Simultaneous Speech Denoising and Super-Resolution Using mGLFB-Based U-Net, Fine-Tuned via Perceptual Loss †
Abstract
1. Introduction
2. DNN for Speech Enhancement
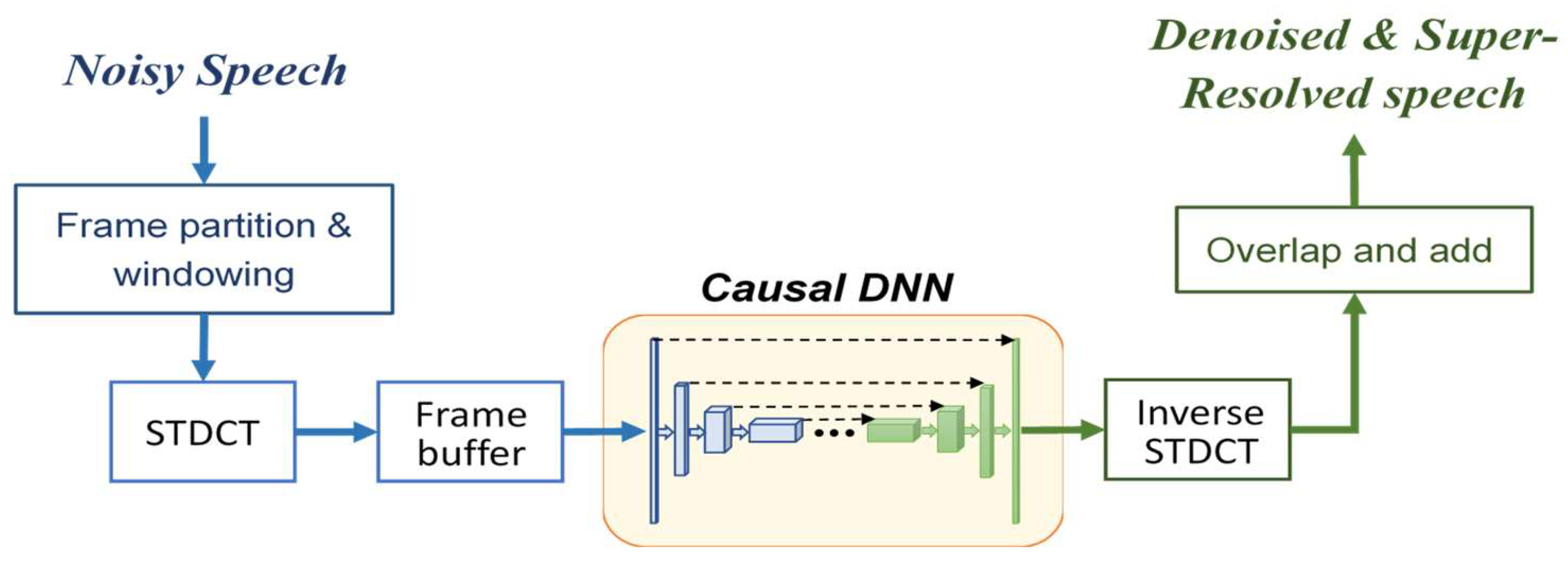
2.1. Processing Framework
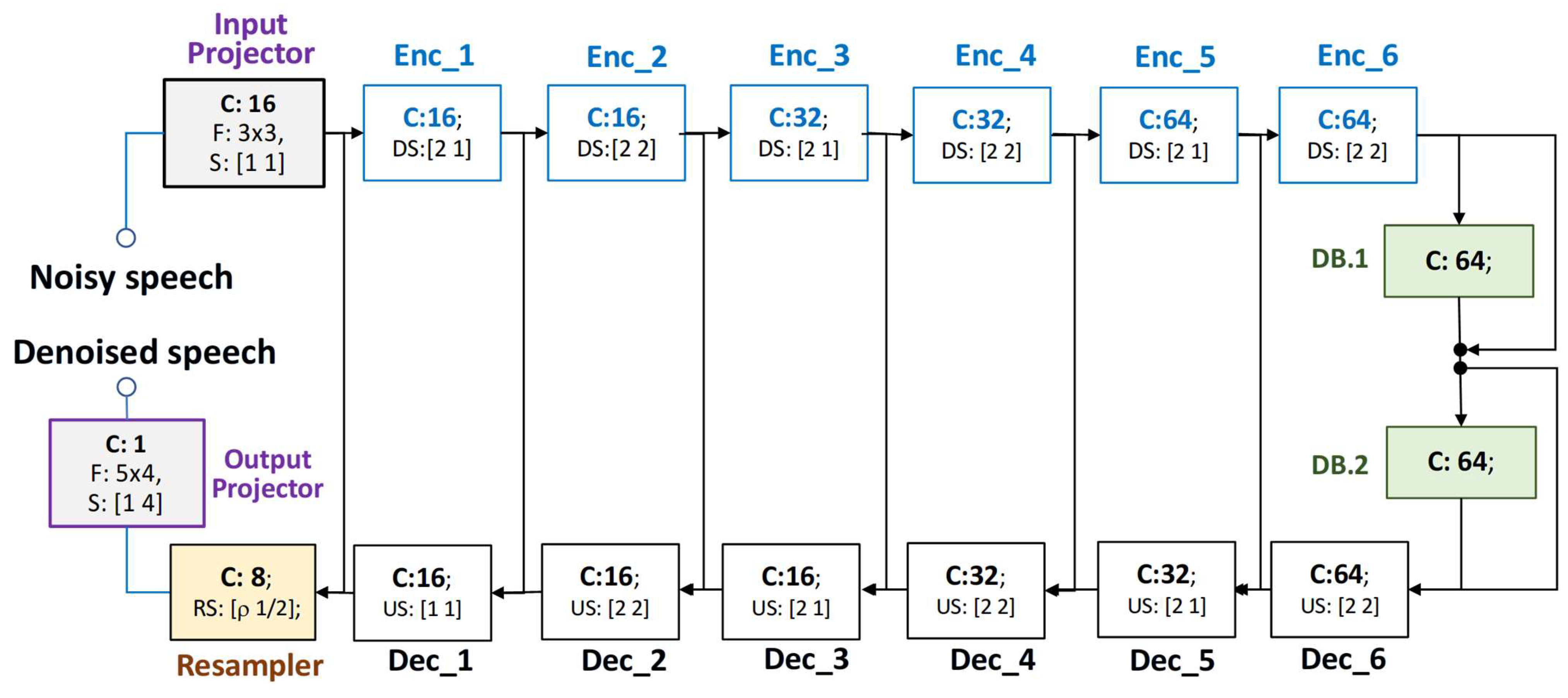
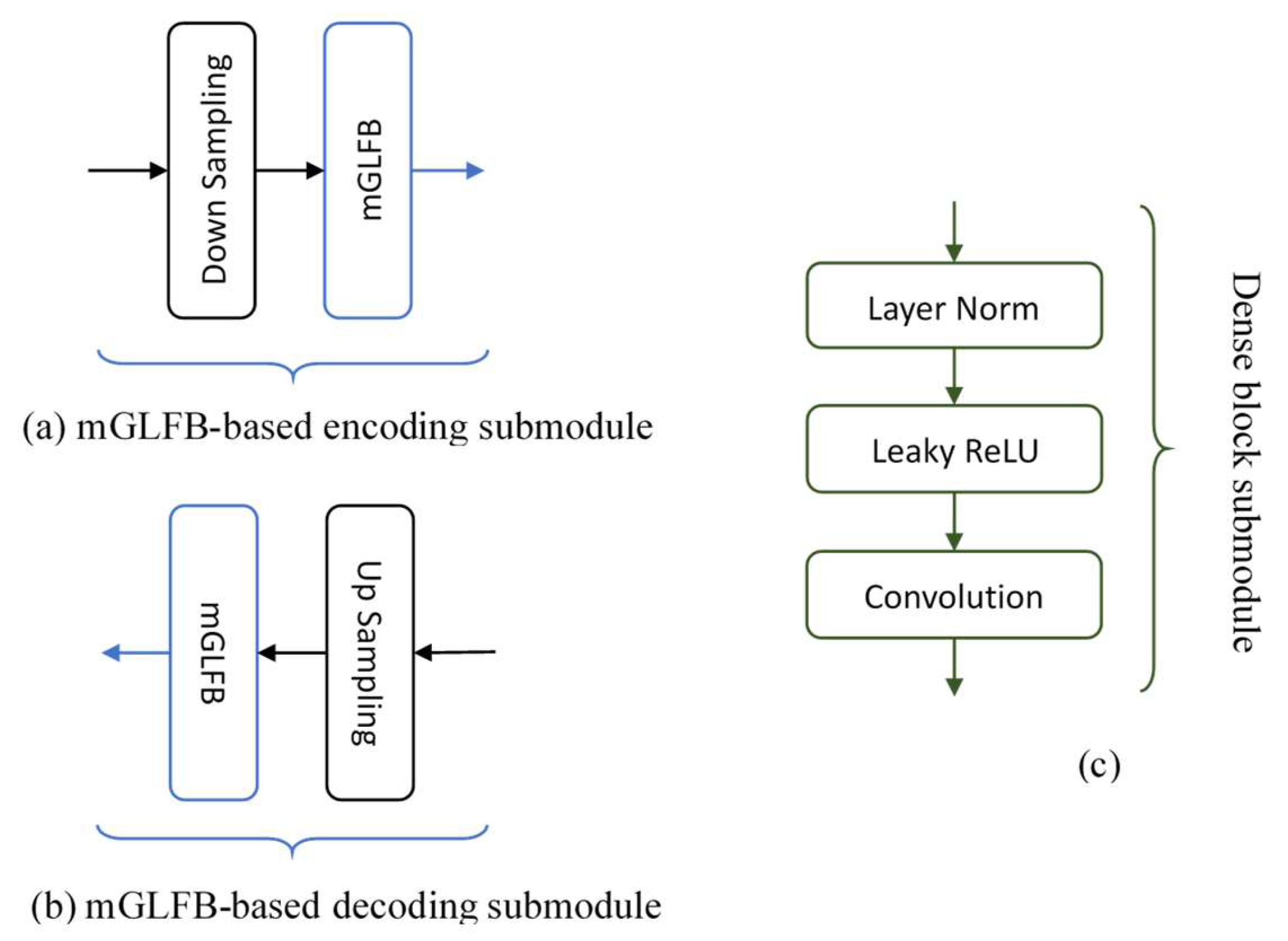
2.2. U-Net Architecture
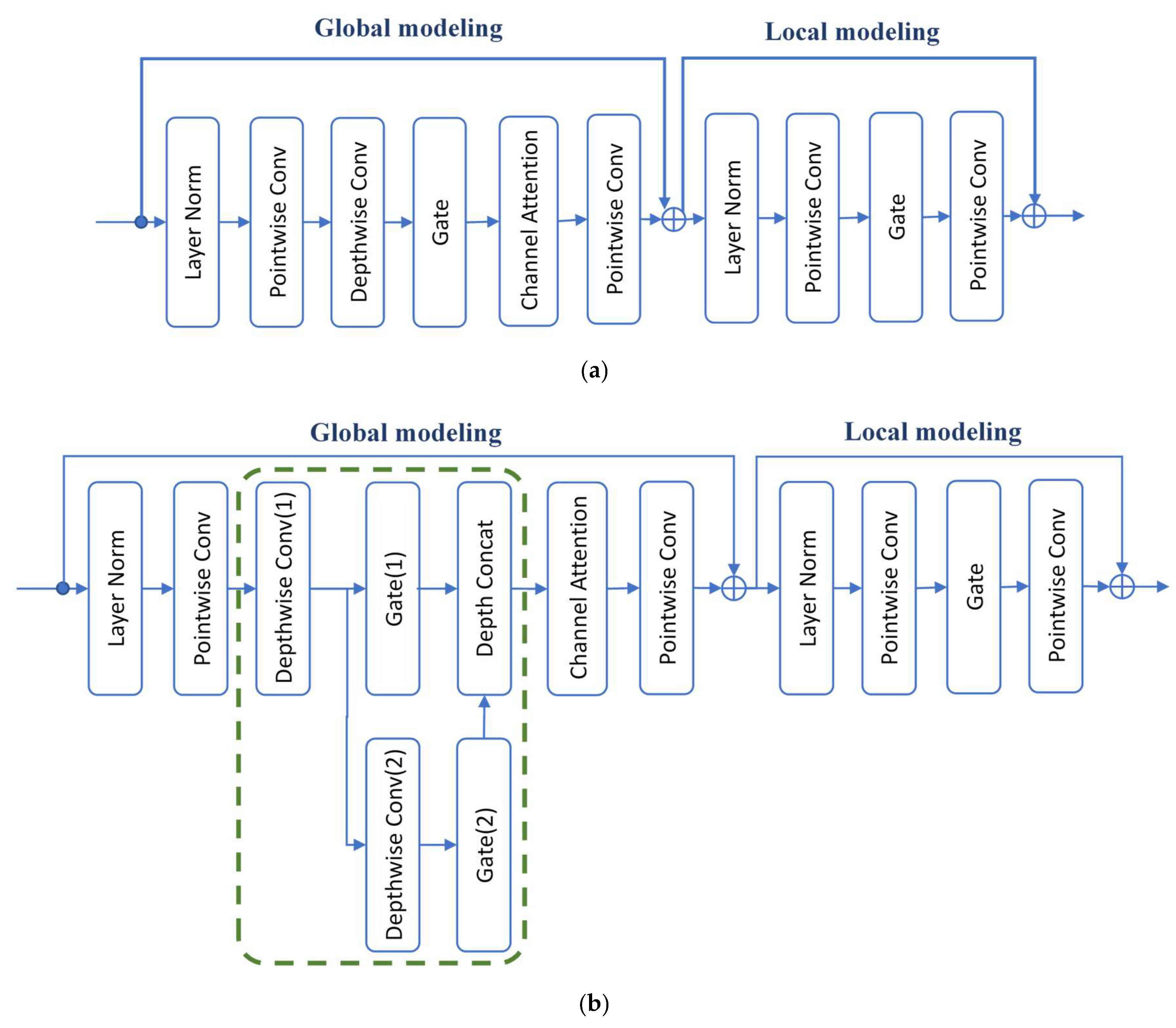
2.3. Inner Composition of mGLFB
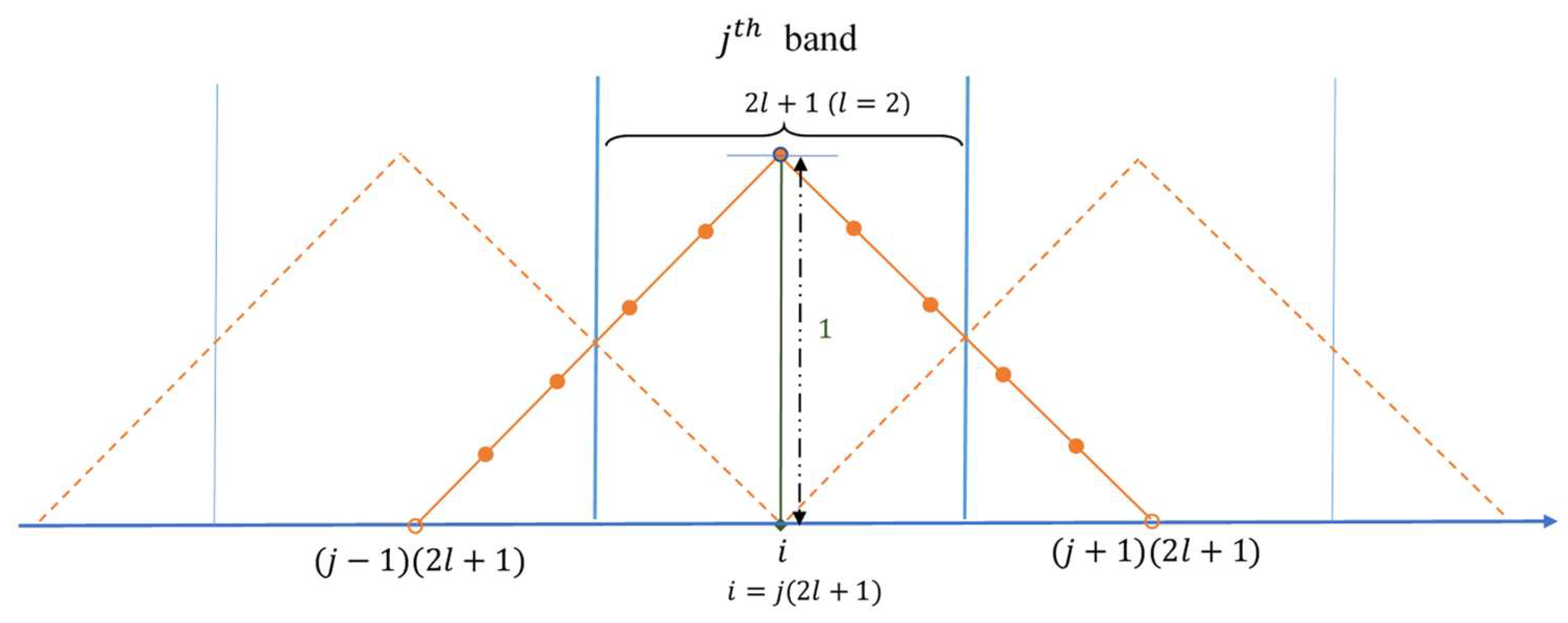
2.4. Super-Resolution Reconstruction
2.5. Perceptual Loss Function
3. Experiment and Assessment Metrics
4. Performance Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kinoshita, K.; Delcroix, M.; Gannot, S.; Habets, E.A.P.; Haeb-Umbach, R.; Kellermann, W.; Leutnant, V.; Maas, R.; Nakatani, T.; Raj, B.; et al. A summary of the REVERB challenge: State-of-the-art and remaining challenges in reverberant speech processing research. EURASIP J. Adv. Signal Process. 2016, 2016, 7. [Google Scholar] [CrossRef]
- Dubey, H.; Gopal, V.; Cutler, R.; Aazami, A.; Matusevych, S.; Braun, S.; Eskimez, S.E.; Thakker, M.; Yoshioka, T.; Gamper, H.; et al. ICASSP 2022 Deep Noise Suppression Challenge. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; pp. 9271–9275. [Google Scholar]
- Sun, Y.; Wang, W.; Chambers, J.A.; Naqvi, S.M. Enhanced Time-Frequency Masking by Using Neural Networks for Monaural Source Separation in Reverberant Room Environments. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Roma, Italy, 3–7 September 2018; pp. 1647–1651. [Google Scholar]
- Choi, H.-S.; Heo, H.; Lee, J.H.; Lee, K. Phase-aware Single-stage Speech Denoising and Dereverberation with U-Net. arXiv 2020, arXiv:2006.00687. [Google Scholar]
- Tan, K.; Wang, D. Learning Complex Spectral Mapping with Gated Convolutional Recurrent Networks for Monaural Speech Enhancement. IEEE/ACM Trans. Audio Speech Lang. Process. 2020, 28, 380–390. [Google Scholar] [CrossRef] [PubMed]
- Choi, H.-S.; Kim, J.-H.; Huh, J.; Kim, A.; Ha, J.-W.; Lee, K. Phase-aware Speech Enhancement with Deep Complex U-Net. arXiv 2019, arXiv:1903.03107. [Google Scholar] [CrossRef]
- Li, A.; Liu, W.; Zheng, C.; Fan, C.; Li, X. Two Heads are Better Than One: A Two-Stage Complex Spectral Mapping Approach for Monaural Speech Enhancement. IEEE/ACM Trans. Audio Speech Lang. Process. 2021, 29, 1829–1843. [Google Scholar] [CrossRef]
- Yuan, W. A time–frequency smoothing neural network for speech enhancement. Speech Commun. 2020, 124, 75–84. [Google Scholar] [CrossRef]
- Zhao, H.; Zarar, S.; Tashev, I.; Lee, C.H. Convolutional-Recurrent Neural Networks for Speech Enhancement. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 2401–2405. [Google Scholar]
- Tan, K.; Wang, D. A Convolutional Recurrent Neural Network for Real-Time Speech Enhancement. In Proceedings of the Interspeech, Hyderabad, India, 2–6 September 2018; pp. 3229–3233. [Google Scholar]
- Liu, L.; Guan, H.; Ma, J.; Dai, W.; Wang, G.-Y.; Ding, S. A Mask Free Neural Network for Monaural Speech Enhancement. arXiv 2023, arXiv:2306.04286. [Google Scholar] [CrossRef]
- Hu, H.-T.; Lee, T.-T. Options for Performing DNN-Based Causal Speech Denoising Using the U-Net Architecture. Appl. Syst. Innov. 2024, 7, 120. [Google Scholar] [CrossRef]
- Abdulatif, S.; Cao, R.; Yang, B. CMGAN: Conformer-Based Metric-GAN for Monaural Speech Enhancement. IEEE/ACM Trans. Audio Speech Lang. Process. 2024, 32, 2477–2493. [Google Scholar] [CrossRef]
- Kuleshov, V.; Enam, S.Z.; Ermon, S. Audio Super Resolution using Neural Networks. arXiv 2017, arXiv:1708.00853. [Google Scholar] [CrossRef]
- Birnbaum, S.; Kuleshov, V.; Enam, S.Z.; Koh, P.W.; Ermon, S. Temporal FiLM: Capturing long-range sequence dependencies with feature-wise modulation. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; p. 923. [Google Scholar]
- Lim, T.Y.; Yeh, R.A.; Xu, Y.; Do, M.N.; Hasegawa-Johnson, M. Time-Frequency Networks for Audio Super-Resolution. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 646–650. [Google Scholar]
- Wang, H.; Wang, D. Towards Robust Speech Super-Resolution. IEEE/ACM Trans. Audio Speech Lang. Process. 2021, 29, 2058–2066. [Google Scholar] [CrossRef]
- Li, S.; Villette, S.; Ramadas, P.; Sinder, D.J. Speech Bandwidth Extension Using Generative Adversarial Networks. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 5029–5033. [Google Scholar]
- Eskimez, S.E.; Koishida, K.; Duan, Z. Adversarial Training for Speech Super-Resolution. IEEE J. Sel. Top. Signal Process. 2019, 13, 347–358. [Google Scholar] [CrossRef]
- Lee, J.; Han, S. NU-Wave: A Diffusion Probabilistic Model for Neural Audio Upsampling. arXiv 2021, arXiv:2104.02321. [Google Scholar] [CrossRef]
- Yu, C.Y.; Yeh, S.L.; Fazekas, G.; Tang, H. Conditioning and Sampling in Variational Diffusion Models for Speech Super-Resolution. In Proceedings of the ICASSP 2023—2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar]
- Wang, H.; Healy, E.W.; Wang, D. Combined generative and predictive modeling for speech super-resolution. Comput. Speech Lang. 2025, 94, 101808. [Google Scholar] [CrossRef]
- Dubey, H.; Aazami, A.; Gopal, V.; Naderi, B.; Braun, S.; Cutler, R.; Ju, A.; Zohourian, M.; Tang, M.; Golestaneh, M.; et al. ICASSP 2023 Deep Noise Suppression Challenge. IEEE Open J. Signal Process. 2024, 5, 725–737. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar] [CrossRef]
- Rakotonirina, N.C. Self-Attention for Audio Super-Resolution. In Proceedings of the 2021 IEEE 31st International Workshop on Machine Learning for Signal Processing (MLSP), Gold Coast, Australia, 25–28 October 2021; pp. 1–6. [Google Scholar]
- Vaswani, A.; Shazeer, N.M.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. In Proceedings of the Neural Information Processing Systems, Red Hook, NY, USA, 4–9 December 2017. [Google Scholar]
- Hu, H.-T.; Tsai, H.-H. mGLFB-based U-Net for simultaneous speech denoising and super-resolution. In Proceedings of the 11th International Conference on Advances in Artificial Intelligence, Information Communication Technology, and Digital Convergence (ICAIDC-2025), Jeju City, Jeju Island, Republic of Korea, 10–12 July 2025. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Gelfand, S.A. Hearing: An Introduction to Psychological and Physiological Acoustics, 4th ed.; Marcel Dekker: New York, NY, USA, 2004; 512p. [Google Scholar]
- Munkong, R.; Juang, B.H. Auditory perception and cognition. IEEE Signal Process. Mag. 2008, 25, 98–117. [Google Scholar] [CrossRef]
- Glasberg, B.R.; Moore, B.C.J. Derivation of auditory filter shapes from notched-noise data. Hear. Res. 1990, 47, 103–138. [Google Scholar] [CrossRef]
- Yamagishi, J.; Veaux, C.; MacDonald, K. CSTR VCTK Corpus: English Multi-speaker Corpus for CSTR Voice Cloning Toolkit (Version 0.92); The Centre for Speech Technology Research (CSTR): Edinburgh, UK, 2019. [Google Scholar] [CrossRef]
- Thiemann, J.; Ito, N.; Vincent, E. The Diverse Environments Multi-channel Acoustic Noise Database (DEMAND): A database of multichannel environmental noise recordings. J. Acoust. Soc. Am. 2013, 133, 3591. [Google Scholar] [CrossRef]
- Hu, Y.; Loizou, P.C. Evaluation of Objective Quality Measures for Speech Enhancement. IEEE Trans. Audio Speech Lang. Process. 2008, 16, 229–238. [Google Scholar] [CrossRef]
- ITU-T, R.P. Methods for Subjective Determination of Transmission Quality; International Telecommunications Union: Geneva, Switzerland, 1996. [Google Scholar]
- Hines, A.; Skoglund, J.; Kokaram, A.; Harte, N. ViSQOL: The Virtual Speech Quality Objective Listener. In Proceedings of the International Workshop on Acoustic Signal Enhancement (IWAENC 2012), Aachen, Germany, 4–6 September 2012; pp. 1–4. [Google Scholar]
- Taal, C.H.; Hendriks, R.C.; Heusdens, R.; Jensen, J. An Algorithm for Intelligibility Prediction of Time–Frequency Weighted Noisy Speech. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 2125–2136. [Google Scholar] [CrossRef]
- Rabiner, L.R.; Juang, B.H. Fundamentals of Speech Recognition; PTR Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
| Layer Index | 6-Level U-Net | ||
|---|---|---|---|
| Encoder Side | Decoder Side | ||
| Input/Output Projection | F: 3 3, C: 16; S: [1 1] | F: 5 × 4, C: 1; S: [1 4] | |
| – | Resampler: C: 8; RS: [ρ 1/2]; F1[D1]: 3[1]3[1]; F2[D2]: 3[2]3[2]; | ||
| 1 | F1[D1]: 5[1]3[1]; F2[D2]: 3[3]3[2]; C:16; DS:[2 1] | → | C:16; US: [1 1]; F1[D1]: 3[1]3[1]; F2[D2]: 3[2]3[2]; |
| 2 | F1[D1]: 5[1]3[1]; F2[D2]: 3[3]3[2]; C:16; DS:[2 2] | → | C:16; US: [2 2]; F1[D1]: 5[1]3[1]; F2[D2]: 3[3]3[2]; |
| 3 | F1[D1]: 3[1]3[1]; F2[D2]: 3[2]3[1]; C:32; DS: [2 1] | → | C:16; US: [2 1]; F1[D1]: 5[1]3[1]; F2[D2]: 3[3]3[2]; |
| 4 | F1[D1]: 3[1]3[1]; F2[D2]: 3[2]3[1]; C:32; DS: [2 2] | → | C:32; US: [2 2]; F1[D1]: 3[1]3[1]; F2[D2]: 3[2]3[1]; |
| 5 | F1[D1]: 3[1]3[1]; F2[D2]: 3[2]1[1]; C:64; DS: [2 1] | → | C:32; US: [2 1]; F1[D1]: 3[1]3[1]; F2[D2]: 3[2]3[1]; |
| 6 | F1[D1]: 3[1]3[1]; F2[D2]: 3[2]1[1]; C:64; DS: [2 2] | → | C:64; US: [2 2]; F1[D1]: 3[1]3[1]; F2[D2]: 3[2]1[1]; |
| Latent space (dense block) | C: 64; F[D]: 3[1]1[1]; S: [1 1] | ⇉ | C: 64; F[D]: 3[2]1[2]; S: [1 1] |
| Building Module | Initial SNR | Final SNR (dB) | LSD | CSIG | CBAK | COVL | PESQ | ViSQOL | STOI (%) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Original GLFB | (0, 1) | −2.5 dB | 13.64 | 2.765 | 3.249 | 3.069 | 3.066 | 2.980 | 3.705 | 86.30 |
| 2.5 dB | 16.13 | 2.428 | 3.775 | 3.342 | 3.478 | 3.238 | 4.031 | 90.62 | ||
| 7.5 dB | 18.07 | 2.169 | 4.198 | 3.554 | 3.803 | 3.440 | 4.264 | 90.08 | ||
| 12.5 dB | 20.04 | 1.929 | 4.515 | 3.768 | 4.063 | 3.621 | 4.444 | 89.72 | ||
| Average | 16.97 | 2.323 | 3.934 | 3.433 | 3.603 | 3.320 | 4.111 | 89.18 | ||
| (0.5, 0.5) | −2.5 dB | 13.73 | 2.513 | 3.857 | 3.169 | 3.421 | 3.044 | 3.874 | 88.80 | |
| 2.5 dB | 16.37 | 2.238 | 4.275 | 3.439 | 3.792 | 3.338 | 4.161 | 92.72 | ||
| 7.5 dB | 18.39 | 2.004 | 4.598 | 3.666 | 4.083 | 3.578 | 4.373 | 93.96 | ||
| 12.5 dB | 20.20 | 1.806 | 4.840 | 3.877 | 4.308 | 3.769 | 4.525 | 94.74 | ||
| Average | 17.17 | 2.140 | 4.393 | 3.538 | 3.901 | 3.432 | 4.233 | 92.56 | ||
| Modified GLFB | (0, 1) | −2.5 dB | 13.40 | 2.769 | 3.328 | 3.043 | 3.094 | 2.962 | 3.711 | 85.14 |
| 2.5 dB | 16.03 | 2.424 | 3.832 | 3.316 | 3.493 | 3.218 | 4.029 | 89.56 | ||
| 7.5 dB | 18.04 | 2.137 | 4.246 | 3.544 | 3.822 | 3.433 | 4.280 | 90.28 | ||
| 12.5 dB | 19.97 | 1.895 | 4.555 | 3.763 | 4.081 | 3.619 | 4.468 | 90.51 | ||
| Average | 16.86 | 2.306 | 3.990 | 3.416 | 3.622 | 3.308 | 4.122 | 88.87 | ||
| (0.5, 0.5) | −2.5 dB | 13.65 | 2.530 | 3.872 | 3.168 | 3.428 | 3.039 | 3.855 | 88.55 | |
| 2.5 dB | 16.20 | 2.248 | 4.286 | 3.443 | 3.798 | 3.336 | 4.144 | 92.93 | ||
| 7.5 dB | 18.27 | 2.019 | 4.603 | 3.669 | 4.084 | 3.571 | 4.358 | 93.99 | ||
| 12.5 dB | 20.15 | 1.818 | 4.856 | 3.885 | 4.320 | 3.772 | 4.518 | 94.23 | ||
| Average | 17.07 | 2.153 | 4.404 | 3.541 | 3.907 | 3.430 | 4.219 | 92.42 |
| Approach | Initial SNR | Final SNR (dB) | LSD | CSIG | CBAK | COVL | PESQ | ViSQOL | STOI (%) |
|---|---|---|---|---|---|---|---|---|---|
| (1) mGLFB-based U-Net (8 kHz) + spline interpolation (16 kHz) | −2.5 dB | 11.40 | 3.741 | −1.861 | 3.072 | 0.534 | 2.961 | 3.403 | 88.12 |
| 2.5 dB | 13.07 | 3.545 | −1.636 | 3.330 | 0.815 | 3.269 | 3.644 | 92.62 | |
| 7.5 dB | 14.24 | 3.359 | −1.442 | 3.550 | 1.056 | 3.534 | 3.831 | 93.82 | |
| 12.5 dB | 14.99 | 3.224 | −1.273 | 3.740 | 1.255 | 3.743 | 3.965 | 94.35 | |
| Average | 13.42 | 3.467 | −1.553 | 3.423 | 0.915 | 3.377 | 3.711 | 92.22 | |
| (2) mGLFB-based U-Net (16 kHz) | −2.5 dB | 11.37 | 2.807 | 3.384 | 3.017 | 3.103 | 2.896 | 3.510 | 87.35 |
| 2.5 dB | 13.23 | 2.583 | 3.795 | 3.275 | 3.470 | 3.188 | 3.802 | 92.24 | |
| 7.5 dB | 14.69 | 2.421 | 4.124 | 3.501 | 3.774 | 3.443 | 4.025 | 94.43 | |
| 12.5 dB | 15.66 | 2.313 | 4.359 | 3.694 | 4.002 | 3.645 | 4.174 | 95.15 | |
| Average | 13.74 | 2.531 | 3.916 | 3.372 | 3.587 | 3.293 | 3.878 | 92.29 |
| Approach | Model | Parameters | Real-Time Factor | |||
|---|---|---|---|---|---|---|
| Intel® i5-14500 | Intel® i9-11900 | NVIDIA® RTX-3080Ti | NVIDIA® RTX-4080S | |||
| Approach (1) | GLFB-based U-Net (8 kHz) + spline interpolation (16 kHz) | 238.5 K | 0.338 | 0.381 | 0.053 | 0.046 |
| mGLFB-based U-Net (8 kHz) + spline interpolation (16 kHz) | 206.2 K | 0.450 | 0.447 | 0.100 | 0.071 | |
| Approach (2) | mGLFB-based U-Net (16 kHz) | 207.3 K | 0.482 | 0.476 | 0.107 | 0.070 |
| Approach (2) mGLFB-Based U-Net (16 kHz) | Initial SNR | Final SNR (dB) | LSD | CSIG | CBAK | COVL | PESQ | ViSQOL | STOI (%) |
|---|---|---|---|---|---|---|---|---|---|
| Spectral Smoothing in high frequencies: OFF | −2.5 dB | 10.99 | 3.086 | 3.221 | 2.952 | 2.985 | 2.835 | 3.316 | 85.72 |
| 2.5 dB | 12.97 | 2.945 | 3.518 | 3.224 | 3.301 | 3.134 | 3.603 | 90.89 | |
| 7.5 dB | 14.39 | 2.838 | 3.737 | 3.453 | 3.553 | 3.393 | 3.812 | 92.82 | |
| 12.5 dB | 15.35 | 2.755 | 3.908 | 3.655 | 3.758 | 3.610 | 3.957 | 93.83 | |
| Average | 13.43 | 2.906 | 3.596 | 3.321 | 3.399 | 3.243 | 3.672 | 90.81 | |
| Spectral Smoothing in high frequencies: OFF | −2.5 dB | 11.11 | 2.864 | 3.330 | 2.973 | 3.051 | 2.851 | 3.423 | 85.99 |
| 2.5 dB | 13.06 | 2.658 | 3.702 | 3.239 | 3.404 | 3.152 | 3.713 | 90.47 | |
| 7.5 dB | 14.49 | 2.513 | 3.987 | 3.463 | 3.685 | 3.405 | 3.925 | 92.03 | |
| 12.5 dB | 15.46 | 2.410 | 4.209 | 3.663 | 3.912 | 3.618 | 4.078 | 92.89 | |
| Average | 13.53 | 2.611 | 3.807 | 3.335 | 3.513 | 3.256 | 3.784 | 90.34 | |
| Spectral Smoothing in high frequencies: ON | −2.5 dB | 11.02 | 2.883 | 3.294 | 2.957 | 3.027 | 2.845 | 3.417 | 85.51 |
| 2.5 dB | 13.00 | 2.663 | 3.693 | 3.229 | 3.393 | 3.144 | 3.722 | 90.64 | |
| 7.5 dB | 14.41 | 2.508 | 3.997 | 3.456 | 3.685 | 3.399 | 3.942 | 92.52 | |
| 12.5 dB | 15.36 | 2.395 | 4.226 | 3.653 | 3.915 | 3.608 | 4.095 | 93.18 | |
| Average | 13.45 | 2.612 | 3.803 | 3.324 | 3.505 | 3.249 | 3.794 | 90.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.-T.; Tsai, H.-H. Simultaneous Speech Denoising and Super-Resolution Using mGLFB-Based U-Net, Fine-Tuned via Perceptual Loss. Electronics 2025, 14, 3466. https://doi.org/10.3390/electronics14173466
Hu H-T, Tsai H-H. Simultaneous Speech Denoising and Super-Resolution Using mGLFB-Based U-Net, Fine-Tuned via Perceptual Loss. Electronics. 2025; 14(17):3466. https://doi.org/10.3390/electronics14173466
Chicago/Turabian StyleHu, Hwai-Tsu, and Hao-Hsuan Tsai. 2025. "Simultaneous Speech Denoising and Super-Resolution Using mGLFB-Based U-Net, Fine-Tuned via Perceptual Loss" Electronics 14, no. 17: 3466. https://doi.org/10.3390/electronics14173466
APA StyleHu, H.-T., & Tsai, H.-H. (2025). Simultaneous Speech Denoising and Super-Resolution Using mGLFB-Based U-Net, Fine-Tuned via Perceptual Loss. Electronics, 14(17), 3466. https://doi.org/10.3390/electronics14173466






