1. Introduction
The rapid evolution toward 6G networks promises unprecedented connectivity speeds and ubiquitous intelligence, enabling transformative applications in edge-assisted Artificial Intelligence of Things (AIoT) systems. For example, a central node distributes the well-trained model to mobile edge devices (e.g., unmanned aerial vehicles) for model inference and decision-making, supporting a wide range of AI applications. However, this paradigm shift introduces critical security challenges, particularly in safeguarding sensitive model transmissions against increasingly sophisticated eavesdropping attacks. Physical layer security (PLS) has emerged as a fundamental complement to cryptographic methods by exploiting the inherent randomness of wireless channels to prevent information leakage. Despite significant progress in semantic communication [
1] and IoT security mechanisms [
2,
3,
4], a crucial gap persists in jointly optimizing model accuracy and transmission security for resource-constrained edge AIoT deployments.
Existing approaches suffer from three key limitations: (1) AI model transmission frameworks prioritize bandwidth efficiency but neglect PLS considerations against eavesdroppers. (2) Traditional PLS methods focus on generic data transmission without accounting for the unique accuracy-vs-size tradeoffs in AI model architectures. (3) Static resource allocation strategies cannot adapt to dynamic channel conditions in multi-user edge environments. These limitations create a fundamental tension between model recognition accuracy and transmission security that remains unresolved.
To address these challenges, we propose a novel dynamic user selection framework for physical layer secure transmission in edge AIoT systems. Our core contributions include the following:
Closed-Form Analysis: We derive closed-form expressions for secrecy outage probability (SOP) under Rayleigh fading channels.
Security-Accuracy Metric: We introduce Secure Model Accuracy (SMA) as a unified optimization metric combining recognition accuracy and SOP.
Cross-Layer Optimization: To maximize the SMA of the system, we propose an alternating optimization algorithm that jointly selects AI models and allocates bandwidth under secrecy constraints.
Comprehensive simulations validate that our framework achieves up to 22% higher SMA compared to fixed-model and single-objective baselines across diverse channel conditions, transmit power levels, and eavesdropper capabilities. By fundamentally resolving the accuracy–security tradeoff, this work establishes a foundation for trustworthy edge intelligence in next-generation networks.
2. Related Work
Current research on secure transmission in IoT focuses on several key areas:
2.1. Physical Layer Security in AIoT Communications
Recent research has focused on integrating PLS into AIoT systems to protect model parameters and intermediate feature data transmitted over wireless channels. For example, the S2E-DECI framework [
2] proposes a device-edge co-inference scheme that partitions a deep neural network between resource-constrained AIoT devices and edge servers and jointly optimizes model split and resource allocation under finite-blocklength secrecy capacity constraints via reinforcement learning and convex optimization, demonstrating near-optimal secrecy and energy efficiency tradeoffs. Similarly, ambient backscatter cooperative communication networks [
3] employ wireless-powered backscatter devices and decode-and-forward relays, deriving closed-form SOP and secrecy energy efficiency (SEE) expressions to guide power and relay selection for enhanced PLS in ultra-low-power AIoT scenarios.
2.2. Authentication and Unclonable Feature Extraction for AIoT
Lightweight authentication mechanisms tailored to AIoT leverage physical layer unclonable attributes and channel prediction to detect spoofing and ensure integrity with minimal latency. A channel prediction-based security authentication scheme [
4] uses long short-term memory (LSTM) at the edge node to forecast time-varying channel fingerprints and applies a Savitzky–Golay filter–based feature extractor (SGF-HOCM), achieving over 97% spoofing detection accuracy in industrial AIoT deployments. In addition, unclonable physical functions embedded within spiking neural networks built on threshold-switching devices [
5] offer hardware-intrinsic physical unclonable functions (PUFs) for identity verification with high uniqueness and reliability, making them suitable for neuromorphic AIoT platforms. Nevertheless, lightweight authentication techniques mainly improve device identity assurance, without adequately addressing security risks during AI model transmission.
2.3. Advanced PLS Techniques and Resource Allocation
Beyond basic PLS paradigms, advanced schemes exploit novel physical layer technologies and optimization methods to strengthen secure AIoT transmissions. Reconfigurable intelligent surfaces (RISs) have been integrated with beamforming [
6] to maximize the secrecy sum rate in two-way relay and 6G IoT settings, leveraging alternating optimization and semidefinite programming to jointly configure RIS phase shifts and beamforming weights under eavesdropping threats. Non-orthogonal multiple access (NOMA)-enabled overlay cognitive radio networks [
7] employ full-duplex jamming and optimal power allocation to minimize SOP for both primary and secondary users, illustrating the benefits of cooperative jamming in densely connected AIoT environments. Rate-splitting and artificial noise strategies [
8,
9] further enhance PLS in multi-user MISO AIoT systems by formulating joint beamforming and jamming designs that balance secrecy and throughput under passive eavesdropping.
2.4. Semantic Communication and Model Transmission
Recent advances in semantic communication have introduced innovative approaches to model transmission in 6G networks. Wang et al. [
1] proposed an intellicise model transmission framework for semantic communication in intelligence-native 6G networks. Their work introduced key metrics including model transmission outage probability (MTOP) and effective model accuracy (EMA), and they developed a joint model selection and resource allocation (JMSRA) algorithm that outperformed baseline methods by 22%. Their work established important foundations for understanding the relationship between model size and recognition performance but did not consider security aspects against eavesdroppers. Meanwhile, it lacks comprehensive security frameworks that protect the semantic model’s information under realistic adversarial settings.
Building on this, the concept of model-driven semantic communication has emerged as a new paradigm that facilitates preprocessing of multi-modal data with AI models before transmission [
1]. This approach significantly reduces transmission volume while maintaining semantic fidelity, which is particularly valuable for edge intelligence scenarios where bandwidth and latency are critical constraints.
While recent studies have advanced physical layer security, lightweight authentication, and resource allocation techniques for AIoT, critical gaps remain in jointly optimizing model accuracy and transmission security in edge-assisted systems. Our work addresses this gap by developing a unified framework that simultaneously enhances semantic model performance while ensuring physical layer security through dynamic resource allocation, resolving the fundamental tension between these traditionally separate objectives.
3. System Model
We consider an “edge server-UAV” multi-user physical layer secure communication system with a passive eavesdropping node (
Figure 1). The system consists of
An edge server storing pre-trained models with size .
K resource-constrained edge devices, such as UAVs.
A passive eavesdropper, Eve. (While our analysis assumes a single passive eavesdropper, the framework can be extended to (i) multiple eavesdroppers via max-SNR combining, (ii) active attacks (e.g., jamming) through SINR interference terms, and (iii) mobility via time-varying channel statistics in SOP expressions.)
The edge server distributes the pre-trained models to mobile edge devices (UAVs) for model inference and decision-making, supporting a wide range of AI applications. However, there may be an eavesdropper (Eve) who wants to obtain private model information.
3.1. Model Recognition Accuracy
The pre-trained models stored on the edge server exhibit varying recognition accuracies due to differences in model sizes. Inspired by [
10], the recognition error rate
is a nonlinear function of the model size
, satisfying the following properties:
- (i)
Since is a percentage, it satisfies ;
- (ii)
As larger model sizes contain more parameters, enabling higher performance, is a monotonically decreasing function of ;
- (iii)
The magnitude of the partial derivative decreases as increases. When becomes sufficiently large, the derivative approaches zero, indicating diminishing returns in semantic recognition performance with further increases in model size.
Based on Properties (i)–(iii), the recognition error rate can be modeled as the following function:
where
are tuning parameters determined by the specific intelligent model, characterizing the error rate decay with respect to model size. It can be verified that
satisfies all the above properties.
Following the experimental results reported in [
1], a four-layer convolutional neural network (CNN) was trained on the CIFAR-10 dataset [
11] for semantic communication tasks. By varying the number of channels in the convolutional layers, models with different sizes were obtained, and their recognition error rates were measured. The experimental data were then fitted to the nonlinear function in (1), showing that with parameters
and
, the fitted curve closely matches the empirical results, with the reconstruction error evaluated by the root mean square error (RMSE). Therefore, in this paper, the values of
a and
b used in simulations are directly adopted from the fitting results in [
1], as illustrated in Figure 2 of that work.
Moreover, when , which means that an infinite model size would theoretically lead to 100% accuracy. This reflects the assumption that given infinite model capacity, the error rate of the intelligent model approaches zero.
3.2. Physical Layer Transmission Model
Legitimate UAV Link: The downlink channel gain from the edge server to UAV
k is
. The received signal at UAV
k is given by
where
represents the encrypted model parameter symbols,
is additive white Gaussian noise [
12], and
denotes the bandwidth allocated to UAV
k.
Eavesdropping Link: The channel gain from the edge server to the eavesdropper is
. The intercepted signal at Eve is given by
where
. The eavesdropping link shares the same frequency band and bandwidth
with the legitimate link.
4. Secrecy Capacity and SOP Analysis
In this section, we derive the secrecy outage probability (SOP) for the secrecy analysis of the system.
4.1. Secrecy Capacity
In our considered system, the model transmission rate is given by , where represents the model size. Assuming both the main channel (edge server → User k) and eavesdropping channel (edge server → Eve) experience Rayleigh fading, the squared channel gains and follow exponential distributions with parameters and , respectively.
4.2. SOP Closed-Form Expression
The SOP is defined as the probability that the secrecy capacity falls below the target rate
, where
We derive the closed-form expression for the SOP as follows.
Proposition 1. The SOP for user k in the considered UAV-assisted AIoT system, under Rayleigh fading channels with exponential channel gains and , is given bywhere and are the parameters of the exponential distributions for the legitimate and eavesdropping channels, respectively; is the noise power spectral density; is the bandwidth allocated to user k; P is the transmit power; and is the target secrecy rate. Proof. To derive the SOP, we start with the definition below.
where the secrecy capacity is
, with
and
being the signal-to-noise ratios (SNRs) at the legitimate user
k and eavesdropper, respectively.
Expanding the condition
yields
which can be rewritten as
and further simplifies to
Thus, the SOP is expressed as
where
is the probability density function (PDF) of
since
.
Since
with parameter
, its cumulative distribution function (CDF) is given by
Substituting into the SOP expression, we obtain
We simplify the exponent as
By computing the two integrals separately, we have
For
and using the integral identity
, we have
Combining the items, we obtain
Substitute
, we derive the SOP as
This completes the derivation of the closed-form SOP expression. □
5. Transmission Security Performance Optimization
5.1. Secure Model Accuracy (SMA) Metric
To jointly optimize transmission security and model accuracy, we propose the Secure Model Accuracy (SMA) metric, defined as the product of successful secure transmission probability and model recognition accuracy, which is given by
where
.
The proposed SMA metric in (22) jointly captures the effects of model size
, bandwidth allocation
, and physical layer security on the overall system performance. In our system model, the model transmission rate is defined as
, where
is the target transmission delay. This rate requirement directly corresponds to the target secrecy rate
in the SOP analysis of
Section 4 (i.e.,
). Intuitively, a larger
improves recognition accuracy by reducing
because more parameters enable better semantic representation; however, it also increases
, which raises the term
in the SOP expression and thereby increases the outage probability under fixed
and channel conditions. Similarly, increasing
reduces the transmission time and lowers SOP by improving the legitimate channel’s effective secrecy capacity, but the total available bandwidth is limited and must be shared among all users. From a security perspective, the secrecy capacity depends on the SNR gap between the legitimate user and the eavesdropper. A larger
without sufficient
may cause the transmission time to exceed the target delay threshold, resulting in higher SOP, while allocating more
to a smaller model can improve security but may underutilize the accuracy potential of larger models. Therefore, SMA reflects the fundamental tradeoff:
enhances semantic accuracy but risks security when bandwidth is constrained, while
mitigates security risks but competes with other users for resources. By analyzing SMA under varying
and
, we can observe the dynamic interplay between model accuracy and physical layer security in multi-user edge intelligence systems.
Thus the optimization problem can be formulated as
We can see from the above problem that SMA is influenced by only two parameters: (i) the error rate based on model selection and (ii) bandwidth allocation and channel state .
Thus, we can decompose the problem into two tractable subproblems as follows: (1) Optimal Model Selection Optimization: For fixed bandwidth allocation and channel state , select the model with the smallest to maximize SMA. (2) Bandwidth Allocation Optimization: For fixed model selection , optimize to maximize SMA.
5.2. Optimal Model Selection with Fixed Bandwidth
For the fixed bandwidth allocation
and channel state
, the Algorithm 1 proceeds as follows.
| Algorithm 1 Optimal model selection for multiple UAVs. |
- 1.
For each UAV k, enumerate all available models to obtain . - 2.
Calculate SMA for each model: - 3.
Select the model maximizing .
|
5.3. Bandwidth Allocation with Fixed Model Selection
With the fixed model selection
, the optimization is transformed as follows:
Due to the non-convex nature of this problem, we employ successive convex approximation (SCA). By introducing slack variables and decomposing the problem into fractional and exponential components, the optimization process can be solved using convex optimization methods. Specifically, we introduce
,
, and
, making the problem transform into
where
5.3.1. Fractional Component Approximation
At iteration point
, we linearize
using first-order Taylor expansion as
The partial derivative is computed through the following steps:
where Term 1 is given by
and Term 2 is given by
Combining both terms yields the final derivative
5.3.2. Exponential Component Approximation
Similarly, we approximate
as
with the derivative
5.4. Convex Optimization Solution
Through the convex approximation of and , all constraints in the SMA objective function are transformed into convex constraints. Consequently, the bandwidth allocation optimization problem can be efficiently solved using convex optimization methods, as shown in Algorithm 2.
The complete solution is achieved through alternating optimization between the two subproblems as follow (Algorithm 3).
| Algorithm 2 Bandwidth allocation optimization (subproblem 2). |
- 1.
Initialize bandwidth allocation for all users k - 2.
For each iteration i until convergence,
|
| Algorithm 3 Joint optimization algorithm. |
- 1.
Initialize model selection and bandwidth allocation - 2.
Repeat until convergence:
Fix bandwidth, optimize model selection (Algorithm 1); Fix models, optimize bandwidth (Algorithm 2);
- 3.
Return optimal model–bandwidth pairs.
|
5.5. Computational Complexity Analysis
The computational efficiency of the proposed optimization framework can be determined through careful analysis of its constituent components [
13,
14]. We first examine the model selection subproblem (Algorithm 1), whose computational burden scales linearly with both the number of users
K and available models
N, yielding a complexity of
. This favorable scaling stems from the need to evaluate each model option for every user in the system.
The bandwidth allocation subproblem (Algorithm 2) presents greater computational challenges due to its iterative convex optimization nature [
15,
16]. The overall complexity can be expressed as
, involving 15 outer iterations and an average of 100 line search steps. The cubic term
dominates this expression, reflecting the computational cost of solving the convex approximation problem using interior-point methods.
When considering the complete joint optimization procedure (Algorithm 3), the complexity combines both subproblems through an alternating optimization framework [
17]. The total computational burden becomes
, where a coefficient of 8 represents the number of alternating iterations between model selection and bandwidth allocation. In practical deployment scenarios, the bandwidth allocation subproblem typically governs the overall computational requirements due to its polynomial scaling with the number of users.
Implementation observations demonstrate that the algorithm exhibits robust convergence characteristics in real-world conditions [
13,
14,
15]. Typical operation requires 5–10 alternating iterations, with each bandwidth allocation subproblem converging within 10–20 convex optimization iterations. The line search component generally completes in 3–5 steps per outer iteration. These characteristics enable real-time operation (under 100 ms latency) on modern edge servers equipped with 8-core processors, supporting systems with up to 20 users and 10 model options. Although the theoretical polynomial complexity is higher than some alternatives, it remains manageable for practical edge computing deployments due to these favorable convergence properties and the parallelizable nature of the computations [
16,
17].
Table 1 summarizes conservative, order-of-magnitude estimates for three representative deployment scenarios.
For reproducibility, we clarify the implementation details of alternating optimization. The bandwidth allocation subproblem (Algorithm 2) is initialized with an equal bandwidth share for all users. The model selection subproblem (Algorithm 1) starts from the largest available model size to exploit potential accuracy gains. The convergence criterion is set as the maximum relative change in SMA across iterations falling below .
6. Simulation Analysis
To validate the proposed framework, as shown in
Table 2, we conduct comprehensive simulations using the following parameters:
IoT devices,
models with error rates =
,
= 20–100 MHz,
W,
W/Hz, and
for legitimate channels. The eavesdropper channel strength
varies from 0.1 to 1.5. We compare Algorithm 3 against three benchmarks: (i) fixed error rate models (
), (ii) sum-rate maximization, and (iii) SOP minimization.
6.1. Results
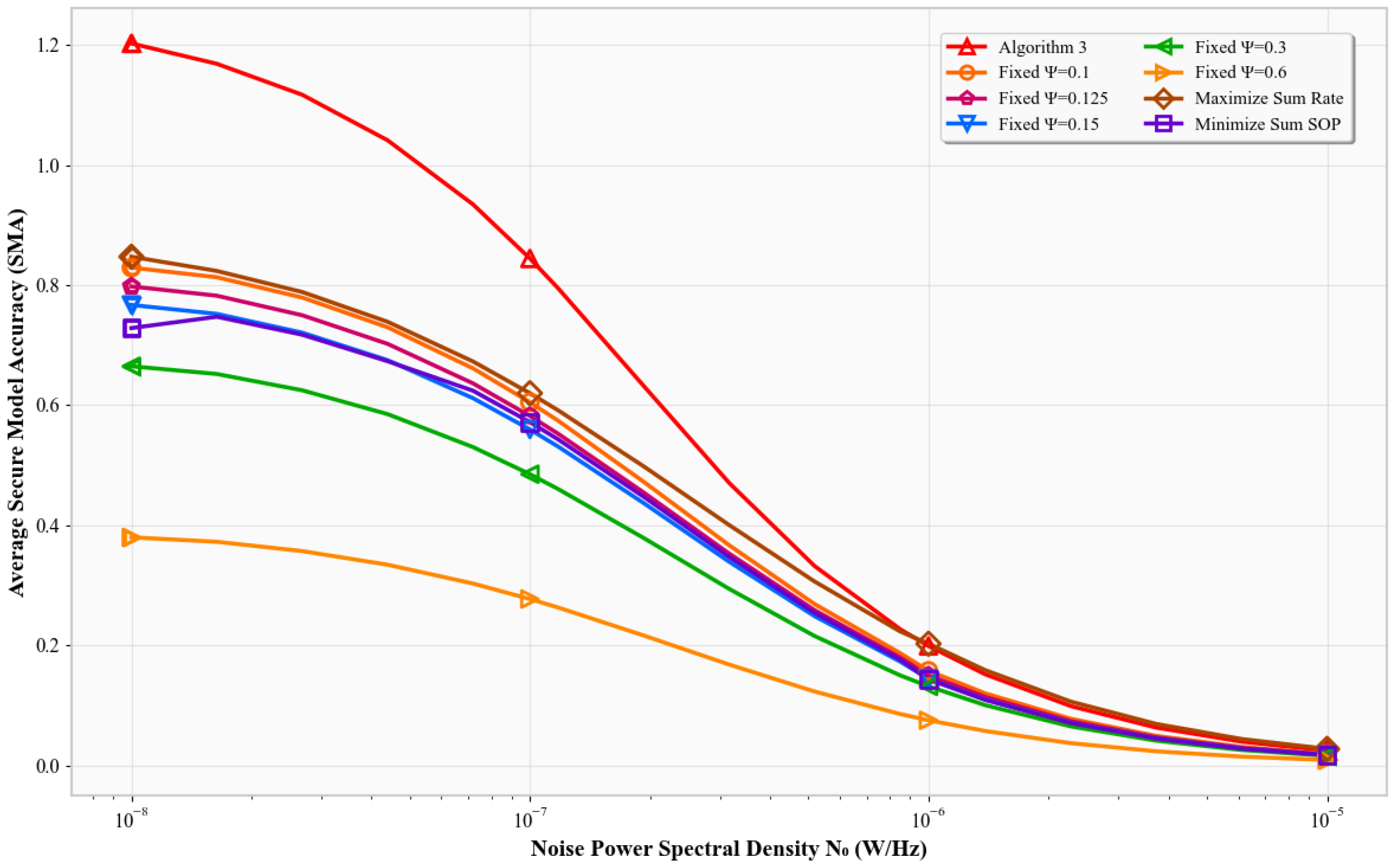
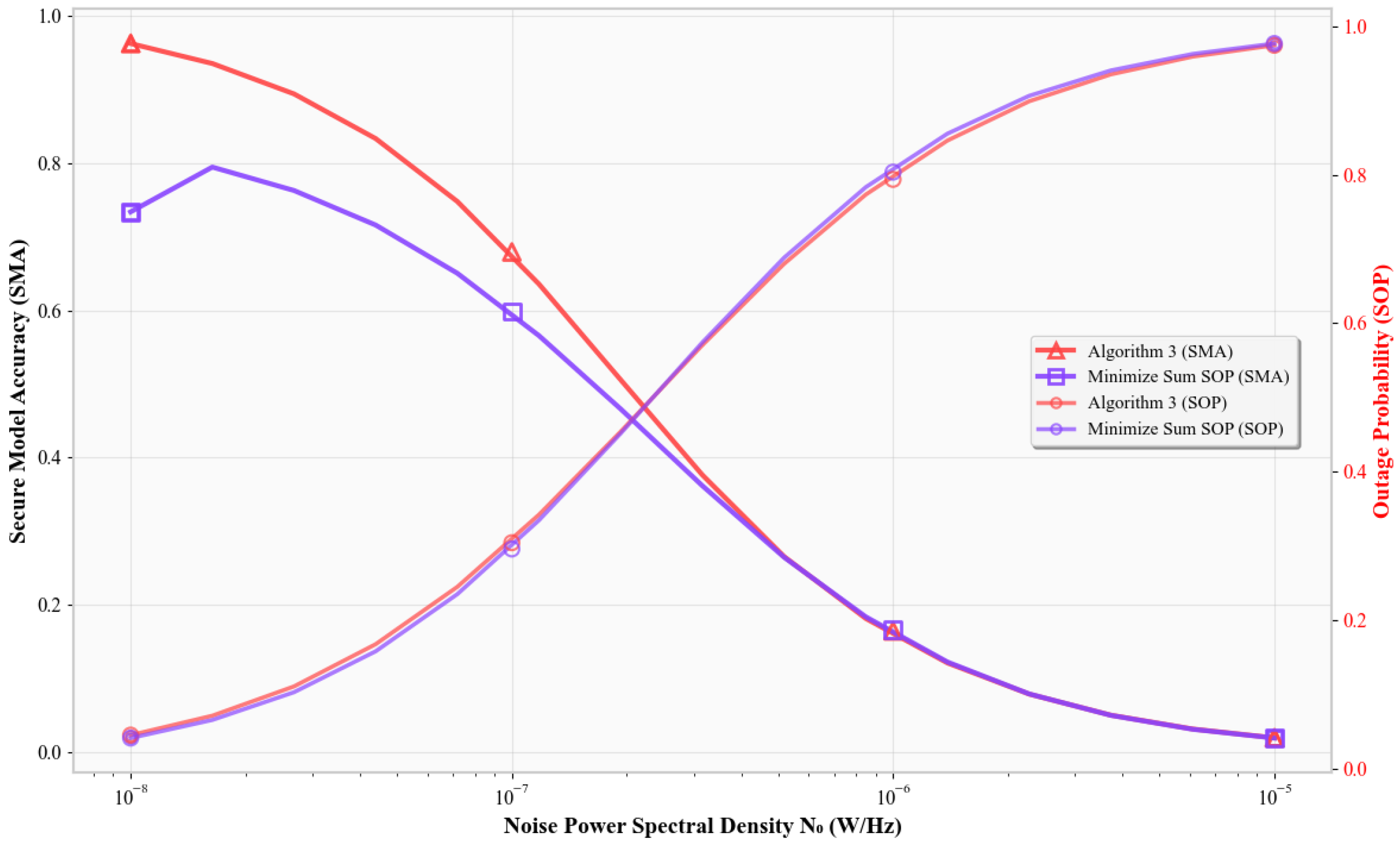
Figure 2 plots SMA versus the noise power spectral density
. As
increases, the signal-to-noise ratio (SNR
) at the legitimate receiver decreases, reducing the channel’s capacity. Consequently, all schemes show a decline in SMA. Algorithm 3 consistently achieves the highest SMA, outperforming the fixed error-rate models, the Max-Sum-Rate scheme, and the Min-SOP scheme. Fixed-
models remain relatively flat since they do not adapt to changing SNRs. The Max-Sum-Rate and Min-SOP schemes degrade more under noise due to their single-objective focus. Algorithm 3 dynamically allocates resources under secrecy constraints to preserve classification accuracy, resulting in significantly better performance.
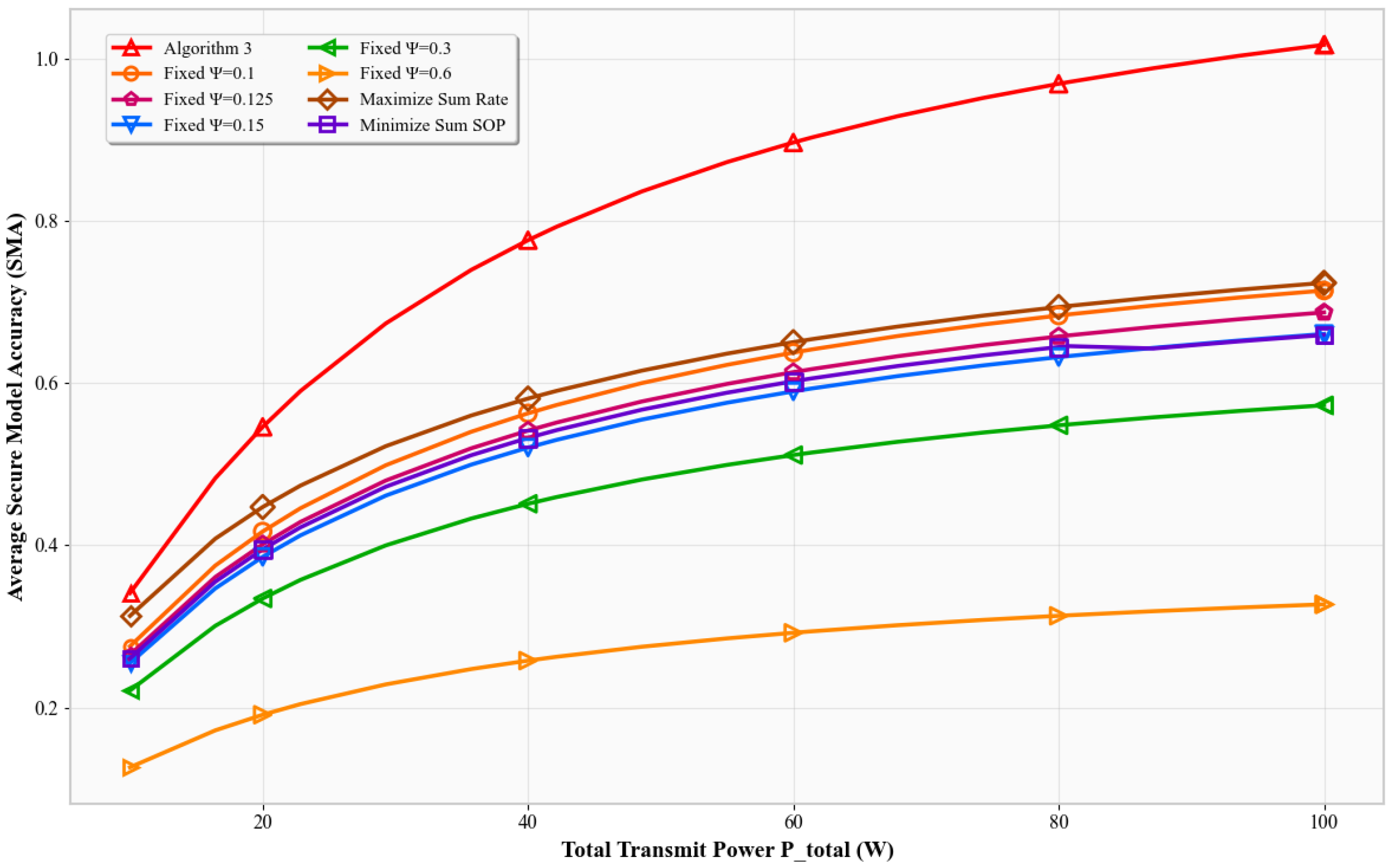
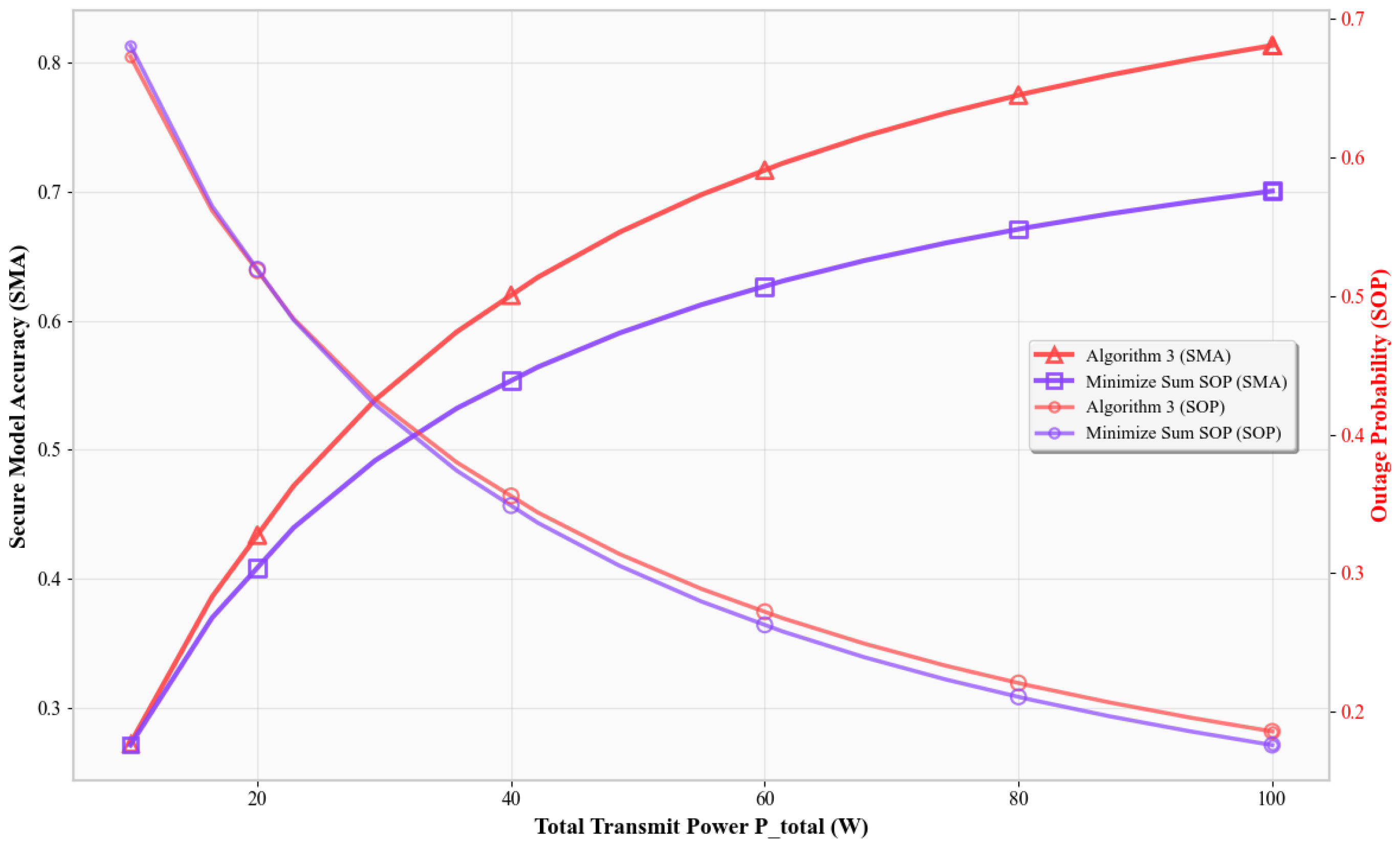
Figure 3 shows SMA versus the total transmit power
. According to Shannon’s capacity, increasing
improves SNR and reliability. All schemes show increased SMA, but Algorithm 3 exhibits the steepest rise. It outperforms other baselines by intelligently using additional power to improve classification while maintaining secrecy. Other schemes fail to exploit higher power as effectively.
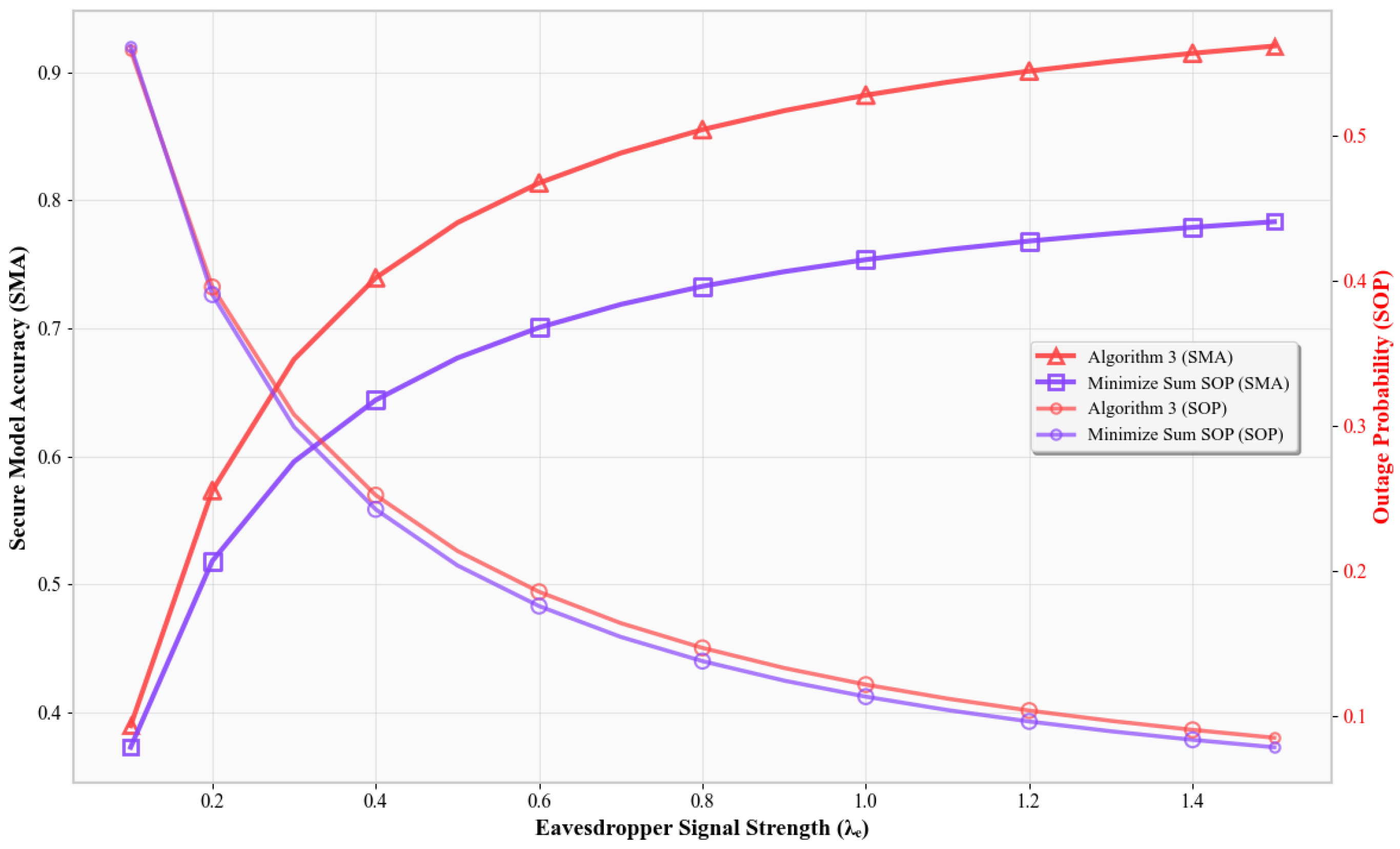
In
Figure 4, SMA is plotted against the eavesdropper’s channel gain
. As derived previously, a higher
value leads to a lower SOP. All schemes experience increased SMA as
increases. Algorithm 3 maintains higher metrics than all others. This is because it adjusts its strategy to maintain reliability under tighter secrecy constraints. Fixed-
models, lacking such adaptation, suffer more accuracy loss. The Max-Sum-Rate and Min-SOP schemes are unable to balance secrecy and throughput as effectively.
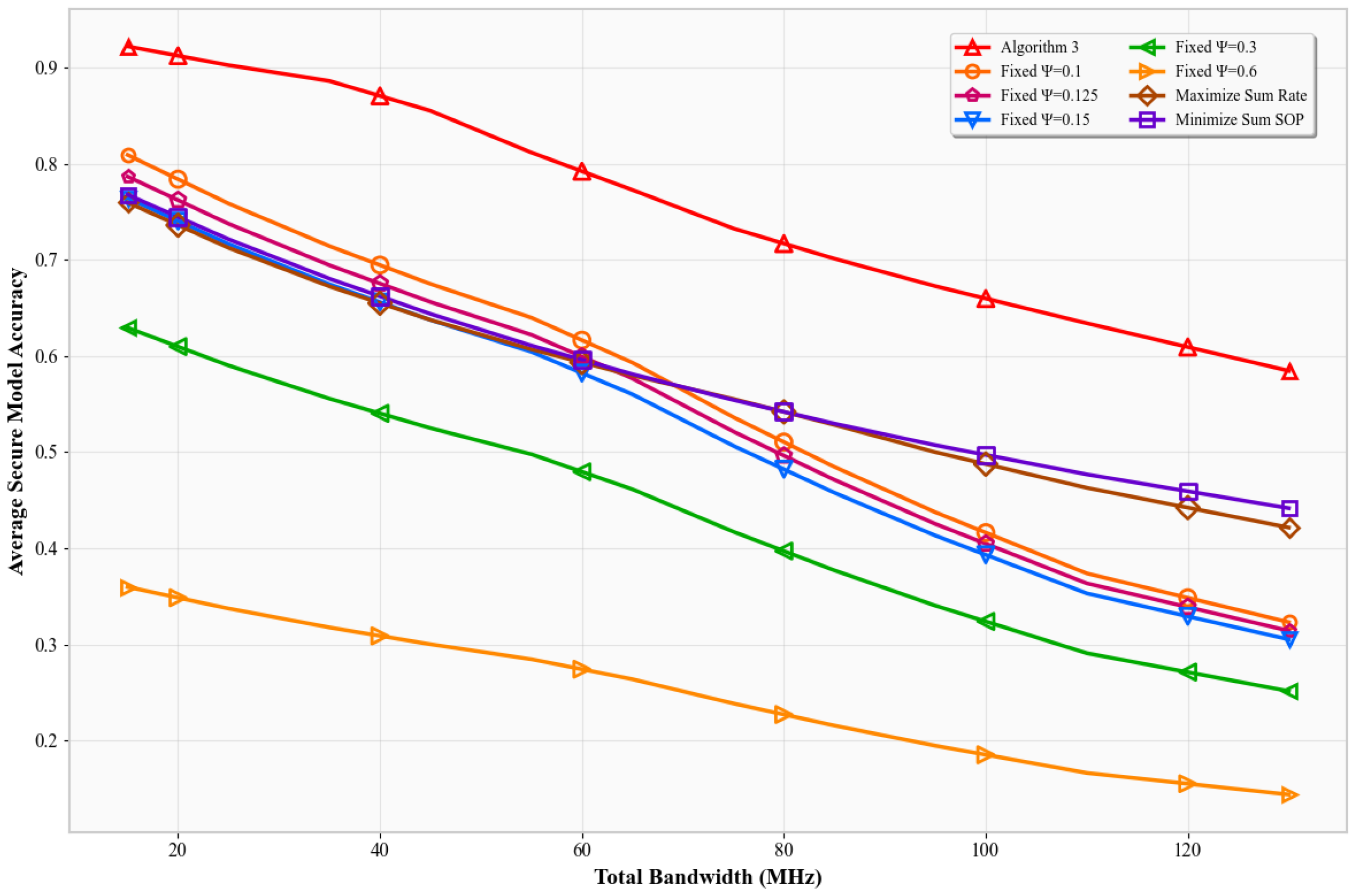
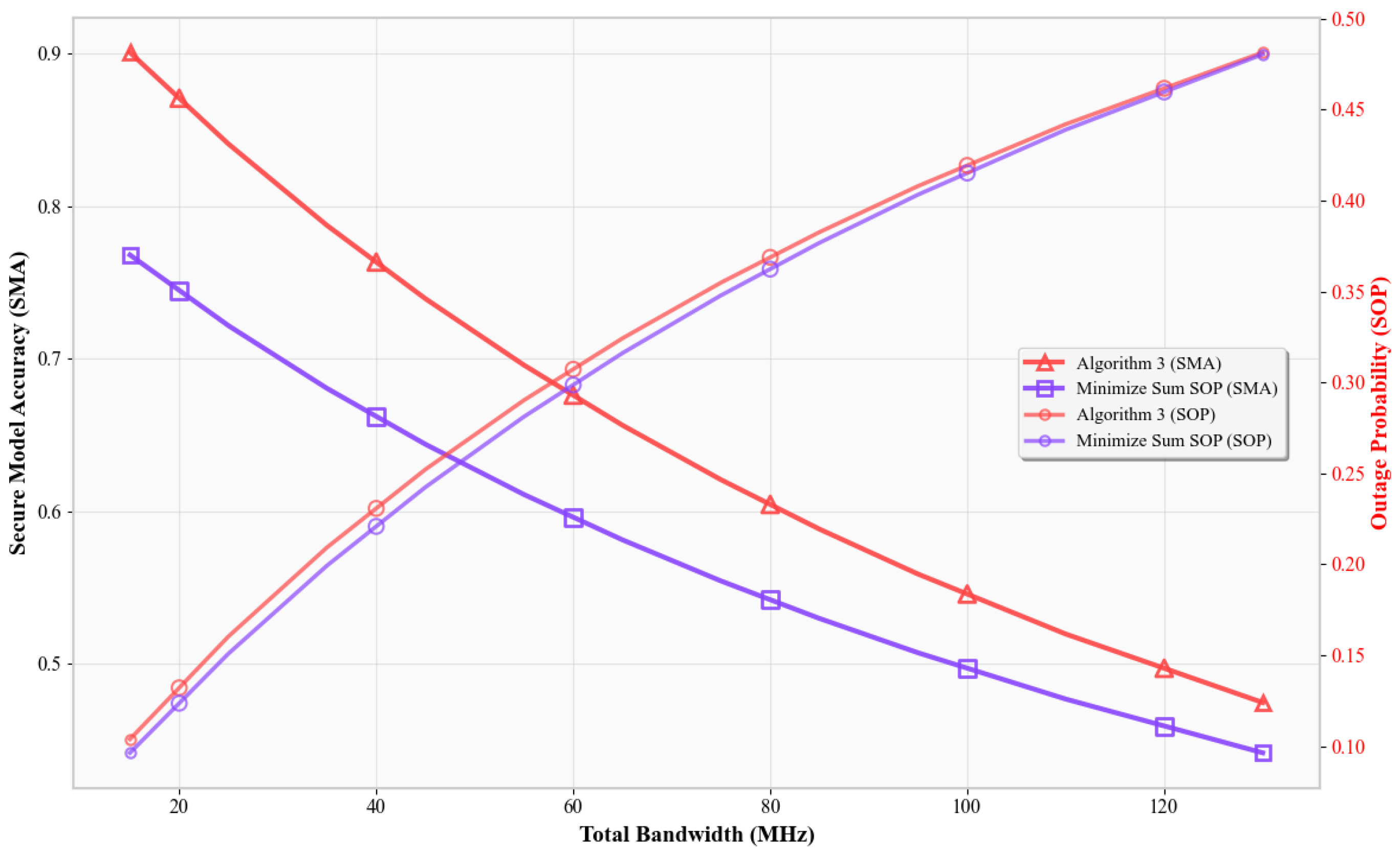
Figure 5 shows SMA versus total bandwidth
. With fixed power, increasing bandwidth reduces the SNR per Hz due to increased noise power (
). As a result, all schemes experience lower SMA. Algorithm 3’s accuracy drops more gently, maintaining superiority across the range. It adapts to bandwidth-induced noise by focusing on the most efficient sub-bands, whereas the others either spread power too thin or sacrifice throughput for secrecy.
Figure 6,
Figure 7,
Figure 8 and
Figure 9 jointly plot SMA and the secrecy outage probability versus various system parameters. In
Figure 6, as
increases, Algorithm 3 achieves the highest SMA and nearly the lowest SOP. In contrast, the Min-SOP scheme reduces SOP more but severely sacrifices SMA. Algorithm 3 balances these objectives better than the others.
In
Figure 7, as bandwidth increases, Algorithm 3 still preserves a better SMA–SOP tradeoff. Higher bandwidth leads to lower SNRs, raising SOP and lowering accuracy. Algorithm 3 adapts through selective power use and subband prioritization, while Min-SOP limits SMA too aggressively.
Figure 8 demonstrates the effect of increasing
. All schemes see rising SOP and falling SMA. However, Algorithm 3 maintains a good balance, with higher SMA and moderate SOP, while the Min-SOP scheme achieves lower SMA.
Finally,
Figure 9 shows that as
grows, all SMAs rise. Yet, Algorithm 3 achieves the best accuracy and near-optimal SOP, whereas the Min-SOP scheme ensures secrecy but loses accuracy.
In all cases, Algorithm 3’s joint optimization achieves superior SMA by dynamically balancing throughput and secrecy. It adapts to system conditions like power, noise, and bandwidth, unlike the fixed- or single-objective benchmarks. These results validate Algorithm 3’s ability to consistently find the optimal tradeoff between classification accuracy and secrecy.
6.2. Practical Implementation Feasibility
Regarding communication constraints, the proposed scheme only requires model parameter transmission once per task period, with incremental updates possible for further bandwidth savings. In real UAV networks, the wireless link bandwidth may fluctuate due to mobility, interference, or environmental conditions. SMA-based optimization inherently adapts to such fluctuations because bandwidth allocation is recomputed in each optimization cycle based on the current channel state information (CSI). Furthermore, the optimization framework can be integrated with link adaptation mechanisms (e.g., adaptive modulation and coding) to mitigate the effect of short-term bandwidth drops.
Additionally, from an energy and hardware perspective, UAVs can offload the optimization computations entirely to edge servers, leaving only lightweight CSI measurement and model identification tasks onboard. This ensures that even resource-constrained UAVs can participate in the system without violating their onboard power budgets. Overall, the computational tractability, adaptability to bandwidth variability, and low onboard resource requirements suggest that the proposed scheme is feasible for near-term deployment in UAV-assisted secure semantic communication systems.
7. Discussion
While the proposed framework demonstrates significant advantages in jointly optimizing model recognition accuracy and physical layer security in UAV-assisted AIoT systems, several limitations should be acknowledged.
First, the current study assumes perfect channel state information (CSI) at the edge server for both legitimate users and potential eavesdroppers. In practical deployments, CSI estimation errors and feedback delays are inevitable, which may degrade the optimization performance. Incorporating robust optimization techniques to mitigate imperfect CSI remains an important direction for future work.
Second, the system model considers a single-task transmission scenario where one trained AI model is delivered to multiple UAVs. In real-world applications, multiple heterogeneous tasks may coexist, each with different latency, accuracy, and security requirements. Extending the framework to multi-task or multi-priority scenarios could enhance its applicability in complex AIoT environments.
Finally, the proposed optimization method focuses on downlink model transmission without considering the computational heterogeneity and battery limitations of UAVs. Although UAVs in our framework can offload optimization computation to edge servers, future research could integrate energy-aware resource allocation and heterogeneous device capabilities into the optimization problem to improve sustainability and fairness.
By addressing these limitations, the proposed framework could be further extended to support more realistic, large-scale, and heterogeneous AIoT deployments, thereby advancing the development of trustworthy edge intelligence in next-generation networks.
8. Conclusions
This study has established a novel framework for physical layer secure transmission in UAV-assisted AIoT systems through three key innovations: First, the closed-form SOP derivation provides theoretical guarantees for secrecy performance under Rayleigh fading channels. Second, the SMA metric fundamentally reconciles the traditionally competing objectives of model recognition accuracy and transmission security. Third, our alternating optimization algorithm dynamically selects optimal model–bandwidth pairs while adapting to channel conditions and eavesdropper capabilities. Extensive simulations demonstrate that the proposed framework achieves significant performance gains compared to fixed-model selection schemes under varying noise conditions. The optimal power utilization of the algorithm allows us to convert additional transmit power into accuracy gains while maintaining security constraints.
Future research will extend the framework to more complex and realistic AIoT scenarios, such as federated learning with heterogeneous devices and dynamic task arrivals, aiming for adaptive and robust optimization in both spatial and temporal dimensions.
Author Contributions
Conceptualization, T.L. and X.F.; Methodology, H.L., M.L. and X.F.; Validation, Y.L.; Formal analysis, T.L. and X.F.; Investigation, H.L., T.L. and X.F.; Writing—original draft, M.L. and Y.L.; Writing—review & editing, H.L. and X.F.; Supervision, H.L., R.L. and X.F.; Project administration, H.L., R.L. and X.F.; Funding acquisition, H.L. and X.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 62302332, 62502036), the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant No. 23KJB510033), the China Postdoctoral Science Foundation under Grant 2024M750199, and the Fundamental Research Funds for the Central Universities (Grant No. BLX202360, QNTD202504).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Runlei Li was employed by the company China Academy of Railway Sciences Corporation Limited. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Wang, Y.; Han, S.; Xu, X.; Rui, M.; Liang, H.; Chen, D.; Zhang, P. Intellicise model transmission for semantic communication in intelligence-native 6G networks. China Commun. 2024, 21, 95–112. [Google Scholar] [CrossRef]
- Han, S.; Zhang, W.; Xu, X.; Wang, B.; Sun, M.; Tao, X.; Zhang, P. S2E-DECI: Secrecy and Energy-Efficient Dual-Aware Device-Edge Co-Inference for AIoT. IEEE Internet Things J. 2024, 11, 39142–39157. [Google Scholar] [CrossRef]
- Jia, S.; Wang, R.; Lou, Y.; Wang, N.; Zhang, D.; Singh, K.; Mumtaz, S. Secrecy performance analysis of UAV-assisted ambient backscatter communications with jamming. IEEE Trans. Wirel. Commun. 2024, 23, 18111–18125. [Google Scholar] [CrossRef]
- Qiu, X.; Yu, J.; Zhuang, W.; Li, G.; Sun, X. Channel prediction-based security authentication for artificial intelligence of things. Sensors 2023, 23, 6711. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhu, Q.; Hu, H.; Li, Y.; Miao, X.; Xu, M. Physical Unclonable Function in Spiking Neural Network Based on in-Te Ovonic Threshold Switching Devices. In Proceedings of the 2025 9th IEEE Electron Devices Technology & Manufacturing Conference (EDTM), Hong Kong, China, 9–12 March 2025; pp. 1–3. [Google Scholar]
- Zhang, Y.; Zhao, S.; Shen, Y.; Jiang, X.; Shiratori, N. Enhancing the physical layer security of two-way relay systems with RIS and beamforming. IEEE Trans. Inf. Forensics Secur. 2024, 19, 5696–5711. [Google Scholar] [CrossRef]
- Hema, P.P.; Babu, A.V. Full-duplex jamming for physical layer security improvement in NOMA-enabled overlay cognitive radio networks. Secur. Priv. 2024, 7, e371. [Google Scholar] [CrossRef]
- Khalid, W.; Rehman, M.A.U.; Van Chien, T.; Kaleem, Z.; Lee, H.; Yu, H. Reconfigurable intelligent surface for physical layer security in 6G-IoT: Designs, issues, and advances. IEEE Internet Things J. 2023, 11, 3599–3613. [Google Scholar] [CrossRef]
- Qiu, B.; Cheng, W.; Zhang, W. Joint information and jamming beamforming for securing IoT networks with ratesplitting. IEEE Internet Things J. 2023, 11, 6338–6351. [Google Scholar] [CrossRef]
- Wang, S.; Wu, Y.C.; Xia, M.; Wang, R.; Poor, H.V. Machine intelligence at the edge with learning centric power allocation. IEEE Trans. Wirel. Commun. 2020, 19, 7293–7308. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. In Handbook of Systemic Autoimmune Diseases; University of Toronto: Toronto, ON, Canada, 2009; Volume 1. [Google Scholar]
- Jin, L.; Xu, X.; Han, S.; Chi, X.; Lv, S.; Zhang, P.; Liu, C. Computation offloading outage probability analysis and min-max fairness optimization in RIS-assisted MEC system. IEEE Trans. Veh. Technol. 2022, 72, 4615–4627. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Gondzio, J. Interior point methods 25 years later. Eur. J. Oper. Res. 2012, 218, 587–601. [Google Scholar] [CrossRef]
- Nesterov, Y.E.; Todd, M.J. Self-scaled barriers and interior-point methods for convex programming. Math. Oper. Res. 1997, 22, 1–42. [Google Scholar] [CrossRef]
- Wright, S.J. Primal-Dual Interior-Point Methods; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1997. [Google Scholar]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).