Robust Helmert Variance Component Estimation for Positioning with Dual-Constellation LEO Satellites’ Signals of Opportunity

Abstract

In Global Navigation Satellite System (GNSS)-denied environments, navigation using signals of opportunity (SOP) from Low Earth Orbit (LEO) satellites is considered a feasible alternative. Compared with single-constellation systems, multiple-constellation LEO systems offer improved satellite visibility and geometric diversity, which enhances positioning continuity and accuracy. To allocate weights among heterogeneous observations, prior studies have employed the Helmert variance component estimation (HVCE) method, which iteratively determines relative weight ratios of different observation types through posterior variance estimation. HVCE enables error modeling and weight adjustment without prior noise information but is highly sensitive to outliers, making it vulnerable to their impact. This study proposes a Robust HVCE-based dual-constellation weighted positioning method. The approach integrates prior weighting based on satellite elevation, observation screening based on characteristic slopes, HVCE, and IGG-III robust estimation to achieve dynamic weight adjustment and suppress outliers. Experimental results over a 33.9 km baseline demonstrate that the proposed method attains Two-Dimensional (2D) and Three-Dimensional (3D) positioning accuracies of 12.824 m and 23.230 m, corresponding to improvements of 29% and 16% over conventional HVCE weighting, respectively. It also outperforms single-constellation positioning and equal-weighted fusion, confirming the effectiveness of the proposed approach.

1. Introduction

Global Navigation Satellite System (GNSS) services are widely used across various sectors. However, in challenging environments such as urban canyons, tunnels, and forests, GNSS signals are vulnerable to blockage and multipath interference, limiting their reliability for certain applications [1,2]. To overcome this challenge, navigation using Signals of Opportunity (SOP) has recently emerged as a promising alternative for positioning. SOP refers to non-navigation radio signals available in space, which can be categorized as terrestrial-based or space-based according to their sources [3,4,5]. With the rapid growth of Low Earth Orbit (LEO) constellations, communication downlink signals transmitted by numerous non-navigation satellites, such as Iridium Next, Starlink, and OneWeb, have become a major component of SOP. LEO satellites provide strong signal power, wide coverage, and rapidly changing geometry [6,7], enabling SOP-based navigation schemes constructed from their downlink signals to offer substantial positioning potential in environments where GNSS is unavailable or restricted [8,9,10]. Notably, the high-density deployment of large-scale LEO constellations such as Starlink and OneWeb not only expands spatial coverage, but also significantly enhances satellite visibility and spatial redundancy across different latitudes. This ensures more stable observation geometry even in regions where GNSS availability is limited [11].

Compared with single-constellation LEO systems, SOP positioning that integrates multiple LEO constellations offers notable advantages in terms of the number of available observations, spatial geometry, and orbital diversity. Studies have shown that multi-constellation integration can effectively optimize geometric configurations and improve positioning stability and continuity. For example, combining Iridium Next and Orbcomm improves positioning accuracy by over 43% compared with single-constellation solutions [12]; experiments with Starlink and OneWeb achieve accuracies within 5 m [9]; and joint use of Starlink, OneWeb, ORBCOMM, and Iridium Next yields a Three-Dimensional (3D) positioning error of 9.5 m [8].The complementarity among constellations in terms of frequencies, orbital structures, and signal formats enhances the overall system reliability and robustness [13,14]. The improvement in geometric diversity brought by constellation integration is often assessed through Geometric Dilution of Precision (GDOP). While GDOP is traditionally used in pseudorange-based GNSS positioning to describe the spatial distribution of satellites relative to the user, Doppler-based SOP positioning requires a fundamentally different interpretation. Specifically, Doppler GDOP is influenced not by satellite positions alone, but by their velocities and the directions of signal propagation. The GDOP formulation must account for the angular relationship between the satellite motion vectors and the line-of-sight directions to the user. This distinction is essential for accurate modeling of geometry-induced error propagation in Doppler-based systems and should not be confused with conventional pseudorange GDOP metrics [11,15].

Determining appropriate weight ratios among multi-system observations is essential for achieving high-precision multi-satellite navigation. Improper weight allocation can bias posterior unit variances and compromise parameter estimation. Common prior weighting models primarily rely on satellite elevation and Carrier-to-Noise Ratio (CNR) to assign weights at each epoch [16,17]. Observations at higher elevations are given greater weights due to shorter propagation paths and reduced multipath effects, while signals with higher CNR, indicative of better quality, also receive larger weights. However, such models fail to reflect the true statistical behavior of LEO observation errors. Different constellations exhibit marked variations in orbital accuracy and noise characteristics, while abrupt outliers or non-Gaussian error distributions can further distort prior precision-based weighting, degrading solution stability and accuracy [18,19,20].

To enhance integrated positioning accuracy, observation weights should be adaptively adjusted according to the characteristics of observation errors. Posterior variance estimation is a commonly employed strategy, which derives the variance components of different observation types from initial residuals and iteratively updates the weight matrix. Among these methods, Helmert Variance Component Estimation (HVCE) is widely adopted in multi-source weighting for integrated GNSS and LEO positioning due to its reliable convergence and numerical stability [21,22,23]. However, because HVCE is formulated as a least-squares method, it is highly sensitive to outliers. When outliers exist within the observations, residual statistics can be severely biased, leading to distorted variance modeling, unstable or divergent solutions, and significantly degraded performance of integrated positioning [24,25,26,27].

This study focuses on the Iridium Next and Starlink constellations, systematically investigating joint positioning method based on SOP. To improve positioning robustness, an HVCE method enhanced with a robust estimation mechanism is proposed. In this approach, robust weight functions are incorporated into the variance estimation process to dynamically reduce the impact of residuals and suppress the effects of outliers. These enhancements aim to improve the stability and accuracy of integrated positioning using multiple LEO constellations. The proposed method is further validated through experiments with real signal data.

2. Fusion Positioning Model for Iridium Next and Starlink

This section introduces the direct fusion positioning model and the weighted fusion positioning model for Iridium Next and Starlink.

2.1. Direct Fusion Positioning Model

The Doppler observation equations for Iridium Next and Starlink signals can be formulated as follows:

$$\begin{array}{l}{f}_{d,i}^{\mathrm{Iri}}=f_{c,i}^{\mathrm{Iri}}\cdot {\displaystyle \frac{{\left({\overrightarrow{V}}_i^{\mathrm{Iri}}-{\overrightarrow{V}}_u\right)}^{\mathrm{T}}\cdot \left({\overrightarrow{P}}_u-{\overrightarrow{P}}_i^{\mathrm{Iri}}\right)}{c\cdot ‖{\overrightarrow{P}}_u-{\overrightarrow{P}}_i^{\mathrm{Iri}}‖}}+\delta {\dot{t}}^{\mathrm{Iri}}+{\epsilon }_i^{\mathrm{Iri}}\\ f_{d,j}^{\mathrm{Sta}}=f_{c,j}^{\mathrm{Sta}}\cdot {\displaystyle \frac{{\left({\overrightarrow{V}}_j^{\mathrm{Sta}}-{\overrightarrow{V}}_u\right)}^{\mathrm{T}}\cdot \left({\overrightarrow{P}}_u-{\overrightarrow{P}}_j^{\mathrm{Sta}}\right)}{c\cdot ‖{\overrightarrow{P}}_u-{\overrightarrow{P}}_j^{\mathrm{Sta}}‖}}+\delta {\dot{t}}^{\mathrm{Sta}}+{\epsilon }_j^{\mathrm{Sta}}\end{array}$$

(1)

In Equation (1), $\mathrm{Iri}$ and $\mathrm{Sta}$ denote Iridium Next and Starlink, respectively. $f_{d,i}^{\mathrm{Iri}}$ and $f_{d,j}^{\mathrm{Sta}}$ represent the Doppler measurements. ${f_c}^{\mathrm{Iri}}$ and ${f_c}^{\mathrm{Sta}}$ indicate the carrier frequencies. The user position is expressed as ${\overrightarrow{P}}_u={\left[x_u,y_u,z_u\right]}^{\mathrm{T}}$, and the velocity as ${\overrightarrow{V}}_u={\left[v_{u,x},v_{u,y},v_{u,z}\right]}^{\mathrm{T}}$. The satellite positions are ${\overrightarrow{P}}_i^{\mathrm{Iri}}={\left[x_i^{\mathrm{Iri}},y_i^{\mathrm{Iri}},z_i^{\mathrm{Iri}}\right]}^{\mathrm{T}}$ for Iridium Next and ${\overrightarrow{P}}_j^{\mathrm{Sta}}={\left[x_j^{\mathrm{Sta}},y_j^{\mathrm{Sta}},z_j^{\mathrm{Sta}}\right]}^{\mathrm{T}}$ for Starlink. The satellite velocities are given by ${\overrightarrow{V}}_i^{\mathrm{Iri}}={\left[v_{i,x}^{\mathrm{Iri}},v_{i,y}^{\mathrm{Iri}},v_{i,z}^{\mathrm{Iri}}\right]}^{\mathrm{T}}$ and ${\overrightarrow{V}}_j^{\mathrm{Sta}}={\left[v_{j,x}^{\mathrm{Sta}},v_{j,y}^{\mathrm{Sta}},v_{j,z}^{\mathrm{Sta}}\right]}^{\mathrm{T}}$. $c$ denotes the speed of light. $\delta {\dot{t}}^{\mathrm{Iri}}$ and $\delta {\dot{t}}^{\mathrm{Sta}}$ represent the clock drifts between the receiver and the two constellations, respectively. ${\epsilon }_i^{\mathrm{Iri}}$ and ${\epsilon }_j^{\mathrm{Sta}}$ represent the residual errors, which include contributions from the Doppler measurements.

When the user is assumed to be stationary (i.e., ${\overrightarrow{V}}_u=0$) in the Earth-Centered, Earth-Fixed (ECEF) coordinate frame, the observation equation for Iridium Next is used as an example to construct the function:

$$f^i({\overrightarrow{P}}_u^{\mathrm{T}},\delta {\dot{t}}^{\mathrm{Iri}})=f_{d,i}^{\mathrm{Iri}}$$

(2)

The equation can then be derived as:

$$f^i({\overrightarrow{P}}_u^{\mathrm{T}},\delta {\dot{t}}^{\mathrm{Iri}})=f^i(x_{k-1}+\Delta x_u,y_{k-1}+\Delta y_u,z_{k-1}+\Delta z_u,\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}+\Delta \delta {\dot{t}}^{\mathrm{Iri}})$$

(3)

where ${\overrightarrow{X}}_{k-1}={\left[x_{k-1},y_{k-1},z_{k-1},\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}\right]}^{\mathrm{T}}={\left[{\overrightarrow{P}}_{k-1}^{\mathrm{T}},\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}\right]}^{\mathrm{T}}$ represents the initial estimated state vector; $\Delta x_u=x_u-x_{k-1}$, $\Delta y_u=y_u-y_{k-1}$, and $\Delta z_u=z_u-z_{k-1}$ denote the corrections for the user position; and $\Delta \delta {\dot{t}}^{\mathrm{Iri}}=\delta {\dot{t}}^{\mathrm{Iri}}-\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}$ represents the clock drift correction. Using the first-order Taylor series expansion, the result can be expressed as follows:

$$\begin{array}{l}{f}^i\left(x_{k-1}+\Delta x_u,y_{k-1}+\Delta y_u,z_{k-1}+\Delta z_u,\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}+\Delta \delta {\dot{t}}^{\mathrm{Iri}}\right)=f^i\left({\overrightarrow{P}}_{k-1}^{\mathrm{T}},\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}\right)+\\ {\displaystyle \frac{\partial f^i\left({\overrightarrow{P}}_{k-1}^{\mathrm{T}},\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}\right)}{\partial P_{u,x}}}\Delta x_u+{\displaystyle \frac{\partial f^i\left({\overrightarrow{P}}_{k-1}^{\mathrm{T}},\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}\right)}{\partial P_{u,y}}}\Delta y_u+\\ {\displaystyle \frac{\partial f^i\left({\overrightarrow{P}}_{k-1}^{\mathrm{T}},\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}\right)}{\partial P_{u,z}}}\Delta z_u+{\displaystyle \frac{\partial f^i\left({\overrightarrow{P}}_{k-1}^{\mathrm{T}},\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}\right)}{\partial \delta {\dot{t}}^{\mathrm{Iri}}}}\Delta \delta {\dot{t}}^{\mathrm{Iri}}\end{array}$$

(4)

$$\begin{array}{l}{\displaystyle \frac{\partial f^i\left({\overrightarrow{P}}_{k-1}^{\mathrm{T}},\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}\right)}{\partial x_u}}={\displaystyle \frac{f_{c,i}^{\mathrm{Iri}}}{c}}\left({\displaystyle \frac{v_{i,x}^{\mathrm{Iri}}}{d_i}}-{\displaystyle \frac{\left({\overrightarrow{V}}_i^{\mathrm{Iri}}\cdot {\overrightarrow{r}}_i\right)\left(x_{k-1}-x_i^{\mathrm{Iri}}\right)}{d_i^3}}\right)\\ {\displaystyle \frac{\partial f^i\left({\overrightarrow{P}}_{k-1}^{\mathrm{T}},\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}\right)}{\partial y_u}}={\displaystyle \frac{f_{c,i}^{\mathrm{Iri}}}{c}}\left({\displaystyle \frac{v_{i,y}^{\mathrm{Iri}}}{d_i}}-{\displaystyle \frac{\left({\overrightarrow{V}}_i^{\mathrm{Iri}}\cdot {\overrightarrow{r}}_i\right)\left(y_{k-1}-y_i^{\mathrm{Iri}}\right)}{d_i^3}}\right)\\ {\displaystyle \frac{\partial f^i\left({\overrightarrow{P}}_{k-1}^{\mathrm{T}},\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}\right)}{\partial z_u}}={\displaystyle \frac{f_{c,i}^{\mathrm{Iri}}}{c}}\left({\displaystyle \frac{v_{i,z}^{\mathrm{Iri}}}{d_i}}-{\displaystyle \frac{\left({\overrightarrow{V}}_i^{\mathrm{Iri}}\cdot {\overrightarrow{r}}_i\right)\left(z_{k-1}-z_i^{\mathrm{Iri}}\right)}{d_i^3}}\right)\\ {\displaystyle \frac{\partial f^i\left({\overrightarrow{P}}_{k-1}^{\mathrm{T}},\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}\right)}{\partial \delta {\dot{t}}^{\mathrm{Iri}}}}=1\\ f^i\left(x_{k-1}+\Delta x_u,y_{k-1}+\Delta y_u,z_{k-1}+\Delta z_u,\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}+\Delta \delta {\dot{t}}^{\mathrm{Iri}}\right)-f^i\left({\overrightarrow{P}}_{k-1}^{\mathrm{T}},\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}\right)=\Delta f_{d,i}^{\mathrm{Iri}}\end{array}$$

(5)

where ${\overrightarrow{r}}_i={\overrightarrow{P}}_u-{\overrightarrow{P}}_i^{\mathrm{Iri}}$, $d_i=\sqrt{{\left(x_{k-1}-x_i^{\mathrm{Iri}}\right)}^2+{\left(y_{k-1}-y_i^{\mathrm{Iri}}\right)}^2+{\left(z_{k-1}-z_i^{\mathrm{Iri}}\right)}^2}$.

Similarly, the linearized observation equation for Starlink at ${\overrightarrow{X}}_0$ can be obtained. Therefore, the combined linearized observation equation for positioning using Iridium Next and Starlink signals can be expressed as:

$$G\Delta X=b$$

(6)

where

$$\begin{array}{c}G=\left[\begin{array}{c}{G}_{\mathrm{Iri}}\\ G_{\mathrm{Sta}}\end{array}\right]=\left[\begin{array}{ccccc}⋮& ⋮& ⋮& ⋮& ⋮\\ {\displaystyle \frac{\partial f^i\left({\overrightarrow{P}}_{k-1}^{\mathrm{T}},\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}\right)}{\partial x_u}}& {\displaystyle \frac{\partial f^i\left({\overrightarrow{P}}_{k-1}^{\mathrm{T}},\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}\right)}{\partial y_u}}& {\displaystyle \frac{\partial f^i\left({\overrightarrow{P}}_{k-1}^{\mathrm{T}},\delta {\dot{t}}_{k-1}^{\mathrm{Iri}}\right)}{\partial z_u}}& 1& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ {\displaystyle \frac{\partial f^j\left({\overrightarrow{P}}_{k-1}^{\mathrm{T}},\delta {\dot{t}}_{k-1}^{\mathrm{Sta}}\right)}{\partial x_u}}& {\displaystyle \frac{\partial f^j\left({\overrightarrow{P}}_{k-1}^{\mathrm{T}},\delta {\dot{t}}_{k-1}^{\mathrm{Sta}}\right)}{\partial x_u}}& {\displaystyle \frac{\partial f^j\left({\overrightarrow{P}}_{k-1}^{\mathrm{T}},\delta {\dot{t}}_{k-1}^{\mathrm{Sta}}\right)}{\partial x_u}}& 0& 1\\ ⋮& ⋮& ⋮& ⋮& ⋮\end{array}\right]\\ \Delta X=\left[\begin{array}{c}\Delta x_u\\ \Delta y_u\\ \Delta z_u\\ \Delta \delta {\dot{t}}^{\mathrm{Iri}}\\ \Delta \delta {\dot{t}}^{\mathrm{Sta}}\end{array}\right] b=\left[\begin{array}{c}{b}_{\mathrm{Iri}}\\ b_{\mathrm{Sta}}\end{array}\right]=\left[\begin{array}{c}⋮\\ \Delta f_{d,i}^{\mathrm{Iri}}\\ ⋮\\ \Delta f_{d,j}^{\mathrm{Sta}}\\ ⋮\end{array}\right]\end{array}$$

According to the least-squares principle, the position update can be expressed as:

$$\Delta X={\left(G^{\mathrm{T}}G\right)}^{-1}{G}^{\mathrm{T}}b$$

(7)

By performing continuous iterations until convergence, the final user position can be obtained.

2.2. Weighted Fusion Positioning Model

To implement the weighted least-squares method, a weight matrix $W$ is introduced, where n represents the total number of Iridium Next and Starlink signals received.

$$W=\left[\begin{array}{cccc}{w}_1& 0& \dots & 0\\ 0& w_2& \dots & 0\\ ⋮& ⋮& \ddots & 0\\ 0& 0& 0& w_n\end{array}\right]$$

(8)

Typically, the weight $w_i$ is defined as the inverse of the standard deviation ${\sigma }_i$ of the measurement error, i.e.,

$$w_i={\displaystyle \frac{1}{{\sigma }_i}}$$

(9)

Each equation in Equation (6) is multiplied by its corresponding weight, resulting in the following expression:

$$WG\Delta X=Wb$$

(10)

The least-squares solution for this system is given by:

$$\Delta X={\left(G^{\mathrm{T}}{W}^{\mathrm{T}}WG\right)}^{-1}{G}^{\mathrm{T}}{W}^{\mathrm{T}}Wb$$

(11)

where $P=W^{\mathrm{T}}W$.

3. Dual-Constellation Weighted Positioning Method Based on Robust HVCE

This section introduces a dual-constellation weighted positioning method based on Robust HVCE. The method dynamically adjusts the weight ratio of fused observations from the Iridium Next and Starlink systems to improve the overall accuracy of dual-constellation fusion positioning.

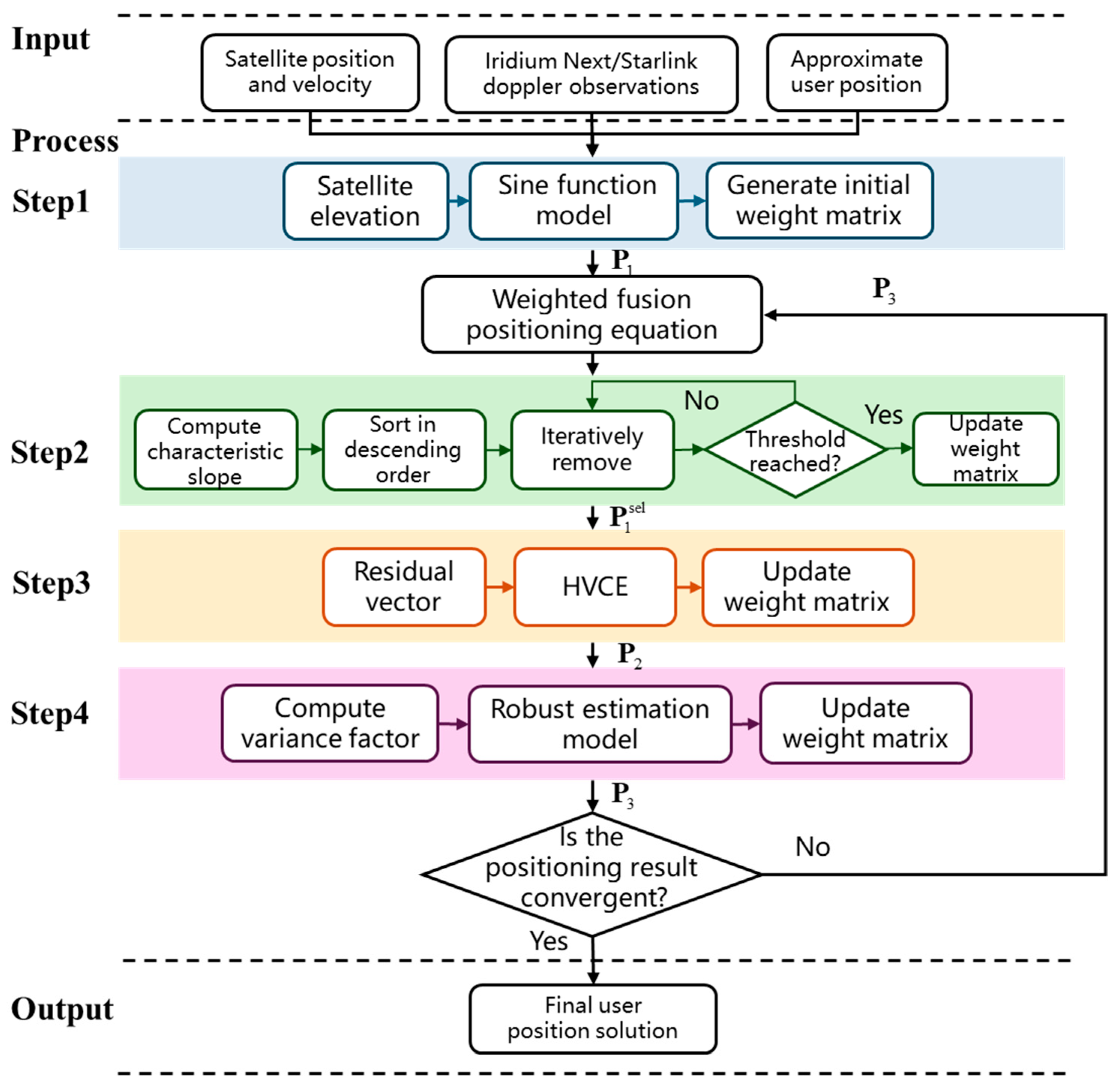
3.1. Positioning Flow

The overall positioning flow is illustrated in Figure 1, and the related principles and theoretical models are elaborated in the following subsections. First, satellite positions and velocities at any observation epoch are obtained using a combination of the Lagrange interpolation algorithm and the Simplified General Perturbations 4 (SGP4) model, based on publicly available Two Line Element (TLE) data provided by Celestrak (https://celestrak.org/, accessed on 16 December 2024) and Space-Track (https://www.space-track.org/, accessed on 31 December 2024). Considering that the satellite orbits predicted by SGP4 are expressed in the True Equator, Mean Equinox (TEME) coordinate system, the orbital information is subsequently transformed into the ECEF frame to ensure consistency with the observation model. Next, the downlink signals from Starlink and Iridium Next are processed using a high-sensitivity frequency detection algorithm and a carrier frequency–code phase joint estimation algorithm, respectively. These methods estimate the carrier frequencies and derive the Doppler observations [28,29]. After constructing the Doppler observations for the two constellations, the subsequent step is to assign appropriate weights to each type of observation to improve the accuracy and robustness of the fusion solution. As a solution, this study proposes a weight estimation method based on Robust HVCE, which consists of the following four main steps:

Step 1: A priori weighting based on elevation

A priori weighting matrix is constructed using an elevation-based weighting model to assign initial weights to different observations.

Step 2: Observation screening based on characteristic slopes

The characteristic slope of each observation epoch is calculated to assess its contribution to the positioning geometry. Observations with minor influence are subsequently removed.

Step 3: Weight adjustment based on HVCE

After observation screening, the residuals of the retained observations are used with the HVCE method to estimate the variance components of the two systems. The weight matrix is then updated accordingly.

Step 4: Outlier elimination based on robust estimation

A robust estimation model is employed to determine the equivalent weight matrix, where the weights of outliers are adaptively reduced. The optimized weight matrix is subsequently used as the initial input for the next iteration of the solution.

This study embeds the weight estimation and updating process within the iterative framework of dual-constellation fusion Doppler positioning. During the positioning process, observation selection and weight optimization continue until the results satisfy the convergence criterion. The final user position is then stably determined.

3.2. Elevation-Based Prior Weighting Model

In positioning based on LEO satellites, the elevation angle of the observed satellites has a significant impact on the quality of the measurements. Typically, observations at low elevation angles are more susceptible to atmospheric delay, ionospheric disturbances, and multipath effects, which reduce the reliability of the measurements. Therefore, satellites with low elevation angles should be assigned lower weights during the observation weighting process. In this study, a sine function model is used to construct the prior weight matrix [30]:

$${\sigma }_i={\displaystyle \frac{1}{\sin \left(E_i\right)}}$$

(12)

In this equation, $E_i$ denotes the elevation angle of the satellite. The initial weight matrix $P_1$ is given as:

$$P_1=\left[\begin{array}{cc}{P}_{\mathrm{Iri},1}& 0\\ 0& P_{\mathrm{Sta},1}\end{array}\right]=\left[\begin{array}{cccc}1/{\sigma }_1^2& 0& \dots & 0\\ 0& 1/{\sigma }_2^2& \dots & 0\\ ⋮& ⋮& \ddots & 0\\ 0& 0& 0& 1/{\sigma }_n^2\end{array}\right]$$

(13)

where $P_{\mathrm{Iri}}$ and $P_{\mathrm{Sta}}$ represent the initial weight matrices for the Iridium Next and Starlink systems, respectively, determined based on the sine function model.

3.3. Characteristic Slope-Based Observation Screening

In dual-constellation SOP-based positioning, some observations contribute minimally to positioning accuracy in terms of geometric structure. If these observations are directly included in the solution, they not only lead to higher computational complexity but may also degrade the overall geometric quality. Therefore, this study performs observation screening based on characteristic slopes by evaluating each observation’s geometric contribution to the Doppler Position Dilution of Precision (DPDOP). Redundant observations are iteratively removed to construct a refined observation set with an improved geometric distribution.

In GNSS navigation, the Position Dilution of Precision (PDOP) is used to quantify the impact of satellite geometry on positioning accuracy. A smaller PDOP value indicates a more favorable spatial satellite configuration, which helps improve the accuracy of positioning results [29]. Similarly, in Doppler positioning using LEO satellites, DPDOP is employed to characterize the effect of satellite spatial distribution on Doppler-based positioning results, and is defined as:

$$DPDOP=\sqrt{H_{\left(1,1\right)}+H_{\left(2,2\right)}+H_{\left(3,3\right)}}$$

(14)

where $H={\left(G^{\mathrm{T}}G\right)}^{-1}$.

To further assess the influence of each observation on DPDOP, this study employs the characteristic slope as a quantitative metric. The characteristic slope is derived based on a linear noise-free model to quantify the geometric relationship between positioning error and test statistics. The characteristic slope of each observation is equivalent to its contribution to the DPDOP value [31] and is defined as:

$$Slop{e}_i=\sqrt{{\displaystyle \frac{{\displaystyle \sum _{j=1}^3{p}_{j,i}^2}}{S_{\left(i,i\right)}}}}=\sqrt{DPDO{P}_i^2-DPDOP}$$

(15)

where $P={\left(G^{\mathrm{T}}G\right)}^{-1}{G}^{\mathrm{T}}$, $S=I-G{\left(G^{\mathrm{T}}G\right)}^{-1}{G}^{\mathrm{T}}$.

The specific processing procedure is as follows:

Step 1: With all available observations retained, compute the initial DPDOP value corresponding to the current observation set, given by $DPDO{P}_n$.

Step 2: Compute the characteristic slope for each observation, denoted as $Slop{e}_i$, according to Equation (15).

Step 3: Sort the characteristic slopes of all observations in descending order, and denote the total number of observations as $n$.

Step 4: Determine whether the current number of observations $n$ exceeds the predefined minimum threshold $n_{th}$. If $n>n_{th}$, temporarily remove the observation positioned at rank $n$ in the ranking by characteristic slope from the observation set; otherwise, terminate the screening process and retain the current set.

Step 5: Compute the $DPDO{P}_{n-1}$ for the remaining observation set, and then calculate the relative change rate of DPDOP, denoted as $\delta DPDOP$, after removing the observation.

$$\delta DPDOP={\displaystyle \frac{DPDO{P}_{n-1}-DPDO{P}_n}{DPDO{P}_n}}$$

(16)

Step 6: If $\delta DPDOP$ exceeds the predefined threshold ${\lambda }_{th}$, the observation is deemed to contribute significantly and is retained, terminating the screening process. Otherwise, the observation is removed, $n=n-1$, and the process returns to Step 4 for the next iteration of screening.

Finally, the initial weight matrix corresponding to the screened observation set is constructed and denoted as $P_1^{\mathrm{sel}}$:

$$P_1^{\mathrm{sel}}=\left[\begin{array}{cc}{P}_{\mathrm{Iri},1}^{\mathrm{sel}}& 0\\ 0& P_{\mathrm{Sta},1}^{\mathrm{sel}}\end{array}\right]$$

(17)

3.4. HVCE

After completing the observation screening based on characteristic slopes, redundant observations with minimal contribution to positioning accuracy are initially removed. This step improves the quality of the geometric configuration. On this basis, this study then adjusts the initial weights using HVCE. Assuming that the Doppler observations from Iridium Next and Starlink satellites are independent, the residual equation formed by the parameter adjustment model is given as:

$$\left[\begin{array}{c}{V}_{\mathrm{Iri}}\\ V_{\mathrm{Sta}}\end{array}\right]=\left[\begin{array}{c}{G}_{\mathrm{Iri}}\\ G_{\mathrm{Sta}}\end{array}\right]\Delta \widehat{X}-\left[\begin{array}{c}{b}_{\mathrm{Iri}}\\ b_{\mathrm{Sta}}\end{array}\right]$$

(18)

The rigorous formula for HVCE is given as:

$$S_{2\times 2}{\widehat{\theta }}_{2\times 1}=W_{2\times 1}$$

(19)

where

$$\begin{array}{c}{S}_{2\times 2}=\left[\begin{array}{cc}{n}_{\mathrm{Iri}}-2\mathrm{tr}\left(N^{-1}{N}_{\mathrm{Iri}}\right)+\mathrm{tr}{\left(N^{-1}{N}_{\mathrm{Iri}}\right)}^2& \mathrm{tr}\left(N^{-1}{N}_{\mathrm{Iri}}{N}^{-1}{N}_{\mathrm{Sta}}\right)\\ \mathrm{tr}\left(N^{-1}{N}_{\mathrm{Iri}}{N}^{-1}{N}_{\mathrm{Sta}}\right)& n_{\mathrm{Sta}}-2\mathrm{tr}\left(N^{-1}{N}_{\mathrm{Sta}}\right)+\mathrm{tr}{\left(N^{-1}{N}_{\mathrm{Sta}}\right)}^2\end{array}\right]\\ {\widehat{\theta }}_{2\times 1}=\left[\begin{array}{c}{\widehat{\sigma }}_{\mathrm{Iri}}^2\\ {\widehat{\sigma }}_{\mathrm{Sta}}^2\end{array}\right]W_{2\times 1}=\left[\begin{array}{c}{V}_{\mathrm{Iri}}^{\mathrm{T}}{P}_{\mathrm{Iri}}{V}_{\mathrm{Iri}}\\ V_{\mathrm{Sta}}^{\mathrm{T}}{P}_{\mathrm{Sta}}{V}_{\mathrm{Sta}}\end{array}\right]\end{array}$$

$n_{\mathrm{Iri}}$ and $n_{\mathrm{Sta}}$ represent the numbers of observations from the Iridium Next and Starlink systems, respectively. ${\widehat{\sigma }}_{\mathrm{Iri}}^2$ and ${\widehat{\sigma }}_{\mathrm{Sta}}^2$ denote the unit weight variance estimates for the Iridium Next and Starlink systems, respectively.

$$N=\left(G^{\mathrm{T}}{P}_{1}G\right)={G_{\mathrm{Iri}}}^{\mathrm{T}}{P}_{\mathrm{Iri},1}{G}_{\mathrm{Iri}}+{G_{\mathrm{Sta}}}^{\mathrm{T}}{P}_{\mathrm{Sta},1}{G}_{\mathrm{Sta}}=N_{\mathrm{Iri}}+N_{\mathrm{Sta}}$$

(20)

The solution to Equation (19) is given as:

$${\widehat{\theta }}_{2\times 1}=S_{2\times 2}^{-1}{W}_{2\times 1}$$

(21)

After obtaining ${\widehat{\sigma }}_{\mathrm{Iri}}^2$ and ${\widehat{\sigma }}_{\mathrm{Sta}}^2$, the weights of the observations from the two systems are readjusted to derive the weight matrix $P_2$:

$$P_2=\left[\begin{array}{cc}{P}_{\mathrm{Iri},2}& 0\\ 0& P_{\mathrm{Sta},2}\end{array}\right]=\left[\begin{array}{cc}{P}_{\mathrm{Iri},1}^{\mathrm{sel}}\cdot C/{\widehat{\sigma }}_{\mathrm{Iri}}^2& 0\\ 0& P_{\mathrm{Sta},1}^{\mathrm{sel}}\cdot C/{\widehat{\sigma }}_{\mathrm{Sta}}^2\end{array}\right]$$

(22)

where $C$ is a constant.

3.5. IGG-III Equivalent Weight Function

Because HVCE lacks robustness, the presence of outliers in the observation data can lead to significant deviations in the estimates and even cause divergence in the solution process. To enhance the model’s robustness, this study incorporates a robust estimation mechanism that constructs an equivalent weight matrix to assign reduced weights to outliers and eliminate them when necessary. This process effectively mitigates the impact of outliers.

Commonly used equivalent weight functions include the Huber, Tukey, Hampel, Andrews, and IGG-III schemes. A comparison of these equivalent weight functions is presented in the table below [32,33,34]. Among them, $k$, $k_0$, $k_1$ are empirical robustness parameters that determine the robustness and estimation efficiency of the robust scheme, $v_i$ represents the residual of the corresponding observation, and $\sigma$ denotes the variance factor, defined as:

$$\sigma =1.483\cdot \mathrm{med}\left(\left|\left(v-\mathrm{med}\left(v\right)\right)\right|\right)$$

(23)

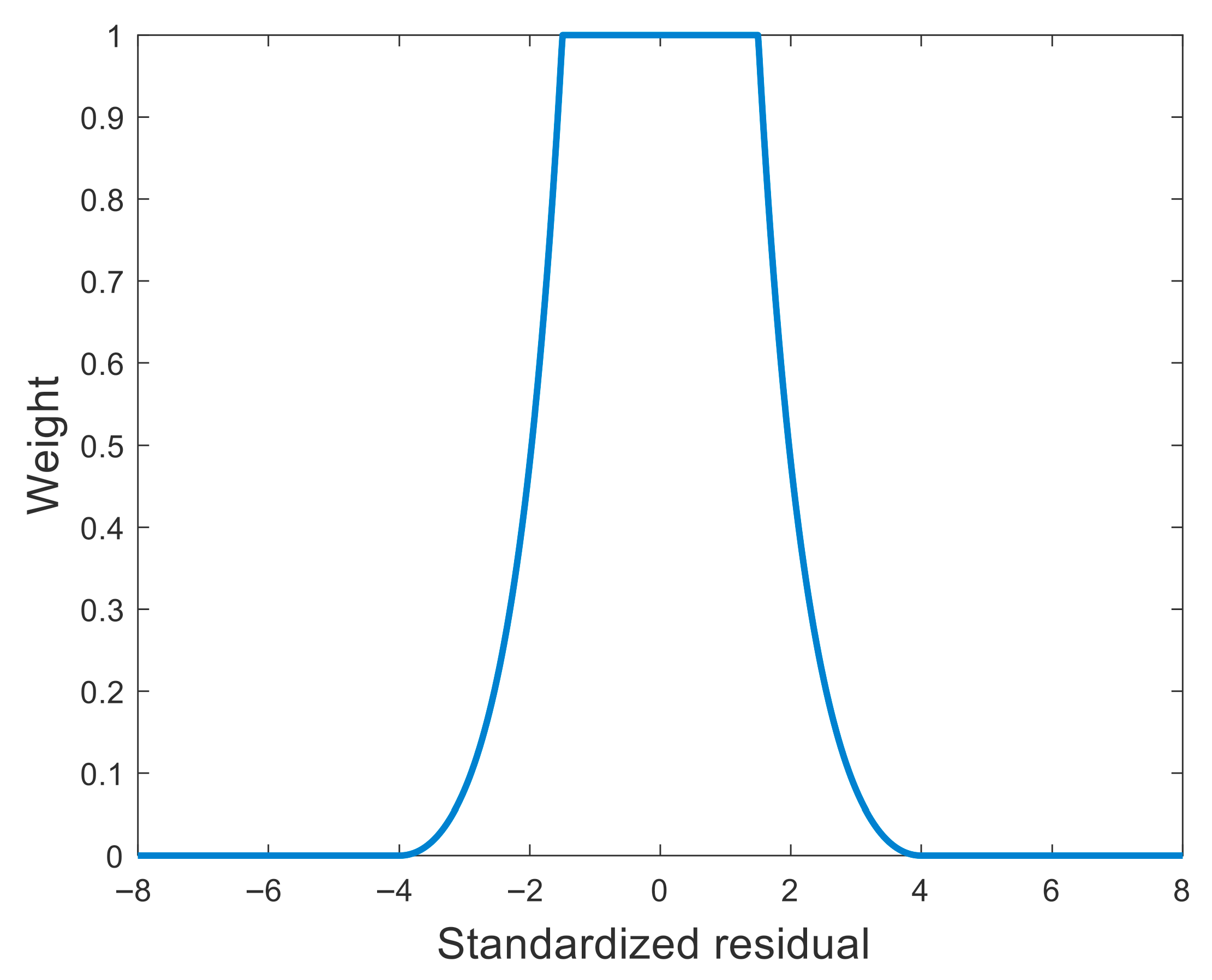
As shown in

Table 1. Equivalent Weight Functions of Robust Schemes.

Scheme	Function	Parameter
Huber	${\overline{\rho }}_i=\left\{\begin{array}{ll}1\hfill & \left|v_i\right|<k\sigma \hfill \\ {\displaystyle \frac{k\sigma }{\left|v_i\right|}}\hfill & \left|v_i\right|\ge k\sigma \hfill \end{array}\right.$	$k=1.345$
Tukey	${\overline{\rho }}_i=\left\{\begin{array}{ll}{\left|1-{\left|{\displaystyle \frac{v_i}{k}}\right|}^2\right|}^2\hfill & \left|v_i\right|<k\sigma \hfill \\ 0\hfill & \left|v_i\right|\ge k\sigma \hfill \end{array}\right.$	$k=4.685$ 1
Andrews	${\overline{\rho }}_i=\left\{\begin{array}{ll}\sin \left(v_i/k\sigma \right)/\sin \left(v_i/k\sigma \right)\hfill & \left|v_i\right|\le k\pi \sigma \hfill \\ 0\hfill & \left|v_i\right|>k\pi \sigma \hfill \end{array}\right.$	$k=1.339$
IGG-III	${\overline{\rho }}_i=\left\{\begin{array}{ll}1\hfill & \left|v_i\right|\le k_0\sigma \hfill \\ {\displaystyle \frac{k_0}{\left|v_i\right|}}\cdot {\left({\displaystyle \frac{k_1-\left|v_i\right|}{k_1-k_0}}\right)}^2\hfill & k_0\sigma \le \left|v_i\right|<k_1\sigma \hfill \\ 0\hfill & \left|v_i\right|\ge k_1\sigma \hfill \end{array}\right.$	$\begin{array}{l}{k}_0=1.0\sim 2.0\\ k_1=2.5\sim 3.5\end{array}$

¹ Empirical robust parameter.

, the Huber scheme is a two-segment weight function that consists of a retained-weight zone and a reduced-weight zone but lacks a zero-weight zone, resulting in relatively low robustness efficiency. The Tukey and Andrews schemes also employ a two-segment structure with reduced-weight and zero-weight zones but no retained-weight zone, which limits the utilization of valid observational information. In contrast, the IGG-III scheme is a three-segment function incorporating retained-weight, reduced-weight, and zero-weight zones (as illustrated in Figure 2), achieving a better balance between robustness efficiency and the use of valid information. Therefore, this study adopts the IGG-III equivalent weight function as the implementation scheme for robust estimation. In this study, the threshold parameters of the IGG-III weight function are set to $k_0=1.6$ and $k_1=2.8$, following commonly used empirical values reported in the literature and further refined through adjustment based on the characteristics of the collected observation data [34].

The variance factors ${\sigma }_{\mathrm{Iri}}$ and ${\sigma }_{\mathrm{Sta}}$ are estimated, respectively, based on the residuals of the Iridium Next and Starlink systems, and are substituted into the IGG-III equivalent weight function to construct the individual weight matrices ${\overline{\rho }}_{\mathrm{Iri}}$ and ${\overline{\rho }}_{\mathrm{Iri}}$ for the Iridium Next and Starlink systems. Finally, the two are combined to form the robustly processed weight matrix $P_3$:

$$P_3=\left[\begin{array}{cc}{P}_{\mathrm{Iri},3}& 0\\ 0& P_{\mathrm{Sta},3}\end{array}\right]=\left[\begin{array}{cc}{P}_{\mathrm{Iri},2}\cdot {\overline{\rho }}_{\mathrm{Iri}}& 0\\ 0& P_{\mathrm{Sta},2}\cdot {\overline{\rho }}_{\mathrm{Sta}}\end{array}\right]$$

(24)

4. Experimental Results and Analysis

This section validates the proposed algorithm using real Starlink and Iridium NEXT satellite signals. A brief description of the platform for receiving and processing these signals is provided, followed by positioning experiments and an analysis of the algorithm’s performance.

4.1. Experimental Scenario Setup

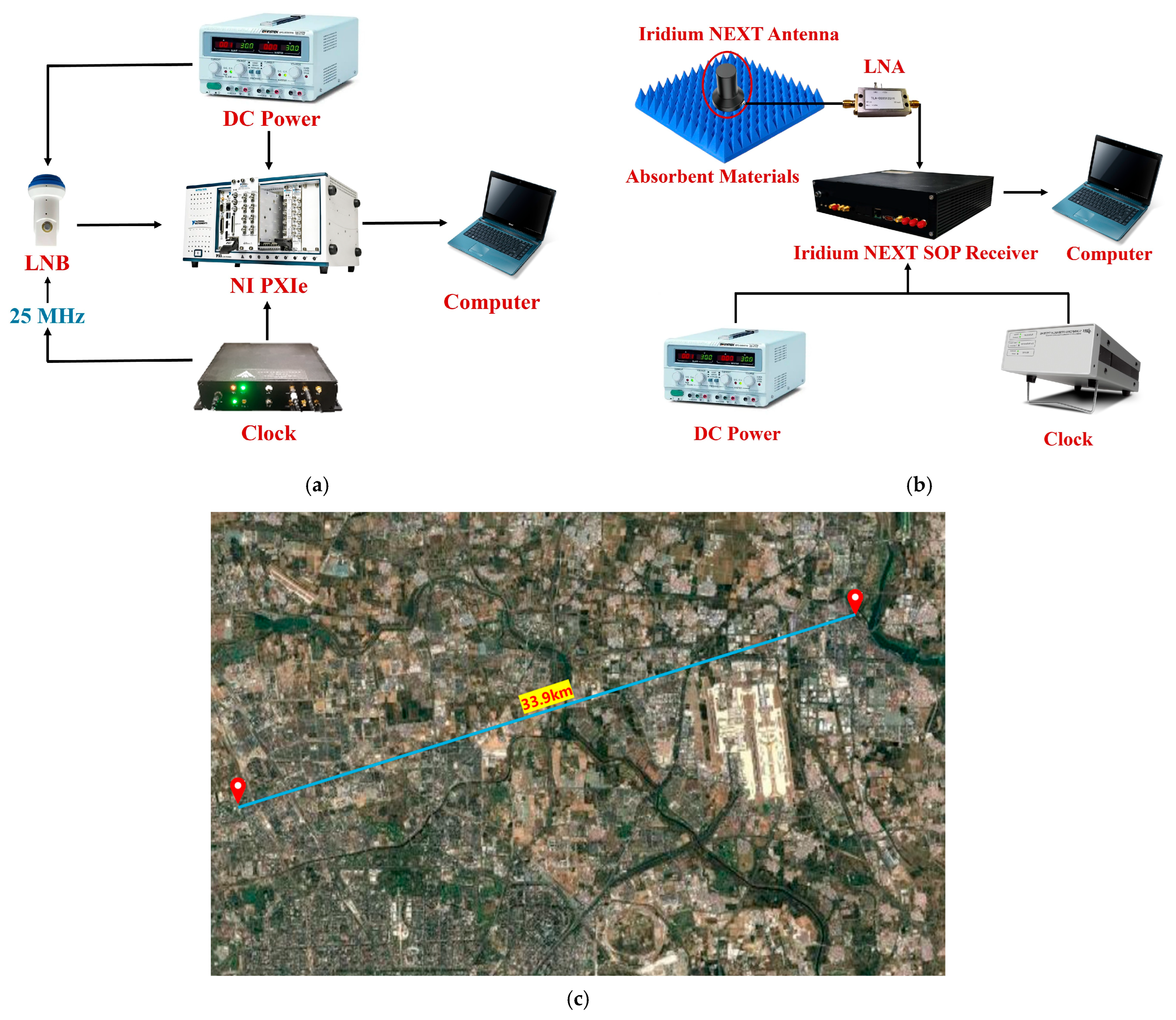
The Starlink signal acquisition platform, as illustrated in Figure 3a, primarily consists of a Ku-band Low-Noise Block (LNB), signal acquisition equipment, a timing clock, a DC power supply, and a workstation (laptop computer). The LNB is used to receive Starlink signals, operating within the frequency range of 10.7–12.75 GHz, with a half-power beamwidth of ±20°. The signal acquisition unit is an NI PXIe-5644R (National Instruments Corporation, Austin, Texas, United States), the clock is provided by a GNSS timing receiver, and the laptop is used to estimate the frequency of the Starlink signals.

The Iridium NEXT signal acquisition platform, as illustrated in Figure 3b, primarily consists of an Iridium NEXT antenna, a custom-built Iridium NEXT signal receiver, a timing clock, a DC power supply, and a workstation (laptop computer). The receiver was developed in-house, the clock is provided by a GNSS timing receiver, and the laptop is used to estimate the frequency of the Iridium NEXT signals. Additionally, as shown in Figure 3b, absorbing materials were placed around the antenna to mitigate multipath interference, and a Low Noise Amplifier (LNA) was connected between the antenna and the receiver to reduce noise effects.

In the experiment, the reference station was located on the rooftop of Building D at No. 9 Dengzhuang South Road, Haidian District, Beijing, with coordinates (40.0709° N, 116.2743° E). The user was positioned at Constitution Square in Shunyi District, Beijing, with coordinates (40.1435° N, 116.6756° E). The baseline length between the two sites was approximately 33.9 km, as illustrated in Figure 3c.

4.2. Experimental Positioning Results

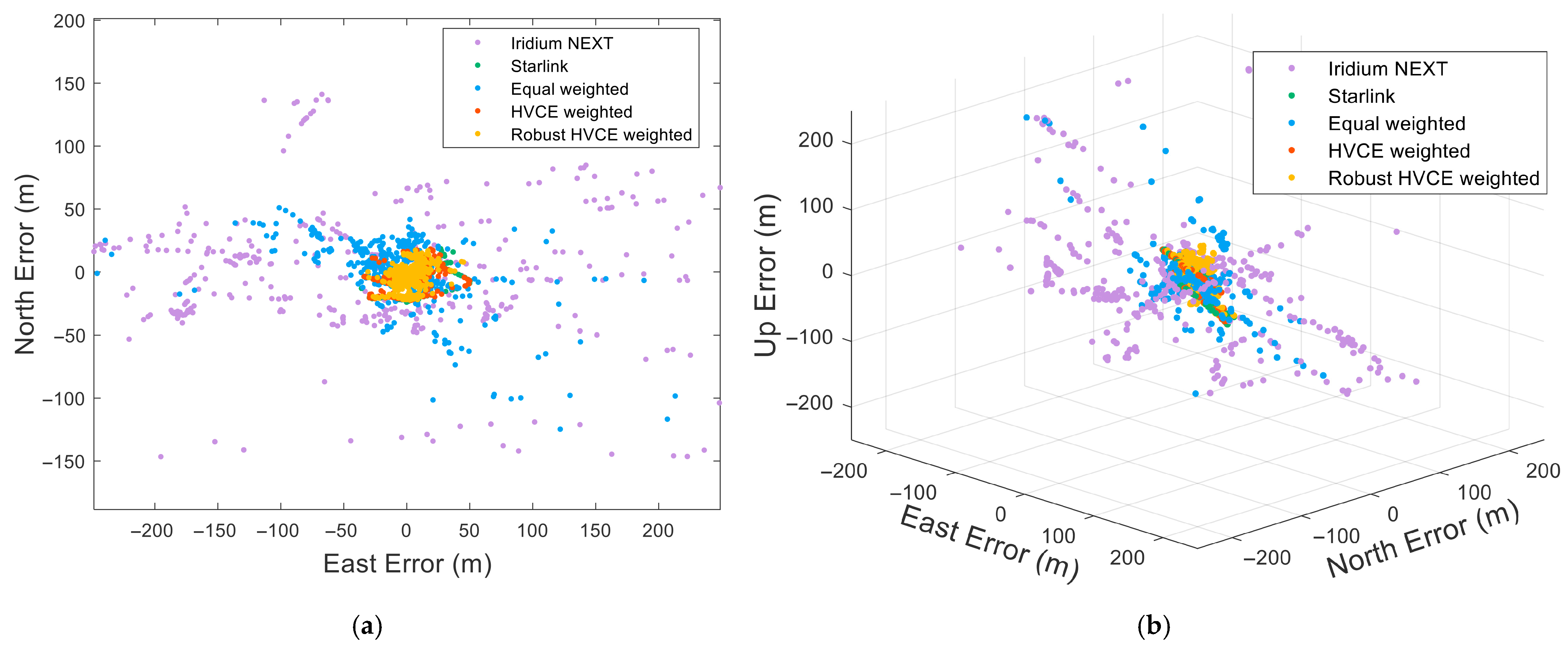
The performance of the proposed algorithm is evaluated using frequency observations obtained from real satellite signals. A positioning experiment was conducted over the 33.9 km baseline described earlier, using Starlink signals at 12.45 GHz and Ring Alert signals from Iridium NEXT operating at 1626.270833 MHz. The experiment lasted for approximately six hours, during which Doppler frequency measurements were continuously collected. The successfully acquired observations at each epoch were uniformly grouped into 500 data sets of 10 min each to assess the positioning performance. High-precision GNSS positioning results served as the reference, and the Root Mean Square Errors (RMSE) for the Two-Dimensional (2D) and Three-Dimensional (3D) positioning results were computed to evaluate algorithm accuracy. The satellite observation geometry and positioning results are shown in Figure 4 and Figure 5, respectively, and the detailed numerical results are summarized in

Table 2. Comparison of positioning performance for different algorithms.

Positioning Algorithm	Average Number of Observed Satellites	2D RMSE (m)	3D RMSE (m)
Iridium NEXT	3.5	212.636	256.820
Starlink	8.5	20.084	30.209
Equal weighted	12.0	63.211	75.000
HVCE weighted	12.0	18.071	27.738
Robust HVCE weighted	12.0	12.824	23.230

.

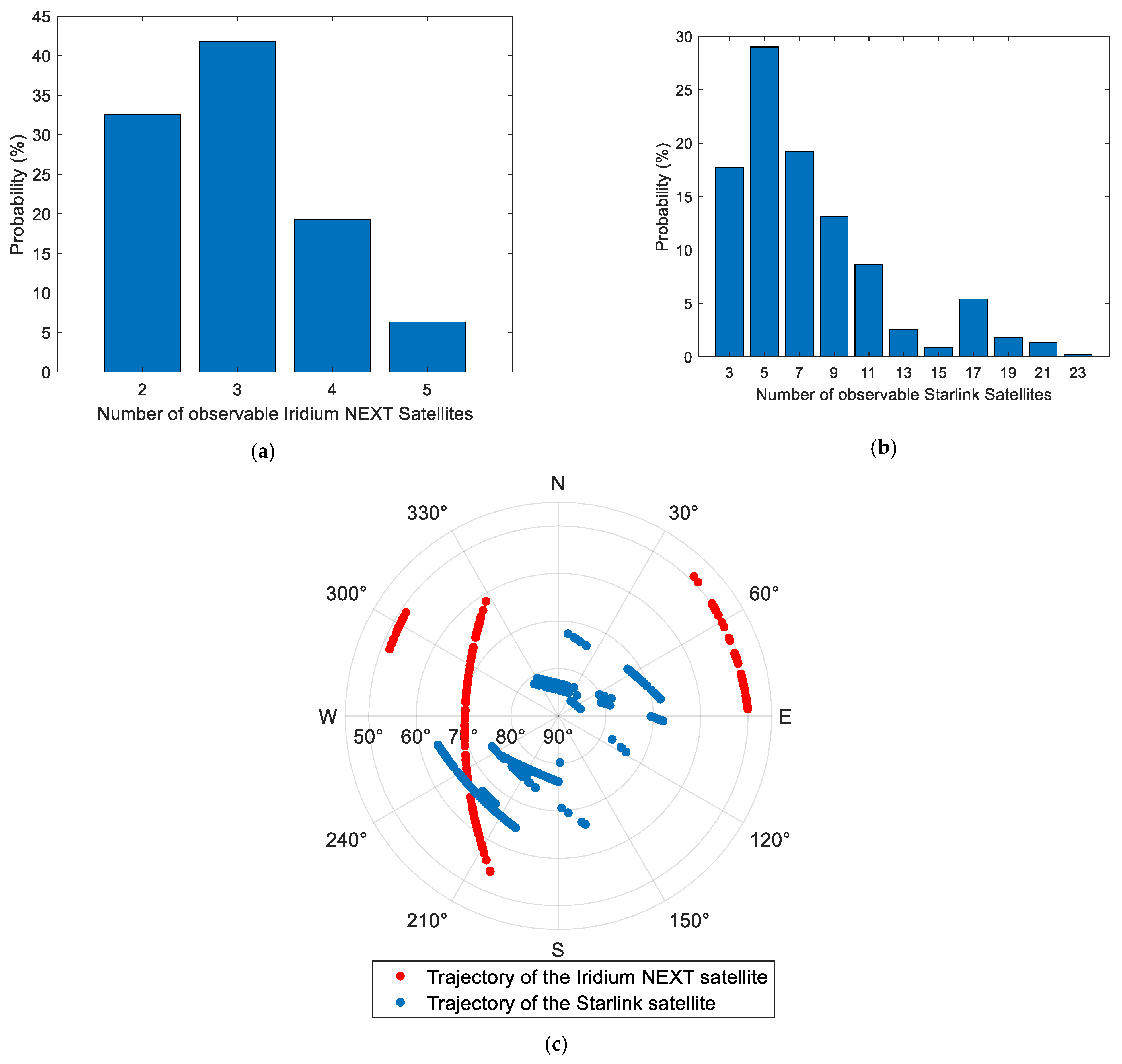
As shown in Figure 4a,b, within a 10 min observation period, signals from at least two Iridium NEXT satellites and three Starlink satellites can be received. As presented in Table 2, compared with a single LEO constellation, dual LEO constellations significantly increase the number of visible satellites, with an average of 12 satellites observed. Such an increase effectively improves the spatial geometry of the observed satellites, as illustrated in Figure 4c.

As shown in Figure 5 and Table 2, Doppler positioning with Iridium NEXT yields the lowest accuracy. The equal-weighted combination with Starlink performs better, while the weighted positioning algorithm based on the Robust HVCE model achieves the highest accuracy. Doppler positioning using Starlink signals results in relatively small errors. However, when these signals are combined with Iridium NEXT signals using equal weights, the substantial accuracy disparity between the two constellations causes the Iridium NEXT observations, which have higher noise levels, to disproportionately influence the final solution. This reduces the overall positioning accuracy to a level inferior to that achieved using Starlink alone. By determining the weights of Iridium NEXT and Starlink observations through HVCE, the positioning accuracy is enhanced relative to both single-constellation solutions and equal-weighted integration. The Robust HVCE model further improves positioning accuracy over standard HVCE weighting by effectively mitigating the impact of outliers. Overall, the proposed algorithm achieves 12.8 m 2D positioning accuracy and 23.2 m 3D positioning accuracy, delivering at least a 29% improvement over the HVCE-weighted positioning algorithm.

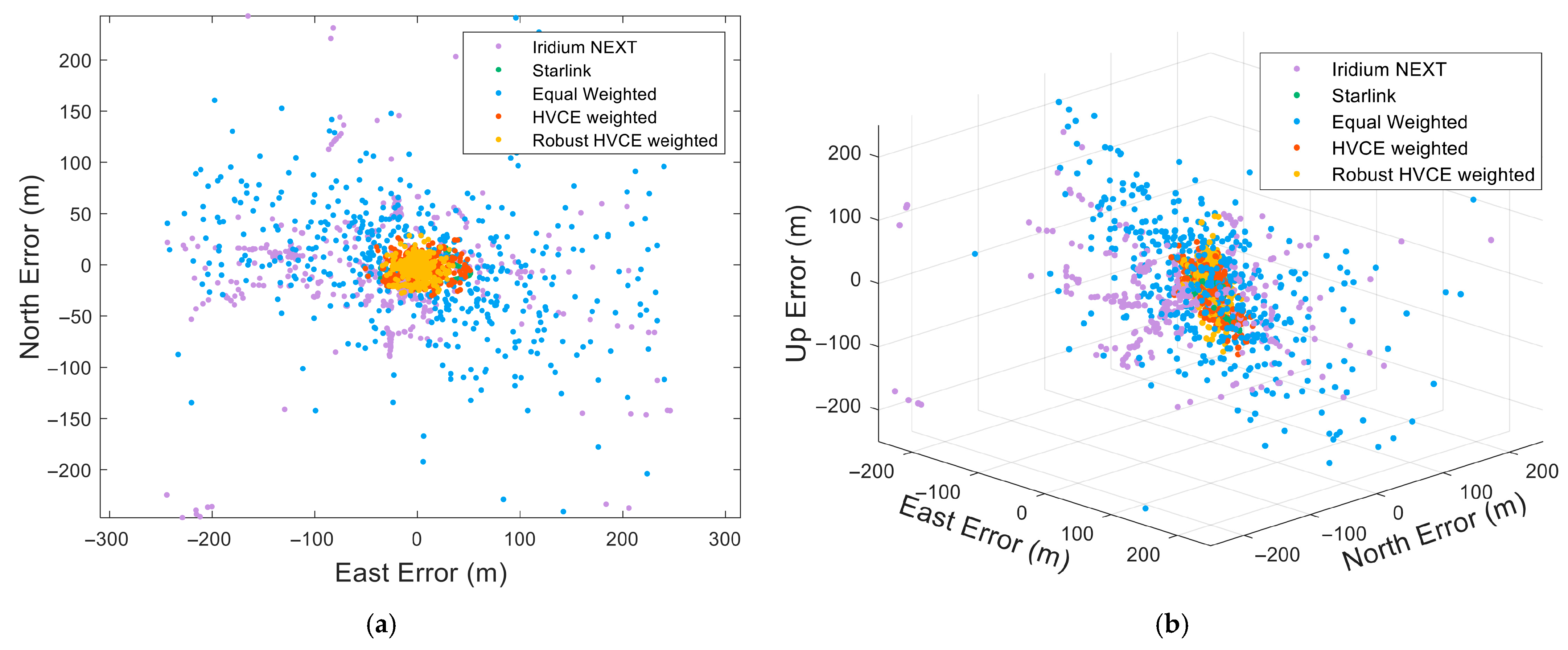
In addition, to further examine the robustness of the proposed method under controlled outlier conditions, an additional experiment was performed. Specifically, we randomly selected 5% of the Doppler observations and introduced simulated outliers with perturbations of ±100 Hz, which were randomly assigned to both Iridium NEXT and Starlink measurements.

As illustrated in Figure 6 and

Table 3. Comparison of positioning performance for different algorithms with added outliers.

Positioning Algorithm	Average Number of Observed Satellites	2D RMSE (m)	3D RMSE (m)
Iridium NEXT	3.5	232.618	267.958
Starlink	8.5	25.713	35.830
Equal weighted	12.0	162.705	193.421
HVCE weighted	12.0	20.035	32.164
Robust HVCE weighted	12.0	13.793	27.147

, introducing outliers leads to distinct performance changes across algorithms. Iridium NEXT single-constellation positioning consistently attains the lowest accuracy and exhibits further error increases once outliers are present. Starlink single-constellation positioning achieves higher accuracy overall, yet its performance also declines under contaminated observations. The equal-weighted fusion is inherently influenced by the larger positioning errors associated with Iridium NEXT; adding outliers further steers the solution toward poorer accuracy. Conventional HVCE weighting shows a certain degree of stability, with only moderate increases in error; however, the proposed Robust HVCE consistently achieves the smallest errors and exhibits relatively small changes compared with the uncontaminated case, thereby demonstrating superior robustness to data contamination.

In summary, based on real experimental data, the proposed Robust HVCE method achieves the highest positioning accuracy compared with single-constellation, equal-weighted, and conventional HVCE solutions. Furthermore, when simulated outliers are introduced on top of the real data, the method is less affected by the outliers and consistently maintains the best positioning accuracy. The results demonstrate that the Robust HVCE method improves positioning accuracy by effectively suppressing and eliminating outliers, while maintaining strong robustness under contaminated observations.

5. Conclusions

This study develops a dual-constellation Doppler positioning framework for Iridium Next and Starlink SOPs. The framework integrates prior weighting based on satellite elevation, characteristic slope-based observation screening, HVCE, and the IGG-III robust weight function. Experimental results over a 33.9 km baseline show that the proposed method achieves 12.8 m 2D and 23.2 m 3D positioning accuracies. Compared to HVCE solutions, this represents improvements of 29% and 16% and outperforms both single-constellation and equal-weighted solutions. This work is the first to introduce Robust HVCE into SOP-based positioning with dual LEO constellations. It addresses redundant observations and geometric degradation through the characteristic slope mechanism, offering a feasible approach for adaptive weighting and outlier suppression under heterogeneous error conditions. Future work may include additional LEO constellations, such as OneWeb and Orbcomm, and incorporate heterogeneous observations such as pseudorange and carrier phase. These extensions will help further validate the applicability of Robust HVCE in more complex configurations. In addition, given the limited precision and infrequent updates of publicly available TLE data, analyzing the impact of ephemeris uncertainty on positioning performance warrants further attention. Building on this analysis, refining satellite orbital parameters during the estimation process may further enhance positioning accuracy.