Abstract
Monocular fisheye camera distance estimation is a crucial visual perception task for autonomous driving. Due to the practical challenges of acquiring precise depth annotations, existing self-supervised methods usually consist of a monocular distance model and an ego-motion predictor with the goal of minimizing a reconstruction matching loss. However, they suffer from inaccurate distance estimation in low-texture regions, especially road surfaces. In this paper, we introduce a weakly supervised learning strategy that incorporates semantic segmentation, instance segmentation, and optical flow as additional sources of supervision. In addition to the self-supervised reconstruction loss, we introduce a road surface flatness loss, an instance smoothness loss, and an optical flow loss to enhance the accuracy of distance estimation. We evaluate the proposed method on the WoodScape and SynWoodScape datasets, and it outperforms the self-supervised monocular baseline, FisheyeDistanceNet.
1. Introduction
Depth estimation is a vital problem in visual perception for autonomous driving. As distance measurement by LiDAR is sparse and costly [1], learning-based approaches have been developed to estimate distance from image sequences. However, most of the previous works [2,3] have focused on rectified images captured by pinhole cameras. Given the widespread adoption of surround-view fisheye cameras in modern vehicles, the importance of monocular depth estimation specifically tailored to fisheye imagery has grown substantially.
Supervised methods [4,5] rely on sparse LiDAR depth ground truth. In contrast, self-supervised methods [6,7,8] are based on the Structure-from-Motion (SfM) framework, which estimates distance and ego-motion from video sequence. Their loss function consists of an image reconstruction term and a depth smoothness term. The effectiveness of these approaches has been demonstrated on WoodScape dataset [9]. However, these methods have two limitations, as shown in Figure 1b. First, they crop the raw fisheye image and miss the distance estimation on image edges. Second, distance predictions on homogeneous regions are inaccurate.

Figure 1.
Results of distance estimation models on a fisheye image. (a) Rear-camera input image. (b) Distance map by FisheyeDistanceNet. (c) Distance map by our method.
In this paper, we propose a weakly supervised learning framework for monocular fisheye distance estimation. First, semantic and instance segmentation labels are adopted to penalize flatness of the road surface region and smoothness within objects. Second, to improve the estimation accuracy, optical flow results generated by a state-of-the-art flow network are used to guide the coordinate mapping between two images. Moreover, our method predicts all valid region of fisheye image without any information loss, as depicted in Figure 1c.
The remainder of this paper is structured as follows: Section 2 presents a review of related work. In Section 3, we revisit a self-supervised framework for monocular fisheye distance estimation. Section 4 details our proposed weakly supervised approach. Experimental results are provided in Section 5, and Section 6 concludes the paper.
2. Related Work
This section presents an overview of existing approaches for depth or distance estimation using monocular fisheye cameras. These methods are generally classified into self-supervised and supervised learning approaches, depending on the absence or presence of ground-truth depth labels.
Most of the current monocular distance estimation works are on the rectified KITTI [10] sequences. Structure-from-Motion (SfM) techniques [2,3] introduce self-supervised learning frameworks for estimating depth and ego-motion from pinhole camera video sequences with no manual labeling.
In the case of fisheye camera, Ravi Kumar et al. [7] developed a FisheyeDistanceNet within the SfM framework. Its training loss consists of an image reconstruction photometric error, an edge-aware distance smoothness term and a cross-sequence distance consistency term. It verified the validity of self-supervised method on WoodScape dataset. Afterwards, to improve the distance estimation accuracy of dynamic objects, thin structure, and homogeneous areas, SynDistNet [8] jointly learns semantic segmentation network and adopts the prediction to guide self-supervised distance estimation. Moreover, OmniDet [6] is another multi-task learning network designed for fisheye images, including depth estimation, semantic segmentation, motion segmentation, and object detection, and outperforms other single-task versions. In addition to the loss terms in FisheyeDistanceNet, OmniDet incorporate feature-metric losses from [11] to penalize the consistency of low-texture regions. However, these methods crop the raw fisheye image and miss the depth estimation of marginal areas. Moreover, Yan et al. [12] combined self-supervised depth estimation with knowledge distillation to handle the challenge of large homogeneous areas in indoor scenes. Zhao et al. [13] proposed a self-supervised method which replaces the pose network with real-scale pose information but relies on the ground-truth pose data from the KITTI-360 dataset [14].
In addition, Lee et al. [5] introduced a supervised fisheye depth estimation method, which represents distance in the slanted cylindrical layer to alleviate distortion of side camera image. Son et al. [4] presented a knowledge-distillation technique by using sparse LiDAR-depth ground truth for supervision. These supervised learning-based methods both rely on dense or sparse depth labels for training.
In this paper, we aim to improve the accuracy of self-supervised monocular distance estimation for fisheye images. Within our proposed weakly supervised learning framework, no ground-truth distance labels are used; instead, we incorporate semantic segmentation, instance segmentation, and optical flow labels as additional constraints.
3. Self-Supervised Distance Estimation Baseline
In this section, we review a self-supervised framework based on FisheyeDistanceNet [7] for monocular fisheye distance estimation. It is built within a self-supervised Structure-from-Motion (SfM) framework tailored for monocular fisheye imagery. It involves training two separate networks:
- A monocular depth predictor that generates a depth map for each pixel p in the target frame .
- A pose estimation network predicting a 6-DoF camera transformation between the target frame and a reference frame .
The loss function used for self-supervised learning comprises two components: a reconstruction loss , which calculates the photometric discrepancy between the reconstructed view and the original target frame , and an edge-aware smoothness loss for estimated distance . The total objective loss is computed as the average across image batches, spatial locations, and scales:
where is term weight factor.
Image reconstruction loss. Using the estimated distance at time t and the camera intrinsic parameters, pixel set in can be unreprojected to a 3D point cloud , stated as
where denotes the unreprojection operation that transforms image coordinates into the camera’s 3D coordinate, as explained in [7]. Using the predicted pose transformation from the pose estimation network, the point cloud under the camera coordinate at time is calculated as . By projecting from camera to image coordinates at time , a mapping from to is obtained as
By warping the source frame , we reconstruct an image .
The image reconstruction loss between the reconstructed image and the target frame is computed by combining the L1 loss and the Structural Similarity Index (SSIM) [15], stated as
where , is the binary mask, and ⊙ denotes element-wise multiplication. is used to filter out invalid mapping regions and pixels that do not change their appearance between frames, which helps to remove effect of low-texture regions.
Additionally, large photometric cost between reconstructed and target images may arise in regions with brightness variations, occlusions and dynamic objects. To mitigate the impact of large photometric of some pixels, which are treated as outliers, errors larger than are clipped to zero gradient.
Edge-aware smoothness loss. To regularize distance for low-gradient regions, smoothness term is defined as
where denotes the mean normalization of to shrink distance.
4. Weakly Supervised Distance Estimation
In this section, we describe our weakly supervised method for distance estimation using monocular fisheye camera. We adopt SfM framework, which is the same with the self-supervised baseline. In contrast, our objective loss consists of a reconstruction term , which is defined the same with the baseline, a road surface flatness term , which is obtained using semantic labels, an instance smoothness term for estimated distance using instance segmentation labels, and an optical flow error term . All these terms are computed as the average across image batches, spatial locations, and scales. The total objective loss is
where , , and are term weight factors. The pipeline of our method is shown in Figure 2.
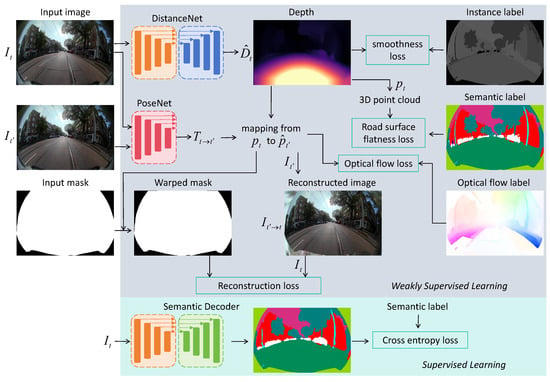
Figure 2.
The pipeline of our proposed weakly supervised learning framework for monocular fisheye camera distance estimation.
4.1. Road Surface Flatness Loss
Road surface is a category that almost always appears in semantic segmentation labels of autonomous driving scene images and often has only a single instance. As road surface regions are low-texture in raw images, it is hard to accurately estimate distance for these pixels by optimizing image reconstruction loss. Moreover, as the depth of the road surface varies drastically from near to far, smoothness loss measuring gradient of estimated distance is not suitable. In order to regularize the distance of road surface pixels, we consider penalizing their corresponding 3D point cloud to a flat surface.
By Equation (2), a 3D point set is obtained from image coordinates and estimated distance . A 3D point is on a plane, if it satisfies , where is plane parameter. Since is unknown, we first estimate them from the 3D point cloud before computing the point-to-plane distance errors for each 3D point. Given a set of 3D points whose labels are road surface, we can solve the plane parameter by solving a linear least-square problem,
where is the binary mask of road surface pixels, generated from semantic segmentation annotations. Thus, we define the road surface flatness loss to penalize road surface point cloud to a single plane by the L1 residual error,
Due to the correlation between and , calculating gradients for becomes numerically unstable. To address this, we detach from the computational graph during training, effectively stopping gradient back-propagation through this variable.
4.2. Instance Smoothness Loss
As depths of pixels from the same objects vary smoothly, we regularize distance for every instance regions separately. Given the instance segmentation label, we can first calculate an instance division map . If pixels , , and in are from the same instance, ; otherwise, . Thus, we define the instance smoothness term as
where is the mean-normalization of .
4.3. Optical Flow Loss
To further improve the accuracy of distance estimation, state-of-the-art optical flow approaches can provide constraint for mapping from pixel set in to projecting coordinates at time . Additionally, the optical flow constraint can compensate for the reconstruction term’s limitations in aligning dynamic objects. In our method, pretrained model FlowFormer [16] is adopted to obtain optical flow labels . Thus, the optical flow loss is defined by L1 loss as
where is calculated by Equation (3). Moreover, as the optical flow labels generated by existing model are sometimes not accurate in some low-texture regions, to mitigate the impact of error labels, L1 error larger than 3.0 for each pixel is clipped to zero gradient.
4.4. Implementation Details
Following previous works [6,8], training distance estimation along with semantic segmentation in a multi-task framework simultaneously improves the performance of a single self-supervised distance estimation network. The distance estimation network, pose estimation network, and semantic segmentation network are all based on an encoder–decoder architecture. ResNet18 [17] is chosen as the encoder in the baseline and our approach. The network details of distance estimation and pose estimation network are the same with FisheyeDistanceNet [7]. The semantic segmentation and the distance estimation network share the same encoder. Layers of semantic segmentation decoder are similar to corresponding ones in distance estimation decoder expect the predicting head.
We employ Adam [18] optimizer for training with a learning rate of . The model is trained for 100 epochs with a batch size of 24 on an RTX 3090 GPU, requiring approximately 10 h to complete training. The input resolution of the fisheye image is pixels. Different from previous works which crop the original fisheye image to remove regions of vehicle’s body, to preserve more valid regions, we use a binary mask obtained from semantic segmentation annotation. The mask is used to calculate in Equation (4).
5. The Experimental Verification
5.1. Datasets
WoodScape dataset [9]. The WoodScape dataset contains real-world 8234 images obtained with four surround-view fisheye cameras from driving scenes. It contains raw images of two consecutive frames, vehicle speed, and time interval, which can be used to predict ego-motion. In addition, it consists of instance and semantic segmentation annotations. However, depth estimation ground truth is not available. The dataset is split into a training set of 8029 images and a test set of 205 images.
SynWoodScape dataset [19]. The SynWoodScape dataset is a synthetic counterpart of the real-world WoodScape dataset, maintaining nearly identical semantic class distributions across urban driving scenarios. It provides 2000 pairs of synthetic fisheye images along with corresponding depth ground truth for four surrounding views.
5.2. Quantitative Evaluation
We adopt the depth estimation accuracy metrics provided in [20], which are used as a standard in some previous works [5,7]. The metrics contain the mean absolute relative error (Abs Rel), the root mean square relative error (Sq Rel), the root mean square error (RMSE), the root mean square log error (RMSE log), and the -accuracy.
Since the WoodScape dataset contains 8234 real-world images but lacks depth ground truth, and the SynWoodScape dataset contains a smaller number of synthetic images with ground truth, we aim to evaluate the prediction accuracy of the depth estimation model while ensuring its generalization ability across different datasets. Therefore, in the quantitative evaluation experiments, we merge the two datasets for training and testing. The training set consists of 8029 images from the WoodScape dataset and 1800 randomly selected images from the SynWoodScape dataset. The testing set comprises the remaining 200 images from the SynWoodScape dataset, which include depth ground truth.
Since the self-supervised models [6,8,21] for fisheye images lack open-source implementations, our comparative analysis uses FisheyeDistanceNet [7] as the primary baseline, based on the authors’ released code. Additionally, we present the results of the proposed method with certain loss terms removed. To ensure fairness, the network architecture and training details for each method are identical, except for the differences in the loss functions. The depth estimation evaluation metrics are presented in Table 1. Our proposed instance smoothness term achieves smaller depth estimation errors compared to FisheyeDistanceNet’s edge-aware smoothness term. Comparing the second and fourth rows in Table 1, the addition of the road surface flatness term slightly reduces depth estimation accuracy. This performance trade-off likely stems from the fact that real-world road surfaces are not perfectly planar. However, the flatness constraint remains essential to prevent significant distance estimation errors along the road surface, ensuring reasonable depth prediction consistency for road areas. Furthermore, the addition of the optical flow term further improves the accuracy of depth estimation.

Table 1.
Quantitative results on SynWoodScape dataset. Note: The arrows ↓ and ↑ indicate that smaller values are better and larger values are better, respectively. The bold values indicate the optimal results.
5.3. Qualitative Evaluation
In qualitative evaluation, we compare our method with FisheyeDistanceNet, as well as our method with certain loss term removed. In Figure 3, all models are trained and evaluated on the WoodScape dataset. The figure presents experimental results from four real-world scenes, shown from left to right. In the first and fourth examples, when the fisheye camera is mounted at the front and rear of the vehicle, FisheyeDistanceNet tends to incorrectly predict nearby ground regions as being at a farther distance. In contrast, our method effectively corrects this issue by jointly leveraging the instance smoothness loss and road surface flatness loss. Comparing Figure 3b,c, our instance smoothness loss achieves smoother depth estimations within each instance compared to the edge-aware smoothness loss used in FisheyeDistanceNet. Furthermore, as shown in Figure 3e,f, the optical flow loss further refines the depth estimation results.

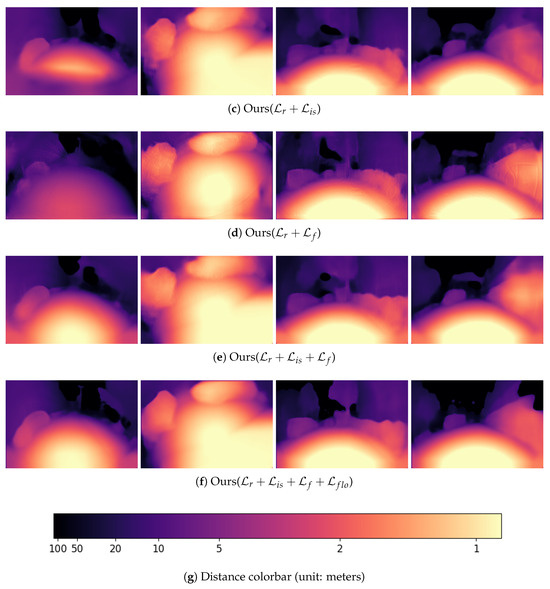
Figure 3.
Qualitative results on the WoodScape dataset.
In Figure 4, both our method and FisheyeDistanceNet are trained on the combined WoodScape and SynWoodScape datasets and evaluated on the SynWoodScape test set. Our method produces depth estimation results that are closer to the ground truth compared to FisheyeDistanceNet. However, it still shows limited accuracy on some fine-scale objects. The limited training data results in inadequate representation of fine-scale objects that infrequently occur in road environments, consequently causing degraded prediction performance for these under-represented categories.

Figure 4.
Qualitative results on the SynWoodScape dataset. Depth map color scale is the same as in Figure 3.
6. Conclusions
In this paper, a weakly supervised learning framework for monocular fisheye distance estimation is proposed. First, to ensure accurate depth estimation in low-texture road surface regions, a planar constraint is introduced on the 3D point cloud of the ground area. Second, instance segmentation labels are used to enforce smoothness in depth estimation within each instance. Third, optical flow fields generated by a state-of-the-art optical flow estimation model are incorporated to further enhance image registration accuracy. By integrating these constraints into the loss function, our method achieves more accurate depth estimation compared to self-supervised approaches on both real-world and synthetic datasets. However, depth estimation accuracy for fine-grained objects still has room for improvement, particularly for low-frequency categories that lack sufficient training samples. Future work will address this through targeted dataset expansion to better represent these under-represented objects.
Author Contributions
Conceptualization, Z.Z.; methodology, Z.Z.; software, Z.Z.; validation, Z.Z. and X.Y.; formal analysis, Z.Z.; investigation, Z.Z.; resources, Z.Z.; data curation, X.Y.; writing—original draft preparation, Z.Z.; writing—review and editing, Z.Z.; visualization, Z.Z.; supervision, Z.Z.; project administration, Z.Z.; funding acquisition, Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the National Natural Science Foundation of China (Grant No. 62303216). Project funded by the China Postdoctoral Science Foundation (Grant No. 2023M731647).
Data Availability Statement
Code is available at https://github.com/zhihao0512/weakly-supervised-fisheye-distance (accessed on 26 July 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gunes, U.; Turkulainen, M.; Ren, X.; Solin, A.; Kannala, J.; Rahtu, E. FIORD: A fisheye indoor-outdoor dataset with LIDAR ground truth for 3D scene reconstruction and benchmarking. arXiv 2025, arXiv:2504.01732. [Google Scholar] [CrossRef]
- Zhou, T.; Brown, M.; Snavely, N.; Lowe, D.G. Unsupervised learning of depth and ego-motion from video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1851–1858. [Google Scholar]
- Godard, C.; Mac Aodha, O.; Firman, M.; Brostow, G.J. Digging into self-supervised monocular depth estimation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3828–3838. [Google Scholar]
- Son, E.; Choi, J.; Song, J.; Jin, Y.; Lee, S.J. Monocular Depth Estimation from a Fisheye Camera Based on Knowledge Distillation. Sensors 2023, 23, 9866. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Cho, G.; Park, J.; Kim, K.; Lee, S.; Kim, J.-H.; Jeong, S.-G.; Joo, K. Slabins: Fisheye depth estimation using slanted bins on road environments. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2–6 October 2023; pp. 8765–8774. [Google Scholar]
- Kumar, V.R.; Yogamani, S.; Rashed, H.; Sitsu, G.; Witt, C.; Leang, I.; Milz, S.; Mäder, P. Omnidet: Surround view cameras based multi-task visual perception network for autonomous driving. IEEE Robot. Autom. Lett. 2021, 6, 2830–2837. [Google Scholar] [CrossRef]
- Kumar, V.R.; Hiremath, S.A.; Bach, M.; Milz, S.; Witt, C.; Pinard, C.; Yogamani, S.; Mäder, P. FisheyeDistanceNet: Self-supervised scale-aware distance estimation using monocular fisheye camera for autonomous driving. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 574–581. [Google Scholar]
- Kumar, V.R.; Klingner, M.; Yogamani, S.; Milz, S.; Fingscheidt, T.; Mäder, P. SynDistNet: Self-supervised monocular fisheye camera distance estimation synergized with semantic segmentation for autonomous driving. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 5–9 January 2021; pp. 61–71. [Google Scholar]
- Yogamani, S.; Hughes, C.; Horgan, J.; Sistu, G.; Varley, P.; O’Dea, D.; Uricár, M.; Milz, S.; Simon, M.; Amende, K.; et al. Woodscape: A multi-task, multi-camera fisheye dataset for autonomous driving. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 9308–9318. [Google Scholar]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets robotics: The KITTI dataset. Int. J. Robot. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef]
- Shu, C.; Yu, K.; Duan, Z.; Yang, K. Feature-metric loss for self-supervised learning of depth and egomotion. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020; pp. 572–588. [Google Scholar]
- Yan, Q.; Ji, P.; Bansal, N.; Ma, Y.; Tian, Y.; Xu, Y. FisheyeDistill: Self-Supervised Monocular Depth Estimation with Ordinal Distillation for Fisheye Cameras. arXiv 2022, arXiv:2205.02930. [Google Scholar]
- Zhao, G.; Liu, Y.; Qi, W.; Ma, F.; Liu, M.; Ma, J. FisheyeDepth: A Real Scale Self-Supervised Depth Estimation Model for Fisheye Camera. arXiv 2024, arXiv:2409.15054. [Google Scholar]
- Liao, Y.; Xie, J.; Geiger, A. KITTI-360: A novel dataset and benchmarks for urban scene understanding in 2D and 3D. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 3292–3310. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Shi, X.; Zhang, C.; Wang, Q.; Cheung, K.C.; Qin, H.; Dai, J.; Li, H. Flowformer: A transformer architecture for optical flow. In Proceedings of the European Conference on Computer Vision (ECCV), Tel Aviv, Israel, 23–27 October 2022; pp. 668–685. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Kingma, D.P. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sekkat, A.R.; Dupuis, Y.; Kumar, V.R.; Rashed, H.; Yogamani, S.; Vasseur, P.; Honeine, P. SynWoodScape: Synthetic surround-view fisheye camera dataset for autonomous driving. IEEE Robot. Autom. Lett. 2022, 7, 8502–8509. [Google Scholar] [CrossRef]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth map prediction from a single image using a multi-scale deep network. Adv. Neural Inf. Process. Syst. 2014, 27, 2366–2374. [Google Scholar]
- Kumar, V.R.; Yogamani, S.; Bach, M.; Witt, C.; Milz, S.; Mäder, P. UnrectDepthNet: Self-supervised monocular depth estimation using a generic framework for handling common camera distortion models. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 8177–8183. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).