Fully DC Aggregation Topology with Power Self-Balancing Capacitors for Offshore Wind Power Transmission: Simulation Study
Abstract
1. Introduction
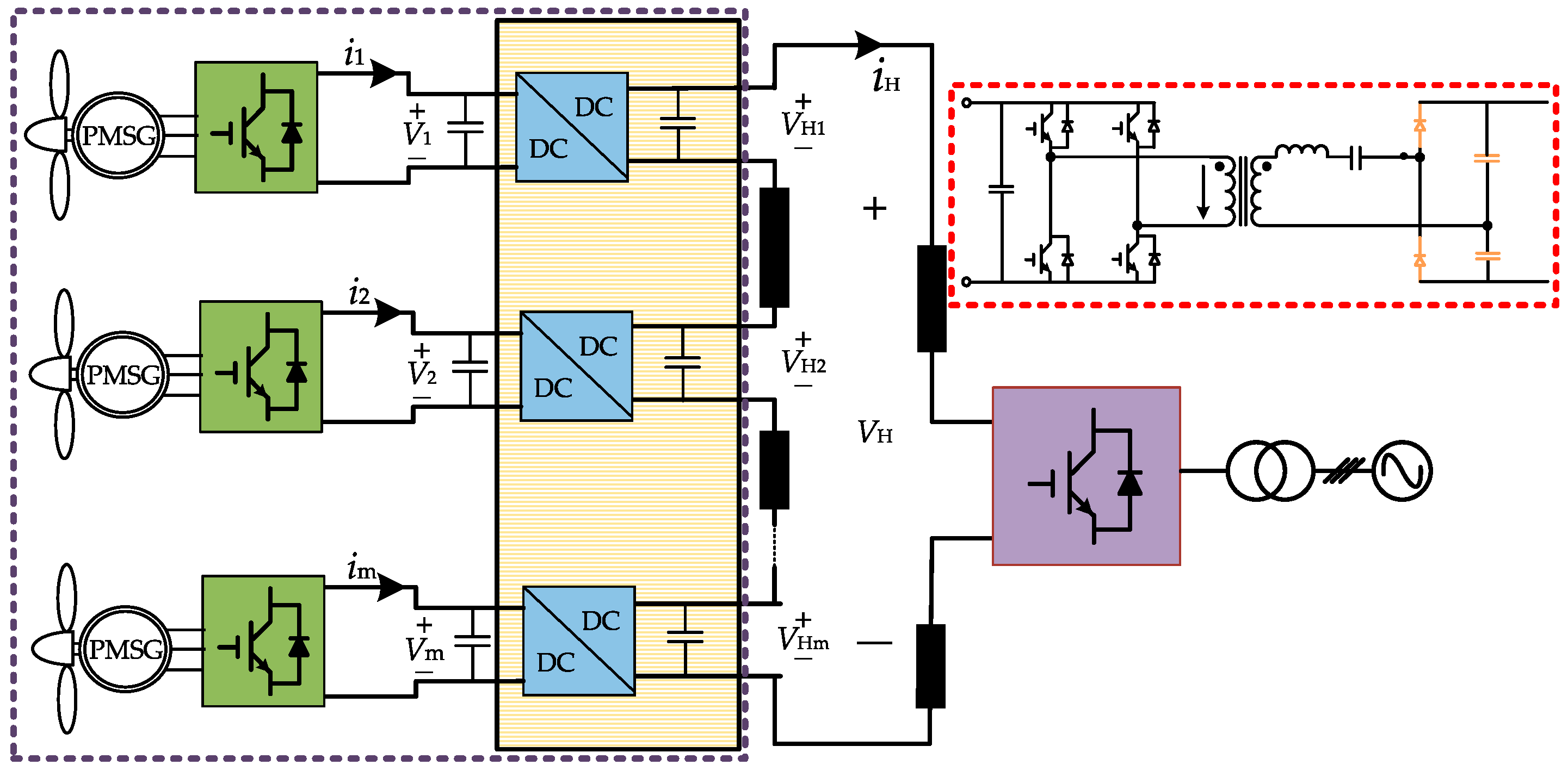
2. Proposed Topology and Operation
2.1. Topology Description
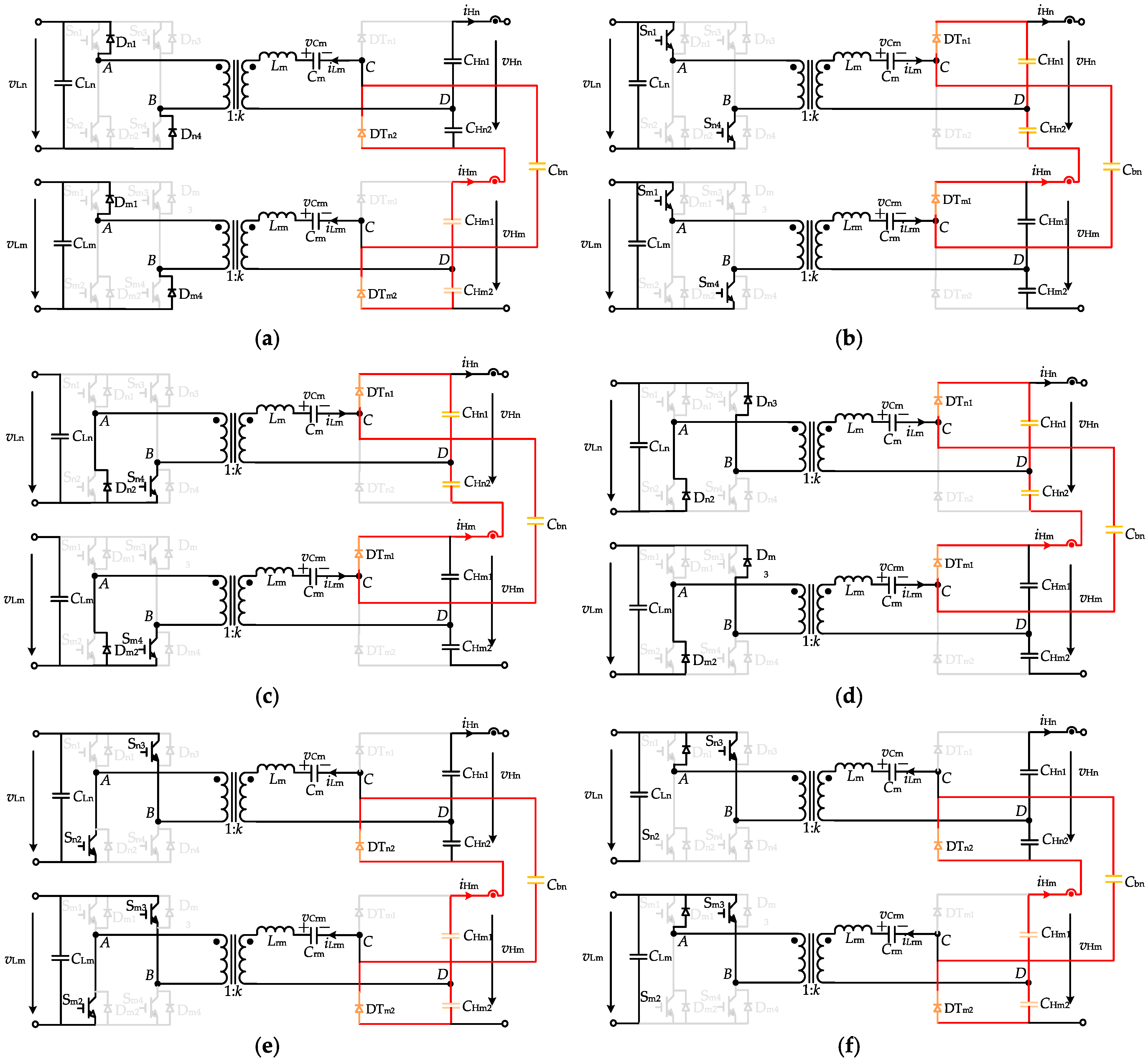
2.2. Operation Principle
- Operation principles and waveforms of the nth submodule within the proposed DC/DC topology.
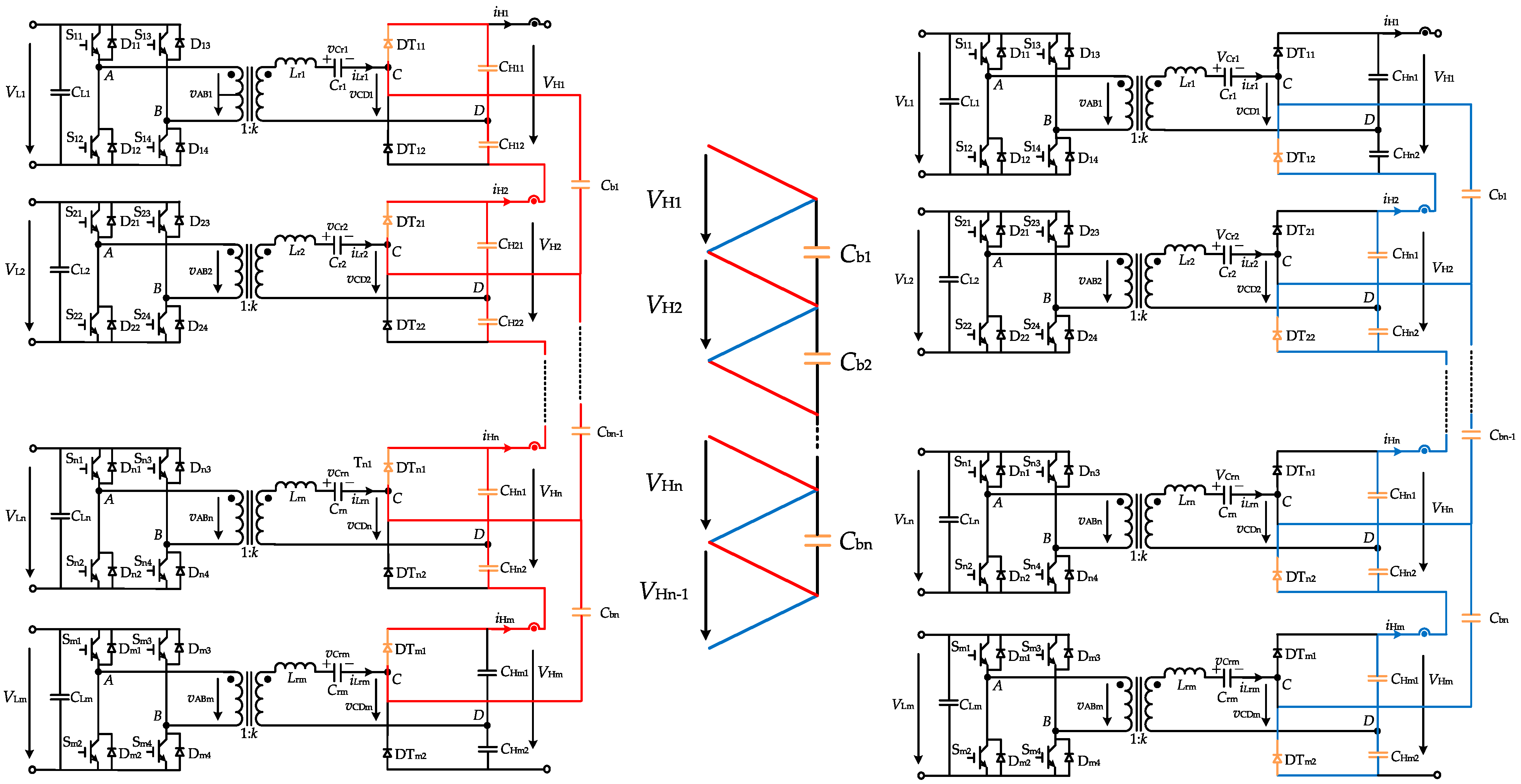
- Energy transfer between the nth and mth submodules via the power-balancing capacitor Cbn.
2.3. Power Balancing Principle
2.4. Soft-Switching Implementation
2.5. Performance Comparison with Other IIOS Converters
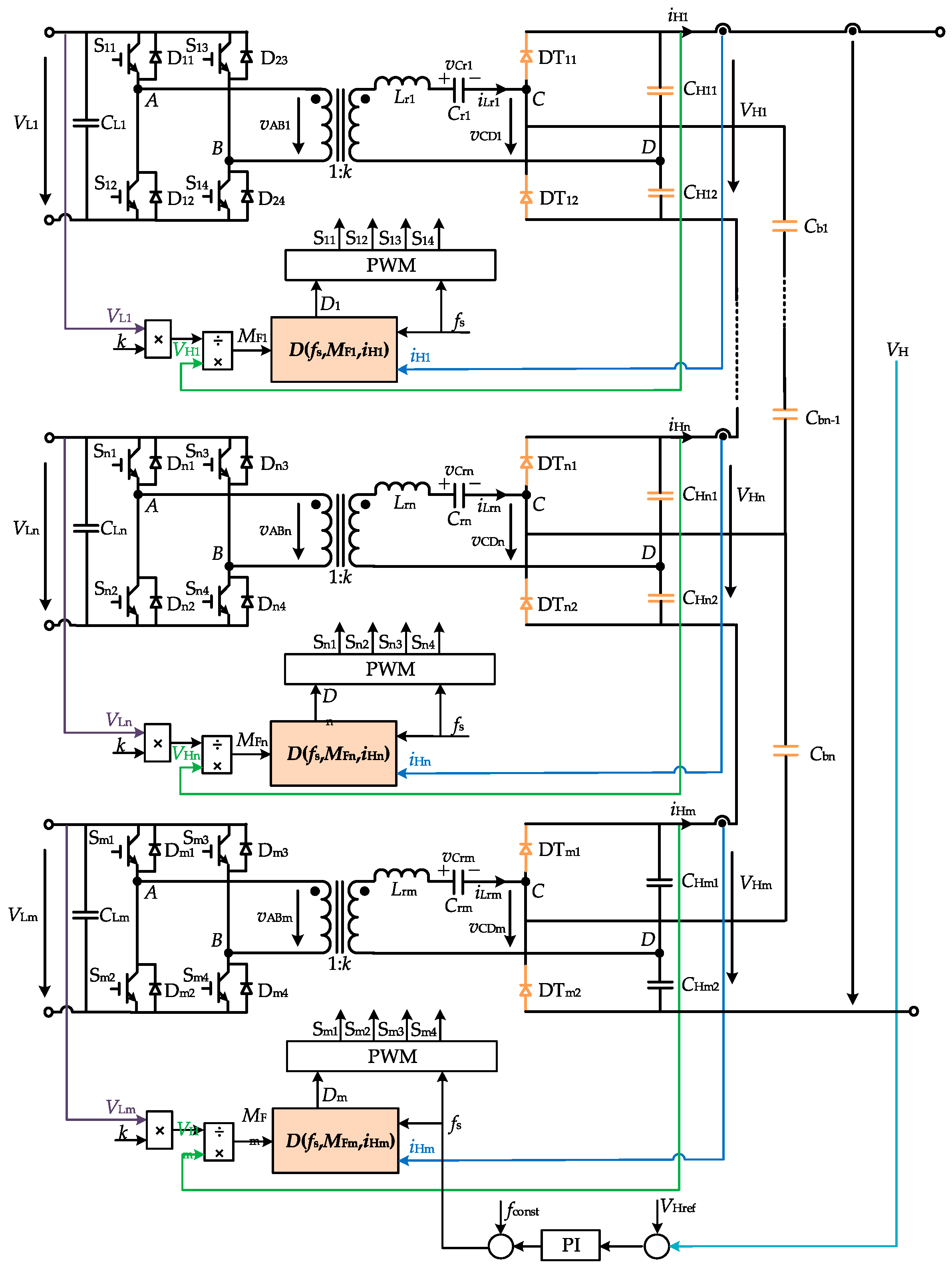
3. PFMT-PSMN Hybrid Control Strategy for Proposed Topology and Simulation
3.1. PFMT-PSMN Hybrid Control Strategy
3.2. PFMT-PSMN Hybrid Control for Proposed Topology
4. Simulation Results
4.1. Simulation Parameters
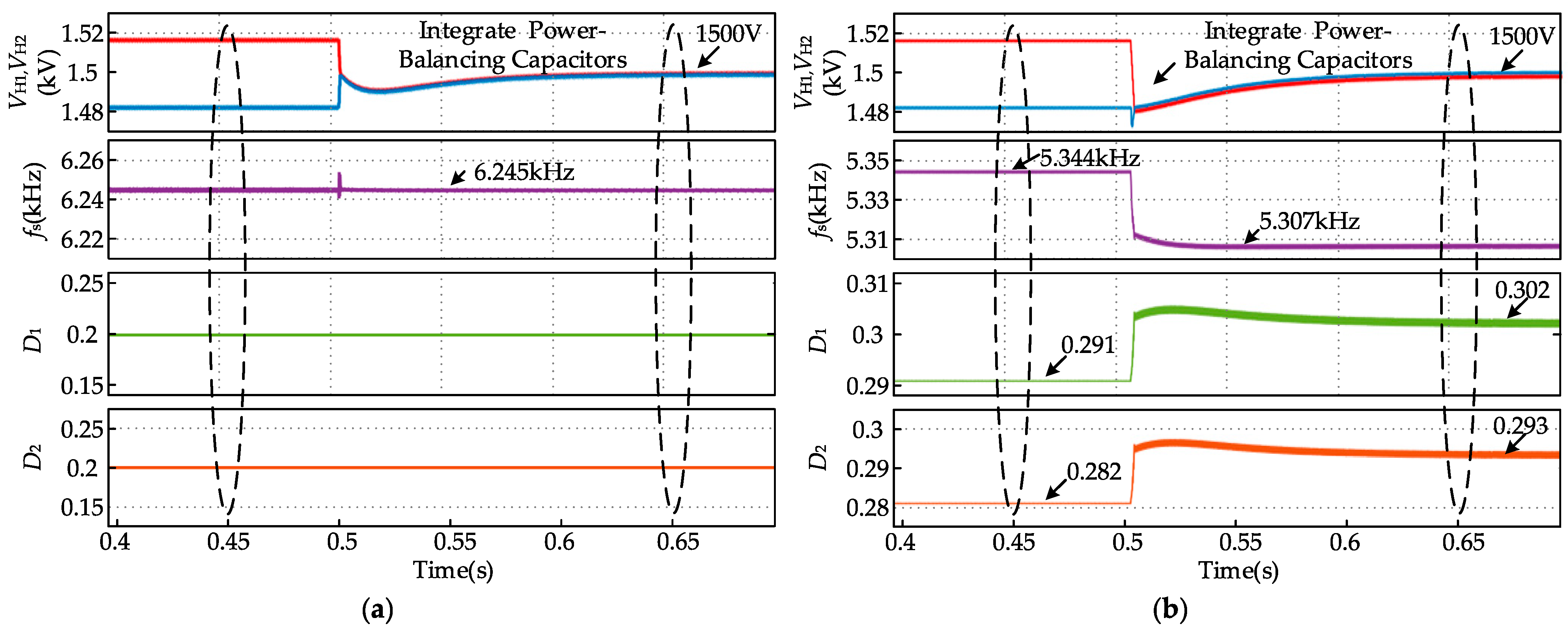
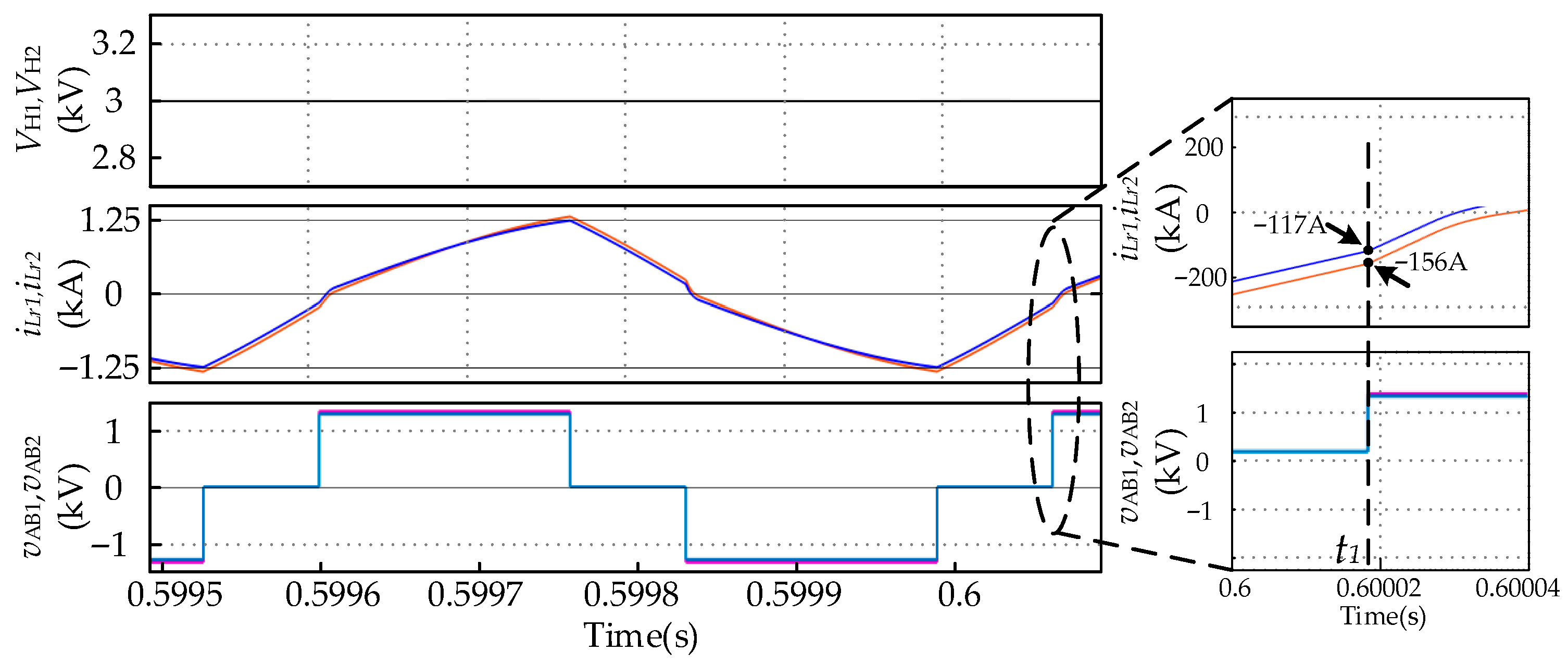
4.2. Simulation Results of PFMT-PSMN Hybrid Control
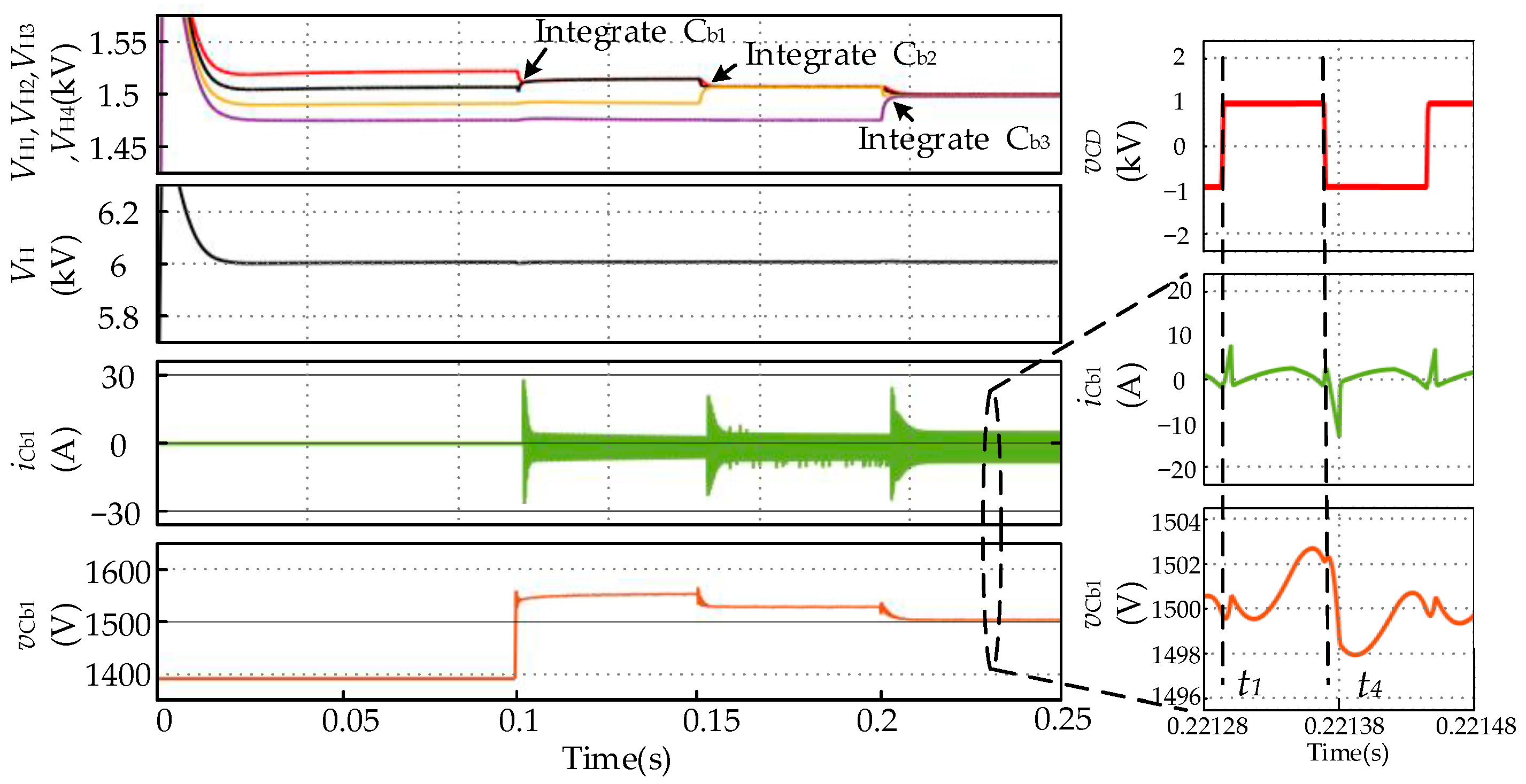
4.3. Simulation Results of the Operating Characteristics of Series-Connected Submodules and the Power-Balancing Capacitor
5. Conclusions
- A series-connected DC aggregation topology incorporating power-balancing capacitors is proposed. The working principles of the balancing capacitor and the resonant components are analyzed using time-domain methods.
- Based on soft-switching boundary constraints, conventional PFM and PSM methods are refined and a PFMT-PSMN hybrid control strategy is proposed. This strategy enables simultaneous adjustment of the switching frequency and phase-shift duty cycle, achieving soft-switching operation while reducing the switching frequency. It is well suited for series-connected DC aggregation topologies with power self-balancing capacitors. The PFMT-PSMN control method adopted in this paper requires real-time monitoring of multiple parameters (voltage, current, and gain), which may increase the control cost; however, it can be appropriately simplified for practical applications.
- The effectiveness of the proposed power-balancing topology and PFMT-PSMN control strategy is verified through MATLAB/Simulink simulations. A hardware prototype is currently under design, and future work will involve experimental validation to further corroborate the theoretical analysis and simulation results presented in this paper.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Li, B.; Liu, J.; Wang, Z.; Zhang, S.; Xu, D. Modular High-Power DC–DC Converter for MVDC Renewable Energy Collection Systems. IEEE Trans. Ind. Electron. 2021, 68, 5875–5886. [Google Scholar] [CrossRef]
- Meyer, C.; Hoing, M.; Peterson, A.; De Doncker, R.W. Control and Design of DC Grids for Offshore Wind Farms. IEEE Trans. Ind. Appl. 2007, 43, 1475–1482. [Google Scholar] [CrossRef]
- Jiao, Z.; Sun, J.; Yao, X.; Le, Y.; Chen, J.; Wang, A. Lightning Overvoltage Simulation and Design of a Novel Surge Protective Device for High-Power Offshore Wind Farms. IEEE Trans. Power Deliv. 2024, 39, 2306–2316. [Google Scholar] [CrossRef]
- Xiao, H.; Huang, X.; Huang, Y.; Liu, T.; Yang, P. Black Start Strategy of DRU-Based Low-Frequency AC Transmission System for Offshore Wind Power Integration. IEEE Trans. Ind. Appl. 2024, 60, 8319–8328. [Google Scholar] [CrossRef]
- Hassan Zamani, M.; Hossein Riahy, G.; Abedi, M. Rotor-Speed Stability Improvement of Dual Stator-Winding Induction Generator-Based Wind Farms by Control-Windings Voltage Oriented Control. IEEE Trans. Power Electron. 2016, 31, 5538–5546. [Google Scholar] [CrossRef]
- Ning, G.; Du, L.; Yuan, L.; Sun, Y.; Liu, Y.; Xu, G.; Han, H.; Su, M. Single-Stage IIOS Converter with Auto-Voltage-Sharing for Distributed Photovoltaic MVDC Collection System. IEEE Trans. Power Electron. 2024, 39, 14172–14178. [Google Scholar] [CrossRef]
- Bui, D.-V.; Cha, H.; Nguyen, C.V. Asymmetrical PWM Scheme Eliminating Duty Cycle Limitation in Input-Parallel Output-Series DC–DC Converter. IEEE Trans. Power Electron. 2022, 37, 2485–2490. [Google Scholar] [CrossRef]
- Fang, T.; Ruan, X.; Tse, C.K. Control Strategy to Achieve Input and Output Voltage Sharing for Input-Series–Output-Series-Connected Inverter Systems. IEEE Trans. Power Electron. 2010, 25, 1585–1596. [Google Scholar] [CrossRef]
- Shi, J.; Zhou, L.; He, X. Common-Duty-Ratio Control of Input-Parallel Output-Parallel (IPOP) Connected DC–DC Converter Modules with Automatic Sharing of Currents. IEEE Trans. Power Electron. 2012, 27, 3277–3291. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Z.; Zhang, Y.; Shu, J.; Liu, J.; Li, X. Unified Modeling and Control Methods for Ripple Power Decoupling Circuit Based on DC-Split Capacitor. IEEE Trans. Power Electron. 2025, 40, 665–678. [Google Scholar] [CrossRef]
- Vazquez, A.; Rodriguez, A.; Lamar, D.G.; Hernando, M.M. Advanced Control Techniques to Improve the Efficiency of IPOP Modular QSW-ZVS Converters. IEEE Trans. Power Electron. 2018, 33, 73–86. [Google Scholar] [CrossRef]
- Xia, Y.; Yu, M.; Zhang, Y.; Lv, Z.; Wei, W. Decentralized Suppression Strategy of Circulating Currents Among IPOP Single-Phase DC/AC Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1571–1583. [Google Scholar] [CrossRef]
- Sun, K.; Su, M.; Xu, G.; Chen, X.; Xiong, W. Modulated Coupled Inductor-Based IPOP-DAB Converter with Optimized Modulation Trajectory Considering the Phase-Shift Angle Between Submodules for SST Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 6112–6123. [Google Scholar] [CrossRef]
- Zhuang, Y.; Liu, F.; Huang, W.; Wang, S.; Jiang, J.; Pan, S.; Zha, X. A Peak Current Reducing Method for Input-Independent and Output-Series Modular Converters with LC-Branch-Based Power Balancing Unit. IEEE Trans. Ind. Electron. 2023, 70, 418–429. [Google Scholar] [CrossRef]
- Wei, C.; Zhu, X.; Jin, K.; Wu, Y. Modular Multiport Voltage Balance Topology Based on Boost Half-Bridge and Quadruple Semiactive Rectifier for MVdc Integration of Distributed PVs. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 3147–3161. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, L.; Jin, K.; Zhang, B. Current-Fed Multiactive Bridge Converter with Inherently Output Voltage Balance for Distributed Photovoltaics MVDC Integration. IEEE Trans. Ind. Electron. 2025, 72, 2563–2575. [Google Scholar] [CrossRef]
- Zhuang, Y.; Zhang, Y.; Chen, X.; Zhu, H.; Huang, Y.; Liu, F. A Novel Fault-Tolerant Topology for MVDC Grids Interface of Photovoltaic Generation Systems. IEEE Trans. Ind. Electron. 2025, 72, 547–558. [Google Scholar] [CrossRef]
- Chen, W.; Wang, G. Decentralized Voltage-Sharing Control Strategy for Fully Modular Input-Series–Output-Series System with Improved Voltage Regulation. IEEE Trans. Ind. Electron. 2015, 62, 2777–2787. [Google Scholar] [CrossRef]
- Kuperman, A. Simple Enhancement of Series–Series-Compensated Inductive Wireless Power Transfer Links Operating with Load-Independent Voltage Output at Fixed Frequency to Attain Zero Inverter Phase Angle. IEEE Trans. Power Electron. 2023, 38, 5670–5674. [Google Scholar] [CrossRef]
- Chen, W.; Wang, G.; Ruan, X.; Jiang, W.; Gu, W. Wireless Input-Voltage-Sharing Control Strategy for Input-Series Output-Parallel (ISOP) System Based on Positive Output-Voltage Gradient Method. IEEE Trans. Ind. Electron. 2014, 61, 6022–6030. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, H.; Wang, X.; Gang, Y.; Li, Y. Voltage Balance Scheme for Input-Series Output-Series DAB DC–DC Converter with Bidirectional Power Flow. IEEE Trans. Power Electron. 2024, 39, 12030–12034. [Google Scholar] [CrossRef]
- Ma, D.; Chen, W.; Ruan, X. A Review of Voltage/Current Sharing Techniques for Series–Parallel-Connected Modular Power Conversion Systems. IEEE Trans. Power Electron. 2020, 35, 12383–12400. [Google Scholar] [CrossRef]
- Barzegarkhoo, R.; Farhangi, M.; Lee, S.S.; Aguilera, R.P.; Blaabjerg, F.; Siwakoti, Y.P. A Novel Active Neutral Point-Clamped Five-Level Inverter with Single-Stage-Integrated Dynamic Voltage Boosting Feature. IEEE Trans. Power Electron. 2023, 38, 7796–7809. [Google Scholar] [CrossRef]
- Sun, L.; Wang, F.; Zhuo, F.; Zhu, T. Multi-Modular Cascaded Phase-Shifted Full-Bridge Converter for DC Grid Connection of Large-Scale Photovoltaic Power Systems. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 1561–1565. [Google Scholar]
- Liu, Y.; Abu-Rub, H.; Ge, B. Front-End Isolated Quasi-Z-Source DC–DC Converter Modules in Series for High-Power Photovoltaic Systems—Part I: Configuration, Operation, and Evaluation. IEEE Trans. Ind. Electron. 2017, 64, 347–358. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, F.; Zhuang, Y. Bidirectional Buck-Boost and Series LC-Based Power Balancing Units for Photovoltaic DC Collection System. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 6726–6738. [Google Scholar] [CrossRef]
- Li, X.; Zhu, M.; Su, M.; Ma, J.; Li, Y.; Cai, X. Input-Independent and Output-Series Connected Modular DC–DC Converter with Intermodule Power Balancing Units for MVdc Integration of Distributed PV. IEEE Trans. Power Electron. 2020, 35, 1622–1636. [Google Scholar] [CrossRef]
- Rong, F.; Wu, G.; Li, X.; Huang, S.; Zhou, B. ALL-DC Offshore Wind Farm with Series-Connected Wind Turbines to Overcome Unequal Wind Speeds. IEEE Trans. Power Electron. 2019, 34, 1370–1381. [Google Scholar] [CrossRef]
- Zhuang, Y.; Liu, F.; Huang, Y.; Liu, P.; Zhang, B. A Multiport Modular DC–DC Converter with Low-Loss Series LC Power Balancing Unit for MVDC Interface of Distributed Photovoltaics. IEEE Trans. Power Electron. 2021, 36, 7736–7749. [Google Scholar] [CrossRef]
- Hilal, A.; Raulet, M.-A.; Martin, C.; Sixdenier, F. Power Loss Prediction and Precise Modeling of Magnetic Powder Components in DC–DC Power Converter Application. IEEE Trans. Power Electron. 2015, 30, 2232–2238. [Google Scholar] [CrossRef]
- Imaoka, J.; Okamoto, K.; Shoyama, M.; Ishikura, Y.; Noah, M.; Yamamoto, M. Modeling, Magnetic Design, Simulation Methods, and Experimental Evaluation of Various Powder Cores Used in Power Converters Considering Their DC Superimposition Characteristics. IEEE Trans. Power Electron. 2019, 34, 9033–9051. [Google Scholar] [CrossRef]
- Wang, C.; Wang, H.; Zhang, T. Hybrid Four-Quadrant DC–DC Converter for DC Wind Farm Collection Systems. J. Power Electron. 2024, 24, 42–54. [Google Scholar] [CrossRef]


| Proposed Converter | PSFB + Buck-Boost Converter [26] | PSFB + Buck-Boost + Phase-Shift LC Solution [28] | DAB + Self-Balancing LC Solution [29] | |
|---|---|---|---|---|
| Semiconductor device | 4m IGBTs and 2m Diodes | 4m + 2(m − 1) IGBTs and 2m Diodes | 4m + 2(m − 1) IGBTs and 2m Diodes | 8m IGBTs |
| Additionally circuits | (m − 1) capacitor circuits | 2(m−1) Buck-Boost circuits | 2(m − 1) Buck-Boost and LC circuits | (m − 1) LC circuits |
| Control loop | m | 2m − 1 | 2m − 1 | m |
| Implementation and control complexity | Simple | Complex | Very Complex | Simple |
| Input ripple | Low | Large | Large | Large |
| Cost | Very Low | High | Very High | High |
| Dynamic response | Slightly Slow | Fast | Very Fast | Slow |
| Switching loss | Low | Large | Large | Low |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Output power Pout | 360 kW | Transformer ratio 1:k | 1:2.2 |
| Resonant frequency fr | 4 kHz | Rated voltage VHN | 1.5 kV |
| Commutation turn-off time tc-off | 50 μs | Resonant inductance Lrn | 400 µH |
| Resonant capacitance Crn | 4 µF | Dead time td | 1 µs |
| The high-voltage capacitors CHn1/CHn2 | 1 mF | Power-balancing capacitor Cbn | 0.1 mF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Xin, Q.; Hong, R.; Li, Q. Fully DC Aggregation Topology with Power Self-Balancing Capacitors for Offshore Wind Power Transmission: Simulation Study. Electronics 2025, 14, 3422. https://doi.org/10.3390/electronics14173422
Li H, Xin Q, Hong R, Li Q. Fully DC Aggregation Topology with Power Self-Balancing Capacitors for Offshore Wind Power Transmission: Simulation Study. Electronics. 2025; 14(17):3422. https://doi.org/10.3390/electronics14173422
Chicago/Turabian StyleLi, Huan, Qingming Xin, Ruoqing Hong, and Qingmin Li. 2025. "Fully DC Aggregation Topology with Power Self-Balancing Capacitors for Offshore Wind Power Transmission: Simulation Study" Electronics 14, no. 17: 3422. https://doi.org/10.3390/electronics14173422
APA StyleLi, H., Xin, Q., Hong, R., & Li, Q. (2025). Fully DC Aggregation Topology with Power Self-Balancing Capacitors for Offshore Wind Power Transmission: Simulation Study. Electronics, 14(17), 3422. https://doi.org/10.3390/electronics14173422






