An Energy-Saving Clustering Algorithm for Wireless Sensor Networks Based on Multi-Objective Walrus Optimization
Abstract
1. Introduction
2. System Model
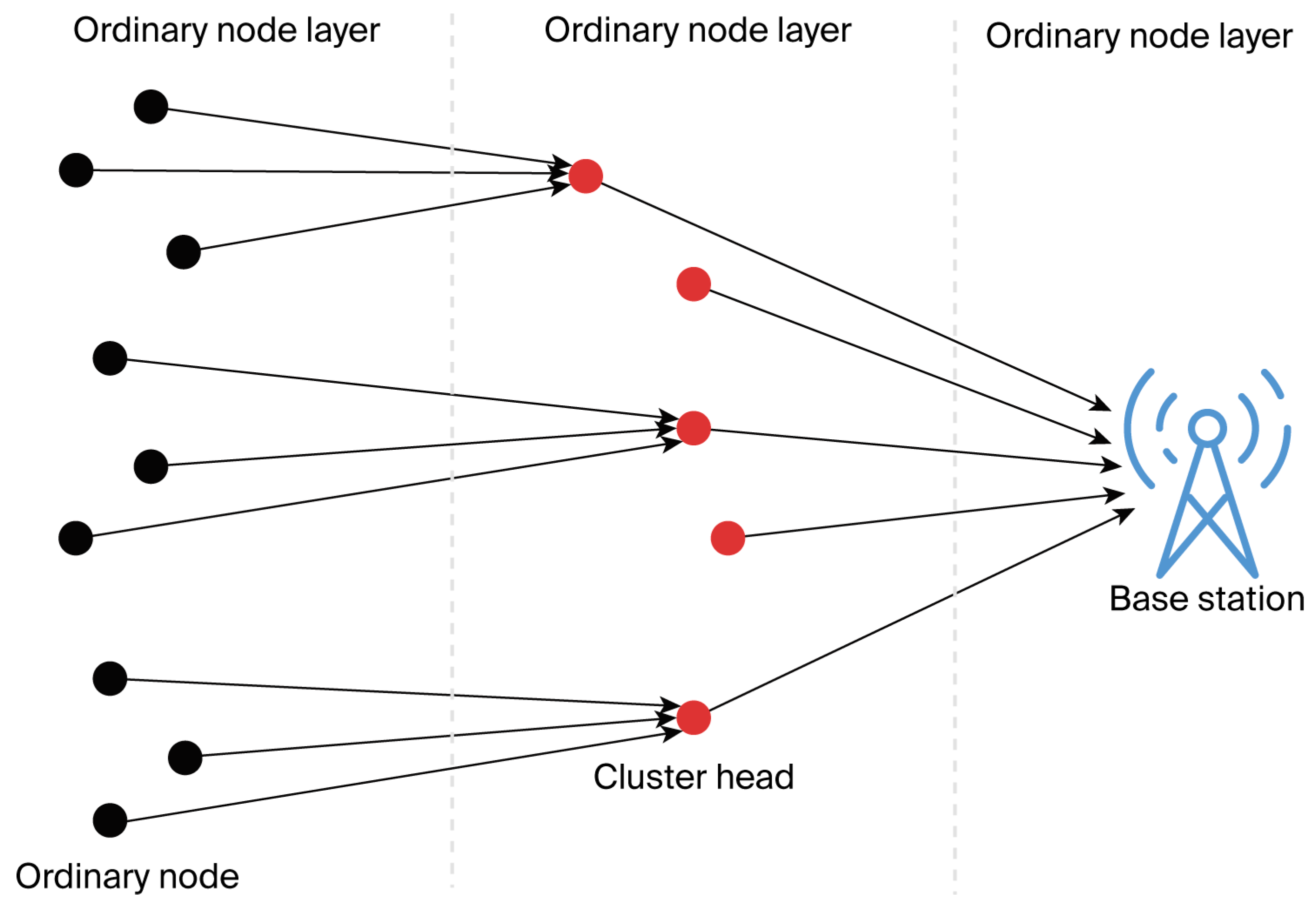
2.1. Sensor Network Structure Model
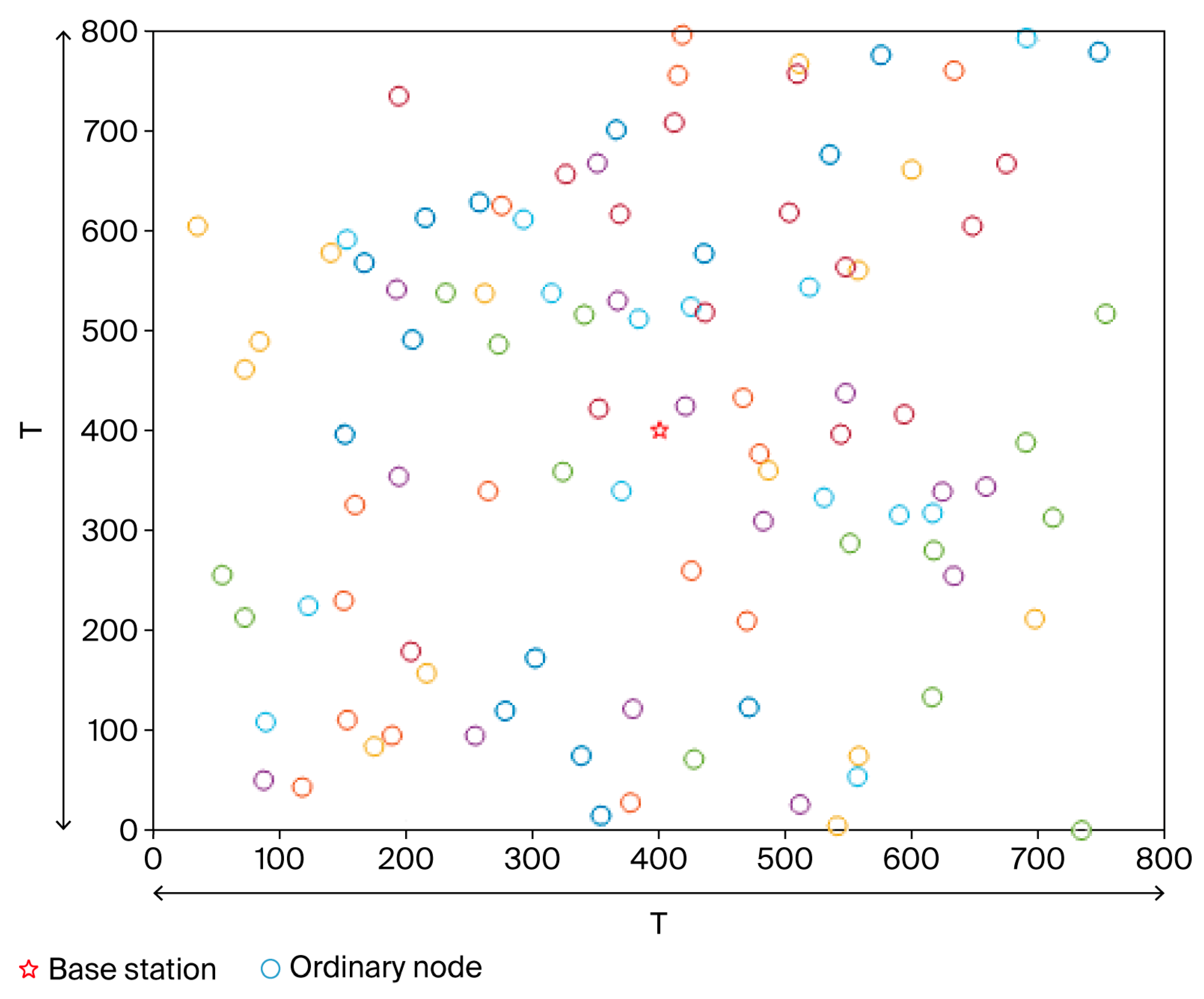
- N sensors are randomly deployed within a T × T area, and their positions remain fixed after deployment.
- Each sensor has a unique and distinct ID.
- It is assumed that there is no signal interference within the coverage area of the base station, and the energy supply of the base station can be used indefinitely.
- The power for each sensor node to send and receive data can be controlled.
- All sensor nodes share identical characteristics, and their locations relative to the base station remain fixed.
2.2. Energy Drain Model
3. Network Energy Drain Analysis
- Selection of the appropriate cluster heads for data collection and aggregation.
- Mitigation of the hotspot effect to prevent the premature death of nodes near the base station.
- Choice of suitable nodes to perform multi-hop data transmission.
3.1. Reasonable Cluster Head Combination
3.1.1. K-Means++ Clustering Algorithm
3.1.2. Chaotic Mapping Optimization
3.1.3. The CM-WaOA Follows the Procedure Outlined Below
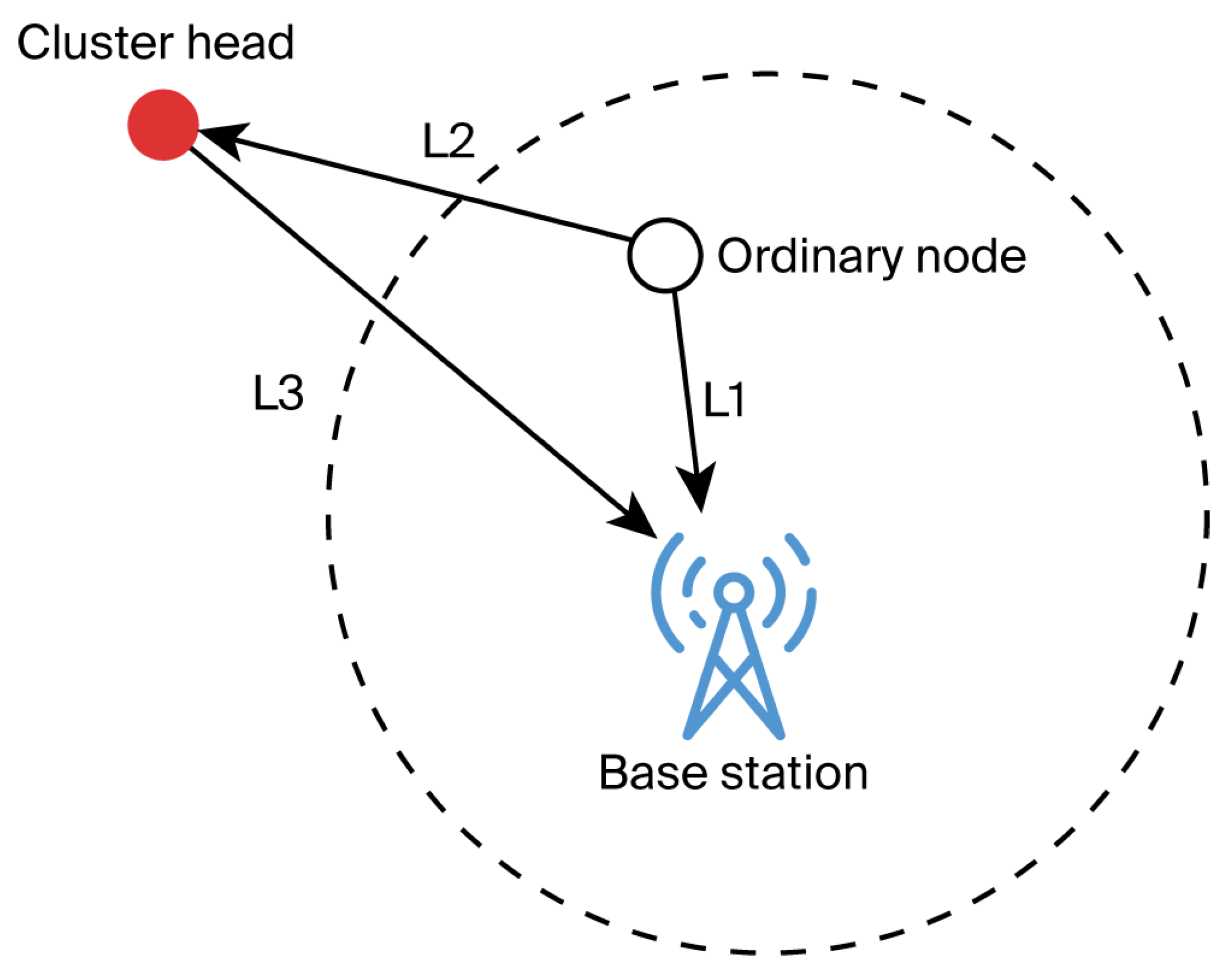
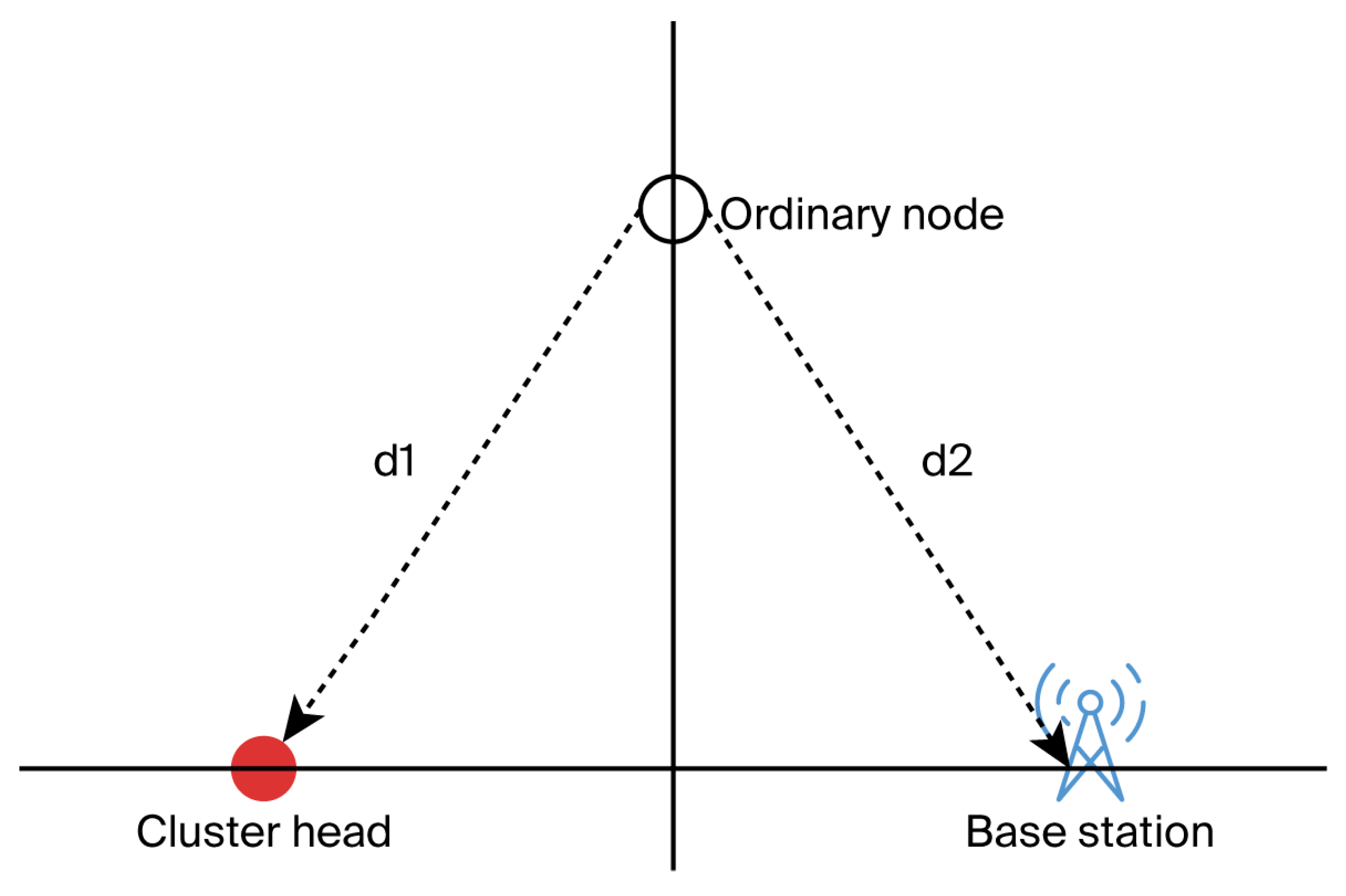
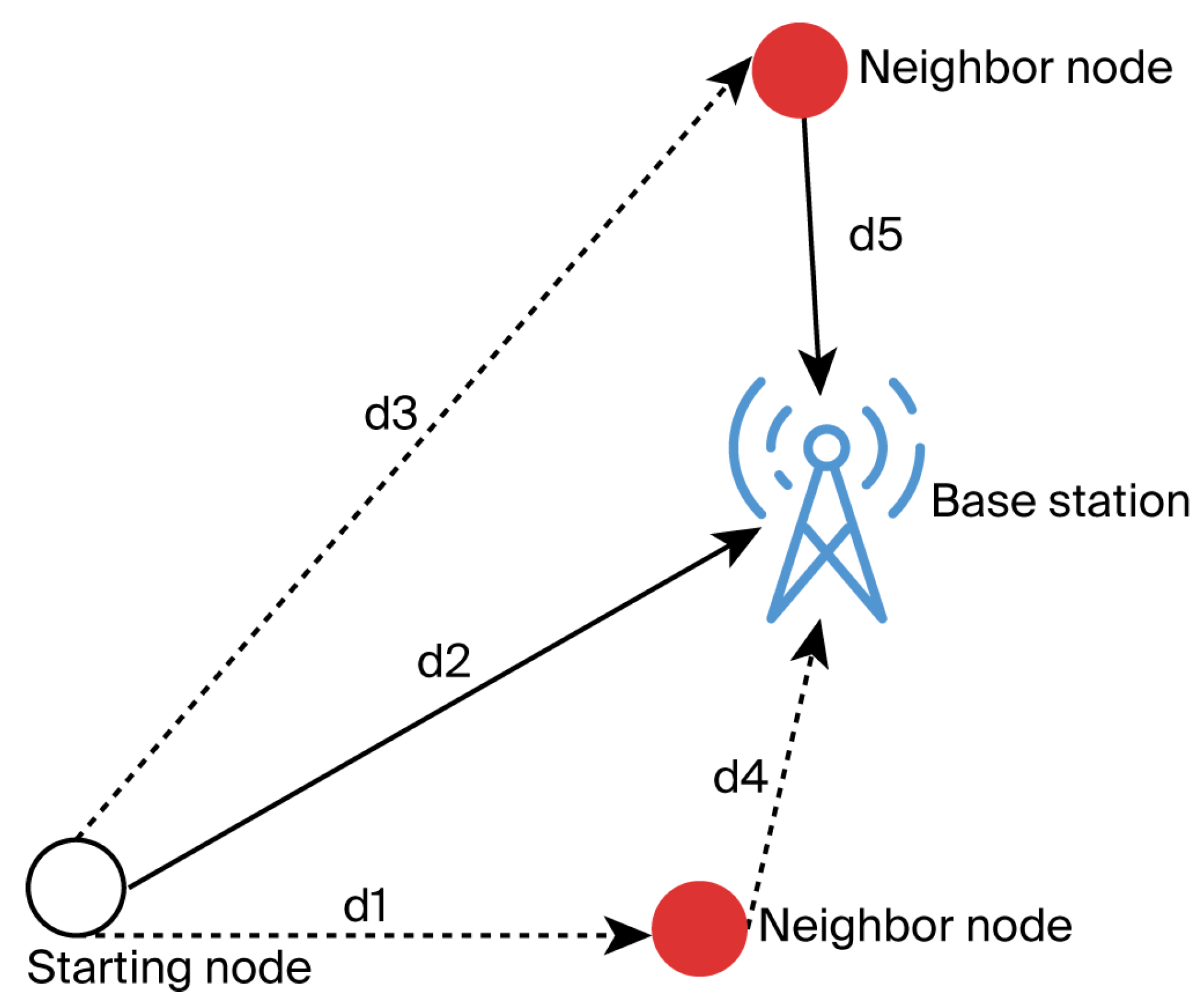
3.2. Data Transmission Direction Planning
3.3. Optimal Next-Hop Node
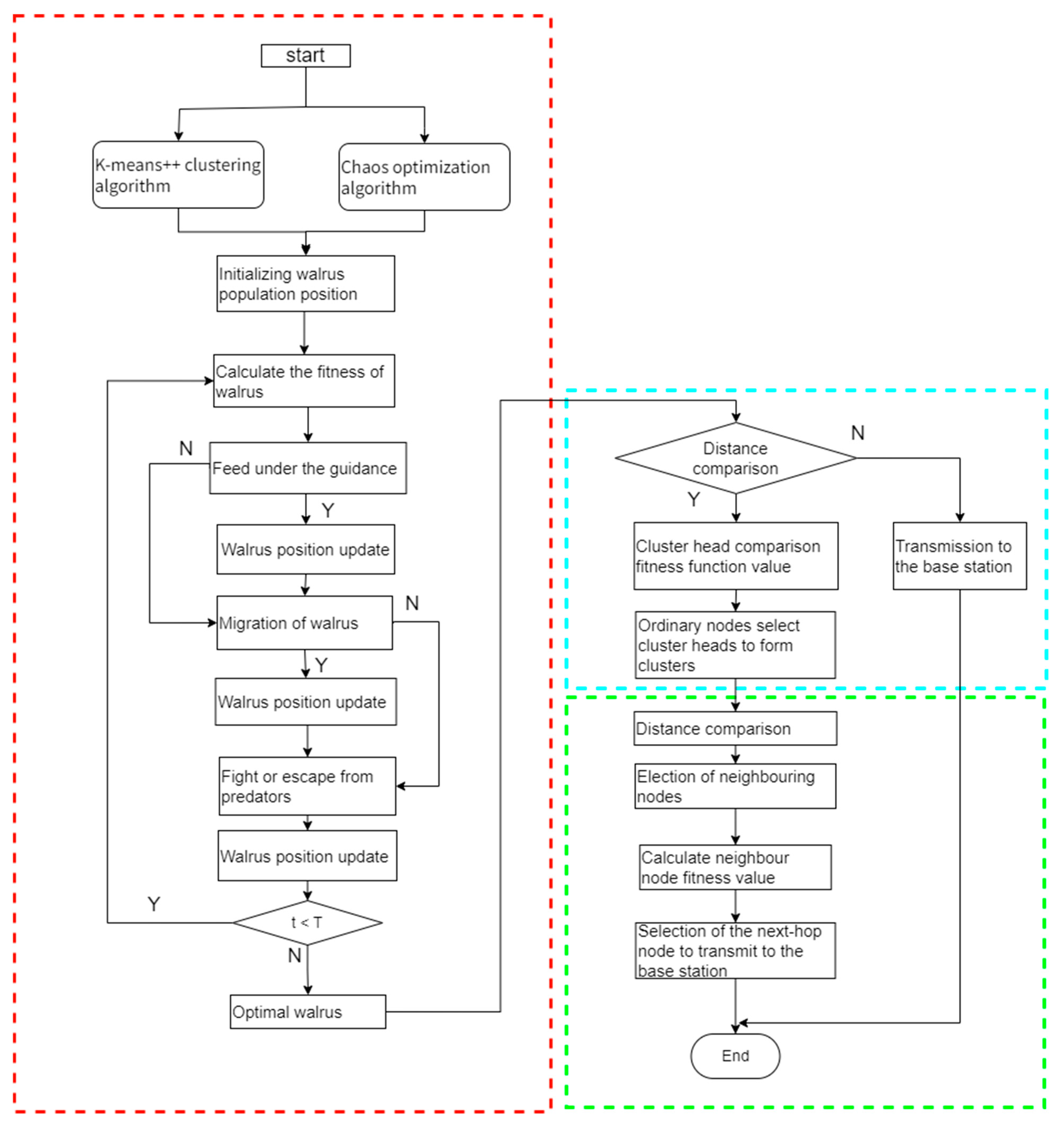
4. Design and Implementation of the CM-WaOA
4.1. Cluster Head Selection
4.1.1. Optimal Number of Cluster Heads
4.1.2. Population Initialization
- Algorithm 1: Pseudo-code of circular symmetric chaotic mapping algorithm.
| Algorithm 1: Initialization of Walrus Population by the Chaotic Mapping Algorithm |
| input: |
| The relative positions of the computing nodes and the base stations |
| Acquire the relative positions and transform it into the initial value for mapping |
| Logistic mapping is applied in Equations (9)–(15) to introduce chaotic behavior |
| This chaotic output is then inversely transformed to generate a new relative position, which is subsequently used to calculate a new position that does not exist. |
| output |
4.1.3. Position Mapping
- Algorithm 2: Pseudo-code of position mapping algorithm.
| Algorithm 2: Obtain the Actual Position Using the Mapping Function |
| input: |
| Calculate the distance from the computing node to the virtual location |
| Retrieve the energy of each node |
| Compute the position mapping function using Equations (4) and (5) |
| Select the node indices corresponding to the virtual coordinates projected onto the real network by comparing the function values |
| output |
4.1.4. Design of the CM-WaOA Functions
- Algorithm 3: Pseudo-code of cluster head node selection algorithm.
| Algorithm 3: CM-WaOA Cluster Head Optimization Algorithm |
| input |
| Initialize the network nodes to determine the positions of the walrus population |
| Compute the objective function value for each walrus individual, and retain the position and corresponding value of the one with the lowest function value |
| By comparing the function values of the walrus population, a new walrus population was generated |
| Feeding strategy: When walruses forage on the seabed, they create a new position for themselves. If the optimization function metric enhances, the updated location supersedes the prior one |
| If migration results in a new location that yields a better objective function value, it replaces the walrus’s previous position |
| Avoiding and resisting predators has created new positions for the walruses. If the objective function value improves, the previous position is updated with the new one |
| Based on the sea elephant’s position and the objective function defined by Equations (32)–(35), the set of non-dominated solutions is calculated: |
| + 1 |
| The best non-dominated solution obtained serves as the solution for the given problem, and the optimal position of the sea lion is obtained, which is the optimal cluster head combination |
| output |
4.2. Cluster Formation Stage
- Algorithm 4: Selecting the cluster head for ordinary nodes.
| Algorithm 4: Network Node Cluster Establishment |
| input |
| Select the appropriate cluster head |
| If the ordinary nodes satisfy the operation of joining a cluster |
| Calculate the fitness function of each common node to every cluster head using Equation (38). Ordinary nodes perform clustering operations |
| Else |
| Ordinary nodes directly establish links with the base station |
| End |
| output |
4.3. Node Data Transmission Based on the SSA
| Algorithm 5: Network Data Transmission |
| input |
| Obtain cluster heads and clusters from Algorithm 3 and Algorithm 4 |
| If ordinary nodes link to the cluster head |
| Selecting the path through the sparrow search algorithm |
| The node transmits data to the cluster head |
| After receiving the data, the cluster head performs fusion and then transmits the data to the base station via a single hop or multiple hops |
| Else |
| Ordinary nodes relay data directly to the base station |
| output |
5. Simulation Study and Performance Comparison
5.1. Parameter Configuration for Experiments
5.2. Energy Fluctuations in WSNs
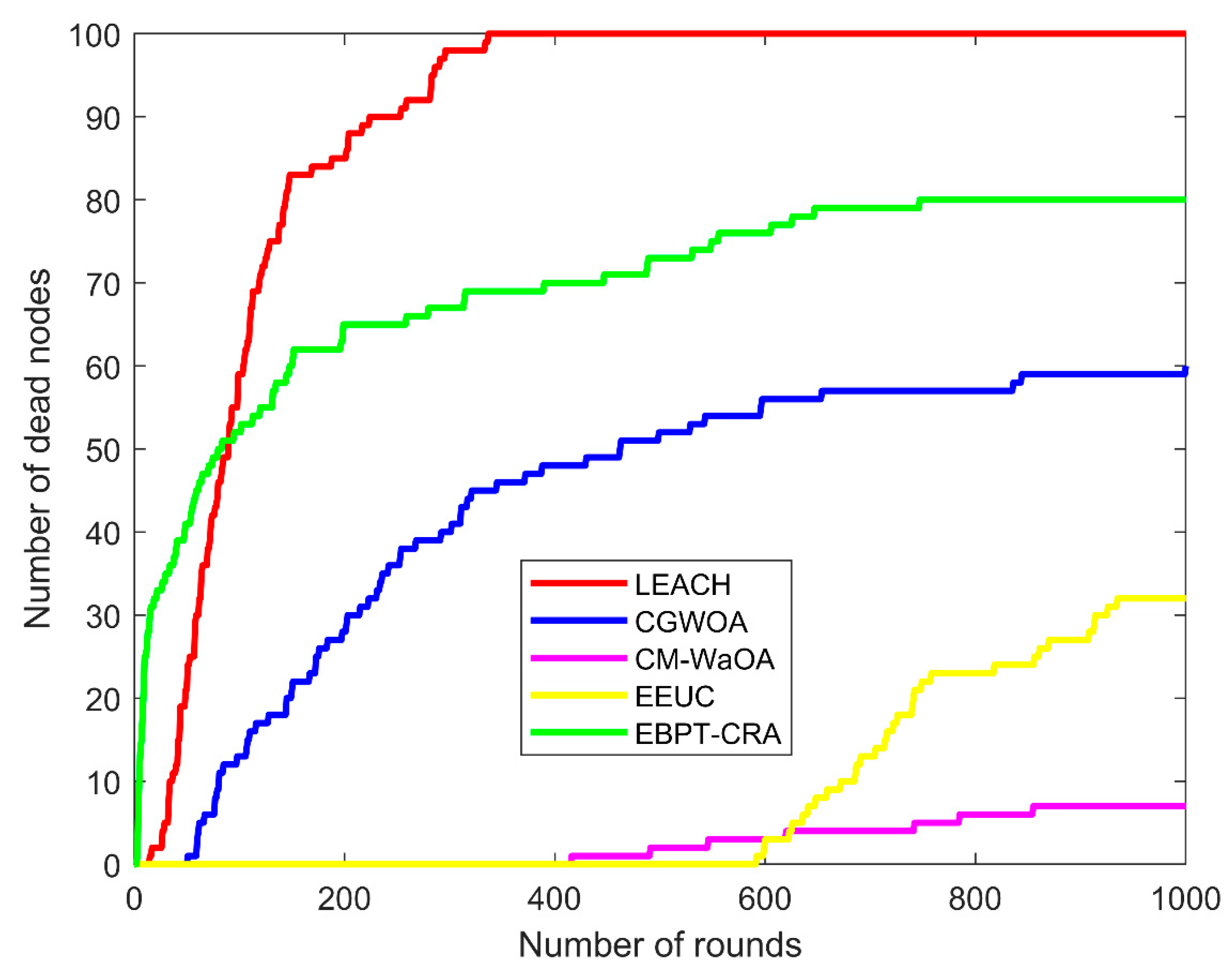
5.3. Evaluation of Dead Node Count in the WSN
5.4. Evaluation of Surviving Node Count in the WSN
5.5. Transmission Delay Comparison
5.6. Comparative Analysis of Surviving Nodes Across Different Network Scales
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| WSN | Wireless sensor networks |
| LEACH | Low-energy adaptive clustering hierarchy |
| EEUC | Energy-efficient unequal clustering |
| CGWOA | Chaotic Grey Wolf Optimization Algorithm |
| EBPT-CRA | Clustering and routing algorithm based on an energy-balanced path tree |
| CM-WaOA | Chaotic Mapping Walrus Optimization Algorithm |
| SSA | Sparrow Search Algorithm |
References
- Tang, M.; Cai, S.; Lau, V.K.N. Radix-partition-based over-the-air aggregation and low-complexity state estimation for IoT systems over wireless fading channels. IEEE Trans. Signal Process 2022, 70, 1464–1477. [Google Scholar] [CrossRef]
- Ranjan Kumar, M.; Yajunath, K.; Shet, N.S.V.; Ranjan, M.S.; Swarnadh, S.G.; Bhanjan, P.S.; Shivalal, P.B. A survey on wireless sensor network (applications and architecture). Int. J. Commun. Netw. Distrib. Syst. 2024, 30, 136–201. [Google Scholar]
- Sourav, R.; Dipnarayan, D.; Bibhash, S. Secure and lightweight authentication protocol using PUF for the IoT-based wireless sensor network. ACM J. Emerg. Technol. Comput. Syst. 2023, 20, 1–17. [Google Scholar]
- Kubra, G.; Nuri Alperen, K.; Damilola, O.; Fan, L. A dynamic wireless sensor network deployment algorithm for emergency communications. In Proceedings of the 2023 IEEE/ACIS 21st International Conference on Software Engineering Research, Management and Applications (SERA), Orlando, FL, USA, 23–25 May 2023; pp. 28–34. [Google Scholar]
- Hudda, S.; Haribabu, K. A review on WSN based resource constrained smart IoT systems. Discov. Internet Things 2025, 5, 56. [Google Scholar] [CrossRef]
- Shiyang, W.; Andrew, A.C.M.; Ameer, I.; Akshat, B.; Wang, K.I.-K. Long range wide area network for agricultural wireless underground sensor networks. J. Ambient Intell. Humaniz. Comput. 2023, 14, 4903–4913. [Google Scholar]
- Adil, K.O.; Nawaf, A.; Alaa, K.O.; Mohammed, A.; Ayman, F.G.; Mahmoud, R. Efficient key distribution for secure and energy-optimized communication in wireless sensor network using bioinspired algorithms. Alex. Eng. J. 2024, 92, 63–73. [Google Scholar] [CrossRef]
- Yuki, N.; Aoto, H.; Chihiro, Y.; Kyohei, T.; Tetsuya, O.; Leonard, B. Experimental results of a wireless sensor network testbed for monitoring a water reservoir tank considering multi-flows. Lect. Notes Data Eng. Commun. Technol. 2023, 161, 331–340. [Google Scholar]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-efficient communication protocol for wireless microsensor networks. In Proceedings of the Hawaii International Conference on System Sciences, Maui, HI, USA, 7 January 2000; p. 10. [Google Scholar]
- Madhvi, S.; Aarti, S.; Shefali, R. An approach to increase the lifetime of traditional LEACH protocol using CHME-LEACH and CHP-LEACH. In Fourth Congress on Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2024; Volume 868, pp. 133–145. [Google Scholar]
- Suman, J.; Shyamala, K.; Roja, G.; Pranay, N. Testbed Implementation of MAX LEACH Routing Protocol and Sinkhole Attack in WSN. In Proceedings of Third International Conference on Advances in Computer Engineering and Communication Systems; Springer: Berlin/Heidelberg, Germany, 2023; Volume 612, pp. 153–162. [Google Scholar]
- Gülbaş, G.; Çetin, G. Lifetime Optimization of the LEACH Protocol in WSNs with Simulated Annealing Algorithm. Wirel. Pers. Commun. 2023, 132, 2857–2883. [Google Scholar] [CrossRef]
- Mishra, R.; Yadav, R.K. Energy efficient cluster-based routing protocol for WSN using nature inspired algorithm. Wirel. Pers. Commun. 2023, 130, 2407–2440. [Google Scholar] [CrossRef]
- Almusawi, M.; Ravindran, G.; Bhasker, B.; NL, L. Chaotic Grey Wolf Optimization for Energy-Efficient Clustering and Routing in Wireless Sensor Networks. In Proceedings of the 2024 International Conference on Integrated Circuits and Communication Systems (ICICACS), Raichur, India, 23–24 February 2024; pp. 1–8. [Google Scholar]
- Li, C.; Ye, M.; Chen, G.; Wu, J. An energy-efficient unequal clustering mechanism for wireless sensor networks. In Proceedings of the IEEE International Conference on Mobile Adhoc and Sensor Systems Conference, Washington, DC, USA, 7 November 2005; pp. 597–604. [Google Scholar]
- Akshay, V.; Sunil, K.; Prateek Raj, G.; Tarique, R.; Arvind, K. Enhanced Cost and Sub-epoch Based Stable Energy-Efficient Clustering Algorithm for Heterogeneous Wireless Sensor Networks. Wirel. Pers. Commun. 2023, 131, 3053–3072. [Google Scholar]
- Fan, B.; Xin, Y. EBPT-CRA: A clustering and routing algorithm based on energy-balanced path tree for wireless sensor networks. Expert Syst. Appl. 2025, 259, 125232. [Google Scholar] [CrossRef]
- Li, B.; Wang, H.; Liu, Y.; Zhang, X. Chaos-based optimization in WSNs. IEEE Trans. Wirel. Commun. 2016, 15, 2145–2156. [Google Scholar]
- Shahid, I.M.; Faiyaj Ahmed, L.M.; Monirul, K.M.; Khurram Monir, R.M. A hybrid optimization algorithm for improving load frequency control in interconnected power systems. Expert Syst. Appl. 2024, 249, 695–701. [Google Scholar] [CrossRef]
- Jasim, K.M.O.; Salih, B.M. Improving Task Scheduling in Cloud Datacenters by Implementation of an Intelligent Scheduling Algorithm. Informatica 2024, 48, 77–88. [Google Scholar] [CrossRef]
- Suhag, S.; Aarit. Challenges and Potential Approaches in Wireless Sensor Network Security. J. Electr. Eng. Technol. 2024, 19, 2693–2700. [Google Scholar] [CrossRef]
- Heidari, E. A novel energy-aware method for clustering and routing in IoT based on whale optimization algorithm & Harris Hawks optimization. Computing 2024, 106, 1013–1045. [Google Scholar]
- Funaki, M.; Tanaka, Y.; Murata, D.; Yamamoto, T. Wireless Sensor System, Wireless Terminal Device, Communication Control Method and Communication Control Program. U.S. Patent 11930431, 12 March 2024. [Google Scholar]
- Jae Young, J.; Boun, S.; Young Jin, H. Optimal design method of a wireless charging system for HTS magnets using a genetic algorithm. IEEE Trans. Appl. Supercond. 2024, 34, 4901806. [Google Scholar] [CrossRef]
- Trojovský, P.; Dehghani, M. A new bio-inspired metaheuristic algorithm for solving optimization problems based on walruses behavior. Sci. Rep. 2023, 13, 8775. [Google Scholar] [CrossRef]
- Dinesh, K.; Santhosh Kumar, S.V.N. GWO-SMSLO: Grey wolf optimization-based clustering with secured modified Sea Lion optimization routing algorithm in wireless sensor networks. Peer-to-Peer Netw. Appl. 2024, 17, 585–611. [Google Scholar] [CrossRef]
- Sakhri, A.; Arsalan, M.; Maimour, M.; Kherbache, E.; Rondeau, E.; Doghmane, N. A digital twin-based energy-efficient wireless multimedia sensor network for waterbirds monitoring. Future Gener. Comput. Syst. 2024, 155, 146–163. [Google Scholar] [CrossRef]
- Preethi, R. Assault Type Detection in WSN Based on Modified DBSCAN with Osprey Optimization Using Hybrid Classifier LSTM with XGBOOST for Military Sector. Opt. Mem. Neural Netw. (Inf. Opt.) 2024, 33, 53–71. [Google Scholar] [CrossRef]
- Qader, K.B.A.; Mezaal, H.D.; Abdulwahab, K.Y.; Alkenani, J.; Alshawi, I.S. Lifetime Maximization Using Grey Wolf Optimization Routing Protocol with statistical Technique in WSNs. Informatica 2023, 47, 75–82. [Google Scholar] [CrossRef]
- Deena, S.; Suganthi, D.S.; Nalini, T. Energy aware clustering protocol using chaotic gorilla troops optimization algorithm for Wireless Sensor Networks. Multimed. Tools Appl. 2024, 83, 23853–23871. [Google Scholar]
- Vikhyath, V.K.; Prasad, A.P. Optimal Cluster Head Selection in Wireless Sensor Network via Combined Osprey-Chimp Optimization Algorithm: CIOO. Int. J. Adv. Comput. Sci. Appl. 2023, 14, 401–407. [Google Scholar] [CrossRef]
- Fransen, K.; Van Eekelen, J. Efficient path planning for automated guided vehicles using A (Astar) algorithm incorporating turning costs in search heuristic. Int. J. Prod. Res. 2023, 61, 707–725. [Google Scholar] [CrossRef]
- Soleimanian Gharehchopogh, F.; Namazi, M.H.; Ebrahimi, L.; Abdollahzadeh, B. Advances in Sparrow Search Algorithm: A comprehensive survey. Arch. Comput. Methods Eng. 2022, 30, 427–455. [Google Scholar] [CrossRef]
- Dinesh, K.; Kumar, S.V.N.S. Energy-efficient trust-aware secured neuro-fuzzy clustering with sparrow search optimization in wireless sensor network. Int. J. Inf. Secur. 2024, 23, 199–223. [Google Scholar] [CrossRef]
- Ikkurthi Bhanu, P.; Saumitra, G.; Yogita; Singh, Y.S.; Pal, V. HCM: A hierarchical clustering framework with MOORA based cluster head selection approach for energy efficient wireless sensor networks. Microsyst. Technol. 2024, 30, 393–409. [Google Scholar]
- Alhijaj, A.; Khuder, B.A.Q.; Alshawi, I. Fuzzy Data Aggregation Approach to Enhance Energy-Efficient Routing Protocol for HWSNs-Efficient Routing Protocol for HWSNs. Informatica 2022, 46, 45–47. [Google Scholar]
- Ustun, D.; Erkan, U.; Toktas, A.; Lai, Q.; Yang, L. 2D hyperchaotic Styblinski-Tang map for image encryption and its hardware implementation. Multimed. Tools Appl. 2024, 83, 34759–34772. [Google Scholar] [CrossRef]
- Meenakshi, N.; Ahmad, S.; Prabu, A.V.; Rao, J.N.; Othman, N.A.; Abdeljaber, H.A.M.; Sekar, R.; Nazeer, J. Efficient Communication in Wireless Sensor Networks Using Optimized Energy Efficient Engroove Leach Clustering Protocol. Tsinghua Sci. Technol. 2024, 29, 985–1001. [Google Scholar] [CrossRef]





| Model | Algorithm | Advantages | Disadvantages |
|---|---|---|---|
| Threshold protocol | LEACH.2000 [9] | The algorithm is relatively simple, and it selects the coarse head by calculating the threshold. | The selection of cluster heads through the calculation of thresholds, with a random selection probability, will lead to an unreasonable distribution of cluster heads. |
| CHP-LEACH.2024 [10] | |||
| MAX LEACH.2023 [11] | |||
| Machine learning protocol | LEACH-SA.2023 [12] | Selecting the appropriate cluster heads through swarm intelligence algorithms. | Using swarm intelligence algorithms to select cluster heads may result in uneven distribution of cluster head positions, which can lead to excessive energy drain during transmission. |
| Mishra Rashmi.2023 [13] | |||
| CGWOA.2024 [14] | |||
| Non-uniform protocol | EEUC.2005 [15] | Different numbers of nodes and cluster heads within the cluster can prevent the cluster head nodes from dying prematurely. | The difference in the number of nodes within a cluster may result in significant variations in energy drain among different clusters. |
| ECSSEEC.2023 [16] | |||
| EBPY-CRA.2024 [17] |
| WSN | CM-WaOA |
|---|---|
| Number of sensor nodes | Size and position |
| Node groups | All combinations of preselected cluster heads |
| Cluster head node combinations | Best positions of walrus individuals |
| All combinations of preselected cluster heads | All positions in the walrus population |
| Transmission Direction | |
|---|---|
| Move away from the best solution toward , exploring new paths. | |
| , fine-tuning the path. | |
| Make no directional change, relying solely on random perturbations. |
| Parameter | Value |
|---|---|
| Total number of sensor nodes | 100 |
| Network coverage area | 800 × 800 m2 |
| Base station coordinates | (400,400) |
| Energy loss coefficient (free-space model) | /bit/m2 |
| Energy loss coefficient (multipath model) | /bit/m2 |
| Initial node energy | 4 J |
| Number of network operation rounds | 1000 rounds |
| Area Size | Round | LEACH | CGWOA | EEUC | EBPT-CRA | CM-WaOA |
|---|---|---|---|---|---|---|
| 1000 × 1000 | 0r | 100 | 100 | 100 | 100 | 100 |
| 500r | 0 | 33 | 79 | 9 | 93 | |
| 1000r | 0 | 25 | 3 | 5 | 62 | |
| 800 × 800 | 0r | 100 | 100 | 100 | 100 | 100 |
| 500r | 0 | 48 | 100 | 27 | 100 | |
| 1000r | 0 | 40 | 68 | 20 | 93 | |
| 600 × 600 | 0r | 100 | 100 | 100 | 100 | 100 |
| 500r | 31 | 80 | 100 | 42 | 100 | |
| 1000r | 2 | 67 | 100 | 27 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, S.; Yuan, Y.; Shao, W. An Energy-Saving Clustering Algorithm for Wireless Sensor Networks Based on Multi-Objective Walrus Optimization. Electronics 2025, 14, 3421. https://doi.org/10.3390/electronics14173421
Jia S, Yuan Y, Shao W. An Energy-Saving Clustering Algorithm for Wireless Sensor Networks Based on Multi-Objective Walrus Optimization. Electronics. 2025; 14(17):3421. https://doi.org/10.3390/electronics14173421
Chicago/Turabian StyleJia, Songhao, Yaohui Yuan, and Wenqian Shao. 2025. "An Energy-Saving Clustering Algorithm for Wireless Sensor Networks Based on Multi-Objective Walrus Optimization" Electronics 14, no. 17: 3421. https://doi.org/10.3390/electronics14173421
APA StyleJia, S., Yuan, Y., & Shao, W. (2025). An Energy-Saving Clustering Algorithm for Wireless Sensor Networks Based on Multi-Objective Walrus Optimization. Electronics, 14(17), 3421. https://doi.org/10.3390/electronics14173421





