Ultra-Short-Term Wind Power Prediction Based on Spatiotemporal Contrastive Learning

Abstract

With the accelerating global energy transition, wind power has become a core pillar of renewable energy systems. However, its inherent intermittency and volatility pose significant challenges to the safe, stable, and economical operation of power grids—making ultra-short-term wind power prediction a critical technical link in optimizing grid scheduling and promoting large-scale wind power integration. Current forecasting techniques are plagued by problems like the inadequate representation of features, the poor separation of features, and the challenging clarity of deep learning models. This study introduces a method for the prediction of wind energy using spatiotemporal contrastive learning, employing seasonal trend decomposition to encapsulate the diverse characteristics of time series. A contrastive learning framework and a feature disentanglement loss function are employed to effectively decouple spatiotemporal features. Data on geographical positions are integrated to simulate spatial correlations, and a convolutional network of spatiotemporal graphs, integrated with a multi-head attention system, is crafted to improve the clarity. The proposed method is validated using operational data from two actual wind farms in Northwestern China. The research indicates that, compared with typical baselines (e.g., STGCN), this method reduces the RMSE by up to 38.47% and the MAE by up to 44.71% for ultra-short-term wind power prediction, markedly enhancing the prediction precision and offering a more efficient way to forecast wind power.

1. Introduction

With the deepening of the global energy transition and sustainable development strategies [1,2,3], wind power, as a vital component of clean energy, is assuming an increasingly important role in the energy structure [4,5]. However, its intermittent, volatile, and random nature poses significant challenges to the safe and stable operation of power grids [6,7,8].

Accurate wind power prediction is crucial for grid scheduling, energy management, and economic operation [9,10]. The power output of wind farms is influenced by various factors, including meteorological variables such as the wind speed, wind direction, temperature, and humidity, as well as spatial features like the terrain and turbine distribution. The complex nonlinear relationships among these factors present multifaceted challenges for power prediction [11,12]. The wind power prediction methods that are available today fall broadly into three types. Specifically, physical methods construct prediction models based on numerical weather prediction (NWP) and the physical attributes of wind farms [13]. Studies [14,15] use NWP data as input and employ Kalman filtering and machine learning to predict short-term wind power.

The physical model method requires the creation of numerical weather forecast models, which are usually based on a large number of assumptions and are more suitable for long-term prediction. The statistical method [16,17,18,19] has low requirements regarding data samples and high accuracy for stationary sequences but is not able to deal with high-dimensional nonlinear problems.

As deep learning continues to advance, deep learning methods have achieved significant progress in wind power prediction. Recurrent neural networks like LSTM effectively capture temporal dependencies, CNNs excel in processing spatial features, and graph neural networks (GNNs) model complex spatial topological relationships. Ref. [20] employs an extensive short-term memory network coupled with backpropagation learning for complex training to forecast wind power in the ultra-short term. Ref. [21] suggests a comprehensive spatiotemporal network framework that merges a CNN with a bidirectional GRU for the accurate prediction of the wind velocity throughout the entire farm. Ref. [22] develops a spatiotemporal feature extraction module for adjacent wind farms and integrates these features into a Temporal Fusion Transformer to identify time-related correlations.

However, these neural network models—containing activation functions like sigmoid and tanh—are generally “black-box” models. The “black-box” nature of deep learning arises from the high complexity of their multi-layer nonlinear transformations: hidden layers map raw inputs to abstract high-dimensional features via activation functions, and complex parameter dependencies cause feature contributions to overlap, making it impossible to trace how specific inputs influence decision boundaries or model conclusions. Currently, most approaches rely on machine learning process parameter extraction to achieve interpretability. Ref. [23] points out that the multi-head attention mechanism can analyze input features in parallel, capture diverse spatiotemporal features of time series through different attention heads, decompose model decisions, and improve transparency. Ref. [24] proposes that the attention weights generated by it can be visualized in the form of heatmaps, showing the importance of data from different wind farms and power features in different time periods and presenting the decision logic in a quantitative manner. Therefore, this paper introduces attention mechanisms into deep learning models to improve model interpretability. Ref. [25] introduced a seasonal trend contrastive learning framework, which, for the first time, removed the seasonal trend representation used in contrastive learning to decouple time series, significantly enhancing the accuracy of time series prediction.

In addition to designing improved prediction models, decomposing the complex information contained in time series—with the aim of reducing the computational complexity in short-term WPF—is also an essential research focus [26]. Refs. [27,28] tackle wind power time series’ volatility and complexity via optimal VMD, improved complete ensemble empirical mode decomposition, and permutation entropy. Ref. [29] enhances differential evolution parameters through a sparrow search algorithm, integrating them with BiLSTM to boost the predictive accuracy, yet these models are unable to detect more profound temporal changes, leading to inadequate feature depiction for further analysis. Ref. [30] suggests a hybrid STL-IAOA-iTransformer model for brief WPF, employing STL decomposition to isolate seasonal and trend elements. Ref. [31] introduces a PA-TimesNet-BiLSTM model utilizing STL decomposition, markedly improving the prediction of photovoltaic power by detecting more profound trends and seasonal variations.

In wind power prediction, methods utilizing the spatial location information of wind farms have become a research hotspot. Studies enhance the predictive precision by amalgamating geographical coordinates, landscape characteristics, and adjacent wind farm data to develop models of spatial correlation. Ref. [32] introduces an IWC-DELM framework, utilizing past records from adjacent wind farms to construct input collections and procedures for absent data, employing a multifaceted averaging approach, thereby accurately recording the spatial relationships of the wind velocity in clusters. Ref. [33] utilizes convolutional neural networks (CNNs) to derive spatial characteristics from data on multi-turbine power and integrates them with long short-term memory (LSTM) to identify time-related patterns, facilitating the simultaneous forecasting of multi-turbine power and the analysis of terrain influences and wake effects. Utilizing wind farm spatial data markedly enhances the accuracy of predictions, offering essential support for precise wind energy predictions.

Recent studies have explored spatiotemporal contrastive learning (STCL) for wind power forecasting. Ref. [34] proposed a spatiotemporal graph contrastive learning framework with graph structure augmentation to enhance spatial modeling, but its single-branch encoder fails to explicitly decouple temporal features. Ref. [35] developed a hierarchical STCL approach emphasizing multi-scale spatial aggregation, yet it overlooks the critical temporal periodicity of wind power data. Ref. [36] introduced multi-graph contrastive learning via diverse graph structures, but this lacks feature interpretability. Beyond wind power, Ref. [37] applied STCL to weather forecasting (requiring adaptation to wind power’s periodic patterns), Ref. [38] modeled spatiotemporal correlations without contrastive learning, and Ref. [39] analyzed grid spatiotemporal dependencies but lacked STCL’s feature enhancement. While these works validate STCL’s potential, they neglect temporal decoupling, interpretability, or domain-specific tuning—gaps that are addressed here through seasonal trend disentanglement, multi-head attention, and wind-tailored STCL.

Aiming to address the issues of insufficient feature representation, inadequate feature decoupling, and poor interpretability in “black-box” deep learning models in existing short-term wind power prediction, this paper proposes a wind power prediction method based on spatiotemporal contrastive learning. The main concept revolves around employing a contrastive learning approach to automatically derive latent data representations, coupled with a dual-branch encoder designed for the effective separation of spatiotemporal features. Initially, STL decomposition is utilized to break down wind speed and power time series into their trend, seasonal, and residual elements, thereby capturing variations across multiple time scales. The geographical location data are then incorporated through a dedicated geographic encoder, transforming the coordinates of wind farms into spatial feature vectors that model positional relationships. This contrastive learning setup facilitates the unsupervised extraction of trend and seasonal features, ensuring that similar instances are represented by closely aligned embeddings, while dissimilar ones are spaced apart. An innovative aspect of this framework is the integration of a feature disentanglement loss function within the dual-branch encoder, which effectively isolates spatiotemporal features and prevents the feature confusion often encountered in conventional methods. Finally, an improved spatiotemporal graph convolutional network with a multi-head attention mechanism is designed to enhance model interpretability. Experiments on datasets from Wind Farm A and Wind Farm B in Northwestern China show that the proposed method significantly improves the prediction accuracy compared to common baselines.

The structure of the subsequent sections of this paper is as follows:

Section 2, titled “Wind Power Prediction Model Based on Spatiotemporal Contrastive Learning”, expounds on the overall architecture and operation mode of the prediction model;

Section 3, titled “Theoretical Methodology”, introduces the relevant theoretical knowledge and specific methods used in the research;

Section 4, titled “Example Analysis”, explains the specific situations of the experimental examples and the analysis process;

Section 5, the “Results and Discussion”, presents the experimental results and carries out relevant discussions;

Section 6, the “Conclusions and Summary”, summarizes the study’s core content, key conclusions, significance, limitations, and future directions.

2. Wind Power Prediction Model Based on Spatiotemporal Contrastive Learning

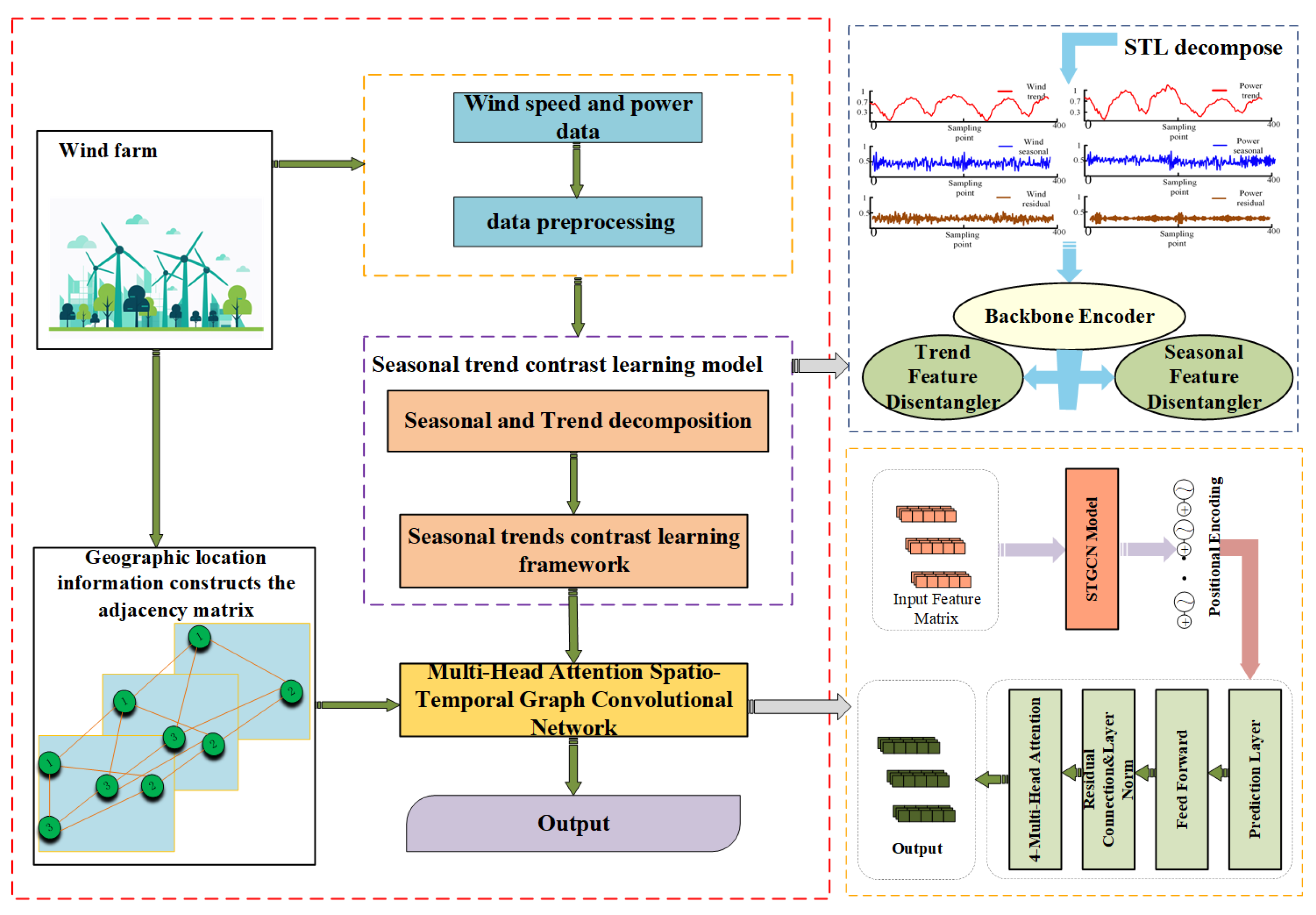
The structure of the wind power prediction model based on spatiotemporal contrastive learning, proposed in this paper, is shown in Figure 1.

First, wind speed and power data are collected and subjected to preliminary processing. Concurrently, an adjacency matrix is developed using geographic location details to characterize spatial correlations. To identify these spatial correlations, a seasonal trend contrastive learning model is employed: the data are first decomposed into seasonal and trend components, which are then used in the model for analysis. The contrast learning framework is employed to explore the correlations and differences between features. The trend and seasonal feature disentanglers independently examine their signals by incorporating STL decomposition for improved data refinement and using the primary encoder for the initial feature encoding. Additionally, a multi-head attention-based spatiotemporal graph convolutional network is utilized. The graph convolutional layer leverages the adjacency matrix to capture spatial relationships, while the multi-head attention mechanism emphasizes critical information through weighted focus, and the temporal convolutional layer uncovers temporal dynamics. Ultimately, the insights gained from this comprehensive process are applied to optimize wind farm operations and improve power forecasting, transforming data-driven insights into tangible real-world solutions.

3. Theoretical Methodology

3.1. Seasonal Trend Contrastive Learning Model

3.1.1. Seasonal Trend Decomposition (STL)

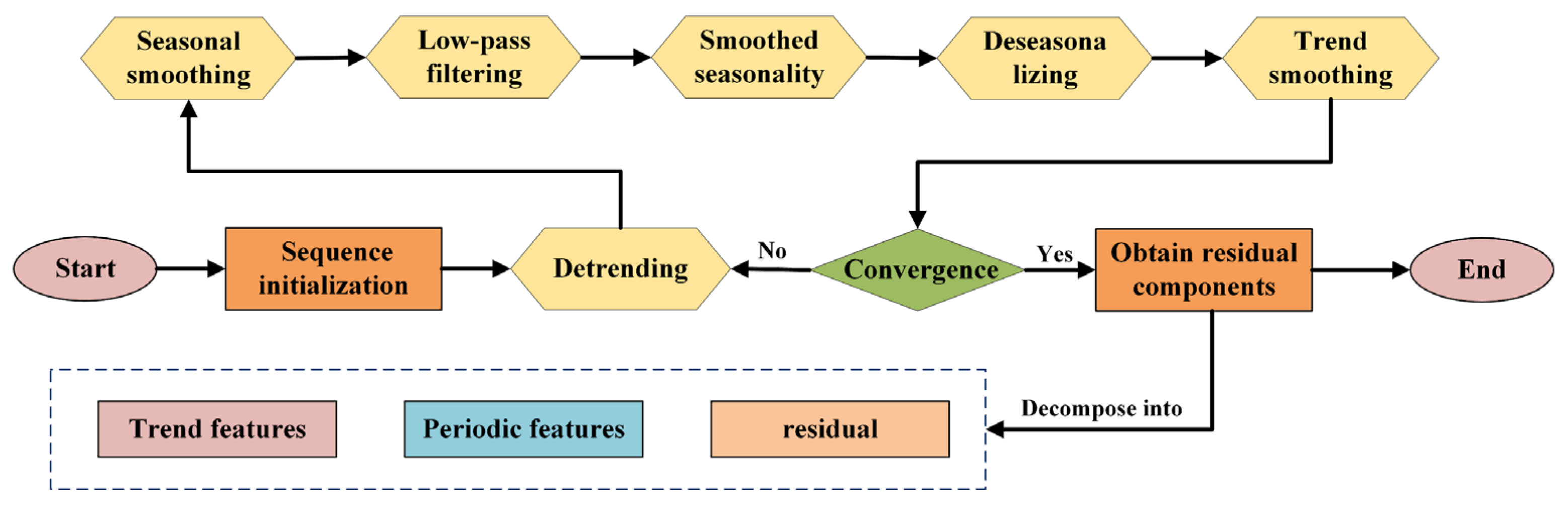
STL splits the time series into trend, seasonal, and residual components. The STL algorithm flowchart is shown in Figure 2.

The inner loop updates the seasonal and trend components through detrending and smoothing, while the outer loop reduces the impact of outliers via robust weights. The steps are as follows, with (1)–(6) being the inner loop.

(1) Detrending: In the (k + 1)-th inner iteration, first, remove the trend component obtained from the previous round from the original series to obtain a detrended sequence $Y_t^{\det rend}=Y_t-T_t^{(k)}$.

(2) Seasonal Smoothing: Perform preliminary smoothing on the seasonal component to obtain $C_t^{(k+1)}$.

(3) Low-Pass Filtering: Proceed to refine the aforementioned outcome by employing moving average and local weighted regression techniques to create a refined sequence $L_t^{(k+1)}$.

(4) Seasonal Component Extraction: Compute $S_t^{(k+1)}=C_t^{(k+1)}-L_t^{(k+1)}$ to obtain the pure seasonal component.

(5) Seasonal Adjustment: Calculate $Y_t^{\mathrm{de}season}=Y_t-S_t^{(k+1)}$ and remove the seasonal influence from the original data.

(6) Trend Estimation: Apply local weighted regression to smooth the seasonally adjusted data and extract the trend component $T_t^{(k+1)}$.

(7) In the outer loop, the residual component is obtained through calculating $R_t^{(k+1)}=Y_t-S_t^{(k+1)}-T_t^{(k+1)}$.

In the algorithm, $Y_t$ represents the original time series value at time step t;

$T_t^{(k)}$ stands for the trend component at time step t after the k-th inner iteration;

$Y_t^{\det rend}$ is the detrended sequence, obtained by subtracting the trend component from the original series at time step t;

$C_t^{(k+1)}$ denotes the temporarily smoothed seasonal component result at time step t in the (k + 1)-th inner iteration;

$L_t^{(k+1)}$ is the refined seasonal sequence at time step t after low-pass filtering in the (k + 1)-th inner iteration;

$S_t^{(k+1)}$ is the pure seasonal component extracted at time step t in the (k + 1)-th inner iteration;

$Y_t^{\mathrm{de}season}$ is the seasonally adjusted sequence at time step t;

$T_t^{(k+1)}$ is the updated trend component at time step t after seasonal adjustment in the (k + 1)-th inner iteration;

$R_t^{(k+1)}$ is the residual component at time step t, calculated as the original series minus the seasonal and trend components in the (k + 1)-th iteration.

For data points that stand out as anomalies within the residual sequence, the algorithm assigns specific weight factors to diminish their influence in later inner iterations. Given that wind power data display clear daily patterns, this research opts for an additive time series decomposition approach rather than a multiplicative one. This decision better reflects the inherent characteristics of the data and allows for the more precise extraction of each underlying component in the dataset.

For the key parameters of the STL decomposition in this study, the window size for seasonal smoothing is set to 144 (corresponding to 144 sampling points per day, consistent with the 10 min sampling frequency of the wind farm data) to ensure the effective capture of daily seasonal patterns of wind power. The number of inner iterations is set to 15 and that of outer iterations to 5, a configuration that balances decomposition accuracy and computational efficiency—pre-experiments verify that increasing the number of iterations beyond this range does not significantly improve component separation but doubles the runtime.

3.1.2. Seasonal Trend Contrastive Learning Framework

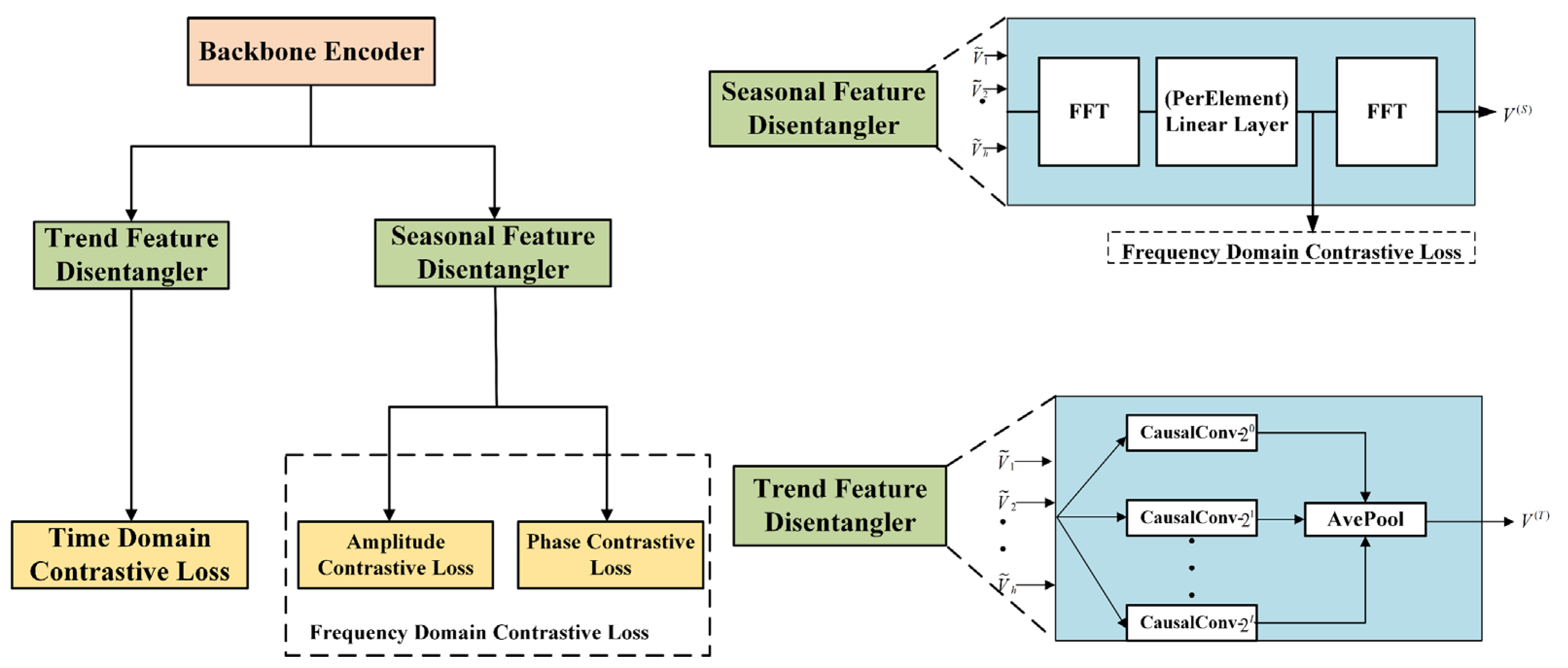
The framework learns disentangled seasonal trend representations by ensuring that, for each time step, the model captures separate seasonal and trend components. The seasonal trend contrastive learning framework is shown in Figure 3.

First, a backbone encoder projects the observed time series data into a latent space, and trend and seasonal representations are constructed using these intermediate latent embeddings. Specifically, to extract trend representations, the trend feature disentangler employs a set of autoregressive experts, and its learning is driven by a temporal contrastive loss ${\mathcal{L}}_{time}$. The seasonal feature disentangler employs a trainable Fourier layer to identify seasonal patterns and leverages a frequency-domain contrastive loss that considers both amplitude ${\mathcal{L}}_{amp}$ and phase components ${\mathcal{L}}_{phase}$ during the learning process.

The model is learned in an end-to-end manner, and the overall loss function is

$$\mathcal{L}={\mathcal{L}}_{time}+{\displaystyle \frac{\alpha }{2}}({\mathcal{L}}_{amp}+{\mathcal{L}}_{phase})$$

(1)

where α is a hyperparameter that balances the trade-off between the trend factor and the seasonal factor. To obtain the final output representation, the outputs from the trend disentangler and the seasonal feature disentangler are combined via concatenation.

3.1.3. Trend Feature Disentangler (TFD)

The TFD is a mixture of $L+1$ autoregressive experts, where $L={\log }_2(h/2)$, and h is the hidden feature dimension that controls the scale of the number of experts. Each expert is implemented as a one-dimensional causal convolution, where the ith expert has a kernel size of $2^i$ (i is the expert index, ranging from [0, L], with a total of L + 1 experts). Each expert outputs a matrix ${\tilde{V}}^{(T,i)}=\mathrm{CausalConv}(\tilde{V},2^i)$. Ultimately, an average pooling operation is applied to these outputs, yielding the final trend representations:

$$V^{(T)}=\mathrm{AvePool}({\tilde{V}}^{(T,0)},{\tilde{V}}^{(T,1)},\dots ,{\tilde{V}}^{(T,L)})={\displaystyle \frac{1}{(L+1)}}{\displaystyle \sum _{i=0}^L{\tilde{V}}^{(T,i)}}$$

(2)

where $V^{(T)}=\mathrm{AvePool}(\dots )$ denotes the average pooling operation.

Time-domain contrastive loss is employed to help differentiate between various trend representations over time. This method leverages a momentum encoder to generate positive pairs, ensuring consistent and reliable similarity, while a dynamic queue acts as a dictionary to supply negative pairs, facilitating contrastive learning in the temporal dimension. Given N samples and K negative samples, the time-domain contrast loss is

$${\mathcal{L}}_{\mathrm{time}}={\displaystyle \sum _{i=1}^N-}\log {\displaystyle \frac{\exp (q_i\cdot k_i/\tau )}{\exp (q_i\cdot k_i/\tau )+{\displaystyle \sum _{j=1}^K\exp }(q_i\cdot k_j/\tau )}}$$

(3)

Given a sample V (T), we first select a random time step t for contrast loss calculation, and then use a projection head (implemented as a one-layer MLP) to generate q and k—these two vectors correspond to the augmented versions of the relevant samples in the momentum encoder and dynamic dictionary, respectively. $\tau$ is a temperature coefficient in the time-domain contrastive loss, controlling the sharpness of the contrastive distribution.

3.1.4. Seasonal Feature Disentangler (SFD)

The SFD primarily adopts the DFT to convert intermediate features to the frequency domain, followed by a learnable Fourier layer. The DFT is applied along the time dimension and maps the time-domain representation into the frequency domain, $\mathcal{F}(\tilde{V})\in {ℂ}^{F\times d}$, where $\mathrm{F}=|\mathrm{h}/2|+1$ is the number of frequencies. Next, the learnable Fourier layer—designed to enable interactions between frequency components—is implemented via a chained linear layer. It applies an affine transformation to each frequency, and each frequency is assigned a unique set of complex-valued parameters, as translation invariance is not required for this layer. Finally, we use an inverse DFT operation to transform the representation back to the time domain.

This layer produces a final output matrix, which functions as the seasonal representation, $V^{(S)}\in {ℝ}^{h\times d_S}$. Formally, the i,k-th element of the output can be denoted as

$$V_{i,k}^{(S)}={\mathcal{F}}^{-1}\left({\displaystyle \sum _{j=1}^d{A}_{i,j,k}}\mathcal{F}{(\tilde{V})}_{i,j}+B_{i,k}\right)$$

(4)

where $A\in {ℂ}^{F\times d\times d_S}$, $B\in {ℂ}^{F\times d_S}$ are the parameters of each elemental linear layer.

The frequency-domain contrast loss is shown in Figure 3. The inputs to the frequency-domain loss function are ex-ifft representations, denoted by F ∈ CF × dS. In the frequency domain, these representations take the form of complex values. In order to learn representations that can distinguish between different seasonal patterns, a frequency-domain loss function is introduced. Because our data augmentation essentially acts as an intervention on the error term, the seasonal patterns remain unaffected. To address the challenge of designing a loss function using complex-valued representations, each frequency can be uniquely characterized by its amplitude and phase, $|F_{i,:}|$ and $\varphi (F_{i,:})$.

$${\mathcal{L}}_{\mathrm{amp}}={\displaystyle \frac{1}{FN}}{\displaystyle \sum _{i=1}^F{\displaystyle \sum _{j=1}^N-}}\log {\displaystyle \frac{\exp (|F_{i,:}^{(j)}|\cdot |{(F_{i,:}^{(j)})}^{\prime }|)}{\exp (|F_{i,:}^{(j)}|\cdot |{(F_{i,:}^{(j)})}^{\prime }|)+{\displaystyle \sum _{k\ne j}^N\exp }(|F_{i,:}^{(j)}|\cdot |F_{i,:}^{(k)}|)}}$$

(5)

$${\mathcal{L}}_{\mathrm{phase}}={\displaystyle \frac{1}{FN}}{\displaystyle \sum _{i=1}^F{\displaystyle \sum _{j=1}^N-}}\log {\displaystyle \frac{\exp (\varphi (F_{i,:}^{(j)})\cdot \varphi ({(F_{i,:}^{(j)})}^{\prime }))}{\exp (\varphi (F_{i,:}^{(j)})\cdot \varphi ({(F_{i,:}^{(j)})}^{\prime }))+{\displaystyle \sum _{k\ne j}^N\exp }(\varphi (F_{i,:}^{(j)})\cdot \varphi (F_{i,:}^{(k)}))}}$$

(6)

where $F_{i,:}^{(j)}$ is the jth sample in the small batch; ${(F_{i,:}^{(j)})}^{\prime }$ is the expanded version of this sample; F is the number of frequency components; N is the number of samples in each positive sample group in the frequency-domain contrastive loss; and $\varphi (*)$ is a phase projection function.

3.2. Multi-Head Attention Spatiotemporal Graph Convolutional Network

Considering the spatial dependence and temporal dynamics of data in wind power prediction is crucial. Spatiotemporal graph convolutional networks bring together the strengths of graph convolutional networks and temporal convolutional networks, enabling them to effectively analyze data across both space and time. In addition, the multi-attention mechanism enhances the model’s ability to capture information by learning different subspace representations of the information in parallel, which improves the accuracy of prediction. The multi-head attention spatiotemporal graph convolutional network is shown in Figure 4.

3.2.1. Graph Convolution Layer

The graph convolution layer focuses on the spatial characteristics of nodes, identifying spatial interdependencies through the dissemination and consolidation of data from adjacent nodes within the graph’s framework. The formula for the graph convolution layer is

$$H^{(l+1)}=\sigma ({\tilde{D}}^{-{\displaystyle \frac{1}{2}}}\tilde{A}{\tilde{D}}^{-{\displaystyle \frac{1}{2}}}{H}^{(l)}{W}^{(l)})$$

(7)

$\sigma$ is the activation function, and ReLU is used in this paper. $H^{(l)}$ is the node feature matrix of the $\tilde{A}=A+1$ layer; $\tilde{A}$ is the adjacency matrix A plus the unit matrix $l$, which is intended to include each node’s own features; $W^{(l)}$ is the weight matrix of the layer; and $\tilde{D}$ is the degree matrix of $\tilde{A}$, whose diagonal elements are ${\tilde{D}}_{ii}={\displaystyle {\sum }_{ j}{\tilde{A}}_{ij}}$.

3.2.2. Time Convolution Layer

A time convolution layer is used to capture dynamic features of time series data. It usually uses one-dimensional convolution to deal with features in the time dimension:

$$H_t^{(l+1)}=\sigma (W^{(l)}*H_t^{(l)}+b^{(l)})$$

(8)

$H_t^{(l)}$ denotes the time step in the $l$ th layer; $W^{(l)}$ and $b^{(l)}$ are the convolution kernel and bias, respectively. The size of the convolution kernel used in this paper is 6, and the bias is 64.

3.2.3. Multi-Attention Layer

The multi-attention layer combines spatial and temporal features, enhancing the model’s ability to detect and distinguish key information by simultaneously attending to various subspaces.

$$\left\{\begin{array}{l}\mathrm{MultiHead}(Q,K,V)=\mathrm{Concat}({\mathrm{head}}_1,{\mathrm{head}}_2,\dots ,{\mathrm{head}}_h)W^o\\ {\mathrm{head}}_i=\mathrm{Attention}(Q{W}_i^Q,K{W}_i^K,V{W}_i^V)\\ \mathrm{Attention}(Q,K,V)=\mathrm{sofmax}({\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}})V\end{array}\right.$$

(9)

$Q,K,V$ are the query, key, and value matrices, respectively. $W_i^Q$, $W_i^K$, $W_i^V$ and $W^o$ are the learnable parameter matrices. $d_k$ is the dimension of the key vector, and $h$ is the number of heads, where $h=4$.

3.3. Explanation of the Core Process of the Methodological Framework

To clarify the implementation logic of the proposed spatiotemporal contrastive learning-based wind power prediction model, its core process is as follows.

Data Preprocessing and STL Decomposition: Input time series data such as wind speed and power. First, perform min-max normalization (calculate the difference between the original variable and the minimum value of the variable and then divide it by the difference between the maximum and minimum values of the variable) to eliminate the influence of dimension differences among different features. Then, use the STL decomposition method (with a window size of 144, 15 inner iterations, and 15 outer iterations) to decompose the time series data into trend components, seasonal components, and residual components. Combine these three components to form a new decomposed feature matrix, laying the foundation for subsequent feature learning.

Spatiotemporal Contrastive Feature Learning: Generate two types of augmented views for each sample in the decomposed feature matrix. In the time domain, randomly crop the sample sequence, with the length of the cropped sequence being 70–100% of the original sequence length. In the spatial domain, add Gaussian noise with a standard deviation of 0.05 to the samples to simulate minor fluctuations in actual data. Next, input the two types of augmented views into the dual-branch encoder to obtain the corresponding feature embedding vectors. To optimize the effect of feature learning, introduce the temporal contrastive loss and frequency-domain contrastive loss. The temperature coefficient of the temporal contrastive loss is set to 0.07, and the frequency-domain contrastive loss includes the amplitude loss and phase loss. The total contrastive loss is calculated by the weighted sum of the temporal contrastive loss, amplitude loss, and phase loss, where the weight coefficient is used to balance the influences of trend factors and seasonal factors.

Multi-Head Attention STGCN Prediction: Input the features optimized by contrastive learning into the spatiotemporal graph convolutional network (STGCN), which consists of a graph convolution layer, a temporal convolution layer, and a multi-head attention layer. The graph convolution layer captures the spatial correlations between different nodes (wind turbines) in the wind farm based on the adjusted adjacency matrix (original adjacency matrix plus identity matrix). The temporal convolution layer adopts one-dimensional convolution operations, with a convolution kernel size of 6 and bias of 64, to extract the dynamic features of the time series data. The multi-head attention layer is set with 4 attention heads and weights the key features by concatenating the output of each attention head and multiplying it with the learnable parameter matrix, so as to highlight the role of important information. Finally, input the features processed by the above layers into the linear layer to obtain the final predicted wind power value.

Joint Training: The total loss of the model is composed of three parts: prediction loss, contrastive loss, and disentanglement loss. The prediction loss is calculated using the mean absolute error (MAE). The contrastive loss and disentanglement loss are weighted and summed with the prediction loss through weight coefficients of 0.1 and 0.05, respectively, to obtain the total loss function. During the training process, the Adam optimizer is used, with a learning rate of 0.001, and the model is trained iteratively for 100 epochs. At the same time, the dataset is divided into a training set, a validation set, and a test set in a ratio of 6:2:2. The training set is used for model parameter learning, the validation set is used for the optimization and adjustment of the model’s hyperparameters, and the test set is used to evaluate the final generalization ability of the model.

4. Example Analysis

For experimental validation, datasets from Wind Farm A and Wind Farm B, both located in Northwest China, are utilized, and corresponding experiments are conducted. Each wind farm’s dataset is split into three parts: a training set, a validation set, and a test set. To guarantee experimental fairness and validate the overall stability of the model, each model is tested 10 times independently. The final evaluation metrics of each model are determined by averaging the evaluation metrics from these 10 repetitions, and all experimental results in this paper are retained to three decimal places.

The operational datasets of Wind Farms A and B are private, provided by local wind power management for academic research only. Due to commercial and operational confidentiality, the raw data cannot be shared publicly. However, the study’s methodology, experimental design, and result analysis are detailed and transparent, enabling replication with other accessible wind farm datasets.

The mean absolute error (MAE) and the root mean square error (RMSE) are adopted as the evaluation metrics of the model, as shown in

Table 1. Error index.

Metric	Equation	Definition
RMSE	$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{\left(y_{\mathrm{i}}-{\widehat{y}}_{\mathrm{i}}\right)}^2}}$	Root mean square error
MAE	$MAE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\left|y_{\mathrm{i}}-{\widehat{y}}_{\mathrm{i}}\right|}$	Mean absolute error

.

The RMSE quantifies the square root of the average squared difference between the predicted values $y_i$ and actual values ${\widehat{y}}_i$, emphasizing larger errors due to the squaring operation. The formula is

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{\left(y_{\mathrm{i}}-{\widehat{y}}_{\mathrm{i}}\right)}^2}}$$

(10)

where $n$ denotes the number of samples. A lower RMSE indicates higher prediction accuracy, being especially sensitive to outliers.

The MAE calculates the average of the absolute differences between the predicted and actual values, reflecting the overall error magnitude linearly. The formula is

$$MAE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\left|y_{\mathrm{i}}-{\widehat{y}}_{\mathrm{i}}\right|}$$

(11)

The MAE is robust to extreme values and provides a straightforward measure of the average prediction deviation.

4.1. Data Preprocessing

There are many abnormal operation data in the original wind power dataset, which will affect the overall operation performance of the model. In order to establish a high-precision wind power prediction model, this paper adopts the following steps to preprocess the original data.

(1) There are many missing values in the original wind power data, whose existence will affect the accuracy of the model. In order to reduce the effect of the missing values on the model’s accuracy, this paper proposes to use the interpolation method to fill in the missing values of the system.

(2) The interpolated dataset is divided into training set, validation set, and test set according to the ratio of 6:2:2; among them, the training set and validation set are used to optimize and adjust the hyperparameters of the model, and the test set is used to evaluate the final generalization ability of the model.

(3) In order to further improve the convergence effect of the prediction model, it is necessary to normalize the data, and the data normalization formula is as follows:

$$x^{*}={\displaystyle \frac{x-x_{\min }}{x_{\max }-x_{\min }}}$$

(12)

where $x$ is the input variable to be normalized; $x^{*}$ denotes the normalized value; and $x_{\max }$ and $x_{\min }$ are the maximum and minimum values of the input variable, respectively.

(4) For the spatial distance information between different wind turbines, the adjacency matrix is constructed as an input to the graph network, and the results of the adjacency matrix visualization for wind farms are shown in Appendix A.

4.2. Analysis of Prediction Results

4.2.1. Wind Farm A Power Prediction Results

The time interval of the historical operation data of Wind Farm A is 10 min, with a total of 144 sampling points in a day, and the time span is from 1 March 2022 to 1 June 2022, with a total of 13,247 pieces of operation data. The training set contains 7949 entries, while both the validation and test sets have 2649 entries each.

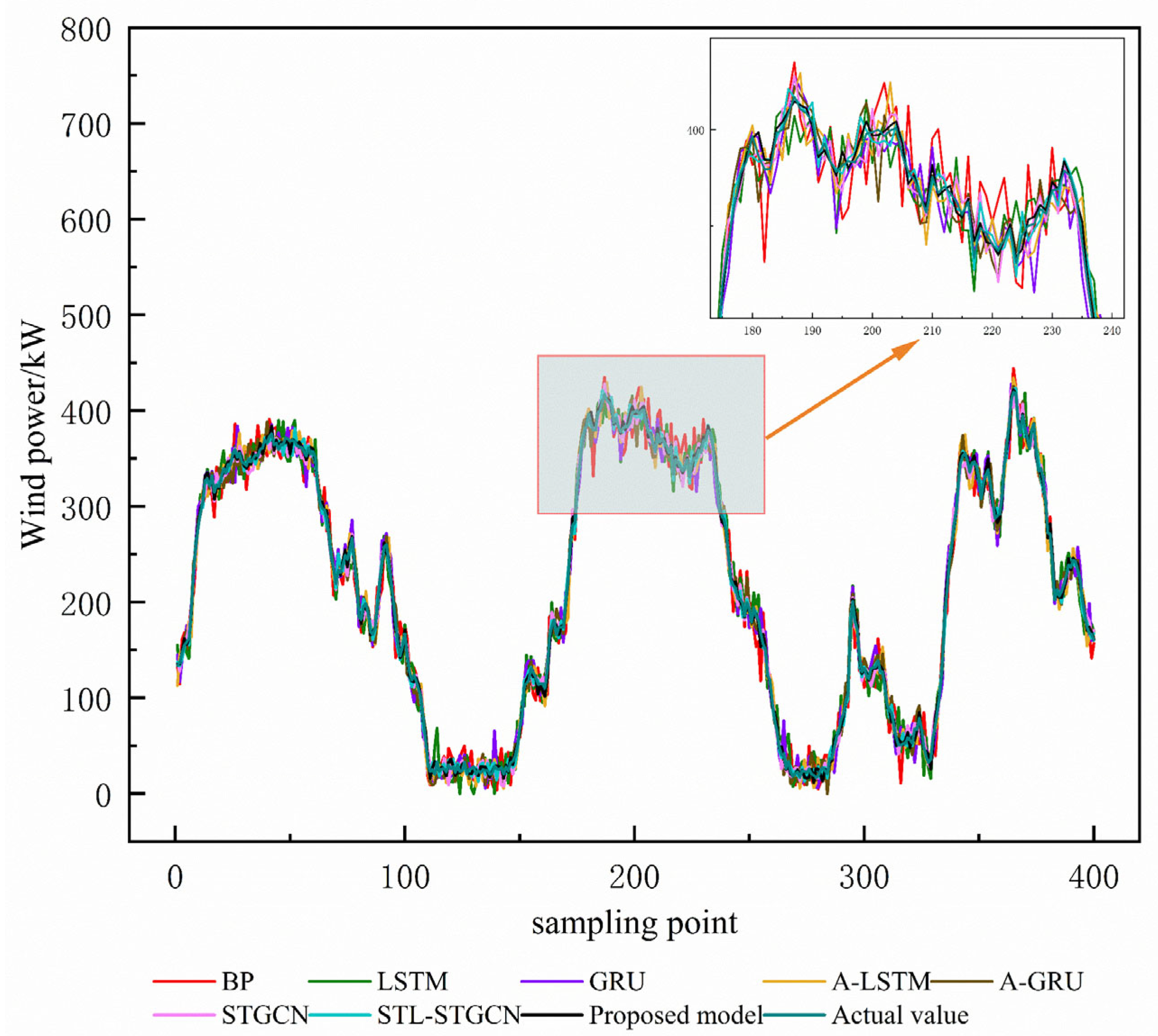
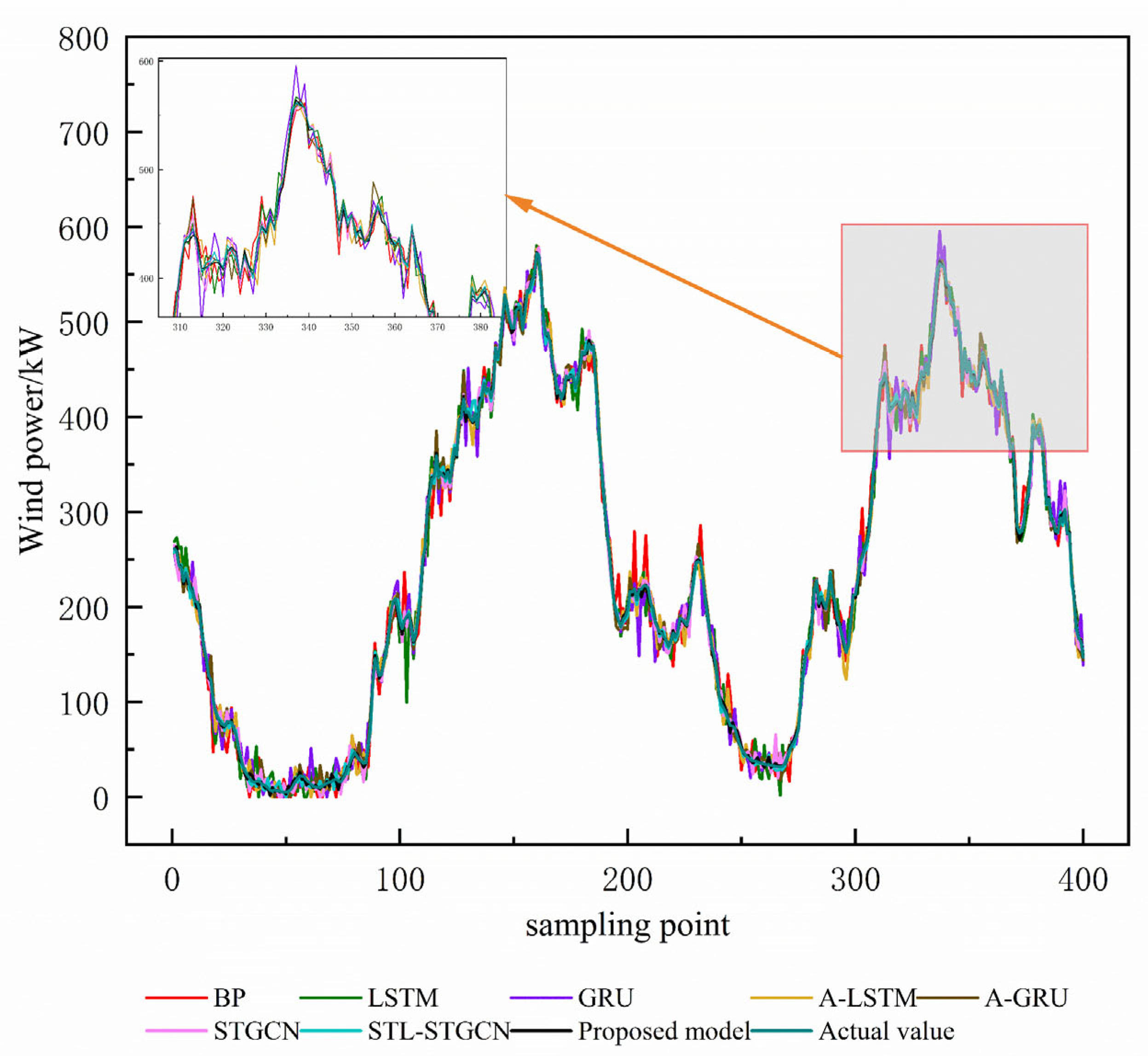
The wind power prediction results of the above models are shown in Figure 5. The evaluation index results of each model are listed in

Table 2. Results of the RMSE and MAE assessment for Wind Farm A.

Model	RMSE	MAE
BP	8.748	7.881
LSTM	6.388	4.535
GRU	7.223	5.342
A-LSTM	5.625	3.856
A-GRU	5.918	3.965
STGCN	3.871	2.410
STL-STGCN	2.940	1.371
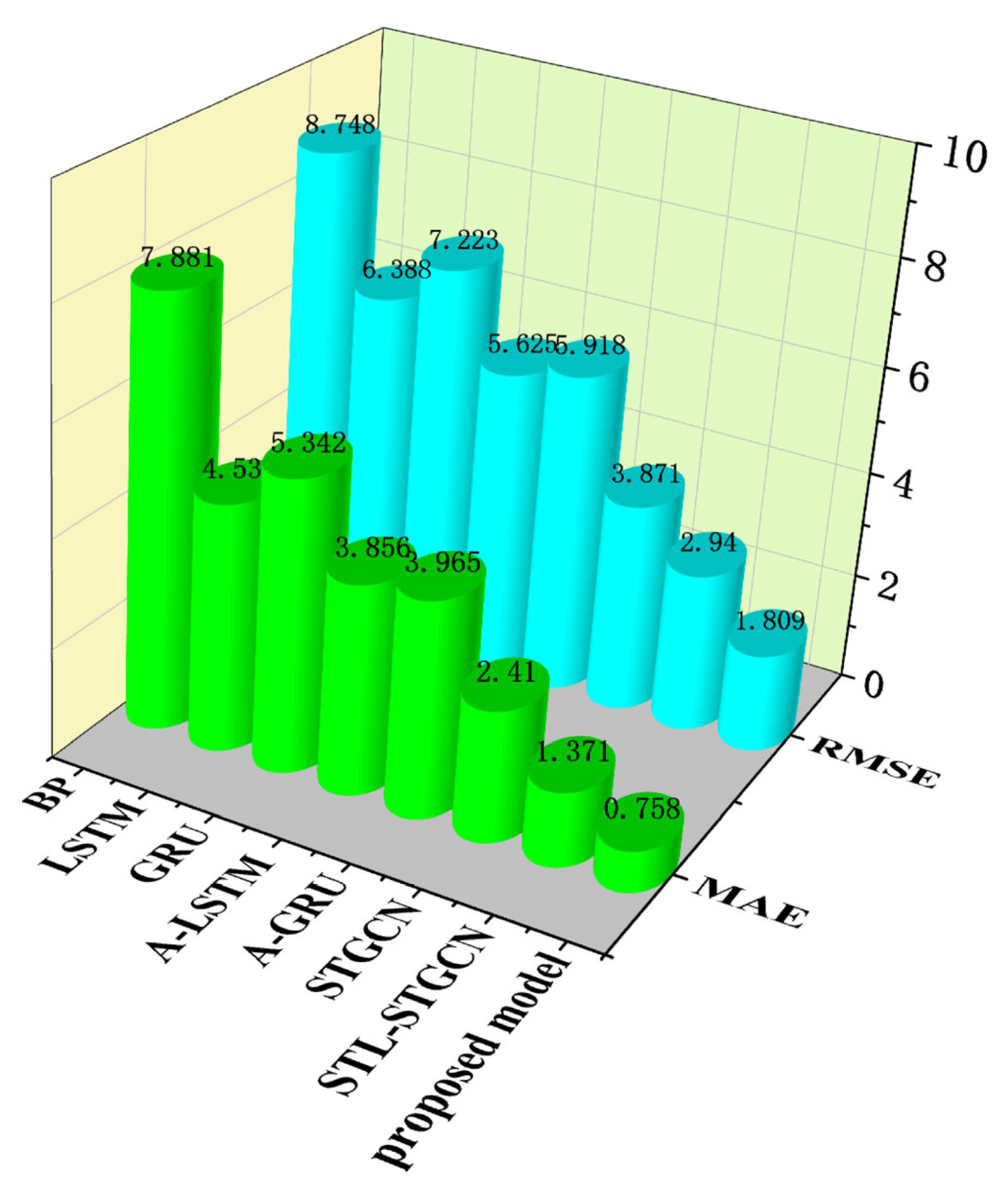
Proposed model	1.809	0.758

. The experimental data show that the prediction performance of the BP model lags behind that of other deep learning algorithms significantly. This phenomenon reveals the limitations of traditional shallow neural networks in deep feature extraction from wind power data. As improved structures of recurrent neural networks, LSTM and the GRU can effectively capture the time dependence of long sequence data and alleviate the problems of gradient vanishing and gradient explosion. Compared with the traditional BP neural network, the GRU and LSTM reduce the MAE by 42.45% and 32.20% and the RMSE by 26.98% and 17.43%.

The introduction of the attention mechanism significantly improves the model performance. Compared with the GRU and LSTM without adding the attention module, the MAEs of A-GRU and A-LSTM are reduced by 25.78% and 14.97%, and the RMSE is reduced by 18.08% and 11.94%, respectively. Compared with the traditional attention construction methods, this paper designs a multi-head attention mechanism that can extract effective features from nonlinear WT sequences more efficiently. In comparison to the outstanding results achieved by the A-LSTM model, the approach presented in this paper reduces the MAE and RMSE metrics by an impressive 80.34% and 67.84%, respectively.

This substantial improvement demonstrates that incorporating a multi-head attention mechanism enables the more thorough extraction of the complex spatiotemporal relationships within multi-dimensional wind power data, leading to a notable boost in prediction precision. The results regarding the predicted RMSE and MAE evaluation metrics for different models for Wind Farm A are shown in Figure 6.

Differing from the traditional network structure mentioned above, the prediction model proposed in this paper is able to strongly decouple the graph structural correlation and temporal features of the original wind power data by comparing the learning frameworks, thus obtaining more accurate prediction results. Compared with the STL-STGCN algorithm, the MAE and RMSE metrics of the model exhibit reductions of 44.71% and 38.47%, respectively.

The introduction of the STL module effectively enhances the node feature extraction capability. Compared with the STGCN model, the MAE of the model with the STL decomposition method is reduced by 43.11%. The experimental results demonstrate that the model introduced in this study outperforms all other network architectures, with every error metric reaching its best possible score. This confirms the model’s cutting-edge capabilities and its strong, reliable prediction performance.

4.2.2. Wind Farm B Power Prediction Results

In order to further verify the robustness and accuracy of the proposed wind power prediction method, this paper adopts the prediction method to train and predict the data of Wind Farm B. The time interval of the historical operation data of Wind Farm B is 10 min, and there are 144 sampling points with 13,103 data per day. Figure 7 shows the prediction results of Wind Farm B under different models, and

Table 3. Results of the RMSE and MAE assessment for Wind Farm B.

Model	RMSE	MAE
BP	16.247	10.206
LSTM	14.232	9.179
GRU	14.212	9.164
A-LSTM	8.193	6.149
A-GRU	8.970	6.036
STGCN	5.697	4.076
STL-STGCN	3.389	2.903
Proposed model	1.881	1.130

and Figure 8 show the evaluation index results for each model in Wind Farm B.

When analyzing the power prediction curve, it can be clearly perceived that the wind power is characterized by stochasticity, volatility, and dispersion due to the wind, presenting a complex and variable situation. In the past, the traditional single deep neural network models, when faced with different datasets, exhibited different strengths and weaknesses, with poor stability. This demonstrates that traditional deep learning algorithms have obvious adaptability shortcomings when dealing with various situations involving complex data.

The model proposed in this paper has significant advantages in terms of prediction accuracy. The data in the table show that the model is optimal in all error evaluation indices. It can more accurately identify the trends of wind power data and then provide accurate predictions of power changes. Compared with traditional neural network models, the MAE value of the model in this paper is only 1.130, and the RMSE value is 1.881, which intuitively show the excellent stability and prediction accuracy of the model.

The model constructed in this paper has excellent performance in feature extraction and nonlinear mapping, and its performance is far better than that of traditional machine learning algorithms. By integrating the multi-attention mechanism alongside a spatiotemporal map convolutional network, the model’s input features are significantly refined, leading to a marked boost in its ability to extract pertinent information. This paper adopts a seasonal trend comparison learning framework, which successfully disentangles spatiotemporal features—sidestepping the common issue of feature overlap that plagues conventional approaches. Moreover, the model proposed in this paper achieves the best results in all evaluation indices. The experimental results strongly confirm the effectiveness and superiority of the spatiotemporal contrast learning wind power prediction model. Even when the wind turbine’s output undergoes substantial fluctuations and falls within a phase of rapid power variation, the prediction approach outlined in this paper continues to deliver reliable and accurate forecasts.

4.3. Comparison of Multi-Step Prediction Results

In the previous experiments, we used a single-step prediction method. To delve deeper into how well the proposed prediction method performs in a multi-step forecasting setting, this section evaluates its accuracy against alternative models using data from Wind Farm A and Wind Farm B. The comparison aims to shed light on the strengths and limitations of our approach in predicting multiple steps ahead. The results of the multi-step prediction experiments are summarized in the following. Specifically, we conduct one-step, two-step, and three-step wind power prediction experiments. The RMSE and MAE results for Wind Farm A and Wind Farm B in multi-step prediction are displayed in

Table 4. RMSE and MAE evaluation index results of multi-step prediction for different models.

Wind Farm	Model	1 Step		2 Steps		3 Steps
		RMSE	MAE	RMSE	MAE	RMSE	MAE
A	BP	8.748	7.881	25.784	17.226	31.154	22.877
	LSTM	6.388	4.535	21.423	13.448	25.976	18.762
	GRU	7.223	5.342	21.803	13.783	28.062	20.162
	A-LSTM	5.625	3.856	19.778	12.483	23.590	17.284
	A-GRU	5.918	3.965	19.422	12.768	22.429	16.375
	STGCN	3.871	2.410	8.382	6.313	11.391	9.325
	STL-STGCN	1.940	1.371	4.950	3.287	6.359	5.298
	Proposed model	1.809	0.758	2.918	1.961	3.826	2.771
B	BP	16.247	10.206	30.319	21.268	41.387	30.328
	LSTM	14.232	9.179	27.965	19.203	38.316	28.250
	GRU	14.212	9.164	27.043	18.886	37.289	27.729
	A-LSTM	8.193	6.149	19.221	12.169	25.263	18.208
	A-GRU	8.970	6.036	18.715	11.819	22.857	16.270
	STGCN	5.697	4.076	10.142	8.974	17.201	11.910
	STL-STGCN	3.389	2.903	5.713	4.643	7.901	6.501
	Proposed model	1.881	1.130	3.185	2.312	4.701	3.092

.

(1) The BP model is significantly inferior to other deep learning algorithms in multi-step prediction. Taking the Wind Farm A dataset as an example, compared with the BP neural network model, the MAEs of the GRU and LSTM are reduced by about 19.98% and 21.88% in two-step prediction and 11.88% and 17.99% in three-step prediction, respectively.

(2) The attention mechanism shows good results in multi-step prediction. Taking the Wind Farm B dataset as an example, compared with the GRU network model, the MAE of A-GRU is reduced by 7.58% and 18.78% in two-step prediction and three-step prediction, respectively, which confirms the effectiveness of the attention mechanism applied to wind power prediction.

(3) The graph structure network also shows good results in multi-step prediction. Compared with other deep learning models, the prediction accuracy of the model with STGCN has a significant improvement.

(4) Due to the cumulative effect of errors, most of the models show an increase in the error evaluation index with an increase in the prediction time step. However, the model in this paper performs well, with MAE values of 1.961 and 2.771 in the two-step and three-step prediction of the Wind Farm A dataset, respectively. Moreover, it has MAE values of 2.312 and 3.092 in the two-step and three-step prediction of the Wind Farm B dataset, respectively, indicating that the method proposed in this paper is significantly better than the other comparative models.

To further substantiate the statistical significance of the proposed model’s performance improvements, a two-tailed paired t-test was conducted on the prediction error residuals (RMSE/MAE) of the proposed model and baseline models (STGCN, LSTM, BP) across 50 independent test subsets (each containing 200 samples randomly selected from the test set). The results show that, for Wind Farm A’s single-step prediction, the p-values when comparing the proposed model with STGCN, LSTM, and BP are 3.2 × 10⁻⁸, 1.5 × 10⁻⁹, and 4.7 × 10⁻¹¹, respectively; for Wind Farm B, the corresponding p-values are 5.1 × 10⁻⁷, 2.3 × 10⁻⁸, and 6.9 × 10⁻¹⁰. All p-values are far lower than the significance level α = 0.05, indicating that the reduction in the prediction errors of the proposed model compared to the baseline models is statistically significant, thus confirming the model’s stable superiority.

4.4. Ablation Experiment

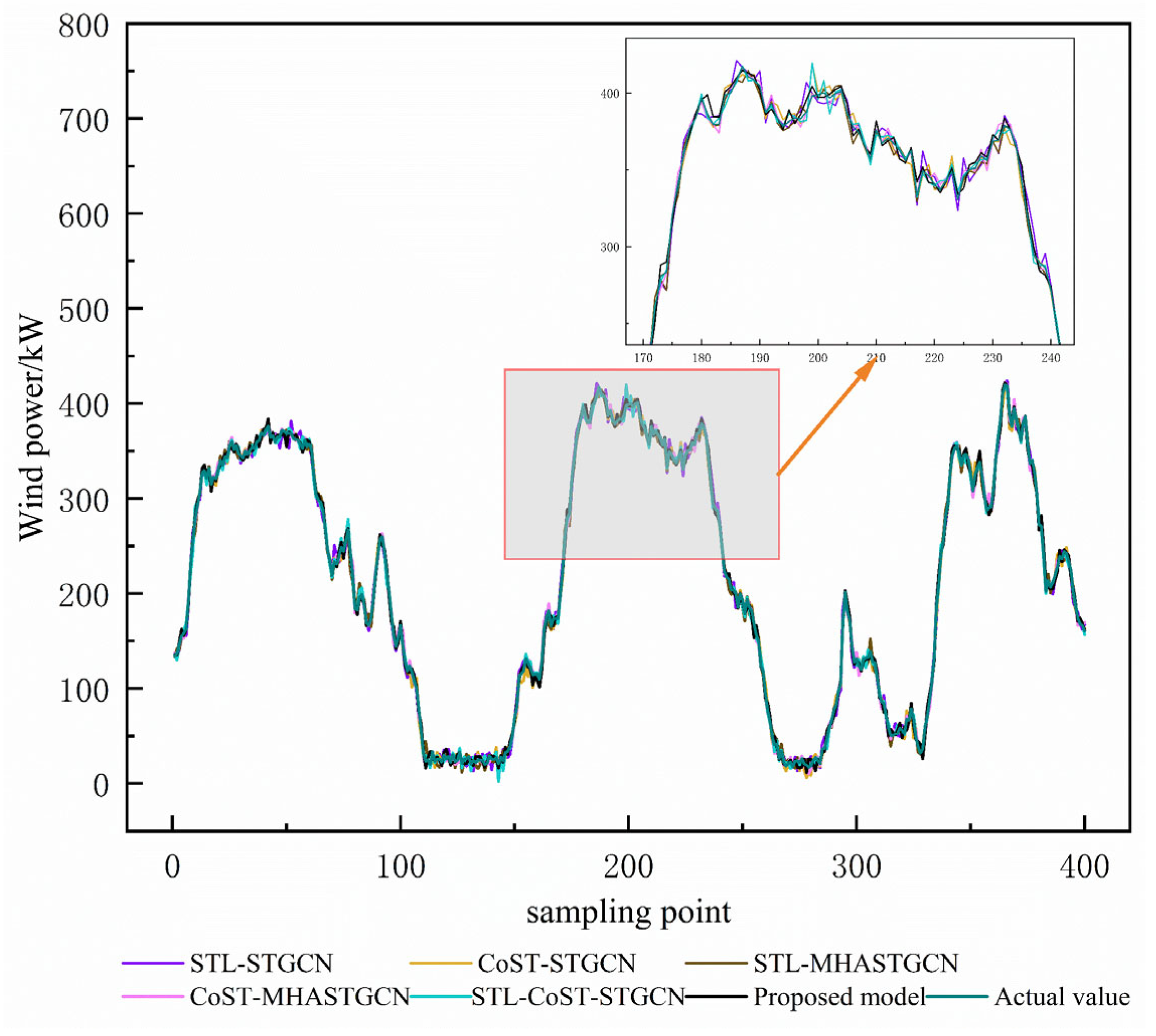
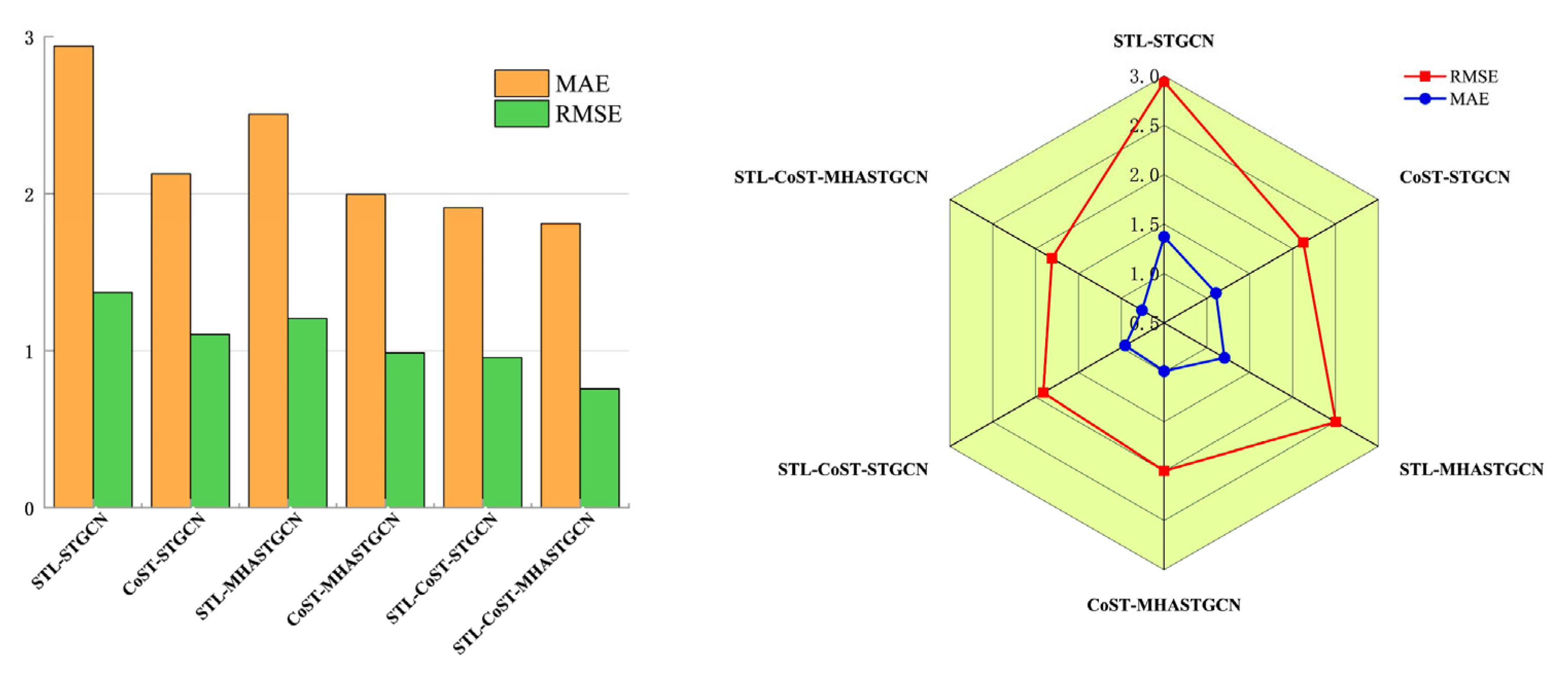
Figure 9 shows a comparison of the prediction results from the ablation experiment for Wind Farm A. The accuracy of wind power prediction according to the ablation experiments is shown in

Table 5. Different prediction model error indicators for ablation experiments.

Model	Assessment Indicator
	RMSE	MAE
STL-STGCN	2.94	1.371
CoST-STGCN	2.126	1.105
STL-MHASTGCN	2.505	1.206
CoST-MHASTGCN	1.996	0.987
STL-CoST-STGCN	1.910	0.955
STL-CoST-MHASTGCN	1.809	0.758

and Figure 10. The table shows the RMSE and MAE values for the proposed prediction model and the ablation model. In the ablation study, it was found that the application of STL decomposition reduced the average running time of the model by 2.3 s. It not only reduces the computation time but also improves the prediction accuracy, illustrating the need for STL decomposition. The model implementing the comparative learning framework fully separates data features, greatly enhancing the prediction accuracy.

Table 6. The DM test results of the ablation experiment.

Model	STGCN	STL-STGCN	CoST-STGCN	STL-CoST-STGCN	STL-CoST-MHASTGCN
STGCN	1	0.44 (0.55)	1.87 (0.15)	5.33 (0.56)	4.11 * (0.00)
STL-STGCN		1	1.44 * (0.04)	4.11 * (0.01)	3.29 * (0.00)
CoST-STGCN			1	3.17 * (0.00)	3.69 * (0.00)
STL-CoST-STGCN				1	1.81 * (0.00)
STL-CoST-MHASTGCN					1

Note: * indicates p < 0.05; p-values in parentheses.

takes the prediction results of Wind Farm A as the DM test results. Taking the DM test results of STL-STGCN and STL-CoST-STGCN as an example, the p-value is less than 0.05, so the alternative hypothesis is chosen, which indicates that the two predicted sequences are not the same. The DM test value is greater than 0, which indicates that the predicted sequences of STL-CoST-STGCN are closer to the actual sequences than the predicted sequences of STL-STGCN, and it thus has better forecasting performance. The DM test reveals the superiority of the STL-CoST-MHASTGCN model proposed in this paper.

5. Results and Discussion

In this study, a wind power prediction method based on spatiotemporal contrast learning is proposed, which significantly improves the accuracy and interpretability of wind power prediction by combining the seasonal trend contrast learning model and the improved spatiotemporal graph convolutional network. The conclusions are as follows.

(1) The effective decoupling of spatiotemporal features is achieved by a two-branch encoder, which avoids the problem of insufficient feature representation in the traditional method, significantly improves the model’s ability to model complex nonlinear relationships, and effectively solves the problem of feature aliasing. Compared with the STGCN model without using the comparative learning framework, the RMSE and MAE of this paper’s method are reduced by 38.47% and 44.71%, respectively.

(2) STL decomposition decomposes the wind speed and power time series into trend, seasonal, and residual components, making it able to capture the changing features on different time scales, and it further improves the accuracy of the model in extracting long-term trend and periodic features. After the introduction of STL decomposition, the MAE of the model on the Wind Farm A dataset decreased by 43.11%.

(3) The multi-head attention mechanism boosts the model’s capacity to identify crucial features by simultaneously learning various subspace representations of the data, leading to a notable gain in prediction precision. When contrasted with the standard STGCN model that lacked this attention component, the approach discussed here achieved a 53.27% reduction in the RMSE on the Wind Farm A dataset.

(4) The method in this paper performs well in both single-step and multi-step prediction. Compared with traditional models such as BP, LSTM, and GRU models, the error indicators of this paper’s method on both wind farm datasets were significantly reduced, especially in multi-step prediction. The error accumulation effect was effectively suppressed, which verifies the robustness and generalization ability of the model.

The research results described in this paper have important practical application value in the wind power industry and even the renewable energy sector. For wind farm operators, the accurate prediction of wind power can optimize the scheduling of power generation, reduce the cost of power grid regulation, and improve the stability of the power supply. With more precise power prediction, operators can better coordinate the operation of wind turbines, arrange maintenance plans reasonably, and avoid the waste of power resources caused by inaccurate prediction. For the renewable energy industry, this method can provide a reliable technical support for the large-scale integration of wind power into the power grid. It would help to reduce the impact of wind power fluctuations on the power grid, promote the consumption of renewable energy, and thus accelerate the transformation of the energy structure. In terms of policy recommendations, relevant government departments can promote the application of advanced prediction technologies in the renewable energy industry through financial subsidies and tax incentives. They can also establish a data sharing mechanism among wind farms to improve the accuracy and generalization abilities of prediction models. In addition, formulating technical standards for wind power prediction can guide the healthy development of the industry.

This study also has certain limitations. First, the data used in the experiment are mainly from two wind farms, and the geographical and climatic conditions of these wind farms are relatively similar, which may limit the generalization ability of the model in more complex and diverse environments. Second, the current model focuses more on short-term and medium-term wind power prediction, and its performance in long-term prediction (such as monthly or annual prediction) needs to be further verified. Third, the model’s computational complexity is relatively high, which may increase the cost of practical application, especially for small and medium-sized wind farms with limited computing resources.

In future research, the scope of the dataset can be expanded to include wind farms in different geographic locations and climatic zones, serving to improve the generalization ability of the model. We will also optimize the model structure to reduce the computational complexity while ensuring prediction accuracy, making it more suitable for practical application scenarios. In addition, we will explore the application of the model in long-term wind power prediction and combine it with other factors such as meteorological forecast data to further improve the prediction performance. Moreover, we will study the integration of the proposed prediction method with energy storage systems to better solve the problem of wind power fluctuations and improve the stability of the renewable energy power supply.

In addition to dataset and long-term prediction limitations, this study also experienced constraints in terms of computational complexity. Regarding the training time, when training the proposed model on a hardware configuration consisting of an Intel Core i7-12700H CPU (2.30 GHz) and NVIDIA RTX 3060 GPU (6 GB VRAM), the average training time per epoch is approximately 8.5 min for the full dataset (13,000+ samples), which is about 1.8 times longer than that of the baseline STGCN model (≈4.7 min per epoch). The increased training time is mainly attributed to the dual-branch encoder of the spatiotemporal contrastive learning framework and the multi-head attention mechanism, which introduce additional feature decoupling and subspace learning computations. In terms of hardware requirements, the model requires a GPU with at least 4 GB VRAM to avoid out-of-memory errors during training—this may limit its direct deployment on low-resource devices (e.g., edge computing platforms for small wind farms) in real-world scenarios. These computational constraints need to be addressed in future work by optimizing the model structure to reduce the time and hardware costs while maintaining the prediction accuracy.

6. Conclusions and Summary

This study addresses the core issues of insufficient feature representation, poor feature decoupling, and the weak interpretability of “black-box” models in existing ultra-short-term wind power prediction. A wind power prediction method based on spatiotemporal contrastive learning is proposed, and its effectiveness is verified through experiments. The core content and conclusions are as follows.

Research Background and Objectives: Amid the global energy transition, wind power intermittency threatens power grid stability, making ultra-short-term prediction critical. Traditional methods (physical models, shallow machine learning, etc.) struggle to balance feature extraction accuracy, spatiotemporal decoupling, and interpretability. This study fills this gap by integrating spatiotemporal contrastive learning with multi-scale feature processing.

Core Methods and Innovations: A dual-branch encoder is used to achieve effective spatiotemporal feature decoupling. ① Seasonal Trend Decomposition (STL) splits wind speed and power time series into trend, seasonal, and residual components to capture multi-scale patterns. ② A spatiotemporal contrastive learning framework (with trend/seasonal feature disentanglers) extracts features in an unsupervised manner, and a feature disentanglement loss function avoids feature confusion. ③ Geographic location data are integrated to construct an adjacency matrix for the simulation of spatial correlations between wind turbines. ④ An improved spatiotemporal graph convolutional network (STGCN) with multi-head attention enhances interpretability and key feature capture.

Experimental Validation and Results: The method is validated using data from two wind farms in Northwest China (Wind Farm A: March–June 2022, 13,247 data points; Wind Farm B: 13,103 data points). ① In single-step prediction, the proposed model reduces the RMSE by 38.47% and the MAE by 44.71% compared to STGCN on Wind Farm A (final RMSE = 1.809, MAE = 0.758) and achieves optimal metrics (RMSE = 1.881, MAE = 1.130) on Wind Farm B. ② In multi-step prediction (1–3 steps), it suppresses error accumulation—for example, Wind Farm A’s three-step prediction MAE = 2.771, far lower than BP’s 22.877. ③ Ablation experiments confirm that STL decomposition shortens the runtime by 2.3 s while improving the accuracy, and multi-head attention reduces the RMSE by 53.27% compared to the standard STGCN.

Significance and Prospects: This method provides a reliable technical solution for ultra-short-term prediction, aiding wind farm scheduling optimization, grid cost reduction, and large-scale wind power integration. Limitations include datasets limited to two wind farms with similar geographic/climatic conditions and the need to optimize the long-term prediction performance and computational complexity. Future work will expand the datasets to multi-region wind farms, simplify the model structure, and explore long-term prediction applications.