Resilience Enhancement for Power System State Estimation Against FDIAs with Moving Target Defense
Abstract
1. Introduction
- First, we use a new metric (i.e., resiliency) to quantify the effectiveness of MTD in defending against FDIAs.
- Second, the analytical upper bounds for the resiliency of PSSE against FDIAs under different MTD scenarios are derived.
- Third, the deployment cost of MTD is optimized to realize a cost-effective defense strategy.
- Fourth, extensive simulations are conducted to validate the performance of MTD in enhancing the resiliency of PSSE against FDIAs.
2. System Model and Attack Model
2.1. System Model
2.2. Formulation of the Measurement Matrix
2.3. Power System State Estimation
2.4. Attack Model
- Initial Access: The attackers gained access to the corporate networks of three Ukrainian energy distribution companies through spear-phishing emails containing the BlackEnergy 3 malware. This initial compromise occurred months before the actual attack, allowing the hackers to conduct reconnaissance.
- Reconnaissance and Planning: Over several months, the attackers used the malware to map out the networks, steal credentials, and identify vulnerabilities. They moved from the corporate IT networks to the operational technology (OT) networks that control the power grid’s physical components.
- The Attack Phase: On the day of the attack, the hackers remotely took control of the supervisory control and data acquisition (SCADA) systems at the utility companies’ control centers. They used the operators’ human–machine interfaces (HMIs) to open circuit breakers at about 30 substations, causing a blackout for over 230,000 customers in the Ivano-Frankivsk region.
- Other coordinated attacks: The attacker wiped data from servers and workstations using KillDisk malware and flooded the customer service call centers with fake calls in a denial-of-service (DoS) attack, preventing customers from reporting the outage.
- Random FDIA (R-FDIA): A random error is injected into the measurement, i.e.,
- Noise-based FDIA (N-FDIA): A very small error is injected into the measurement with the attempt to avoid being detected, i.e.,
- Stealthy FDIA (S-FDIA): A strategically designed error is injected into the measurement with the attempt to bypass the bad data detector (BDD), i.e.,
3. Resiliency Enhancement for PSSE with Moving Target Defense
3.1. Moving Target Defense
3.2. Resiliency Enhancement with MTD
3.2.1. Fully Measured Power Injections
3.2.2. Partially Measured Measurements
3.3. Optimal MTD for Enhancing the Resiliency of PSSE
4. Simulation Results
4.1. Resiliency Enhancement of PSSE After pMTD and nMTD
4.2. Optimal MTD for Enhancing the Resiliency of PSSE
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FDIA | false data injection attack |
| PSSE | power system state estimation |
| MTD | moving target defense |
| R-FDIA | random false data injection attack |
| N-FDIA | noise-based false data injection attack |
| S-FDIA | stealthy false data injection attack |
| pMTD | physical moving target defense |
| nMTD | network moving target defense |
| OPF | optimal power flow |
| ISO | independent system operation |
| FACTS | flexible alternating current transmission system |
References
- Illera, A.G.; Vidal, J.V. Lights Off! The Darkness of the Smart Meters. 2014. Available online: http://youtube.be/Z_y_vjYtAWM (accessed on 19 August 2025).
- Geiger, M.; Bauer, J.; Masuch, M.; Franke, J. An Analysis of Black Energy 3, Crashoverride, and Trisis, Three Malware Approaches Targeting Operational Technology Systems. In Proceedings of the 25th IEEE International Conference on Emerging Technologies and Factory Automation, Vienna, Austria, 8–11 September 2020; pp. 1537–1543. [Google Scholar]
- Liang, G.; Zhao, J.; Luo, F.; Weller, S.R.; Dong, Z.Y. A Review of False Data Injection Attacks Against Modern Power Systems. IEEE Trans. Smart Grid 2017, 8, 1630–1638. [Google Scholar] [CrossRef]
- Yang, Q.; Yang, J.; Yu, W.; An, D.; Zhang, N.; Zhao, W. On false data-injection attacks against power system state estimation: Modeling and countermeasures. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 717–729. [Google Scholar] [CrossRef]
- Usama, M.; Aman, M.N. Command Injection Attacks in Smart Grids: A Survey. IEEE Open J. Ind. App. 2024, 5, 75–85. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, M.; Sun, M.; Deng, R.; Cheng, P.; Niyato, D. Vulnerability of Machine Learning Approaches Applied in IoT-Based Smart Grid: A Review. IEEE Internet Things J. 2024, 11, 18951–18975. [Google Scholar] [CrossRef]
- Sayed, M.A.; Ghafouri, M.; Atallah, R.; Debbabi, M.; Assi, C. Grid Chaos: An uncertainty-conscious robust dynamic EV load-altering attack strategy on power grid stability. Appl. Energy 2024, 363, 122972. [Google Scholar] [CrossRef]
- Liu, Y.; Ning, P.; Reiter, M.K. False data injection attacks against state estimation in electric power grid. ACM Trans. Inform. Syst. Secur. 2011, 14, 13. [Google Scholar] [CrossRef]
- Rahman, M.A.; Datta, A. Impact of Stealthy Attacks on Optimal Power Flow: A Simulink-Driven Formal Analysis. IEEE Trans. Dependable Secur. Comput. 2020, 17, 451–464. [Google Scholar] [CrossRef]
- Huang, R.; Li, Y. Adversarial Attack Mitigation Strategy for Machine Learning-Based Network Attack Detection Model in Power System. IEEE Trans. Smart Grid 2023, 14, 2367–2376. [Google Scholar] [CrossRef]
- Zhang, Z.; Deng, R.; Tian, Y.; Cheng, P.; Ma, J. SPMA: Stealthy physics-manipulated attack and countermeasures in cyber-physical smart grid. IEEE Trans. Inf. Forensics Secur. 2022, 18, 581–596. [Google Scholar] [CrossRef]
- Selim, A.; Zhao, J. Cyber-Physical Testbed Integrating RTAC with RTDS for Game-Theoretic Topology Control Under Load Altering Attacks. In Proceedings of the 2024 IEEE Texas Power and Energy Conference, College Station, TX, USA, 12–13 February 2024; pp. 1–6. [Google Scholar]
- Zhang, Z.; Deng, R.; Cheng, P.; Wei, Q. On Feasibility of Coordinated Time-Delay and False Data Injection Attacks on Cyber–Physical Systems. IEEE Internet Things J. 2022, 9, 8720–8736. [Google Scholar] [CrossRef]
- Tang, D.; Fang, Y.-P.; Zio, E. Vulnerability analysis of demand-response with renewable energy integration in smart grids to cyber attacks and online detection methods. Reliab. Eng. Syst. Saf. 2023, 235, 109212. [Google Scholar] [CrossRef]
- Tian, J.; Tan, R.; Guan, X.; Liu, T. Enhanced Hidden Moving Target Defense in Smart Grids. IEEE Trans. Smart Grid 2018, 10, 2208–2223. [Google Scholar] [CrossRef]
- Hu, Y.; Zhu, P.; Xun, P.; Liu, B.; Kang, W.; Xiong, Y.; Shi, W. CPMTD: Cyber-physical moving target defense for hardening the security of power system against false data injected attack. Comput. Secur. 2024, 111, 102465. [Google Scholar] [CrossRef]
- Deng, R.; Xiao, G.; Lu, R.; Liang, H.; Vasilakos, A.V. False Data Injection on State Estimation in Power Systems Attacks, Impacts, and Defense: A Survey. IEEE Trans. Ind. Infrom. 2017, 13, 411–423. [Google Scholar] [CrossRef]
- Lakshminarayana, S.; Yau, D.K.Y. Cost-Benefit Analysis of Moving-Target Defense in Power Grids. IEEE Trans. Power Syst. 2021, 36, 1152–1163. [Google Scholar] [CrossRef]
- Wang, Z.-Y.; Chiang, H.-D. On the Feasibility of AC and DC Optimal Power Flow Models: Analytics and Comparison. In Proceedings of the IEEE Power Energy Society General Meeting, Washington, DC, USA, 26–29 July 2021; pp. 1–5. [Google Scholar]
- Kamel, O.M.; Elzein, I.; Mahmoud, M.M.; Abdelaziz, A.Y.; Hussein, M.M.; Diab, A. Effective energy management strategy with a novel design of fuzzy logic and JAYA-based controllers in isolated DC/AC microgrids: A comparative analysis. Wind Eng. 2024, 49, 199. [Google Scholar] [CrossRef]
- Ericsson, G.N. Cyber Security and Power System Communication—Essential Parts of a Smart Grid Infrastructure. IEEE Trans. Power Deliv. 2010, 25, 1501–1507. [Google Scholar] [CrossRef]
- Zhao, T.; Tu, H.; Jin, R.; Xia, Y.; Wang, F. Improving resilience of cyber–physical power systems against cyber attacks through strategic energy storage deployment. Reliab. Eng. Syst. Safety 2024, 252, 110438. [Google Scholar] [CrossRef]
- Divan, D.; Johal, H. Distributed FACTs: A new concept for realizing grid power flow control. IEEE Trans. Power Electron. 2007, 22, 2253–2260. [Google Scholar] [CrossRef]
- Liu, C.; Tang, Y.; Deng, R.; Zhou, M.; Du, W. Joint Meter Coding and Moving Target Defense for Detecting Stealthy False Data Injection Attacks in Power System State Estimation. IEEE Trans. Ind. Inform. 2024, 20, 3371–3381. [Google Scholar] [CrossRef]
- Penrose, R. On best approximate solution of linear matrix equations. Proc. Camb. Philos. Soc. 2008, 52, 17–19. [Google Scholar] [CrossRef]
- Condren, C.; Gedra, T.W.; Damrongkulkamjorn, P. Optimal power flow with expected security costs. IEEE Trans. Power Syst. 2006, 21, 541–547. [Google Scholar] [CrossRef]
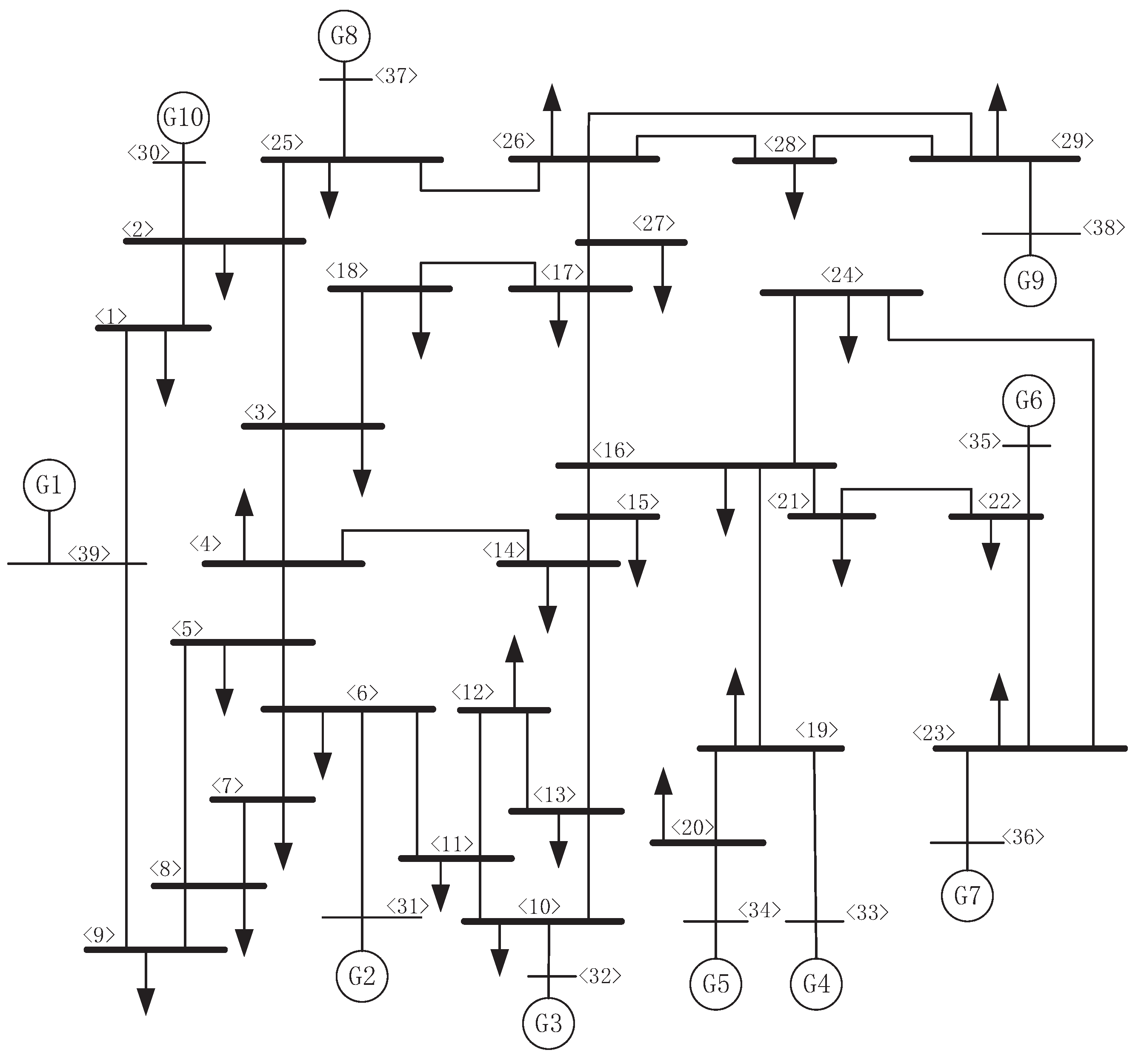

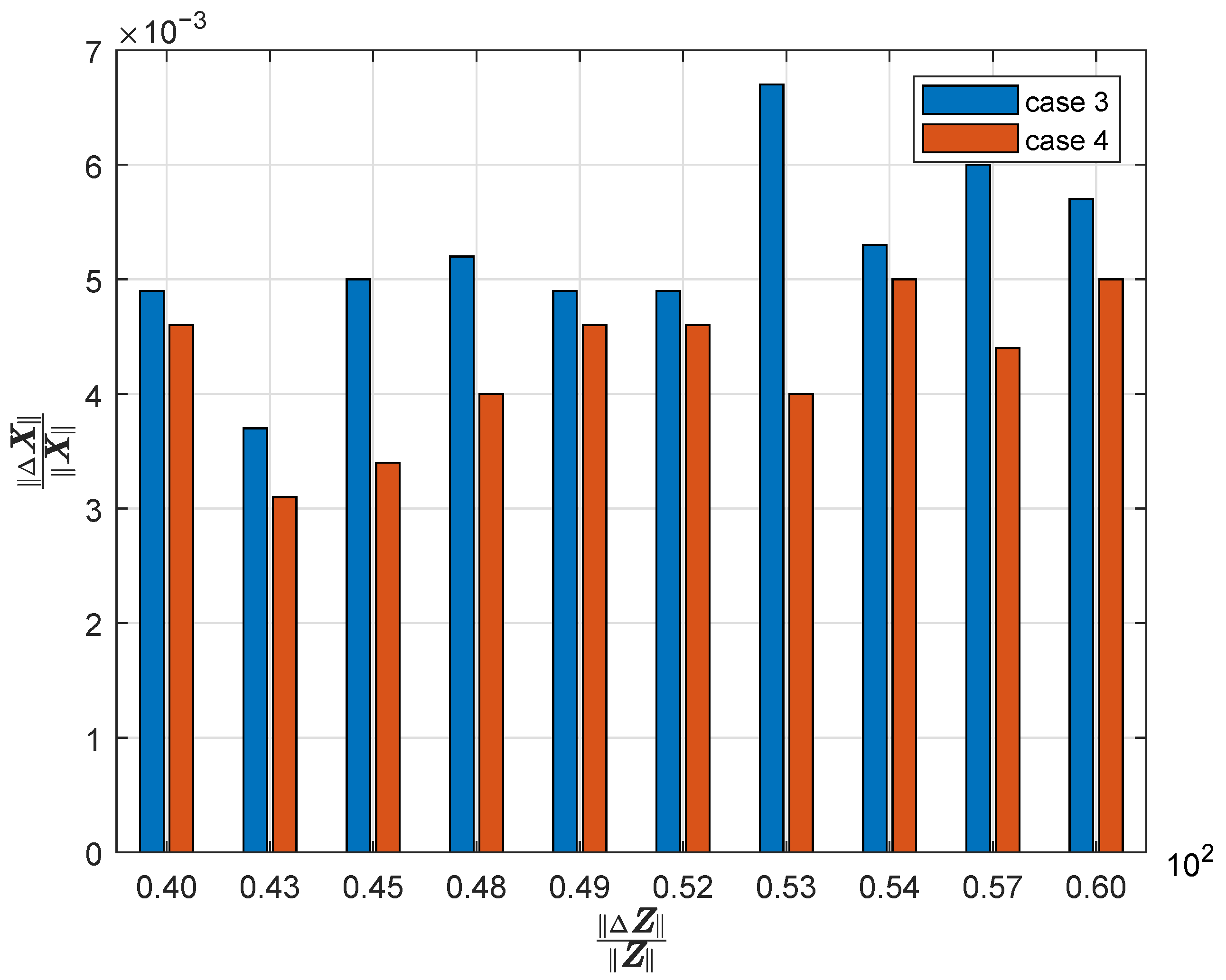
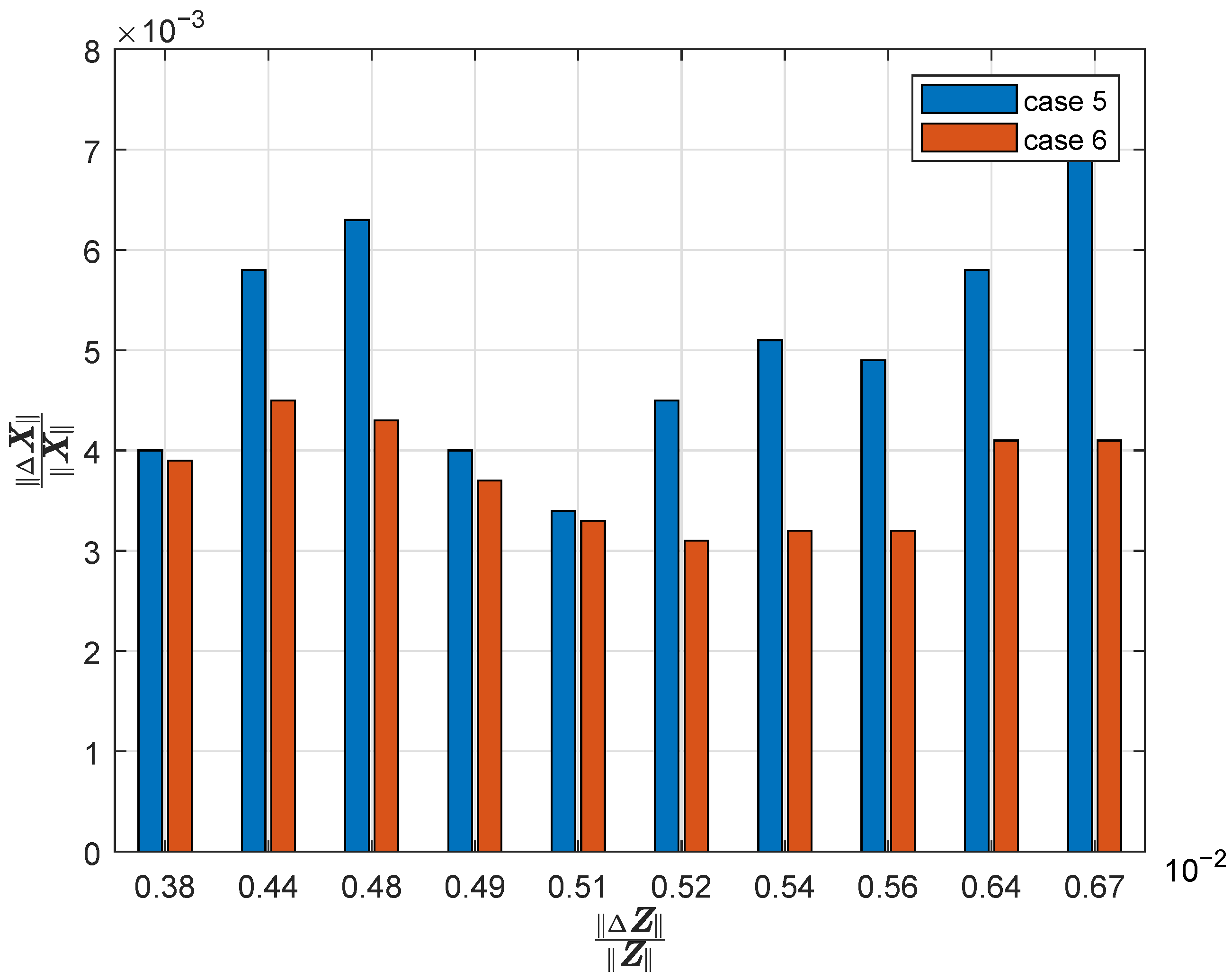

| Line | Susceptances in Case 1 (Before pMTD) | Susceptances in Case 2 (After pMTD) |
|---|---|---|
| 16.67 | 20 | |
| 5.26 | 7.37 | |
| 5.88 | 8.24 | |
| 25 | 25 | |
| 5 | 5 | |
| 5.56 | 5.56 | |
| 25 | 5 | |
| 8.33 | 1.67 | |
| 12.5 | 12.5 | |
| 25 | 25 | |
| 4.76 | 4.76 | |
| 1.79 | 1.79 | |
| 4.76 | 5.24 | |
| 9.10 | 9.10 | |
| 3.85 | 3.85 | |
| 7.14 | 7.14 | |
| 3.85 | 3.85 | |
| 7.69 | 7.69 | |
| 5 | 5 | |
| 5 | 5 | |
| 5.26 | 5.26 | |
| 4.54 | 4.54 | |
| 7.69 | 7.69 | |
| 14.29 | 11.43 | |
| 4.76 | 4.76 | |
| 12.5 | 12.5 | |
| 14.29 | 14.29 | |
| 6.67 | 6 | |
| 50 | 50 | |
| 5 | 5 | |
| 5.56 | 5.56 | |
| 3.70 | 3.70 | |
| 3.03 | 3.03 | |
| 2.63 | 2.63 | |
| 4.76 | 4.76 | |
| 2.5 | 2.5 | |
| 2.38 | 2.38 | |
| 1.67 | 1.67 | |
| 2.22 | 2.22 | |
| 5 | 5 | |
| 16.67 | 7 |
| Resiliency Factor | Case 1 | Case 2 |
|---|---|---|
| 961.5342 | 961.5342 | |
| 110.1516 | 105.7965 | |
| 961.5342 | 961.5342 |
| Before MTD | After pMTD | After nMTD | After the Coordinated pMTD and nMTD |
|---|---|---|---|
| 110.1516 | 105.7965 | 103.0243 | 102.583 |
| Dimension | Existing Methods | Proposed Method |
|---|---|---|
| Primary Objective | Attack detection | Resilience enhancement |
| Evaluation Metric | Detection Rate, False alarm rate | “Resiliency Factor” (quantifies system robustness) |
| Core Concept | Make attacks visible to detectors | Minimize the impact of undetected attacks |
| Economic Focus | Cost as a constraint (if considered) | Cost as an optimization objective (cost-effective design with potential savings) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Bi, J.; Zhang, Z. Resilience Enhancement for Power System State Estimation Against FDIAs with Moving Target Defense. Electronics 2025, 14, 3367. https://doi.org/10.3390/electronics14173367
Zhou Z, Bi J, Zhang Z. Resilience Enhancement for Power System State Estimation Against FDIAs with Moving Target Defense. Electronics. 2025; 14(17):3367. https://doi.org/10.3390/electronics14173367
Chicago/Turabian StyleZhou, Zeyuan, Jichao Bi, and Zhenyong Zhang. 2025. "Resilience Enhancement for Power System State Estimation Against FDIAs with Moving Target Defense" Electronics 14, no. 17: 3367. https://doi.org/10.3390/electronics14173367
APA StyleZhou, Z., Bi, J., & Zhang, Z. (2025). Resilience Enhancement for Power System State Estimation Against FDIAs with Moving Target Defense. Electronics, 14(17), 3367. https://doi.org/10.3390/electronics14173367






