A Real-Time UWB-Based Device-Free Localization and Tracking System
Abstract
1. Introduction
- We design and implement a real-time DFLT system based on COTS UWB sensors, which have been demonstrated to be more robust to multipath interference.
- We propose two RSS measurements based on total paths and the LoS path for our UWB-based system and LoS measurements are more attractive in cluttered environments.
- We design a fast measurement protocol for UWB-based sensor networks and analyze practical radio frequency configurations for real-time tracking.
- We conduct various experiments in outdoor and indoor environments to evaluate the performance improvement of our UWB-based system, and the results show that our UWB-based system improves the localization and tracking accuracy significantly compared to narrowband ones.
2. Related Work
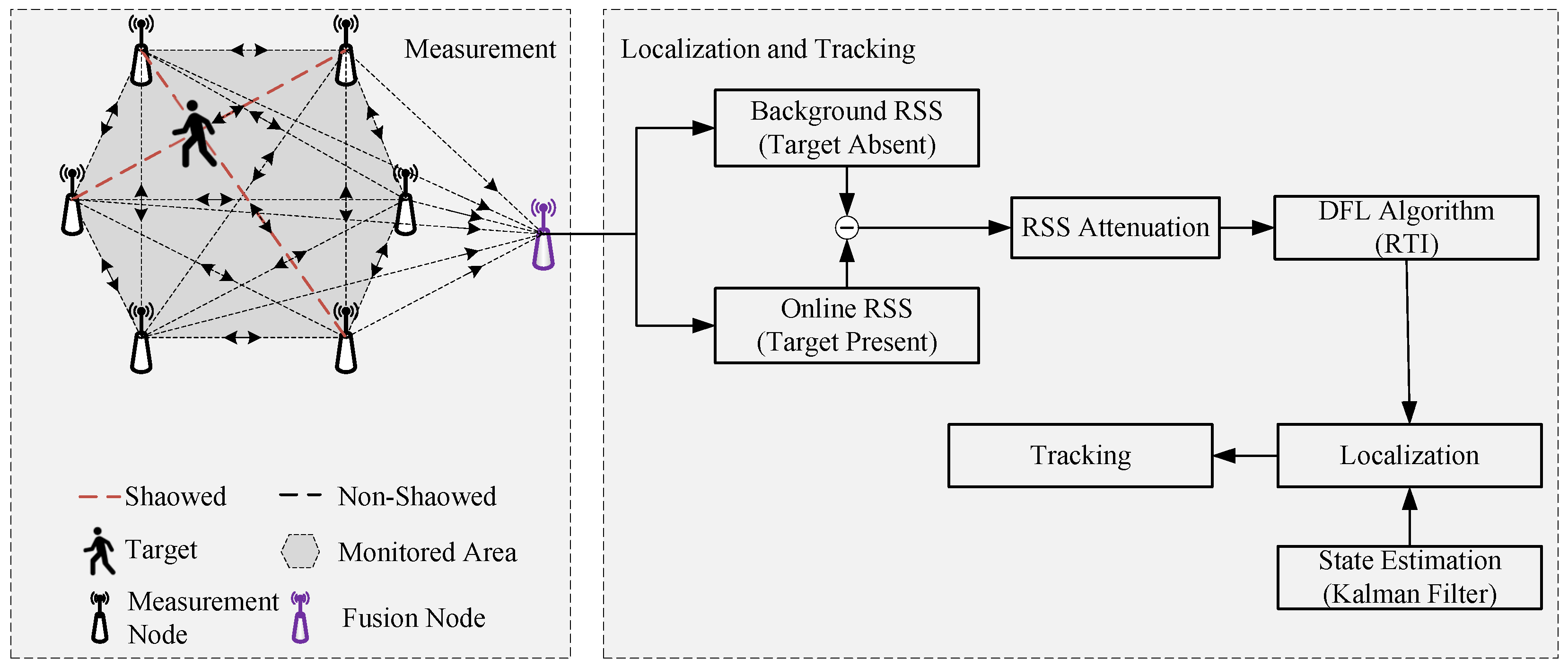
3. System Overview
4. Analysis of RSS Change
5. Target Localization and Tracking
5.1. Localization
5.2. Tracking
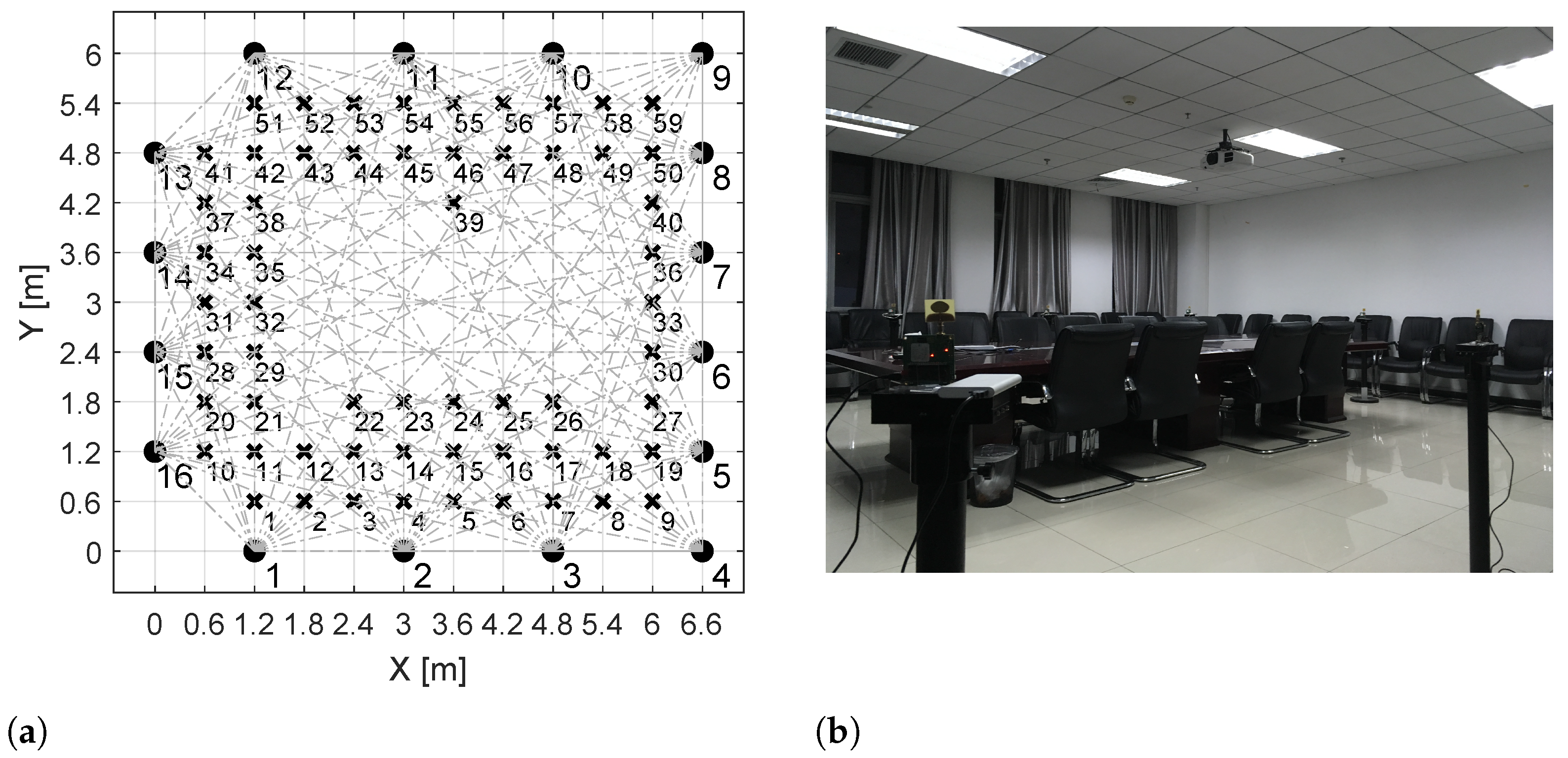
6. Experimental Setup
6.1. Hardware Description
6.2. Communication Protocol
6.3. RF Configuration
6.4. Field Experiments
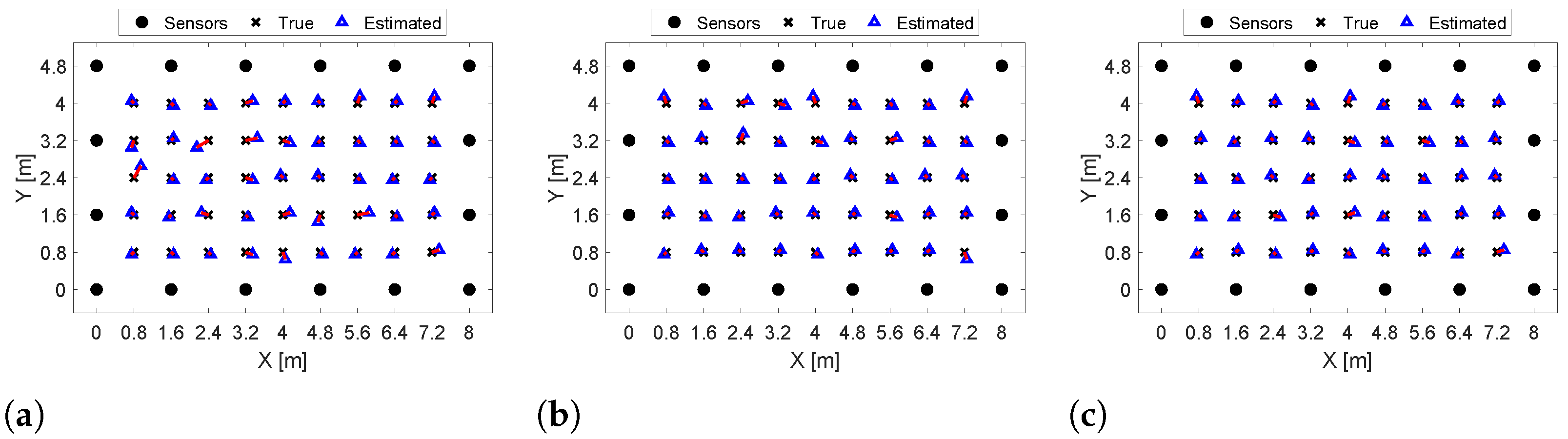
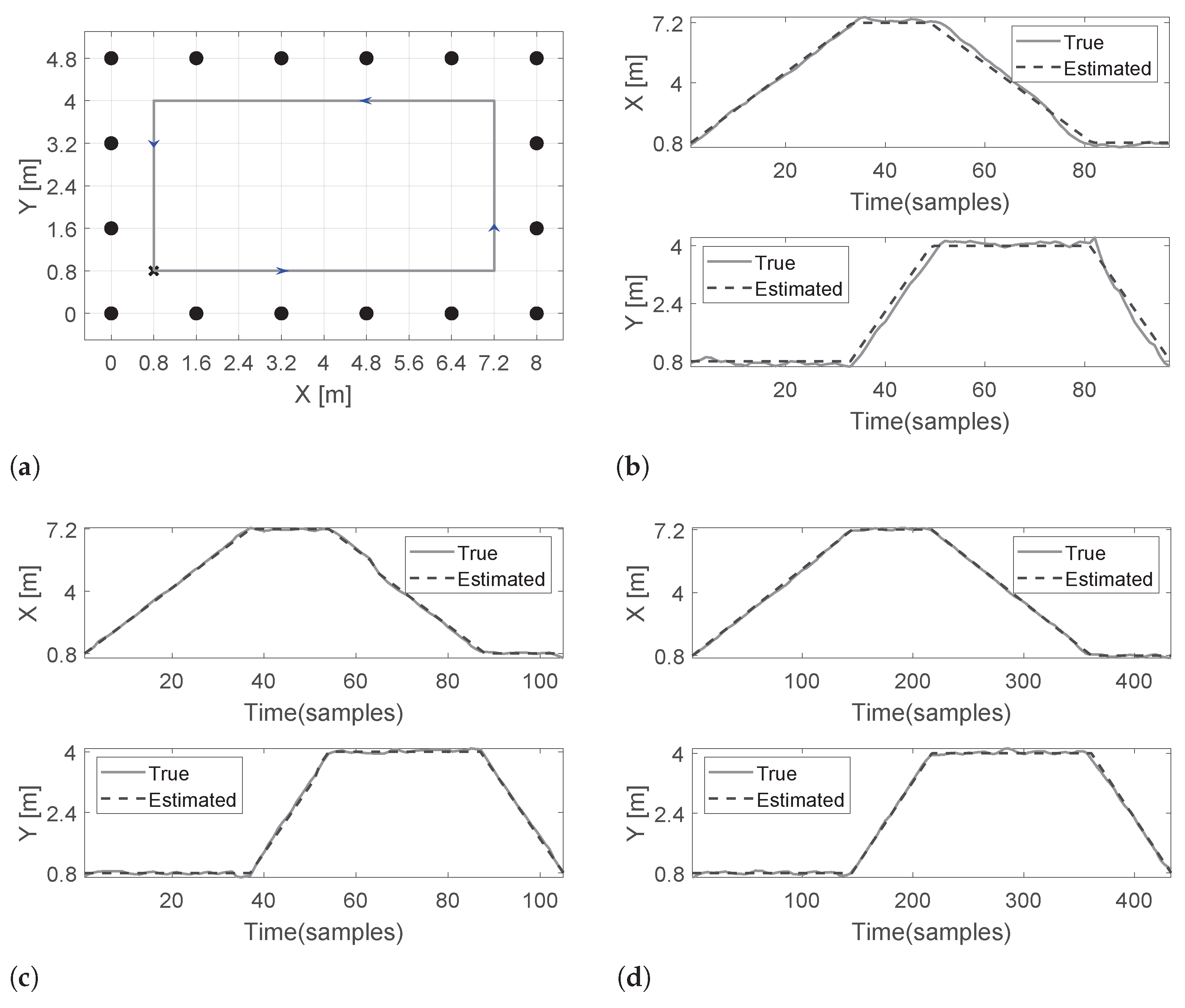
7. Performance Evaluation
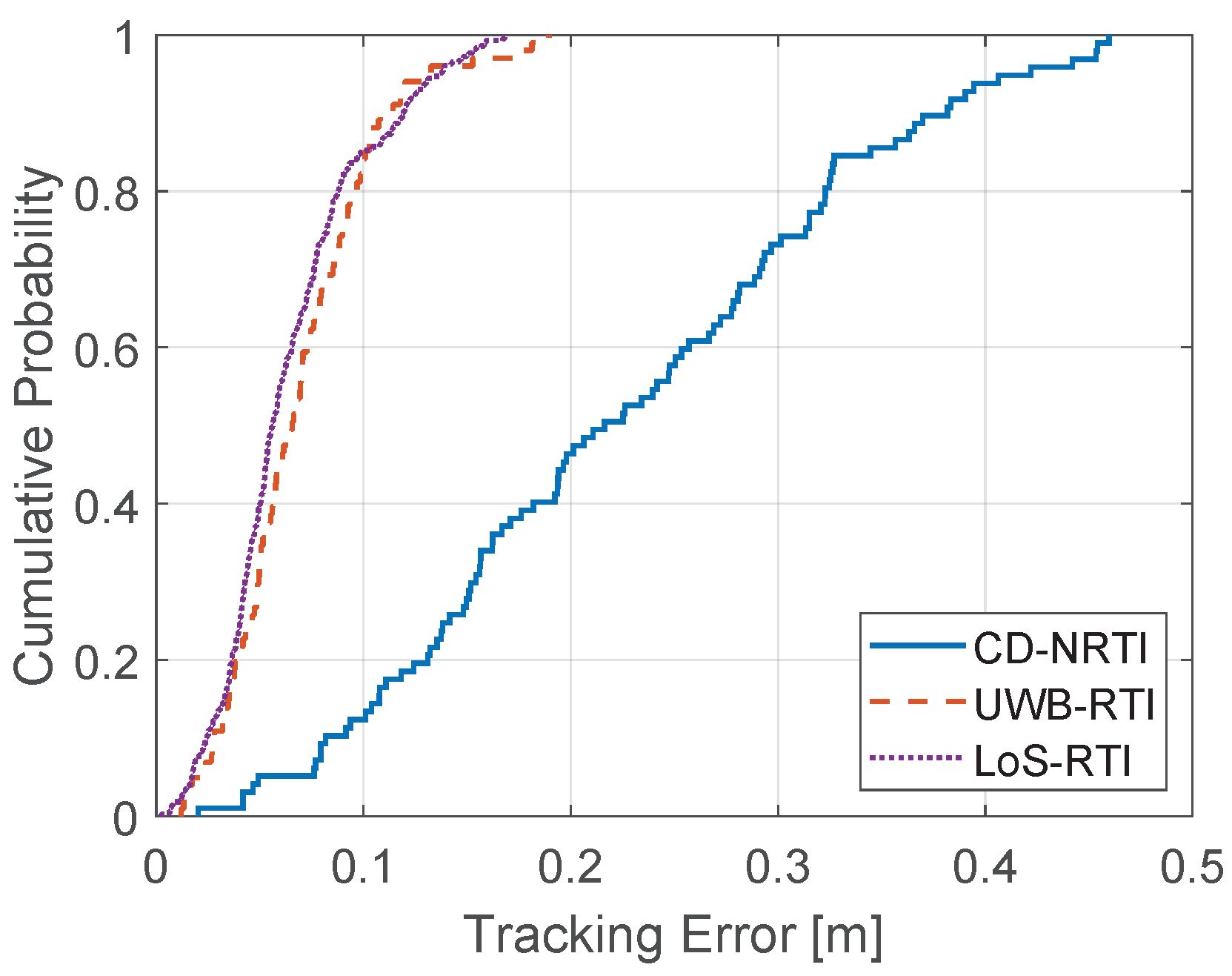
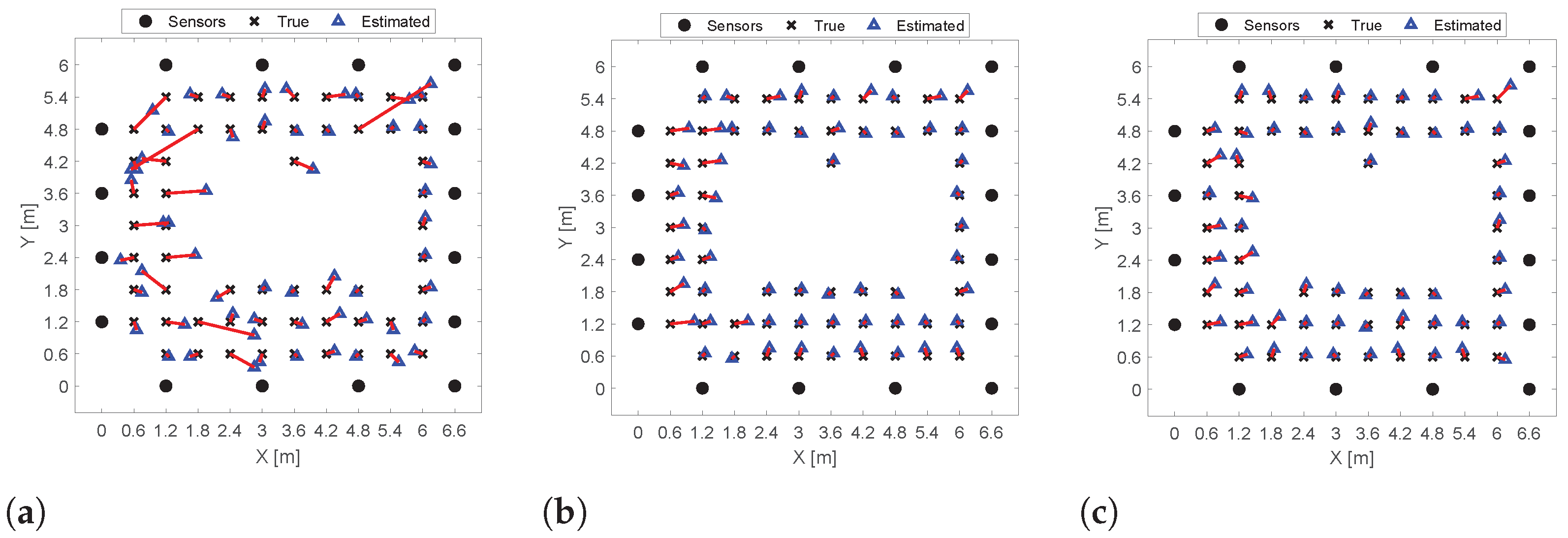
7.1. Results of Experiment 1
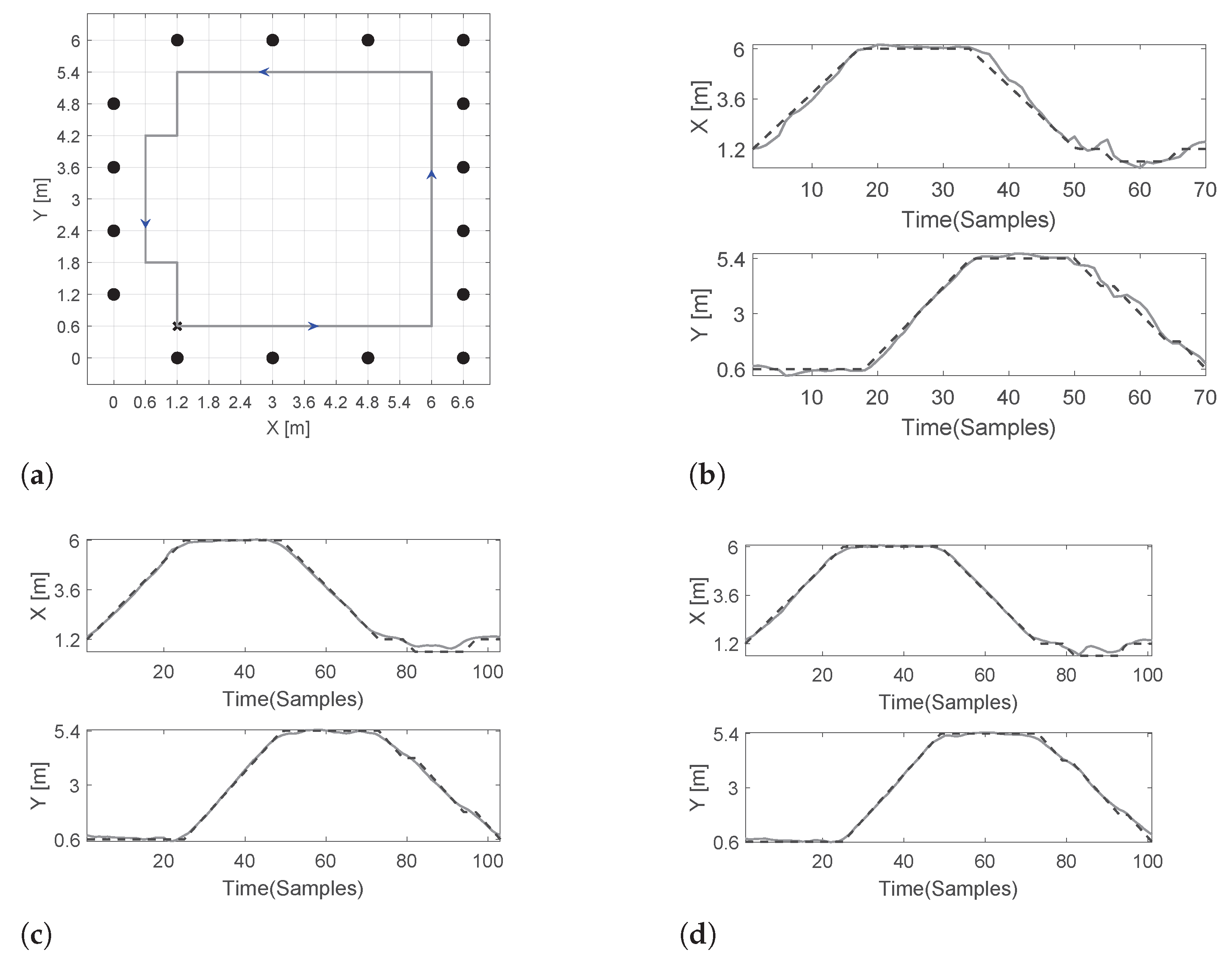
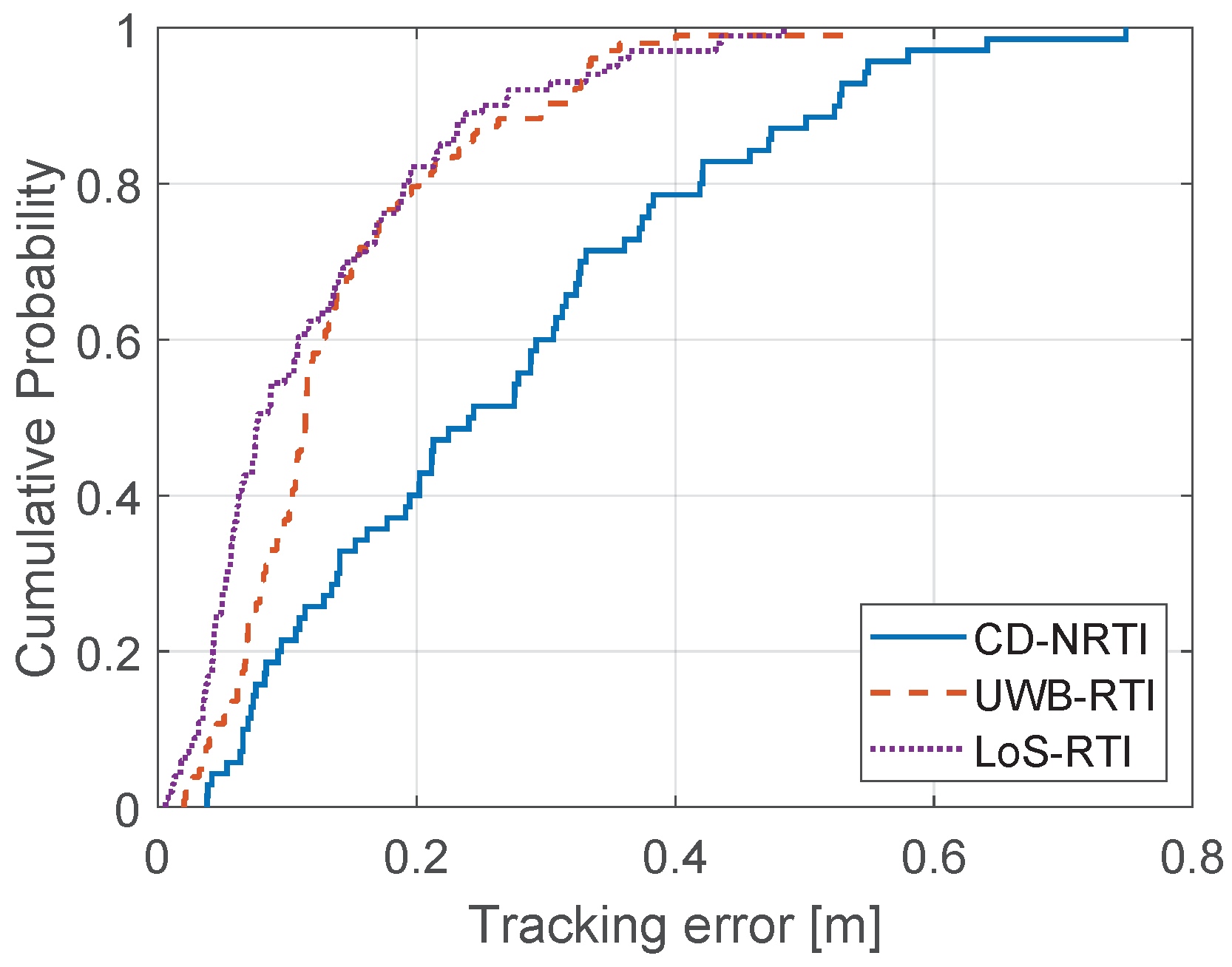
7.2. Results of Experiment 2
8. Discussion
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bi, J.; Wang, J.; Cao, H.; Yao, G.; Wang, Y.; Li, Z.; Sun, M.; Yang, H.; Zhen, J.; Zheng, G. Inverse distance weight-assisted particle swarm optimized indoor localization. Appl. Soft Comput. 2024, 164, 112032. [Google Scholar] [CrossRef]
- Luoh, L. ZigBee-based intelligent indoor positioning system soft computing. Soft Comput. 2014, 18, 443–456. [Google Scholar] [CrossRef]
- Tan, P.; Tsinakwadi, T.H.; Xu, Z.; Xu, H. Sing-Ant: RFID indoor positioning system using single antenna with multiple beams based on LANDMARC algorithm. Appl. Sci. 2022, 12, 6751. [Google Scholar] [CrossRef]
- Azaddel, M.H.; Nourian, M.A.; Shahhosseini, K.; Junoh, S.A.; Akbari, A. SPOTTER: A novel asynchronous and independent WiFi and BLE fusion method based on particle filter for indoor positioning. Internet Things 2023, 24, 100967. [Google Scholar] [CrossRef]
- Mager, B.; Lundrigan, P.; Patwari, N. Fingerprint-based device-free localization performance in changing environments. IEEE J. Sel. Areas Commun. 2015, 33, 2429–2438. [Google Scholar] [CrossRef]
- Wilson, J.; Patwari, N. Radio tomographic imaging with wireless networks. IEEE Trans. Mob. Comput. 2010, 9, 621–632. [Google Scholar] [CrossRef]
- Savazzi, S.; Nicoli, M.; Carminati, F.; Riva, M. A Bayesian approach to device-free localization: Modeling and experimental assessment. IEEE J. Sel. Top. Signal Process. 2014, 8, 16–29. [Google Scholar] [CrossRef]
- Kaltiokallio, O.; Yiğitler, H.; Jäntti, R. A three-state received signal strength model for device-free localization. IEEE Trans. Veh. Technol. 2017, 66, 9226–9240. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, H.; Xu, S.; Bu, X.; An, J. A diffraction measurement model and particle filter tracking method for RSS-based DFL. IEEE J. Sel. Areas Commun. 2015, 33, 2391–2403. [Google Scholar] [CrossRef]
- Kaltiokallio, O.; Bocca, M.; Patwari, N. Enhancing the accuracy of radio tomographic imaging using channel diversity. In Proceedings of the 2012 IEEE 9th International Conference on Mobile Ad-Hoc and Sensor Systems (MASS 2012), Las Vegas, NV, USA, 8–11 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 254–262. [Google Scholar]
- Wang, M.; Wang, Z.; Ding, E.; Yang, Y. Dual-band sensor network for accurate device-free localization in indoor environment with wifi interference. IEICE Trans. Inf. Syst. 2015, 98, 596–606. [Google Scholar] [CrossRef]
- Fink, A.; Ritt, T.; Beikirch, H. Redundant radio tomographic imaging for privacy-aware indoor user localization. In Proceedings of the 2015 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Banff, AB, Canada, 13–16 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–7. [Google Scholar]
- Denis, S.; Berkvens, R.; Ergeerts, G.; Bellekens, B.; Weyn, M. Combining multiple sub-1 ghz frequencies in radio tomographic imaging. In Proceedings of the 2016 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Madrid, Spain, 4–7 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–8. [Google Scholar]
- Denis, S.; Berkvens, R.; Ergeerts, G.; Weyn, M. Multi-frequency sub-1 GHz radio tomographic imaging in a complex indoor environment. In Proceedings of the 2017 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–8. [Google Scholar]
- Bocca, M.; Luong, A.; Patwari, N.; Schmid, T. Dial it in: Rotating RF sensors to enhance radio tomography. In Proceedings of the 2014 Eleventh Annual IEEE International Conference on Sensing, Communication, and Networking (SECON), Singapore, 30 June–3 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 600–608. [Google Scholar]
- Xu, S.; Liu, H.; Gao, F.; Wang, Z. Compressive sensing based radio tomographic imaging with spatial diversity. Sensors 2019, 19, 439. [Google Scholar] [CrossRef]
- Wei, B.; Varshney, A.; Patwari, N.; Hu, W.; Voigt, T.; Chou, C.T. dRTI: Directional Radio Tomographic Imaging. In Proceedings of the 14th International Conference on Information Processing in Sensor Networks, New York, NY, USA, 13–16 April 2015; IPSN ’15. pp. 166–177. [Google Scholar]
- Qi, C.; Hillyard, P.; Al-Husseiny, A.; Patwari, N.; Durgin, G.D. On-Wall, Wide Bandwidth E-Shaped Patch Antenna for Improved Whole-Home Radio Tomography. IEEE J. Radio Freq. Identif. 2017, 1, 22–31. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, H.; Ma, X.; An, J.; Xu, S. Enhancing indoor radio tomographic imaging based on interference link elimination. Digit. Signal Process. 2015, 44, 26–36. [Google Scholar] [CrossRef]
- Kaltiokallio, O.; Jäntti, R.; Patwari, N. ARTI: An adaptive radio tomographic imaging system. IEEE Trans. Veh. Technol. 2017, 66, 7302–7316. [Google Scholar] [CrossRef]
- Yiğitler, H.; Jäntti, R.; Kaltiokallio, O.; Patwari, N. Detector based radio tomographic imaging. IEEE Trans. Mob. Comput. 2018, 17, 58–71. [Google Scholar] [CrossRef]
- Patwari, N.; Agrawal, P. Effects of correlated shadowing: Connectivity, localization, and RF tomography. In Proceedings of the 2008 International Conference on Information Processing in Sensor Networks (IPSN 2008), St. Louis, MO, USA, 22–24 April 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 82–93. [Google Scholar]
- Patra, A.; Simic, L.; Petrova, M. mmRTI: Radio tomographic imaging using highly-directional millimeter-wave devices for accurate and robust indoor localization. In Proceedings of the 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–7. [Google Scholar]
- Li, Y.; Chen, X.; Coates, M.; Yang, B. Sequential Monte Carlo radio-frequency tomographic tracking. In Proceedings of the 2011 IEEE International Conference Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 3976–3979. [Google Scholar]
- Nannuru, S.; Li, Y.; Zeng, Y.; Coates, M.; Yang, B. Radio-frequency tomography for passive indoor multitarget tracking. IEEE Trans. Mob. Comput. 2012, 12, 2322–2333. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, K.; Jiang, N.; Guo, X.; Li, Y.; Wang, G. An exponential-Rayleigh model for RSS-based device-free localization and tracking. IEEE Trans. Mob. Comput. 2015, 14, 484–494. [Google Scholar] [CrossRef]
- Savazzi, S.; Sigg, S.; Nicoli, M.; Rampa, V.; Kianoush, S.; Spagnolini, U. Device-free radio vision for assisted living: Leveraging wireless channel quality information for human sensing. IEEE Signal Process. Mag. 2016, 33, 45–58. [Google Scholar] [CrossRef]
- Rampa, V.; Savazzi, S.; Nicoli, M.; D’Amico, M. Physical modeling and performance bounds for device-free localization systems. IEEE Signal Process. Lett. 2015, 22, 1864–1868. [Google Scholar] [CrossRef]
- Nicoli, M.; Rampa, V.; Savazzi, S.; Schiaroli, S. Device-free localization of multiple targets. In Proceedings of the 2016 24th European Signal Processing Conference (EUSIPCO), Budapest, Hungary, 29 August–2 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 738–742. [Google Scholar]
- Wang, J.; Gao, Q.; Pan, M.; Zhang, X.; Yu, Y.; Wang, H. Toward accurate device-free wireless localization with a saddle surface model. IEEE Trans. Veh. Technol. 2015, 65, 6665–6677. [Google Scholar] [CrossRef]
- Wu, H.; Ma, X.; Yang, C.H.H.; Liu, S. Convolutional neural network based radio tomographic imaging. In Proceedings of the 2020 54th Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, USA, 18–20 March 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Wu, H.; Cheng, C.; Peng, T.; Zhou, H.; Chen, T. Combining transformer with a latent variable model for radio tomography based robust device-free localization. Comput. Commun. 2025, 231, 108022. [Google Scholar] [CrossRef]
- Lu, Z.; Liu, H.; Zhang, X. Radio tomographic imaging localization based on transformer model. In Proceedings of the 2023 IEEE 6th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 24–26 February 2023; IEEE: Piscataway, NJ, USA, 2023; Volume 6, pp. 1134–1138. [Google Scholar]
- Cheraghinia, M.; Shahid, A.; Luchie, S.; Gordebeke, G.J.; Caytan, O.; Fontaine, J.; Van Herbruggen, B.; Lemey, S.; De Poorter, E. A comprehensive overview on UWB radar: Applications, standards, signal processing techniques, datasets, radio chips, trends and future research directions. IEEE Commun. Surv. Tutor. 2024, 27, 2283–2324. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, H.; Xu, S.; Gao, F.; Bu, X.; An, J. Towards robust and efficient device-free localization using UWB sensor network. Pervasive Mob. Comput. 2017, 41, 451–469. [Google Scholar] [CrossRef]
- Yang, J.; Wang, M.; Yang, Y.; Wang, J. A device-free localization and size prediction system for road vehicle surveillance via UWB networks. IEEE Trans. Instrum. Meas. 2021, 71, 1–11. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.; Wang, M. Device-free localization and tracking of multiple person in UWB sensor networks. In Proceedings of the 2021 International Conference on Sensing, Measurement & Data Analytics in the era of Artificial Intelligence (ICSMD), Nanjing, China, 21–23 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–7. [Google Scholar]
- Schmidhammer, M.; Gentner, C.; Sand, S.; Fiebig, U.C. Multipath-enhanced device-free localization in wideband wireless networks. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 453–457. [Google Scholar] [CrossRef]
- Schmidhammer, M.; Gentner, C. Multipath-enhanced device-free localization using low-cost ultra-wideband devices. In Proceedings of the 2022 16th European Conference on Antennas and Propagation (EuCAP), Madrid, Spain, 27 March–1 April 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–5. [Google Scholar]
- Cimdins, M.; Schmidt, S.O.; John, F.; Constapel, M.; Hellbrück, H. MA-RTI: Design and Evaluation of a Real-World Multipath-Assisted Device-Free Localization System. Sensors 2023, 23, 2199. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Xu, H.; Li, C.; Wang, Y.; Shi, Z. Passive human sensing based on UWB CIR. In Proceedings of the 2024 IEEE/CIC International Conference on Communications in China (ICCC), Hangzhou, China, 7–9 August 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1680–1685. [Google Scholar]
- Yang, S.; Xiao, X.; Wang, X.; Chen, Z.; Sheng, M.; Yao, Z. Multipath Components Modeling and Measuring in Device-Free Underground Parking Localization. In Proceedings of the 2024 IEEE/CIC International Conference on Communications in China (ICCC), Hangzhou, China, 7–9 August 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 417–422. [Google Scholar]
- Lee, H.S. Device-Free Localization Using Commercial UWB Transceivers. arXiv 2025, arXiv:2507.13938. [Google Scholar] [CrossRef]
- Poeggel, R.; Stahlke, M.; Pirkl, J.; Ott, J.; Yammine, G.; Feigl, T.; Mutschler, C. Passive Channel Charting: Locating Passive Targets using a UWB Mesh. arXiv 2025, arXiv:2505.10194. [Google Scholar] [CrossRef]
- Maas, D.; Firooz, M.H.; Zhang, J.; Patwari, N.; Kasera, S.K. Channel sounding for the masses: Low complexity gnu 802.11 b channel impulse response estimation. IEEE Trans. Wirel. Commun. 2012, 11, 1–8. [Google Scholar] [CrossRef]
- Texas Instruments. CC253x/4x User’s Guide. 2014. Available online: http://www.ti.com/lit/ug/swru191f/swru191f.pdf (accessed on 23 August 2015).
- Wilson, J.; Patwari, N. A fade-level skew-laplace signal strength model for device-free localization with wireless networks. IEEE Trans. Mob. Comput. 2012, 11, 947–958. [Google Scholar] [CrossRef]
- Hillyard, P.; Maas, D.; Premnath, S.; Patwari, N.; Kasera, S. Through-wall person localization using transceivers in motion. arXiv 2015, arXiv:1511.06703. [Google Scholar] [CrossRef]
- Decawave (Qorvo). DW1000 User Manual. 2017. Available online: https://www.qorvo.com/products/d/da007967 (accessed on 23 August 2025).
- Decawave (Qorvo). Decawave Reference Planar Monopole Antenna. 2014. Available online: https://www.decawave.com/uwb-antennae-design-files/ (accessed on 23 August 2025).
- Decawave (Qorvo). Decawave EVK1000 User Manual. 2016. Available online: https://www.qorvo.com/products/d/da007993 (accessed on 10 July 2025).



| Mode | Channel | Center Frequency [GHz] | Bandwidth [MHz] | Data Rate [kbps] | PRF * [MHz] | Preamble Length | Preamble Code | Ns-SFD † |
|---|---|---|---|---|---|---|---|---|
| 5 | 5 | 110 | 16 | 1024 | 3 | Yes |
| Parameter | Value | Description |
|---|---|---|
| grid size [m] | ||
| (narrowband) | maximum extra path length [m] | |
| (UWB) | ||
| 100 | regularization parameter | |
| 2 | correlation distance [m] | |
| movement noise variance [] | ||
| measurement noise variance [] |
| CD-NRTI | UWB-RTI | LoS-RTI | |
|---|---|---|---|
| Localization | |||
| Tracking |
| CD-NRTI | UWB-RTI | LoS-RTI | |
|---|---|---|---|
| Localization | |||
| Tracking |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Lv, D.; Zhang, Z.; Liu, H. A Real-Time UWB-Based Device-Free Localization and Tracking System. Electronics 2025, 14, 3362. https://doi.org/10.3390/electronics14173362
Xu S, Lv D, Zhang Z, Liu H. A Real-Time UWB-Based Device-Free Localization and Tracking System. Electronics. 2025; 14(17):3362. https://doi.org/10.3390/electronics14173362
Chicago/Turabian StyleXu, Shengxin, Dongyue Lv, Zekun Zhang, and Heng Liu. 2025. "A Real-Time UWB-Based Device-Free Localization and Tracking System" Electronics 14, no. 17: 3362. https://doi.org/10.3390/electronics14173362
APA StyleXu, S., Lv, D., Zhang, Z., & Liu, H. (2025). A Real-Time UWB-Based Device-Free Localization and Tracking System. Electronics, 14(17), 3362. https://doi.org/10.3390/electronics14173362







