Abstract
Device-to-device (D2D) communication enhances network efficiency by enabling direct, low-latency links between nearby users or devices. While most existing research assumes that D2D connections occur with the nearest neighbor, this assumption often fails in real-world scenarios—such as dense indoor environments, smart buildings, and industrial IoT deployments—due to factors like channel variability, physical obstructions, or limited user participation. In this paper, we investigate the performance implications of connecting to the n-th nearest neighbor in a cellular network supporting underlay D2D communication. Using a stochastic geometry framework, we derive and analyze key performance metrics, including the coverage probability and average data rate, for both D2D and cellular links under proximity-aware connection strategies. Our results reveal that non-nearest-neighbor associations are not only common but sometimes necessary for maintaining reliable connectivity in highly dense or constrained spaces. These findings are directly relevant to IoT-enhanced localization systems, where fallback mechanisms and adaptive pairing are essential for communication resilience. This work contributes to the development of proximity-aware and spatially adaptive D2D frameworks for next-generation smart environments and 5G-and-beyond wireless networks.
1. Introduction
Device-to-device (D2D) communication enables direct connectivity between nearby devices without relying on centralized infrastructure, thereby reducing latency and offloading cellular traffic. This capability is increasingly important in smart environments, such as shopping malls, industrial facilities, and healthcare settings, where proximity-based services like indoor localization, asset tracking, and context-aware automation depend on timely and resilient device interactions [1,2,3].
D2D enables direct communication between nearby devices without the aid of an evolved node base station (eNB). D2D communication is becoming more important for ultra-reliable low-latency communications (URLLC) and massive machine-type communications (mMTC) as wireless networks move toward 5G-and-beyond architecture [4]. This integration is reshaping traditional LTE cellular networks, offering improved resource allocation efficiency, reduced power consumption, and enhanced capabilities for content sharing, traffic offloading, and social-aware networking [5,6]. D2D principles are leveraged to facilitate direct vehicle-to-vehicle (V2V) and vehicle-to-infrastructure (V2I) communications, enhancing road safety and traffic efficiency [7,8].
In traditional D2D models, a device is assumed to connect with its nearest neighbor to minimize power consumption and transmission delays. However, obstacles such as walls or interference, along with user movement, selective participation, or spectrum constraints, may render the nearest node unavailable or unsuitable for communication. These dynamics call for a more flexible, proximity-aware D2D model that can accommodate connections to farther nodes when needed. As an example, let us consider a platooning scenario in dense urban traffic in which the vehicles may need to maintain their connections with multiple peers at the same time, instead of just connecting to the nearest one. This might be necessary for safety-critical applications, ensuring robust communication [9]. Moreover, the quality and stability of D2D connections in vehicular networks are affected by factors such as urban canyon effects and direction of travel [10].
In realistic deployments, the assumption that a D2D receiver always connects to its nearest neighbor can be overly restrictive. Factors such as obstacles, shadowing, spectrum contention, or user opt-out behavior may render the nearest node unavailable or suboptimal. In such settings (e.g., crowded venues, urban streetscapes, or industrial halls), allowing connections to the n-th nearest neighbor improves flexibility and robustness. This reality highlights a critical gap in current D2D research, where the influence of establishing connections to non-nearest neighbors remains largely unexplored.
This work examines how associating with the closest node in an uplink underlay D2D-enabled network influences system performance. Using stochastic geometry, we evaluate how varying the selected proximity index (n) affects both the coverage probability and the average throughput of a representative active D2D link. Our work contributes to a more realistic understanding of D2D performance in complex network environments, complementing recent advancements in D2D technologies and applications.
The proposed methodology offers a more accurate representation of D2D communication behavior in vehicular networks, encompassing the dynamic and intricate characteristics of actual deployments where vehicles are in continuous motion and connections vary between devices. By taking into account a wider range of possible D2D connections beyond the closest neighbor, it facilitates the creation of more resilient and flexible resource allocation algorithms. Moreover, it provides valuable information on the scalability and performance constraints of vehicular D2D networks, especially when they encounter different connection distances and environmental conditions, such as urban canyons and vehicle speeds. Furthermore, it can guide the development of more effective mode selection and user pairing algorithms that consider the unpredictable characteristics of vehicle surroundings, surpassing conventional nearest-neighbor approaches to enhance communication dependability and network efficiency. Our main contributions are as follows:
- We analyze the performance impact of establishing connections with the nearest neighbor, instead of the nearest neighbor, in D2D-enabled cellular networks using a stochastic geometry framework.
- We derive closed-form expressions for the coverage probability and average data rate for both D2D and cellular links as a function of the proximity parameter n.
- We discuss the relevance of non-nearest-neighbor connections in highly dynamic and dense urban settings, such as vehicular networks. We demonstrate through simulations that the performance degradation from connecting to farther neighbors is non-trivial, highlighting the importance of adaptive connection strategies.
2. Related Works
Traditional methods presume a connection with the nearest neighbor in order to reduce both communication time and power consumption. Nevertheless, several studies have shown that this assumption is frequently impractical in dynamic settings, such as metropolitan vehicular networks, where swift alterations in topology and channel conditions warrant the exploration of alternate connections beyond the closest neighbor. The influence of D2D communication on spectrum use and power management, under the assumption that devices establish connections with their closest neighbor, was reviewed in [11]. The authors of [11] recognized that limitations in the communication channels and the movement of users can result in suboptimal performance, indicating the necessity for the implementation of more adaptable connection schemes. The study in [12] showed that in densely populated urban areas, vehicle nodes often encounter substandard link quality when establishing connections with their closest neighbor as a result of urban canyon effects and mobility patterns, resulting in frequent link failures.
Advancements in stochastic geometry have facilitated the modeling of more realistic D2D communication instances [13]. For instance, the authors of [14] investigated the efficiency of D2D-enabled cellular networks by employing stochastic geometry, with a specific emphasis on the influence of interference and coverage. While their model presupposes nearest-neighbor connections, the authors acknowledge that interference from nodes located far away has a substantial impact on network performance. This observation strengthens the case for exploring connections beyond the nearest neighbor.
Within vehicular networks, the rapid movement of nodes introduces an extra level of intricacy to D2D interactions. The authors of [9] illustrated the constraints of nearest-neighbor connections in vehicular platooning situations when vehicles need to sustain dependable connections with several peers concurrently to guarantee the appropriate functioning of safety-critical applications. In order to improve network resilience, they propose a more robust communication structure by investigating links to distant nodes.
Moreover, the authors of [15] examined the concepts of mode selection and resource allocation algorithms that consider non-nearest-neighbor connections in D2D communications. Their research emphasizes the possibility of enhancing data speeds and coverage probability by enabling devices to establish connections with more distant nodes, especially in network environments with high density.
Considering connections to users beyond the nearest neighbor, alongside the incorporation of exclusion zones [16,17], can provide more realistic and effective solutions for enhancing the performance of cellular networks with D2D capabilities. This approach not only reduces interference but also promotes more balanced resource allocation, addressing practical challenges in dense and heterogeneous network environments. Such strategies are essential for developing robust and scalable D2D communication frameworks in modern wireless systems. In previous work [18], the effect of connecting to the nearest node was studied in a dedicated D2D network with exclusive resources. The present work extends this analysis to an underlay scenario with cellular users, where interference and spectrum sharing play a key role.
The related studies highlight the need to take into account practical circumstances in the design of D2D networks, where the characteristics of the channel, mobility, and user preferences are crucial factors in choosing the most effective connection methodologies. Expanding upon these observations, our study examines the impact of establishing connections with the n-th closest neighbor in D2D-enabled cellular networks, thus enhancing our understanding of D2D link behavior in intricate network infrastructures. Through the analysis of the coverage probability and average data rate for D2D and cellular links, we provide a more precise depiction of actual D2D communication situations, beyond the limitations of idealized nearest-neighbor modeling.
While [15,16] explored non-nearest-neighbor strategies in D2D settings, our work extends this analysis by quantifying how the number of such connections (n) and the density relationships between transmitters and receivers affect key metrics like coverage and rate. Unlike prior studies, we provide insights into the limitations of nearest-neighbor assumptions in dense urban D2D scenarios and include fallback behavior to cellular links when thresholds are exceeded. To better contextualize our contributions, we present a comparative overview of closely related works in Table 1.

Table 1.
Comparison between our work and the most relevant related works.
3. System Model
We consider a D2D-enabled cellular network in the uplink direction. Our system model consists of three user categories: device-to-device transmitters (DTUs), device-to-device receivers (DRUs), and cellular users (CUs). We assume that eNBs are placed in the centers of a hexagonal cell grid with density . DTUs and CUs are assumed to be generated from a Poisson point process (PPP) with density and a D2D traffic controller parameter q (i.e., the density of potential DTUs is ). DRUs are assumed to be generated from another independent PPP, , with density .
It is assumed that the density of DRUs is less than that of DTUs and CUs. Therefore, it is reasonable to think about the situations in which connection to farther nodes is possible in D2D communication. It is possible in densely populated user networks that some popular files are downloaded primarily by transmitter users (DTUs and CUs), and they can deliver them locally to DRUs or through traditional cellular networks. However, it should be noted that the relationship between the density of transmitters and receivers determines the number of more distant users that can be considered. For example, when the density of transmitters is two times that of receivers, investigating the situation of connecting to the fifth nearest node for D2D communication is neither feasible nor can it be formulated, as we demonstrate in the following.
We define a search radius around each DRU and assume that potential DTUs for each DRU are located in a circle, with that DRU at the center and radius . This radius is a key network parameter in a D2D-enabled network and is also used for mode selection. This study primarily explores how link performance changes when devices are associated with the closest node, rather than being restricted to the nearest one, in both D2D and cellular communications. Furthermore, we consider that whenever the distance of a potential D2D link exceeds , such a connection is discarded, and the receiving user is instead served through the cellular network.
3.1. D2D Link Statistics
In the literature, the distance between two D2D nodes is always assumed to be Rayleigh or uniformly distributed. In this paper, farther node connections in D2D mode are considered. The probability density function (PDF) of the distance to the neighbor for a PPP [19] can be expressed as
where is the user density and r is the distance between each node and its nearest neighbor. We assume that the locations of DTUs and DRUs follow independent homogeneous PPPs to enable tractable analysis using stochastic geometry. The density of DRUs is assumed to be less than that of DTUs and CUs. This captures scenarios where a limited number of users request content compared to the number able to transmit. Mobility is not explicitly modeled; the framework applies to time-averaged snapshots or slow-varying D2D configurations. User preferences (e.g., willingness to participate in D2D) are indirectly captured through probabilistic association and coverage modeling. Therefore, the PDF of the length of a D2D link considering the DRU’s search radius is
where is a random variable that represents the length of a D2D link and is the unity function. There is another important D2D link parameter, which is the probability of the existence of the nearest DTU around the intended DRU. Let N denote the random variable representing the count of DTUs located in the vicinity of a DRU. We further denote by the probability that no fewer than n DTUs exist within the coverage radius of the considered DRU, expressed as
where is the lower incomplete gamma function. The value of increases with both the DTU density and the search radius , reflecting the likelihood that at least n transmitters exist within a given distance. For fixed n, increasing or improves D2D link availability, while for fixed and , a higher n reduces .
For analytical tractability, channel-inversion power control is employed, ensuring that the transmit power adjusts proportionally to the path loss to preserve the received signal quality. Accordingly, for a standard communication link of length r, the mean transmit power is expressed as , with denoting the path loss exponent. Therefore, considering (2), the average transmit power of a DTU in the aforementioned system model with respect to n can be expressed as
It is important to acknowledge that in dense urban environments, DRUs may outnumber DTUs. In such cases, our assumptions may not hold, and alternative spatial models (e.g., Poisson cluster processes or correlated point processes) may be required.
3.2. Modeling User Engagement
To account for user participation behavior, we introduce an engagement coefficient , representing the probability that a transmitting user (DTU) agrees to participate in a D2D link. This parameter can capture energy-saving policies, social constraints, or user incentives. The adjusted effective density of DTUs becomes , and the probability of successful link formation in (3) is scaled accordingly:
This adaptation allows evaluation under varying willingness-to-participate scenarios. It is important to note that under channel-inversion power control, the average transmit power increases as the link distance increases. Thus, as the n-th nearest neighbor is farther away, DTUs transmit at higher power, intensifying the interference experienced by both D2D and cellular links.
4. Analysis of SINR and Rate
Consider a typical D2D or cellular link , where c and d stand for cellular and D2D modes, respectively. At any randomly chosen receiver, the experienced SINR is described by
where characterizes the small-scale fading of the typical link, refers to the interference power, and denotes the noise power. The D2D interferers are considered to be the nearest DTUs of the co-channel DRUs. Therefore, the effective D2D interferers constitute an HPPP with density , a PPP thinned from with thinning probability , denoted by . Furthermore, the cellular interferers form another HPPP with density , named (for a cellular link, it is , i.e., the cellular UEs of the intended cell must be excluded). Therefore, the interference powers at typical D2D and cellular links can be expressed as
In these expressions, is the transmit power of the interfering source, is its associated channel fading, and is the distance separating it from the typical receiver. Accounting for the previously discussed interferer density, the SINR’s complementary cumulative distribution function (CCDF), which reflects the coverage probability of a representative D2D or cellular link, can be derived as
where is the Laplace transform of a typical link’s interference and is expressed as
Finally, the average data rates for a D2D link in D2D mode , a cellular link , and a potential D2D link are given by
where is the factor in (14) that arises from the cellular channel share between users on average. The obtained relations show that the number of farther-connected nodes n has an important effect on the coverage probability and rate of D2D and cellular links. The expected rate accounts for the fact that not all DRUs find a suitable n-th nearest DTU within . If the required DTU does not exist, the DRU falls back to cellular mode. Thus, represents the average per-DRU rate combining both successful D2D links and fallback cellular links.
5. Simulation Results
This section explores the influence of linking to the closest node on the coverage performance and achievable throughput of cellular and D2D connections within the network. The simulation setup employed for this analysis is shown in Table 2. It should be noted that refers to the average received signal-to-noise ratio, which is defined as the mean received signal power normalized by the noise power. Figure 1 depicts how varying n alters the CCDF of these representative links. The results show that connecting to the nearest D2D transmitter () yields the best performance in terms of the coverage probability, while selecting farther nodes () leads to degradation due to increased path loss and interference.

Table 2.
Parameters and their corresponding values used in the simulations.
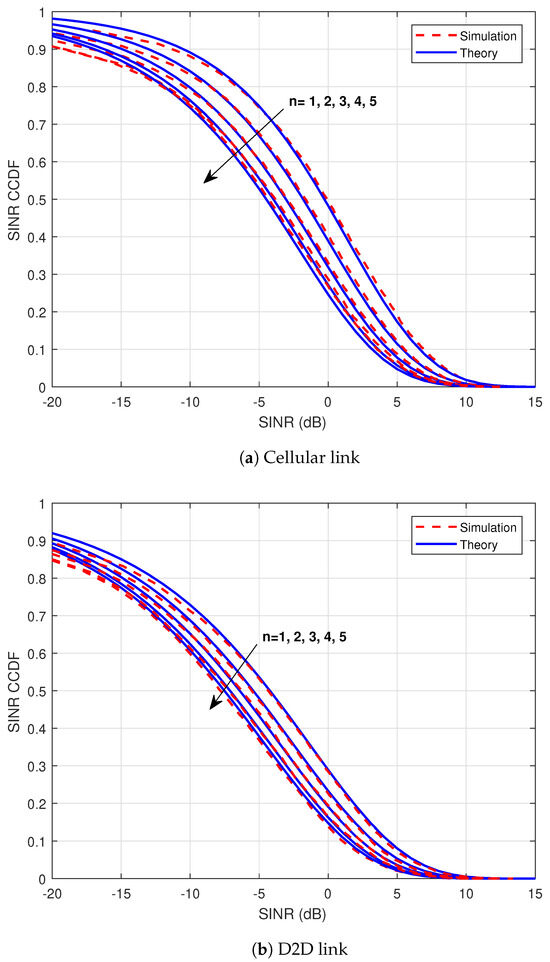
Figure 1.
Coverage probabilities of cellular and D2D links.
Furthermore, connecting to farther nodes causes an increase in DTU power because of channel-inversion power control. Increasing the power of DTUs leads to an increase in interference from all other co-channel D2D connections at the considered link. As expected, selecting a farther transmitter leads to a longer communication distance, which results in higher path loss and reduced SINR. Consequently, the coverage probability decreases with increasing n. However, this trend is not strictly linear; instead, our results highlight a threshold-like behavior. This nonlinear effect reflects the combined influence of path loss and interference in the D2D-enabled network, the channel-inversion power control strategy, and the spatial distribution of transmitting and interfering users, as captured by our stochastic geometry model. Shadowing effects, poor channel states, and users opting out of D2D participation reveal that considering additional, more distant nodes is vital, and relying solely on the nearest node represents an idealized scenario. These findings emphasize the significance of accounting for realistic network conditions in D2D-enabled systems. There is good agreement between simulation and theory.
In the figures below, , and we considered a connection to n = 1–5 farther nodes. As we mentioned earlier, the relationship between the density of transmitting and receiving D2D nodes must be in accordance with the number of farther nodes that are investigated. If the ratio of transmitting D2D nodes to receiving D2D nodes is less than the number of farther nodes to be investigated, the assumption of independence between the DRUs’ PPP and the transmitting nodes is not valid. In other words, in this situation, DTUs form a correlated PPP with the receiving nodes, and considering other point processes for DTUs is necessary.
While our model provides analytical clarity, real-world D2D performance may deviate due to factors such as urban canyon effects, time-varying traffic, and rapid user mobility. For instance, in vehicular networks, link durations are short, and relative velocities may degrade connection stability. Additionally, user participation in D2D may depend on battery constraints, privacy, or the application context. These aspects can be addressed in future work using trace-driven simulations or hybrid stochastic-empirical modeling.
The relationship between the average data rate of potential D2D and cellular links and the maximum search radius () of a typical DRU, for varying values of n, is illustrated in Figure 2. It is evident that higher values of n reduce the average rate across both link types. For D2D links, the radius that maximizes throughput shifts with n, suggesting that the optimal depends on the number of nodes intended for connection. Therefore, appropriately setting relative to the DTU-to-DRU density ratio enhances the achievable data rates in D2D networks. Furthermore, the results capture the performance differences between the nearest and farthest candidates, and the choice of n balances rate performance and connection availability.
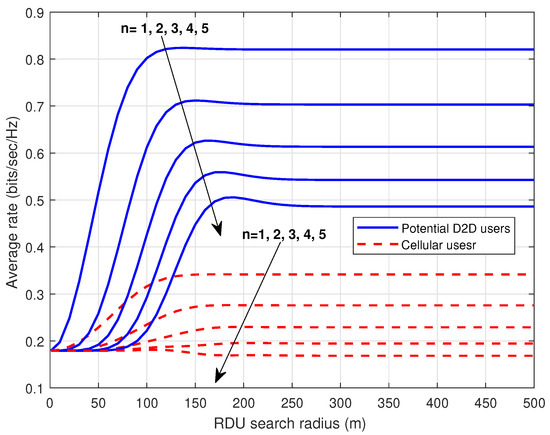
Figure 2.
Average data rate of D2D and cellular links as a function of .
Furthermore, with the increase in , more DRUs choose the D2D mode to connect to the network. This increases traffic offloaded via D2D links; however, the interference from co-channel D2D links will increase. Similar to the results in [20], the increase in interference dominates the offloading gain, and therefore, the cellular rate will decrease with an increase in . However, in this paper, the density of receiving users is five times that of transmitting users. This causes the distance between DRUs and their neighboring DTUs to be relatively small for small values of n, although this distance increases with the increase in n.
Therefore, for small values of n (1 to 3), the power of DTUs in active D2D links is small and leads to an increase in the cellular link data rate with an increase in the search radius . This means that, for small values of n, the offloading gains from the increasing number of D2D links dominate the increase in interference power of co-channel D2D links. However, with an increase in n to larger values (4 and 5), the increase in interference power of co-channel D2D links dominates the offloading gains of increasing active D2D links. Therefore, we see no significant difference in the cellular link data rate for and a slight decrease for .
In our simulation results, we explicitly present the case of as a natural benchmark, corresponding to the conventional scenario in which each user connects to its nearest neighbor. This allows a direct comparison between the standard nearest-neighbor connection and the proposed model with connections to farther nodes (). By including the scenario, we demonstrate how key performance metrics, such as the outage probability and average data rate, vary as the connection distance increases. This approach provides a clear baseline for evaluating the benefits and trade-offs of connecting to the nearest node in D2D-enabled cellular networks.
5.1. Implications for Optimization Algorithms
The analytical expressions derived for the coverage probability and data rate provide insights that can guide algorithmic design. For instance, the sensitivity of performance to the proximity index n and suggests that adaptive search-radius control or mode-switching algorithms could be designed to maximize throughput under interference constraints. Additionally, pairing strategies that consider not just distance but also link quality and traffic load could be developed. These directions open up possibilities for integrating our stochastic geometry models with optimization and machine learning techniques.
5.2. Heuristic for Adaptive Selection
As a proof of concept, we present a simple adaptive heuristic in which each DRU selects the smallest proximity index n such that the expected potential D2D rate exceeds a predefined rate threshold , and the interference remains below a maximum acceptable level . Formally, each DRU solves
This policy improves link efficiency in sparse areas while mitigating interference in dense regions.
6. Future Work and Limitations
This study focuses on the performance implications of connecting to the n-th nearest neighbor in D2D-enabled cellular networks, under the assumption of static users and homogeneous spatial distributions. While this abstraction allows for tractable mathematical modeling and analytical insights, it introduces several limitations. First, user mobility, which significantly affects channel dynamics, link stability, and interference patterns, is not considered. Incorporating realistic mobility models (e.g., random waypoint, group mobility) would require revised outage and rate formulations and is left for future exploration. Second, the analysis is based on a homogeneous PPP for both cellular and D2D users, which may not capture spatial clustering in real urban environments. Extensions using more advanced spatial models, such as Poisson cluster processes, could offer more accurate insights. Third, power control is not fully applied in the current model; all transmitters operate with a channel-inversion power control mechanism, which may not reflect practical resource allocation schemes. Finally, future work could explore adaptive node-selection and search-radius optimization strategies to better balance the trade-off between the coverage and data rate, particularly under varying interference and traffic conditions. The current analysis assumes static selection criteria, which may limit performance in highly dynamic networks. These limitations open avenues for future work to generalize the proposed model and make it more applicable to realistic deployment scenarios.
7. Conclusions
This study examined how connecting to the closest node affects performance in D2D-enabled networks. The underlaid D2D network was evaluated through the coverage probability and average throughput, employing both analytical derivations and simulations to validate our findings. The results indicate strong agreement between the theoretical predictions and simulation outcomes. Importantly, the analysis demonstrates that assuming connections only to the nearest node is idealized, highlighting the significance of considering more distant nodes in D2D communications.
Author Contributions
Conceptualization, S.R. and S.A.G.; methodology, S.R.; software, S.R.; validation, S.R., R.S., and S.A.G.; formal analysis, S.R.; investigation, S.R.; resources, S.R.; data curation, S.R.; writing—original draft preparation, S.R.; writing—review and editing, R.S. and S.A.G.; visualization, S.R.; supervision, S.A.G.; project administration, S.A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
Acknowledgments
During the preparation of this manuscript, the authors used AI-based language editing tools for refinement and formatting suggestions. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| D2D | Device-to-device |
| BS | Base station |
| SINR | Signal-to-interference-plus-noise ratio |
| Probability density function | |
| PPP | Poisson point process |
| CDF | Cumulative distribution function |
| SIR | Signal-to-interference ratio |
| UE | User equipment |
| 5G | Fifth generation |
| QoS | Quality of service |
Appendix A
Proofs of (10) and (11) .
Equality (a) is derived using Slivnyak’s theorem in conjunction with the Laplace functional of a PPP [21], while equality (b) results from assuming Rayleigh fading for H. Considering the channel-inversion power control and the uniform distribution of cellular UEs in each cell with the PDF of the link distance () [20] and the PDF of the D2D link distance in (2), the moment of D2D and cellular link powers can be expressed as
and
References
- Chen, B.; Liang, H.; Wan, J.; Wang, C.; Yan, X.; Xia, X.; AlQahtani, S.A. Exploring NetGPT-enabled dynamic resource management for mobile D2D in Industrial IoT. IEEE Netw. 2025, 39, 37–46. [Google Scholar] [CrossRef]
- Militano, L.; Araniti, G.; Condoluci, M.; Farris, I.; Iera, A. Device-to-device communications for 5G internet of things. EAI Endorsed Trans. Internet Things 2015, 1, 1–15. [Google Scholar] [CrossRef]
- Shastri, A.; Valecha, N.; Bashirov, E.; Tataria, H.; Lentmaier, M.; Tufvesson, F.; Rossi, M.; Casari, P. A review of millimeter wave device-based localization and device-free sensing technologies and applications. IEEE Commun. Surv. Tutor. 2022, 24, 1708–1749. [Google Scholar] [CrossRef]
- Papachary, B.; Arya, R.; Dappuri, B. Power-aware QoS-centric strategy for ultra reliable low latency communication in 5G beyond wireless networks. Clust. Comput. 2024, 27, 7455–7468. [Google Scholar] [CrossRef]
- Nair, A.; Tanwar, S. Resource allocation in V2X communication: State-of-the-art and research challenges. Phys. Commun. 2024, 64, 102351. [Google Scholar] [CrossRef]
- Gopal, M.; Velmurugan, T. Resource allocation algorithm for 5G and B5G D2D underlay wireless cellular networks. Multimed. Tools Appl. 2024, 83, 66841–66868. [Google Scholar] [CrossRef]
- Su, J.; Liu, Z.; Li, Y.; Lee, J.; Guan, X. Communication and Computing Balanced Resource Allocation in D2D-Based Vehicular MEC Networks. IEEE Internet Things J. 2024, 11, 40689–40701. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, H.; Chen, C.W. Caching Optimization in User-Centric Networks: A Stochastic Geometry Perspective. IEEE Trans. Veh. Technol. 2025, 74, 8187–8200. [Google Scholar] [CrossRef]
- Parvini, M.; Schulz, P.; Fettweis, G. Resource Allocation in V2X Networks: From Classical Optimization to Machine Learning-Based Solutions. IEEE Open J. Commun. Soc. 2024, 5, 1958–1974. [Google Scholar] [CrossRef]
- Anwar, W.; Franchi, N.; Fettweis, G. Physical layer evaluation of V2X communications technologies: 5G NR-V2X, LTE-V2X, IEEE 802.11 bd, and IEEE 802.11 p. In Proceedings of the 2019 IEEE 90th Vehicular Technology Conference (VTC2019-Fall), Honolulu, HI, USA, 22–25 September 2019; pp. 1–7. [Google Scholar]
- Lin, X.; Andrews, J.G.; Ghosh, A.; Ratasuk, R. An overview of 3GPP device-to-device proximity services. IEEE Commun. Mag. 2014, 52, 40–48. [Google Scholar] [CrossRef]
- Singh, P.K.; Nandi, S.K.; Nandi, S. A tutorial survey on vehicular communication state of the art, and future research directions. Veh. Commun. 2019, 18, 100164. [Google Scholar] [CrossRef]
- Shatnawi, R.A.; Khodeir, M.A.; Al-Mistarihi, M.F.; Darabkh, K.A.; Al-Zuraiqi, E.T.; Qasaymeh, M.M. The Analysis of Device-to-Device (D2D) Communication System Operating in 5G Underlaying Cellular Networks on Multiple Bands over Nakagami-m Fading Channels. SN Comput. Sci. 2025, 6, 430. [Google Scholar] [CrossRef]
- ElSawy, H.; Hossain, E.; Haenggi, M. Stochastic geometry for modeling, analysis, and design of multi-tier and cognitive cellular wireless networks: A survey. IEEE Commun. Surv. Tutor. 2013, 15, 996–1019. [Google Scholar] [CrossRef]
- Pawar, P.; Trivedi, A. Power Control and Mode Selection Algorithm for D2D Communications. In Proceedings of the 2019 IEEE 89th Vehicular Technology Conference (VTC2019-Spring), Kuala Lumpur, Malaysia, 28 April–1 May 2019; pp. 1–5. [Google Scholar]
- Chu, M.; Liu, A.; Chen, J.; Lau, V.K.; Cui, S. A stochastic geometry analysis for energy-harvesting-based device-to-device communication. IEEE Internet Things J. 2021, 9, 1591–1607. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, L.; Yao, S.; Liang, H.; Shi, H.; Chen, Y. Outage Probability Analysis for D2D-Enabled Heterogeneous Cellular Networks with Exclusion Zone: A Stochastic Geometry Approach. CMES-Comput. Model. Eng. Sci. 2024, 138, 639. [Google Scholar] [CrossRef]
- Rajabi, S.; Ghorashi, S.; Shah-Mansouri, V. Impact of connecting to the nth nearest node in dedicated device-to-device communications. Electron. Lett. 2018, 54, 535–537. [Google Scholar] [CrossRef]
- Song, X.A.; Li, H.; Guo, Z.; Wang, X.P. Coverage probability analysis of D2D communication based on stochastic geometry model. In International Conference in Communications, Signal Processing, and Systems; Springer: Singapore, 2020; pp. 83–93. [Google Scholar]
- Lin, X.; Andrews, J.G.; Ghosh, A. Spectrum sharing for device-to-device communication in cellular networks. IEEE Trans. Wirel. Commun. 2014, 13, 6727–6740. [Google Scholar] [CrossRef]
- Haenggi, M. Stochastic Geometry for Wireless Networks; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).