Fast Identification of Series Arc Faults Based on Singular Spectrum Statistical Features
Abstract
1. Introduction
2. Feature Extraction from Singular Spectrum Statistical Features
2.1. Singular Spectrum Construction
2.2. Statistical Feature Extraction
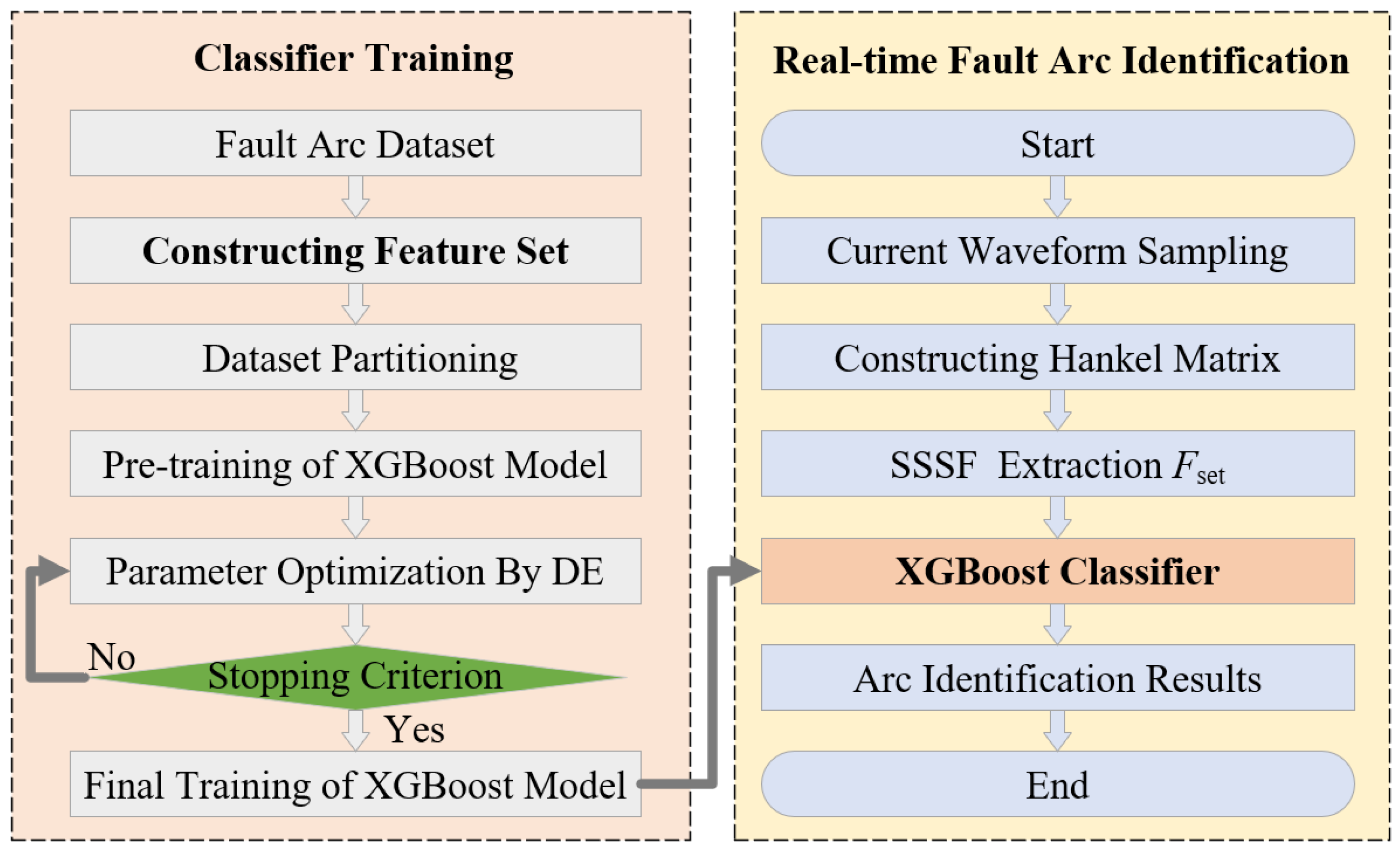
3. Series Arc Fault Rapid Identification
3.1. XGBoost Classifier
3.2. Selection of Classifier Hyperparameters
3.3. The Proposed Arc Fault Identification Method
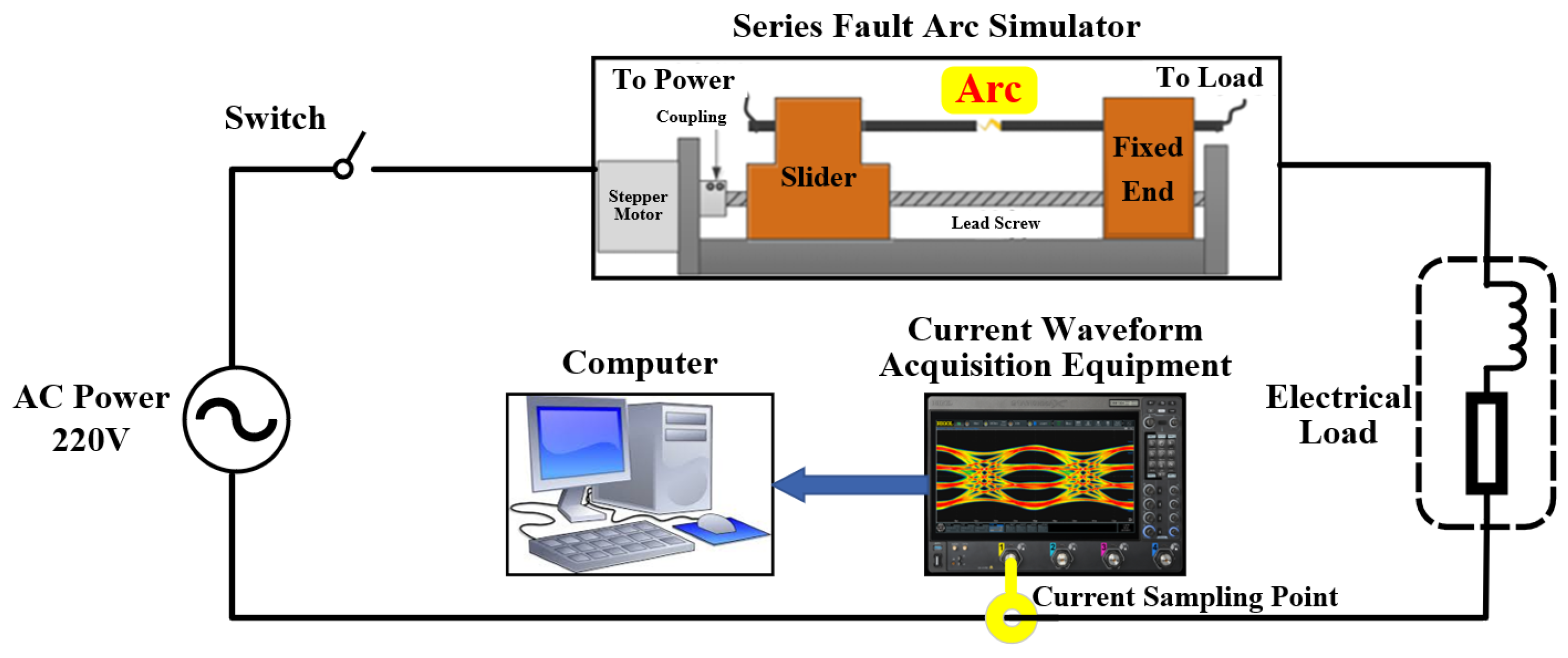
4. Experimental Methods and Results Analysis
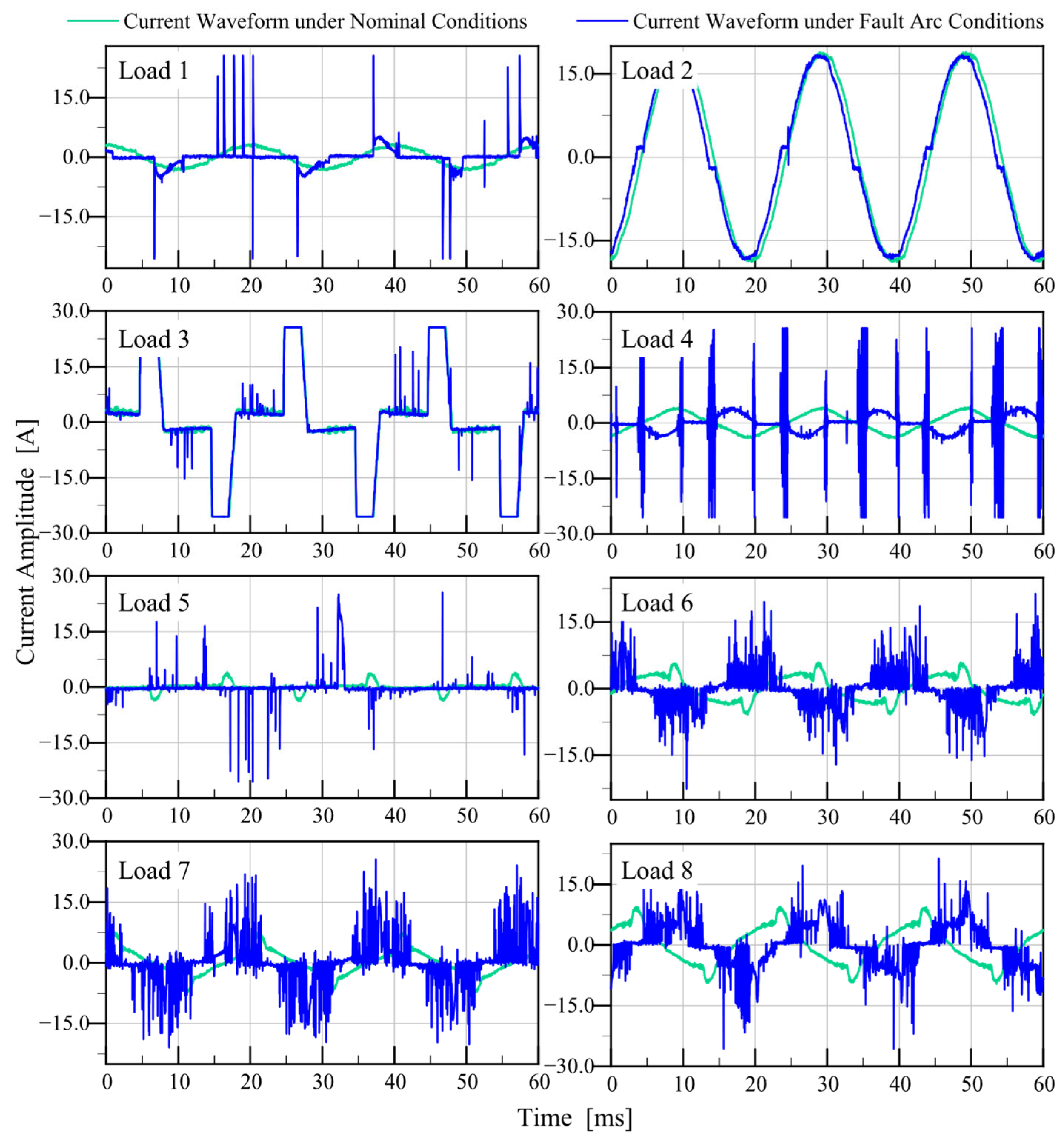
4.1. Experimental Platform and Dataset
4.2. Evaluation Metrics
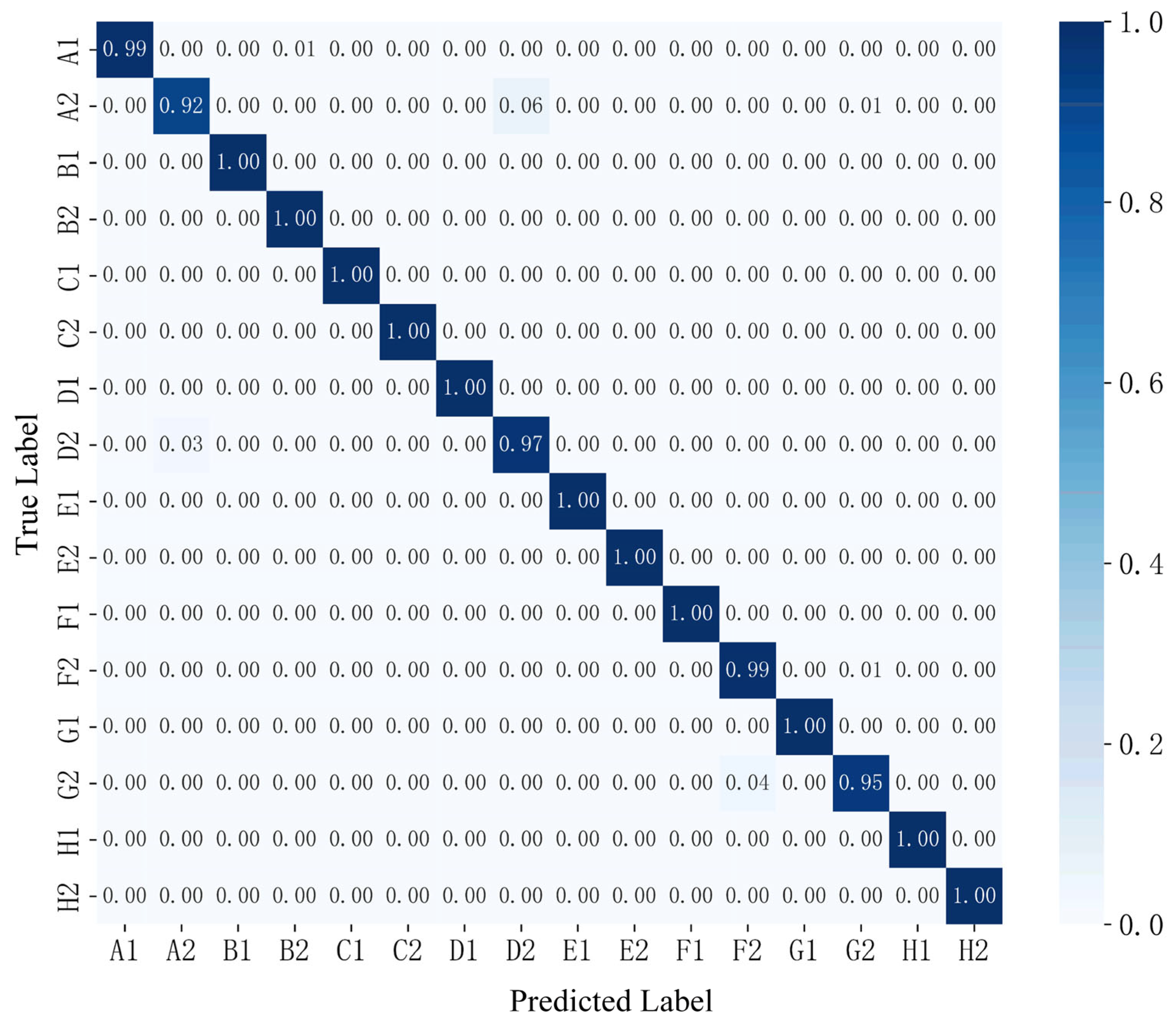
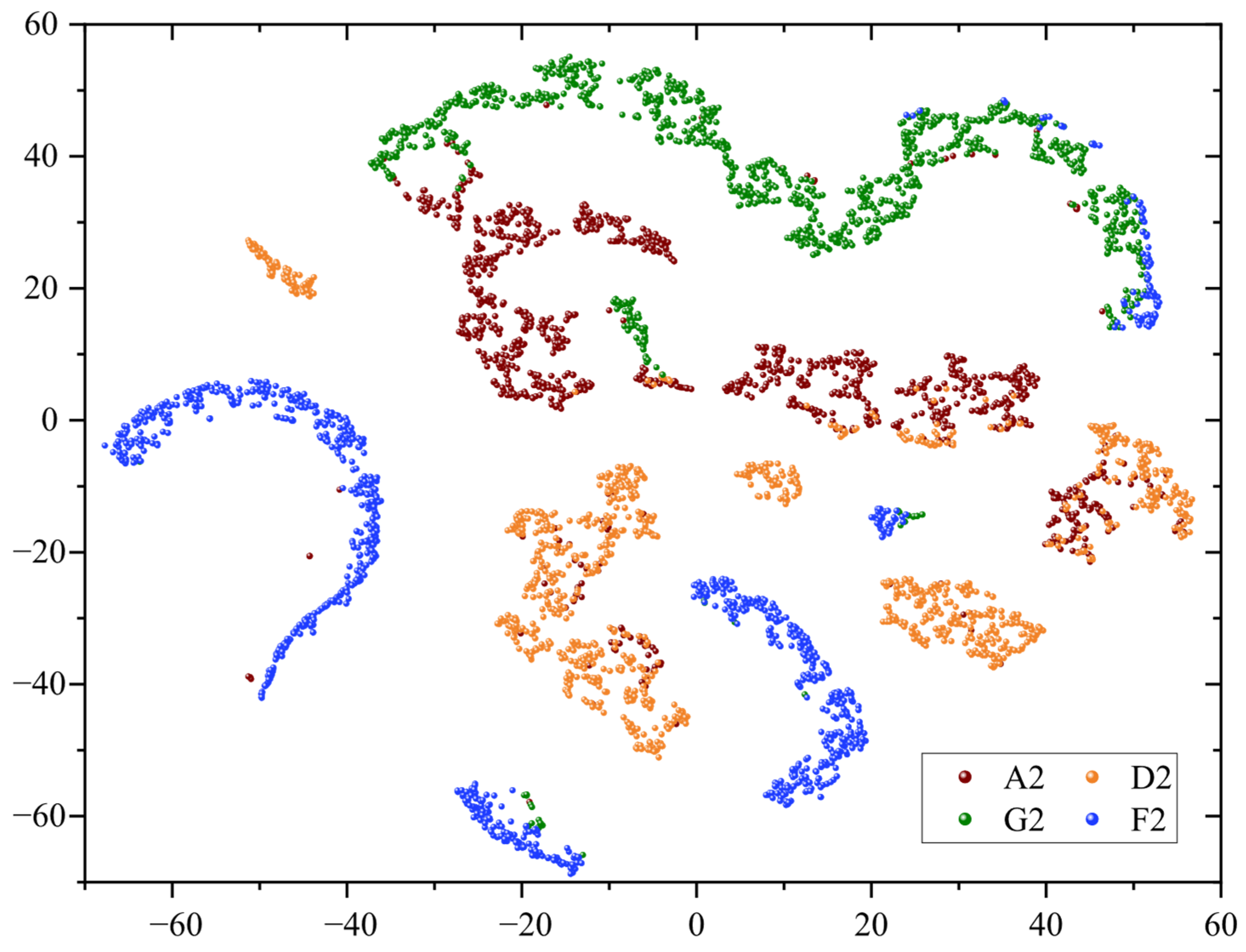
4.3. Test Results
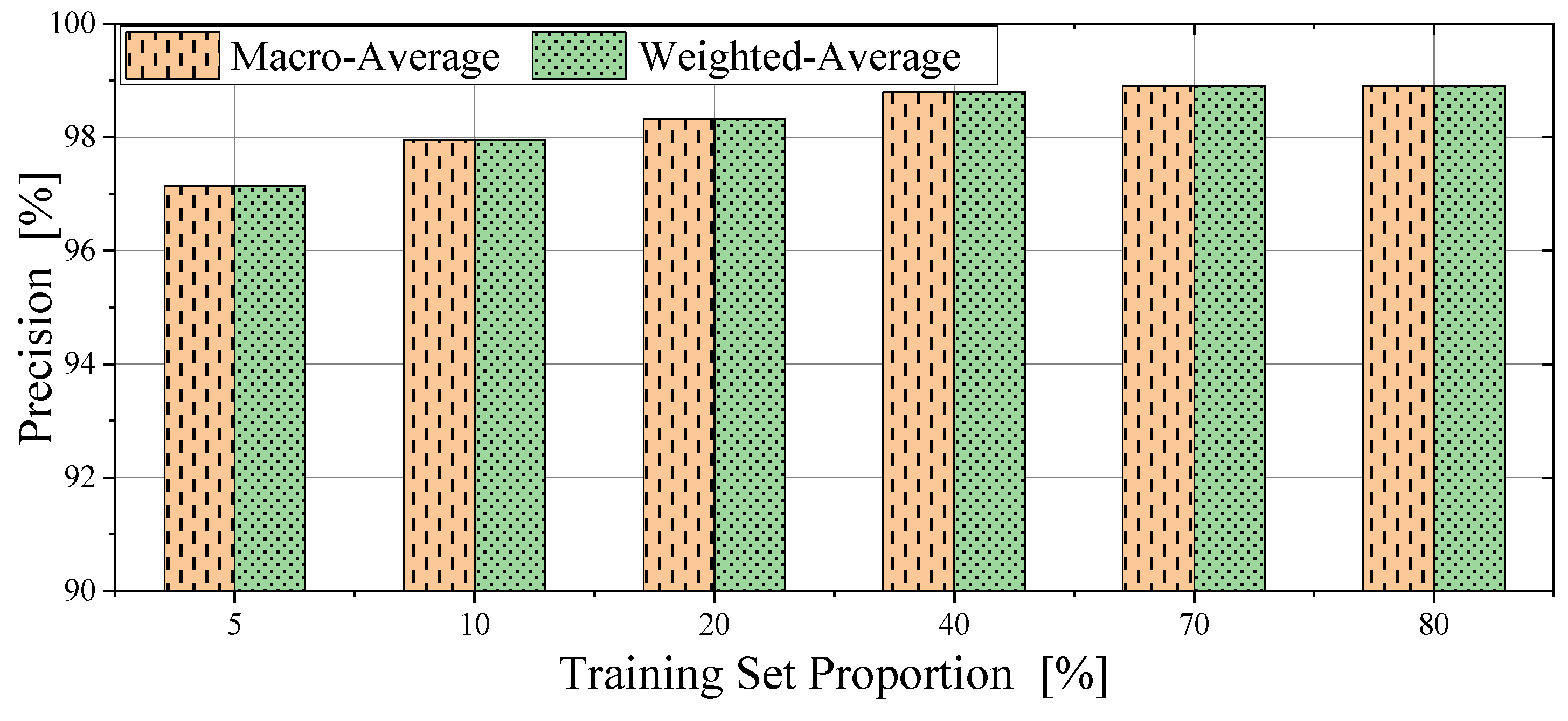
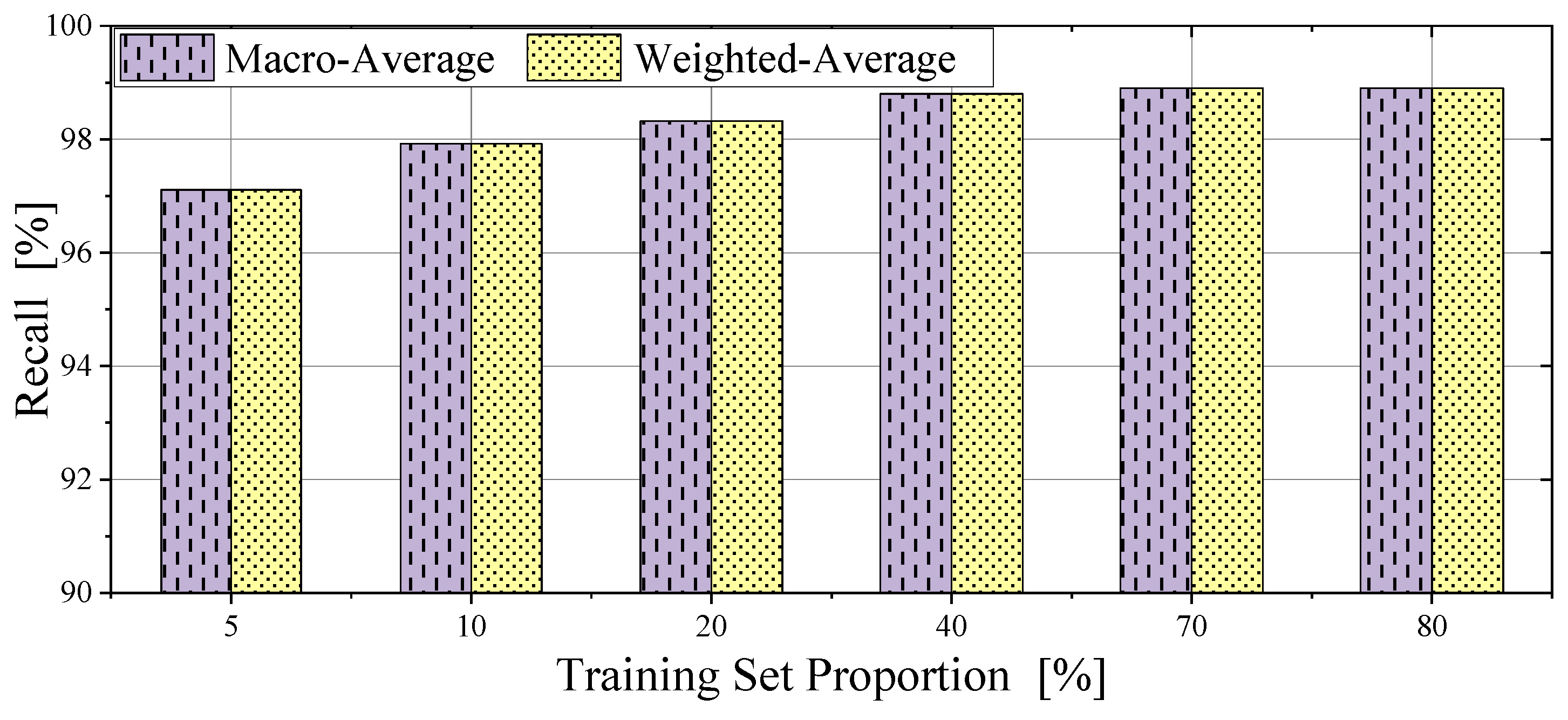
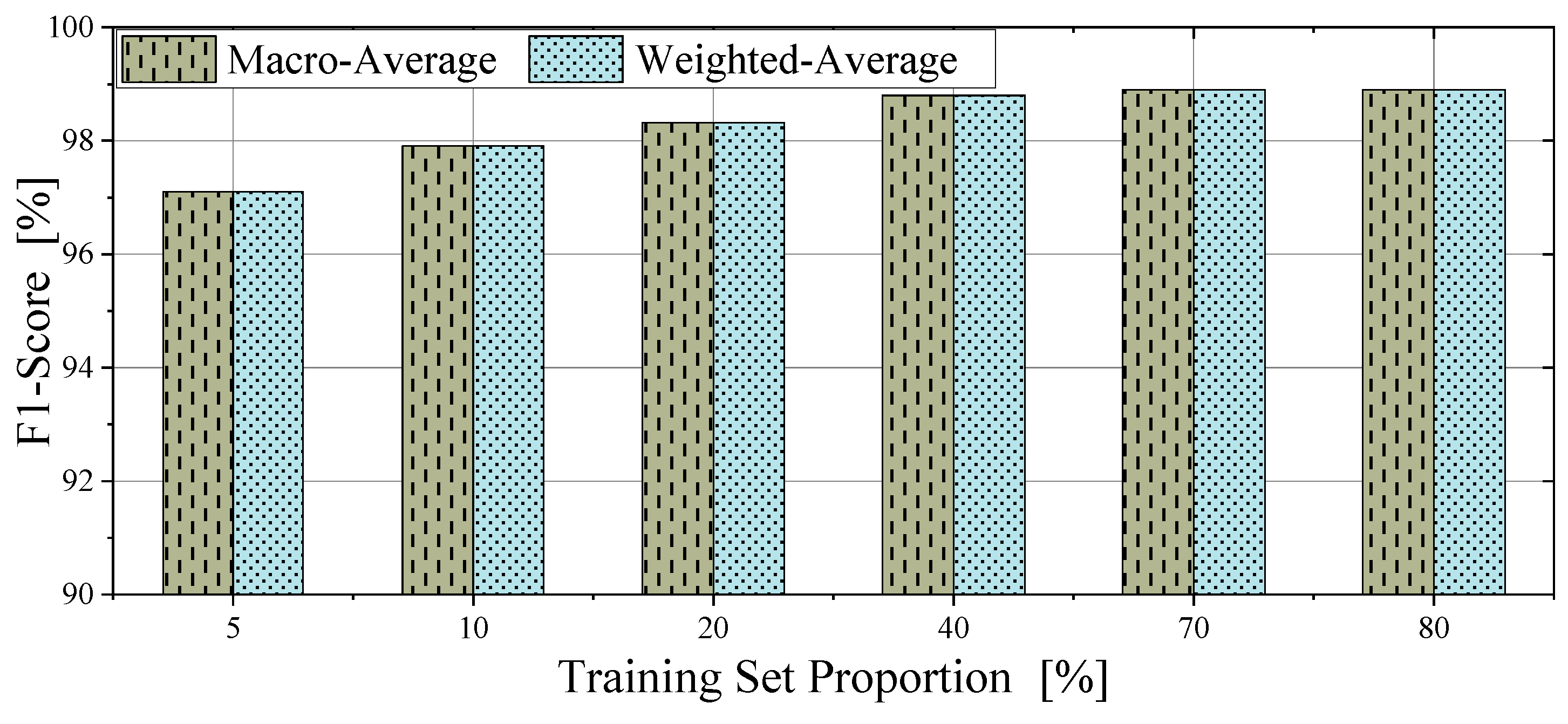
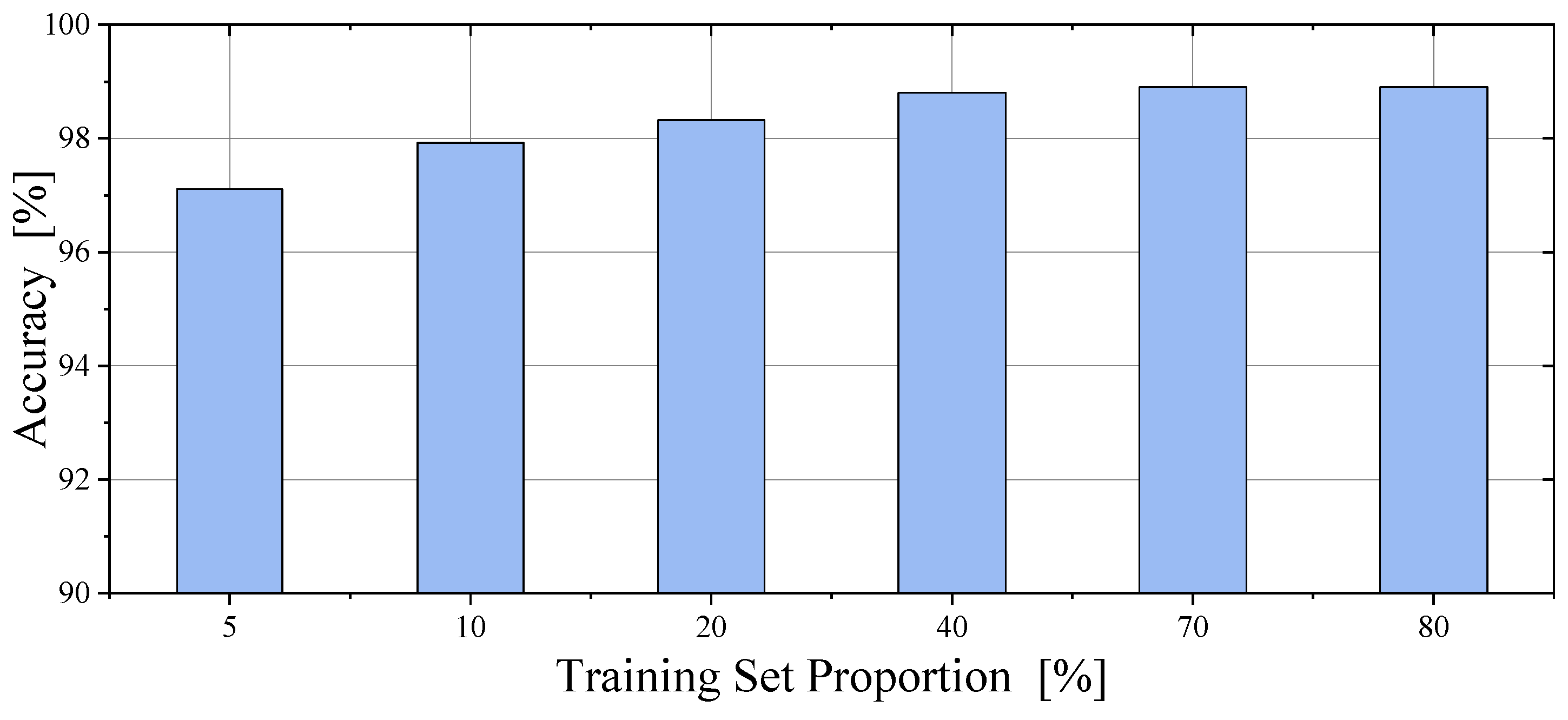
4.4. Validation with Varying Training Set Proportions
4.5. Accuracy Comparison with Other Methods
4.6. Computational Complexity Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Chen, H.C.; Li, Z.; Jia, C.; Du, Y.; Zhang, K.; Wei, H. Lightweight AC Arc Fault Detection Method by Integration of Event-Based Load Classification. IEEE Trans. Ind. Electron. 2024, 71, 4130–4140. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Lin, J.; Hu, S.; Cao, Y.; He, L.; Yang, X.; Xu, Y.; Zeng, L.; Xie, L. A bi-layer coordinated power regulation strategy considering system dynamics and economics for isolated hybrid AC/DC multi-energy microgrid. Sci. China Technol. Sci. 2024, 68, 1121001. [Google Scholar] [CrossRef]
- Liu, B.; Zeng, X. AC Series Arc Fault Modeling for Power Supply Systems Based on Electric-to-Thermal Energy Conversion. IEEE Trans. Ind. Electron. 2023, 70, 4167–4174. [Google Scholar] [CrossRef]
- Ji, C.; Wang, K.; Wang, Q.; Chen, Q.; Fan, M.; Xu, B.; Wang, X.; Zhao, W.; Xiong, L. Arc Detection Method for Single-Phase AC Series Fault Based on Current Convolution. Recent Adv. Electr. Electron. Eng. 2025, 18, 991–998. [Google Scholar] [CrossRef]
- Dhar, S.; Patnaik, R.K.; Dash, P.K. Fault Detection and Location of Photovoltaic Based DC Microgrid Using Differential Protection Strategy. IEEE Trans. Smart Grid 2018, 9, 4303–4312. [Google Scholar] [CrossRef]
- Yuventi, J. DC Electric Arc-Flash Hazard-Risk Evaluations for Photovoltaic Systems. IEEE Trans. Power Deliv. 2014, 29, 161–167. [Google Scholar] [CrossRef]
- Wang, Y.; Hou, L.; Paul, K.C.; Ban, Y.; Chen, C.; Zhao, T. ArcNet: Series AC Arc Fault Detection Based on Raw Current and Convolutional Neural Network. IEEE Trans. Ind. Inform. 2022, 18, 77–86. [Google Scholar] [CrossRef]
- Zhang, J.; Zou, J.; Xu, X.; Li, C.; Song, J.; Wen, H. High accuracy DFT-based frequency estimator for sine-wave in short records. Measurement 2025, 239, 115456. [Google Scholar] [CrossRef]
- Wang, K.; Wang, J.; Song, J.; Tang, L.; Shan, X.; Wen, H. Accurate DFT Method for Power System Frequency Estimation Considering Multi-Component Interference. IEEE Trans. Instrum. Meas. 2023, 72, 1–11. [Google Scholar] [CrossRef]
- Jiang, R.; Zheng, Y. Series Arc Fault Detection Using Regular Signals and Time-Series Reconstruction. IEEE Trans. Ind. Electron. 2023, 70, 2026–2036. [Google Scholar] [CrossRef]
- Miao, W.; Wang, Z.; Wang, F.; Lam, K.H.; Pong, P.W.T. Multicharacteristics Arc Model and Autocorrelation-Algorithm Based Arc Fault Detector for DC Microgrid. IEEE Trans. Ind. Electron. 2023, 70, 4875–4886. [Google Scholar] [CrossRef]
- Saleh, S.A.; Valdes, M.E.; Mardegan, C.S.; Alsayid, B. The State-of-the-Art Methods for Digital Detection and Identification of Arcing Current Faults. IEEE Trans. Ind. Appl. 2019, 55, 4536–4550. [Google Scholar] [CrossRef]
- Ananthan, S.N.; Bastos, A.F.; Santoso, S.; Feng, X.; Penney, C.; Gattozzi, A.; Hebner, R. Signatures of Series Arc Faults to Aid Arc Detection in Low-Voltage DC Systems. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar]
- Tisserand, E.; Lezama, J.; Schweitzer, P.; Berviller, Y. Series arcing detection by algebraic derivative of the current. Electr. Power Syst. Res. 2015, 119, 91–99. [Google Scholar] [CrossRef]
- Georgijevic, N.L.; Jankovic, M.V.; Srdic, S.; Radakovic, Z. The Detection of Series Arc Fault in Photovoltaic Systems Based on the Arc Current Entropy. IEEE Trans. Power Electron. 2016, 31, 5917–5930. [Google Scholar] [CrossRef]
- Zhang, S.; Qu, N.; Zheng, T.; Hu, C. Series Arc Fault Detection Based on Wavelet Compression Reconstruction Data Enhancement and Deep Residual Network. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- He, Z.; Xu, Z.; Zhao, H.; Li, W.; Zhen, Y.; Ning, W. Detecting Series Arc Faults Using High-Frequency Components of Branch Voltage Coupling Signal. IEEE Trans. Instrum. Meas. 2024, 73, 1–13. [Google Scholar] [CrossRef]
- Jiang, J.; Wen, Z.; Zhao, M.; Bie, Y.; Li, C.; Tan, M.; Zhang, C. Series Arc Detection and Complex Load Recognition Based on Principal Component Analysis and Support Vector Machine. IEEE Access 2019, 7, 47221–47229. [Google Scholar] [CrossRef]
- Hwang, S.; Kim, B.; Kim, M.; Park, H.-P. AC Series Arc Fault Detection for Wind Power Systems Based on Phase Lock Loop with Time and Frequency Domain Analyses. IEEE Trans. Power Electron. 2024, 39, 12446–12455. [Google Scholar] [CrossRef]
- Cai, X.; Wai, R.-J. Intelligent DC Arc-Fault Detection of Solar PV Power Generation System via Optimized VMD-Based Signal Processing and PSO–SVM Classifier. IEEE J. Photovolt. 2022, 12, 1058–1077. [Google Scholar] [CrossRef]
- Song, J.; Shan, X.; Zhang, J.; Wen, H. Parameter Estimation of Power System Oscillation Signals under Power Swing Based on Clarke–Discrete Fourier Transform. Electronics 2024, 13, 297. [Google Scholar] [CrossRef]
- Wang, K.; Zhong, F.; Song, J.; Yu, Z.; Tang, L.; Tang, X.; Yao, Q. Power System Frequency Estimation with Zero Response Time Under Abrupt Transients. IEEE Trans. Circuits Syst. I Regul. Pap. 2025, 72, 467–480. [Google Scholar] [CrossRef]
- Song, J.; Mingotti, A.; Zhang, J.; Peretto, L.; Wen, H. Fast Iterative-Interpolated DFT Phasor Estimator Considering Out-of-Band Interference. IEEE Trans. Instrum. Meas. 2022, 71, 1–14. [Google Scholar] [CrossRef]
- Yin, Z.; Wang, L.; Zhang, B.; Meng, L.; Zhang, Y. An Integrated DC Series Arc Fault Detection Method for Different Operating Conditions. IEEE Trans. Ind. Electron. 2021, 68, 12720–12729. [Google Scholar] [CrossRef]
- Qi, P.; Jovanovic, S.; Lezama, J.; Schweitzer, P. Discrete wavelet transform optimal parameters estimation for arc fault detection in low-voltage residential power networks. Electr. Power Syst. Res. 2017, 143, 130–139. [Google Scholar] [CrossRef]
- Shi, B.; Ma, Z.; Liu, J.; Ni, X.; Xiao, W.; Liu, H. Shadow Extraction Method Based on Multi-Information Fusion and Discrete Wavelet Transform. IEEE Trans. Instrum. Meas. 2022, 71, 1–15. [Google Scholar] [CrossRef]
- Osman, S.; Wang, W. A Morphological Hilbert-Huang Transform Technique for Bearing Fault Detection. IEEE Trans. Instrum. Meas. 2016, 65, 2646–2656. [Google Scholar] [CrossRef]
- Artale, G.; Cataliotti, A.; Cosentino, V.; Di Cara, D.; Nuccio, S.; Tine, G. Arc Fault Detection Method Based on CZT Low-Frequency Harmonic Current Analysis. IEEE Trans. Instrum. Meas. 2017, 66, 888–896. [Google Scholar] [CrossRef]
- Da Rocha, G.S.; Pulz, L.T.C.; Gazzana, D.S. Serial Arc Fault Detection Through Wavelet Transform and Support Vector Machine. In Proceedings of the 2021 IEEE International Conference on Environment and Electrical Engineering and 2021 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Bari, Italy, 7–10 September 2021; pp. 1–5. [Google Scholar]
- Wu, N.; Peng, M.; Wang, J.; Wang, H.; Lu, Q.; Wu, M.; Zhang, H.; Ni, F. Research on Series Arc Fault Detection Method Based on the Combination of Load Recognition and MLP-SVM. IEEE Access 2024, 12, 100186–100199. [Google Scholar] [CrossRef]
- Han, C.; Wang, Z.; Tang, A.; Gao, H.; Guo, F. Recognition method of AC series arc fault characteristics under complicated harmonic conditions. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Miao, W.; Xu, Q.; Lam, K.H.; Pong, P.W.T.; Poor, H.V. DC Arc-Fault Detection Based on Empirical Mode Decomposition of Arc Signatures and Support Vector Machine. IEEE Sens. J. 2021, 21, 7024–7033. [Google Scholar] [CrossRef]
- Jegadeeshwaran, R.; Sugumaran, V. Comparative study of decision tree classifier and best first tree classifier for fault diagnosis of automobile hydraulic brake system using statistical features. Measurement 2013, 46, 3247–3260. [Google Scholar] [CrossRef]
- Dong, X.; Li, G.; Jia, Y.; Xu, K. Multiscale feature extraction from the perspective of graph for hob fault diagnosis using spectral graph wavelet transform combined with improved random forest. Measurement 2021, 176, 109178. [Google Scholar] [CrossRef]
- Zhang, D.; Qian, L.; Mao, B.; Huang, C.; Huang, B.; Si, Y. A Data-Driven Design for Fault Detection of Wind Turbines Using Random Forests and XGboost. IEEE Access 2018, 6, 21020–21031. [Google Scholar] [CrossRef]
- Ma, S.; Guan, L. Arc-Fault Recognition Based on BP Neural Network. In Proceedings of the 2011 Third International Conference on Measuring Technology and Mechatronics Automation, Shanghai, China, 6–7 January 2011; pp. 584–586. [Google Scholar]
- Han, X.; Li, D.; Huang, L.; Huang, H.; Yang, J.; Zhang, Y.; Wu, X.; Lu, Q. Series Arc Fault Detection Method Based on Category Recognition and Artificial Neural Network. Electronics 2020, 9, 1367. [Google Scholar] [CrossRef]
- Yang, K.; Chu, R.; Zhang, R.; Xiao, J.; Tu, R. A Novel Methodology for Series Arc Fault Detection by Temporal Domain Visualization and Convolutional Neural Network. Sensors 2019, 20, 162. [Google Scholar] [CrossRef]
- Cao, Y.; Cheng, X.; Mu, J.; Li, D.; Han, F. Detection Method Based on Image Enhancement and an Improved Faster R-CNN for Failed Satellite Components. IEEE Trans. Instrum. Meas. 2023, 72, 1–13. [Google Scholar] [CrossRef]
- Li, W.; Liu, Y.; Li, Y.; Guo, F. Series Arc Fault Diagnosis and Line Selection Method Based on Recurrent Neural Network. IEEE Access 2020, 8, 177815–177822. [Google Scholar] [CrossRef]
- Song, J.; Zhang, J.; Wen, H. Accurate Dynamic Phasor Estimation by Matrix Pencil and Taylor Weighted Least Squares Method. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Yan, Z.; Wen, H. Electricity Theft Detection Base on Extreme Gradient Boosting in AMI. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Liang, B.; Qin, W.; Liao, Z. A Differential Evolutionary-Based XGBoost for Solving Classification of Physical Fitness Test Data of College Students. Mathematics 2025, 13, 1405. [Google Scholar] [CrossRef]
| Parameters | Search Range | Optimal Selection |
|---|---|---|
| learning_rate | [0.02, 0.5] | 0.1321 |
| n_estimators | [10, 50] | 17 |
| max_depth | [5, 30] | 10 |
| subsample | [0.2, 1] | 0.7921 |
| colsample_bytree | [0.2, 1] | 0.5934 |
| reg_lambda | [0, 1] | 0.8 |
| min_child_weight | [0, 1] | 0.4823 |
| Load Types | Load Combination | Power/W |
|---|---|---|
| 1 | Electric Fan | 60 |
| 2 | Incandescent Lamp | 300 |
| 3 | Dust Catcher | 1100 |
| 4 | Evaporative Cooling Fan | 65 |
| 5 | Monitor | 18 |
| 6 | Electric Fan + Monitor | 60 + 18 |
| 7 | Evaporative Cooling Fan + Monitor | 65 + 18 |
| 8 | Electric Fan + Evaporative Cooling Fan + Monitor | 60 + 65 + 18 |
| Load Types | Working Conditions | Label | Load Types | Working Conditions | Label |
|---|---|---|---|---|---|
| 1 | Normal | A1 | 5 | Normal | E1 |
| Fault Arc | A2 | Fault Arc | E2 | ||
| 2 | Normal | B1 | 6 | Normal | F1 |
| Fault Arc | B2 | Fault Arc | F2 | ||
| 3 | Normal | C1 | 7 | Normal | G1 |
| Fault Arc | C2 | Fault Arc | G2 | ||
| 4 | Normal | D1 | 8 | Normal | H1 |
| Fault Arc | D2 | Fault Arc | H2 |
| Label | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|
| A1 | 1.00 | 0.99 | 1.00 | 342 |
| A2 | 0.97 | 0.92 | 0.94 | 342 |
| B1 | 1.00 | 1.00 | 1.00 | 342 |
| B2 | 0.99 | 1.00 | 1.00 | 342 |
| C1 | 1.00 | 1.00 | 1.00 | 342 |
| C2 | 1.00 | 1.00 | 1.00 | 342 |
| D1 | 1.00 | 1.00 | 1.00 | 342 |
| D2 | 0.94 | 0.97 | 0.95 | 342 |
| E1 | 1.00 | 1.00 | 1.00 | 342 |
| E2 | 1.00 | 1.00 | 1.00 | 342 |
| F1 | 1.00 | 1.00 | 1.00 | 342 |
| F2 | 0.96 | 0.99 | 0.97 | 342 |
| G1 | 1.00 | 1.00 | 1.00 | 342 |
| G2 | 0.97 | 0.95 | 0.96 | 342 |
| H1 | 1.00 | 1.00 | 1.00 | 342 |
| H2 | 1.00 | 1.00 | 1.00 | 342 |
| Accuracy | - | - | 0.99 | 5472 |
| Macro-Average | 0.99 | 0.99 | 0.99 | 5472 |
| Weighted Average | 0.99 | 0.99 | 0.99 | 5472 |
| Label | BPNN | SVM | RNN | Proposed |
|---|---|---|---|---|
| A1 | 89.16% | 94.09% | 93.32% | 99.01% |
| A2 | 91.38% | 93.45% | 92.19% | 92.17% |
| B1 | 93.14% | 95.92% | 96.21% | 100.0% |
| B2 | 92.87% | 97.78% | 95.81% | 100.0% |
| C1 | 93.87% | 94.32% | 97.23% | 100.0% |
| C2 | 95.31% | 97.83% | 96.29% | 100.0% |
| D1 | 92.45% | 94.79% | 95.16% | 100.0% |
| D2 | 94.89% | 93.13% | 94.92% | 97.39% |
| E1 | 93.78% | 96.34% | 95.24% | 100.0% |
| E2 | 90.83% | 95.41% | 96.97% | 100.0% |
| F1 | 91.22% | 96.17% | 97.89% | 100.0% |
| F2 | 89.27% | 94.86% | 94.35% | 99.13% |
| G1 | 94.26% | 97.82% | 95.87% | 100.0% |
| G2 | 93.59% | 95.31% | 96.19% | 95.34% |
| H1 | 91.29% | 96.51% | 95.86% | 100.0% |
| H2 | 92.57% | 97.35% | 96.97% | 100.0% |
| Methods | WT-BPNN | WT-SVM | MLP-SVM | RNN | Proposed |
|---|---|---|---|---|---|
| Avg Time | 23.76 ms | 10.34 ms | 17.93 ms | 37.49 ms | 7.21 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, D.; Yang, S.; Xue, Y.; Zhang, P.; Song, R.; Song, J. Fast Identification of Series Arc Faults Based on Singular Spectrum Statistical Features. Electronics 2025, 14, 3337. https://doi.org/10.3390/electronics14163337
Xiong D, Yang S, Xue Y, Zhang P, Song R, Song J. Fast Identification of Series Arc Faults Based on Singular Spectrum Statistical Features. Electronics. 2025; 14(16):3337. https://doi.org/10.3390/electronics14163337
Chicago/Turabian StyleXiong, Dezhi, Shuai Yang, Yang Xue, Penghe Zhang, Runan Song, and Jian Song. 2025. "Fast Identification of Series Arc Faults Based on Singular Spectrum Statistical Features" Electronics 14, no. 16: 3337. https://doi.org/10.3390/electronics14163337
APA StyleXiong, D., Yang, S., Xue, Y., Zhang, P., Song, R., & Song, J. (2025). Fast Identification of Series Arc Faults Based on Singular Spectrum Statistical Features. Electronics, 14(16), 3337. https://doi.org/10.3390/electronics14163337






