Optimization Design of Microwave Filters Based on Deep Learning and Metaheuristic Algorithms
Abstract
1. Introduction
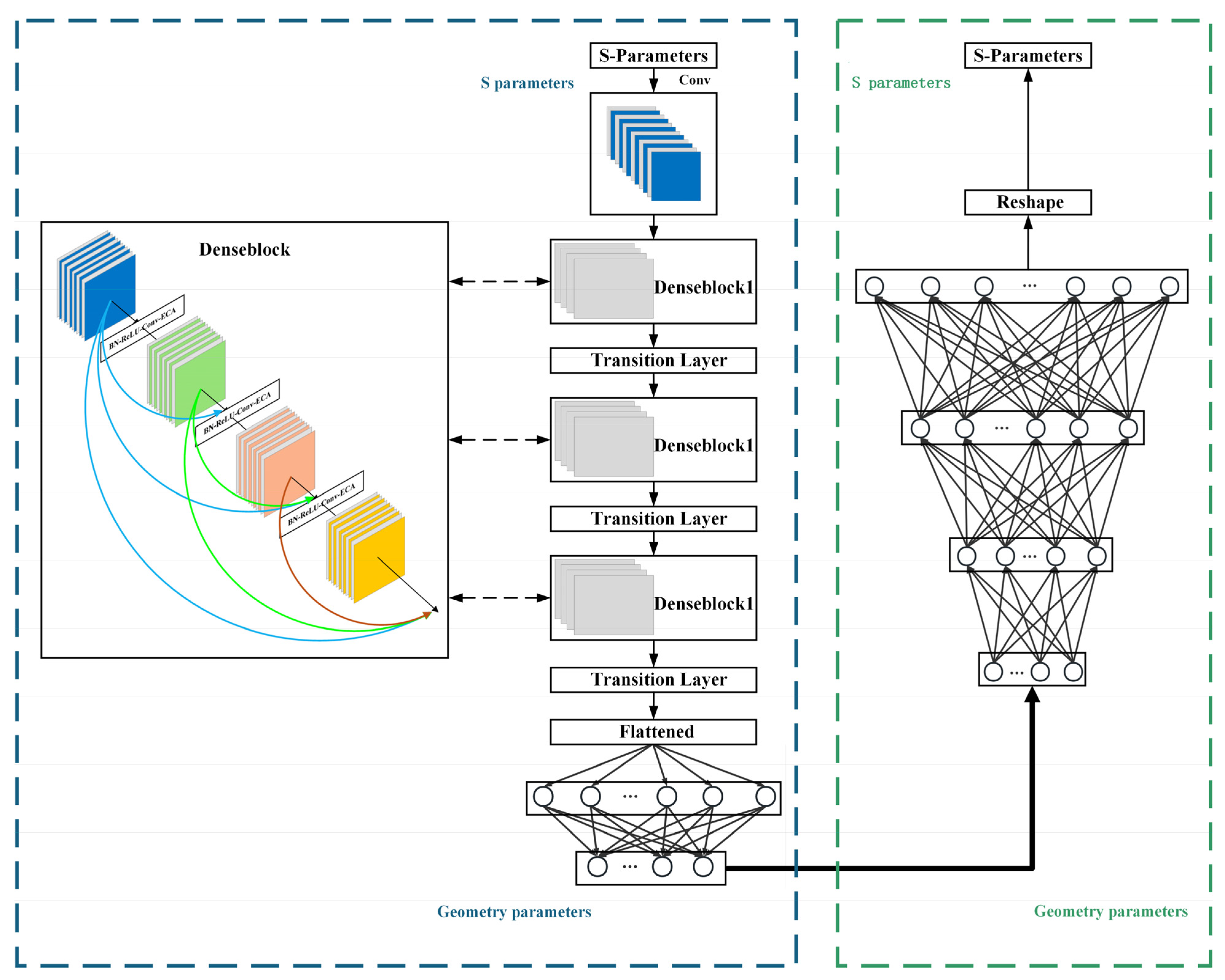
- The proposed 1D-DenseCAE surrogate model incorporates cross-layer feature reuse through DenseNet [19] (densely connected convolutional network) connectivity, effectively mitigating the gradient-vanishing problem. Furthermore, the embedded efficient channel attention (ECA-Net) mechanism dynamically weights key frequency-band features, enhancing the accuracy of S-parameter prediction.
- The IHOA integrates IVYA’s population-collaborative diffusion mechanism with HOA’s terrain-adaptive step-length strategy, establishing a closed-loop optimization framework that balances global exploration and local exploitation.
- The 1D-DenseCAE surrogate model substitutes electromagnetic simulation for fitness evaluation in the optimization process. When integrated with IHOA, this combined approach enables efficient exploration of the parameter space.
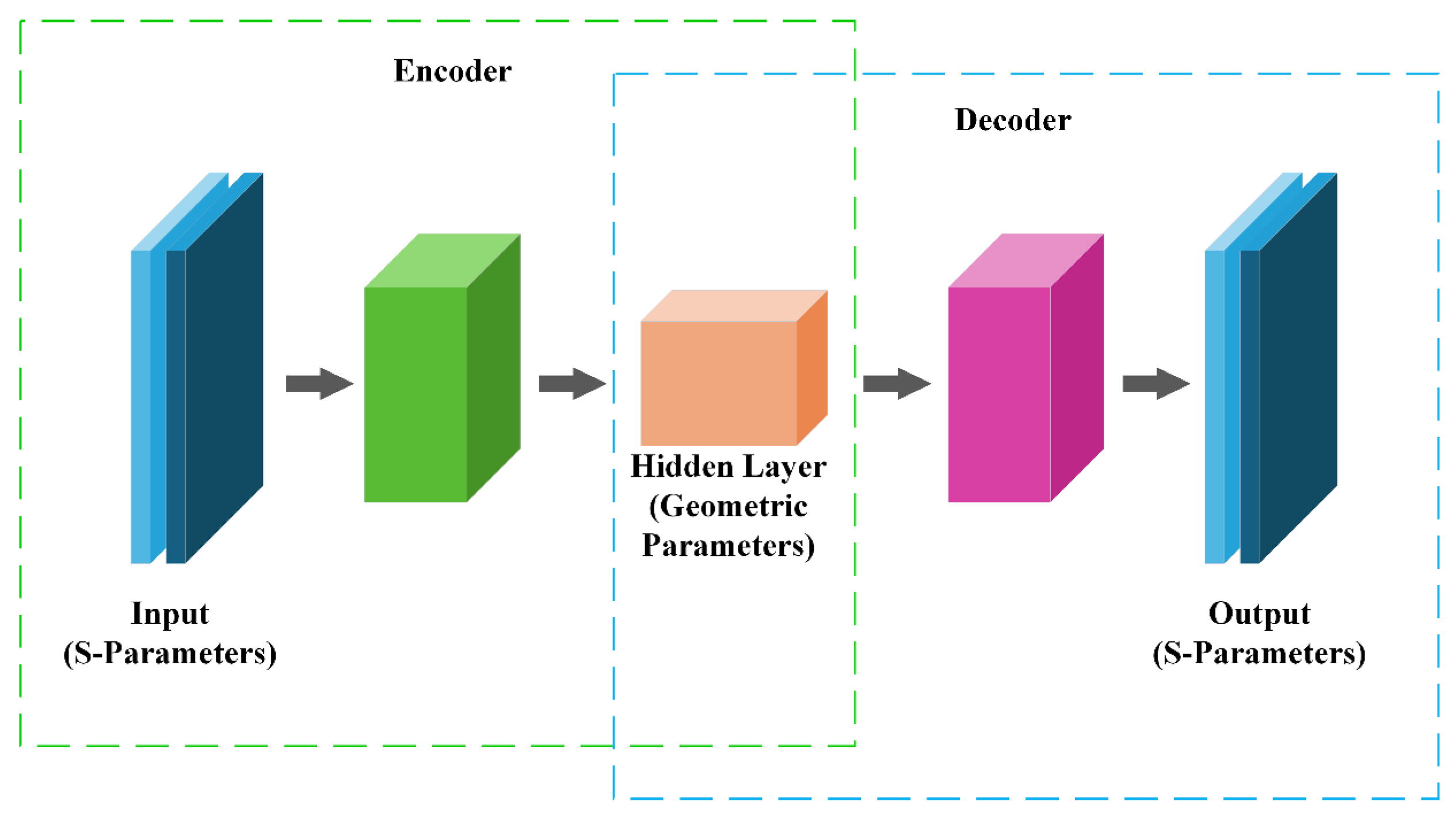
2. Construction of the 1D-DenseCAE Surrogate Model
2.1. Encoder: Multi-Scale Feature Extraction
2.2. Decoder: High-Fidelity Response Reconstruction
2.3. Loss Function
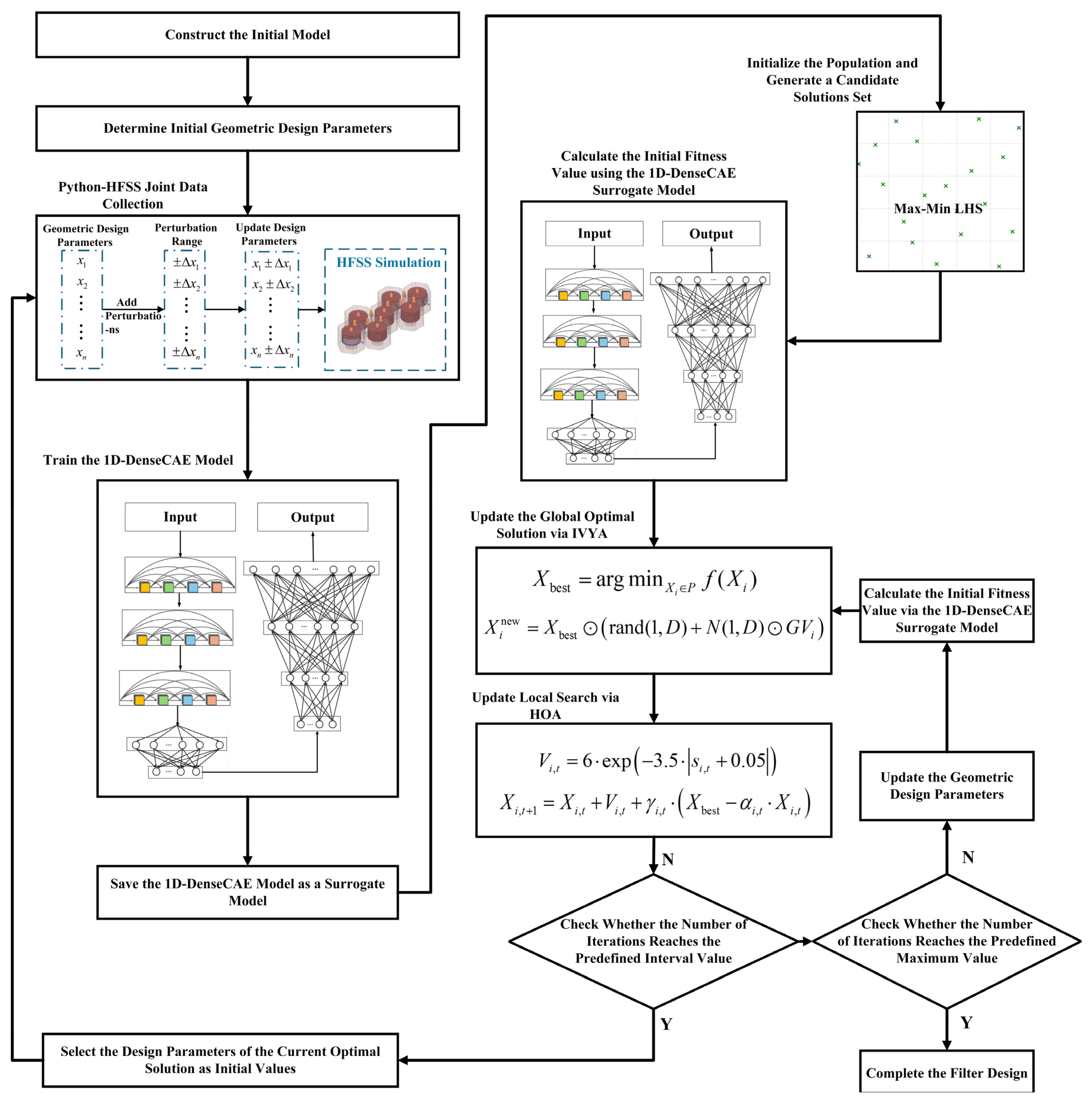
3. Design of IHOA
3.1. Mathematical Models of Algorithm Components
3.1.1. Mathematical Model of the IVYA Global Search Module
3.1.2. The HOA Local Optimization Module
3.2. A Case Study of Filter Design Based on Surrogate Model and IHOA
| Algorithm 1: IHOA (data processing automation and output reading) |
| Input: Population size , dimension D, search bounds and , max iterations MaxIter Output: Global best individual and its fitness 1. Initialize the population using LHS 2. Evaluate the fitness of all individuals 3. Identify current global best and 4. For each iteration until the maximum iteration limit is reached: // IVYA’s global search 5. Generate a new candidate solution by updating position based on global diffusion (Use the IVYA strategy to simulate growth and expansion) 6. If the new fitness is better, Then update the current individual with this new solution 7. Rank individuals based on fitness and select the top-K with the highest fitness for local refinement 8. For each of the selected K individuals: // HOA’s local optimization 9. Randomly generate a terrain slope angle between 0° and 50° 10. Compute walking velocity based on slope using Tobler’s hiking function 11. Calculate a global guidance component to follow the current global best 12. Update the individual’s position based on walking direction and velocity 13. If the new solution improves fitness, Then replace the original individual 14. Return the best solution () and its corresponding fitness () |
4. Experimental Results and Discussion
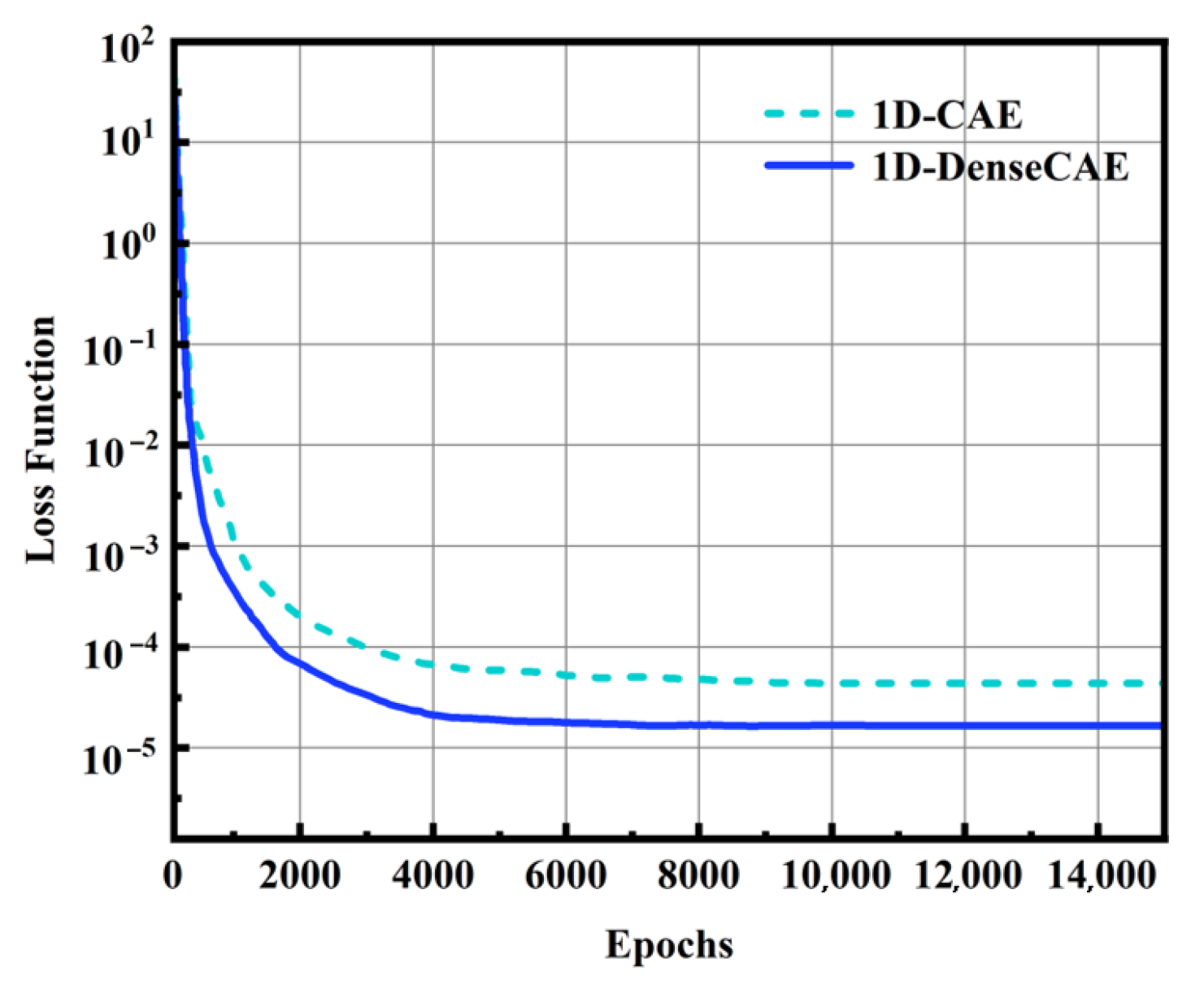
4.1. Validation of the 1D-DenseCAE Model
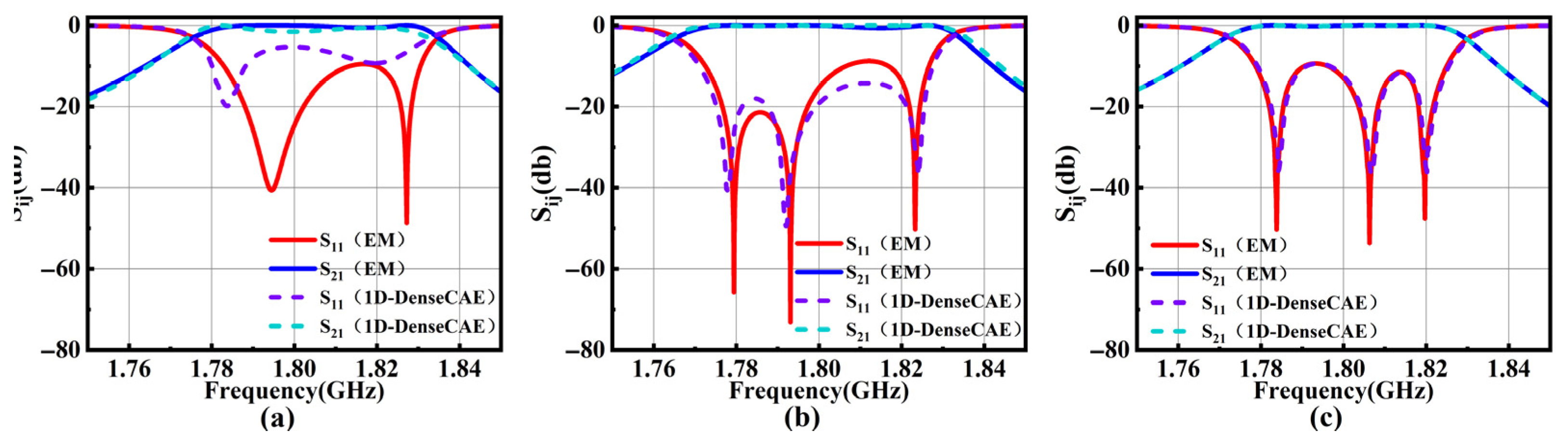
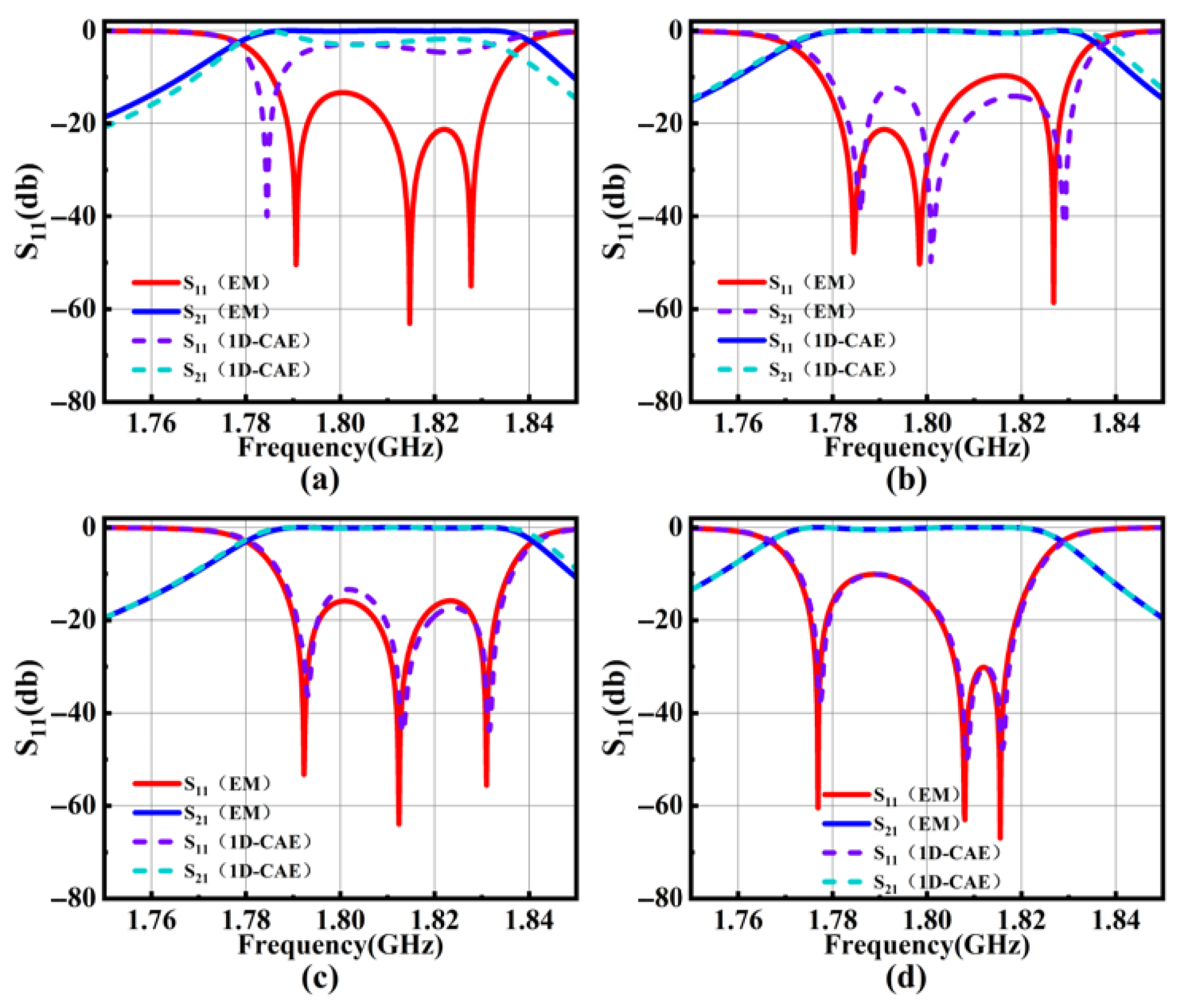
4.2. Verification of the Surrogate Model and IHOA
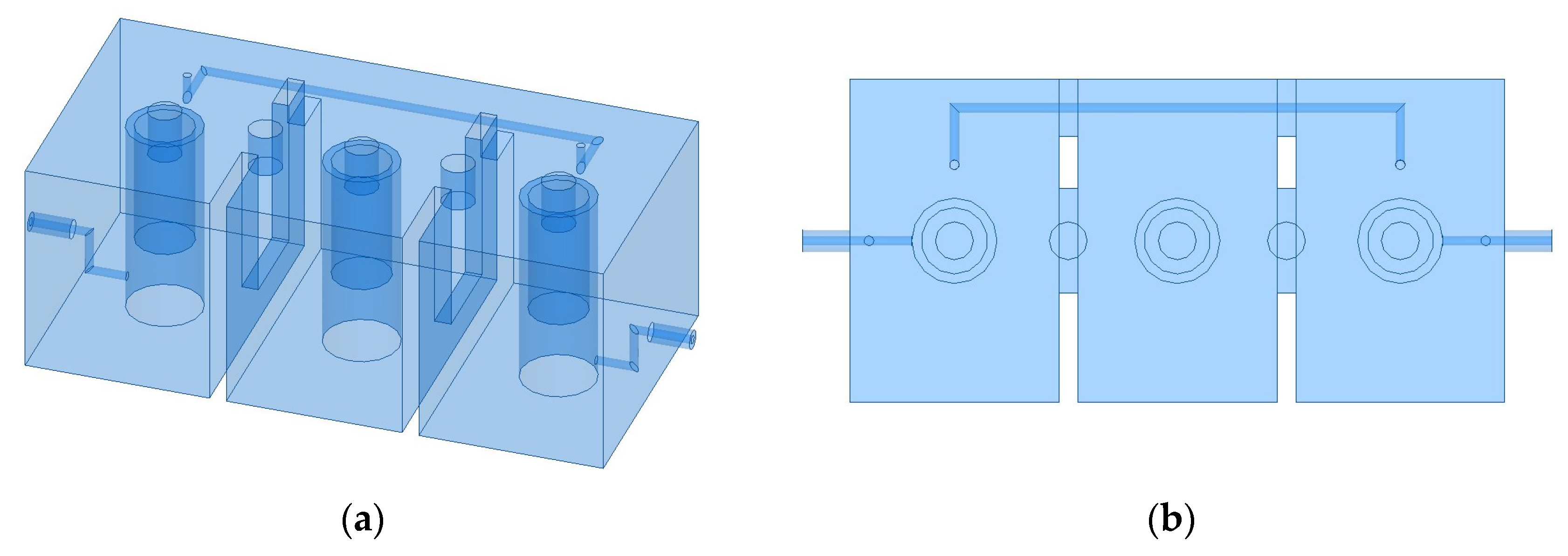
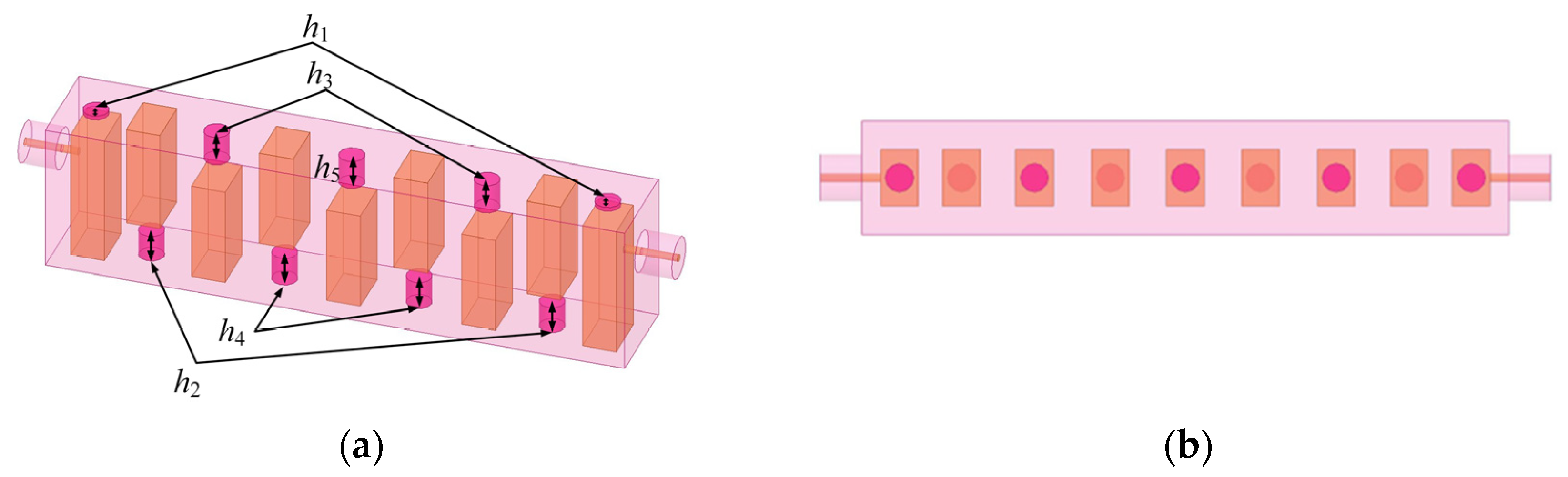
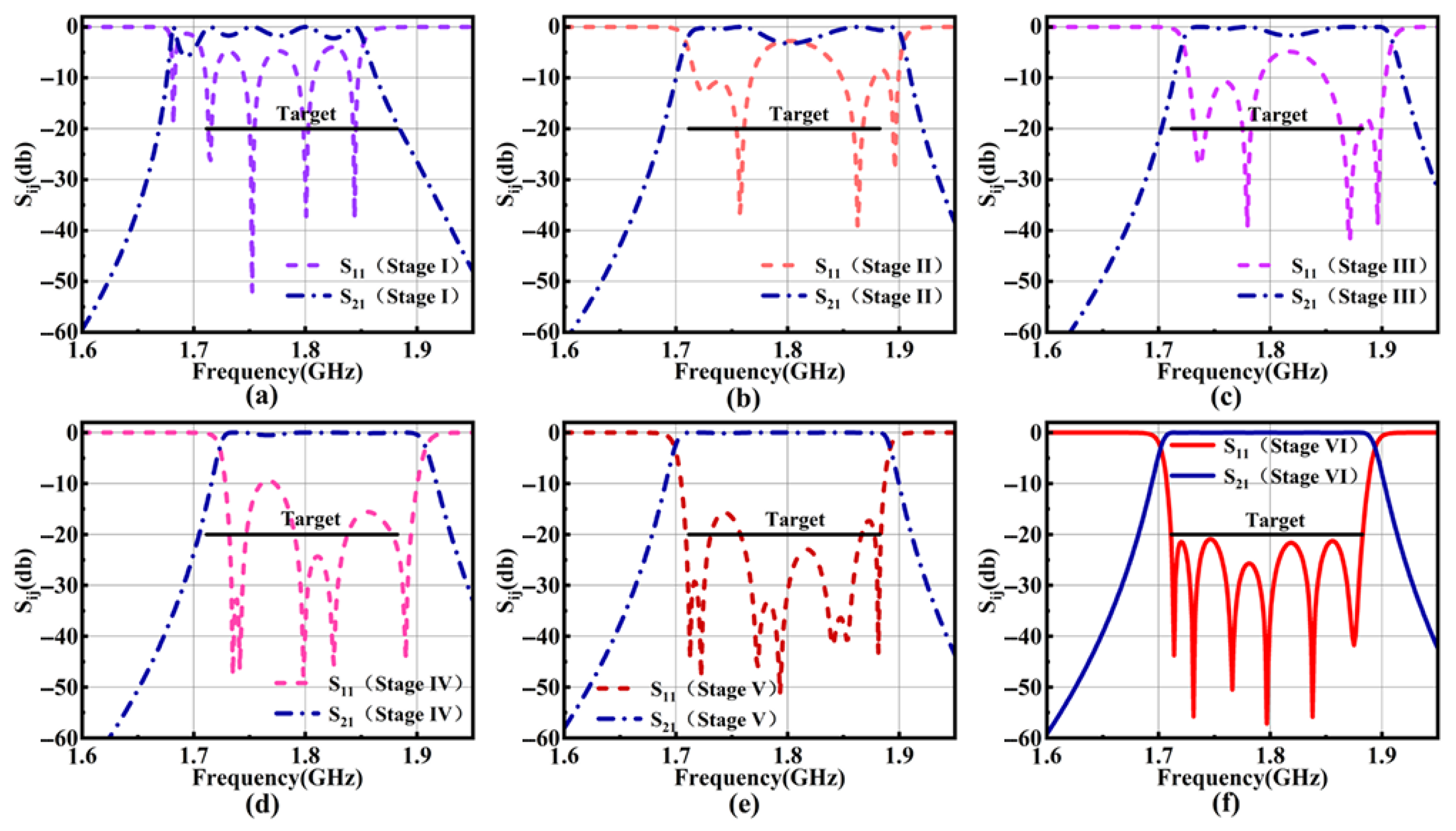
4.2.1. Verification of the Optimization Design of the Interdigital Filter Model
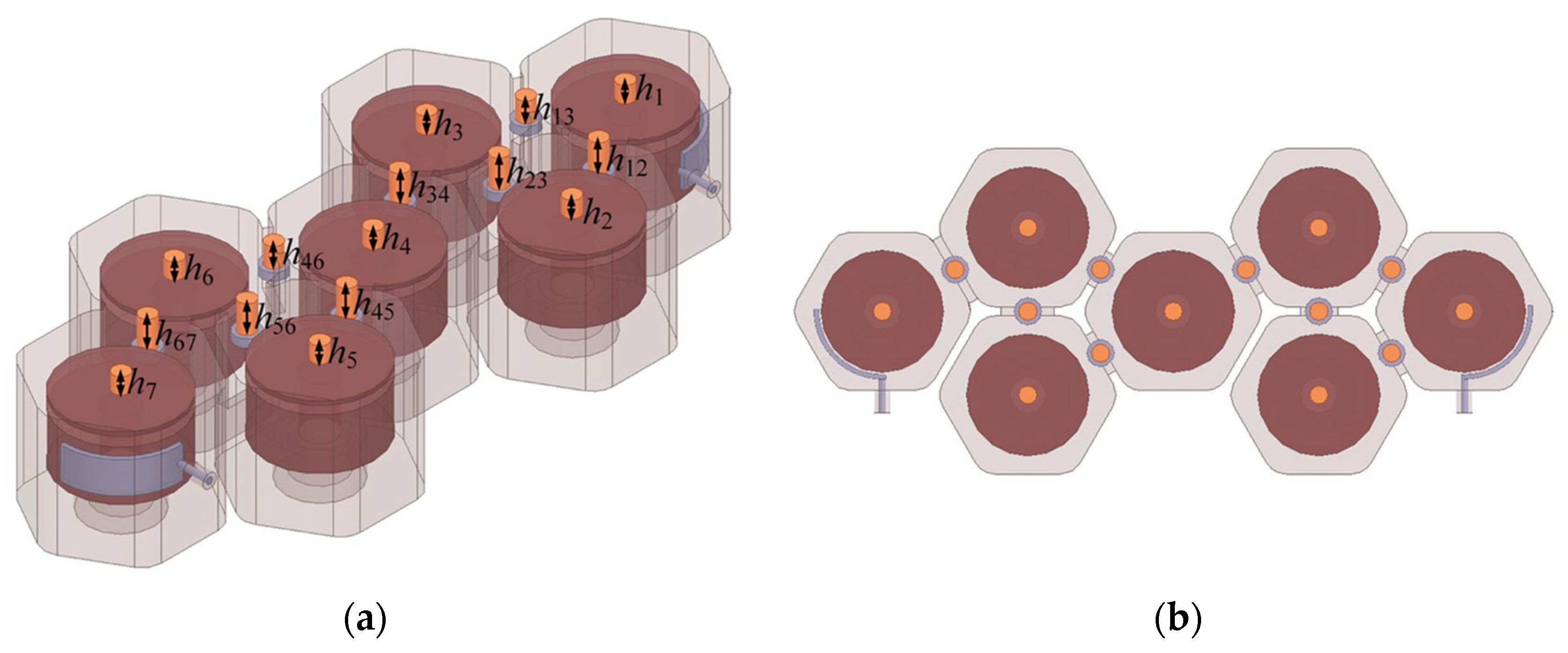
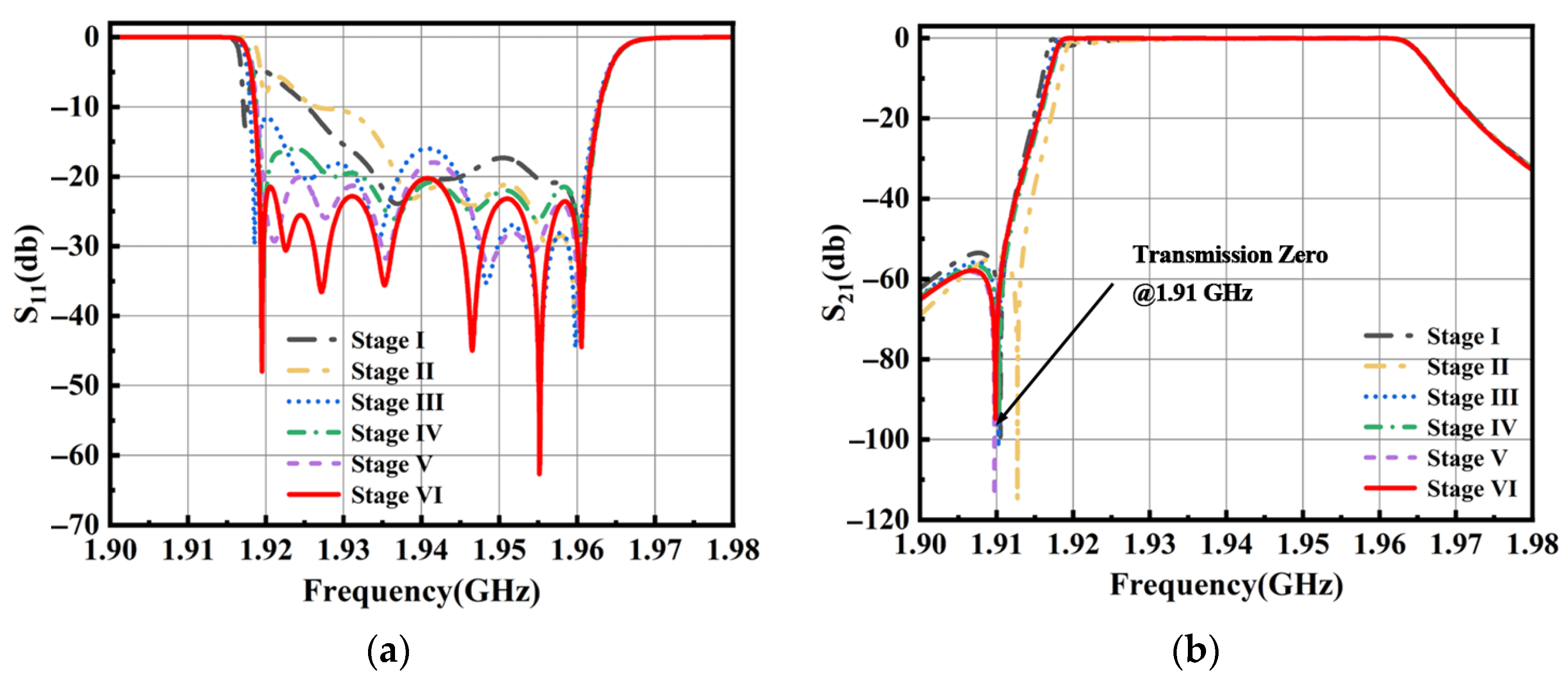
4.2.2. Verification of the Optimization Design of a Seventh-Order Cross-Coupled Cavity Filter
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Feng, F.; Jin, J.; Zhang, W.; Zhao, Z.; Zhang, Q.-J. Adaptively Weighted Yield-Driven EM Optimization Incorporating Neurotransfer Function Surrogate with Applications to Microwave Filters. IEEE Trans. Microw. Theory Tech. 2021, 69, 518–528. [Google Scholar] [CrossRef]
- Bandler, J.W.; Rayas-Sánchez, J.E.; Zhang, Q.-J. Yield-driven electromagnetic optimization via space mapping-based neuromodels. Int. J. RF Microw. Comput.-Aided Eng. 2002, 12, 79–89. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, F.; Na, W.; Yan, S.; Zhang, Q. Parallel Space-Mapping Based Yield-Driven EM Optimization Incorporating Trust Region Algorithm and Polynomial Chaos Expansion. IEEE Access 2019, 7, 143673–143683. [Google Scholar] [CrossRef]
- Pietrenko-Dabrowska, A. Rapidtolerance-awaredesign of miniaturized microwave passives by means ofconfined-domainsurrogates. Int. J. Numer. Model. Electron. Netw. Devices Fields 2020, 33, e2779. [Google Scholar] [CrossRef]
- Koziel, S.; Bekasiewicz, A. Sequential approximate optimisation for statistical analysis and yield optimisation of circularly polarised antennas. IET Microw. Antennas Propag. 2018, 12, 2060–2064. [Google Scholar] [CrossRef]
- Ciccazzo, A.; Di Pillo, G.; Latorre, V. A SVM Surrogate Model-Based Method for Parametric Yield Optimization. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2016, 35, 1224–1228. [Google Scholar] [CrossRef]
- Bo, L.; Qingfu, Z.; Fernández, F.V.; Gielen, G. An Efficient Evolutionary Algorithm for Chance-constrained Bi- objective Stochastic Optimization. IEEE Trans. Evol. Comput. 2013, 17, 786–796. [Google Scholar] [CrossRef]
- Jin, J.; Feng, F.; Na, W.; Zhang, J.; Zhang, W.; Zhao, Z.; Zhang, Q.-J. Advanced Cognition-Driven EM Optimization Incorporating Transfer Function-Based Feature Surrogate for Microwave Filters. IEEE Trans. Microw. Theory Tech. 2021, 69, 15–28. [Google Scholar] [CrossRef]
- Zhao, P.; Wu, K. Homotopy Optimization of Microwave and Millimeter-Wave Filters Based on Neural Network Model. IEEE Trans. Microw. Theory Tech. 2020, 68, 1390–1400. [Google Scholar] [CrossRef]
- Xue, L.; Liu, B.; Yu, Y.; Cheng, Q.S.; Imran, M.; Qiao, T. An Unsupervised Microwave Filter Design Optimization Method Based on a Hybrid Surrogate Model-Assisted Evolutionary Algorithm. IEEE Trans. Microw. Theory Tech. 2023, 71, 1159–1170. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, Z.; Cheng, Q.S.; Liu, B.; Wang, Y.; Guo, C.; Ye, T.T. State-of-the-Art: AI-Assisted Surrogate Modeling and Optimization for Microwave Filters. IEEE Trans. Microw. Theory Tech. 2022, 70, 4635–4651. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, B.; Yu, Y.; Imran, M.; Cheng, Q.S.; Yu, M. A Surrogate Modeling Space Definition Method for Efficient Filter Yield Optimization. IEEE Microw. Wirel. Technol. Lett. 2023, 33, 631–634. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, B.; Yu, Y.; Cheng, Q.S. A Microwave Filter Yield Optimization Method Based on Off-Line Surrogate Model-Assisted Evolutionary Algorithm. IEEE Trans. Microw. Theory Tech. 2022, 70, 2925–2934. [Google Scholar] [CrossRef]
- Zhao, W.-S.; Wang, B.-X.; Wang, D.-W.; You, B.; Liu, Q.; Wang, G. Swarm Intelligence Algorithm-Based Optimal Design of Microwave Microfluidic Sensors. IEEE Trans. Ind. Electron. 2022, 69, 2077–2087. [Google Scholar] [CrossRef]
- Liang, S.; Fang, Z.; Sun, G.; Qu, G. Biogeography-based optimization with adaptive migration and adaptive mutation with its application in sidelobe reduction of antenna arrays. Appl. Soft Comput. 2022, 121, 108772. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A. Efficient Simulation-Based Global Antenna Optimization Using Characteristic Point Method and Nature-Inspired Metaheuristics. IEEE Trans. Antennas Propag. 2024, 72, 3706–3717. [Google Scholar] [CrossRef]
- Ghasemi, M.; Zare, M.; Trojovský, P.; Rao, R.V.; Trojovská, E.; Kandasamy, V. Optimization based on the smart behavior of plants with its engineering applications: Ivy algorithm. Knowl.-Based Syst. 2024, 295, 111850. [Google Scholar] [CrossRef]
- Oladejo, S.O.; Ekwe, S.O.; Mirjalili, S. The Hiking Optimization Algorithm: A novel human-based metaheuristic approach. Knowl. -Based Syst. 2024, 296, 111880. [Google Scholar] [CrossRef]
- Hou, Y.; Wu, Z.; Cai, X.; Zhu, T. The application of improved densenet algorithm in accurate image recognition. Sci. Rep. 2024, 14, 8645. [Google Scholar] [CrossRef]
- Rayas-Sanchez, J.E.; Gutierrez-Ayala, V. EM-Based Monte Carlo Analysis and Yield Prediction of Microwave Circuits Using Linear-Input Neural-Output Space Mapping. IEEE Trans. Microw. Theory Tech. 2006, 54, 4528–4537. [Google Scholar] [CrossRef]
- Sabbagh, M.A.E.; Bakr, M.H.; Bandler, J.W. Adjoint higher order sensitivities for fast full-wave optimization of microwave filters. IEEE Trans. Microw. Theory Tech. 2006, 54, 3339–3351. [Google Scholar] [CrossRef]
- Ochoa, J.S.; Cangellaris, A.C. Random-Space Dimensionality Reduction for Expedient Yield Estimation of Passive Microwave Structures. IEEE Trans. Microw. Theory Tech. 2013, 61, 4313–4321. [Google Scholar] [CrossRef]
- Koziel, S.; Bandler, J.W. Rapid Yield Estimation and Optimization of Microwave Structures Exploiting Feature-Based Statistical Analysis. IEEE Trans. Microw. Theory Tech. 2015, 63, 107–114. [Google Scholar] [CrossRef]
- Du, B.; Xiong, W.; Wu, J.; Zhang, L.; Zhang, L.; Tao, D. Stacked Convolutional Denoising Auto-Encoders for Feature Representation. IEEE Trans. Cybern. 2017, 47, 1017–1027. [Google Scholar] [CrossRef]
- Mondal, A.; Shrivastava, V.K. A novel Parametric Flatten-p Mish activation function based deep CNN model for brain tumor classification. Comput. Biol. Med. 2022, 150, 106183. [Google Scholar] [CrossRef]
- Sheikholeslami, R.; Razavi, S. Progressive Latin Hypercube Sampling: An efficient approach for robust sampling-based analysis of environmental models. Environ. Model. Softw. 2017, 93, 109–126. [Google Scholar] [CrossRef]
- Goodwin, A.; Hammett, M.; Harris, M. The application of Tobler’s hiking function in data-driven traverse modelling for planetary exploration. Acta Astronaut. 2025, 228, 265–273. [Google Scholar] [CrossRef]
- Wyka, T.P. Negative phototropism of the shoots helps temperate liana Hedera helix L. to locate host trees under habitat conditions. Tree Physiol. 2023, 43, 1874–1885. [Google Scholar] [CrossRef]
| Layer | Size/Nodes | Stride | Output Shape | Activation | |
|---|---|---|---|---|---|
| Input Layer | [400, 2] | - | [400, 2] | - | |
| Encoder | |||||
| Initial Conv Layer | 3 × 16 | 1 | [400, 16] | - | |
| Dense Block 1 | Conv1 | 3 × 12 | 1 | [400, 28] | ReLU |
| Conv2 | 3 × 12 | 1 | [400, 40] | ReLU | |
| Conv3 | 3 × 12 | 1 | [400, 52] | ReLU | |
| Conv4 | 3 × 12 | 1 | [400, 64] | ReLU | |
| Transition Layer 1 | 1 × 24 | 2 | [200, 32] | ReLU | |
| Dense Block 2 | Conv1 | 3 × 12 | 1 | [200, 32] | ReLU |
| Conv2 | 3 × 12 | 1 | [200, 44] | ReLU | |
| Conv3 | 3 × 12 | 1 | [200, 56] | ReLU | |
| Conv4 | 3 × 12 | 1 | [200, 68] | ReLU | |
| Transition Layer 2 | 1 × 48 | 2 | [100, 40] | ReLU | |
| Dense Block 3 | Conv1 | 3 × 12 | 1 | [100, 52] | ReLU |
| Conv2 | 3 × 12 | 1 | [100, 64] | ReLU | |
| Conv3 | 3 × 12 | 1 | [100, 76] | ReLU | |
| Conv4 | 3 × 12 | 1 | [100, 88] | ReLU | |
| Transition Layer 3 | 1 × 48 | 2 | [50, 44] | ReLU | |
| Flatten Layer | 2200 | - | [2200] | - | |
| Decoder | |||||
| Fully Connected Layer 1 | 256 Nodes | - | [256] | Mish | |
| Fully Connected Layer 2 | 1024 Nodes | - | [1024] | Mish | |
| Fully Connected Layer 3 | 800 Nodes | - | [800] | Mish | |
| Reshape Layer | - | - | [400, 2] | - | |
| Stage 1 | Stage 2 | Stage 3 | Stage 4 | Stage 5 | Stage 6 | |
|---|---|---|---|---|---|---|
| h1 | 0.329 | 0.418 | 0.378 | 0.259 | 0.288 | 0.274 |
| h2 | 1.674 | 1.593 | 1.733 | 1.631 | 1.653 | 1.642 |
| h3 | 1.838 | 1.677 | 1.718 | 1.812 | 1.834 | 1.805 |
| h4 | 1.678 | 1.698 | 1.671 | 1.734 | 1.753 | 1.779 |
| h5 | 1.628 | 1.583 | 1.794 | 1.822 | 1.797 | 1.806 |
| Stage 1 | Stage 2 | Stage 3 | Stage 4 | Stage 5 | Stage 6 | |
|---|---|---|---|---|---|---|
| h1 | 3.75 | 3.924 | 4.113 | 4.074 | 3.926 | 3.967 |
| h2 | 3.846 | 4.179 | 4.188 | 3.989 | 4.125 | 4.146 |
| h3 | 3.826 | 4.173 | 3.885 | 4.249 | 4.176 | 4.118 |
| h4 | 3.751 | 3.747 | 4.258 | 3.922 | 4.066 | 4.05 |
| h5 | 3.945 | 3.99 | 3.712 | 4.137 | 4.052 | 3.997 |
| h6 | 4.025 | 3.894 | 3.776 | 4.033 | 4.259 | 3.839 |
| h7 | 3.966 | 4.214 | 3.789 | 3.753 | 3.944 | 4.059 |
| h12 | 6.831 | 7 | 6.716 | 6.951 | 6.86 | 6.969 |
| h23 | 7.257 | 7.029 | 7.049 | 7.084 | 7.104 | 7.289 |
| h34 | 7.255 | 6.945 | 7.133 | 7.029 | 6.989 | 7.021 |
| h45 | 6.794 | 6.873 | 6.728 | 7.205 | 7.141 | 7.148 |
| h56 | 7.093 | 7.1 | 7.297 | 7.028 | 7.033 | 6.97 |
| h67 | 6.924 | 7.269 | 7.077 | 7.159 | 7.189 | 7.276 |
| h13 | 5.13 | 4.876 | 4.702 | 5.05 | 5.032 | 4.948 |
| h46 | 5.175 | 4.736 | 4.792 | 4.937 | 5.101 | 5.166 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Gan, S.; Xue, J. Optimization Design of Microwave Filters Based on Deep Learning and Metaheuristic Algorithms. Electronics 2025, 14, 3305. https://doi.org/10.3390/electronics14163305
Zhang L, Gan S, Xue J. Optimization Design of Microwave Filters Based on Deep Learning and Metaheuristic Algorithms. Electronics. 2025; 14(16):3305. https://doi.org/10.3390/electronics14163305
Chicago/Turabian StyleZhang, Lu, Shihai Gan, and Jiabiao Xue. 2025. "Optimization Design of Microwave Filters Based on Deep Learning and Metaheuristic Algorithms" Electronics 14, no. 16: 3305. https://doi.org/10.3390/electronics14163305
APA StyleZhang, L., Gan, S., & Xue, J. (2025). Optimization Design of Microwave Filters Based on Deep Learning and Metaheuristic Algorithms. Electronics, 14(16), 3305. https://doi.org/10.3390/electronics14163305






