A Federated Learning Framework with Attention Mechanism and Gradient Compression for Time-Series Strategy Modeling
Abstract
1. Introduction
- A path attention aggregation mechanism that dynamically evaluates client gradient contributions to enhance strategy performance;
- A gradient clipping and compression mechanism that reduces cross-border communication costs;
- A heterogeneity-aware optimization module that improves local adaptability under varying market structures.
2. Related Work
2.1. The Application of Deep Learning in Quantitative Strategy Modeling
2.2. Federated Learning and Financial Data Privacy Protection
2.3. Heterogeneous Distributed Modeling and Communication Optimization Mechanism
3. Materials and Method
3.1. Data Collection
3.2. Data Preprocessing and Augmentation
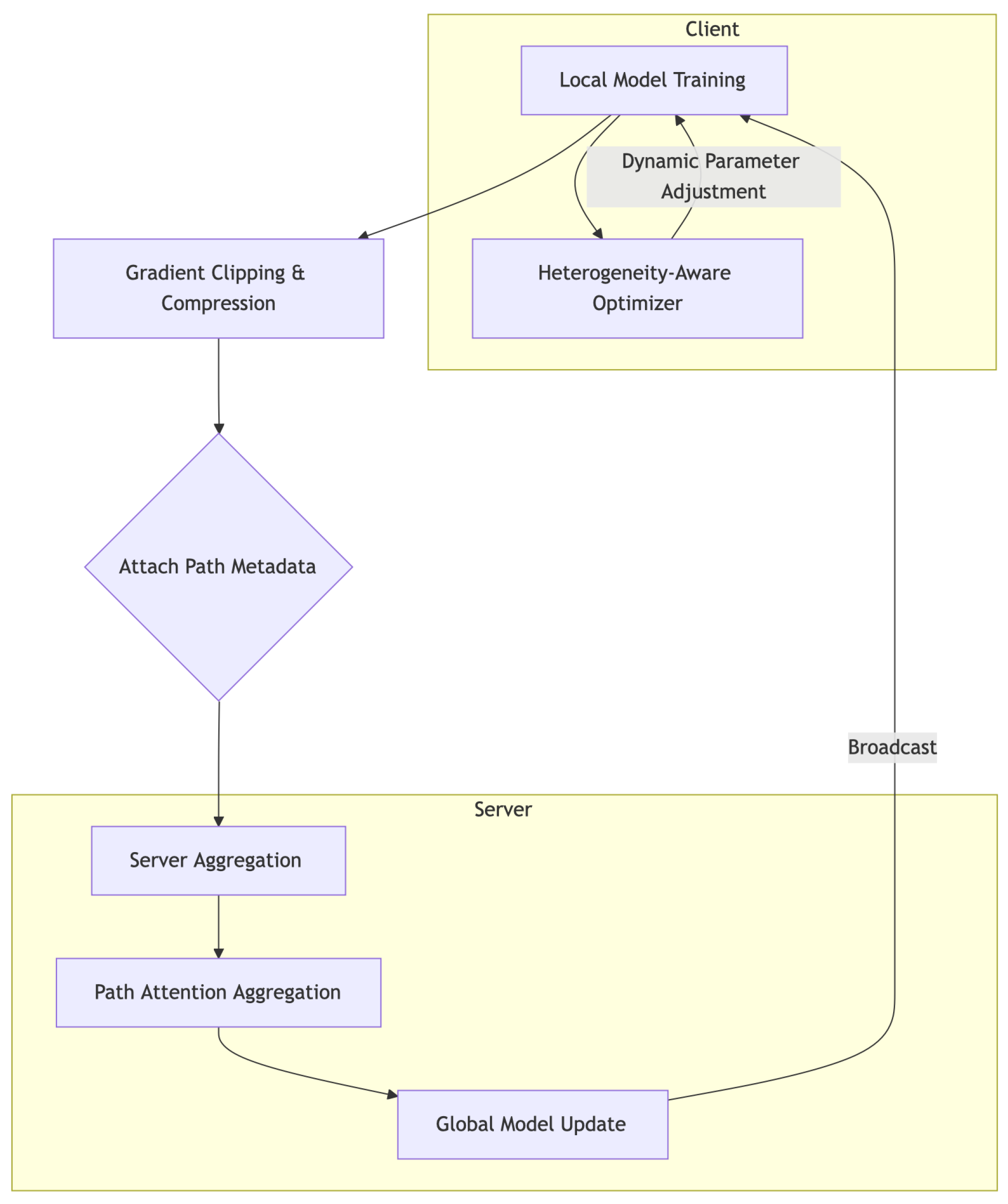
3.3. Proposed Method
3.3.1. Overall
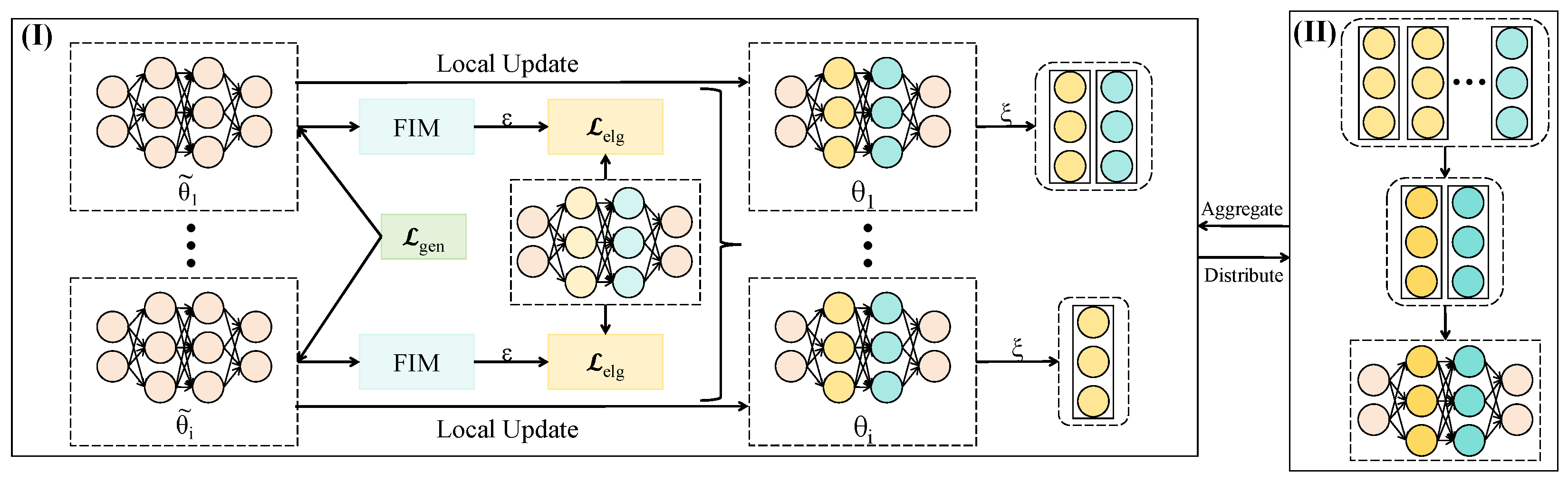
3.3.2. Path Attention Aggregation Module
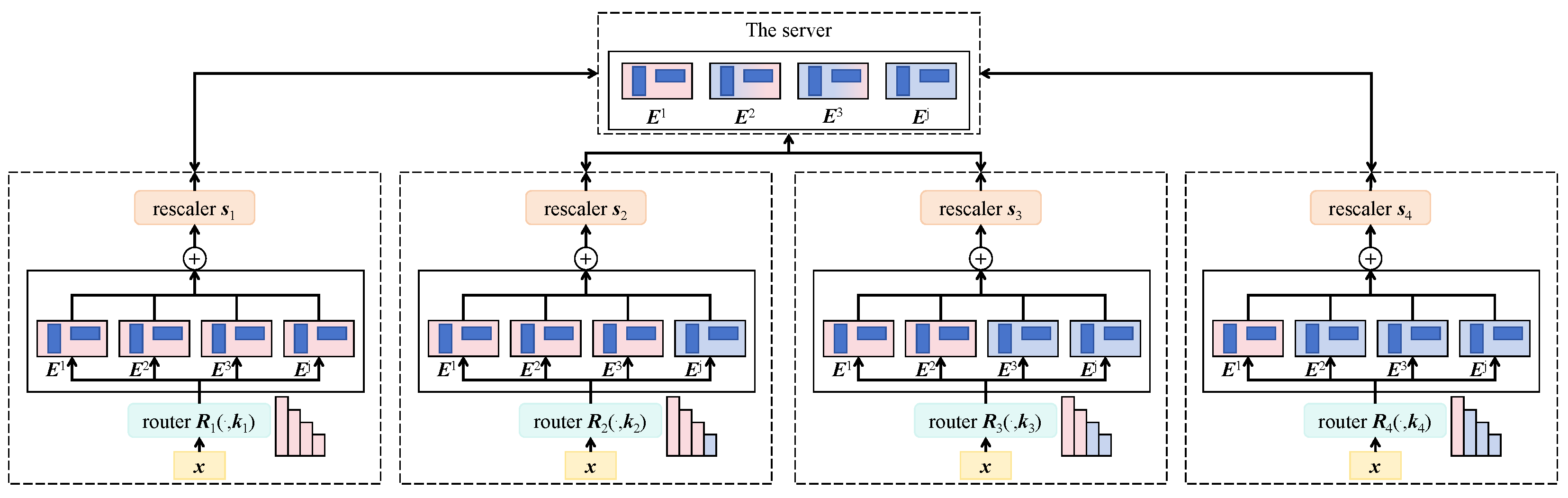
3.3.3. Gradient Clipping and Compression
3.3.4. Heterogeneity-Aware Adaptive Optimizer
4. Results and Discussion
4.1. Experimental Setup
4.1.1. Evaluation Metrics
4.1.2. Baselines
4.1.3. Hardware and Software Platform
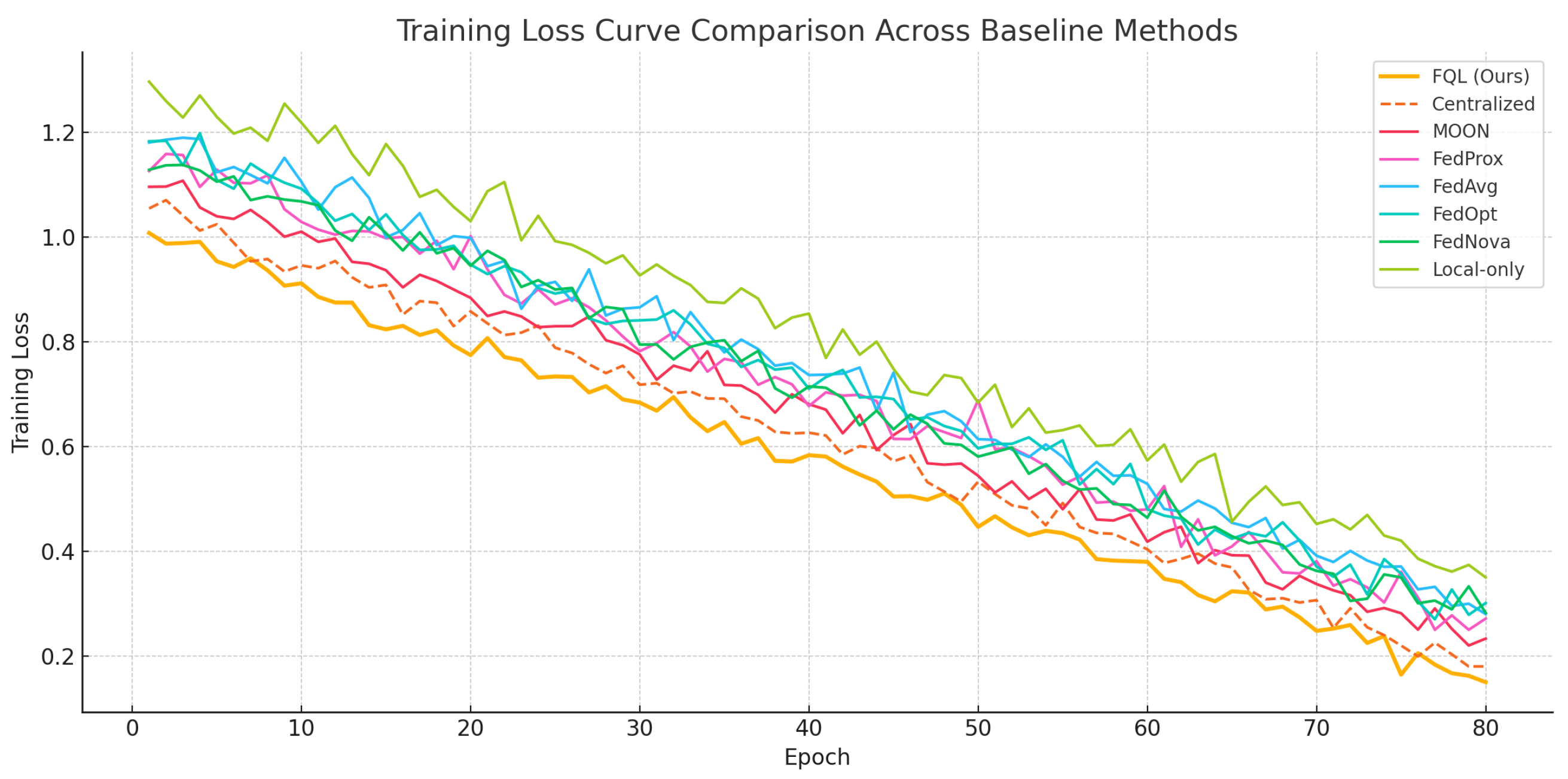
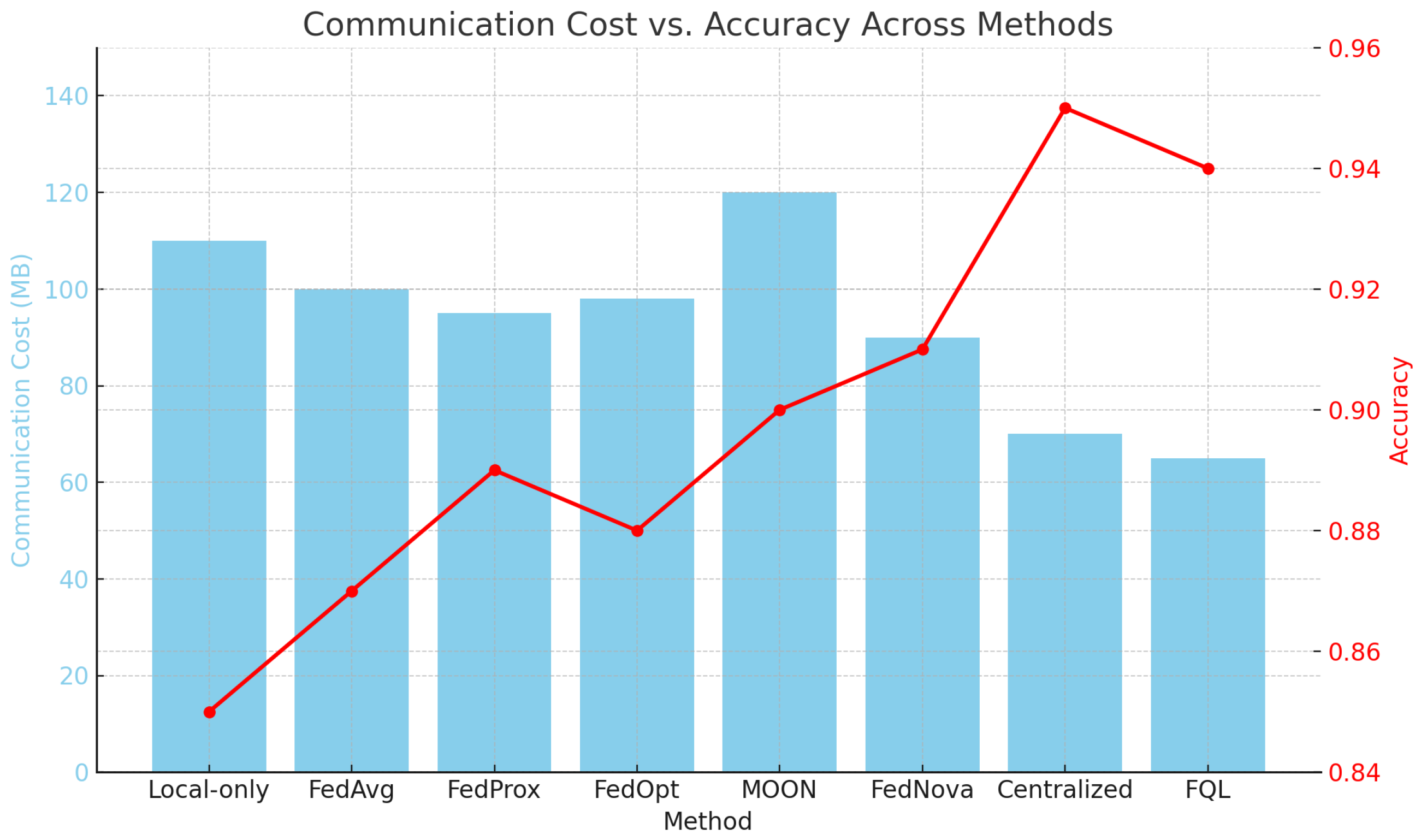
4.2. Performance Comparison Across Baseline Methods in Cross-Market Financial Strategy Modeling
4.3. Module Ablation Study of FQL Components
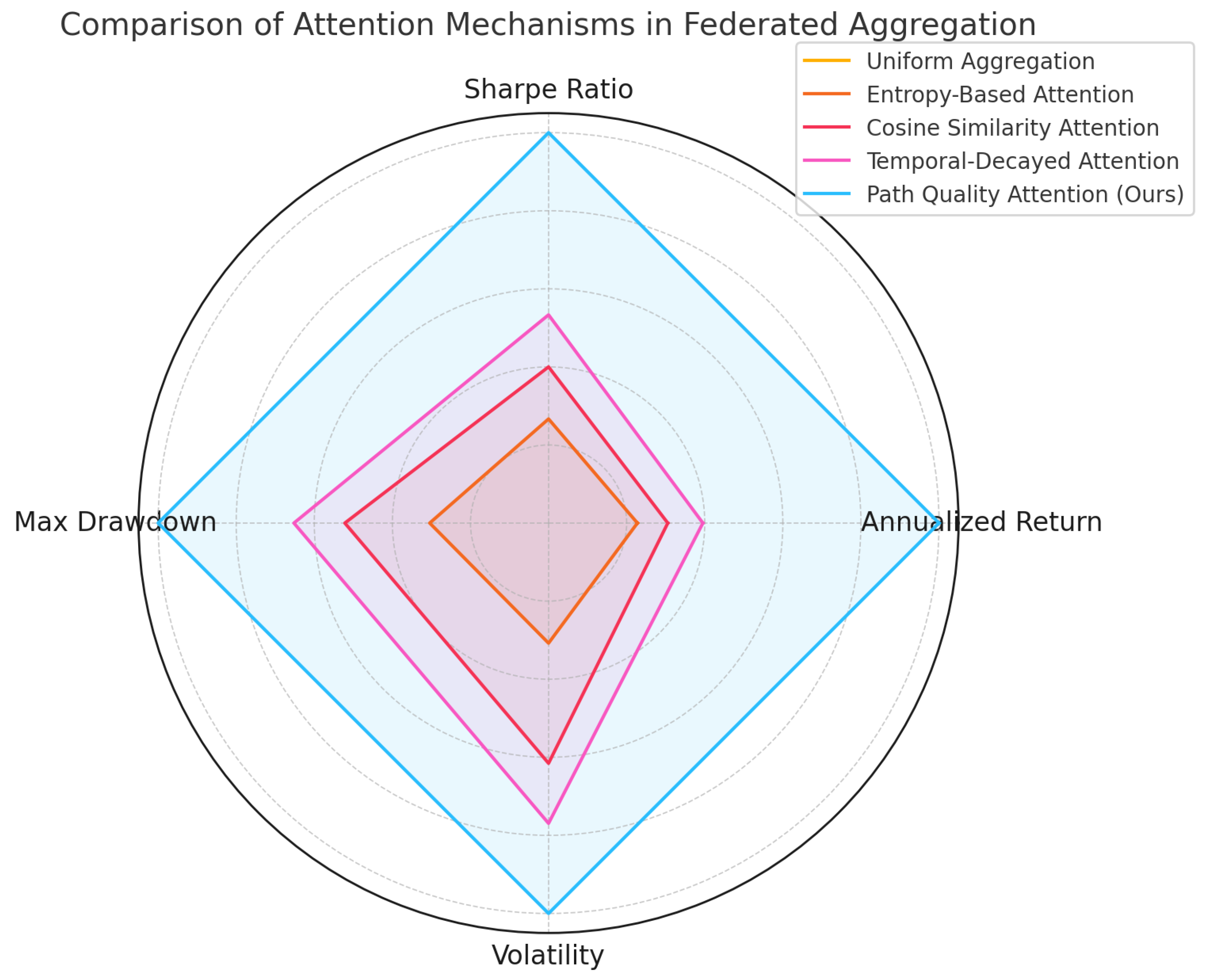
4.4. Comparison of Different Attention Mechanisms in Federated Aggregation
4.5. Discussion
4.5.1. Robust Communication Efficiency Across Diverse Network Scenarios
- Normal Network Environment (10 MB/s bandwidth): This scenario reflects standard enterprise intranet or metropolitan area network speeds. Under such conditions, the proposed method reduced communication volume by an average of 32.7% without sacrificing model accuracy.
- Bandwidth-Constrained Environment (1 MB/s bandwidth): This setting simulates remote agricultural regions or edge devices connected via cellular networks. In this scenario, conventional methods such as FedAvg experienced significantly increased latency. By contrast, our method maintained training stability while reducing gradient volume, achieving a 49.5% reduction in communication overhead and effectively avoiding model divergence.
- Dynamic Client Environment (20% intermittent client dropout): This scenario models unstable client participation, a common issue in federated learning. Thanks to the integration of compression and asynchronous aggregation, the proposed method achieved faster and more reliable model updates with a retransmission rate below 5%. Overall, it reduced communication cost by 41.2%, demonstrating strong robustness to network fluctuations.
4.5.2. Practical Applications Analysis
4.5.3. Analysis of Inter-Module Collaboration Mechanism
4.6. Limitation and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, H.; Malik, A. Reinforcement Learning Pair Trading: A Dynamic Scaling Approach. J. Risk Financ. Manag. 2024, 17, 555. [Google Scholar] [CrossRef]
- Han, W.; Xu, J.; Cheng, Q.; Zhong, Y.; Qin, L. Robo-Advisors: Revolutionizing Wealth Management Through the Integration of Big Data and Artificial Intelligence in Algorithmic Trading Strategies. J. Knowl. Learn. Sci. Technol. 2024, 3, 33–45. [Google Scholar]
- Bentre, S.; Busy, E.; Abiodun, O. Developing a Privacy-Preserving Framework for Machine Learning in Finance. 2024. Available online: https://www.researchgate.net/profile/Abiodun-Okunola-6/publication/386573416_Developing_a_Privacy-Preserving_Framework_for_Machine_Learning_in_Finance/links/675746722c5fa80df7b250c5/Developing-a-Privacy-Preserving-Framework-for-Machine-Learning-in-Finance.pdf (accessed on 4 July 2025).
- Li, Z.; Liu, X.Y.; Zheng, J.; Wang, Z.; Walid, A.; Guo, J. Finrl-podracer: High performance and scalable deep reinforcement learning for quantitative finance. In Proceedings of the Second ACM International Conference on AI in Finance, Virtual, 3–5 November 2021; pp. 1–9. [Google Scholar]
- Fan, B.; Qiao, E.; Jiao, A.; Gu, Z.; Li, W.; Lu, L. Deep learning for solving and estimating dynamic macro-finance models. arXiv 2023, arXiv:2305.09783. [Google Scholar] [CrossRef]
- Jeleel-Ojuade, A. The Role of Information Silos: An Analysis of How the Categorization of Information Creates Silos Within Financial Institutions, Hindering Effective Communication and Collaboration. 2024. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4881342 (accessed on 4 July 2025).
- Johnny, R.; Marie, C. Achieving Consistency in Data Governance Across Global Financial Institutions. Available online: https://www.researchgate.net/profile/Ricky-Johnny/publication/387174359_Achieving_Consistency_in_Data_Governance_Across_Global_Financial_Institutions/links/6762fd5872316e5855fc2ce2/Achieving-Consistency-in-Data-Governance-Across-Global-Financial-Institutions.pdf (accessed on 4 July 2025).
- Chatzigiannis, P.; Gu, W.C.; Raghuraman, S.; Rindal, P.; Zamani, M. Privacy-enhancing technologies for financial data sharing. arXiv 2023, arXiv:2306.10200. [Google Scholar] [CrossRef]
- He, P.; Lin, C.; Montoya, I. DPFedBank: Crafting a Privacy-Preserving Federated Learning Framework for Financial Institutions with Policy Pillars. arXiv 2024, arXiv:2410.13753. [Google Scholar]
- Li, L.; Fan, Y.; Tse, M.; Lin, K.Y. A review of applications in federated learning. Comput. Ind. Eng. 2020, 149, 106854. [Google Scholar] [CrossRef]
- Kang, R.; Li, Q.; Lu, H. Federated machine learning in finance: A systematic review on technical architecture and financial applications. Appl. Comput. Eng. 2024, 102, 61–72. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, S.; Xie, L. Research on analysis and application of quantitative investment strategies based on deep learning. Acad. J. Comput. Inf. Sci. 2023, 6, 24–30. [Google Scholar] [CrossRef]
- Wu, K.; Gu, J.; Meng, L.; Wen, H.; Ma, J. An explainable framework for load forecasting of a regional integrated energy system based on coupled features and multi-task learning. Prot. Control Mod. Power Syst. 2022, 7, 1–14. [Google Scholar] [CrossRef]
- Md, A.Q.; Kapoor, S.; AV, C.J.; Sivaraman, A.K.; Tee, K.F.; Sabireen, H.; Janakiraman, N. Novel optimization approach for stock price forecasting using multi-layered sequential LSTM. Appl. Soft Comput. 2023, 134, 109830. [Google Scholar] [CrossRef]
- Moghar, A.; Hamiche, M. Stock market prediction using LSTM recurrent neural network. Procedia Comput. Sci. 2020, 170, 1168–1173. [Google Scholar] [CrossRef]
- Qi, L. Forex Trading Signal Extraction with Deep Learning Models. Ph.D. Thesis, The University of Sydney, Camperdown, Australia, 2023. [Google Scholar]
- Muhammad, T.; Aftab, A.B.; Ibrahim, M.; Ahsan, M.M.; Muhu, M.M.; Khan, S.I.; Alam, M.S. Transformer-based deep learning model for stock price prediction: A case study on Bangladesh stock market. Int. J. Comput. Intell. Appl. 2023, 22, 2350013. [Google Scholar] [CrossRef]
- Chantrasmee, C.; Jaiyen, S.; Chaikhan, S.; Wattanakitrungroj, N. Stock Trading Signal Prediction Using Transformer Model and Multiple Indicators. In Proceedings of the 2024 28th International Computer Science and Engineering Conference (ICSEC), Khon Kaen, Thailand, 6–8 November 2024; IEEE: Piscataway Township, NJ, USA, 2024; pp. 1–6. [Google Scholar]
- Zhang, Q.; Qin, C.; Zhang, Y.; Bao, F.; Zhang, C.; Liu, P. Transformer-based attention network for stock movement prediction. Expert Syst. Appl. 2022, 202, 117239. [Google Scholar] [CrossRef]
- Ruiru, D.K.; Jouandeau, N.; Odhiambo, D. LSTM versus Transformers: A Practical Comparison of Deep Learning Models for Trading Financial Instruments. In Proceedings of the 16th International Joint Conference on Computational Intelligence, Porto, Portugal, 20–22 November 2024; SCITEPRESS-Science and Technology Publications: Setúbal, Portugal, 2024. [Google Scholar]
- Lin, Z. Comparative study of lstm and transformer for a-share stock price prediction. In Proceedings of the 2023 2nd International Conference on Artificial Intelligence, Internet and Digital Economy (ICAID 2023), Chengdu, China, 21–23 April 2023; Atlantis Press: Dordrecht, The Netherlands, 2023; pp. 72–82. [Google Scholar]
- Ge, Q. Enhancing stock market Forecasting: A hybrid model for accurate prediction of S&P 500 and CSI 300 future prices. Expert Syst. Appl. 2025, 260, 125380. [Google Scholar]
- Yuxin, M.; Honglin, W. Federated learning based on data divergence and differential privacy in financial risk control research. Comput. Mater. Contin. 2023, 75, 863–878. [Google Scholar]
- Fantacci, R.; Picano, B. Federated learning framework for mobile edge computing networks. CAAI Trans. Intell. Technol. 2020, 5, 15–21. [Google Scholar] [CrossRef]
- Abadi, A.; Doyle, B.; Gini, F.; Guinamard, K.; Murakonda, S.K.; Liddell, J.; Mellor, P.; Murdoch, S.J.; Naseri, M.; Page, H.; et al. Starlit: Privacy-preserving federated learning to enhance financial fraud detection. arXiv 2024, arXiv:2401.10765. [Google Scholar] [CrossRef]
- Whitmore, J.; Mehra, P.; Yang, J.; Linford, E. Privacy Preserving Risk Modeling Across Financial Institutions via Federated Learning with Adaptive Optimization. Front. Artif. Intell. Res. 2025, 2, 35–43. [Google Scholar] [CrossRef]
- Chen, C.; Yang, Y.; Liu, M.; Rong, Z.; Shu, S. Regularized joint self-training: A cross-domain generalization method for image classification. Eng. Appl. Artif. Intell. 2024, 134, 108707. [Google Scholar] [CrossRef]
- Zhang, H.; Peng, G.; Wu, Z.; Gong, J.; Xu, D.; Shi, H. MAM: A multipath attention mechanism for image recognition. IET Image Process. 2022, 16, 691–702. [Google Scholar] [CrossRef]
- Jing, Y.; Zhang, L. An Improved Dual-Path Attention Mechanism with Enhanced Discriminative Power for Asset Comparison Based on ResNet50. In Proceedings of the 2025 5th International Conference on Advances in Electrical, Electronics and Computing Technology (EECT), Guangzhou, China, 21–23 March 2025; IEEE: Piscataway Township, NJ, USA, 2025; pp. 1–10. [Google Scholar]
- Chen, S. Local regularization assisted orthogonal least squares regression. Neurocomputing 2006, 69, 559–585. [Google Scholar] [CrossRef]
- Abrahamyan, L.; Chen, Y.; Bekoulis, G.; Deligiannis, N. Learned gradient compression for distributed deep learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 7330–7344. [Google Scholar] [CrossRef]
- Li, X.; Karimi, B.; Li, P. On distributed adaptive optimization with gradient compression. arXiv 2022, arXiv:2205.05632. [Google Scholar] [CrossRef]
- Collins, L.; Hassani, H.; Mokhtari, A.; Shakkottai, S. Fedavg with fine tuning: Local updates lead to representation learning. Adv. Neural Inf. Process. Syst. 2022, 35, 10572–10586. [Google Scholar]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. Proc. Mach. Learn. Syst. 2020, 2, 429–450. [Google Scholar]
- Asad, M.; Moustafa, A.; Ito, T. Fedopt: Towards communication efficiency and privacy preservation in federated learning. Appl. Sci. 2020, 10, 2864. [Google Scholar] [CrossRef]
- Kim, S.; Bae, S.; Yun, S.Y.; Song, H. Lg-fal: Federated active learning strategy using local and global models. In Proceedings of the ICML Workshop on Adaptive Experimental Design and Active Learning in the Real World, Baltimore, MD, USA, 22 July 2022; pp. 127–139. [Google Scholar]
- Augenstein, S.; Hard, A.; Partridge, K.; Mathews, R. Jointly learning from decentralized (federated) and centralized data to mitigate distribution shift. arXiv 2021, arXiv:2111.12150. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Q.; Liang, H.; Joshi, G.; Poor, H.V. Tackling the Objective Inconsistency Problem in Heterogeneous Federated Optimization. arXiv 2020, arXiv:2007.07481. [Google Scholar] [CrossRef]
- Li, Q.; He, B.; Song, D. Model-Contrastive Federated Learning. arXiv 2021, arXiv:2103.16257. [Google Scholar] [CrossRef]

| Region | Asset Class | Number of Tickers | Total Samples (Daily) |
|---|---|---|---|
| United States (US) | NASDAQ-100 Constituents | 100 | 2,520,000 |
| Europe (EU) | Stoxx 600 Representative Stocks | 120 | 3,024,000 |
| Asia-Pacific (APAC) | MSCI Asia ETF Constituents | 80 | 2,016,000 |
| Total | — | 300 | 7,560,000 |
| Method | Annualized Return (%) | Sharpe Ratio | Max Drawdown (%) | Volatility (%) |
|---|---|---|---|---|
| Local-only [36] | 8.32 | 0.77 | 15.8 | 13.6 |
| FedAvg [33] | 9.21 | 0.87 | 14.2 | 12.1 |
| FedProx [34] | 10.35 | 0.91 | 13.5 | 11.8 |
| FedOpt [35] | 10.01 | 0.89 | 14.0 | 12.0 |
| MOON [39] | 10.82 | 0.95 | 13.1 | 11.3 |
| FedNova [38] | 11.05 | 0.98 | 12.6 | 10.9 |
| Centralized [37] | 13.44 | 1.23 | 9.3 | 8.8 |
| FQL (Ours) | 12.72 | 1.12 | 10.3 | 9.7 |
| Method Variant | Annualized Return (%) | Sharpe Ratio | Max Drawdown (%) | Volatility (%) |
|---|---|---|---|---|
| FQL w/o GradClip+Compress | 11.92 | 1.04 | 11.6 | 10.5 |
| FQL w/o Het-Optimizer | 11.58 | 1.00 | 12.3 | 10.9 |
| FQL w/o Path-Attention | 11.23 | 0.96 | 12.7 | 11.2 |
| FQL (Full Model) | 12.72 | 1.12 | 10.3 | 9.7 |
| Attention Type | Annualized Return (%) | Sharpe Ratio | Max Drawdown (%) | Volatility (%) |
|---|---|---|---|---|
| Uniform Aggregation | 11.05 | 0.97 | 12.6 | 11.0 |
| Entropy-Based Attention | 11.43 | 1.01 | 11.9 | 10.6 |
| Cosine Similarity Attention | 11.56 | 1.03 | 11.4 | 10.2 |
| Temporal-Decayed Attention | 11.71 | 1.05 | 11.1 | 10.0 |
| Path Quality Attention (Ours) | 12.72 | 1.12 | 10.3 | 9.7 |
| Method | Normal Bandwidth | Constrained Bandwidth | Client Dropout |
|---|---|---|---|
| FedAvg | 102.5 | 108.3 | 98.4 |
| FedProx | 98.1 | 101.2 | 96.7 |
| MOON | 120.4 | 135.6 | 125.1 |
| FedNova | 91.7 | 96.4 | 89.5 |
| FQL (Ours) | 68.9 | 54.5 | 57.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, W.; Zhang, L.; Sun, Z.; Zhai, Z.; Cai, X.; Lan, Z.; Zhan, Y. A Federated Learning Framework with Attention Mechanism and Gradient Compression for Time-Series Strategy Modeling. Electronics 2025, 14, 3293. https://doi.org/10.3390/electronics14163293
Cui W, Zhang L, Sun Z, Zhai Z, Cai X, Lan Z, Zhan Y. A Federated Learning Framework with Attention Mechanism and Gradient Compression for Time-Series Strategy Modeling. Electronics. 2025; 14(16):3293. https://doi.org/10.3390/electronics14163293
Chicago/Turabian StyleCui, Weiyuan, Liman Zhang, Zhengxi Sun, Ziying Zhai, Xiahuan Cai, Zeyu Lan, and Yan Zhan. 2025. "A Federated Learning Framework with Attention Mechanism and Gradient Compression for Time-Series Strategy Modeling" Electronics 14, no. 16: 3293. https://doi.org/10.3390/electronics14163293
APA StyleCui, W., Zhang, L., Sun, Z., Zhai, Z., Cai, X., Lan, Z., & Zhan, Y. (2025). A Federated Learning Framework with Attention Mechanism and Gradient Compression for Time-Series Strategy Modeling. Electronics, 14(16), 3293. https://doi.org/10.3390/electronics14163293






