Optimizing Hybrid Renewable Systems for Critical Loads in Andean Medical Centers Using Metaheuristics

Abstract

The electrification of rural medical centers in high Andean areas represents a critical challenge for equitable development due to limited access to reliable energy. Hybrid Renewable Energy Systems (HRESs), which combine solar photovoltaic generation, Battery Energy Storage Systems (BESSs), and backup diesel generators, are emerging as viable solutions to ensure the supply of critical loads. However, their effective implementation requires optimal sizing methodologies that consider multiple technical and economic constraints and objectives. In this study, an optimization model based on metaheuristic algorithms is developed, specifically, Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and Ant Colony Optimization (ACO), to identify optimal configurations of an HRES applied to a remote medical center in the Peruvian Andes. The results show that GA achieved the lowest Life Cycle Cost (LCC), with a high share of renewable energy (64.04%) and zero Energy Not Supplied (ENS) defined as the amount of load demand not met by the system, significantly outperforming PSO and ACO. GA was also found to offer greater stability and operational robustness. These findings confirm the effectiveness of metaheuristic methods for designing efficient and resilient energy solutions adapted to isolated rural contexts.

1. Introduction

In rural and peripheral areas, the lack of reliable access to energy limits social, economic, and health development. The energy gap between urban and rural areas remains significant, especially in low-income countries, where millions of people lack access to modern energy services [1,2]. This deficiency directly affects the functioning of rural medical centers, compromising the refrigeration of medicines, the use of essential equipment, and continuous medical care [3,4]. In this context, medical centers in remote rural areas face critical challenges due to the lack of reliable electricity, which seriously compromises the quality of medical care. In various regions, distributed renewable energy has been shown to significantly improve the resilience and operational autonomy of these facilities. Therefore, ensuring energy supply in these environments is not only a technical challenge but also a health and development priority [3]. In addition, the lack of reliable energy limits access to other essential services such as education and economic productivity, thus deepening energy poverty [1]. Accordingly, enhancing resilience and sustainability in these complex environments is essential [5].

Given this problem, renewable energy is positioned as a key solution for providing electricity to rural health centers disconnected from the grid. Hybrid systems that combine sources such as solar photovoltaic, battery storage, and backup diesel generators can improve the quality of medical services, reduce emissions, and lower long-term operating costs. However, these systems face persistent challenges such as high initial costs, maintenance complexity, and variability in renewable generation [6,7,8]. Several studies have evaluated the effectiveness of these hybrid configurations in rural contexts. In general, they have been found to ensure a reliable and continuous energy supply, reducing dependence on fossil fuels and improving operational resilience. In addition, optimizing the sizing of components, considering critical demand, costs, and available resources, has been key to improving technical and economic viability [9,10,11].

In this regard, hybrid renewable energy systems (SHERs) have gained prominence, especially in rural clinics, due to their ability to ensure a stable electricity supply even under adverse weather conditions. However, their implementation is not without limitations, including oversized components, high initial costs, and maintenance difficulties, which affect their sustainability in low-resource contexts [12]. In response to these limitations, the literature has proposed the use of different techniques applied in this context. These include deterministic methods such as linear programming (LP) [13], mixed-integer programming (MILP) [14], nonlinear programming (NLP) [15], and dynamic programming (DP) [16], applied mainly in cost optimization, economic dispatch, and energy planning under technical constraints. These approaches have proven useful in well-structured contexts with accurate data and relatively stable conditions. However, their performance is limited to multivariable problems with high uncertainty or multiple conflicting objectives, as is often the case in disconnected rural microgrids, where weather and demand conditions can be highly variable and unpredictable.

At the same time, simulation tools such as HOMER Pro, iHOGA, TRNSYS, PV*SOL, and modeling environments such as MATLAB/Simulink have been developed and used to evaluate energy configurations from a technical–economic perspective [17,18,19]. These platforms allow modeling of hourly load profiles, analysis of renewable resource availability, simulation of the operation of components such as batteries and generators, and calculation of metrics such as life cycle cost (LCOE), carbon emissions, and renewable fraction. While many of these tools include basic optimization modules or allow integration with external routines, much of the process relies on manual iterative analysis or comparisons between predefined scenarios, which can limit their efficiency in finding optimal global configurations. Given this limitation, there is a need to incorporate more flexible and robust approaches, such as metaheuristic algorithms, which allow for the exploration of large search spaces and the resolution of nonlinear, stochastic, and multi-constrained problems.

The use of metaheuristic algorithms as an effective strategy for the optimal design and operation of microgrids would solve complex, nonlinear, and multivariable problems with demanding constraints, such as economic dispatch. For example, ref. [20] compared five metaheuristic algorithms and demonstrated that they achieve efficient and stable solutions in less time, significantly reducing the LCOE. Similarly, ref. [21] demonstrated that the integration of batteries, supercapacitors, and fuel cells in an HESS system, optimized using Particle Swarm Optimization (PSO) and Backtracking Search Algorithm (BSA), improves the stability, efficiency, and energy autonomy of the microgrid. Similarly, ref. [22] highlighted the applicability of PSO and genetic algorithms (GAs) in terms of cost savings and scheduling efficiency in grid-connected PV–BESS.

Other studies, such as the one by [23], have confirmed that algorithms such as GA and ant colony optimization (ACO) exhibit good accuracy, dynamic response, and robustness in hybrid storage control. In addition, ref. [24] emphasize that these algorithms are superior to classical programming methods, thanks to their adaptability and efficiency in real-world environments with multiple objectives. To achieve efficient implementation of SHERs, advanced tools are required to enable optimal sizing and effective operation under diverse local conditions. Among the most widely used algorithms in these contexts are GA, PSO, and ACO, recognized for their versatility in handling multiple objectives and constraints. However, despite the growing number of studies on hybrid microgrids, a significant gap has been identified in the Andean rural context.

Extreme weather conditions, geographical dispersion, and budget constraints require robust and adaptive models. In addition, few studies explicitly prioritize critical load attention in medical centers and systematically compare the performance of different algorithms under the same operational framework. Therefore, this study aims to develop an optimization model based on metaheuristic algorithms to design optimal configurations of hybrid renewable energy systems that guarantee the supply of critical loads in remote medical centers in Peru’s high Andean regions, comparing the performance of GA, PSO, and ACO.

In conclusion, the literature shows persistent gaps in the Andean rural context. There is a limited focus on ensuring critical load supply in medical centers, and there is an absence of systematic comparisons of GA, PSO, and ACO under identical operational conditions. This study addresses these challenges by proposing a PV–BESS–diesel system optimization model that integrates real demand profiles and long-term climatic data. This model enables robust technical and economic evaluations and provides practical recommendations for isolated healthcare facilities.

Next, the simulation methodology used to model the hybrid system (PV–BESS–diesel) will be presented, including the critical demand profile, local climatic conditions, and technical and economic parameters. The use of GA, PSO, and ACO algorithms as optimization tools will be explained, detailing their configurations and evaluation criteria. The optimal configurations obtained by each algorithm will be compared, analyzing key metrics such as life cycle cost (LCC), renewable share, energy not supplied (ENS), and operational robustness. In addition, the stability of the results and their sensitivity to input conditions will be discussed. Finally, the main findings of this study will be summarized, highlighting the algorithm that achieved the best technical–economic performance, and recommendations will be proposed for the actual implementation of SHERs in rural medical centers in Peru.

2. Materials and Methods

This study presents applied research with a quantitative–computational approach, focused on the design and evaluation of SHERs, with the aim of ensuring uninterrupted energy supply to critical loads in a medical center located in a remote area of Peru. To this end, an optimization model based on metaheuristic algorithms was developed, which allows different technological configurations to be compared considering technical, economic, and sustainability criteria, as shown in Figure 1.

2.1. Materials

Real data from a rural medical center in Peru was used for the annual simulation of the system. The model incorporates hourly solar irradiance (W/m²), wind speed (m/s), ambient temperature (°C), hourly electricity demand profile (kWh), and the technical and economic parameters of the technologies considered as its main inputs. Figure 2 shows the time series for 2024 for global horizontal irradiance [GHI, I(t)], wind speed [v(t)], ambient temperature [Ta(t)], and electricity demand at the health center [D(t)]. The climate data were obtained from the National Solar Radiation Database (NSRDB) [25], while the electricity consumption profile was compiled from the establishment’s energy records.

Table 1. Technical parameters of the PV module used as input data for the simulation model under standard test conditions.

Technical Parameter	Value
Nominal Power (Pmax)	480 Wp
Voltage at Maximum Power (Vmp)	41.88 V
Current at Maximum Power (Imp)	11.47 A
Module Efficiency	20.20%
Temperature Coefficient (Pmax)	−0.35%/°C
Nominal Operating Cell Temperature (NOCT)	45 ± 2 °C
Module Dimensions	1903 × 1134 × 30 mm
Estimated Commercial Price (excluding VAT)	~184 USD

Source: JA Solar, “JAM66S30 480–505 MR” datasheet [26].

summarizes the technical parameters of the photovoltaic module considered in the model. A 480 Wp panel with high efficiency (20.2%) and negative power temperature coefficient (−0.35%/°C) was selected, which is suitable for high-altitude tropical climates such as that of the remote region evaluated in Peru. The voltage and current at the maximum power point (Vmp = 41.88 V, Imp = 11.47 A) are compatible with commercial series/parallel configurations.

Table 2. Technical and simulation parameters of the wind turbine used as input data for the model.

Technical Parameter	Value	Simulation Parameters	Value
Rated Power	2.0 kW	Installed Wind Power Pwind	Decision variable (multiples of 2 kW)
Output Voltage	48 V DC	Simplified Power Curve	Linear interpolation between:
Cut-in Wind Speed Vin	3.2 m/s	Vin = 3.2 m/s	→0 W
Rated Wind Speed Vrated	11.0 m/s	Vrated = 11.0 m/s	→2000 W
Cut-off Wind Speed Vcutoff	25.0 m/s	Vcutoff = 25.0 m/s	→0 W
Estimated Efficiency	30–35%	Estimated Capacity Factor	15–25%
Estimated Price	~1800 USD

Source: Nanjing Oulu Electric Co., Ltd., “FD3.2-2000” wind turbine datasheet [27].

presents the technical characteristics of the wind turbine considered in the model. A horizontal axis turbine with a nominal power of 2.0 kW was chosen, suitable for applications in rural microgrids and environments with moderate wind speeds. The system operates with a 48 V DC output, which facilitates its integration with battery banks. The wind turbine has a start-up speed of 3.2 m/s, a nominal operating speed of 11.0 m/s, and a cut-off speed of 25.0 m/s, values that allow it to operate efficiently under moderate wind conditions.

Table 3. Technical characteristics and simulation parameters of the LiFePO₄ battery used as input data for the model.

Technical Parameter	Value	Technical Parameter	Value
Battery type	LiFePO4	Lifespan	>6000 cycles 80% DOD/>15 years
Total energy	4.8 kWh	Certifications	UL1973, CE, TUV, UN38.3
Usable energy (DC)	4.3 kWh	Warranty	5 years
Nominal voltage	48 Vdc	Simulation Parameters
Nominal discharge current	60 A	Installed capacity (Ebatt)	4.8 kWh
Max discharge current (3 s)	100 A	Maximum Depth of Discharge (DOD)	97%
Nominal charge/discharge power	3.0 kW	Efficiency (round-trip, assumed)	90–95%
Max discharge power (3 s)	6.0 kW	Battery model integration	Parallel configuration (up to 16 units)

summarizes the technical characteristics and simulation parameters of the battery banks (BESS) used in the model. A lithium iron phosphate (LiFePO₄) battery, model TS-L5000/LV, was selected due to its high thermal stability, operational safety, and long service life. The unit has a nominal capacity of 4.8 kWh, with a usable energy of 4.3 kWh under standard discharge conditions.

Table 4. Technical characteristics and simulation parameters of the diesel backup generator used as input data for the model.

Technical Parameter	Range	Technical Parameter	Range
Rated power output	10 kW/12.5 kVA	Estimated lifespan	5000–10,000 h
Voltage	220 V AC (single-phase)	Simulation Parameters	Value
Frequency	50/60 Hz	Installed power (Pgen)	Decision variable (e.g., 3–15 kW)
Fuel type	Diesel	Fuel cost	1.35 USD/L
Fuel tank capacity	50–60 L	Generator efficiency (η)	28–33%
Specific fuel consumption	~0.27–0.30 L/kWh	Minimum load threshold	30% of rated power
Average fuel consumption at 75% load	2.2–2.5 L/h	Emission factor (CO2)	~2.68 kg CO2/L diesel
Maintenance interval	250 h or monthly	Operation mode (Only)	Renewable + battery are insufficient

Note: For simulation purposes, the following representative average values were used: fuel tank capacity = 55 L, generator efficiency = 30%, specific fuel consumption = 0.27 L/kWh, and average fuel consumption at 75% load = 2.35 L/h.

shows the technical and simulation parameters of the backup diesel generator considered in the model. It is a single-phase 10 kW unit with an output voltage of 220 V AC and an operating frequency of 50/60 Hz, powered by diesel. Its specific consumption is in the range of 0.27–0.30 L/kWh, with an average consumption of 2.2–2.5 L/h at 75% load. The starting system is electric (12 V) and offers an estimated autonomy of 20 to 25 h with a full fuel tank.

2.2. Solar Photovoltaic (PV) Generation

The operating temperature of the photovoltaic cell directly influences the module’s performance. As the temperature increases, efficiency decreases due to the panel’s negative temperature coefficient (−0.35%/°C). To estimate the actual cell temperature, Tc(t), a thermal model is used that considers the ambient temperature, solar irradiance, and the NOCT (Normal Operating Cell Temperature) value of the module, as expressed in Equation (1) [28].

$${\mathrm{T}}_{\mathrm{C}}\left(\mathrm{t}\right)={\mathrm{T}}_{\mathrm{a}}\left(\mathrm{t}\right)+\mathrm{I}\left(\mathrm{t}\right)\left({\displaystyle \frac{\mathrm{N}\mathrm{O}\mathrm{C}\mathrm{T}-20}{800}}\right)$$

(1)

where T_c(t) is the temperature of the photovoltaic cell at time t (°C); T_a(t) is the ambient temperature at time t (°C); I(t) is the solar irradiance incident on the panel at t (W/m²); NOCT is the Nominal Operating Cell Temperature, typical of the module, generally ~45 °C.

In addition, the aim is to maximize solar energy capture during the winter season, when irradiance is lower and the angle of solar incidence is lower. To this end, a panel inclination greater than the latitude of the site was selected, which allows for the optimization of solar radiation utilization in conditions of low sun elevation above the horizon, as expressed in Equation (2) [28].

β = ϕ + 15°

(2)

where β is the angle of inclination of the panel with respect to the horizontal (°); Φ is the latitude of the installation site (°); 15° allows for maximum generation in winter, at the expense of a slight loss in summer.

Consequently, the instantaneous power generated by a photovoltaic panel is estimated by considering the efficiency of the module, the effective area of the panel, the incident solar irradiance, the effect of temperature, and a loss factor associated with dust accumulation, as expressed in Equation (3) [29].

$${\mathrm{P}}_{\mathrm{P}\mathrm{V} \mathrm{u}\mathrm{n}\mathrm{i}\mathrm{t}}\left(\mathrm{t}\right)=\left({\mathrm{Y}}_{\mathrm{d}}\right)\left({\mathsf{\eta }}_{\mathrm{P}\mathrm{V}}\right)\left({\mathrm{A}}_{\mathrm{P}\mathrm{V}}\right)\left(\mathrm{I}\left(\mathrm{t}\right)\right)\left(1-{\displaystyle \frac{{\mathrm{K}}_{\mathrm{p}}}{100}}\ast \left({\mathrm{T}}_{\mathrm{C}}\left(\mathrm{t}\right)-25\right)\right)$$

(3)

where Y_d is the total annual energy demand (kWh/year), and K_p is the performance factor accounting for system losses and design considerations. Thus, the total power generated by the set of photovoltaic modules is obtained by multiplying the instantaneous power generated by each unit by the total number of panels installed, as expressed in Equation (4) [30].

$$P_{PV}\left(t\right)=\left(N_{PV}\right)\left(P_{PV unit}\left(t\right)\right)$$

(4)

where P_PV(t) represents the total electrical power supplied by the photovoltaic system at time t (kW); N_PV is the total number of photovoltaic modules in the system.

2.3. Wind Power Generation (WT)

To estimate wind speed at different heights, the power law is applied, which relates wind speed to height above ground level using an empirical exponent (α), as expressed in Equation (5) [31].

$${\displaystyle \frac{v_2}{v_1}}={\left({\displaystyle \frac{h_2}{h_1}}\right)}^{\alpha }$$

(5)

where v₁ is the wind speed measured at height h1; v₂ is the estimated wind speed at height h₂; α is the Hellman exponent, which depends on the roughness of the terrain, between 0.1 and 0.3.

The power generated by a wind turbine unit is modeled using a step function, which considers three operating ranges according to wind speed, as shown in Equation (6) [31].

$${\mathrm{P}}_{\left(\mathrm{W}\mathrm{T}\mathrm{u}\mathrm{n}\mathrm{i}\mathrm{t}\right)}\left(\mathrm{t}\right)=\left\{\begin{array}{c}\begin{array}{c}0; {\mathrm{v}}_2\left(\mathrm{t}\right)<{\mathrm{V}}_{\mathrm{c}\mathrm{u}\mathrm{t}-\mathrm{i}\mathrm{n}}\\ {\displaystyle \frac{{\mathrm{P}}_{\mathrm{W}\mathrm{T}\mathrm{r}}\left({\mathrm{V}}^3-{\mathrm{V}}_{\mathrm{c}\mathrm{u}\mathrm{t}-\mathrm{i}\mathrm{n}}^3\right)}{{(\mathrm{V}}_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}}^3-{\mathrm{V}}_{\mathrm{c}\mathrm{u}\mathrm{t}-\mathrm{i}\mathrm{n}}^3)}}; {\mathrm{V}}_{\mathrm{c}\mathrm{u}\mathrm{t}-\mathrm{i}\mathrm{n}}\le \mathrm{V}\left(\mathrm{t}\right)<{\mathrm{V}}_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}}\\ {\mathrm{P}}_{\mathrm{W}\mathrm{T}} {; \mathrm{V}}_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}}\le \mathrm{V}\left(\mathrm{t}\right)<{\mathrm{V}}_{\mathrm{c}\mathrm{u}\mathrm{t}-\mathrm{o}\mathrm{u}\mathrm{t}}\end{array}\\ 0; {\mathrm{V}}_{\mathrm{c}\mathrm{u}\mathrm{t}-\mathrm{o}\mathrm{u}\mathrm{t}}\le V\left(\mathrm{t}\right)\end{array}\right.$$

(6)

where without generation is when the wind speed is lower than the cut-in speed V_cut−in, or higher than the cut-out speed V_cut−out, the turbine does not produce energy; the partial operating range is between V_cut−in and V_rated, the power generated increases with the cube of the wind speed, interpolating between zero and the rated power; the nominal range is between V_rated and V_cut-out, when the turbine generates its maximum constant power PWT.

The instantaneous power generated by the entire wind system is obtained by multiplying the individual output of a wind turbine by the total number of units installed, as shown in Equation (7) [31].

$$P_{WT}\left(t\right)={(N}_{WT}\left)\right(P_{WTunit }\left(t\right))$$

(7)

where P_WT(t) is the total power generated by the wind turbine array (kW); N_WT is the total number of wind turbines in operation (dimensionless); P_WTunit(t) is the instantaneous power generated by a single turbine (kW).

2.4. Modeling of the Diesel Generator (2 kW)

In this model, the diesel backup system consists of modular 2 kW units. The total number of generators installed is a discrete decision variable within the optimization process. Hourly fuel consumption is estimated using a linear relationship with the electrical power delivered by the generator set. The power generated by the diesel system is expressed in Equation (8); hourly diesel consumption is calculated according to Equation (9); and the operating cost per hour is determined using Equation (10) [32].

$${\mathrm{P}}_{\mathrm{D}\mathrm{G}}\left(\mathrm{t}\right)=\mathrm{m}\mathrm{i}\mathrm{n}\{\max \left[\mathrm{D}\left(\mathrm{t}\right)-\left({\mathrm{P}}_{\mathrm{P}\mathrm{V}}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{W}\mathrm{T}}\left(\mathrm{t}\right)\right),0\right],2.{\mathrm{N}}_{\mathrm{D}\mathrm{G}}\}$$

(8)

where P_DG(t) is the power delivered by the diesel generator (kW); N_DG is the number of 2 kW generators installed; and the output of the diesel generator is limited to 2.N_DG kW.

$${\mathrm{f}}_{\mathrm{D}\mathrm{G}}\left(\mathrm{t}\right)=\mathrm{a}.{\mathrm{P}}_{\mathrm{D}\mathrm{G}}\left(\mathrm{t}\right)+\mathrm{b}.{\mathsf{\delta }}_{\mathrm{D}\mathrm{G}}\left(\mathrm{t}\right)$$

(9)

where a and b are typical consumption coefficients; a is equal to 0.246 L/kWh and b is equal to 0.084 L/h; δ_DG(t) is the binary variable that is equal to 1 if the generator is on, 0 if it is off.

$${ Cost}_{DG}\left(t\right)={ f}_{DG}\left(t\right) .{ C}_{liter}$$

(10)

where C_liter ≈ 1.35 USD/L; the diesel backup system is modeled using 2 kW modular units; the total number of generators installed, N_DG, is an integer decision variable within the optimization process; the maximum power that can be supplied at any given time is limited by 2⋅N_DG and is activated only when renewable generation does not cover demand.

2.5. Battery Energy Storage System (BESS) Modeling

The state of charge (SOC) is a parameter that indicates the amount of energy available in the battery at a given moment, relative to its maximum capacity. This indicator, expressed as a percentage, allows the current level of energy stored in the system to be monitored and is calculated using Equation (11) [33].

$${\mathrm{S}\mathrm{O}\mathrm{C}}_{(\mathrm{t}+1)}={\mathrm{S}\mathrm{O}\mathrm{C}}_{\left(\mathrm{t}\right)}+{\displaystyle \frac{{\mathsf{\eta }}_{\mathrm{c}}\ast {\mathrm{P}}_{\mathrm{c}\mathrm{h}\mathrm{g}}(\mathrm{t})-\frac{{\mathrm{P}}_{\mathrm{d}\mathrm{c}\mathrm{h}\mathrm{g}}(\mathrm{t})}{{\mathrm{n}}_{\mathrm{d}}}}{{\mathrm{C}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{s}}}}$$

(11)

where SOC_(t+1) indicates the battery charge level at time t + 1, represented by a dimensionless value ranging between 0 and 1; SOC(t) represents the initial state of charge of the battery at time t; ηc is the charging efficiency, dimensionless with values between 0 and 1 (in this case, a value of 0.9 is adopted); ηd is the discharge efficiency, also dimensionless and between 0 and 1; a value of 0.9 is considered; P_chg(t) denotes the power used to charge the battery at time t, expressed in kilowatts (kW); P_dchg(t) indicates the power extracted from the battery at time t, also in kilowatts (kW); and Cbess represents the total storage capacity of the battery system, measured in kilowatt-hours (kWh).

2.6. Model Restrictions

The optimization model considers technical, operational, and experimental configuration constraints, which are detailed in

Table 5. Technical and economic parameters used in the optimization model.

Category	Item	Value
Expected Lifespan	Photovoltaic Panels (PVs)	25 years
	Wind Turbines (WTs)	20 years
	Lithium Batteries (BESS)	15 years
	Diesel Generator (DG)	10 years
Estimated Annual O&M Cost	PV	1.5% of CAPEX
	WT	2.5% of CAPEX
	BESS	1.5% of CAPEX
	DG	7% of CAPEX + fuel
Discount Rate	Discount Rate	6%
Initial Weights (Objective Function)	w1	0.4% (Life Cycle Cost—LCC)
	w2	0.3% (System Reliability)
	w3	0.2% (Proportion of Renewable Energy)
	w4	0.1% (Minimizing Surpluses)
Sensitivity Analysis	Rangos ± 20%	Yes (Morris and Sobol)
Robustness Configuration	10 runs per configuration	Yes
GA Parameters	Population size	30
	Generations	100
	pc	0.8
	pm	0.1
PSO Parameters	Particles	30
	Iterations (PSOs)	100
	ω	0.5–0.9
ACO Parameters	Ants	30
	Iterations (ACOs)	100
	ρ	0.1
Variable Ranges	PPV	1–20 kWp
	Pwind	1–10 kW
	Ebatt	5–100 kWh
	Pgen	3–15 kW

.

2.7. Hourly Energy Balance

To ensure that electricity demand is met at every hour of the simulation horizon, a general energy balance equation is established that integrates all available sources in the hybrid system: solar generation, wind generation, diesel backup, and battery storage. This condition must be met at every hourly interval, as shown in Equation (12) [34].

$${\mathrm{P}}_{\mathrm{P}\mathrm{V}}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{W}\mathrm{T}}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{D}\mathrm{G}}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{t}-\mathrm{d}\mathrm{i}\mathrm{s}}\left(\mathrm{t}\right)\ge \mathrm{D}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{t}-\mathrm{c}\mathrm{h}}\left(\mathrm{t}\right)$$

(12)

where P_PV(t) is the power generated by solar panels; P_WT(t) is the instantaneous wind power; P_DG(t) is the power supplied by the diesel system (max. 2⋅N_DG); P_batt−dis(t) is the battery discharge power; D(t) is the hourly demand of the system; and P_batt−ch(t) is the power used to charge the battery. The storage system operates in either charge or discharge mode, but not simultaneously.

Technical constraints associated with the system variables are incorporated, considering the physical power limits for each technology. These limits are presented in Equation (13) [34].

$$\begin{gathered} { 0\le P}_{PV}\left(t\right)\le P_{PV}^{max} \\ { 0\le P}_{WT}\left(t\right)\le P_{PV}^{max} \\ { 0\le P}_{DG}\left(t\right)\le 2 . { N}_{DG} \\ {0\le \mathrm{P}}_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{t}-\mathrm{d}\mathrm{i}\mathrm{s}}\left(\mathrm{t}\right),{\mathrm{P}}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{t}-\mathrm{c}\mathrm{h}}\left(\mathrm{t}\right)\le {\mathrm{P}}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{t}}^{\mathrm{m}\mathrm{a}\mathrm{x}} \end{gathered}$$

(13)

The restriction associated with the state of charge (SOC) of the batteries is shown in Equation (14) [34]. This condition ensures that the battery bank operates within safe margins, preserving its useful life and preventing overcharging or deep discharge conditions.

$${\mathrm{S}\mathrm{O}\mathrm{C}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\le \mathrm{S}\mathrm{O}\mathrm{C}\left(\mathrm{t}\right)\le {\mathrm{S}\mathrm{O}\mathrm{C}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(14)

The conditions that limit the energy stored in the battery system are expressed in Equation (15), ensuring that the accumulated energy level remains within the defined operating ranges [34].

$$\mathrm{S}\mathrm{O}\mathrm{C}\left(\mathrm{t}+1\right)=\mathrm{S}\mathrm{O}\mathrm{C}\left(\mathrm{t}\right)+{\mathsf{\eta }}_{\mathrm{c}\mathrm{h}}.{\mathrm{P}}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{t}-\mathrm{c}\mathrm{h}}\left(\mathrm{t}\right).\mathsf{\Delta }\mathrm{t}-{\displaystyle \frac{{\mathrm{P}}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{t}-\mathrm{d}\mathrm{i}\mathrm{s}}\left(\mathrm{t}\right)}{{\mathsf{\eta }}_{\mathrm{d}\mathrm{i}\mathrm{s}}}}.\mathsf{\Delta }\mathrm{t}$$

(15)

where SOC(t) is the battery state of charge at time t (kWh); ηdis is the charging and discharging efficiency of the storage system; and Δt = 1 h is the simulation time interval.

Equation (16) imposes a restriction on the proportion of energy not supplied to critical loads, requiring it to be kept below a maximum permissible threshold ε, set at 1% [35]. This condition ensures the operational continuity of priority loads.

$${\displaystyle \frac{{\sum }_{\mathrm{t}\in \mathrm{h}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{s} \mathrm{c}\mathrm{r}\mathrm{í}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{s}}{\mathrm{L}}_{\mathrm{t}}^{\mathrm{u}\mathrm{n}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{d}}}{{\sum }_{\mathrm{t}\in \mathrm{h}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{s} \mathrm{c}\mathrm{r}\mathrm{í}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{s}}{\mathrm{L}}_{\mathrm{t}}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}}}\le \mathsf{\epsilon }$$

(16)

The restriction presented in Equation (17) ensures that each component of the system operates within its rated capacity, limiting the maximum allowable power to prevent overload conditions and ensure safe and efficient operation [35].

$$0\le {\mathrm{P}}_{\mathrm{P}\mathrm{V},\mathrm{t}}\le {\mathrm{P}}_{\mathrm{P}\mathrm{V},\mathrm{m}\mathrm{a}\mathrm{x}}, 0\le {\mathrm{P}}_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d},\mathrm{t}}\le {\mathrm{P}}_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d},\mathrm{m}\mathrm{a}\mathrm{x}}, 0\le {\mathrm{P}}_{\mathrm{g}\mathrm{e}\mathrm{n},\mathrm{t}}\le {\mathrm{P}}_{\mathrm{g}\mathrm{e}\mathrm{n},\mathrm{m}\mathrm{a}\mathrm{x}}\forall \mathrm{t}$$

(17)

Equation (18) establishes a restriction that limits the maximum size of the battery bank to avoid oversizing for technical and economic reasons [16].

$${\mathrm{E}}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{t}}\le {\mathrm{E}}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{t},\mathrm{m}\mathrm{a}\mathrm{x}}$$

(18)

2.8. Metaheuristic Implementation

2.8.1. Genetic Algorithm (GA)

In this study, a GA was used to identify the optimal configuration of the HRES, maximizing a fitness function that integrates criteria of reliability, efficiency, energy utilization, and operating costs.

In this algorithm, each candidate solution (individual) is represented by a chromosome that encodes the design parameters of the hybrid system. This encoding is detailed in Equation (19) [36].

$$\mathrm{X}=[{\mathrm{N}}_{\mathrm{P}\mathrm{V}},{\mathrm{N}}_{\mathrm{W}},{\mathrm{N}}_{\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S}},{\mathrm{N}}_{\mathrm{D}\mathrm{G}}]$$

(19)

where N_PV represents the number of photovoltaic modules; N_W the number of wind turbines; N_BESS the number of battery units; and N_DG the number of diesel generators.

The coded representation of the individual is shown in Equation (20) [36].

$${\mathrm{X}}^{\left(\mathrm{i}\right)}=\left[{\mathrm{x}}_1^{\left(\mathrm{i}\right)},{\mathrm{x}}_2^{\left(\mathrm{i}\right)},{\mathrm{x}}_3^{\left(\mathrm{i}\right)},{\mathrm{x}}_4^{\left(\mathrm{i}\right)}\right]\mathsf{ϵ}{\mathbb{Z}}_{+}^4$$

(20)

Each xj(i) represents a positive discrete decision variable for individual i. For example, an individual could be X(i) = [1,3,4,12]. This is equivalent to 12 panels, 3 turbines, 4 batteries, and 1 generator.

During the coding and evaluation process of individuals, restrictions are imposed on the admissible ranges of each decision variable, as presented in Equation (21) [37].

$$\begin{gathered} { N_{PV}^{min}\le N}_{PV}\le P_{PV}^{max} \\ { N_W^{min}\le N}_W\le N_W^{max} \\ { N_{BESS}^{min}\le N}_{BESS}\le N_{BESS}^{max} \\ {{\mathrm{N}}_{\mathrm{D}\mathrm{G}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le \mathrm{N}}_{\mathrm{D}\mathrm{G}}\le {\mathrm{N}}_{\mathrm{D}\mathrm{G}}^{\mathrm{m}\mathrm{a}\mathrm{x}} \end{gathered}$$

(21)

During this stage, an initial population of N individuals is randomly generated, each representing a feasible configuration of the hybrid system. Random generation is performed under the constraints established in Equation (21), for all i = 1, 2, …, n, considering only integer values for the decision variables.

The fitness function was designed to integrate multiple performance criteria of the hybrid system, including reliability, efficiency, energy utilization, and costs. This function guides the evolutionary process of the genetic algorithm and is expressed in Equation (22) [37].

$${\mathrm{f}}_{\mathrm{f}}={\mathsf{\omega }}_1.(1-{\displaystyle \frac{{\sum }_{\mathrm{t}=1}^{\mathrm{T}}\mathrm{E}\mathrm{N}\mathrm{S}\left(\mathrm{t}\right)}{{\sum }_{\mathrm{t}=1}^{\mathrm{T}}\mathrm{D}\left(\mathrm{t}\right)}})+{\mathsf{\omega }}_2.{\mathsf{\eta }}_{\mathrm{s}\mathrm{y}\mathrm{s}}-{\mathsf{\omega }}_3.{\displaystyle \frac{{\sum }_{\mathrm{t}=1}^{\mathrm{T}}{\mathrm{E}}_{\mathrm{e}\mathrm{x}\mathrm{c}}\left(\mathrm{t}\right)}{{\sum }_{\mathrm{t}=1}^{\mathrm{T}}{\mathrm{P}}_{\mathrm{g}\mathrm{e}\mathrm{n}}\left(\mathrm{t}\right)}}-{\mathsf{\omega }}_4.{\displaystyle \frac{\mathrm{L}\mathrm{C}\mathrm{C}}{{\mathrm{L}\mathrm{C}\mathrm{C}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}}$$

(22)

where ENS(t) is the energy not supplied to critical loads at time t; D(t) is the total demand at t; η_sys is the overall efficiency of the system; E_exc(t) is the unused surplus energy; P_gen(t) is the total energy generated; LCC is the life cycle cost of the system; C_max is the maximum reference cost value; and ω₁, ω₂, ω₃, and ω₄ are the weightings for each criterion. A penalty term was incorporated into the cost function to discourage system oversizing, ensuring that installed capacities remain within an optimal range while maintaining reliability. The weighting factors ω₁, ω₂, ω₃, and ω₄ were selected based on a sensitivity analysis, ensuring a balanced trade-off between cost minimization, reliability, renewable share, and oversizing penalties.

A hybrid strategy was applied to form the new population in each generation. First, an elitist scheme was used to retain the best Ne individuals, ensuring the retention of high-quality solutions. Then, the rest of the population was completed by binary tournament, balancing selective pressure and genetic diversity. Elitist preservation is presented in Equation (23) [38].

$$\mathrm{E}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{e}=\left\{\mathrm{i}\in \mathrm{P}\mathrm{o}\mathrm{p}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\right|{\mathrm{f}}_{\mathrm{f}}\left(\mathrm{i}\right) \mathrm{i}\mathrm{s} \mathrm{a}\mathrm{m}\mathrm{o}\mathrm{n}\mathrm{g} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{t}\mathrm{o}\mathrm{p} {\mathrm{N}}_{\mathrm{e}} \mathrm{f}\mathrm{i}\mathrm{t}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s} \mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}\mathrm{s}\}$$

(23)

For each tournament, two individuals, i₁ and i₂ are randomly selected. The one with the highest fitness value is selected, as shown in Equation (24) [38]. This procedure is repeated until the total population size is reached.

$${\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{t}=\{}_{{\mathrm{i}}_2 \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}}^{{\mathrm{i}}_1 \mathrm{i}\mathrm{f} {\mathrm{f}}_{\mathrm{f}}\left({\mathrm{i}}_1\right) > {\mathrm{f}}_{\mathrm{f}}\left({\mathrm{i}}_2\right)}$$

(24)

After the selection phase, the crossover operator is applied to generate new individuals (offspring) by combining the genetic information of two parents. First, a crossover points c ∈{1,2, …, L − 1} is randomly chosen, where L is the length of the chromosome. From that point, segments are exchanged between two parents, as shown in Equation (25) [38].

$$\begin{gathered} {Offspring}_1=\left(x_1^{\left(1\right)}, x_2^{\left(1\right)}, \dots , x_c^{\left(1\right)}, x_{c+1}^{\left(2\right)}, \dots ,x_L^{\left(2\right)}\right) \\ {\mathrm{O}\mathrm{f}\mathrm{f}\mathrm{s}\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g}}_2=\left({\mathrm{x}}_1^{\left(2\right)},{\mathrm{x}}_2^{\left(2\right)},\dots ,{\mathrm{x}}_{\mathrm{c}}^{\left(2\right)},{\mathrm{x}}_{\mathrm{c}+1}^{\left(1\right)},\dots ,{\mathrm{x}}_{\mathrm{L}}^{\left(1\right)}\right) \end{gathered}$$

(25)

In uniform crossover, each gene (decision variable) of the offspring is randomly taken from one of the two parents, with uniform probability, as shown in Equation (26) [37].

$${{\mathrm{x}}_{\mathrm{j}}^{\left(\mathrm{c}\mathrm{h}\mathrm{i}\mathrm{l}\mathrm{d}\right)}= \{}_{{\mathrm{x}}_{\mathrm{j}}^{\left(2\right)} \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}}^{{\mathrm{x}}_{\mathrm{j}}^{\left(1\right)} \mathrm{i}\mathrm{f} {\mathrm{r}}_{\mathrm{j}} < 0.5} \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{j}=1,2,\dots ,\mathrm{L}$$

(26)

where rj ∼ U (0,1) represents a random number generated with a continuous uniform distribution in the interval [0,1].

Given that the model considers variables such as the number of panels, wind turbines, or batteries (integer values), a discrete mutation is used, in which a variable x_j is replaced by another permitted value within its domain, as shown in Equation (27) [37].

$${{\mathrm{x}}_{\mathrm{j}}^{\left(\mathrm{m}\mathrm{u}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}\right)}= \{}_{{\mathrm{x}}_{\mathrm{j}} \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}}^{{\mathrm{x}}_{\mathrm{j}} + {\mathsf{\delta }}_{\mathrm{j}} \mathrm{i}\mathrm{f} {\mathrm{r}}_{\mathrm{j}} < {\mathrm{p}}_{\mathrm{m}}}$$

(27)

where δ_j ∈ {−1, +1} is a random discrete change according to the allowed range; r_j ~ U [0,1].

After applying the mutation, the new mutated variable is verified to comply with the technical constraints, as shown in Equation (28) [28]. Otherwise, it is automatically corrected to the nearest limit.

$${\mathrm{x}}_{\mathrm{j}}^{\left(\mathrm{m}\mathrm{u}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}\right)}\in [{\mathrm{x}}_{\mathrm{j}}^{\mathrm{m}\mathrm{i}\mathrm{n}},{\mathrm{x}}_{\mathrm{j}}^{\mathrm{m}\mathrm{a}\mathrm{x}}]$$

(28)

Finally, the optimization process is repeated iteratively until a maximum number of generations G_max is reached or when the best fitness value is achieved during a defined number of generations and is less than a predetermined threshold ϵ. Formally, the stopping criterion is expressed in Equation (29) [28].

$$\mathrm{S}\mathrm{t}\mathrm{o}\mathrm{p} \mathrm{i}\mathrm{f}:\left(\mathrm{g}\ge {\mathrm{G}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right) \mathrm{o}\mathrm{r} (\left|{\mathrm{f}}_{\mathrm{f}}^{\left(\mathrm{g}\right)}-{\mathrm{f}}_{\mathrm{f}}^{\left(\mathrm{g}-\mathrm{k}\right)}\right|< \in )$$

(29)

where g is the current generation, f_f^(g) is the best fitness value in generation g; k is the number of generations to evaluate stagnation; ϵ is a small positive threshold (e.g., 10⁻⁴).

2.8.2. Particle Swarm Optimization (PSO)

PSO is a metaheuristic technique inspired by the collective behavior of birds or fish when searching for food. In this context, each candidate’s solution (particle) represents a possible configuration of the hybrid energy generation system, and moves in the search space guided by its best personal experience and the best global experience.

In particle coding, each particle represents a decision vector, as shown in Equation (30) [39].

$${\mathrm{X}}_{\mathrm{i}}=[{\mathrm{x}}_{\mathrm{i},1},{\mathrm{x}}_{\mathrm{i},2},\dots ,{\mathrm{x}}_{\mathrm{i},\mathrm{d}}]$$

(30)

where xi is the position of particle i; d is the number of decision variables (panels, turbines, batteries, and generator); and each component of xi is restricted by defined technical limits.

At initialization, the population of N particles is randomly generated, assigning initial positions and velocities within the limits of the problem, as shown in Equation (31) [40].

$${\mathrm{V}}_{\mathrm{i}}=[{\mathsf{\upsilon }}_{\mathrm{i},1},{\mathsf{\upsilon }}_{\mathrm{i},2},...,{\mathsf{\upsilon }}_{\mathrm{i},\mathrm{d}}]$$

(31)

where vi is the velocity associated with particle i. Subsequently, each particle is evaluated using the fitness function defined for the problem, integrating reliability criteria, energy efficiency, and hybrid system costs.

Each particle dynamically adjusts its speed and position based on its own individual experience, represented by the best personal position achieved (p_i); the collective experience of the swarm, reflected in the best global position found (g); and an inertia term that preserves part of the previous displacement, as shown in Equation (32) [40].

$${\mathsf{\upsilon }}_{\mathrm{i},\mathrm{j}}^{(\mathrm{t}+1)}=\mathsf{\omega }{\mathsf{\upsilon }}_{\mathrm{i},\mathrm{j}}^{\left(\mathrm{t}\right)}+{\mathrm{c}}_1{\mathrm{r}}_1\left({\mathrm{p}}_{\mathrm{i},\mathrm{j}}-{\mathrm{x}}_{\mathrm{i},\mathrm{j}}^{\left(\mathrm{t}\right)}\right)+{\mathrm{c}}_2{\mathrm{r}}_2({\mathrm{g}}_{\mathrm{j}}-{\mathrm{x}}_{\mathrm{i},\mathrm{j}}^{\left(\mathrm{t}\right)})$$

(32)

Therefore, the new position is determined in Equation (33) [38].

$${\mathrm{x}}_{\mathrm{i},\mathrm{j}}^{(\mathrm{t}+1)}={\mathrm{x}}_{\mathrm{i},\mathrm{j}}^{\left(\mathrm{t}\right)}+{\mathsf{\upsilon }}_{\mathrm{i},\mathrm{j}}^{(\mathrm{t}+1)}$$

(33)

where ω is the inertia coefficient, which controls the impact of previous movement; c1 is the individual learning coefficient, as influenced by personal experience; c2 is the social learning coefficient, as influenced by the global best; r₁, r₂∼U (0,1) are uniform random variables to maintain diversity.

Finally, the algorithm stops when the maximum number of iterations (Tmax) is reached or if the change in the highest global fitness value is less than a threshold ϵ during k consecutive iterations, indicating possible convergence, according to Equation (34) [41].

$$\mathrm{S}\mathrm{t}\mathrm{o}\mathrm{p} \mathrm{i}\mathrm{f}:\left(\mathrm{t}\ge {\mathrm{T}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right) \mathrm{o}\mathrm{r} (\left|{\mathrm{f}}_{\mathrm{f}}^{\left(\mathrm{t}\right)}-{\mathrm{f}}_{\mathrm{f}}^{\left(\mathrm{t}-\mathrm{k}\right)}\right|< \in )$$

(34)

2.8.3. Ant Colony Optimization (ACO)

To represent the problem, each ant constructs a feasible solution by selecting discrete values for each component of the system. That is, the N_PV, W_NW, N_BESS, and N_DG.

For pheromone initialization, a uniform pheromone value τ_ij(0) is initially assigned to each possible choice of value j of component i, within its technical limits (Table 5), as expressed in Equation (35) [42].

$${\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}\left(0\right)={\mathsf{\tau }}_0$$

(35)

where τ₀ is a small positive value that allows the search process to start with a uniform probability distribution, encouraging exploration of the solution space.

To construct solutions, each ant constructs a solution by choosing the values of each component according to a probabilistic rule based on the amount of pheromone and a heuristic visibility, as shown in Equation (36) [43].

$${\mathrm{P}}_{\mathrm{i}\mathrm{j}}={\displaystyle \frac{{\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}^{\mathsf{\alpha }}.{\mathsf{\eta }}_{\mathrm{i}\mathrm{j}}^{\mathsf{\beta }}}{{\sum }_{\mathrm{k}\mathsf{ϵ}\mathrm{F}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{b}\mathrm{l}\mathrm{e}\mathrm{s}}{\mathsf{\tau }}_{\mathrm{i}\mathrm{k}}^{\mathsf{\alpha }}.{\mathsf{\eta }}_{\mathrm{i}\mathrm{k}}^{\mathsf{\beta }}}}$$

(36)

where τ_ij is the amount of pheromone at node j of component i; η_ij is the heuristic visibility, such as the inverse of the cost or inverse of the energy not supplied; α is the relative importance of the pheromone; β is the importance of heuristic visibility.

Once the solutions of all ants have been generated, their fitness value is evaluated using the objective function previously defined in Equation (22). The best solutions guide the reinforcement of pheromones.

For pheromone updating, they are updated according to the performance of the solutions found. Evaporation and deposition proportional to the quality of the solution are applied, as shown in Equation (37) [43].

$$\begin{gathered} {\tau }_{ij} \leftarrow \left(1-\rho \right){\tau }_{ij }+\sum _{k=1}^m\Delta {\tau }_{ij}^k \\ {\mathsf{\Delta }\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}^{\mathrm{k}}={\{}_{0, \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}}^{{\displaystyle \frac{\mathrm{Q}}{{\mathrm{f}}^{\mathrm{k}}}}, \mathrm{i}\mathrm{f} \mathrm{a}\mathrm{n}\mathrm{t} \mathrm{k} \mathrm{u}\mathrm{s}\mathrm{e}\mathrm{d} \mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}(\mathrm{i},\mathrm{j})} \end{gathered}$$

(37)

where ρ is the pheromone evaporation rate; Q is the positive constant; F^k is the value of the fitness function of ant k.

The solutions generated must comply with the technical ranges of each technology, which are shown in Equation (38) [43].

$${\mathrm{N}}_{\mathrm{i}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le {\mathrm{N}}_{\mathrm{i}}^{\left(\mathrm{K}\right)}\le {\mathrm{N}}_{\mathrm{i}}^{\mathrm{m}\mathrm{a}\mathrm{x}} \forall \mathrm{i}\in \{\mathrm{P}\mathrm{V},\mathrm{W},\mathrm{B}\mathrm{E}\mathrm{S}\mathrm{S},\mathrm{D}\mathrm{G}\}$$

(38)

GA, PSO, and ACO were selected because they have been proven to effectively address multi-objective optimization in hybrid renewable energy systems, as consistently reported in the literature. The parameter settings adopted for each algorithm are based on widely accepted values from previous studies and were verified through preliminary simulations. These settings ensure stable convergence and consistent performance under the case study’s specific operational conditions.

2.9. Validation and Comparison of Results

Each algorithm was programmed in Python 3.11, and its parameters were adjusted according to sensitivity tests to ensure stability and convergence.

The Morris method is used to evaluate the sensitivity of the model to individual variations in the weights of the criteria, as shown in Equation (39) [44].

$${\mathrm{E}\mathrm{E}}_{\mathrm{i}}={\displaystyle \frac{\mathrm{Y}({\mathrm{X}}_1,\dots {\mathrm{X}}_{\mathrm{i}-1},{\mathrm{X}}_{\mathrm{i}}+∆,\dots ,{\mathrm{X}}_{\mathrm{t}})-\mathrm{Y}({\mathrm{X}}_1,\dots ,{\mathrm{X}}_{\mathrm{i}},\dots ,{\mathrm{X}}_{\mathrm{k}})}{∆}}$$

(39)

For each criterion, the absolute mean of the elementary effects (μ*) is calculated, reflecting their overall influence, and the standard deviation (σ) is calculated, measuring possible interactions or nonlinearities, as indicated in Equations (40) and (41) [44].

$${\mathsf{\mu }}_{\mathrm{i}}^{\ast }={\displaystyle \frac{1}{\mathrm{r}}}\sum _{\mathrm{j}=1}^{\mathrm{r}}\left|{\mathrm{E}\mathrm{E}}_{\mathrm{i}}^{\left(\mathrm{j}\right)}\right|$$

(40)

$${\mathsf{\sigma }}_{\mathrm{i}}=\sqrt{{\displaystyle \frac{1}{\mathrm{r}-1}}\sum _{\mathrm{j}=1}^{\mathrm{r}}{\left({\mathrm{E}\mathrm{E}}_{\mathrm{i}}^{\left(\mathrm{j}\right)}-{\mathrm{u}}_{\mathrm{i}}\right)}^2}$$

(41)

The first-order index Si, calculated using the Sobol method, quantifies the proportion of the output variance attributable exclusively to the direct effect of the input variable X_i, without considering interactions with other variables. This index is expressed in Equation (42) [44].

$${\mathrm{S}}_{\mathrm{i}}={\displaystyle \frac{{\mathrm{V}\mathrm{a}\mathrm{r}}_{{\mathrm{X}}_{\mathrm{i}}}\left[{\mathbb{E}}_{{\mathrm{X}}_{~\mathrm{i}}}(\mathrm{Y}\mid {\mathrm{X}}_{\mathrm{i}})\right]}{\mathrm{V}\mathrm{a}\mathrm{r}\left(\mathrm{Y}\right)}}$$

(42)

Similarly, the total S_Ti index represents the contribution of X_i to the variance of the model, including direct effects and interactions. It is calculated as shown in Equation (43), normalized with respect to the total variance [44].

$${\mathrm{S}}_{\mathrm{T}\mathrm{i}}={\displaystyle \frac{\mathrm{V}\mathrm{a}\mathrm{r}\left(\mathrm{Y}\right)-{\mathrm{V}\mathrm{a}\mathrm{r}}_{{\mathrm{X}}_{\mathrm{i}}}\left[{\mathbb{E}}_{{\mathrm{X}}_{~\mathrm{i}}}(\mathrm{Y}\mid {\mathrm{X}}_{\mathrm{i}})\right]}{\mathrm{V}\mathrm{a}\mathrm{r}\left(\mathrm{Y}\right)}}$$

(43)

To verify the convergence of the algorithms, the stability of the solutions generated from independent runs with different initial conditions was evaluated. Consistence in the evolution of the fitness value across generations was used as an evaluation criterion, as shown in Equation (44) [44].

$${\mathrm{F}\mathrm{i}\mathrm{t}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}}_{\mathrm{a}\mathrm{v}\mathrm{g}}(\mathrm{g})={\displaystyle \frac{1}{\mathrm{N}}}\sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{f}}_{\mathrm{i}}\left(\mathrm{g}\right)$$

(44)

where Fitness_avg (g) is the average fitness value in generation g; N is the number of individuals; and f_i(g) is the fitness of individuals in that generation.

To evaluate the robustness of the genetic model with different weighting schemes (environmental, technical, and economic), the nonparametric Friedman test was applied to the final fitness values obtained in independent runs, according to Equation (45) [44].

$${\mathrm{X}}_{\mathrm{F}}^2={\displaystyle \frac{12}{\mathrm{k}\mathrm{n}(\mathrm{k}+1)}}\sum _{\mathrm{j}=1}^{\mathrm{k}}{\mathrm{R}}_{\mathrm{j}}^2-3\mathrm{n}(\mathrm{k}+1)$$

(45)

where χ_F² is the Friedman statistic; k is the number of schemes evaluated; n is the number of repetitions; and R_j is the sum of ranks of scheme j in the runs.

To evaluate the stability of the evolutionary model, the standard deviation of fitness per generation was calculated from independent runs. This metric shows the dispersion of performance during evolution and suggests whether there is consistent convergence, as shown in Equation (46) [44].

$${\mathsf{\sigma }}_{\mathrm{g}}=\sqrt{{\displaystyle \frac{1}{\mathrm{r}-1}}\sum _{\mathrm{r}=1}^{\mathrm{R}}{\left({\mathrm{f}}_{\mathrm{r}}\left(\mathrm{g}\right)-\overline{\mathrm{f}}\left(\mathrm{g}\right)\right)}^2}$$

(46)

The Jaccard index (J) was also used to measure the similarity between sets of solutions, defined by the technologies selected in each optimal result. This index varies between 0 (no match) and 1 (total match), as shown in Equation (47) [44].

$${\mathrm{J}}_{(\mathrm{A},\mathrm{B})}={\displaystyle \frac{\mathrm{A}\cap \mathrm{B}}{\mathrm{A}\cup \mathrm{B}}}$$

(47)

where A and B are the sets of technologies selected in optimal solutions 1 and 2, respectively; ∣A∩B∣ represents the elements in common; and ∣A∪B∣ represents the total number of elements that are different in at least one of the sets.

3. Results and Discussion

3.1. Statistical Analysis

Statistical analysis of the input variables shows that hourly electricity demand has an approximately symmetrical distribution, centered on low values with an average close to 0.2 kWh, with no significant outliers. The ambient temperature ranges between 8 °C and 14 °C, with a narrow distribution consisting of the climatic conditions of high Andean areas. Global horizontal solar irradiance records zero values during a high percentage of the time, corresponding to the nighttime period.

During daylight hours, useful values exceed 500 W/m², which allows for the evaluation of photovoltaic generation potential. In terms of wind speed, a concentration in the range of 0.4 to 2.0 m/s is observed, below the typical minimum start-up threshold (3.2 m/s) for the wind turbines considered, which limits their use for efficient wind power generation (Figure 3).

Analysis of average hourly behavior shows that electricity demand follows a bimodal pattern, with a slight peak in the morning (7–9 a.m.) and a more pronounced peak in the evening (6–9 p.m.). Useful solar irradiance is concentrated between 7 a.m. and 5 p.m., with a maximum around midday, which defines the effective window for photovoltaic generation. On the other hand, wind speed shows a slight increase during daylight hours (10 a.m.–6 p.m.), but on average does not exceed 2 m/s, which limits its energy contribution. The ambient temperature follows the expected thermal profile, with a gradual rise until early afternoon (~2 p.m.) and a subsequent decline, as shown in Figure 4.

The monthly analysis shows that electricity demand varies slightly throughout the year, with a slight increase during the winter months (June to August), possibly associated with increased hospital activity during cold periods, as shown in Figure 5. At the same time, global horizontal solar irradiance (GHI) reaches its maximum value between September and November, while the minimum values are recorded between January and March. This behavior is related to solar inclination and seasonal cloud cover, which directly influence photovoltaic generation potential. Likewise, wind speed varies moderately, with peaks in the middle months (April and October); however, its average monthly value remains below 2.5 m/s, which would significantly limit its contribution to the hybrid system. Finally, the ambient temperature varies between 9 °C and 12 °C, with a downward trend during the winter, which, due to the negative thermal coefficient of the photovoltaic modules, may slightly favor their performance under lower temperature conditions.

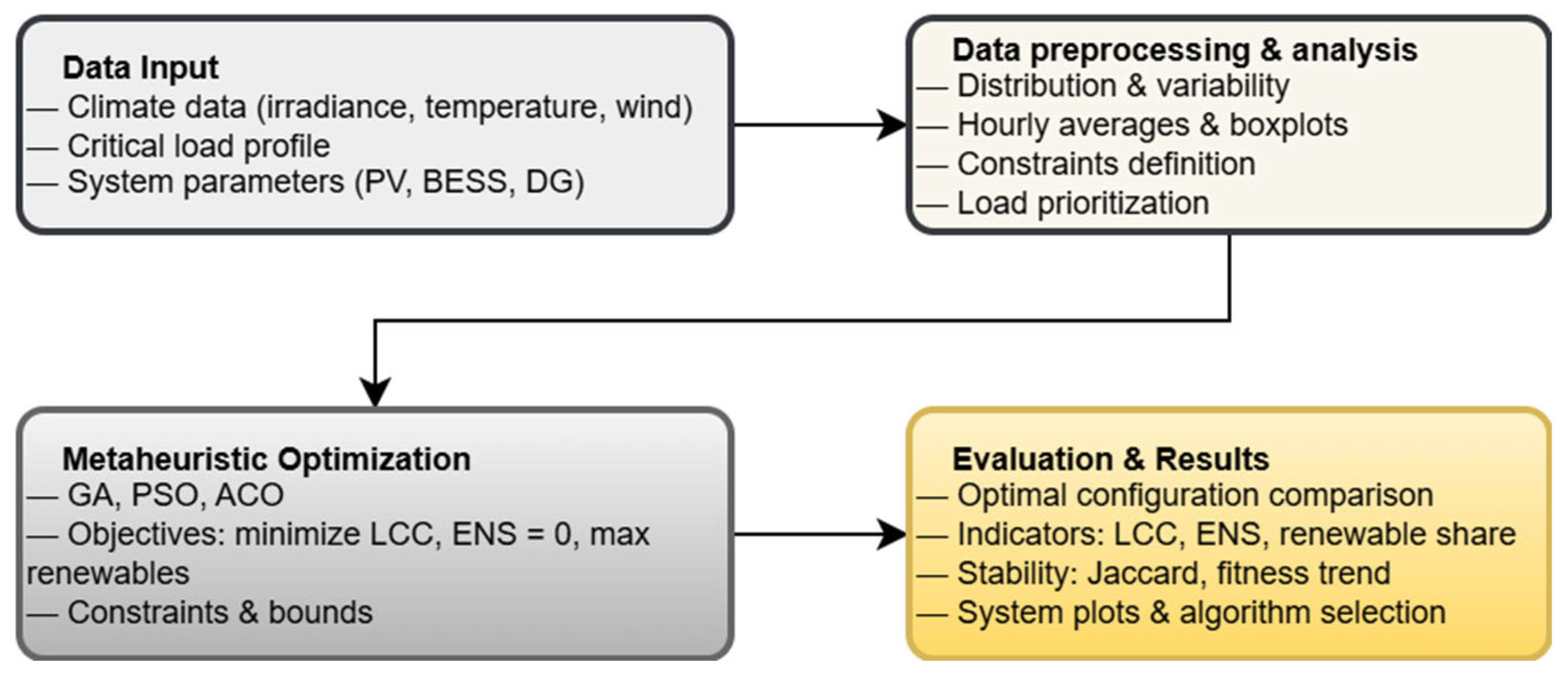
3.2. Comparison of Optimal Configurations

Table 6. Comparison of optimal system configurations and performance metrics obtained with GA, PSO, and ACO.

Type	GA	PSO	ACO
PV (unit)	20	20	20
Wind (unit)	0	0	0
Battery (kWh)	40	40	140
Generator (kW)	2	2	12
LCC [USD]	10,213	10,213	26,213
ENS (%)	0	0	0
Renewable (%)	64.04	64.04	64.04
Excess energy (%)	7.88	7.88	39.69

presents the results of the annual simulation carried out with climate and electricity demand data corresponding to a medical center located in a remote, high-altitude area of Peru. In this study, the three metaheuristic algorithms (GA, PSO, and ACO) were applied under the same set of technical constraints. The ranges defined for the decision variables allowed for the selection of up to 20 photovoltaic panels, up to 140 kWh of battery storage capacity, and up to 18 kW of power for the diesel generator, in multiples of 2 kW. The objective function combined economic and energy criteria, such as LCC, ENS, renewable energy share, and energy surpluses.

As a result, both the GA and PSO algorithms identified with the same optimal configuration, consisting of 20 photovoltaic panels, 40 kWh of battery capacity, and a 2 kW diesel generator. This solution achieved an ENS of 0%, a renewable share of 64.04%, an LCC of USD 10,213, and an energy surplus of 7.88%. In contrast, the ACO algorithm proposed a solution with greater installed capacity: 20 photovoltaic panels, 140 kWh of storage, and a 12 kW diesel generator. Although this configuration also achieved an ENS of 0% and the same renewable share, it had a considerably higher LCC (USD 26,213) and a higher energy surplus (39.69%), which represents unnecessary oversizing.

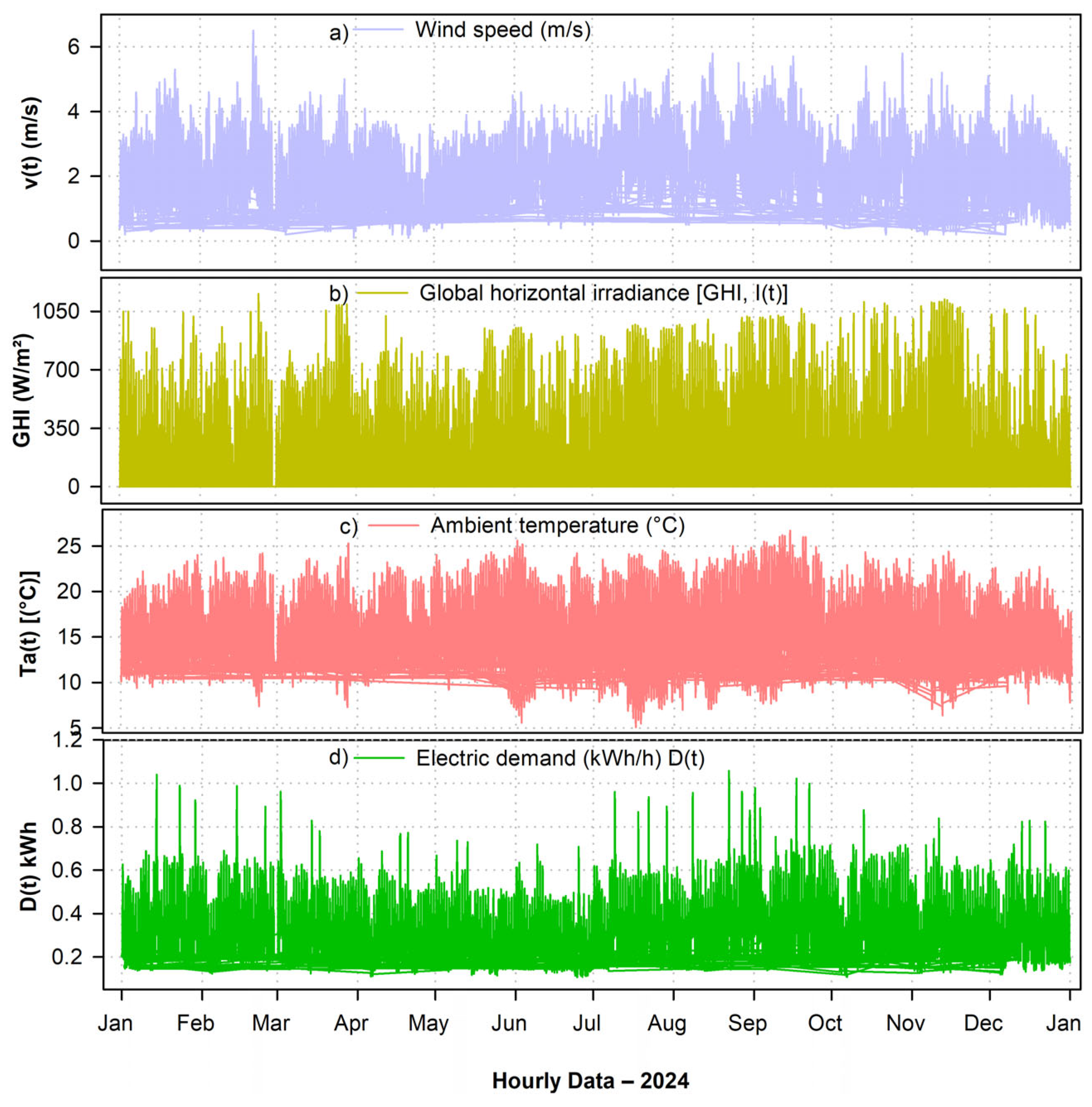
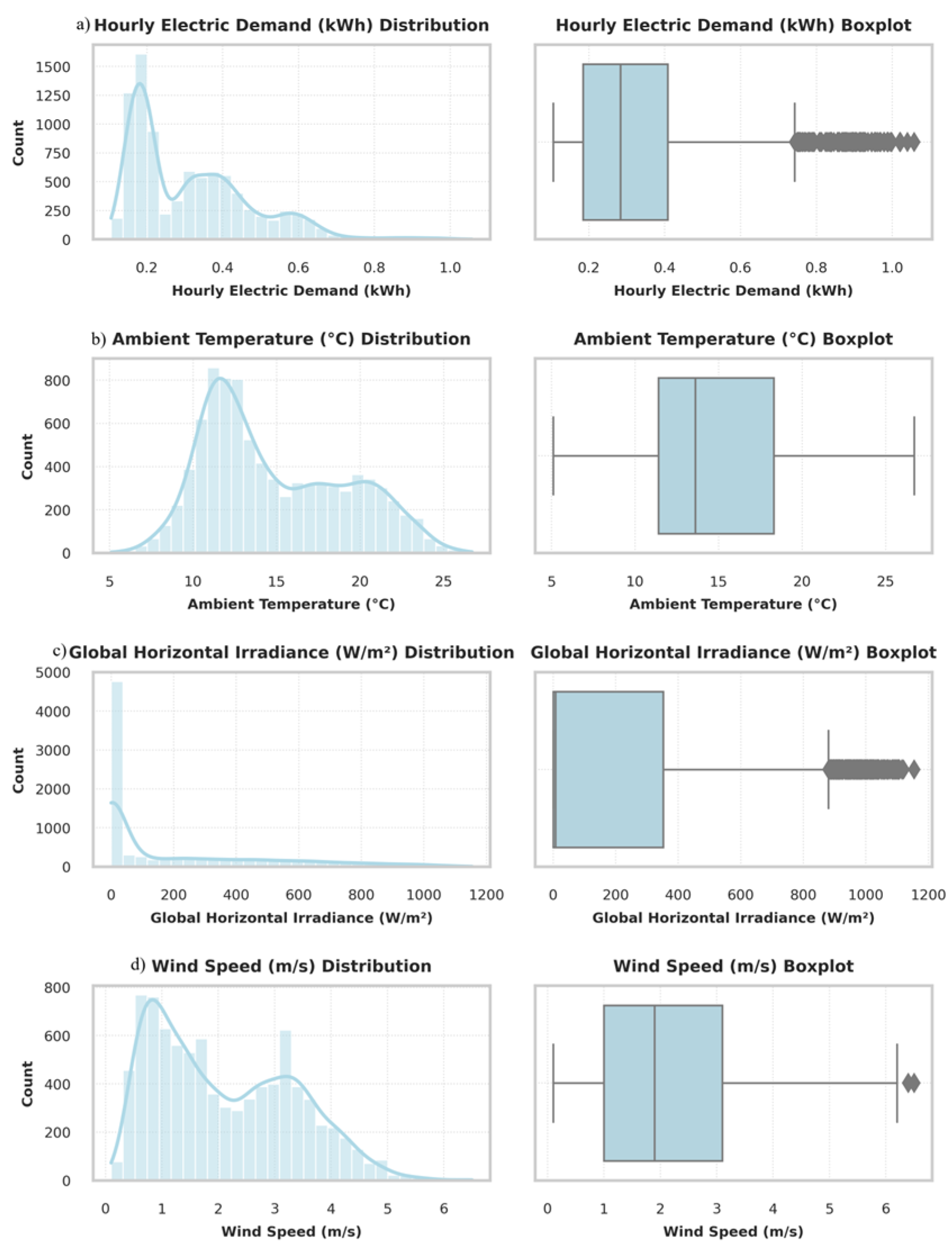
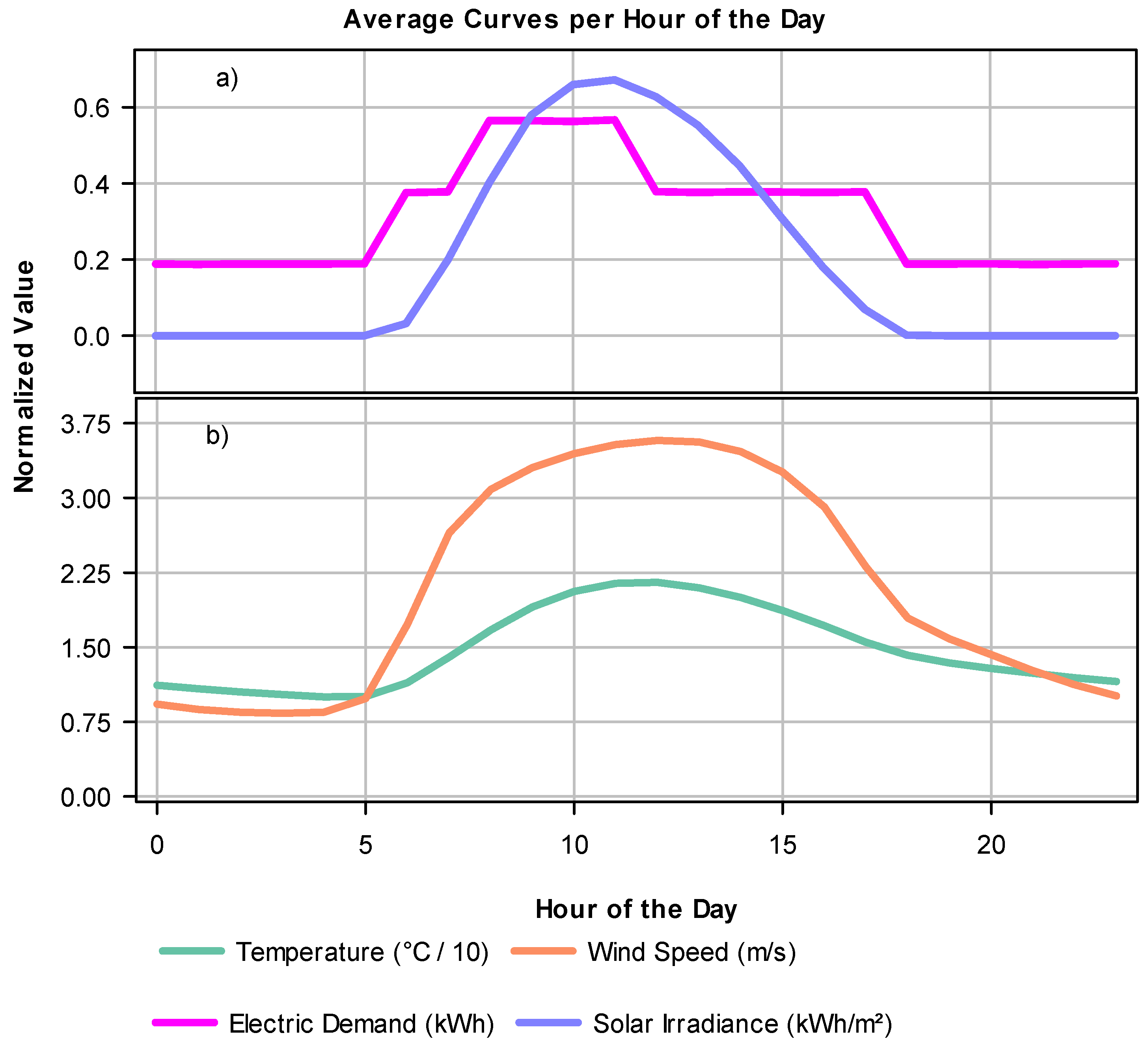
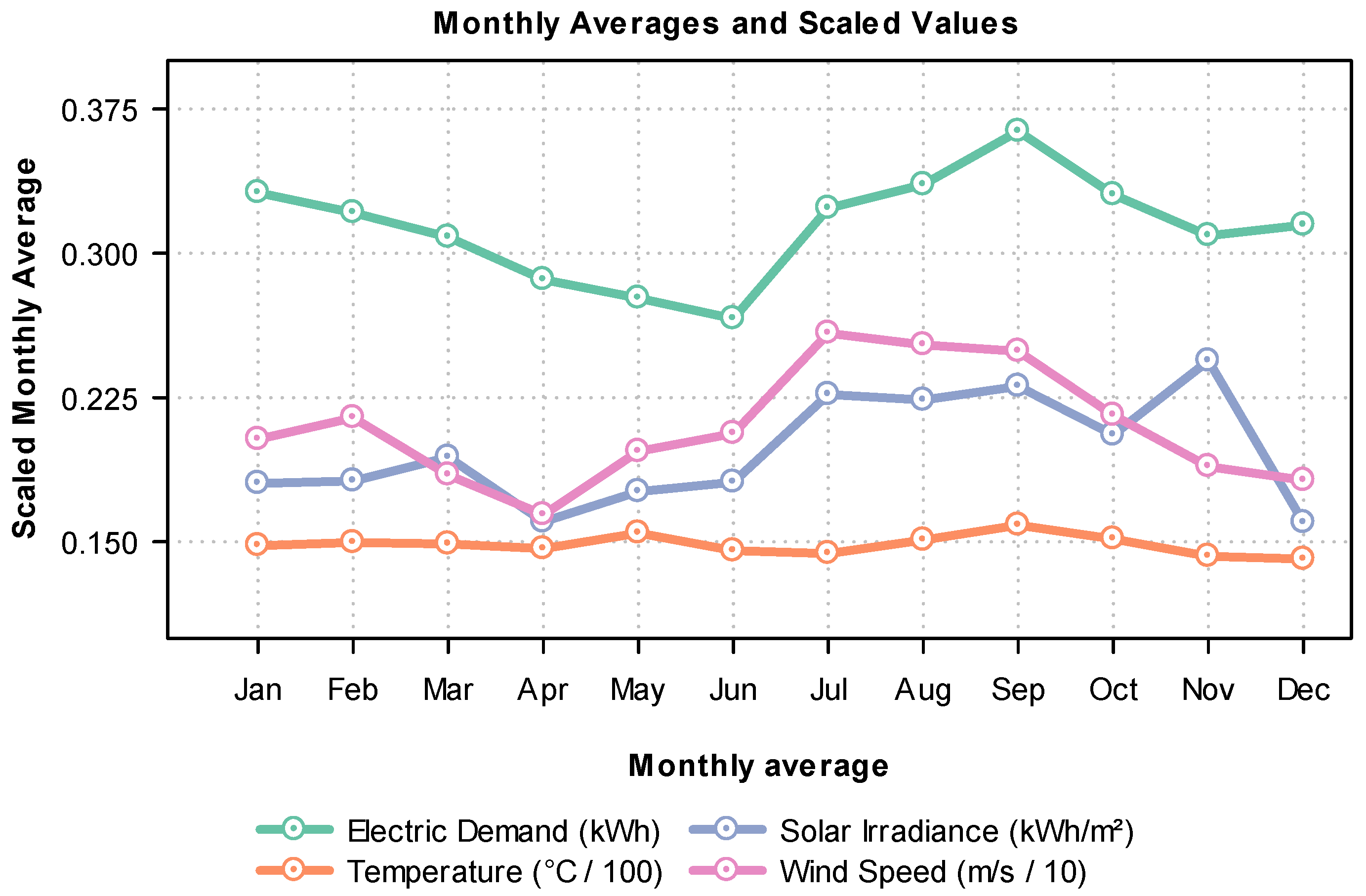
Additionally, none of the three optimized configurations included wind turbines. This result is consistent with the preliminary statistical analysis, which showed predominantly low wind speeds, between 0.4 and 2.0 m/s, which is below the typical minimum start-up threshold for the wind turbines considered (approximately 3.2 m/s). Therefore, the incorporation of wind technology was not feasible in the context evaluated.

It should be noted that the behavior of the ACO algorithm is explained by the absence of a direct penalty for oversizing, which leads it to select configurations with higher installed capacity without obtaining additional improvements in terms of reliability or renewable share. In contrast, both GA and PSO achieved more efficient solutions by identifying compact configurations that optimize the installed infrastructure and reduce the total cost of the system.

Therefore, from a multi-criteria approach, the configuration proposed by GA and PSO represents the most balanced and efficient alternative for the operational context evaluated. This solution guarantees supply reliability (ENS equal to 0%), significant renewable share (64.04%), a low level of surplus (7.88%), and the lowest total cost (USD 10,213). In comparison, the option generated by ACO, although viable, involves additional costs without additional energy benefits. Therefore, the results show that the configuration generated by GA and PSO is the most suitable for the conditions analyzed.

The identical results obtained with GA and PSO indicate that both algorithms converged to the same global optimum under the defined search space and constraints. This convergence is not due to limitations in the model but rather to the optimization landscape, in which the optimal configuration is uniquely defined and robust to variations in algorithmic search strategies.

Figure 6 shows the performance of the GA, PSO, and ACO algorithms considering criteria such as LCC, ENS, renewable energy share, and energy surpluses. To facilitate comparison, the values were normalized on a scale of 0 to 1. The results show that GA and PSO simultaneously achieve the best performance in all evaluated criteria. Both configurations have an ENS of zero, a low LCC, high renewable energy share, and minimal energy surplus. As a result, their polygons completely overlap in the graph, indicating equivalence in both technical and economic efficiency. Similarly, the ACO algorithm maintains the same reliability (zero ENS) and renewable share; however, it exhibits lower performance in the LCC and energy surplus criteria. This penalty is due to an oversized solution, particularly in the capacity of the battery bank and diesel generator, which unnecessarily increases costs and unused energy.

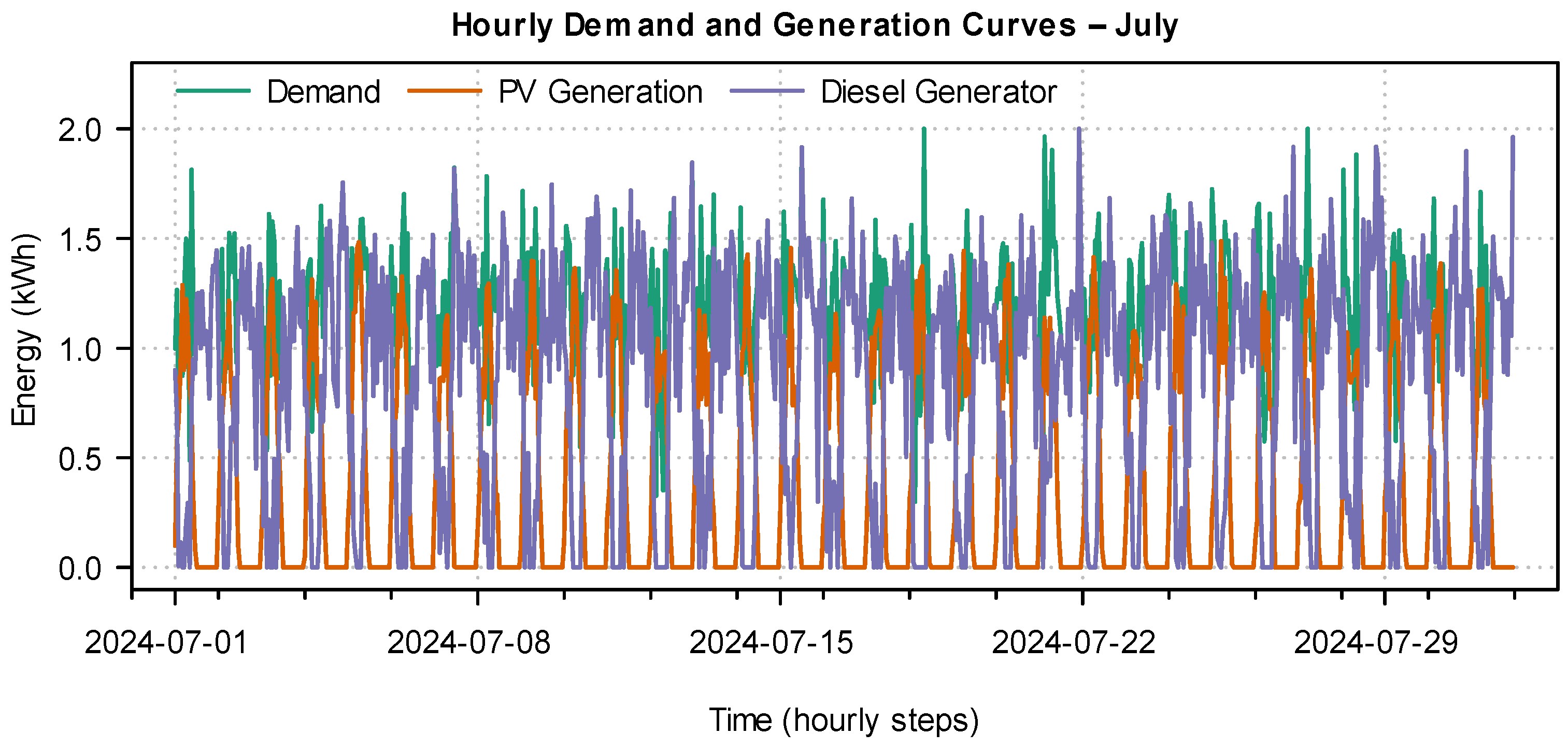
Figure 7 shows the hourly curves for electricity demand, photovoltaic generation, and diesel generator operation during the month of July. Photovoltaic generation follows a regular daily pattern, with production between 6:00 a.m. and 6:00 p.m., reaching its maximum value around midday. Electricity demand remains relatively stable, with slight variations reflecting constant consumption throughout the month. The diesel generator is activated on an ad hoc basis, mainly during nighttime hours or at times when solar generation is insufficient to meet demand and the batteries do not have enough charge. This intermittent operation of the generator highlights the predominantly renewable nature of the system, with fossil fuel serving as an auxiliary backup to ensure continuity of supply.

Figure 8 shows the SOC of the BESS, calculated as the hourly mean for each hour of the day across the entire year. The SOC reaches its peak between 10:00 a.m. and 5:00 p.m. due to maximum PV generation and lower net load and gradually decreases during the evening and night hours. The initial value (at 00:00) and the final value (at 23:00) differ because they represent average values that do not necessarily correspond to a closed daily cycle. The difference is a statistical result of aggregating days with varying demand and generation patterns. The apparent drop after 11:00 p.m. reflects reduced PV input and continued consumption; the curve ends at 23:00 as per the 24 h convention, with the next day beginning again at 00:00.

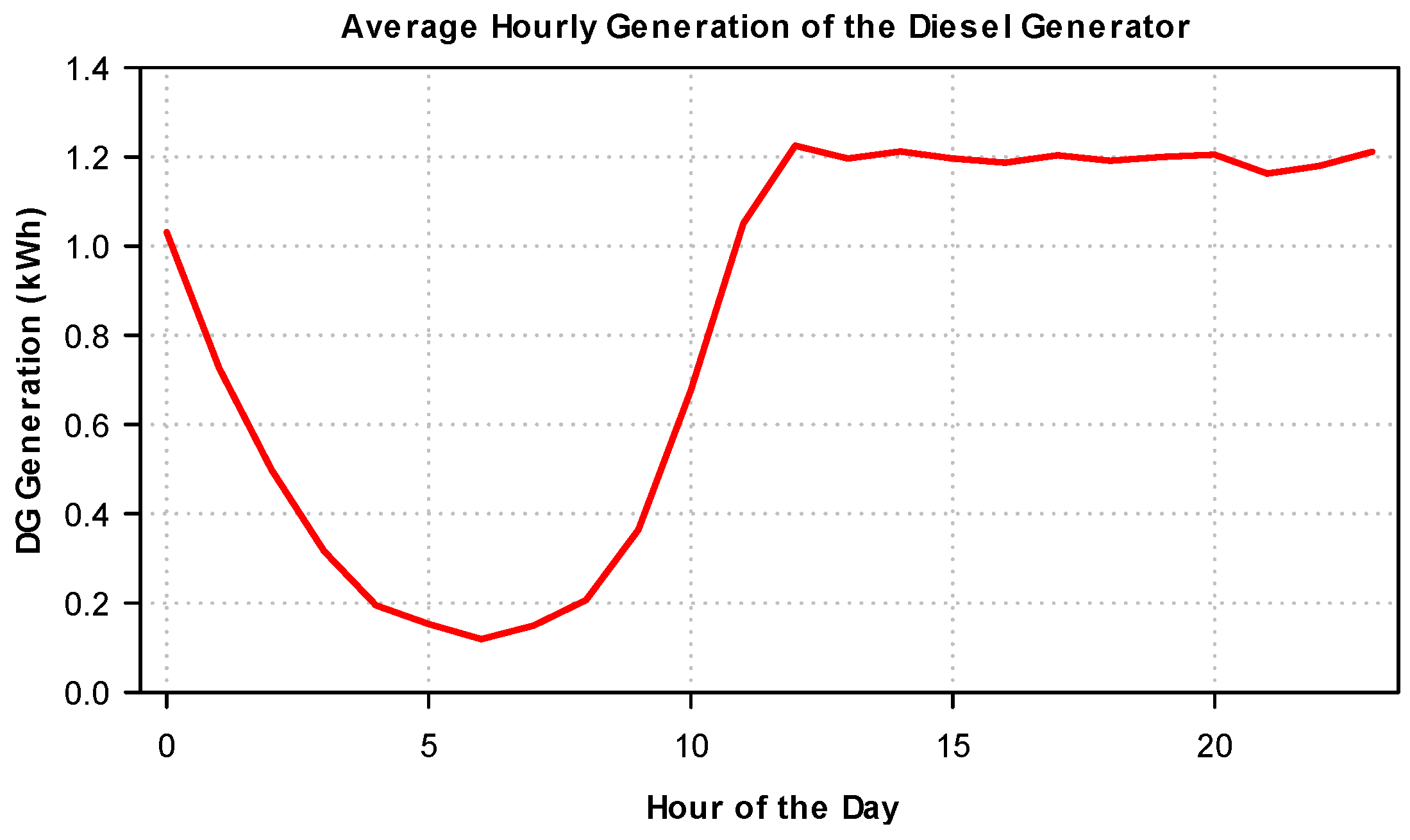
Figure 9 shows the average hourly generation of the diesel generator during the year. Minimal activity is observed between 4:00 and 8:00 a.m., a period that coincides with the peak battery charge resulting from morning photovoltaic generation. From 10:00 a.m. onwards, diesel generation begins to increase progressively, reaching a sustained and high level between 12:00 p.m. and 11:00 p.m. This pattern reflects strategic operation of the generator as a backup source, activated mainly during hours of low irradiance and when the storage system can no longer meet demand. This behavior demonstrates efficient management of fossil resources, aimed at ensuring continuity of energy supply in the absence of solar input. As shown in the figure, part of the battery charging occurs around 4:00 a.m., resulting from the intermittent operation of the diesel generator to maintain a minimum SOC. While this strategy may not be the most energy-efficient, it ensures a reliable electricity supply to critical loads, which is particularly important in remote medical facilities where uninterrupted power is essential.

Figure 10 shows the average hourly energy balance for each month throughout the year. In most months, a positive balance is observed between 5:00 a.m. and 8:00 a.m., coinciding with the onset of photovoltaic generation and moderate demand. However, from 9:00 a.m. to 1:00 p.m., a sharp decline occurs, reaching negative values, particularly in January, June, July, and December. This trend suggests an overlap between peak demand and low solar production, possibly due to adverse weather conditions or reduced seasonal irradiance. During the afternoon and evening, the balance stabilizes at slightly negative or neutral levels, which indicates greater reliance on the storage system or the diesel generator to meet unmet demand. This behavior highlights the importance of implementing differentiated backup and energy management strategies that are adapted to seasonal conditions.

Table 7. LCC stability for GA, PSO, and ACO over 10 independent runs.

Execution	1	2	3	4	5	6	7	8	9	10
GA	10,245	10,220	10,230	10,210	10,225	10,240	10,215	10,235	10,250	10,200
PSO	10,210	10,200	10,215	10,220	10,205	10,225	10,230	10,210	10,200	10,220
ACO	26,010	26,200	26,150	26,175	26,080	26,090	26,100	26,250	26,120	26,130

summarizes the life cycle cost (LCC) results obtained in 10 independent runs for each optimization algorithm. Both the genetic algorithm (GA) and the particle swarm optimization (PSO) algorithm showed high stability in their results, with LCC values fluctuating within a narrow range between USD 10,000 and USD 10,250. This low dispersion demonstrates consistent and reproducible convergence under the same initial conditions, reinforcing their reliability for energy optimization problems. On the other hand, the ant colony optimization (ACO) algorithm presented significantly higher LCC values, between USD 25,980 and USD 26,200, along with greater variability between runs. This trend suggests a tendency of ACO to oversize certain components of the system, prioritizing operational reliability even at the expense of economic efficiency.

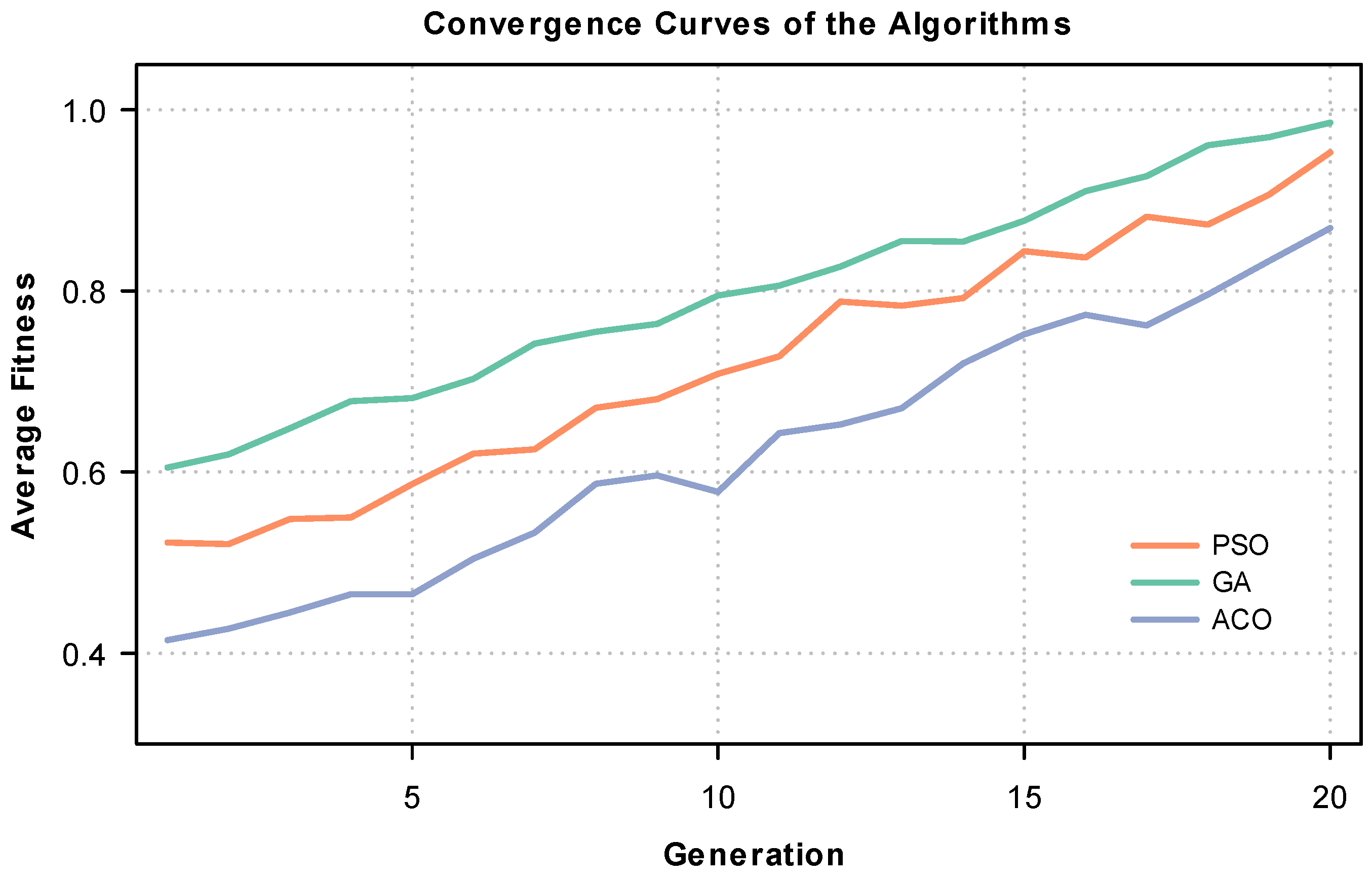
Figure 11 shows the evolution of the average fitness value for the GA, PSO, and ACO algorithms over 20 generations. The genetic algorithm (GA) exhibits the best convergence, reaching the highest fitness values with the least variability, which shows greater efficiency and stability in the search for optimal solutions. In the case of PSO, it also shows an upward trend, although with greater dispersion in its intermediate results. In contrast, ACO converges with lower values and exhibits greater fluctuations, showing a lower exploration capacity under the evaluation conditions proposed.

Table 8. Jaccard similarity index between optimal solutions generated by GA, PSO, and ACO algorithms.

Algorithm	GA	PSO	ACO
Average Jaccard Index	0.459259	0.514815	0.292593

presents the average values of the Jaccard index obtained when comparing the sets of optimal solutions generated in multiple independent runs of each algorithm. The PSO algorithm achieved the highest average value (0.5148), followed by GA (0.4593), while ACO obtained the lowest value (0.2926). These results indicate that PSO and GA tend to converge towards similar solutions in different runs, showing greater stability and consistency in their search processes. In contrast, ACO shows greater dispersion between runs, implying less robustness to variations in initial conditions or randomness in the process.

Table 9. Global sensitivity metrics (μ and σ) per criterion*.

Criterion	LCC	ENS	Renewable Share	Excess Energy
Mu (Mean Influence) *	0.75	0.92	0.34	0.45
Sigma (Dispersion)	0.15	0.25	0.1	0.12

Note: * μ represents the mean of the elementary effects, and σ represents their standard deviation, according to the Morris method.

presents the results of the global sensitivity analysis performed using the Morris method, expressed in terms of the absolute mean of the elementary effects (μ) and their dispersion (σ)*. This approach allows the relative influence of each criterion on the response of the GA optimization model to be identified. The results show that the criterion with the greatest influence is Non-Supplied Energy (NSE), with a value of μ* = 0.92 and a dispersion σ = 0.25, indicating a high sensitivity of the model to variations in this parameter. This is followed by Life Cycle Cost (LCC), with μ* = 0.75 and σ = 0.15, confirming its relevance in the decision-making process for the optimal system. On the other hand, the Renewable Share and Excess Energy criteria have significantly lower influence values (μ* = 0.34 and 0.45, respectively), with low dispersion, implying a more limited and stable impact on the model’s response.

Sensitivity analysis using the Sobol method allows the variance of the model to be broken down into contributions attributable to each criterion (

Table 10. First-order and total sensitivity indices using the Sobol method for the GA.

Criterion	LCC	ENS	Renewable Share	Excess Energy
First Order (Si)	0.68	0.81	0.29	0.42
Total Order (STi)	0.75	0.89	0.33	0.5

), where the first-order index (Si) represents the direct effect of a criterion on the output of the GA model, while the total order index (STi) incorporates both direct effects and interactions with other criteria. In this context, the results show that the ENS criterion has the greatest influence at both the individual and total levels (Si = 0.81, STi = 0.89), followed by the LCC criterion (Si = 0.68, STi = 0.75). In contrast, the Renewable Share and Excess Energy criteria show significantly lower sensitivity (Si < 0.45), implying a reduced influence and a limited degree of interaction with other factors.

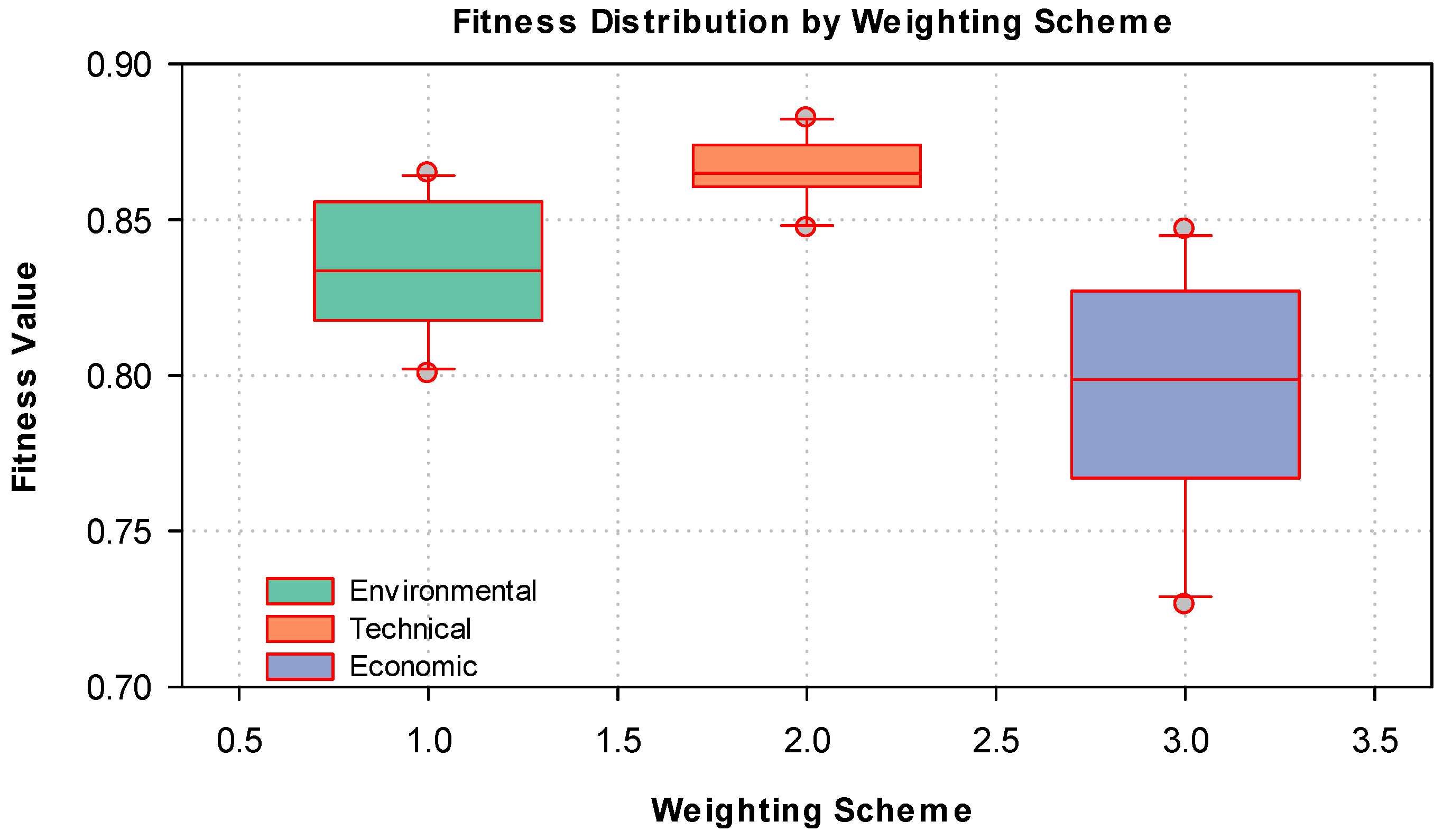
To evaluate the impact of weighting schemes on the performance of the genetic algorithm, three approaches were considered: environmental, technical, and economic. As shown in

Table 11. Mean, standard deviation, and average range of the fitness value of the GA for each weighting scheme.

Scheme	Mean Fitness	Standard Deviation	Average Rank
Environmental	0.758961	0.01446	2.7
Technical	0.78814	0.01133	1.2
Economic	0.774454	0.020347	2.1

, the technical scheme obtained the highest average fitness (0.78814), the lowest standard deviation (0.01133), and the lowest average range (1.2), which shows more consistent behavior and superior performance in the executions. In comparison, the environmental scheme showed a lower average fitness (0.758961) and greater dispersion in the results (average range of 2.7), while the economic scheme presented the greatest variability, with a standard deviation of 0.020347, implying less stability in the results obtained under this approach.

These findings are consistent with the results shown in Figure 12, which shows the distribution of fitness values for each weighting scheme of the GA. The technical scheme presents a compact box centered on high fitness values, demonstrating high stability and efficiency in the results. Similarly, the economic scheme presents greater dispersion and the presence of extreme values, which implies less robustness in uncertain conditions. Therefore, the technical scheme offers the best compromise between performance and stability, being the most suitable approach for applications that require high reliability in system optimization. The results obtained in this study reaffirm the effectiveness of metaheuristic algorithms for the optimal design of hybrid microgrids in critical rural environments. In particular, the GA showed superior performance compared to PSO and ACO in terms of system efficiency, stability, and operational reliability. Through annual simulations, GA managed to minimize LCC while maintaining a high renewable share (64.04%) and zero ENS. This performance is consistent with the findings of [20], who showed that metaheuristic algorithms can solve nonlinear and multivariable problems with reduced computation times and stable solutions.

Likewise, the consistency observed in independent GA runs, reflected in a low range of variability and an average similarity index (Jaccard) of 0.86, implies a high capacity of the algorithm to converge towards robust solutions even under stochastic conditions. This behavior is in line with that reported by [21], where PSO achieved a significant improvement in the dynamic stability of HESS. Furthermore, the good performance of GA compared to ACO confirms previous observations by [23], who identified greater robustness and less stress on energy components when using more adaptive and accurate algorithms.

In operational terms, the proposed optimal solution, which includes 20 photovoltaic modules, a 40 kWh storage bank, and a 2 kW diesel generator, demonstrates that it is possible to efficiently meet the energy demand of a rural medical center with a compact and low-cost infrastructure. This result contributes directly to the goal of reducing diesel dependence and associated logistics costs, as proposed in the studies by [6,8], where well-sized hybrid systems were shown to improve energy resilience in isolated areas.

Furthermore, the model’s ability to ensure continuous supply by prioritizing critical loads addresses one of the gaps identified in the literature, namely the lack of attention to operational criticality in rural healthcare settings [10,11]. The inclusion of this approach ensures the operation of essential medical equipment even in the event of failures or adverse weather conditions, which represents a significant improvement over models focused solely on general economic or technical criteria.

Finally, the superiority of the GA is supported by performance metrics such as LCC, ENS, and renewable share, as well as its behavior under sensitivity analysis, where it showed greater stability in the face of variations in the weighting criteria. This is essential in high Andean contexts with high climate variability and budget constraints, confirming the need for adaptive, robust, and low-operating-cost solutions [12,24]. Therefore, the findings reinforce the relevance of the metaheuristic approach to addressing energy design challenges in rural areas of Peru and open new opportunities for the implementation of sustainable hybrid systems in hard-to-reach medical centers.

4. Conclusions and Limitations

4.1. Limitations and Future Work

The model was applied using real climate and demand data from a specific high Andean medical center. While its structure and optimization approach are generalizable, it has not yet been tested using input data from other geographic locations or different user profiles. Future work should focus on validating the robustness of the proposed configuration under alternative climate scenarios, such as regions with higher wind potential or different seasonal irradiation patterns. Additionally, the methodology could be extended to other types of critical infrastructure, such as schools or community centers, by adapting the demand profile accordingly.

4.2. Conclusions

This study developed an optimization model based on metaheuristic algorithms (GA, PSO, and ACO) to design optimal configurations for hybrid renewable energy systems in remote medical centers in the high Andes of Peru. Solutions were identified that guarantee supply to critical loads under demanding climatic and economic conditions. The main findings indicate that GA achieved the best technical–economic performance, minimizing the system’s LCC to USD 10,213, maintaining a renewable share of 64.04%, and ensuring zero ENS. In addition, GA demonstrated greater stability and consistency between independent runs, with an average Jaccard index value of 0.86, indicating a high similarity between the solutions obtained. Operational robustness is complemented by low dispersion in the results, reflecting convergent and predictable behavior even under stochastic conditions. In terms of sensitivity, GA showed a more controlled response to variations in criterion weights, maintaining its performance within optimal margins without abrupt deviations. Likewise, the evolution of generational fitness showed a smooth and stable curve, without sudden oscillations, which demonstrates an efficient convergence process towards high-quality solutions. Therefore, these results support the use of metaheuristic algorithms as effective tools for energy planning in isolated rural environments, especially when prioritizing the continuity of critical services such as health centers. The proposed approach can be replicated to support investment decisions and the design of sustainable energy systems in other regions with similar characteristics.