Quantifying Effects of Dataset Size, Data Variability, and Data Curvature on Modelling of Simulated Age-Related Motor Development Data
Abstract
1. Introduction
2. Background
3. Methods
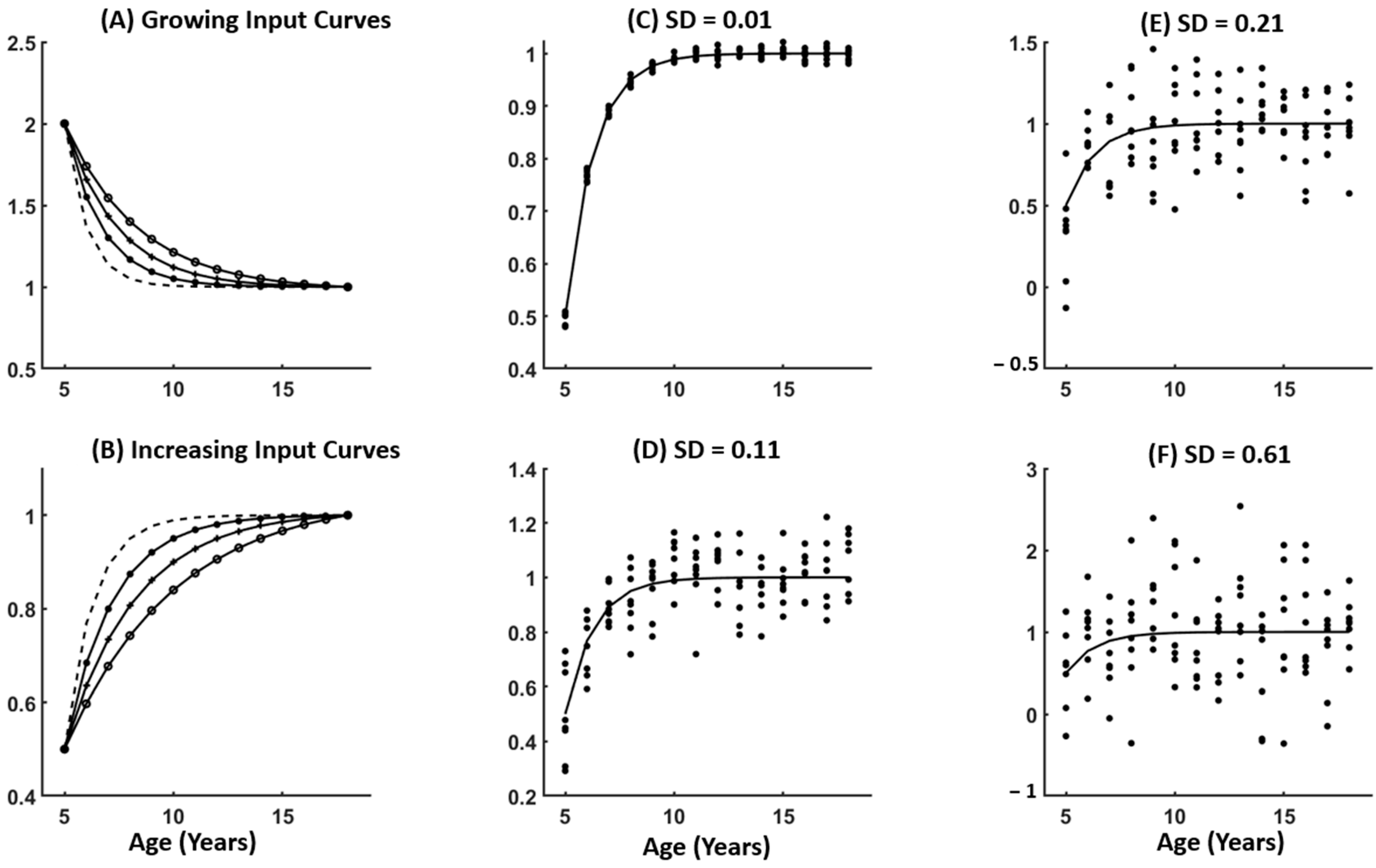
3.1. Simulated Data with Uniform Distributions
3.2. Simulated Data with Non-Uniform Distributions
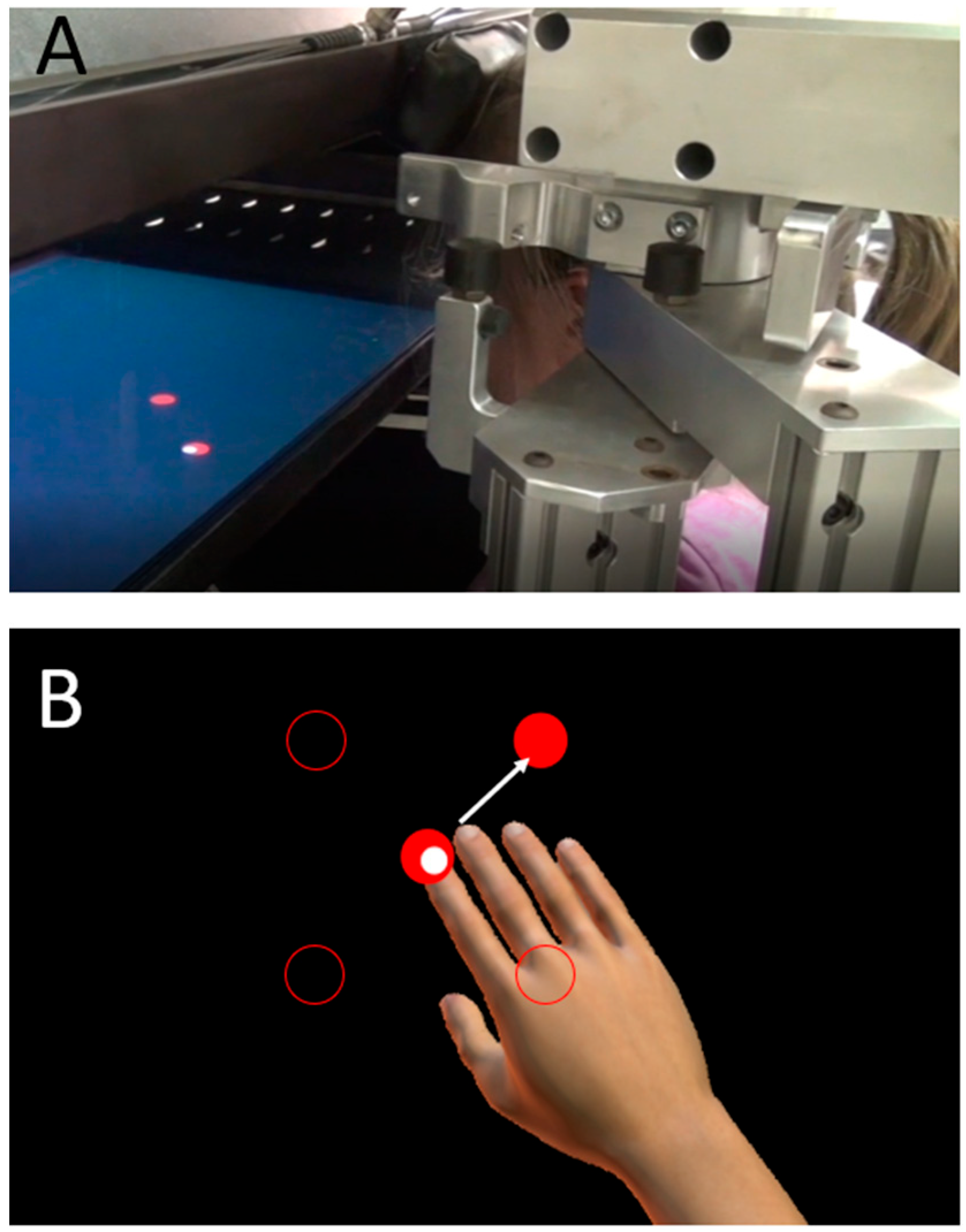
3.3. Applying Confidence Intervals from Both Uniform and Non-Uniform Data Distributions to Data Collected from Child Participants
4. Results
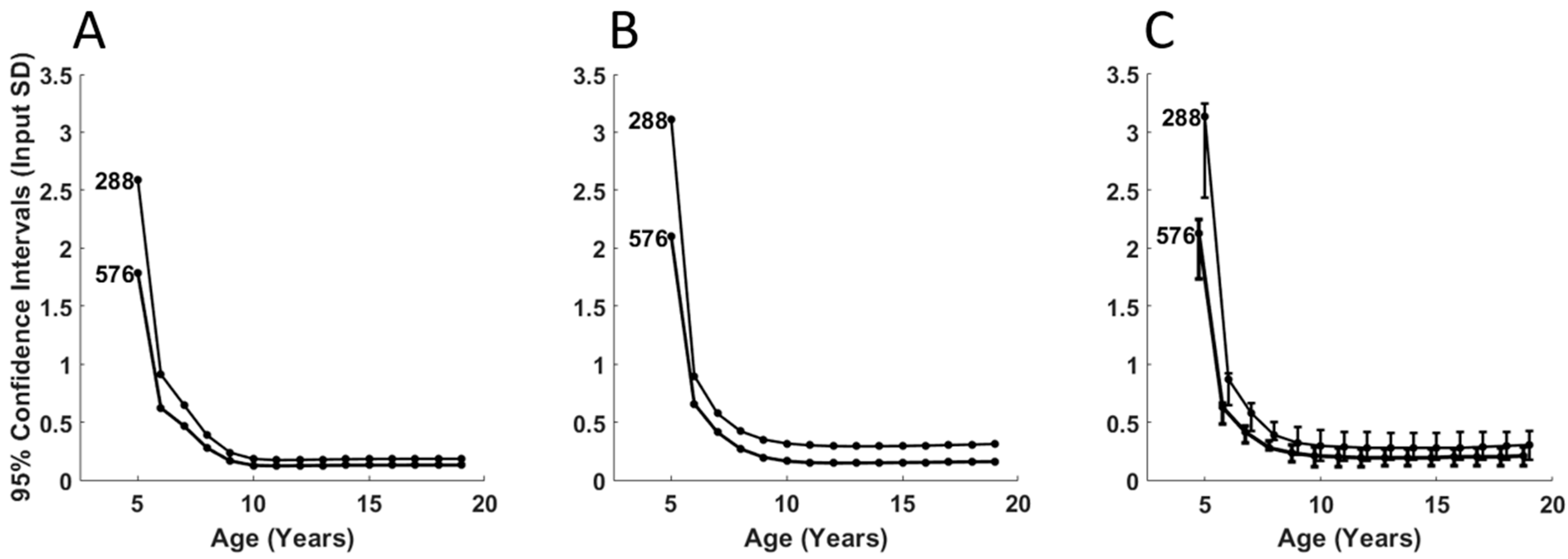
4.1. Simulated Data with Uniform Distributions
4.2. Simulated Data with Non-Uniform Distributions
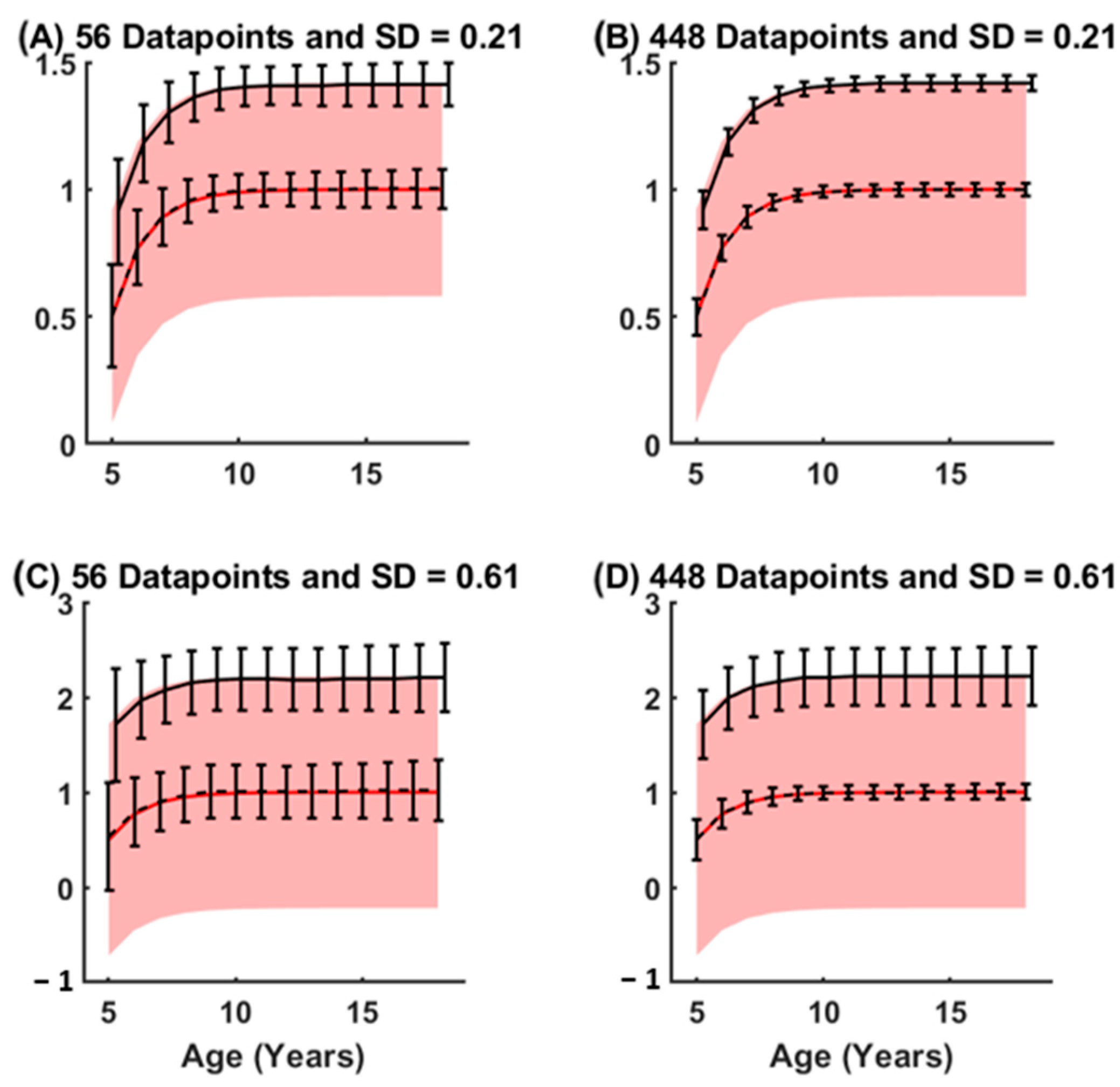
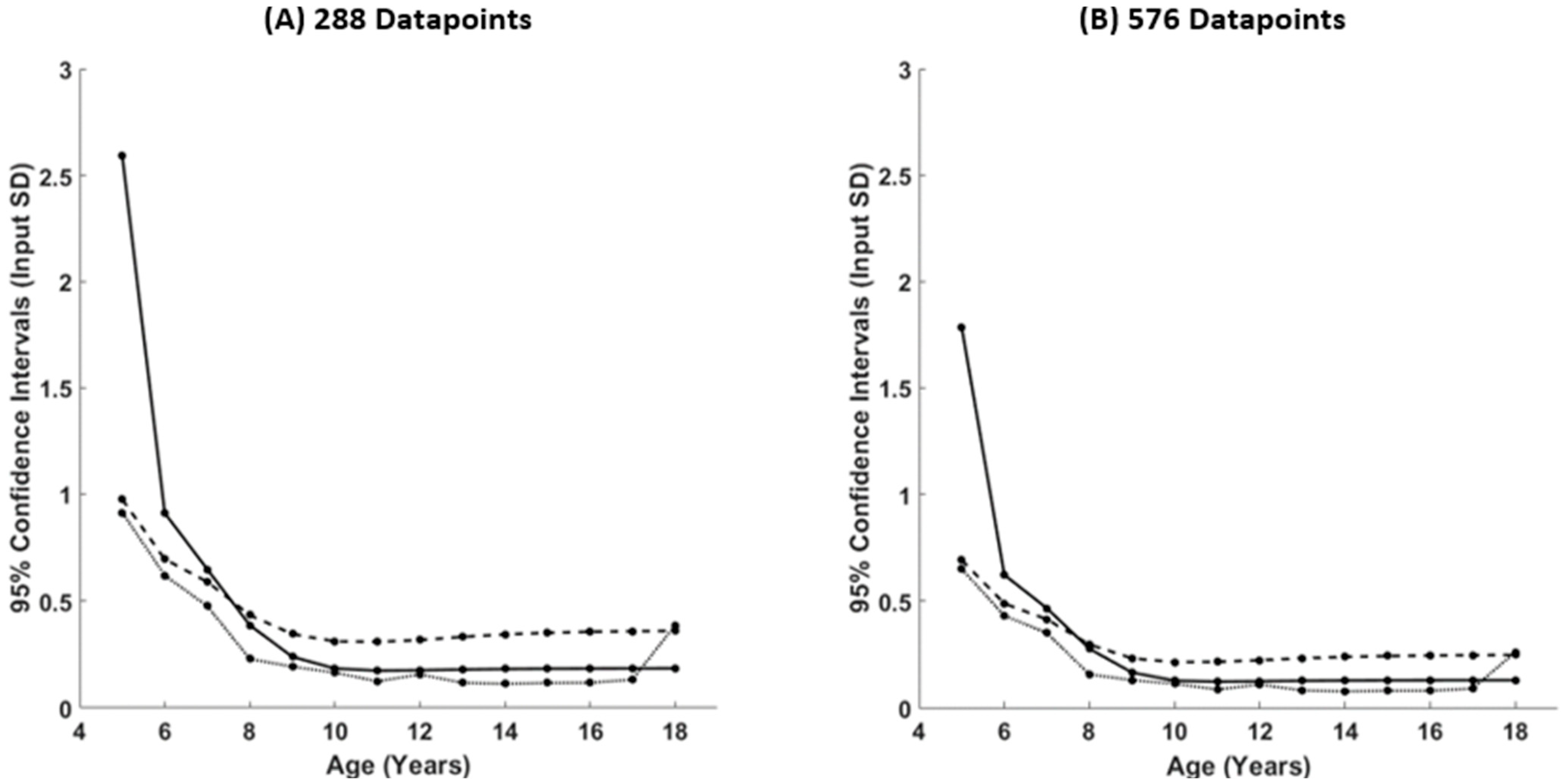
4.3. Assessing Accuracy and Repeatability of Curve Fitting: Fitting Confidence Intervals to Participant Data
5. Discussion
5.1. Repeatability of Curve Fitting
5.2. Confidence Intervals Based on Normative Models
5.3. Limitations
5.4. Clinical Implications
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Haywood, K.M.; Getchell, N. Life Span Motor Development, 6th ed.; Human Kinetics: Champaign, IL, USA, 2014. [Google Scholar]
- Gilliaux, M.; Dierckx, F.; Berghe, L.V.; Lejeune, T.M.; Sapin, J.; Dehez, B.; Stoquart, G.; Detrembleur, C. Age Effects on Upper Limb Kinematics Assessed by the REAplan Robot in Healthy School-Aged Children. Ann. Biomed. Eng. 2014, 43, 1123–1131. [Google Scholar] [CrossRef]
- Gilliaux, M.; Lejeune, T.M.; Sapin, J.; Dehez, B.; Stoquart, G.; Detrembleur, C. Age Effects on Upper Limb Kinematics Assessed by the REAplan Robot in Healthy Subjects Aged 3 to 93 Years. Ann. Biomed. Eng. 2015, 44, 1224–1233. [Google Scholar] [CrossRef]
- Goodenough, F.L. The development of the reactive process from early childhood to maturity. J. Exp. Psychol. 1935, 18, 431–450. [Google Scholar] [CrossRef]
- Kail, R. Developmental change in speed of processing during childhood and adolescence. Psychol. Bull. 1991, 109, 490–501. [Google Scholar] [CrossRef]
- Grohs, M.N.; Hawe, R.L.; Dukelow, S.P.; Dewey, D. Unimanual and bimanual motor performance in children with developmental coordination disorder (DCD) provide evidence for underlying motor control deficits. Sci. Rep. 2021, 11, 5982. [Google Scholar] [CrossRef] [PubMed]
- Hawe, R.L.; Kuczynski, A.M.; Kirton, A.; Dukelow, S.P. Robotic assessment of rapid motor decision making in children with perinatal stroke (in English). J. Neuroeng. Rehabil. 2020, 17, 94. [Google Scholar] [CrossRef]
- Hawe, R.L.; Kuczynski, A.M.; Kirton, A.; Dukelow, S.P. Assessment of bilateral motor skills and visuospatial attention in children with perinatal stroke using a robotic object hitting task (in English). J. Neuroeng. Rehabil. 2020, 17, 18. [Google Scholar] [CrossRef]
- Dobri, S.C.; Ready, H.M.; Davies, T.C. Tools and Techniques Used With Robotic Devices to Quantify Upper-Limb Function in Typically Developing Children: A Systematic Review. Rehabil. Process. Outcome 2020, 9. [Google Scholar] [CrossRef] [PubMed]
- Dobri, S.C.; Samdup, D.; Scott, S.H.; Davies, T.C. Differentiating Motor Coordination in Children with Cerebral Palsy and Typically Developing Populations Through Exploratory Factor Analysis of Robotic Assessments. In Proceedings of the 2021 43rd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Mexico, 1–5 November 2021; pp. 5936–5939. [Google Scholar]
- Dobri, S.C.; Samdup, D.; Scott, S.H.; Davies, T.C. Differentiating Motor Coordination and Position Sense in Children with Cerebral Palsy and Typically Developing Populations Through Robotic Assessments. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 3654–3657. [Google Scholar] [CrossRef]
- Rutherford, S.; Kia, S.M.; Wolfers, T.; Fraza, C.; Zabihi, M.; Dinga, R.; Berthet, P.; Worker, A.; Verdi, S.; Ruhe, H.G.; et al. The normative modeling framework for computational psychiatry (in English). Nat. Protoc. 2022, 17, 1750–2799. [Google Scholar]
- Walters, G.W.; Cooper, S.; Carlevaro, F.; Magno, F.; Boat, R.; Vagnetti, R.; D’ANna, C.; Musella, G.; Magistro, D. Normative percentile values for the TGMD-3 for Italian children aged 3–11+ years. J. Sci. Med. Sport 2024, 28, 398–407. [Google Scholar] [CrossRef] [PubMed]
- Little, C.E.; Emery, C.; Black, A.; Scott, S.H.; Meeuwisse, W.; Nettel-Aguirre, A.; Benson, B.; Dukelow, S. Test–retest reliability of KINARM robot sensorimotor and cognitive assessment: In pediatric ice hockey players. J. Neuroeng. Rehabil. 2015, 12, 78. [Google Scholar] [CrossRef]
- Wang, Y.; Han, X.; Xin, B.; Zhao, P. Innovations in Upper Limb Rehabilitation Robots: A Review of Mechanisms, Optimization, and Clinical Applications. Robotics 2025, 14, 81. [Google Scholar] [CrossRef]
- Skarsgard, M.; Dobri, S.C.D.; Samdup, D.; Scott, S.H.; Davies, T.C. Toward Robot-Assisted Diagnosis of Developmental Coordination Disorder. IEEE Robot. Autom. Lett. 2018, 4, 346–350. [Google Scholar] [CrossRef]
- Germanotta, M.; Vasco, G.; Petrarca, M.; Rossi, S.; Carniel, S.; Bertini, E.; Cappa, P.; Castelli, E. Robotic and clinical evaluation of upper limb motor performance in patients with Friedreich’s Ataxia: An observational study (in English). J. Neuroeng. Rehabil. 2015, 12, 41. [Google Scholar] [CrossRef]
- Largo, R.H.; Caflisch, J.A.; Hug, F.; Muggli, K.; Molnar, A.A.; Molinari, L.; Sheehy, A.; Gasser, T. Neuromotor development from 5 to 18 years. Part 1: Timed performance. Dev. Med. Child Neurol. 2001, 43, 436–443. [Google Scholar] [CrossRef] [PubMed]
- Kuczynski, A.M.; Dukelow, S.P.; Semrau, J.A.; Kirton, A. Robotic quantification of position sense in children with perinatal stroke (in English). Neurorehabilit. Neural Repair 2016, 30, 762–772. [Google Scholar] [CrossRef]
- Kuczynski, A.M.; Carlson, H.L.; Lebel, C.; Hodge, J.A.; Dukelow, S.P.; Semrau, J.A.; Kirton, A. Sensory tractography and robot-quantified proprioception in hemiparetic children with perinatal stroke (in English). Hum. Brain Mapp. 2017, 38, 2424–2440. [Google Scholar] [CrossRef] [PubMed]
- Kuczynski, A.M.; Kirton, A.; Semrau, J.A.; Dukelow, S.P. Bilateral reaching deficits after unilateral perinatal ischemic stroke: A population-based case-control study (in English). J. Neuroeng. Rehabil. 2018, 15, 77. [Google Scholar] [CrossRef] [PubMed]
- Williams, L.; Jackson, C.P.T.; Choe, N.; Pelland, L.; Scott, S.H.; Reynolds, J.N. Sensory-Motor Deficits in Children with Fetal Alcohol Spectrum Disorder Assessed Using a Robotic Virtual Reality Platform (in English). Alcohol. Clin. Exp. Res. 2013, 38, 116–125. [Google Scholar] [CrossRef]
- Scott, S.H. Method and Apparatus for Assessing or Detecting Brain Injury and Neurological Disorders. US8740794B2, 3 June 2012. [Google Scholar]
- Coderre, A.M.; Zeid, A.A.; Dukelow, S.P.; Demmer, M.J.; Moore, K.D.; Demers, M.J.; Bretzke, H.; Herter, T.M.; Glasgow, J.I.; Norman, K.E.; et al. Assessment of Upper-Limb Sensorimotor Function of Subacute Stroke Patients Using Visually Guided Reaching. Neurorehabilit. Neural Repair 2010, 24, 528–541. [Google Scholar] [CrossRef]
- van der Schaaf, A.; Xu, C.-J.; van Luijk, P.; Veld, A.A.V.; Langendijk, J.A.; Schilstra, C. Multivariate modeling of complications with data driven variable selection: Guarding against overfitting and effects of data set size. Radiother. Oncol. 2012, 105, 115–121. [Google Scholar] [CrossRef] [PubMed]
- Schönbrodt, F.; Perugini, M. At what sample size do correlations stabilize? J. Res. Pers. 2013, 47, 609–612. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dobri, S.C.D.; Scott, S.H.; Davies, T.C. Quantifying Effects of Dataset Size, Data Variability, and Data Curvature on Modelling of Simulated Age-Related Motor Development Data. Electronics 2025, 14, 3271. https://doi.org/10.3390/electronics14163271
Dobri SCD, Scott SH, Davies TC. Quantifying Effects of Dataset Size, Data Variability, and Data Curvature on Modelling of Simulated Age-Related Motor Development Data. Electronics. 2025; 14(16):3271. https://doi.org/10.3390/electronics14163271
Chicago/Turabian StyleDobri, Stephan C. D., Stephen H. Scott, and T. Claire Davies. 2025. "Quantifying Effects of Dataset Size, Data Variability, and Data Curvature on Modelling of Simulated Age-Related Motor Development Data" Electronics 14, no. 16: 3271. https://doi.org/10.3390/electronics14163271
APA StyleDobri, S. C. D., Scott, S. H., & Davies, T. C. (2025). Quantifying Effects of Dataset Size, Data Variability, and Data Curvature on Modelling of Simulated Age-Related Motor Development Data. Electronics, 14(16), 3271. https://doi.org/10.3390/electronics14163271





