1. Introduction
Backscatter communication systems are attracting growing attention from researchers due to their potential applications in Internet of Things (IoT) systems [
1,
2,
3]. With the increasing number of sensors and tags that act as backscatter devices (BD), which are key components for the implementation of IoT, there is a growing need for a power supply to support their operation and information transmission. However, in many situations, batteries are not a practical solution for powering these devices. Ambient backscatter communication provides an effective solution to the energy and communication challenges faced by low power communication systems [
3,
4,
5].
Backscatter communication systems can be implemented as monostatic backscatter communication systems (MBCS), bistatic backscatter communication systems (BBCS), and ambient backscatter communication systems (ABCS) [
2]. In an MBCS, the carrier emitter and the backscatter receiver are integrated into one device. The reader functions as both the emitter of the carrier signal and the receiver of the signal reflected from the BD. Radio Frequency Identification (RFID) systems are typically implemented as MBCS communication systems. In a BBCS, the carrier emitter and backscatter receiver are separate devices [
2]. This architecture is proposed to increase the communication range, which is crucial for systems powered by ambient energy sources [
6]. Separation of the carrier emitter and receiver allows for optimal positioning of the carrier emitter, regardless of the position of the receiver, relative to the BD, thus increasing the chances of successful data transmission [
7]. BD gathers energy from the signal emitted by the carrier emitter and uses it for powering and communication. The BD then reflects the signal received from the carrier emitter. The phase and amplitude of the reflected signal depend on the impedance of the BD’s antenna load. Information transmission is achieved by modulating the impedance based on a binary sequence that is being transmitted. In ABCS, the carrier emitter is separated from the receiver, and it is available from ambient radio frequency (RF) sources such as TV towers or cellular base station. Ambient backscatter communication systems are typically implemented with binary modulation due to the required simplicity and low energy harvesting efficiency [
3].
In a bistatic backscatter communication system, the carrier emitter is a controllable source whose location and transmission can be optimized by the system designer, whereas in an ambient backscatter system, the “carrier” arises from uncontrolled RF emitters such as broadcast TV or cellular infrastructure. A BBCS therefore allows the emitter to be placed close to the tag to maximize harvested power and does not rely on ambient sources, while an ABCS must harvest opportunistic signals of opportunity and cannot adjust the waveform or position of the carrier emitter. This clarification emphasizes that the carrier transmitter in a BBCS does not fall into the category of ambient energy sources, as it can be deliberately positioned and scheduled to support the tag.
Noncoherent detection in the receiver is widely used because of its simplicity, while coherent detection offers superior performance, but with the trade-off in increased complexity [
2]. The carrier emitter and receiver in a BBCS are separated devices, and their local oscillators have slight frequency differences, causing a carrier frequency offset (CFO) at the receiver’s side. To achieve coherent detection, which provides a lower probability of decoding errors, compensation for CFO is necessary at the receiver end [
7]. Another important factor to consider in signal detection in a BBCS is the relative phase between the signal emitted by the carrier emitter and the backscattered signal from the BD, which are received by the receiver as a superposition. The relative phase between these signals is dependent on the channel properties and has a significant impact on the system’s reliability, robustness, and communication range [
8].
In [
6], the authors proposed a correlation-based demodulator for a BBCS with frequency-shift keying (FSK) modulation. The carrier frequency offset (CFO) is estimated from the periodogram, which is calculated with high frequency resolution using the fast Fourier transform (FFT). Additionally, the authors proposed an optimum threshold-based detection method for the magnitude of the received samples of the on–off-keying (OOK) signal. The detection of the magnitude eliminates the synchronization problem, but at the cost of a higher bit error probability. In [
7], a coherent detection method in BBCS systems is proposed, but for the FSK modulation. In [
9], the authors propose a coherent detection method for collided FM0 line coded signals in a monostatic architecture, where the CFO is zero. In [
10], the authors propose a detector for the FM0 coded binary sequence on software-defined radio (SDR). However, the proposed detector is only applicable to a setup in which the carrier emitter and receiver are implemented on the same board, sharing the same local oscillator and thus having a CFO of zero.
FM0 line encoding and Miller encoded sequences can be considered equivalent to Manchester encoded sequences because both involve alternating between low and high levels to transmit binary sequences, either from low to high or vice versa. In [
10], the authors show that if the FM0 encoded transmitted waveform is shifted by
, where
T represents the bit interval, only two pulse shapes are possible. In the first shape, the signal level is low during the first half of the bit duration and high during the second half. In the second shape, the signal level is high during the first half of the bit duration and low during the second half. Similarly, the Miller encoded waveform can be represented by a combination of elementary pulse shapes that have a low level in the first half of the pulse shape duration and a high level in the second half, and vice versa. In this research, the focus is on Manchester line encoding, as it can be adapted to FM0 or Miller encoding techniques that are commonly used in commercial RFID systems.
In the BBCS system, the most critical aspect is the estimation of the CFO in order to achieve coherent detection. This paper proposes a method for the coherent detection of Manchester-encoded sequences in BBCS communication systems. The method includes coarse CFO estimation and compensation from the preamble sequence, followed by the application of the proposed algorithm for fine CFO correction. The preamble refers to a predefined sequence of binary symbols known to the receiver. From the received signal samples corresponding to the preamble, the receiver computes reference values for the binary symbols “0” and “1”, which are then used for detecting the data bits. It has been shown that the bit error rate (BER) can be reduced if, after a coarse CFO estimation from the signal preamble, an additional fine CFO correction is performed using the signal samples corresponding to the data. The proposed method was compared with an approach in which the CFO was estimated from the preamble using the maximum likelihood estimator (MLE), but without additional fine CFO correction.
The proposed method eliminates the need for channel estimation, thereby further simplifying decoding. It is shown that the system is equivalent to a binary frequency-shift keying (FSK) modulation, and its performances are also compared with FSK through simulations. The simulation results demonstrate good performance in scenarios with a large CFO and a small sampling rate, which is especially relevant in the context of applying backscattered-based communication systems in IoT applications. The proposed method is suitable for implementation on an SDR type of receiver. An SDR receiver, as a fully reconfigurable device capable of detecting any type of digitally modulated signal, can be utilized as a platform for demodulation and detection of the backscattered signal, regardless of the type of modulation and line coding technique applied [
10,
11]. As the SDR allows for the observation of both the in-phase (I) and quadrature (Q) components of the received signal amplitude, it enables coherent detection of the BBCS signal.
This paper is organized as follows: the system model is presented in
Section 2, and the method for coherent detection is described in
Section 3. The simulation results are presented in
Section 4, and the conclusions is given in
Section 5.
2. System Model
Figure 1 displays a BBCS system. It consists of the carrier emitter, an SDR receiver, and passive tag. Channel responses between carrier emitter and SDR receiver, carrier emitter and tag, and tag and an SDR receiver are denoted with
, respectively:
Throughout this paper, we index the channel responses as
with
(1 for the direct path, 2 for the emitter-to-tag path, and 3 for the tag-to-receiver path).
Here,
and
denote channel attenuation and delay of the corresponding channels, respectively, and have positive values. Here, it is assumed that the symbol duration is much longer than the maximum duration of the channel response. The carrier emitter transmits a continuous carrier of frequency
, amplitude
, and phase offset
:
where
refers to the real part of the signal, and
. The receiver receives the signal from the carrier emitter and the signal scattered from the tag. The tag scatters the signal that propagates from the carrier emitter to the tag, and it can be expressed as follows:
where the symbol ∗ denotes convolution, and
represents a term that depends on the structural mode of the antenna and the antenna load of the tag. Information transmission is achieved by altering the impedance of the antenna load, resulting in a change in the modulation signal
. Signal received at the receiver is superposition of the signal transmitted from the carrier emitter and signal scattered from the tag:
Approximation: Since the symbol period
T is much larger than the delay spread, we approximate
in (
6).
Here,
denotes additive white Gaussian noise (AWGN) with the power spectral density (PSD)
. In the receiver, as shown in
Figure 2, the signal is down-converted using the local oscillator with a frequency of
and filtered through an ideal low-pass filter (LPF) with an impulse response of
:
resulting in the received baseband signal
:
where
,
,
,
,
, and
denotes an angular frequency mismatch between the frequencies of the local oscillators in the transmitter and receiver. Clarification. In (
8), the factor
is a global rotation and does not change
; the envelope depends on
through
. The tag-load phase contribution is absorbed into
, while amplitude asymmetry is captured by
.
denotes circularly symmetric, complex baseband additive Gaussian noise with the following power spectral density:
where
W denotes the bandwidth of the LPF in the receiver. The impulse response of the received filter has the unit energy, i.e.,
.
The received sampled signal
simply follows from (
8):
where
represents the sampling period,
are samples of the complex additive white Gaussian noise (AWGN) with a variance of
per complex dimension, and
denotes the normalized frequency offset. Multiplying
in the exponent of (
10) yields
, so the form of (
10) remains unchanged.
3. Proposed Method for Coherent Detection
For this analysis, perfect symbol synchronization is assumed. The receiver takes
samples of the received signal during the bit duration
T. SDR receivers typically sample the received signal with a higher number of samples per symbol or bit to ensure more reliable clock and waveform reconstruction [
12]. In the case of Manchester encoding, the modulated signal waveforms for binary symbols “0” and “1” are as follows:
It is assumed that
is an even number. For simplicity, and without loss of generality, it is taken that
if the tag backscatters the signal, and
if the tag does not backscatter the signal. This assumption is based on perfect electromagnetic wave absorption by the tag when it does not backscatter the signal.
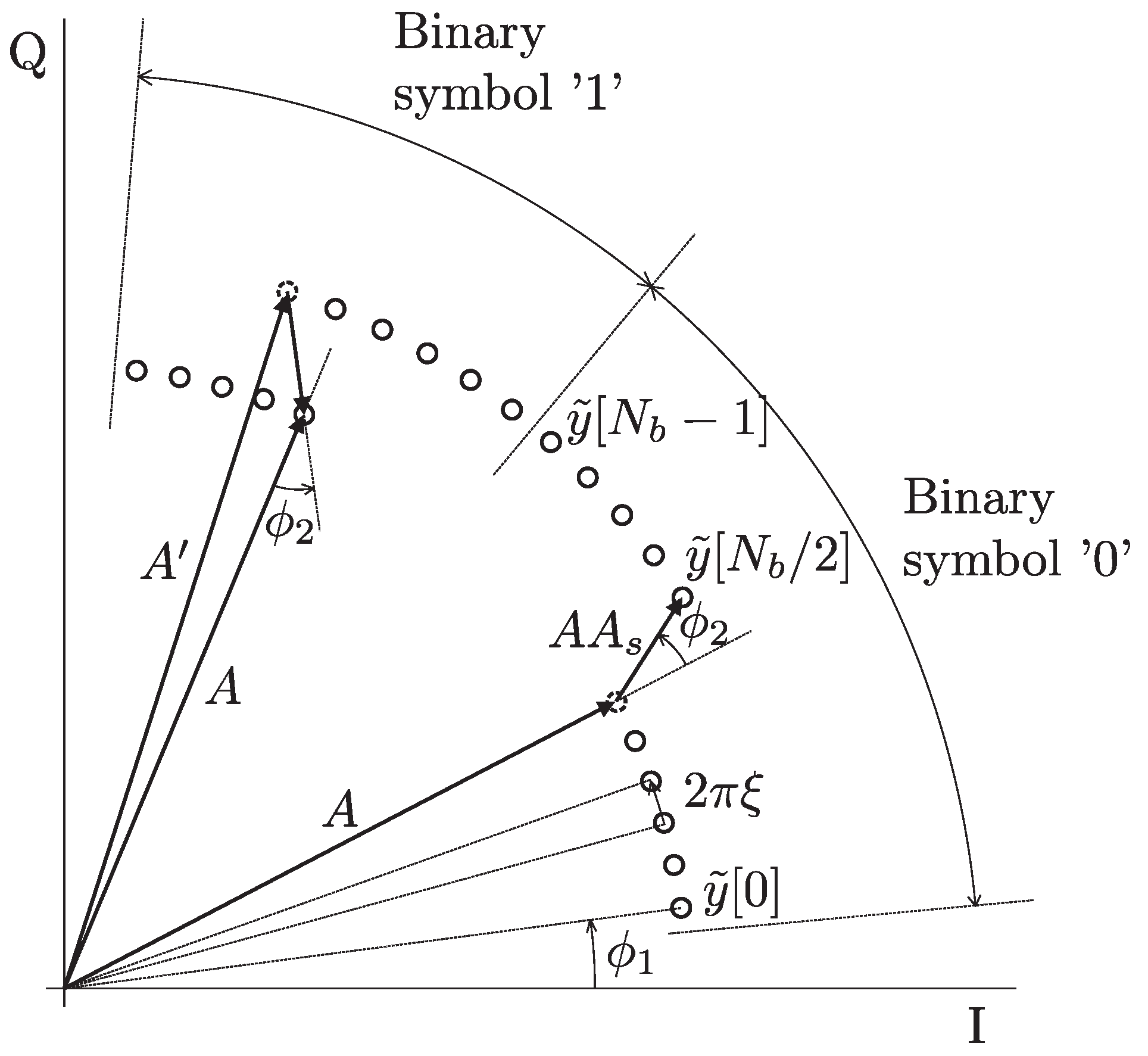
Figure 3 shows an example of received signal samples in a constellation diagram for successive binary symbols “0” and “1”. The phase of each subsequent sample is incremented by
due to frequency mismatch. As a result, each subsequent received sample moves (rotates) in a counterclockwise direction for positive frequency mismatch and in a clockwise direction for negative frequency mismatch. Additionally, in the middle of the signaling interval, due to the Manchester encoding, there is a change in phase and amplitude due to the impedance change in the tag.
It is noteworthy, contrary to intuition, that the magnitude of the received samples
can be lower when the tag backscatters the signal than when it does not. This phenomenon is governed by the relative phase between the direct and backscattered components rather than their absolute phases. Although Equation (
8) shows that
and
include different delay terms, both phases share the common component
from the direct path. Consequently, they are not independent; however,
appears in (
8) only as a common phase rotation
and therefore does not affect the instantaneous magnitude. The constructive or destructive superposition depends only on
, since
In particular, when the backscattered amplitude
is weaker than the direct component
A and when
, the instantaneous magnitude decreases. For small
, this condition is well approximated by
(more precisely,
with
). Under these conditions, a tag reply can reduce the total amplitude, rendering the bits indistinguishable without a known preamble of “0” s and “1” s to provide phase reference.
Coarse estimation of the parameter
can be calculated from the phase difference of the received signal between the end and the beginning of the preamble sequence:
Note: We use the two edge samples of the preamble to maximize phase separation; the denominator reflects their
spacing. In our SNR range, averaging the phase difference across all preamble samples gives indistinguishable
.
Here,
denotes phase of the received signal
,
is the length of the preamble sequence, and
^ is symbol for the estimation. The received signal after coarse CFO correction is as follows:
The estimation of parameter
is critical for correct decoding. If the parameter
is not perfectly estimated from the preamble, the signal samples
will continue to rotate in the constellation diagram even after compensation. Since perfect estimation is not possible using only the preamble, additional fine compensation of the received signal samples is required for each received data symbol, i.e., “0” and “1”. The parameter
can be estimated by computing the periodogram of the received signal and finding its peak [
13]. To estimate the parameter
by finding the peak of the periodogram, high resolution in the frequency domain is required, which means a sufficiently large number of signal samples for computing the FFT used to calculate the periodogram. The nonlinearity of the periodogram further complicates the estimation of the parameter
using this method [
14]. Additionally, the CFO may vary during data transmission, which makes this approach inadequate [
6]. The parameter
can also be estimated using the signal model (
10) by first estimating the parameters
A,
, and
, and
after which
can be estimated by minimizing the norm of the vector obtained from the difference between the received preamble signal samples and the signal model. More details about this approach are provided in
Section 3.1.
Coherent detection requires the reconstruction of the vectors; let them be denoted as and , which represent the binary symbols “0” and “1”, along with the fine CFO correction remaining after the coarse CFO correction of the signal . The vectors and can be determined from the preamble sequence. Once the vectors and are determined, the detection of the transmitted symbol can be performed by calculating the Euclidean distance between the received samples of that symbol and the and .
Figure 4 illustrates the two-dimensional complex vectors,
(on the left) and
(on the right), which represent the binary symbols “0” and “1”, respectively, along with the corresponding samples received in the case of ideal reception without noise. For clarity,
and
are computed from no-backscatter samples (
), whereas
and
are computed from backscatter samples (
B).
Figure 4 illustrates calculation of the vectors
and
from the samples of the received signal
. The magnitudes
A and
are related to the received signal when the tag does not backscatter the signal and when it does backscatter the signal, respectively. The phases
and
are related to the received samples when the tag sends “0” and “1”, respectively. The preamble sequence is an alternating sequence of “0” and “1”, starting with “0” and ending with “1”. Let
, and
denote the index sets of samples of the preamble received signal
, corresponding to the “0” and “1” symbols transmitted by the tag, respectively, when the tag does not backscatter the signal. Similarly, let
and
denote the index sets of samples of the preamble received signal
, corresponding to the “0” and “1” symbols transmitted by the tag, respectively, when the tag backscatters the signal. The magnitudes of the received signal
A when the tag does not backscatter a signal and
when it does can be estimated as follows:
where
denotes the set cardinality or the absolute value operation, depending on whether the input is a set or a scalar. The phase
can be calculated from
and
, which represent the mean phase of the received symbols when the tag does not backscatter the signal and when it does backscatter the signal during the transmission of “0”, respectively. Estimation of
and
can be calculated as follows:
where
denotes the phase of the samples
. Note that before calculating the average, it is necessary to unwrap the phase of the signal
. The phase difference estimation for the binary symbol “0” is as follows:
Subtracting
from
removes the common phase associated with the direct path. The strong carrier emitted by the carrier emitter thus becomes a reference whose contribution is canceled out, leaving only the phase shift introduced by the backscattered component. The same procedure is used for the “1” symbol so that the strong direct signal does not impair detection.The vector
, representing the binary symbol “0” with compensated CFO at the receiver, can be derived by utilizing the estimated values of
A,
, and
:
where
and
can be calculated as follows:
The same procedure is also applicable for the binary symbol “1”. In Equation (
17), to calculate the mean phase
and
when the tag does not backscatter a signal and when it does, respectively, one should use
and
instead of
and
. The phase difference estimation for the binary symbol “1” is as follows:
Vector
, representing the binary symbol “1” with compensated CFO at the receiver, is as follows:
where
and
can be calculated as follows:
To decode the received symbol, it is necessary to calculate the Euclidean distance between the vector
, corresponding to the symbol being decoded, and the vectors
and
. The values
and
are calculated from the first
and the last
samples of the signal
, respectively. The first step is to estimate the magnitudes from the
:
where
and
denote the average magnitudes of the first and second halves of the received samples, respectively, of the symbol to be decoded. The corresponding average phases are computed as follows:
where
and
denote the average phases of the first and second halves of the received samples, respectively. The elements of the two-dimensional complex vector
are as follows:
The decision on the received symbol follows from comparing the Euclidean distance between the vector
and both
and
:
where
denotes the vector norm. In summary, the proposed detection procedure operates as follows: (1) compute the coarse CFO estimate from the preamble via (
13) and rotate the samples using (
14); (2) estimate the amplitudes
and
and the phase differences
and
from the preamble using (
15)–(
18) and (
21); (3) construct the orthogonal reference vectors
and
using (
20) and (
23); (4) for each data symbol, form the two-element vector
by averaging the first and second halves of the samples as in (
24)–(
26); (5) compare the Euclidean distances between
and the references
and
to decide the transmitted bit as in (
27), thereby performing fine CFO correction on a symbol-by-symbol basis. Because
and
are orthogonal, the BBCS signal is mathematically equivalent to coherent binary FSK, and the coherent FSK error probability serves as a theoretical benchmark for our detector.
3.1. Detection Using MLE of Parameter from the Preamble Without Fine CFO Correction
The MLE-based estimator described in
Section 3.1 is presented as a baseline for comparison only. The proposed detection scheme described earlier relies solely on the coarse estimator (
13) for CFO estimation and does not use the MLE; our goal is to illustrate the performance gap between the simple coarse estimator with fine correction and the more complex MLE that lacks per-symbol refinement.
While one could, in principle, perform a maximum-likelihood estimation of the CFO parameter and the phases and using the entire data sequence, such a three-dimensional search over the full frame is computationally prohibitive. A full-sequence MLE would require a joint search over a very fine grid of CFO values and phase offsets across hundreds of data samples; this complexity grows rapidly with the frame length and makes the method unsuitable for low-power SDR platforms. By restricting the MLE benchmark to the preamble, we ensure a fair comparison: both detectors use the same amount of pilot information, and any performance improvement in the proposed method arises from the fine correction applied to the data symbols rather than an artificially longer observation window. This highlights the practical benefit of our approach for resource-constrai- ned devices.
Section 3.1 describes a detection method in which the parameters
A,
,
, and
are first estimated from the preamble. These values are then used to estimate the parameter
using MLE, followed by phase correction. After phase correction, the vectors
and
representing the symbols “0” and “1”, respectively, are determined from the preamble. Finally, the data symbols are decoded from the received signal samples based on the minimum Euclidean distance criterion. From Equations (
15) and (
16), and based on
Figure 3, the vector
can be estimated as follows:
where
denotes phase of the vector
, and
and
follow from:
Estimation of the product
is
, and estimation of the phases
and
follow from:
where
can be calculated using Equation (
13), and
. The parameter
is estimated using the MLE by maximizing the log-likelihood function
[
13]:
where
is calculated from the signal model (
10):
and
. The MLE of the parameter
is equivalent to the minimization of the following expression:
The initial estimate of the parameter
can be taken as
, calculated using (
13). After estimating the parameter
, phase correction is performed using expression (
14).
Similarly to the proposed method, the vectors
and
are calculated from the corresponding preamble samples; that is,
where
and
is calculated using the following expression:
Phase
represents the averaging of sample phases on a symbol-by-symbol basis. In an equivalent manner, the vector
is calculated from the received signal samples corresponding to the symbol being decoded, where:
where:
The decision on the received symbol follows from:
3.2. On Equivalence Between the Analyzed System and Orthogonal FSK
The probability of error in the receiver, in the case of the AWGN channel, can be calculated by using the Euclidean distance between the vectors that represent the symbols “0” and “1” [
15]:
where
and
denote the vectors of the received signal samples
in the case of ideal reception without noise, when the transmitter sends “1” and “0”, respectively. The probability of error depends on the distance between the points in the constellation diagram when the tag reflects the signal and when it does not; that is, according to
Figure 3, on the value of
. Since the distance does not depend on phases
and
, nor on CFO, for the sake of computational simplicity and without loss of generality, one can assume
. Then, it follows:
Energy per bit follows from Equations (
11) and (
12), taking into account Equation (
10):
Probability of error follows from (
43), (
44), and (
45):
The obtained expression is equivalent to the probability of error for a coherently decoded orthogonal FSK modulation [
16].
4. Numerical Results and Discussion
Section 4 presents the performance of the proposed method. The simulations were carried out using Monte Carlo simulations in MATLAB. For each operating point, the channel delays
,
, and
were drawn independently from uniform distributions to emulate random propagation paths. Specifically,
,
, and
were chosen uniformly from the interval
. Packets of
data bits were transmitted repeatedly under independent noise realizations and random delays until the cumulative number of bit errors exceeded 2000. The bit error rate at each SNR and parameter setting was then computed as the ratio of bit errors to total transmitted bits over these runs. For the MLE baseline described in
Section 3.1, the CFO parameter
was obtained via direct numerical minimization of (
35) using MATLAB’s
fminsearch (Nelder–Mead), initialized at the coarse estimate
and constrained to
by clipping during evaluation.
Figure 5 presents the bit error rate (BER) performance of the proposed detection method as a function of the preamble length,
. The results are presented for
dB and 12 dB, at different values of the parameters
and
. The parameter
is introduced to generalize the results, as the signal model in the baseband domain includes the frequency offset and sampling period appearing as a product according to Equation (
10). The parameter
is modeled as a random variable with a uniform distribution in the range from
to
. This modeling approach makes the simulation results more realistic, as the frequency offset of the local oscillator in an SDR receiver is independent of the frequency of the local oscillator in the transmitter and can thus be modeled as a random variable. A larger
value indicates a greater nominal frequency offset of the receiver’s local oscillator relative to that of the transmitter, which is characteristic of receivers with lower precision in generating a stable cosine signal. The parameter
represents the relative proportion of the signal magnitude reflected by the tag to the magnitude of the directly received signal generated by the carrier transmitter in dB at the receiver location. A lower value of the parameter
refers to a situation where the tag is much closer to the receiver than to the carrier emitter. In all simulations, the length of the data sequence is
bits, and
. The same figure also shows the theoretical bound for the FSK system at
and 12 dB, respectively. The theoretical bound is corrected for the energy loss that occurs due to the transmission of the preamble of length
, i.e.,
, where
denotes the energy per channel use [
17]. Since channel coding was not applied, the corrected curve represents the lower limit that can be achieved. The simulation results show that for different values of the parameters
and
, there is no need for a preamble longer than six symbols, as no significant reduction in the error probability is achieved. For this reason, in all simulations,
. It is also important to emphasize that a shorter preamble allows for the transmission of longer data sequences, considering that the tag is powered by the received signal and has limited energy storage capacity required for its operation.
In practical BBCS deployments, the ratio of the direct carrier amplitude to the backscattered signal amplitude can vary widely. We characterize this ratio by the parameter : larger values correspond to weaker backscattering relative to the direct path (for example, 15 dB means the backscattered signal is roughly 15 dB below the direct signal). Conversely, implies equal magnitudes, while negative would indicate unrealistically strong backscattering. Our simulations therefore explore values of 5–15 dB to model typical scenarios ranging from moderately weak to very weak backscatter. A higher naturally leads to larger BERs for all detection schemes, but, as the results will show, the proposed method still maintains an advantage in this regime.
Figure 6,
Figure 7 and
Figure 8 show the dependence of BER on the
ratio in dB for different values of the parameters
and
. The label PM refers to the proposed method, while AVR denotes detection performance of the detector described in
Section 3.1. Two conclusions can be drawn from the presented figures.
At lower values of the parameter , the BER is significantly worse compared to when is higher. This is expected, given that the values of the received signal are such that they are closer to the origin in the constellation diagram, and due to the rotation caused by CFO and the effect of Gaussian noise, the estimation of parameters required for detection becomes more challenging.
The proposed algorithm shows better results for higher values of the parameter , while for lower values, it exhibits slightly worse performance compared to the situation where it is not applied. For lower values of the parameter , there is no need to apply the algorithm for fine phase correction, as even without the correction, the BER achieved is very close to the theoretical limit.
Figure 9,
Figure 10 and
Figure 11 show the dependence of BER on the parameter
for different values of the parameter
at
, 10, and 12 dB. The presented results show that the proposed algorithm for fine CFO correction (PM) performs better compared to the algorithm that does not account for fine CFO correction (AVR) when
exceeds a certain threshold value, which depends on the values of
and
. It can also be observed that the threshold value of the parameter
depends on the parameter
. The threshold value of the parameter
varies from 0.25 when
dB to 0.4 when
dB. A higher value of the parameter
corresponds to a situation with a larger CFO, which is characteristic of lower-cost receivers. Additionally, for a given value of the parameter
, the performance of the proposed algorithm also depends on the
ratio. At lower
values, the threshold value of the parameter
is smaller. From the presented simulation results, it can be concluded that the probability of decoding errors can be reduced by applying additional phase compensation, rather than relying solely on the estimation of the parameter
from the preamble. This is especially true for higher values of the parameter
, i.e., for larger CFO.
For example, at a normalized CFO of and amplitude ratio dB, the bit error rate (BER) at dB is approximately for the MLE-only baseline. The proposed method reduces this to about , representing a fourfold improvement. Similarly, at and dB with dB, the BER improves from roughly (MLE-only) to about (proposed scheme). These results illustrate the clear advantage of incorporating fine CFO correction after the coarse estimate. We also clarify that corresponds to typical frequency offsets in the tens of kilohertz range for sampling intervals around 1 µs, which are representative of low-cost software-defined radio (SDR) platforms.
Figure 12 shows a comparison of the estimation error variance of the parameter
, calculated using Equations (
13) and (
35), for different values of the parameters
and
.
where
denotes expectation. From the presented results, it can be concluded that the estimation of the parameter
using Expression (35) is not better than the simple estimation obtained using expression (13), except in the case when
dB and
. It can be concluded that for higher values of
and lower values of
, the estimation of the parameter
cannot be improved compared to the simple estimation using Equation (
13). For this reason, the proposed algorithm provides better performance at higher CFO values and lower
, since it performs additional CFO correction, as the estimation of the parameter
from the preamble is not sufficiently accurate.