KAN-and-Attention Based Precoding for Massive MIMO ISAC Systems

Abstract

Precoding technology is one of the core technologies that significantly impacts the performance of massive Multiple-Input Multiple-Output (MIMO) Integrated Sensing and Communication (ISAC) systems. Traditional precoding methods, due to their inherent limitations, struggle to adapt to complex channel conditions. Although more advanced neural network-based precoding schemes can accommodate complex channel environments, they suffer from high computational complexity. To address these issues, this paper proposes a KAN-and-Attention based ISAC Precoding (KAIP) scheme for massive MIMO ISAC systems. KAIP extracts channel interference features through multi-layer attention mechanisms and leverages the nonlinear fitting capability of the Kolmogorov–Arnold Network (KAN) to generate precoding matrices, significantly enhancing system performance. Simulation results demonstrate that compared with conventional precoding schemes, the proposed KAIP scheme exhibits significant performance enhancements, including a 70% increase in sum rate (SR) and a 96% decrease in computing time (CT) compared with fully connected neural network (FCNN) based precoding, and a 4% improvement in received power (RP) over the precoding based on convolutional neural network (CNN).

1. Introduction

Massive Multiple-Input Multiple-Output (MIMO) technology is one of the key enablers of 6G [1]. It can achieve multi-user parallel services on the same time-frequency resource by deploying hundreds of antennas at the base station (BS) [2]. Massive MIMO technology, with its excellent energy efficiency performance and spectrum utilization efficiency, is regarded as the core driving force for the development of next-generation communication systems. Meanwhile, based on the ultra-high spatial degree of freedom, massive MIMO technology is also a supporting technology for Integrated Sensing and Communication (ISAC) [3], which enables joint communications and wireless sensing and has received extensive research attention [4].

In the downlink, beamforming techniques or efficient precoding underpin the excellent functionality of massive MIMO. Related studies include traditional precoding methods [5,6,7,8,9,10] and neural network based precoding methods [11,12,13,14,15,16,17,18,19].

Matched Filter (MF) precoding is the simplest precoding scheme, where the precoding matrix is directly obtained by the conjugate transpose of the channel matrix, but its performance is limited [5]. Therefore, Zero Forcing (ZF) and Minimum Mean Square Error (MMSE) further take the inter-user interference into account, yet their capability still falls short of modern requirements due to inherent limitations [6,7]. Subsequently, more advanced precoding methods are devised. For example, a Gradient Descent (GD) based precoding scheme is proposed in [10], where it is implicitly used to solve the Lagrangian formulation of the precoding problem under power constraints. The authors of [8,9] employed Semidefinite Relaxation (SDR) in precoding design, which reformulates the nonconvex precoding design problems into tractable semidefinite programs (SDPs). However, the high computational complexity restricts the practical use of these approaches.

To further enhance the performance of the MIMO system, neural network-based precoding methods have been proposed. Liquid Neural Networks (LNN) is used in [11] to generate precoding matrices, which utilize gradient-based optimization to extract high-order channel information and incorporate a residual connection to ease training. Fully connected neural networks (FCNN) are employed in [12,13], which use fully connected layers to map estimated channels to precoding vectors, incorporating a scalar quantization layer to handle discrete phase constraints. The authors of [14,15,16] adopted deep reinforcement learning (DRL) by formulating the NP-hard precoding problem as a Markov decision process (MDP). DRL’s model-free nature proves particularly effective in multi-hop and multi-user scenarios, where conventional optimization struggles with non-convexity and high dimensionality. Meta-learning (ML) is leveraged in [17,18,19] by enabling the neural networks to learn optimization strategies across diverse scenarios, thereby improving the efficiency in solving the non-convex precoding problem. By feeding the gradients of precoding matrices into lightweight neural networks and employing nested optimization loops, the frameworks dynamically adjust parameters to navigate complex environments, ensuring consistent performance under varying channel conditions. All the above research demonstrates extraordinary precoding operations. However, the use of large-scale networks leads to a steep increase in computational complexity with a large number of antennas.

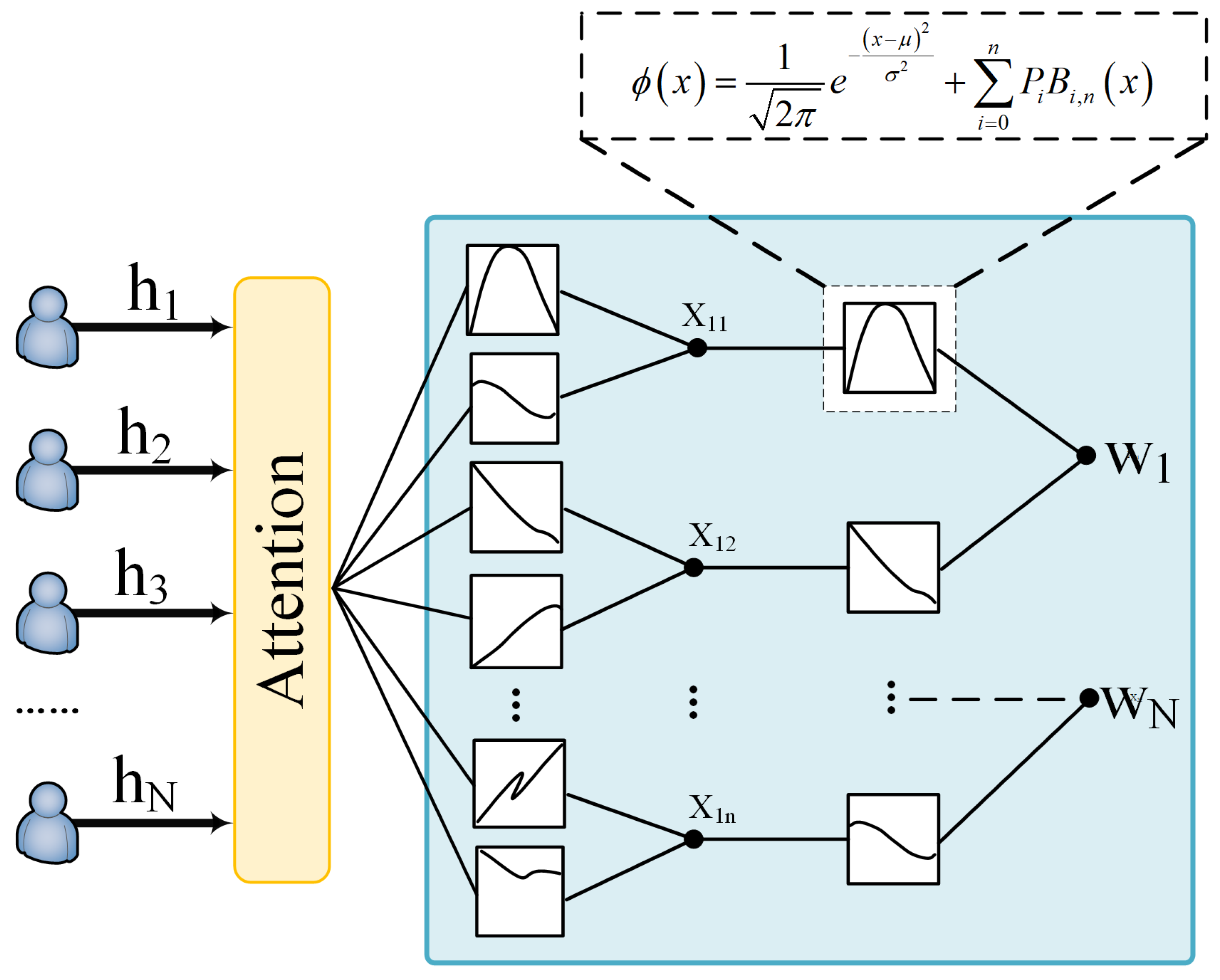
In the case of ISAC, where the communication users require high data rate services and the sensing users require accurate target detection and environment sensing capabilities, a multidimensional challenge is posed to the downlink precoding design. To address this issue, we propose a novel KAN and Attention-based ISAC Precoding (KAIP) scheme for massive MIMO ISAC systems. Based on the attention mechanism and Kolmogorov–Arnold Network (KAN) [20], we design a neural network to generate the precoding matrix for both the communication and the sensing users, with consideration of the received power (RP) for the sensing users as well as the sum rate (SR) obtained by the communication users. The detailed contributions of this work are summarized as follows:

• The precoding problem is formulated for massive MIMO ISAC systems, which takes both the communication users and the sensing users into consideration.
• We propose the novel KAIP scheme that employs KAN and the self-attention mechanism for precoding design in massive MIMO ISAC systems. The attention mechanism in KAIP deeply extracts interference features from the channel matrix to reduce multi-user interference, while the KAN network is responsible for directly generating the precoding matrix with low complexity.
• In order to evaluate the performance of KAIP, extensive simulations are carried out. The proposed KAIP is compared with existing approaches such as ZF, MMSE, FCNN-based scheme, and CNN-based scheme. Numerical results show that the proposed KAIP scheme exhibits significant performance enhancements with a rather low complexity.

The rest of the paper is organized as follows: In Section 2, the system model and the problem formulation is provided. The proposed KAIP scheme is introduced in Section 3. The numerical results are presented in Section 4, and conclusions are drawn in Section 5.

2. System Model and Problem Formulation

Consider the downlink of a massive MIMO ISAC system. The BS is equipped with M antennas. There are N single-antenna users in the system, including $N_1$ communication users and $N_2$ sensing users. The distance between different users and the BS varies, and there are obstacles between them. An illustration of the considered scenario is given in Figure 1.

The signal received by the n-th user is denoted as $y_n$. Let $\mathbf{y}=\left[y_1,\dots ,y_n\right]$ be the received signal vector at all the N users, which is expressed as (1).

$$\mathbf{y}=\mathbf{HWx}+\mathbf{n},$$

(1)

where $\mathbf{H}\in {\mathbb{C}}^{N\times M}$ is the channel matrix from the BS to the N users; $\mathbf{W}\in {\mathbb{C}}^{M\times N}$ is the precoding matrix; $\mathbf{x}={\left[x_1,\dots ,x_N\right]}^T$ with $x_n\in \mathcal{CN}(0,1)$ denotes the symbols for the n-th user, $\mathbf{n}\in {\mathbb{C}}^N$ is the noise vector, and $\mathbf{n}\in \mathcal{CN}\left(0,{\sigma }^2{\mathbf{I}}_N\right)$.

Using (1), we can obtain the received signal vector of the communicating users ${\mathbf{y}}_c\in {\mathbb{C}}^{N_1}$ and that of the sensing user ${\mathbf{y}}_s\in {\mathbb{C}}^{N_2}$, respectively, as (2).

$$\left[\begin{array}{c}{\mathbf{y}}_c\\ {\mathbf{y}}_s\end{array}\right]=\left[\begin{array}{c}{\mathbf{H}}_c\\ {\mathbf{H}}_s\end{array}\right]\left[\begin{array}{cc}{\mathbf{W}}_c& {\mathbf{W}}_s\end{array}\right]\left[\begin{array}{c}{\mathbf{x}}_c\\ {\mathbf{x}}_s\end{array}\right]+\left[\begin{array}{c}{\mathbf{n}}_c\\ {\mathbf{n}}_s\end{array}\right],$$

(2)

where ${\mathbf{H}}_c\in {\mathbb{C}}^{N_1\times M}$ and ${\mathbf{H}}_{\mathbf{s}}\in {\mathbb{C}}^{{\mathbf{N}}_{\mathbf{2}}\times \mathbf{M}}$ are the channel matrix for $N_1$ communicating users and $N_2$ sensing users, respectively; ${\mathbf{W}}_c\in {\mathbb{C}}^{M\times N_1}$ and ${\mathbf{W}}_s\in {\mathbb{C}}^{M\times N_2}$ are the precoding matrix for the communicating users and the sensing users, respectively; ${\mathbf{x}}_c={\left[x_{c1},\dots x_{c{N}_1}\right]}^{\mathrm{T}}$ and ${\mathbf{x}}_s={\left[x_{s1},\dots ,x_{s{N}_2}\right]}^{\mathrm{T}}$ with $x_{ci}$ and $x_{sj}$ denote the symbols for the i-th communicating user and the j-th sensing user, respectively; ${\mathbf{n}}_c\in {\mathbb{C}}^{N_1}$, ${\mathbf{n}}_c\in \mathcal{CN}\left(0,{\sigma }^2{\mathbf{I}}_{N1}\right)$ and ${\mathbf{n}}_s\in {\mathbb{C}}^{N_2}$, ${\mathbf{n}}_s\in \mathcal{CN}\left(0,{\sigma }^2{\mathbf{I}}_{N2}\right)$ denote the noise matrix of the communicating users and the sensing users, respectively.

The received signal at the i-th communication user, i.e., $y_{ci}$ is given by (3).

$$y_{ci}=x_{ci}{\mathbf{h}}_{ci}^H{\mathbf{w}}_{ci}+\sum _{j\ne i}{x}_{cj}{\mathbf{h}}_{ci}^H{\mathbf{w}}_{cj}+\sum _{k=1}^{N_2}{x}_{sk}{\mathbf{h}}_{ci}^H{\mathbf{w}}_{sk}+n_{ci},$$

(3)

where ${\mathbf{w}}_{ci}$ and ${\mathbf{w}}_{sj}$ are the i-th and the j-th column of ${\mathbf{W}}_c$ and ${\mathbf{W}}_s$, respectively; $n_{ci}$ is the noise of the i-th communication user; ${\sum }_{j\ne i}{x}_{cj}{\mathbf{h}}_{ci}^H{\mathbf{w}}_{cj}$ represents the interference from other communication users and ${\sum }_{k=1}^{N_2}{x}_{sk}{\mathbf{h}}_{ci}^H{\mathbf{w}}_{sk}$ represents the interference from all the sensing users to the communication user’s received signal, respectively. ${\mathbf{h}}_{ci}^{\mathrm{H}}$ is the i-th row of ${\mathbf{H}}_c$, denoting the channel for the i-th communication user, which is modeled as (4).

$${\mathbf{h}}_{ci}=\sqrt{L_{ci}\left(d_{ci}\right)}{\tilde{\mathbf{h}}}_{ci},$$

(4)

where ${\tilde{\mathbf{h}}}_{ci}$ denotes the small-scale fading coefficients and $L_{ci}\left(d_{ci}\right)$ denotes the pathloss of the i-th communication user, which is at a distance of $d_{ci}$ from the BS. The pathloss is modeled as $L_{ci}\left(d_{ci}\right)=c{d}_{ci}^{-\alpha }$, where $\alpha$ is the path loss exponent, which usually takes values ranging from 2.0 to 6.0 [21]; c is the pathloss at a reference distance and can be treated as a constant.

For the i-th communication user, the signal to interference plus noise ratio (SINR) is given by (5).

$${\mathrm{SINR}}_i={\displaystyle \frac{{\left|{\mathbf{h}}_{ci}^H{\mathbf{w}}_{ci}\right|}^2}{{\left|{\sum }_{j\ne i}{\mathbf{h}}_{ci}^H{\mathbf{w}}_{cj}\right|}^2+{\left|{\sum }_{k=1}^{N_2}{\mathbf{h}}_{ci}^H{\mathbf{w}}_{sk}\right|}^2+{\sigma }^2}}.$$

(5)

The achievable rate can be expressed as (6).

$$R_i={\log }_2(1+{\mathrm{SINR}}_i).$$

(6)

Then the SR of the MIMO system can be obtained as (7).

$$R=\sum _{i=1}^{N_1}{R}_i.$$

(7)

The massive MIMO ISAC system also needs to sense the position of the sensing users. In this work, we take the RP at the sensing user as a metric for evaluating the system perception performance [22]. The RP for the j-th sensing user $P_{sj}$ is denoted as (8).

$$P_{sj}={∥{\mathbf{h}}_{sj}^H{\mathbf{w}}_{sj}∥}_2^2,$$

(8)

where ${\mathbf{h}}_{sj}$ is modeled in the same way as the communication users. To ensure the sensing accuracy, the RP should be no less than a predefined threshold $\overline{P}$. Therefore, we have (9).

$$P_{sj}\ge \overline{P},1\le j\le N_2.$$

(9)

To this end, we can formulate the precoding problem for massive MIMO ISAC systems as

$$\begin{array}{cc}\hfill & \underset{W}{max}R\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \mathrm{C}1:\mathrm{Tr}\left({\mathbf{W}}^H\mathbf{W}\right)=1,\hfill \\ \hfill & \mathrm{C}2:P_{sj}\ge \overline{P},1\le j\le N_2.\hfill \end{array}$$

(10)

This optimization problem is difficult to solve due to the non-convex objective and the constraint of C2. In the following section, we propose to use a machine learning-based scheme to solve (10) and introduce the novel KAIP scheme.

3. The Proposed KAN and Attention-Based ISAC Precoding Method

This section introduces the novel KAN and Attention-based ISAC Precoding, i.e., KAIP method. The proposed scheme is mainly composed of the attention layer and the KAN layer. The simple structure not only allows for low-complexity processing but also improves system behavior.

3.1. Network Model of KAIP

The structure of the KAIP network is shown in Figure 2, which consists of an input layer, an output layer, an attention layer, and two hidden KAN layers. To be specific, the input of the network is the channel matrix $\mathbf{H}$, which is fed into the attention layer. The output of the attention layer is then input into the KAN layer, which outputs the precoding matrix. The attention layer is responsible for deeply extracting the interference between different users in the system, which facilitates the subsequent suppression of strongly interfering users. The KAN layers are responsible for directly generating the precoding matrix.

The data flow process in the attention layer is shown in Figure 3. There are three learnable parameter matrices in the attention layer, namely ${\mathbf{W}}_q$, ${\mathbf{W}}_k$ and ${\mathbf{W}}_v$. Firstly, $\mathbf{Q}$, $\mathbf{K}$, $\mathbf{V}$ can be obtained by calculating $\mathbf{Q}={\mathbf{HW}}_q$, $\mathbf{K}={\mathbf{HW}}_k$ and $\mathbf{V}={\mathbf{HW}}_v$. Secondly, the matrix $\mathbf{A}$ is obtained by $\mathbf{A}={\mathbf{QK}}^T$. To ensure gradient stability during training, each element of matrix $\mathbf{A}$ is divided by $d_K$, where $d_K$ is the dimension of $\mathbf{K}$. Thirdly, softmax normalization is computed for the matrix $\mathbf{A}$ on a row-by-row basis, and finally the final output ${\mathbf{D}}_{out}$ is obtained by ${\mathbf{D}}_{out}=\mathrm{softmax}\left({\displaystyle \frac{\mathbf{A}}{\sqrt{{\mathit{d}}_k}}}\right)\mathbf{V}$. The entire computation process of the attention layer can be summarized by (11).

$${\mathbf{D}}_{out}=\mathrm{softmax}\left({\displaystyle \frac{\mathbf{A}}{\sqrt{{\mathit{d}}_k}}}\right)\mathbf{V}.$$

(11)

Through the strong feature extraction capability of the attention mechanism, the interference between different users can be extracted from the channel matrix, which facilitates the subsequent assignment of lower gains and weights to the strongly interfering users, thus reducing the interference between multiple users and improving the generalization capability of the algorithm.

Existing neural network-based precoding schemes face high computational complexity. To solve this problem, we propose to introduce KAN, which is inspired by the Kolmogorov–Arnold representation theorem [20]. KAN is different from traditional MLPs in its unique structural design, which achieves effective modeling of complex functions by placing the activation functions on edges instead of nodes. By carefully designing the nonlinear activation function, KAN is able to adapt to various types of complex channel environments, thus improving the generalization ability of the algorithm as well as reducing the number of network parameters.

The following briefly describes the KAN layers and the computational procedure of the KAN layers. Each edge in the two KAN layers corresponds to an activation function, and the activation function we adopt is given by (12), where $\mu$, $P_i$ and $\sigma$ are learnable parameters, and $B_{i,n}\left(x\right)$ is the B-spline basis function.

$$\varphi \left(x\right)={\displaystyle \frac{1}{\sqrt{2\pi }}}{\mathrm{e}}^{-{\displaystyle \frac{{\left(x-\mu \right)}^2}{{\sigma }^2}}}+\sum _{i=0}^n{P}_i{B}_{i,n}\left(x\right).$$

(12)

The input matrix from the previous attention layer ${\mathbf{D}}_{out}$ is fed into the first KAN layer. The computation from the first KAN layer to the second KAN layer is performed by the formula ${\mathbf{x}}_1={\mathsf{\Phi }}_l{D}_{out}$. ${\Phi }_{\mathit{l}}\in {\mathbb{F}}^{{\mathbf{n}}_{\mathbf{1}}\times \mathbf{1}}$ is a vector consisting of activation functions at the first KAN layer as shown in (13), where $\mathbb{F}$ is the set of functions.

$${\Phi }_{\mathit{l}}={\left[\begin{array}{cccc}{\varphi }_{\mathbf{0},\mathbf{1},\mathbf{1}}(·)& {\varphi }_{\mathbf{0},\mathbf{1},\mathbf{2}}(·)& \dots & {\varphi }_{\mathbf{0},\mathbf{1},{\mathbf{n}}_{\mathbf{1}}}(·)\end{array}\right]}^{\mathrm{T}},$$

(13)

where $n_1$ represents the number of nodes in the first KAN layer; each element ${\varphi }_{l,j,i}(·)$ is the function corresponding to the edge connecting the i-th node of layer l to the j-th node of layer $l+1$. Finally, the precoding matrix $\mathbf{W}$ can be calculated by (14).

$$\mathbf{W}=\left[\begin{array}{cccc}{\varphi }_{1,1,1}(·)& {\varphi }_{1,1,2}(·)& \dots & {\varphi }_{1,1,n_1}(·)\\ {\varphi }_{1,2,1}(·)& {\varphi }_{1,2,2}(·)& \dots & {\varphi }_{1,2,n_1}(·)\\ \dots & \dots & \dots & \dots \\ {\varphi }_{1,n_2,1}(·)& {\varphi }_{1,n_2,2}(·)& \dots & {\varphi }_{1,n_2,n_1}(·)\end{array}\right]{\mathbf{x}}_1,$$

(14)

where $n_2$ represents the number of nodes in the second layer and ${\mathbf{x}}_1$ is the output of the first KAN layer.

3.2. Training Process

3.2.1. Design of Loss Function

The constraints are not easy to handle when neural networks are used to solve the optimization problem. Therefore, we introduce a penalty function.

The constraint C1: $\mathrm{Tr}\left({\mathbf{W}}^H\mathbf{W}\right)=1$ enforces total transmit power normalization at the BS in the massive MIMO system. Specifically, it ensures that the sum of squared magnitudes of all precoding matrix elements equal 1, thereby limiting the BS’s radiated power to a fixed budget. We use ${\psi }_2(\mathrm{Tr}\left({\mathbf{W}}^H\mathbf{W}\right)-1)={\lambda }_2{(\mathrm{Tr}\left({\mathbf{W}}^H\mathbf{W}\right)-1)}^2$ to describe this constraint. The quadratic term smoothly penalizes deviations from unit power while maintaining convexity near the feasible region.

The constraint C2: $P_{sj}\ge \overline{P},1\le j\le N_2$ ensures minimum RP requirements for sensing users in the system. Physically, it guarantees that each sensing user receives sufficient signal power ($P_{sj}$) to maintain reliable sensing accuracy, defined by a threshold $\overline{P}$. We use ${\psi }_1(P_{sj}-\overline{P})={\lambda }_{1}log(P_{sj}-\overline{P})$ to describe this constraint. The logarithmic function imposes an infinite penalty as $P_{sj}$ approaches $\overline{P}$ from above, ensuring strict satisfaction of the minimum RP requirement while remaining differentiable.

In summary, the optimization problem is converted into (15).

$$\underset{\mathbf{W}}{max}R+{\psi }_1(P_{sj}-\overline{P})+{\psi }_2(\mathrm{Tr}\left({\mathbf{W}}^H\mathbf{W}\right)-1),$$

(15)

where ${\psi }_1\left(x\right)={\lambda }_{1}log\left(x\right)$, where ${\lambda }_1\ge 0$ is the penalty weight. When $P_{sj}$ approaches $\overline{P}$, the value of the function tends to $-\infty$, which ensures the constraint C2. In (15), ${\psi }_2\left(x\right)={\lambda }_2{x}^2$, where ${\lambda }_2\ge 0$ is the penalty weight.

Based on the above objective function, we can design the loss function as (16).

$$\begin{array}{cc}\hfill \mathcal{L}& =-\alpha R+\beta \mathrm{Var}\left({\left\{R_i\right\}}_{i=1}^{N_1}\right)+\gamma \mathrm{Var}\left({\left\{R_i|\mathbf{H}\right\}}_{i=1}^{N_1}\right)\hfill \\ \hfill & +{\psi }_1\left(P_{sj}-\overline{P}\right)+{\psi }_2\left(\mathrm{Tr}\left({\mathbf{W}}^{\mathrm{H}}\mathbf{W}\right)-1\right).\hfill \end{array}$$

(16)

The loss function is divided into five parts. The first part $-\alpha R$ is responsible for ensuring that the maximum SR is obtained, in which $\alpha$ is the weight coefficient. The second part $\beta \mathrm{Var}\left({\left\{{\mathrm{R}}_{\mathrm{i}}\right\}}_{\mathrm{i}=1}^{{\mathrm{N}}_1}\right)$ is responsible for ensuring fairness among users in the multi-user scenario, which means the achievable rate obtained by each user is as close as possible, where $\beta$ is the weight coefficient, Var represents the variance of the achievable rates for each communication user. The third part $\gamma \mathrm{Var}\left({\left\{{\mathrm{R}}_{\mathrm{i}}|\mathbf{H}\right\}}_{\mathrm{i}=1}^{{\mathrm{N}}_1}\right)$ is responsible for improving the adaptive ability of the model in a complex channel environment, where $\gamma$ is the weight coefficient. By calculating the dispersion of the SR under the current complex channel conditions, the adaptive ability of the channel can be obtained. The fourth and the fifth parts are used to ensure the constraints in (10) are met. The weights were indeed determined empirically through extensive experimentation and tuning to balance the contributions of each term effectively.

In order to avoid the overfitting phenomenon during the training process, we also add L2 regularization to the learnable parameters $\theta$ of the activation function as

$${\mathcal{L}}_{L2}=\mathcal{L}+\tau {∥\theta ∥}_2^2,$$

(17)

where $\tau$ represents the regularized intensity.

3.2.2. Training Method

The training method used in this paper is Adam algorithm [23]. Firstly, all the parameters of the KAIP network are initialized. Then we split the real and imaginary parts of each element of the channel matrix $\mathbf{H}$ to form the real matrix ${\mathbf{H}}^{\prime }$ as the input to KAIP. The output of KAIP is the real precoding matrix ${\mathbf{W}}^{\prime }$, which is then transformed into the complex precoding matrix $\mathbf{W}$. $\mathbf{W}$ is used to compute the loss ${\mathcal{L}}_{L2}$, and the gradient is calculated as ${\nabla }_{\theta }{\mathcal{L}}_{L2}$. Finally, the Adam optimizer is used to update $\theta$ as

$${\theta }^{*}=\theta +\alpha ·Adam\left({▽}_{\theta }{\mathcal{L}}_{L2},\theta \right).$$

(18)

In order to further reduce the network size and decrease the computational complexity, we adopt pruning operations in the training process. For a node in the KAN layer, we design an afferent function and an efferent function, which are used to measure the importance of a node receiving/transmitting information from a node in its previous/subsequent layer.

For the i-th node in layer l, the afferent function $I_{l,i}$ is given by

$$I_{l,i}^{in}=\underset{k}{max}\left({∥{\varphi }_{l-1,i,k}∥}_1\right),$$

(19)

where ${\varphi }_{l-1,i,k}$ denotes the activation function (edge) connecting the k-th node of the $(l-1)$-th layer to the i-th node of the l-th layer. $I_{l,i}$ denotes the maximum value of the L1-norm of all edges (activation functions) connected to that node. In this way, it is possible to highlight the connections that have the greatest impact on the input of that node. Thus, the incoming function reflects the strength of the most dominant message received by the node from its previous layer.

For the i-th neuron in layer l, the efferent fraction $I_{l,i}$ is given by

$$I_{l,i}^{out}=\underset{k}{max}\left({∥{\varphi }_{l+1,i,k}∥}_1\right),$$

(20)

where ${\varphi }_{l+1,i,k}$ denotes the activation function (edge) connecting the k-th node of layer $(l+1)$ to the i-th node of layer l. The efferent function takes the maximum value of the L1 norm of all activation functions from that node. It is able to highlight the connection that has the greatest impact on the output of the nodes in the subsequent layer.

The node is viewed as an important node and is retained if both afferent and efferent values of it are greater than a threshold $\xi$. Otherwise, the node will be removed from the network. In this way, the redundant nodes in the network are removed, and the network structure is simplified. In this way, it is possible to avoid the overfitting situation and enhance the generalization performance.

4. Numerical Results and Analysis

In order to evaluate the behavior of the proposed KAIP scheme, we carried out extensive numerical studies. We consider a scenario where the number of antennas at the BS is M = 256 and randomly generate a set of 10,000 channel matrices, including 5000 Rician fading channel samples and 5000 Rayleigh fading channel samples. The transmit power is normalized to 1 W, whilst the threshold power is set as $\overline{P}=0.15$ W. The path loss exponent $\alpha$ is set to 3.0. The weights in the loss function are set to $\lambda =1, \alpha =0.6, \beta =0.2, \gamma =0.2, \eta =1$, and the training set and test set for the KAIP model training are divided in an 8:2 ratio. The parameters for training KAIP are shown in

Table 1. Parameters for Training KAIP.

Parameter	Value
Number of neurons in hidden layer 1	512
Number of neurons in hidden layer 2	512
Grid size	3
Learning rate	0.001
Batch size	64
Epoch	500

. The proposed KAIP is trained and tested using an Intel i7-12700H CPU (made by Hewlett-Packard in Beijing, China) with Python 3.11 and Pytorch 2.1.2.

In order to show the superiority of the proposed KAIP, the following schemes are used for comparison:

• ZF: inter-user interference is eliminated by finding the pseudo-inverse of the channel matrix to generate the precoding matrix.
• MMSE: the precoding matrix is generated by balancing inter-user interference and noise enhancement.
• FCNN-based precoding scheme [24]: Two fully connected neural layers are adopted in FCNN. The parameters of FCNN are summarized in

  Table 2. The setting of FCNN parameters.

  Parameters	Value
  Number of nodes in the first FCNN layer	512
  Number of nodes in the second FCNN layer	512
  Learning rate	0.001
  Batch	64
  Epoch	500

  .
• CNN precoding scheme [25]: Two convolutional layers are adopted in CNN. The parameters of CNN are summarized in

  Table 3. The setting of CNN parameters.

  Parameters	Value
  Kernel size of CNN	4 × 4
  Learning rate	0.001
  Batch	64
  Epoch	500

  .

4.1. Convergence Analysis

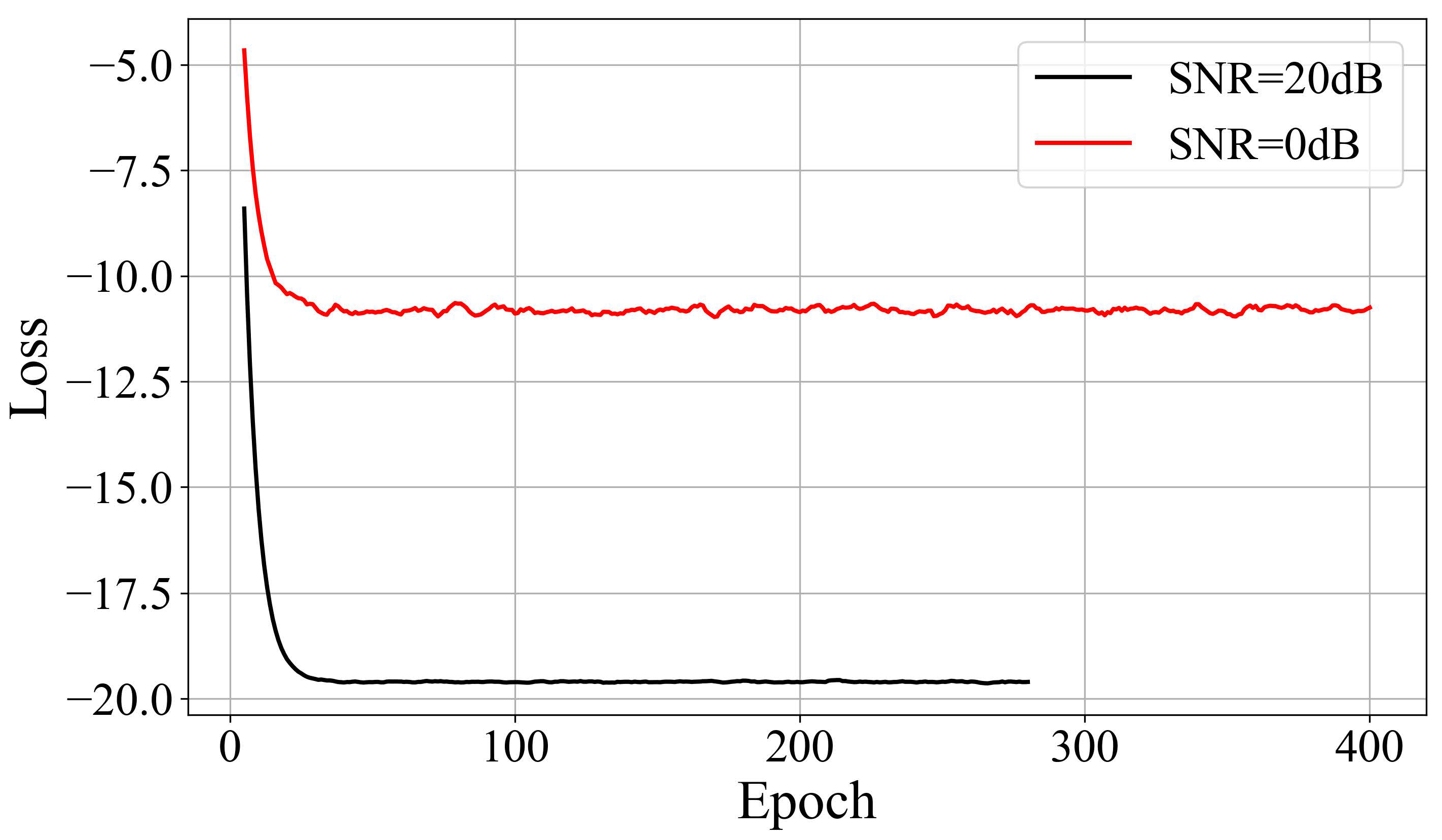
In Figure 4, we show the local best convergence curves for two of the most interesting experiments in terms of number of epochs needed to reach the convergence.

The convergence curves illustrate the training dynamics of the proposed KAIP scheme in a Rician fading channel with 16 communication users and 4 sensing users. The horizontal axis (Epoch) represents the number of training iterations, where each epoch corresponds to a full pass of the training dataset through the network. The vertical axis (Loss) quantifies the value of the composite loss function defined in Equation (16).

The first curve (black line, SNR = 20 dB) shows rapid convergence, with the loss stabilizing near −19.6 by epoch 280, accompanied by minimal oscillations. This behavior reflects KAIP’s ability to efficiently optimize precoding matrices under high-SNR conditions, where strong signal dominance reduces gradient noise during training. In contrast, the second curve (red line, SNR = 0 dB) converges more slowly, reaching −10.8 by epoch 400, with larger fluctuations due to heightened interference and channel uncertainty in low-SNR scenarios. The distinct convergence patterns underscore KAIP’s adaptability: higher SNR accelerates optimization by providing clearer gradient directions, while lower SNR introduces instability, necessitating more iterations to mitigate noise-induced perturbations in the loss landscape. The reduced oscillation amplitude at SNR = 20 dB further confirms the scheme’s stability in favorable channel conditions.

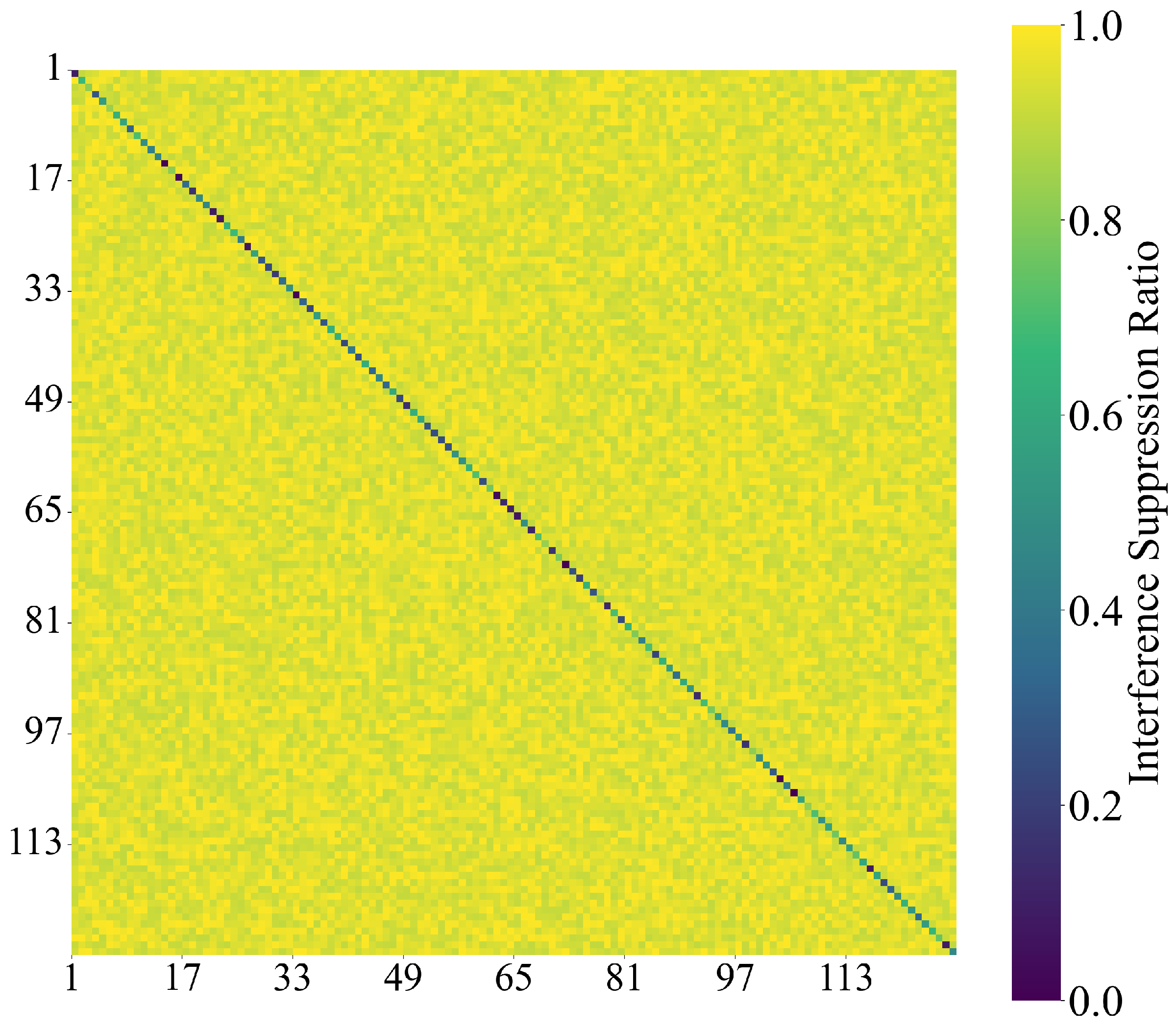
4.2. ISR

To quantitatively validate the attention mechanism’s interference suppression capability, we analyze the Interference Suppression Ratio (ISR) heatmap generated from a 128-user scenario, where ISR is defined as follows: $\mathrm{ISR}=1-\frac{\mathbf{A}}{max\left(\mathbf{A}\right)}$. The larger the ISR, the stronger the interference suppression capability. The simulation results of ISR is shown in Figure 5.

The simulation results show that off-diagonal blocks exhibit graduated suppression levels (close to yellow, ratio = 0.4–0.8), reflecting strong interference suppression capability. However, strong diagonal dominance (close to purple, ratio ≈ 0.2) confirms effective self-signal preservation.

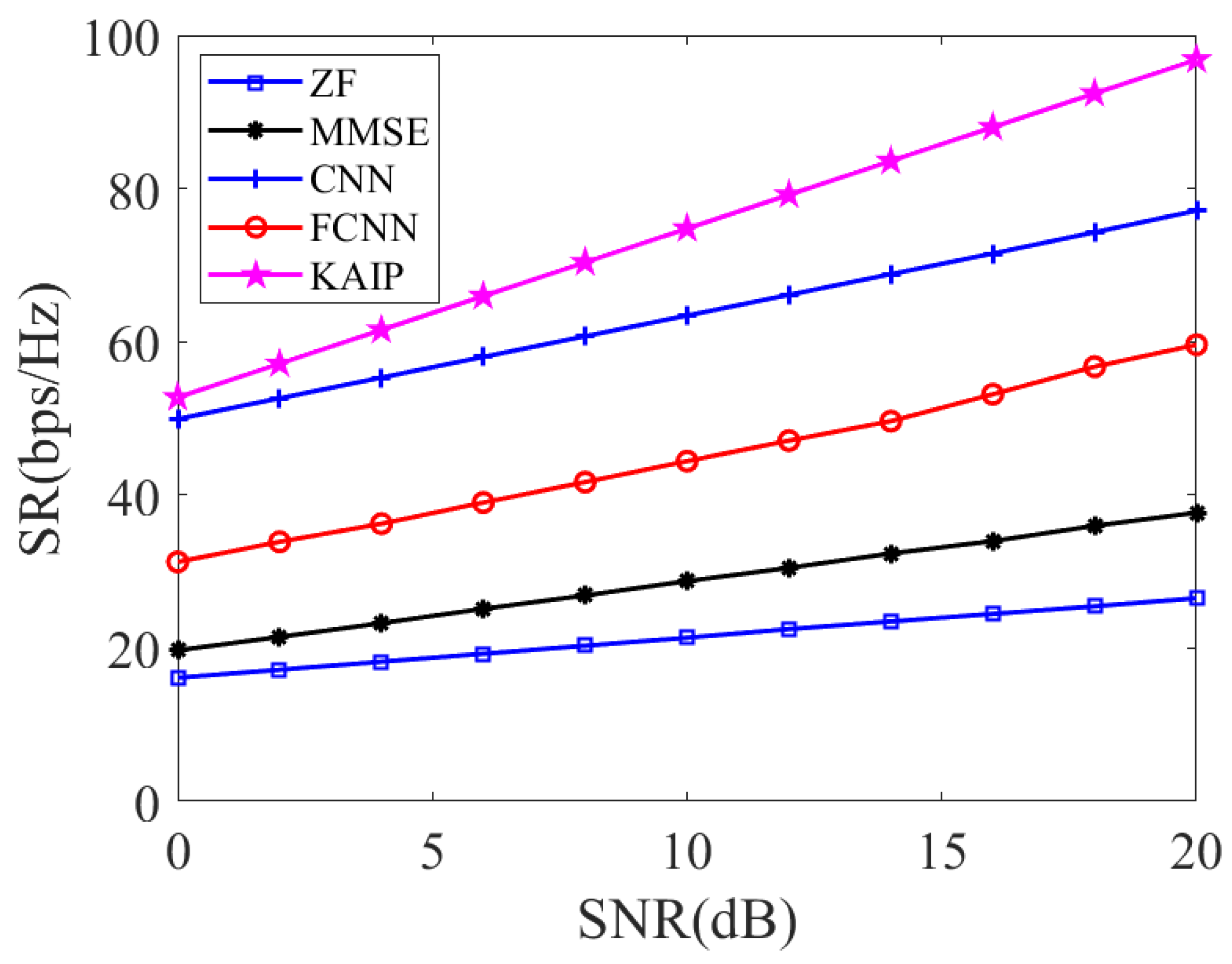
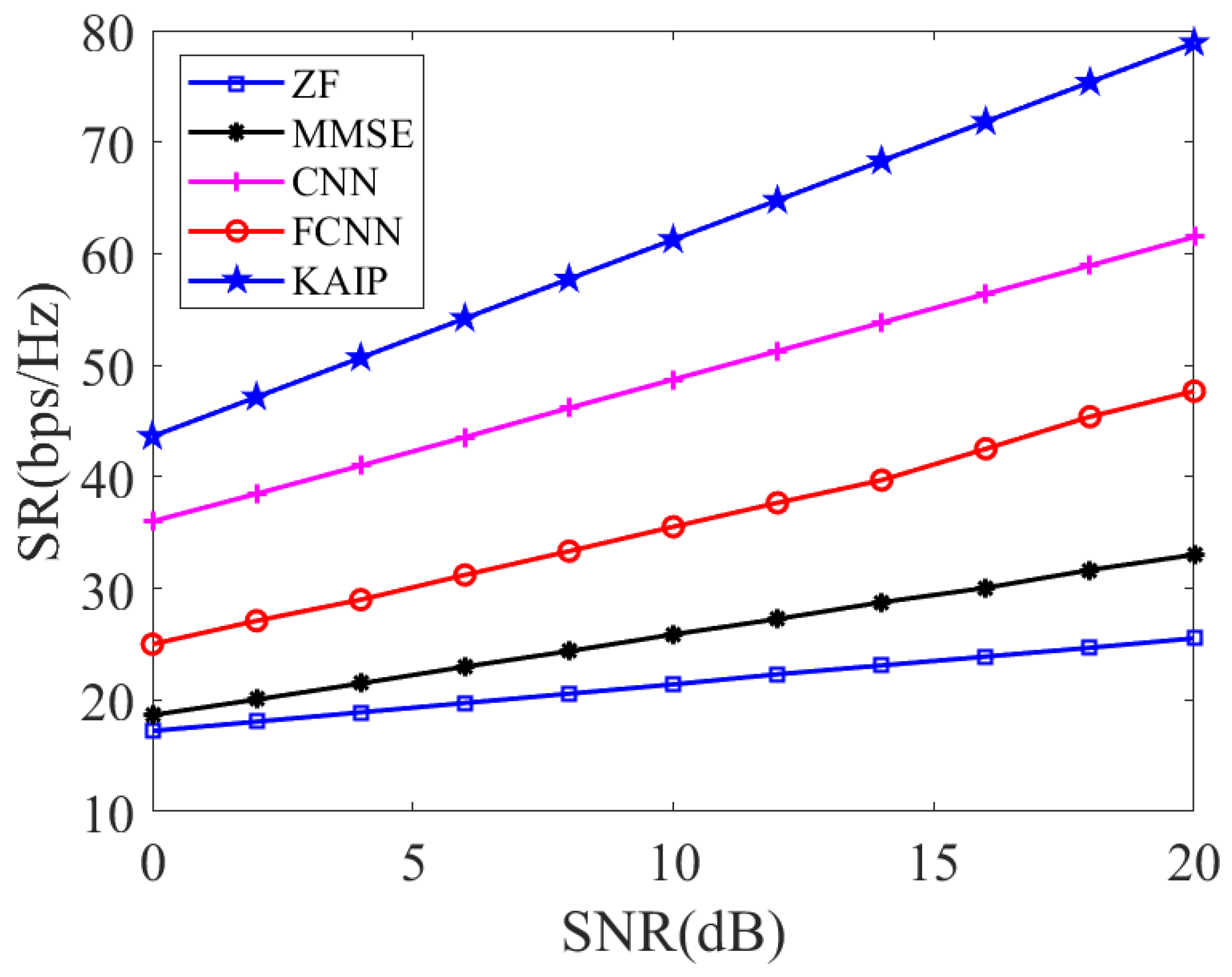
4.3. SR

The SR performance is tested with different signal-to-noise ratios (SNRs) in both Rician and Rayleigh fading channels, where the number of communication users is $N_1=16$. The SNR is defined as $\frac{1}{{\sigma }^2}$. As shown in Figure 6 and Figure 7, whether in Rician or Rayleigh fading channel, the SR always increases with respect to SNR. The deep learning-based schemes (i.e., FCNN, CNN, and KAIP) significantly outperform the conventional ZF and MMSE. Moreover, it can be clearly seen that the proposed KAIP achieves the highest SR, with a gain of around 15% over CNN-based precoding and 70% over FCNN-based precoding. The outstanding performance of the proposed KAIP comes from the fact that KAN has a stronger ability for nonlinear fitting than FCNN and CNN. Therefore, KAIP is more adapted to different channel environments.

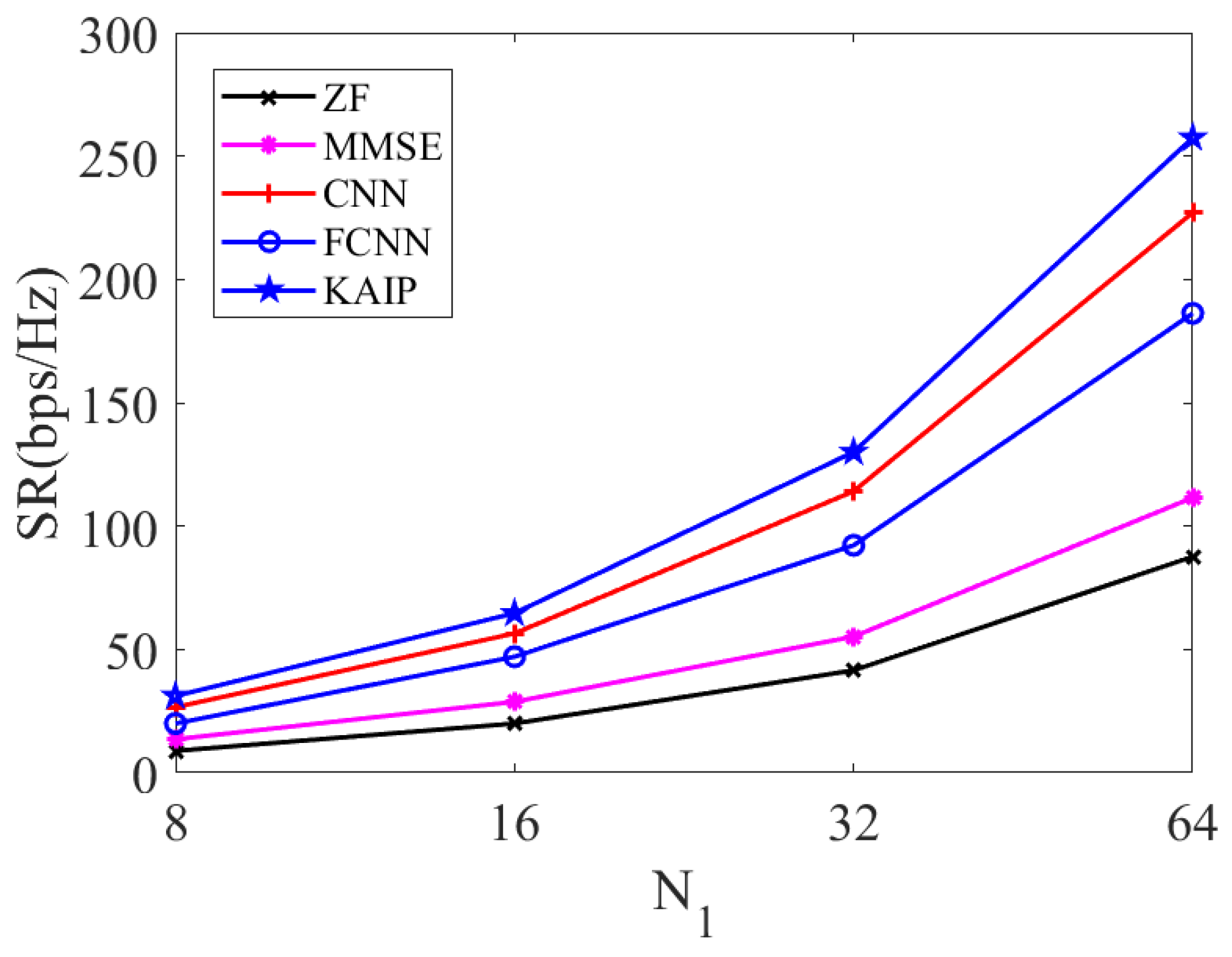
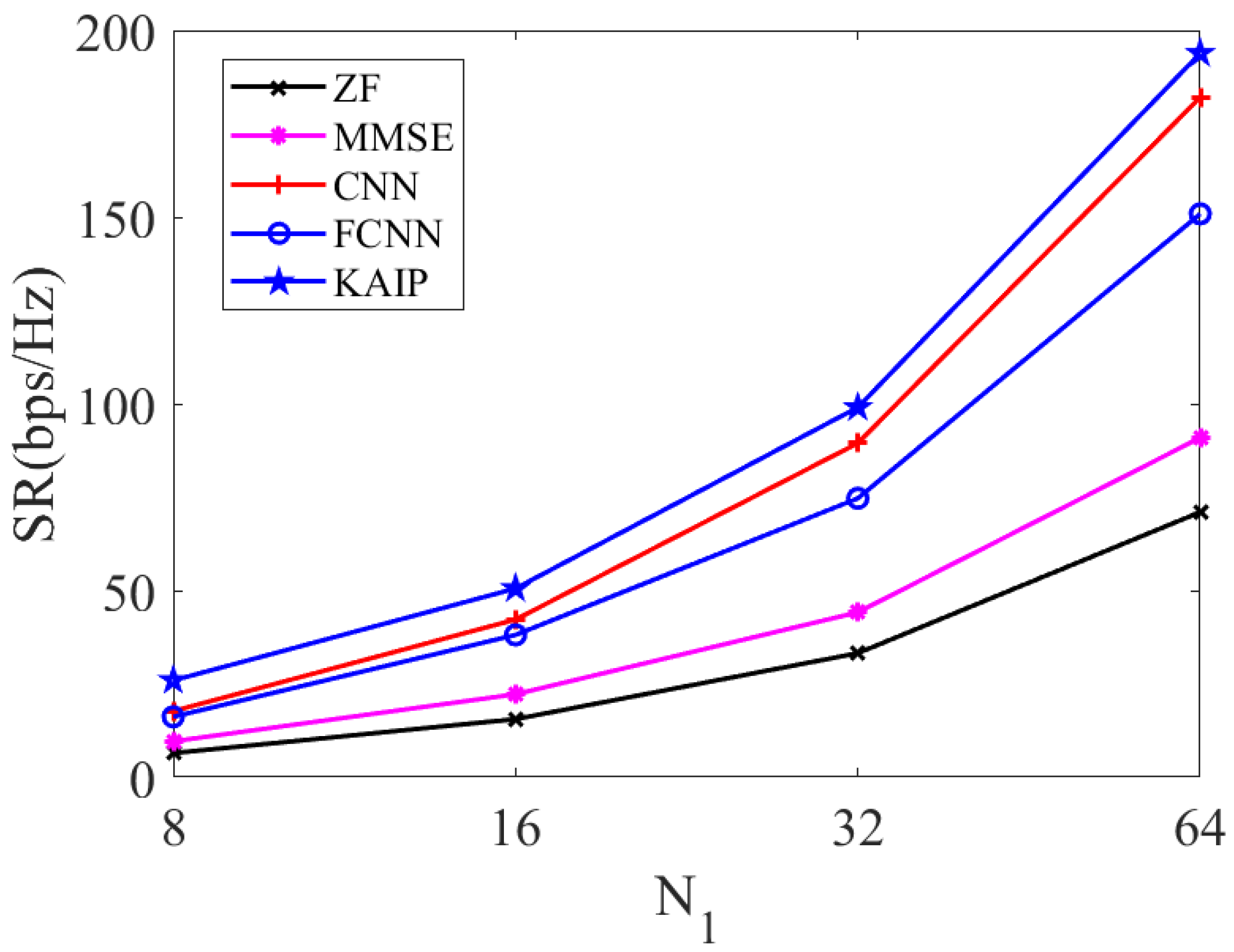
The SR performance under Rician and Rayleigh fading channels for different numbers of communicating users is given in Figure 8 and Figure 9, respectively, where the SNR is set to 10 dB. From the figures, it can be seen that the SR increases with the number of users in both fading cases. Among all the curves, the proposed KAIP obtains the highest SR, with a significant gain over its counterparts.

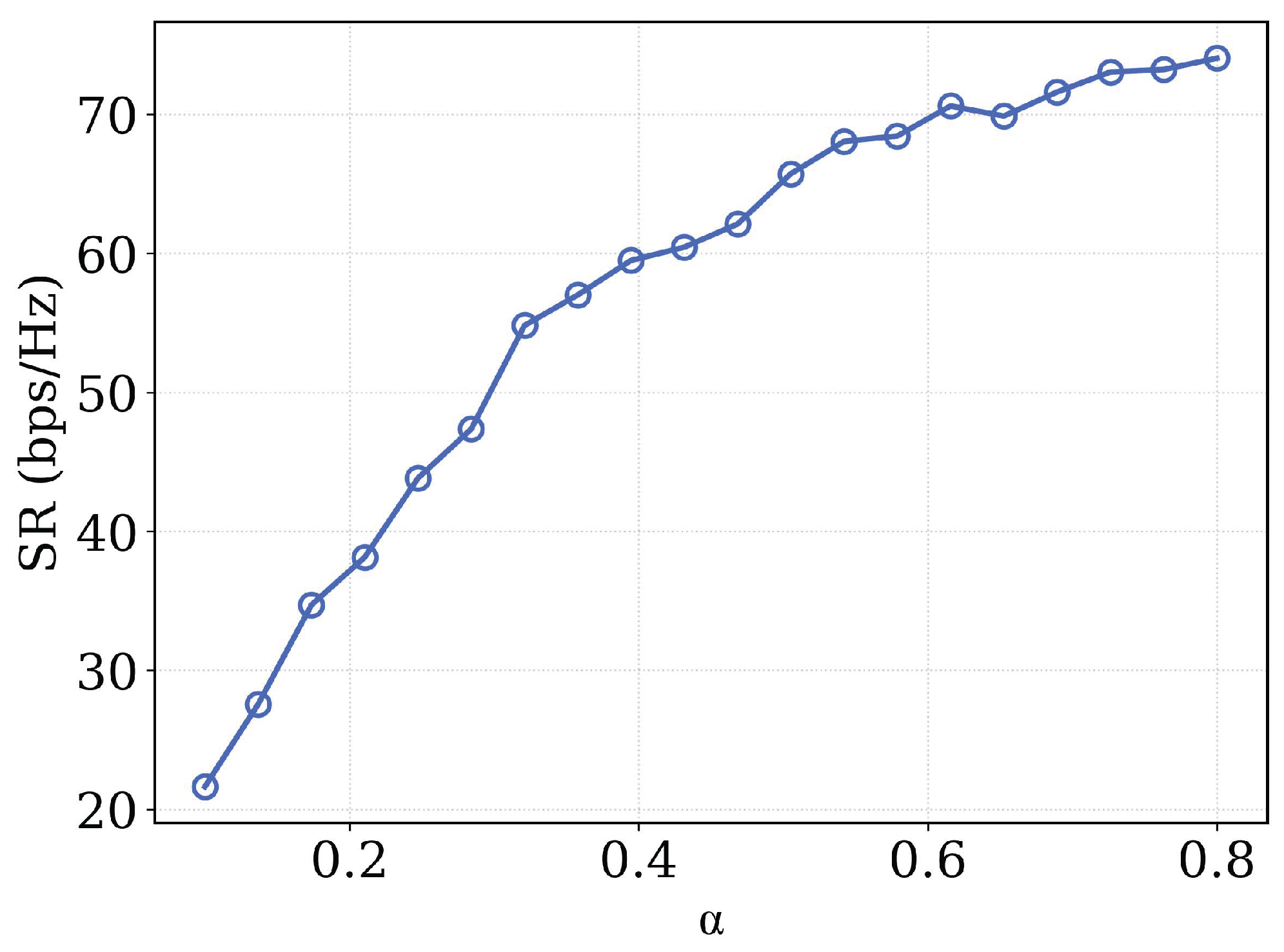
4.4. Analysis of $\alpha$, $\beta$ and $\gamma$

The experimental results presented in Figure 10, Figure 11 and Figure 12 provide a comprehensive analysis of how the key parameters $\alpha$, $\beta$ and $\gamma$ influence overall system performance across their respective operational ranges of 0.1–0.8, 0.1–0.5 and 0.1–0.5. The spectral efficiency (SR) demonstrates characteristic saturating growth behavior as parameter $\alpha$ increases, where initial rapid improvements in data rates gradually approach an asymptotic limit at higher $\alpha$ values, suggesting the existence of fundamental capacity constraints within the system architecture. This enhancement in spectral efficiency, however, introduces significant performance trade-offs that manifest through two distinct mechanisms. First, the system experiences progressively higher rate variance among users as $\alpha$ increases, indicating a substantial degradation in fairness metrics where certain users achieve disproportionately higher throughput compared to others in the network. Second, the inverse relationship observed between $\alpha$ and the channel adaptability parameter $\gamma$ reveals that the improved spectral efficiency comes at the expense of reduced system agility in responding to dynamic channel conditions, potentially compromising performance in time-varying wireless environments. Similarly, the inverse correlation between $\alpha$ and $\beta$ further confirms that gains in spectral efficiency directly impact fairness considerations, establishing a fundamental performance trade-off that system designers must carefully balance when optimizing these parameters for specific operational requirements and quality of service objectives. The comprehensive analysis of these interrelated effects provides valuable insights for developing adaptive parameter tuning strategies that can maintain optimal system performance across diverse network conditions and user requirements.

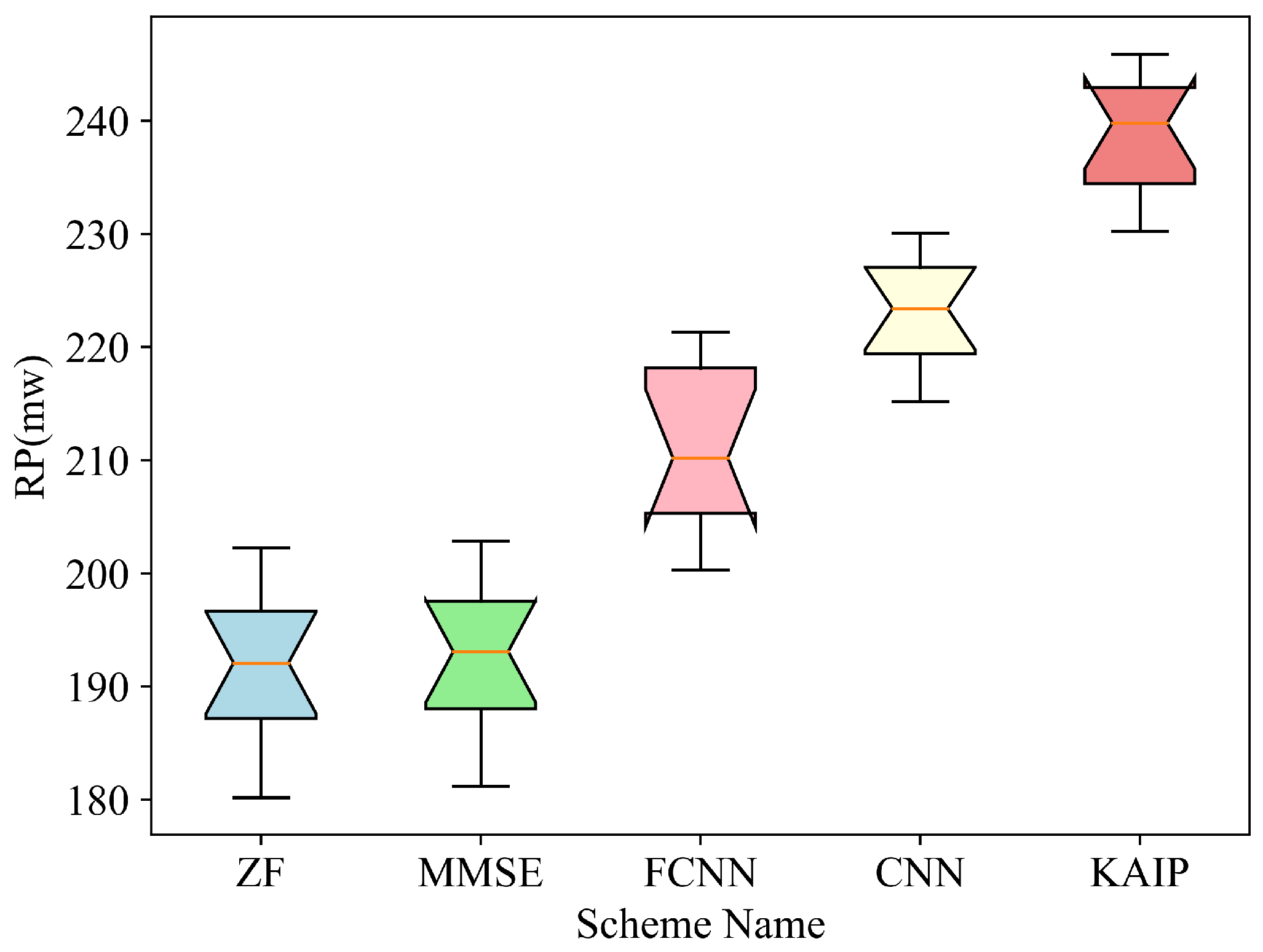
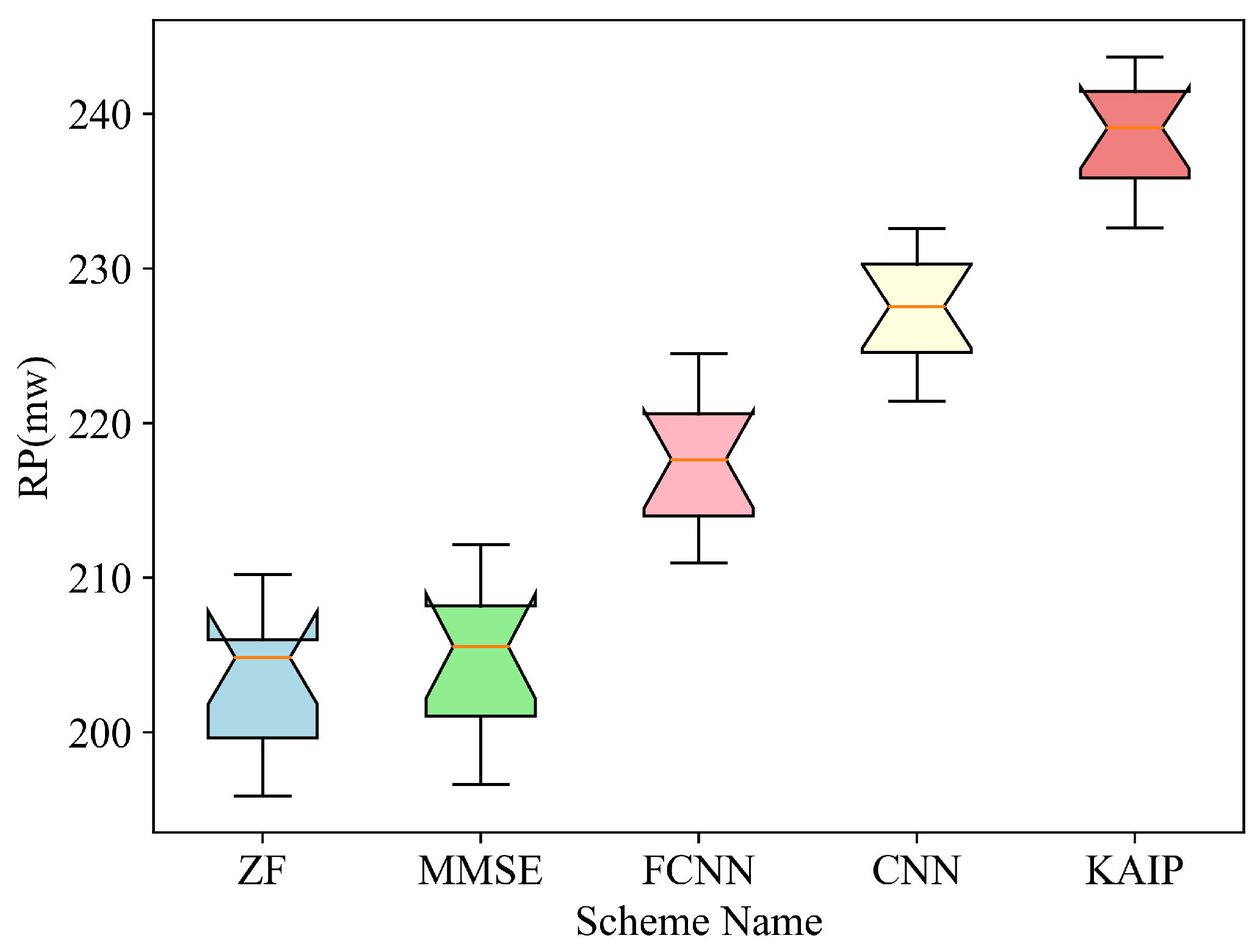
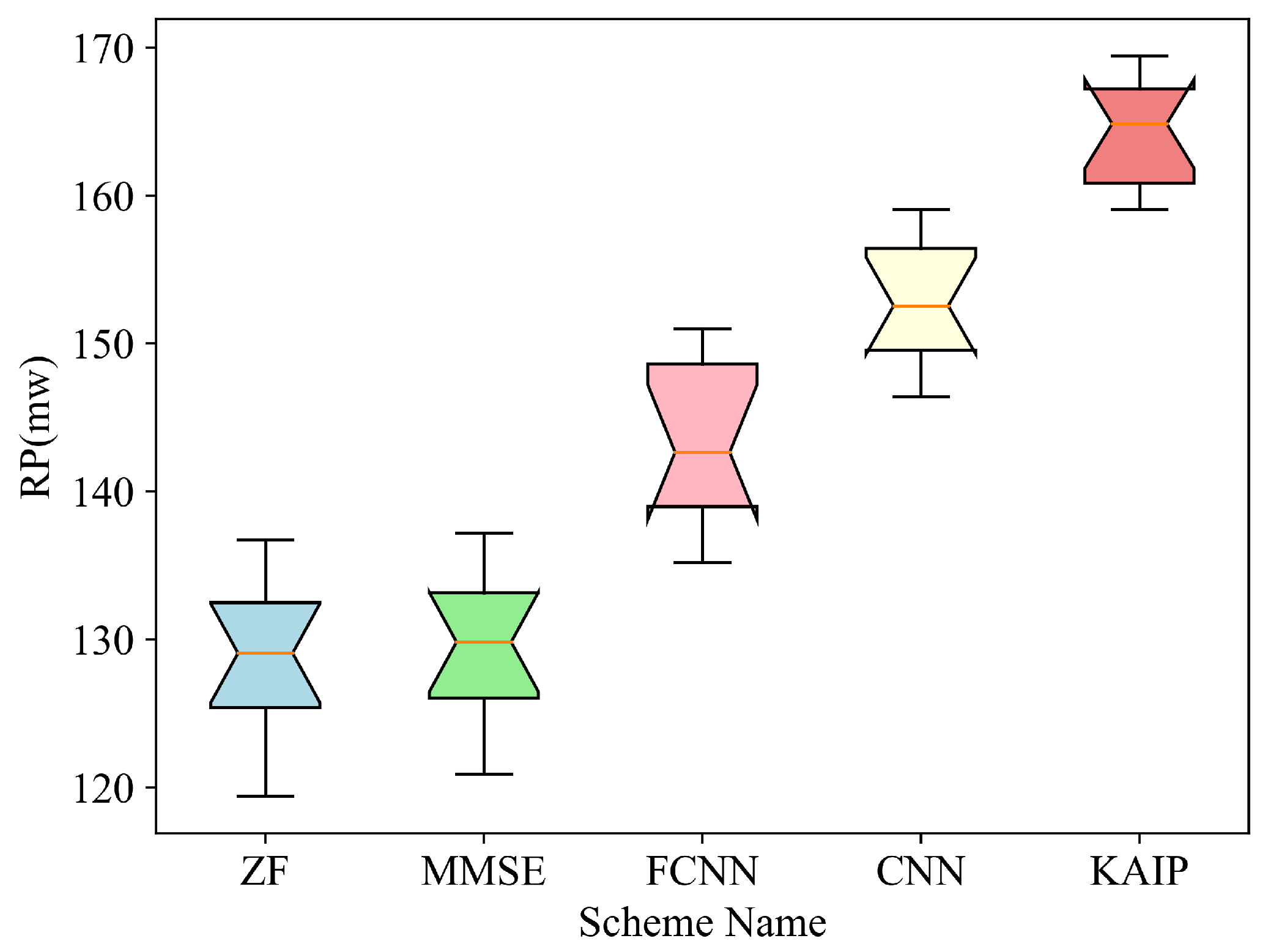
4.5. RP

The RP of four sensing users is tested at different distances from the BS (30 m and 40 m, respectively) in both Rician and Rayleigh fading channels. As shown in Figure 13, Figure 14, Figure 15 and Figure 16, the deep learning based schemes (i.e., FCNN, CNN and KAIP) significantly outperform the conventional ZF and MMSE. It can be seen that the proposed KAIP achieves the highest RP, with a gain of around 4% over CNN-based precoding and 11% over FCNN-based precoding. The RP decreases as the distance between the sensing user and the BS increases. The exceptional performance of the proposed KAIP is attributed to the fact that the neurons of KAN are composed of nonlinear functions, and its nonlinear fitting ability is much stronger than FCNN and CNN. Therefore, the KAIP-generated precoding matrix is more adapted to the different channel conditions at the same distance.

4.6. Complexity

The computation time (CT) of all the algorithms is given in Figure 17 with regard to different number of users. As shown in Figure 17, the CT of the deep learning based schemes (i.e., FCNN, CNN and KAIP) are significantly higher than the conventional ZF and MMSE. However, KAIP outperforms the FCNN and CNN based schemes, with a decrease in CT of around 90% and 96% compared with the CNN and FCNN based precoding, respectively. The proposed KAIP owns a superior behavior in that KAN layer in KAIP can complete the data fitting by using less hidden layers and fewer neurons. Therefore, the computational complexity of KAIP is much lower than the other deep learning based schemes.

Furthermore,

Table 4. Comparison of computational complex.

Method	Computational Complex
ZF	$O(N^3+M{N}^2)$
MMSE	$O(N^3+M{N}^2)$
FCNN	$O\left(N(M{k}_1+k_1{k}_2+k_{2}M)\right)$
CNN	$O(MN(s_1^2+s_2^2)+N{M}^2)$
KAIP	$O(N^2{d}_k+NM{d}_k+d_k{n}_1+n_{2}MN)$

provides a theoretical analysis of the computational complexity between KAIP and other baselines. The computational complexity of ZF is primarily determined by the matrix inversion and multiplication operations [26], represented as $O(N^3+M{N}^2)$. MMSE shares a similar complexity of $O(N^3+M{N}^2)$ due to its reliance on regularized matrix inversion [26]. FCNN involves dense matrix multiplications across layers [27], leading to a complexity of $O\left(N(M{k}_1+k_1{k}_2+k_{2}M)\right)$. $k_1$ is the number of nodes in the first FCNN layer. $k_2$ is the number of nodes in the second FCNN layer. The computational complexity of CNN is determined by its convolution operations [28], represented as $O(MN(s_1^2+s_2^2)+N{M}^2)$, where $s_1$ represents the first kernel size and $s_2$ represents the second kernel size. KAIP combines KAN and attention mechanisms [29], leading to a complexity of $O(N^2{d}_k+NM{d}_k+d_k{n}_1+n_{2}MN)$, where $n_1$ represents the number of neurons in hidden layer 1 after pruning, and $n_2$ represents the number of neurons in hidden layer 2 after pruning.

4.7. Ablation Experiments

The ablation experiments were conducted under 256 BS antennas serving 16 communication users and 4 sensing users, evaluating three scheme variants (KAIP, No Attention, No KAN) across key metrics (RP, SR, CT) with parameters including SNR (14 dB, 16 dB, 18 dB, 20 dB), user distances (30 m, 40 m and 50 m), and system scale (N = 10 and 100 users), using mixed Rician/Rayleigh fading channels to validate the individual contributions of attention mechanisms and KAN layers. The ablation experiment results are shown in

Table 5. Ablation Study on RP.

RP (mw)	Distance (m)	30	40	50
Scheme
KAIP		322	237	178
No Attention		287 (−10%)	208 (−12%)	149 (−16%)
No KAN		311 (−3%)	225 (−5%)	165 (−7%)

and

Table 6. Ablation study on SR.

SR (bps/Hz)	SNR	14	16	18	20
Scheme
KAIP		81	87	92	98
No Attention		62 (−23%)	67 (−23%)	71 (−23%)	76 (−22%)
No KAN		71 (−12%)	77 (−11%)	80 (−12%)	77 (−12%)

.

For RP, removing the attention mechanism reduces RP by 10–16% across distances (30–50 m), demonstrating its critical role in interference suppression and power allocation for sensing users. The degradation worsens with distance (e.g., −16% at 50 m), highlighting attention’s adaptability to pathloss. Without KAN, RP drops by 3–7%, showing KAN’s ability to fine-tune precoding weights for optimal power delivery, especially in far-field scenarios.

For SR, the absence of attention causes a severe 22–23% SR loss at all SNRs, proving its necessity for multi-user interference management and channel feature extraction. The absence of KAN layers reduces SR by 11–12%, as KAN’s nonlinear fitting capability better adapts to complex channel conditions.

4.8. SR-Weighted (SW)

Finally, from a cost-benefit trade-off perspective, we define a new SW precoding metric inspired by [30] under a Rayleigh fading channel. SW is defined as $\mathrm{SW}=\frac{\mathrm{SR}\times \mathrm{RP}}{\mathrm{CT}}$. The proposed precoding metric SW quantifies the system efficiency by measuring the joint communication-sensing performance per unit of computational cost. The results are depicted in Figure 18.

The experimental evaluation reveals that KAIP achieves an optimal balance between performance gains and computational efficiency from a cost-benefit standpoint, establishing its superiority over conventional approaches. Compared with traditional ZF and MMSE methods, KAIP demonstrates substantial performance improvements with 62–137% higher system welfare (SW), while maintaining a consistent 14–23% advantage over deep learning baselines, including FCNN and CNN architectures. These significant gains are attributed to KAIP’s innovative synergistic design that effectively combines complementary technologies. The integrated attention mechanism contributes a notable 23% enhancement in spectral efficiency (SR) through its sophisticated interference suppression capabilities, while the KAN layers provide a 12% improvement in resource partitioning (RP) with remarkable computational efficiency—requiring only an 8% incremental processing overhead. Ablation studies further validate the architectural choices, confirming that each component contributes meaningfully to the overall system performance without introducing excessive complexity. This carefully engineered balance between performance enhancement and computational cost positions KAIP as a practical solution for real-world deployment scenarios where both efficiency and effectiveness are critical considerations. The results demonstrate how intelligent architectural design can achieve substantial quality-of-service improvements while maintaining reasonable implementation costs, addressing a key challenge in modern communication system optimization.

5. Conclusions

In this work, we have proposed a novel precoding scheme, i.e., KAIP, to improve the performance of massive MIMO ISAC systems in both Rayleigh and Rician fading scenarios. KAIP’s attention layer has shown to be able to suppress the inter-user interference, whilst KAN’s spline-based nonlinear activation can adapt to dynamic channel conditions with low complexity. The proposed KAIP based precoding scheme outperforms ZF, MMSE, FCNN and CNN based precoding schemes, achieving significant improvement in both SR and RP over existing schemes with a over 90% reduction in CT compared with other performance-harvesting deep learning based schemes. Furthermore, from a theoretical perspective, we provide an analysis of KAIP’s computational complexity, convergence, and the interference suppression capability of the attention layers, along with experimental verification.

However, this study does not consider scenarios where users are in high-speed motion or channels are time-varying, which imposes limitations on the applicability of KAIP. The adaption to high mobility scenarios is important and is remained for future work. As KAN is a key component of KAIP, we do not analyze its intrinsic performance (e.g., approximation guarantees). The rationality and specific performance of KAN have been thoroughly discussed in [31], and thus, they are not elaborated on in this paper.