A Fractional-Order State Estimation Method for Supercapacitor Energy Storage
Abstract
1. Introduction
- SC single-cell dynamics: Section 2 reviews the equivalent circuit model (ECM) and the governing equations for a single-cell SC.
- SC bank dynamical model: In Section 3, a new model for the SC bank is proposed, leveraging information from single-cell models. In previous studies, the model of a single SC cell has typically been used to represent the entire SC bank. However, in this work, a model specifically for a series–parallel combination of SC cells is derived based on the characteristics of a single-cell model. To the best of our knowledge, this is the first time such an approach has been proposed. This ECM is subsequently utilized for designing the observer.
- Observability analysis: The SC bank observability is analyzed in Section 4, demonstrating that its dynamic model is not inherently observable (the root cause for conventional observers to fail in accurately estimating the states). This is a novel approach that has not been previously explored.
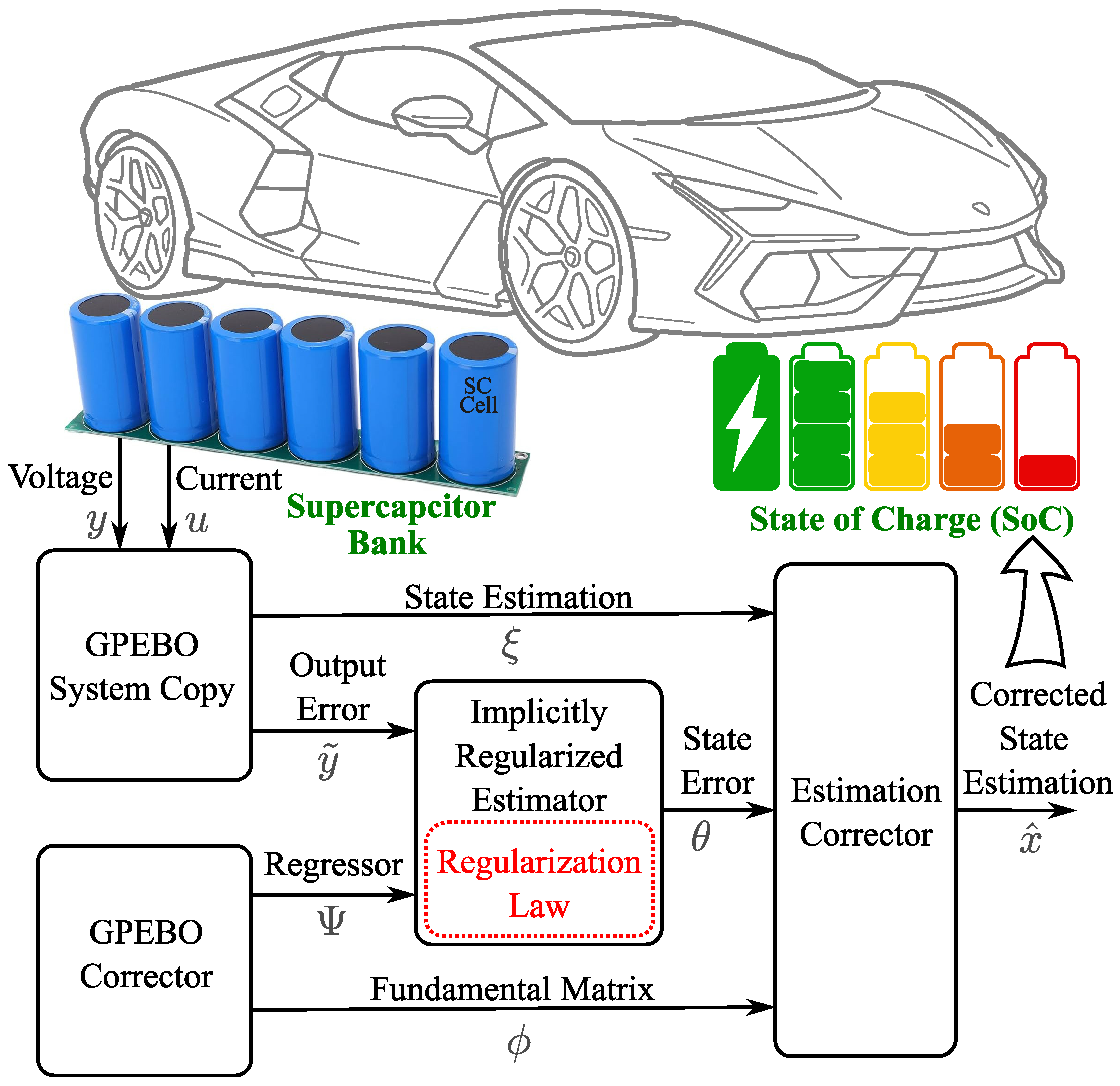
- Qualitative study on the proposed observer: Section 5, for the first time, elaborates on the proposed observer to address the weak observability issue, and an implicit regularization law is subsequently proposed. This feature is embedded into a generalized parameter estimation-based observer (GPEBO). The red dashed line in Figure 1 highlights this module.
- Experimental study: To validate the proposed observer and its parameter identification method, a series of experiments was conducted, with results presented in Section 6. To this end, a novel approach for identifying the fractional-order system using the MATLAB integer-order identification tool is proposed for the first time.
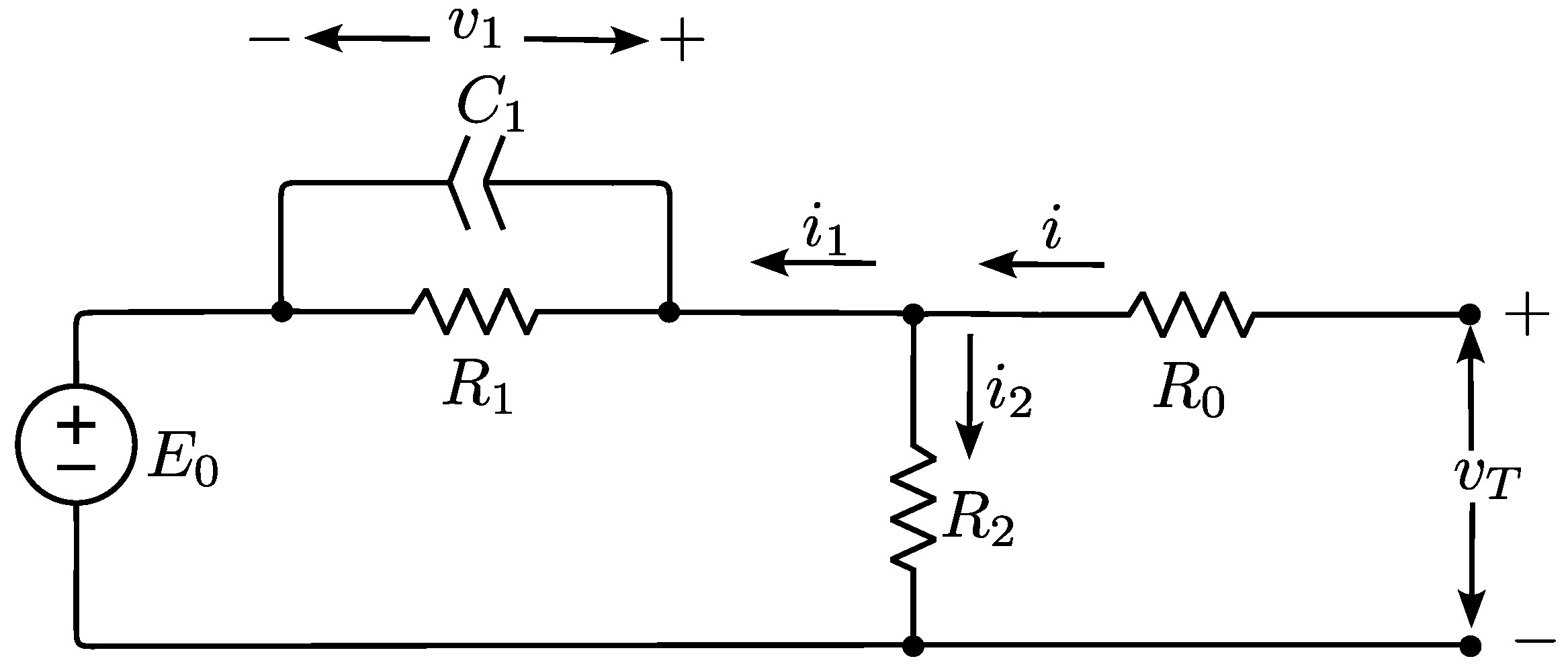
2. Modeling of a Single-Cell Supercapacitor
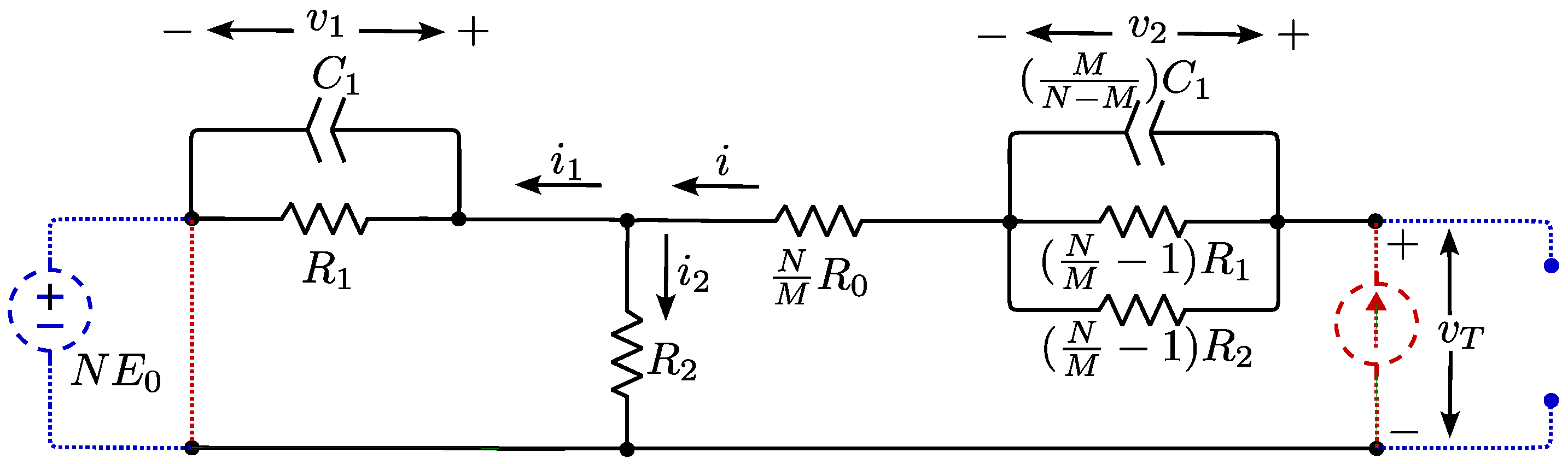
3. Supercapacitors Bank Model
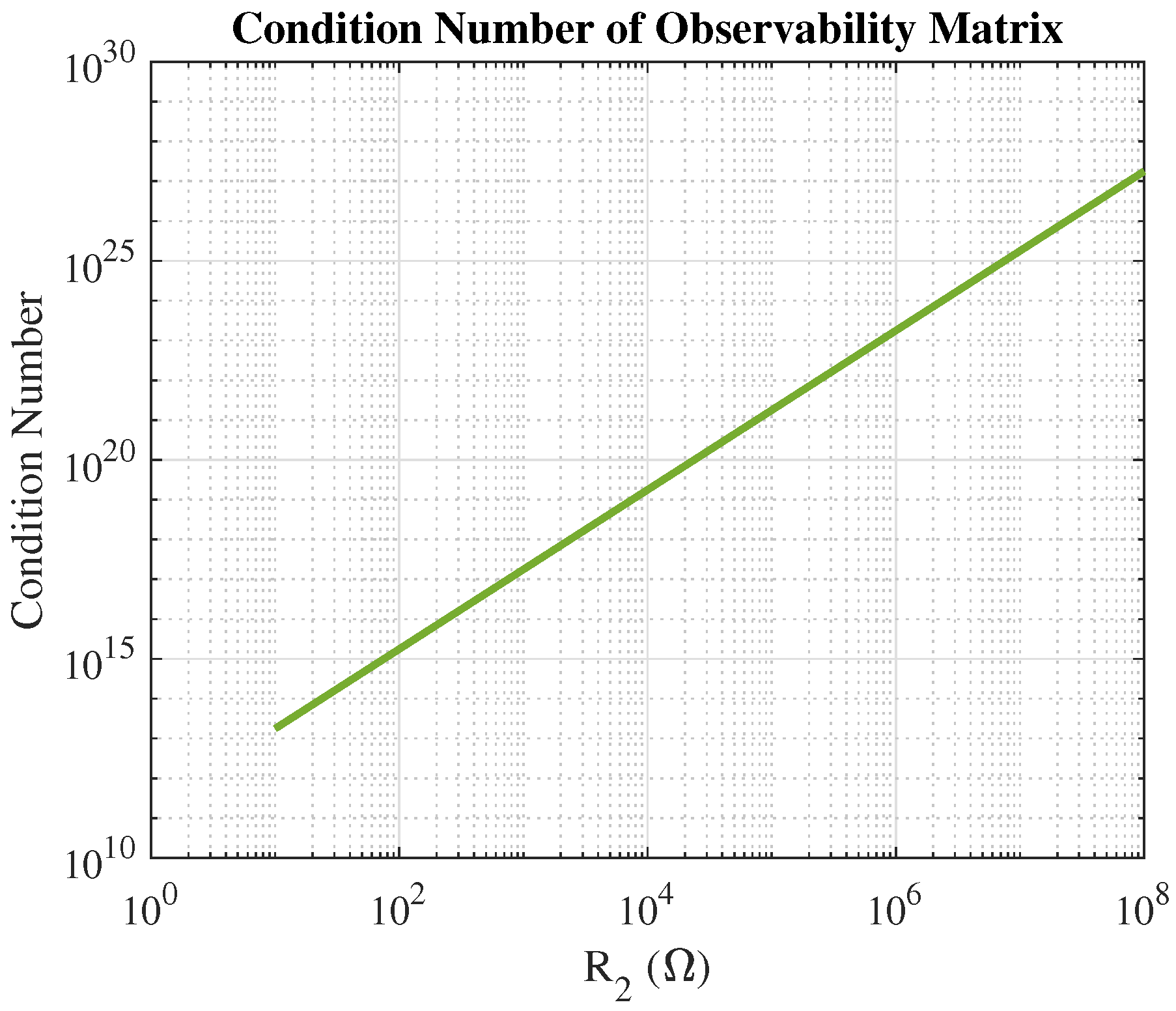
4. Observability of the SC Bank System
5. Observer Design for the Weakly Observable System
Regularization Law
- The observer should be discretized.
- A proper number of samples should be chosen for truncation of the Grunwald–Letnikov Derivative (GLD); for this system, depending on the processor speed and RAM, 10 to 100 samples provide sufficient accuracy while keeping the computational burden low.
- Based on the the characteristics of and using the Newton–Raphson method, the initial value of is calculated.
- A timer with a period of 1 sec is activated. Every 1 s, the following routines will be executed:
- -
- The new data of voltage and current get updated.
- -
- The voltage and currents of the 10–100 latest samples should be saved by shifting the old samples and entering the new sample.
- -
- One round of the discretized observer is executed.
- -
- New state estimations can be extracted from the new run of the observer.
- -
- The state variables of the 10–100 latest samples should be saved by shifting the old samples and entering the new sample.
6. Experimental Results
6.1. Test Setup
6.2. Test Procedure
6.2.1. Pulse Train Charging Mode
- Current injection: A pulse train of 1 A charging current, with an active duration of 1 min followed by a 279 min rest period, is injected into the SC bank. The current setpoint is continuously transmitted from MATLAB to the DC power supply via GPIB.
- Rest mode: During the rest period, the diodes between the power supply and SC bank prevent the SC from discharging through the power supply output.
- Voltage measurement: The DC voltage across the SC bank is measured using a multimeter, controlled by measurement commands sent from the computer. The internal leakage resistance of the multimeter is approximately 10 M, which is sufficiently high to avoid significant disturbance to the SOC or the measurements.
- Current measurement: The current injected into the SC bank is measured by the SC power supply via a GPIB query command. The power supply current measurement is calibrated beforehand and exhibits an accuracy of 1%.
- Data logging: The measured voltage, current, and corresponding time stamps for each sample are recorded and stored in a .txt file for further analysis inside MATLAB software.
6.2.2. Pulse Train Discharging Mode
- Current draw: A pulse train of 0.5 A discharging current, with an active duration of 1 min followed by a 279 min rest period, is drawn from the SC bank. The current setpoint is continuously transmitted from MATLAB to the DC electronic load via GPIB. Due to the higher time constant of redistribution voltage in discharge mode and the slower redistribution dynamics in discharge mode, a lower current pulse is used for discharge mode.
- Rest mode: During the rest period, the relay between the SC bank and the load is de-energized, preventing any discharge through the power supply or electronic load. The relay coil is controlled via a GPIB-connected power supply.
- Voltage measurement: The DC voltage across the SC bank is measured using a multimeter, with measurement commands sent from the computer to the multimeter.
- Current measurement: The current drawn by the SC bank is measured by the electronic load via a GPIB query command.
- Data logging: The measured voltage, current, and corresponding time stamps for each sample are recorded and stored in a .txt file for further analysis.
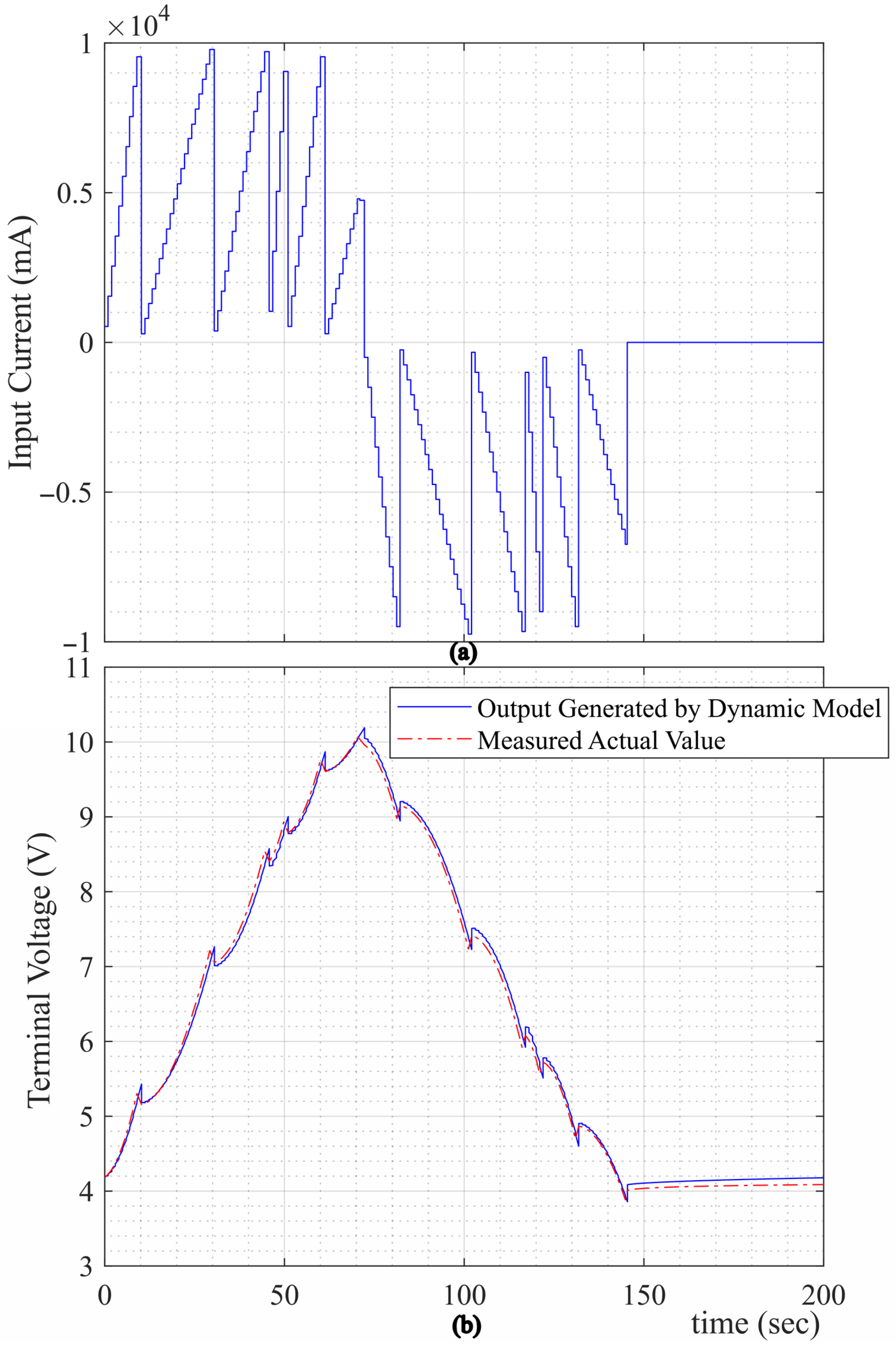
6.2.3. Sawtooth Charging and Discharging Mode
- This mode is intended to verify the identified parameters and evaluate the performance of the observers.
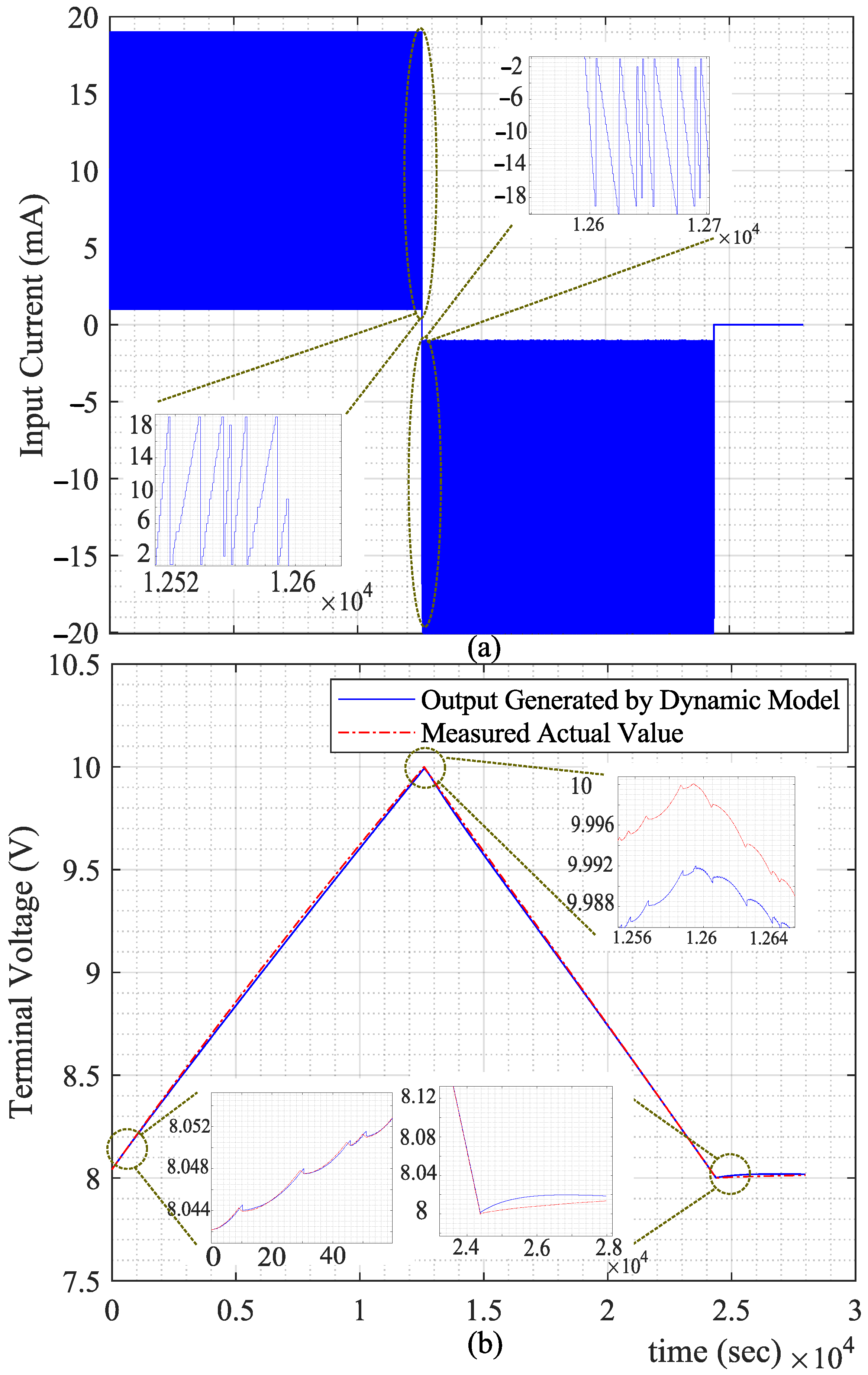
- Current injection: A repetitive sawtooth current with an amplitude of 20 mA is injected into the SC bank. The current waveform is applied at multiple frequencies, 1/10, 1/20, 1/15, and 1/5 Hz, with the objective of increasing the SC bank voltage from 8 V to 10 V. Voltage, current, and corresponding time stamps are recorded at a sampling interval of 1 s. In other separate tests, the current amplitude is increased to 200 mA and 10 A.
- Current draw: A repetitive sawtooth current with an amplitude of 20 mA is drawn from the SC bank. The current waveform is applied at multiple frequencies, 1/10, 1/20, 1/15, and 1/5 Hz, with the objective of decreasing the SC bank voltage from 10 V to 8 V. Voltage, current, and corresponding time stamps are recorded at a sampling interval of 1 s. In other separate tests, the current amplitude is increased to 200 mA and 10 A.
- Rest mode: The voltage across the SC bank is monitored and recorded continuously over a rest period.
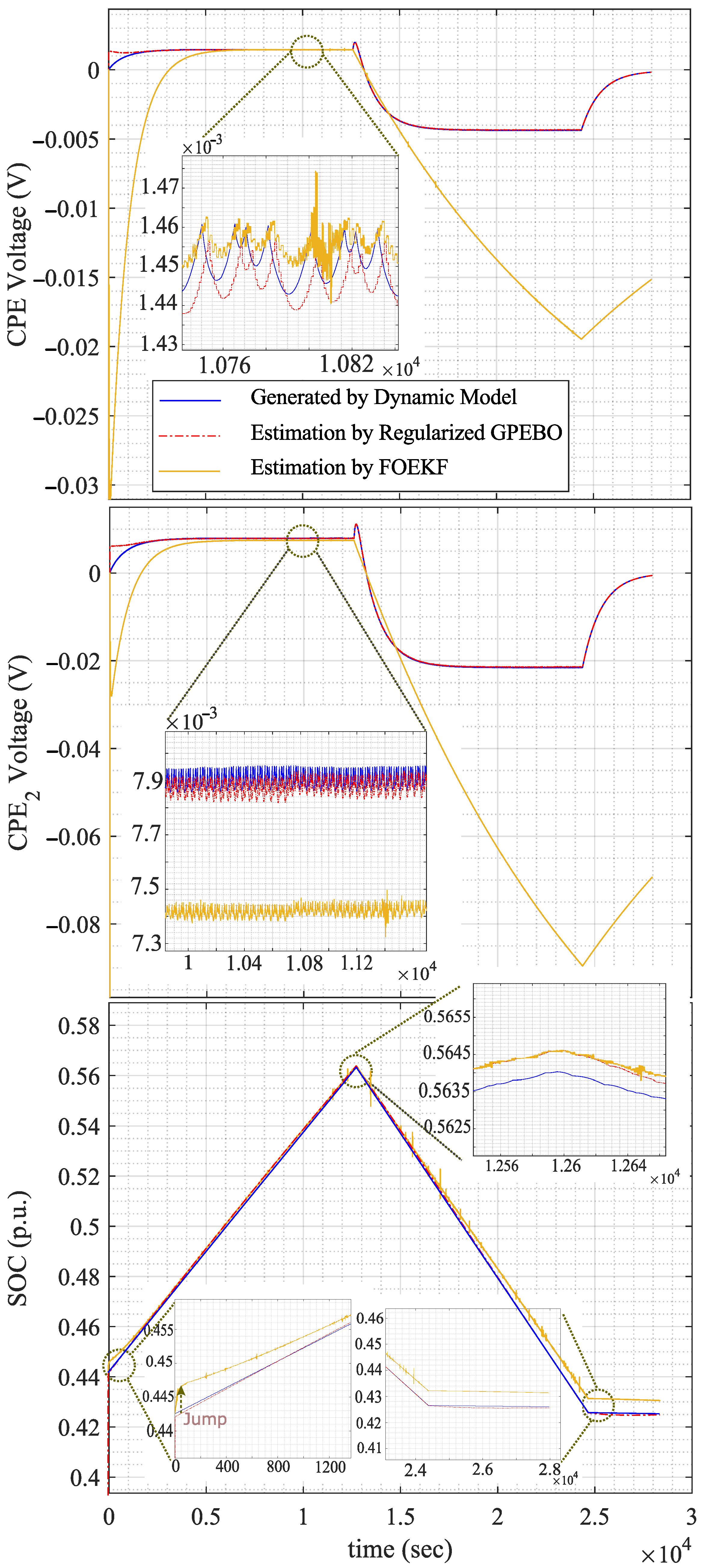
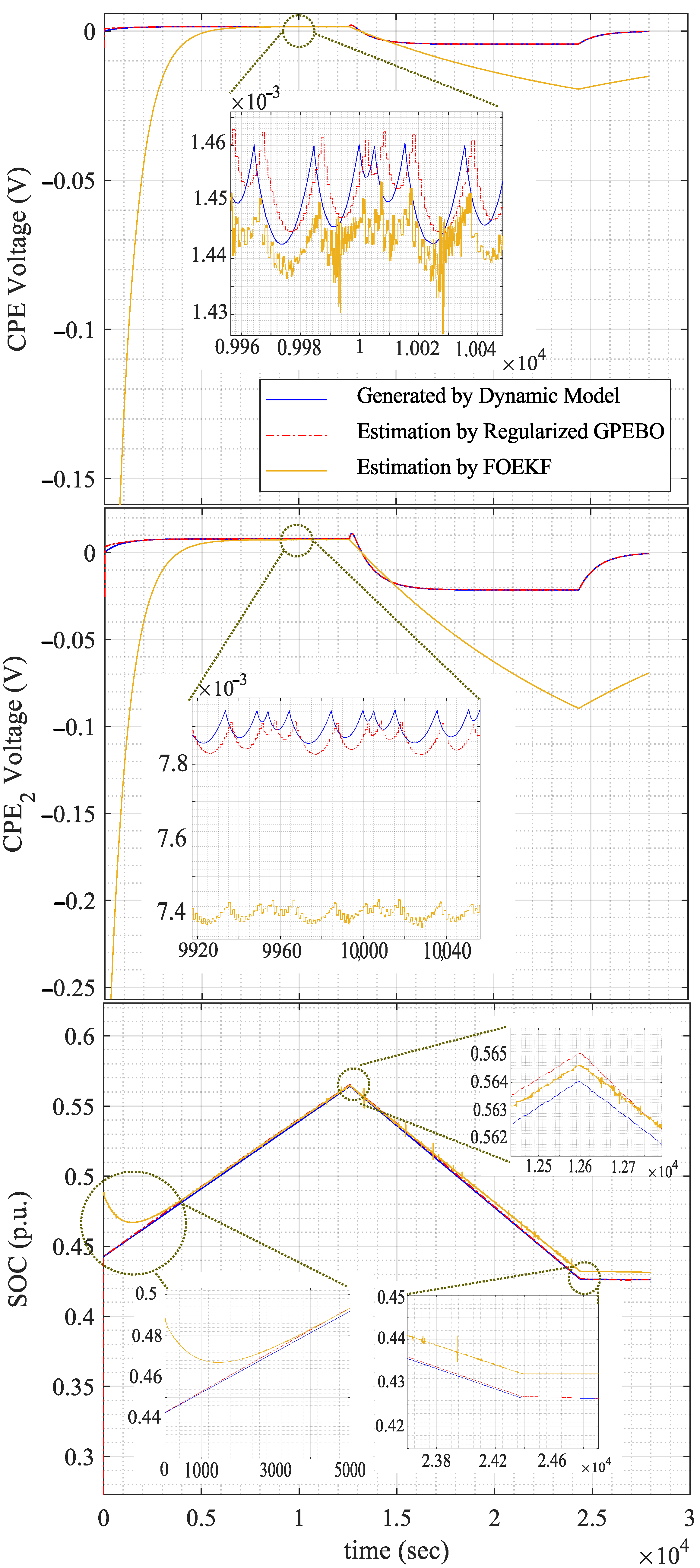
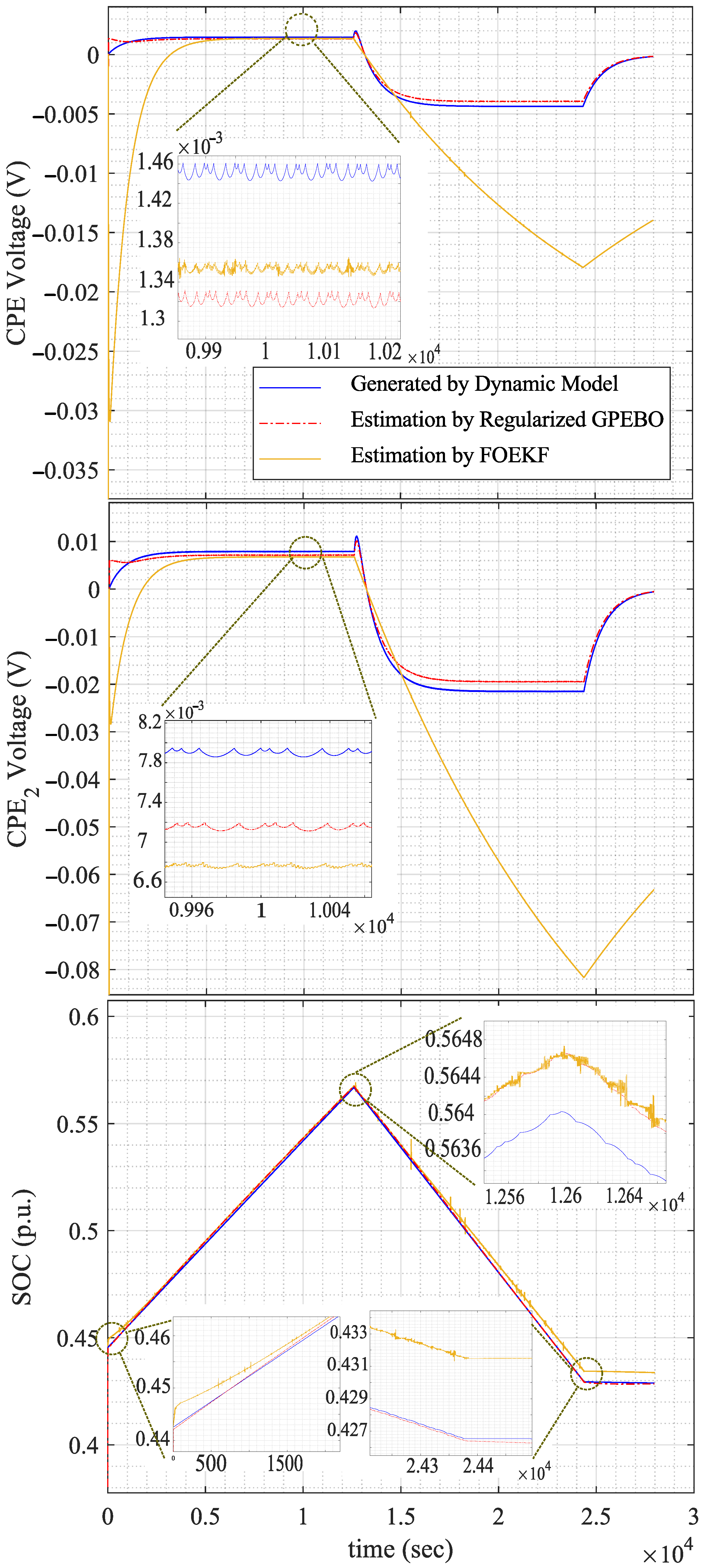
6.3. Test Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CPE | Constant Phase Element |
| LSE | Least Squares Error |
| SOC | State of Charge |
| SC | Supercapacitor |
| ESR | Equivalent Circuit Model |
| OCV | Open-Circuit Voltage |
| EESS | Electrochemical Energy Storage System |
| SoH | State of Health |
Appendix A. Offline Identification of System
Appendix A.1. OCV-SOC Relation
- The SC should be completely discharged by short-circuiting the terminals for a long time based on the SC bank size for example several days.
- The pulse train is applied to the SC and continues until the terminal voltage reaches the nominal voltage .
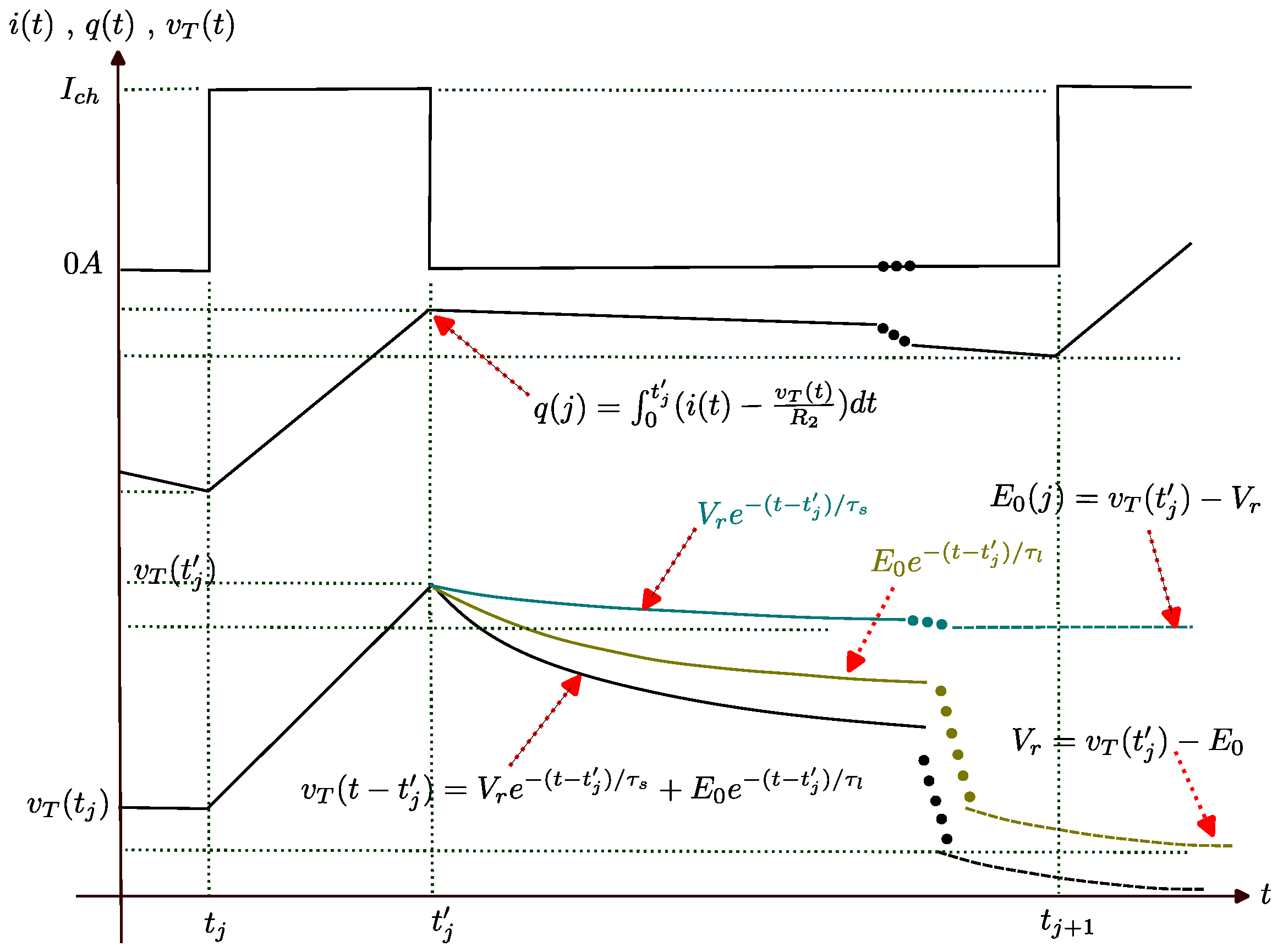
- The values of are recorded during the rest mode of each period. The start time of the rest mode of the jth period is regarded as . To estimate the exact value of , for the jth rest mode period must be decomposed into two exponential components. One component, with a larger time constant, is attributed to the leakage current, while the other, with a shorter time constant, is due to charge redistribution. To accurately calculate , the contribution from charge redistribution must be removed from the measured voltage , i.e., , in which denotes the contribution of charge redistribution. The decomposition of two decaying DCs can be applied to each rest period. Figure A1 demonstrates this decomposition for one of the periods, which can correspond to
- The of the period is calculated by dividing the amount of by , in which
- Using the values of - for each period, the curve is interpolated and fitted to a polynomial.
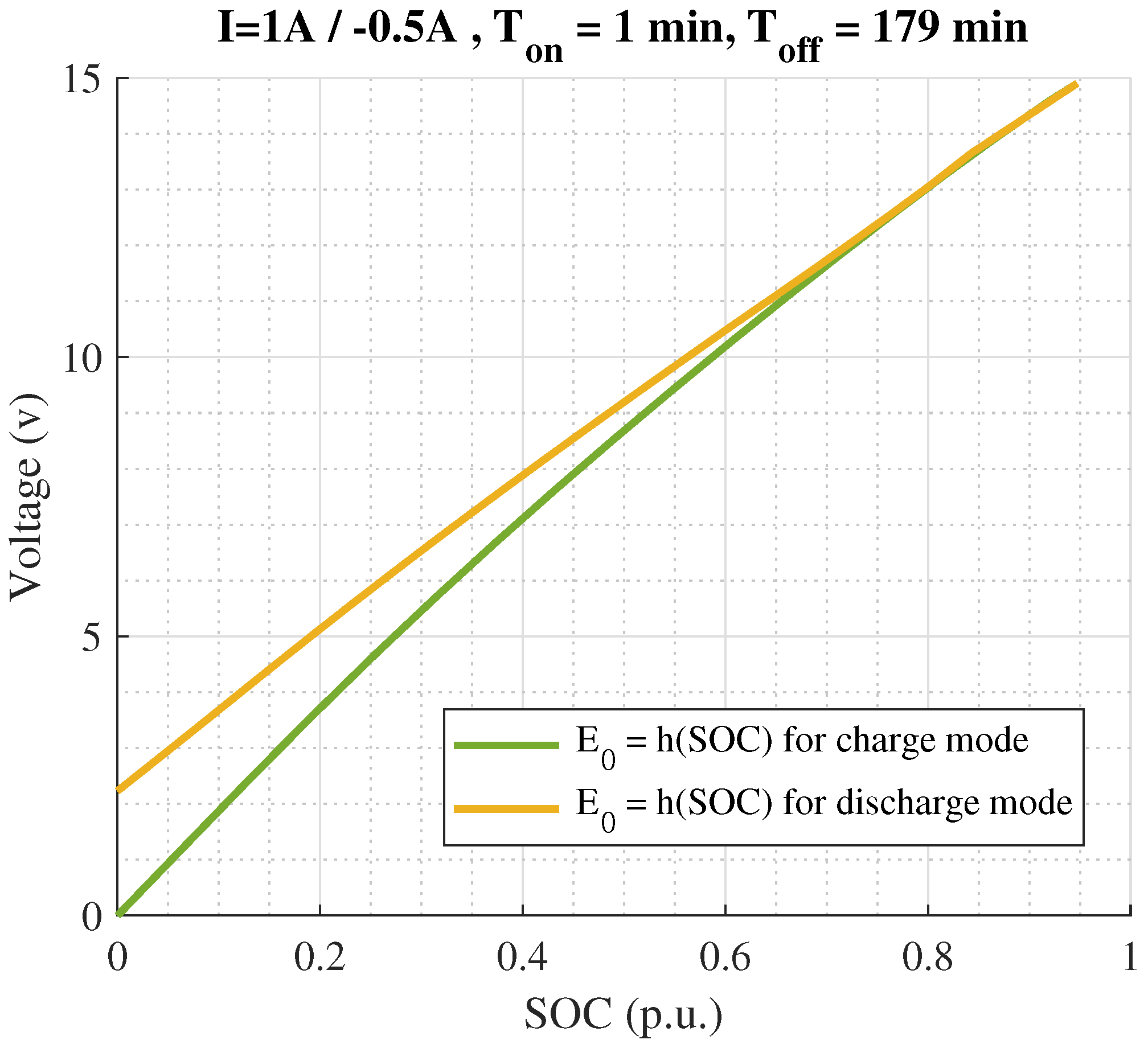
| Parameter | ||||||
|---|---|---|---|---|---|---|
| Charge | 0 | −0.675 | 1.798 | −5.23 | 19.9 | −0.0282 |
| Discharge | −9.67 | 33.95 | −42.1 | 21.09 | 10.2 | −0.012 + |
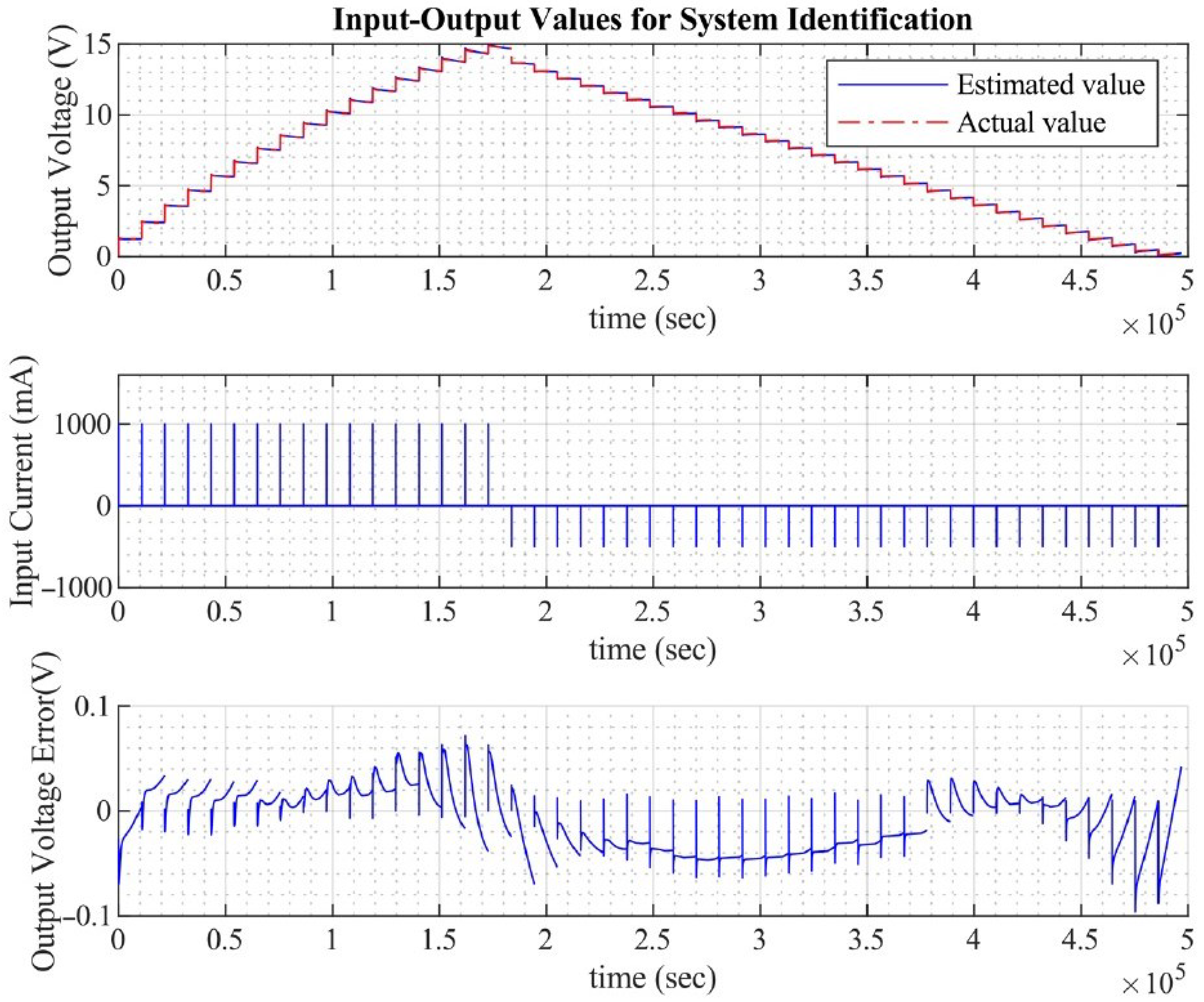
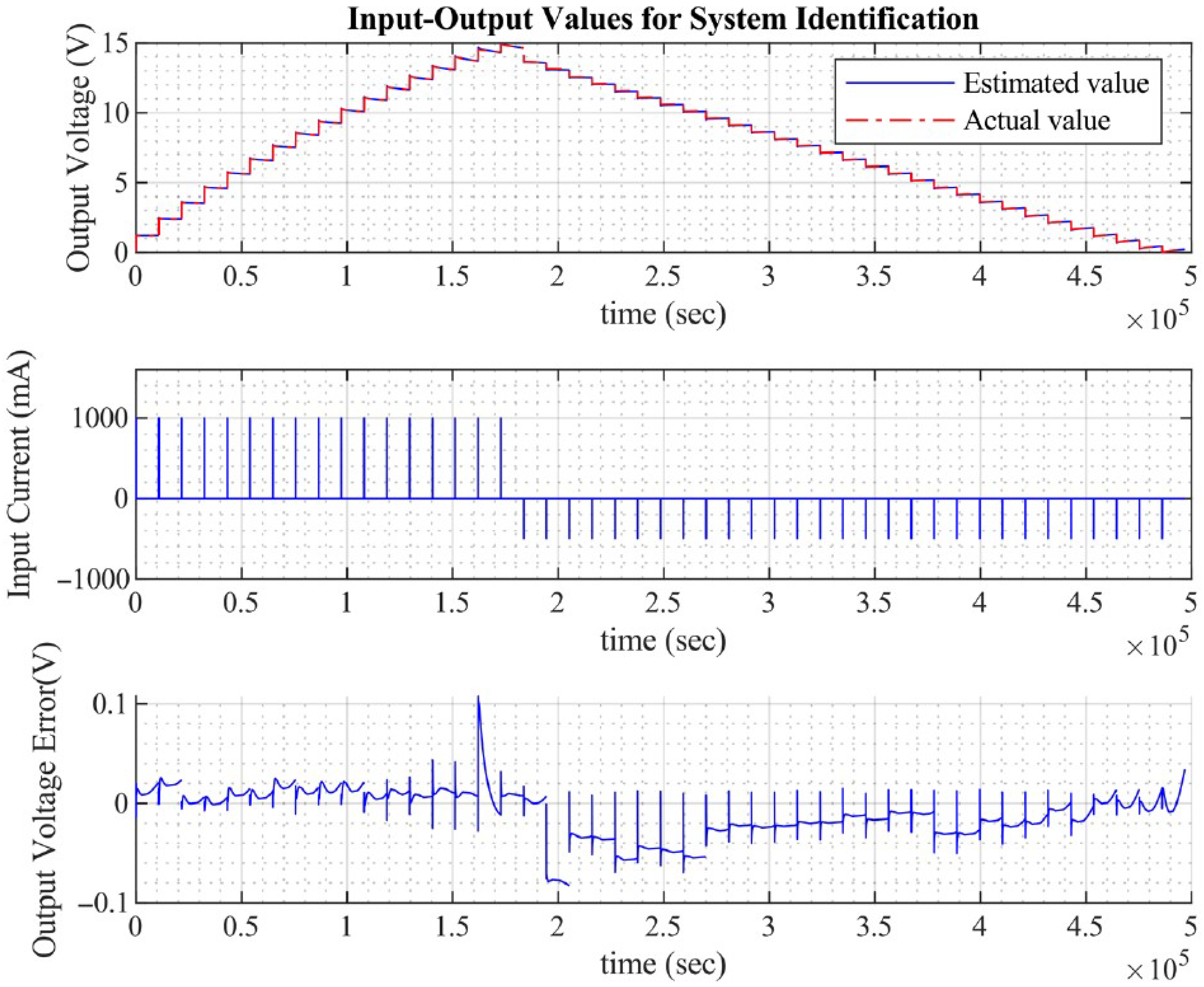
Appendix A.2. Parameter Identification
- Create the experimental data structure using the following function:z = iddata(vo, io, Ts, ’Name’, ’SC’);
- Define a separate function file to model system dynamics:function [dx, y] = model(t, x, u, R1, C1, R2, Cah, R0, alpha, varargin)
- Construct the nonlinear gray-box model:nlgr = idnlgrey(FileName, Order, Parameters, InitialStates, Ts, ’Name’, ’SC_dyn’);
- Perform parameter identification using the toolbox:nlgr = nlgreyest(z, nlgr, opt);
- Extract the identified parameters from the estimated model:nlgr.Parameters(i).Value
| Parameter | Charge | Discharge | Discharge | Unit |
|---|---|---|---|---|
| 0–100% | 100–40% | 40–0% | ||
| 705.3 | 1470.9 | 1636.8 | Mohm | |
| 11.502 | 60.122 | 122.77 | kohm | |
| 26.55 | 49 | 46.93 | mohm | |
| 2446.9 | 2166.3 | 1261 | F | |
| 268.47 | 247.37 | 268.47 | mAh | |
| 0.8609 | 0.9863 | 0.9856 | - |
References
- Zhao, Y.; Yang, C.; Yu, Y. A review on covalent organic frameworks for rechargeable zinc-ion batteries. Chin. Chem. Lett. 2024, 35, 108865–108879. [Google Scholar] [CrossRef]
- Berrueta, A.; Ursúa, A.; Martín, I.S.; Eftekhari, A.; Sanchis, P. Supercapacitors: Electrical Characteristics, Modeling, Applications, and Future Trends. IEEE Access 2019, 7, 50869–50896. [Google Scholar] [CrossRef]
- Automobili Lamborghini S.p.A. Lamborghini Sián FKP 37. 2025. Available online: https://www.lamborghini.com/en-en/models/limited-series/sian-fkp-37 (accessed on 1 August 2025).
- Bhat, M.Y.; Hashmi, S.A.; Khan, M.; Choi, D.; Qurashi, A. Frontiers and recent developments on supercapacitor’s materials, design, and applications: Transport and power system applications. J. Energy Storage 2023, 58, 106104. [Google Scholar] [CrossRef]
- Bertrand, N.; Sabatier, J.; Briat, O.; Vinassa, J.M. Embedded Fractional Nonlinear Supercapacitor Model and Its Parametric Estimation Method. IEEE Trans. Ind. Electron. 2010, 57, 3991–4000. [Google Scholar] [CrossRef]
- Lewandowski, M.; Orzyłowski, M. Fractional-order models: The case study of the supercapacitor capacitance measurement. Bull. Pol. Acad. Sci. Tech. Sci. 2017, 65, 449–457. [Google Scholar] [CrossRef]
- Buller, S.; Karden, E.; Kok, D.; De Doncker, R.W. Modeling the dynamic behavior of supercapacitors using impedance spectroscopy. IEEE Trans. Ind. Appl. 2002, 38, 1622–1626. [Google Scholar] [CrossRef]
- Buller, S.; Thele, M.; De Doncker, R.; Karden, E. Impedance-based simulation models of supercapacitors and Li-ion batteries for power electronic applications. IEEE Trans. Ind. Appl. 2005, 41, 742–747. [Google Scholar] [CrossRef]
- Prasad, R.; Kothari, K.; Mehta, U. Flexible Fractional Supercapacitor Model Analyzed in Time Domain. IEEE Access 2019, 7, 122626–122633. [Google Scholar] [CrossRef]
- De Carne, G.; Morandi, A.; Karrari, S. Supercapacitor Modeling for Real-Time Simulation Applications. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 509–518. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, L.; Hu, X.; Wang, Z.; Wik, T.; Pecht, M. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef]
- Slaifstein, D.; Ibanez, F.M.; Siwek, K. Supercapacitor Modeling: A System Identification Approach. IEEE Trans. Energy Convers. 2023, 38, 192–202. [Google Scholar] [CrossRef]
- Krpan, M.; Kuzle, I.; Radovanović, A.; Milanović, J.V. Modelling of Supercapacitor Banks for Power System Dynamics Studies. IEEE Trans. Power Syst. 2021, 36, 3987–3996. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, L.; Wang, B.; Ma, G. Modeling of Supercapacitor Behavior with an Improved Two-Branch Equivalent Circuit. IEEE Access 2019, 7, 26379–26390. [Google Scholar] [CrossRef]
- Saha, P.; Dey, S.; Khanra, M. Modeling and State-of-Charge Estimation of Supercapacitor Considering Leakage Effect. IEEE Trans. Ind. Electron. 2020, 67, 350–357. [Google Scholar] [CrossRef]
- Quintáns, C.; Iglesias, R.; Lago, A.; Acevedo, J.M.; Martínez-Peñalver, C. Methodology to Obtain the Voltage-Dependent Parameters of a Fourth-Order Supercapacitor Model with the Transient Response to Current Pulses. IEEE Trans. Power Electron. 2017, 32, 3868–3878. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Mao, J.; Zhou, J.; Xu, D. Fractional Order Equivalent Circuit Model and SOC Estimation of Supercapacitors for Use in HESS. IEEE Access 2019, 7, 52565–52572. [Google Scholar] [CrossRef]
- Chai, R.; Zhang, Y. A Practical Supercapacitor Model for Power Management in Wireless Sensor Nodes. IEEE Trans. Power Electron. 2015, 30, 6720–6730. [Google Scholar] [CrossRef]
- Krishnan, G.; Das, S.; Agarwal, V. An Online Identification Algorithm to Determine the Parameters of the Fractional-Order Model of a Supercapacitor. IEEE Trans. Ind. Appl. 2020, 56, 763–770. [Google Scholar] [CrossRef]
- Song, Z.; Hou, J.; Hofmann, H.F.; Lin, X.; Sun, J. Parameter Identification and Maximum Power Estimation of Battery/Supercapacitor Hybrid Energy Storage System Based on Cramer–Rao Bound Analysis. IEEE Trans. Power Electron. 2019, 34, 4831–4843. [Google Scholar] [CrossRef]
- El Mejdoubi, A.; Chaoui, H.; Gualous, H.; Sabor, J. Online Parameter Identification for Supercapacitor State-of-Health Diagnosis for Vehicular Applications. IEEE Trans. Power Electron. 2017, 32, 9355–9363. [Google Scholar] [CrossRef]
- Naseri, F.; Farjah, E.; Ghanbari, T.; Kazemi, Z.; Schaltz, E.; Schanen, J.L. Online Parameter Estimation for Supercapacitor State-of-Energy and State-of-Health Determination in Vehicular Applications. IEEE Trans. Ind. Electron. 2020, 67, 7963–7972. [Google Scholar] [CrossRef]
- Chaoui, H.; El Mejdoubi, A.; Oukaour, A.; Gualous, H. Online System Identification for Lifetime Diagnostic of Supercapacitors with Guaranteed Stability. IEEE Trans. Control Syst. Technol. 2016, 24, 2094–2102. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Shen, W.; Wang, J.; Yang, R. Online simultaneous identification of parameters and order of a fractional order battery model. J. Clean. Prod. 2020, 247, 119147. [Google Scholar] [CrossRef]
- Maity, S.; Saha, M.; Saha, P.; Khanra, M. Fractional calculus-based modeling and state-of-charge estimation of supercapacitor. J. Energy Storage 2024, 81, 110317. [Google Scholar] [CrossRef]
- Miniguano, H.; Barrado, A.; Lázaro, A. Li-Ion Battery and Supercapacitor Modeling for Electric Vehicles Based on Pulse—Pseudo Random Binary Sequence. IEEE Trans. Veh. Technol. 2021, 70, 11378–11389. [Google Scholar] [CrossRef]
- Li, H.; Peng, J.; He, J.; Huang, Z.; Wang, J. Observer-Driven Charging of Supercapacitors. IEEE Trans. Ind. Informatics 2020, 16, 3439–3450. [Google Scholar] [CrossRef]
- Ceraolo, M.; Lutzemberger, G.; Poli, D. State-of-Charge Evaluation of Supercapacitors. J. Energy Storage 2017, 11, 211–218. [Google Scholar] [CrossRef]
- Chiang, C.J.; Yang, J.L.; Cheng, W.C. EKF-based estimation of SOC and temperature in ultracapacitors. In Proceedings of the 2013 10th IEEE International Conference on Control and Automation (ICCA), Hangzhou, China, 12–14 June 2013; pp. 274–279. [Google Scholar] [CrossRef]
- Nadeau, A.; Hassanalieragh, M.; Sharma, G.; Soyata, T. Energy awareness for supercapacitors using Kalman filter state-of-charge tracking. J. Power Sources 2015, 296, 383–391. [Google Scholar] [CrossRef]
- Shen, X.; Shen, T.; Zha, X.; Hikiri, K. State-of-charge estimation of super-capacitor using dual extended Kalman filter. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 227–232. [Google Scholar] [CrossRef]
- Pavković, D.; Komljenović, A.; Hrgetić, M.; Petrić, J.; Smetko, V. Design of EKF-based SoC estimator for an ultracapacitor module. In Proceedings of the IEEE EUROCON 2015—International Conference on Computer as a Tool (EUROCON), Salamanca, Spain, 8–11 September 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, L.; Su, S.; Hu, X.; Dorrell, D.G. Robust state-of-charge estimation of ultracapacitors for electric vehicles. In Proceedings of the 2015 IEEE 13th International Conference on Industrial Informatics (INDIN), Cambridge, UK, 22–24 July 2015; pp. 1296–1301. [Google Scholar] [CrossRef]
- Li, H.; He, W.; Fang, X.; Li, S. State-of-Charge Estimation of Supercapacitors: A Switched Systems Approach. IEEE Trans. Transp. Electrif. 2024, 10, 5987–5996. [Google Scholar] [CrossRef]
- Dey, S.; Mohon, S.; Ayalew, B.; Arunachalam, H.; Onori, S. A Novel Model-Based Estimation Scheme for Battery-Double-Layer Capacitor Hybrid Energy Storage Systems. IEEE Trans. Control Syst. Technol. 2019, 27, 689–702. [Google Scholar] [CrossRef]
- Fan, S.; Duan, J.; Sun, L.; Zhang, K.; Han, Y. State of charge estimate for super-capacitor based on sliding mode observer. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Harbin, China, 7–10 August 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Weigert, T.; Tian, Q.; Lian, K. State-of-charge prediction of batteries and battery–supercapacitor hybrids using artificial neural networks. J. Power Sources 2011, 196, 4061–4066. [Google Scholar] [CrossRef]
- Tri, V.V.; Huong, D.C.; Diep, P.N.N. State estimation problem for fractional-order neural networks using event-triggered state observers. Proc. Inst. Mech. Eng. Part I 2023, 237, 1078–1086. [Google Scholar] [CrossRef]
- Huong, D.C.; Huynh, V.T.; Thao, N.G.M.; Dang, T.P.; Trinh, H. State Estimation for a New Battery and Motor Circuit Model of an Electric Vehicle Using Event-Triggered Functional Interval Observers. IEEE Trans. Circuits Syst. I: Regul. Pap. 2024, 71, 421–430. [Google Scholar] [CrossRef]
- Rasoolzadeh, A.; Hashemi, S.A.; Pahlevani, M. Online Identification of Differential Order in Supercapacitor Fractional-Order Models: Advancing Practical Implementation. Energies 2025, 18, 1876. [Google Scholar] [CrossRef]
- Krener, A.J.; Ide, K. Measures of unobservability. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 6401–6406. [Google Scholar] [CrossRef]
- Ortega, R.; Bobtsov, A.; Nikolaev, N.; Schiffer, J.; Dochain, D. Generalized parameter estimation-based observers: Application to power systems and chemical–biological reactors. Automatica 2021, 129, 109635. [Google Scholar] [CrossRef]
- Cecilia, A.; Costa-Castelló, R. On state-estimation in weakly-observable scenarios and implicitly regularized observers. In Proceedings of the 2021 60th IEEE Conference on Decision and Control (CDC), Austin, TX, USA, 14–17 December 2021; pp. 3996–4001. [Google Scholar] [CrossRef]
- Castiglia, V.; Campagna, N.; Di Tommaso, A.O.; Miceli, R.; Pellitteri, F.; Puccio, C.; Viola, F. Modelling, Simulation and Characterization of a Supercapacitor in Automotive Applications. In Proceedings of the 2020 Fifteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 10–12 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Rizoug, N.; Bartholomeus, P.; Le Moigne, P. Modeling and Characterizing Supercapacitors Using an Online Method. IEEE Trans. Ind. Electron. 2010, 57, 3980–3990. [Google Scholar] [CrossRef]
- Morandi, A.; Lampasi, A.; Cocchi, A.; Gherdovich, F.; Melaccio, U.; Ribani, P.L.; Rossi, C.; Soavi, F. Characterization and Model Parameters of Large Commercial Supercapacitor Cells. IEEE Access 2021, 9, 20376–20390. [Google Scholar] [CrossRef]
- Parvini, Y.; Siegel, J.B.; Stefanopoulou, A.G.; Vahidi, A. Supercapacitor Electrical and Thermal Modeling, Identification, and Validation for a Wide Range of Temperature and Power Applications. IEEE Trans. Ind. Electron. 2016, 63, 1574–1585. [Google Scholar] [CrossRef]
- Zucca, M.; Hassanzadeh, M.; Conti, O.; Pogliano, U. Accurate Parameters Identification of a Supercapacitor Three-Branch Model. IEEE Access 2023, 11, 122387–122398. [Google Scholar] [CrossRef]
- Yang, H. Dependence of Supercapacitor Peukert Constant on Voltage, Aging, and Temperature. IEEE Trans. Power Electron. 2019, 34, 9978–9992. [Google Scholar] [CrossRef]



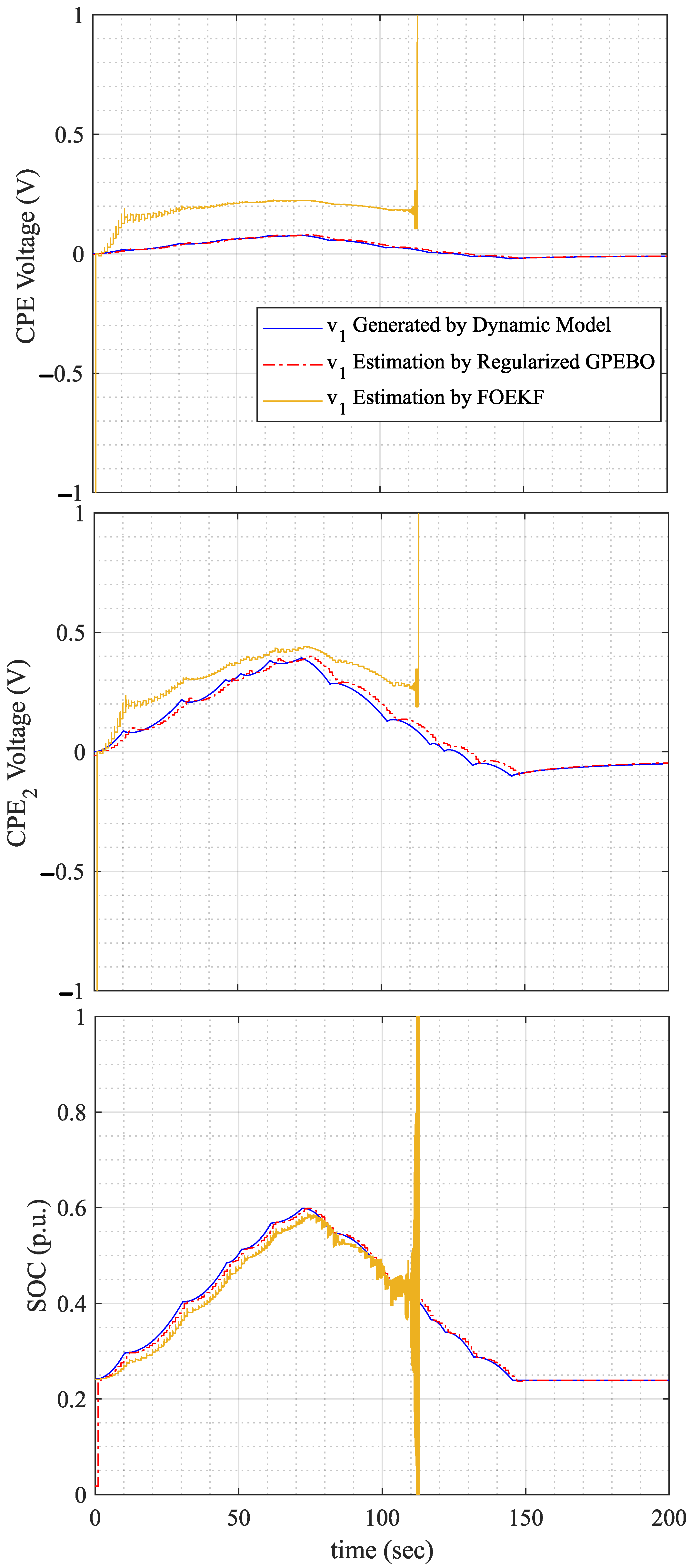
| Truncation | Max Absolute Error | Max Square Error | Mean Squared Error |
|---|---|---|---|
| 10 | 12 | 14 | 8 |
| 50 | 7.7 | 6 | 3 |
| 100 | 3.7 | 14 | 4 |
| Instrument | Brand | Model | Communication |
|---|---|---|---|
| Power supply | Xantrex, San Diego, CA, USA | XT60-1 & XHR20-50 | GPIB |
| Electronic load | Chroma, Wu-Ku, Taipei, Taiwan | 6314-63102 | GPIB |
| Multimeter | Keithley, Cleveland, OH, USA | 2700 | GPIB |
| Observer | SOC Initial | SOC | SOC | |
|---|---|---|---|---|
| Error | (s) | MSE | ||
| 10% initial error of SOC | FOEKF | 0.045 | 3500 | 4.4 |
| GPEBO | 0.0001 | 2 | 6.45 | |
| 10% uncertainty in parameters | FOEKF | 0.003 | 1500 | 6.01 |
| GPEBO | 0.0005 | 3 | 6.07 | |
| 200 mA amplitude current | FOEKF | 0.0027 | unstable | unstable |
| GPEBO | 0.0006 | 2 | 6.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasoolzadeh, A.; Hashemi, S.A.; Pahlevani, M. A Fractional-Order State Estimation Method for Supercapacitor Energy Storage. Electronics 2025, 14, 3231. https://doi.org/10.3390/electronics14163231
Rasoolzadeh A, Hashemi SA, Pahlevani M. A Fractional-Order State Estimation Method for Supercapacitor Energy Storage. Electronics. 2025; 14(16):3231. https://doi.org/10.3390/electronics14163231
Chicago/Turabian StyleRasoolzadeh, Arsalan, Sayed Amir Hashemi, and Majid Pahlevani. 2025. "A Fractional-Order State Estimation Method for Supercapacitor Energy Storage" Electronics 14, no. 16: 3231. https://doi.org/10.3390/electronics14163231
APA StyleRasoolzadeh, A., Hashemi, S. A., & Pahlevani, M. (2025). A Fractional-Order State Estimation Method for Supercapacitor Energy Storage. Electronics, 14(16), 3231. https://doi.org/10.3390/electronics14163231








