Novel Adaptive Intelligent Control System Design
Abstract
1. Introduction
2. AICS Design Strategy and Motivation
2.1. First-Order Lyapunov Stability Analysis of the MRAC System for a Single SISO Plant
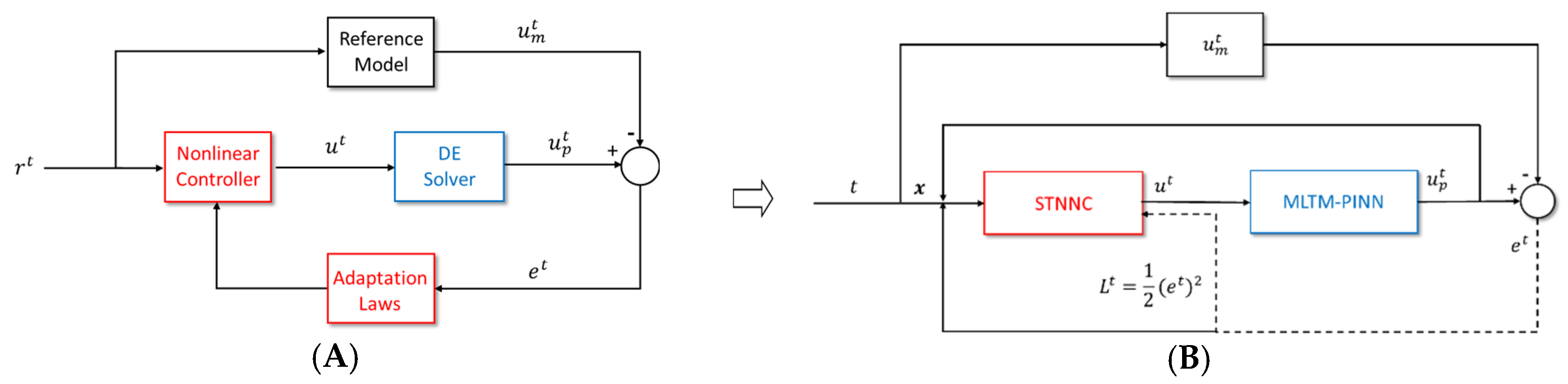
2.2. AICS Design Strategy Derived from the MRAC Framework
2.3. Motivation Behind the AICS Design
3. AICS Design
3.1. MLP and PINN
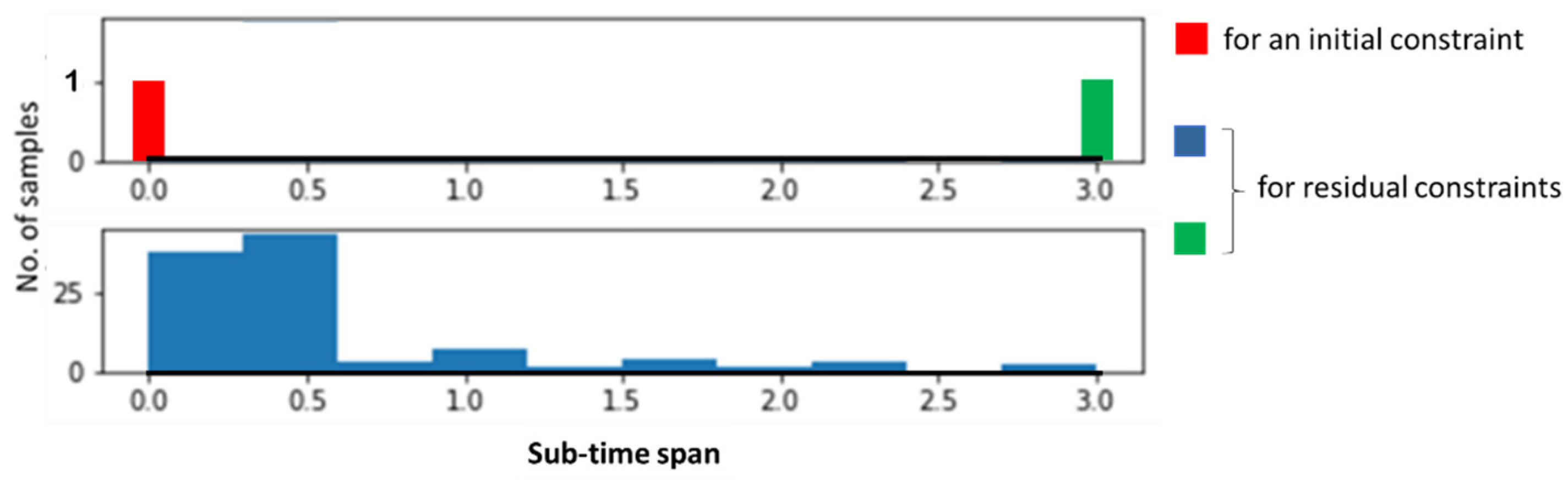
3.2. MLTM-PINN Design
| Algorithm 1 MLTM-PINN algorithm |
|
3.3. STNNC Design
| Algorithm 2 Bi-level optimization process for the GP-BO |
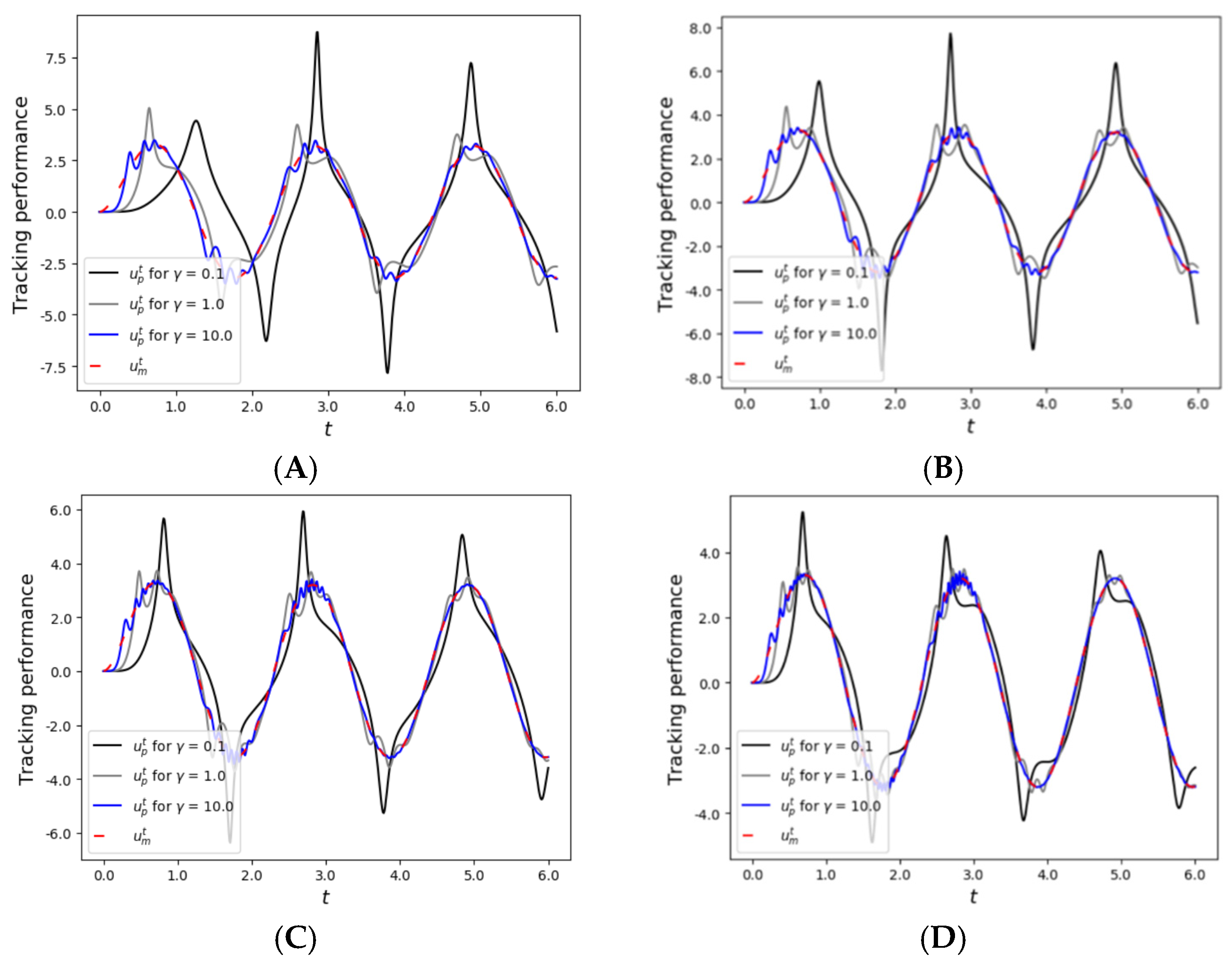
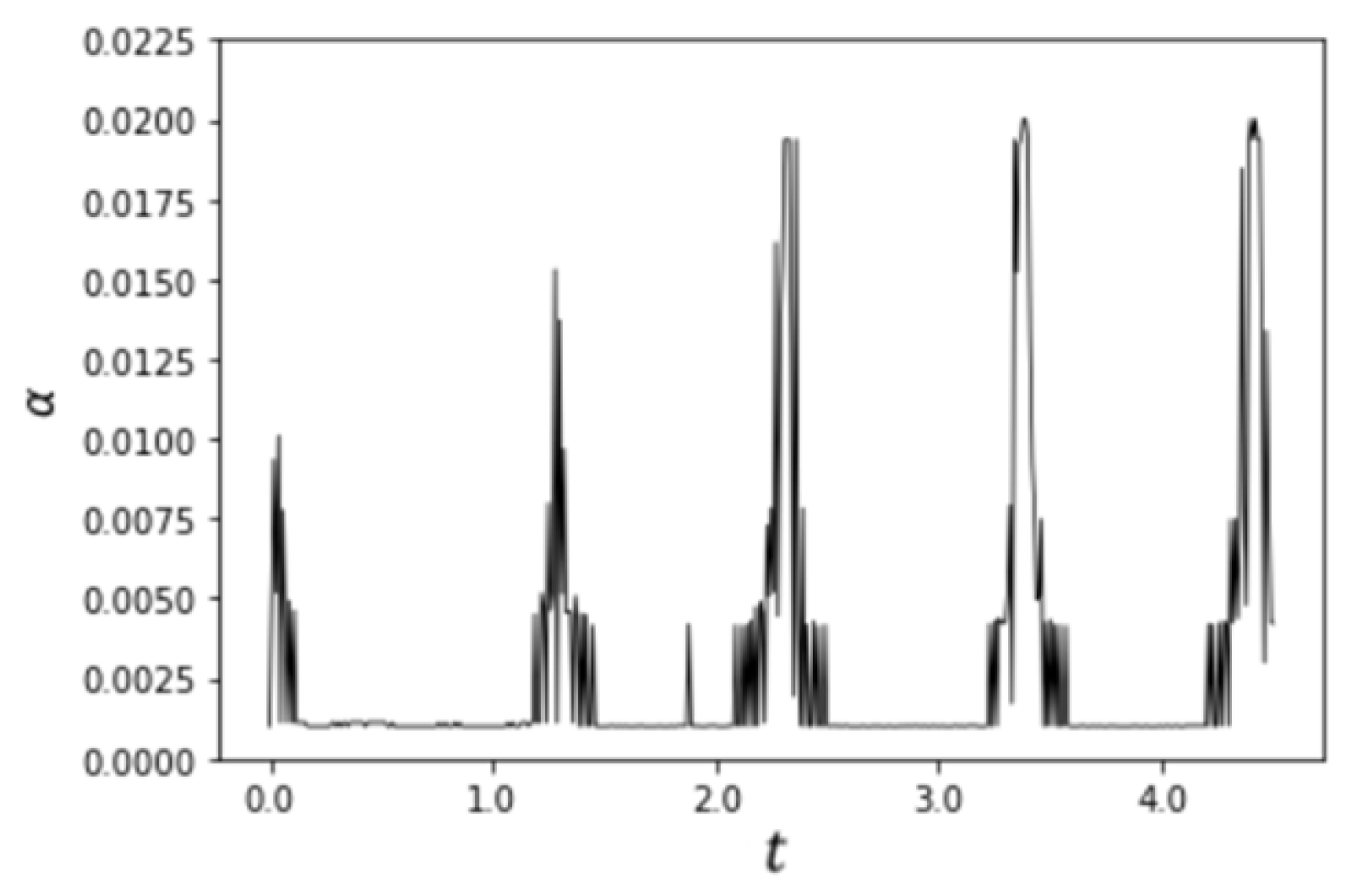
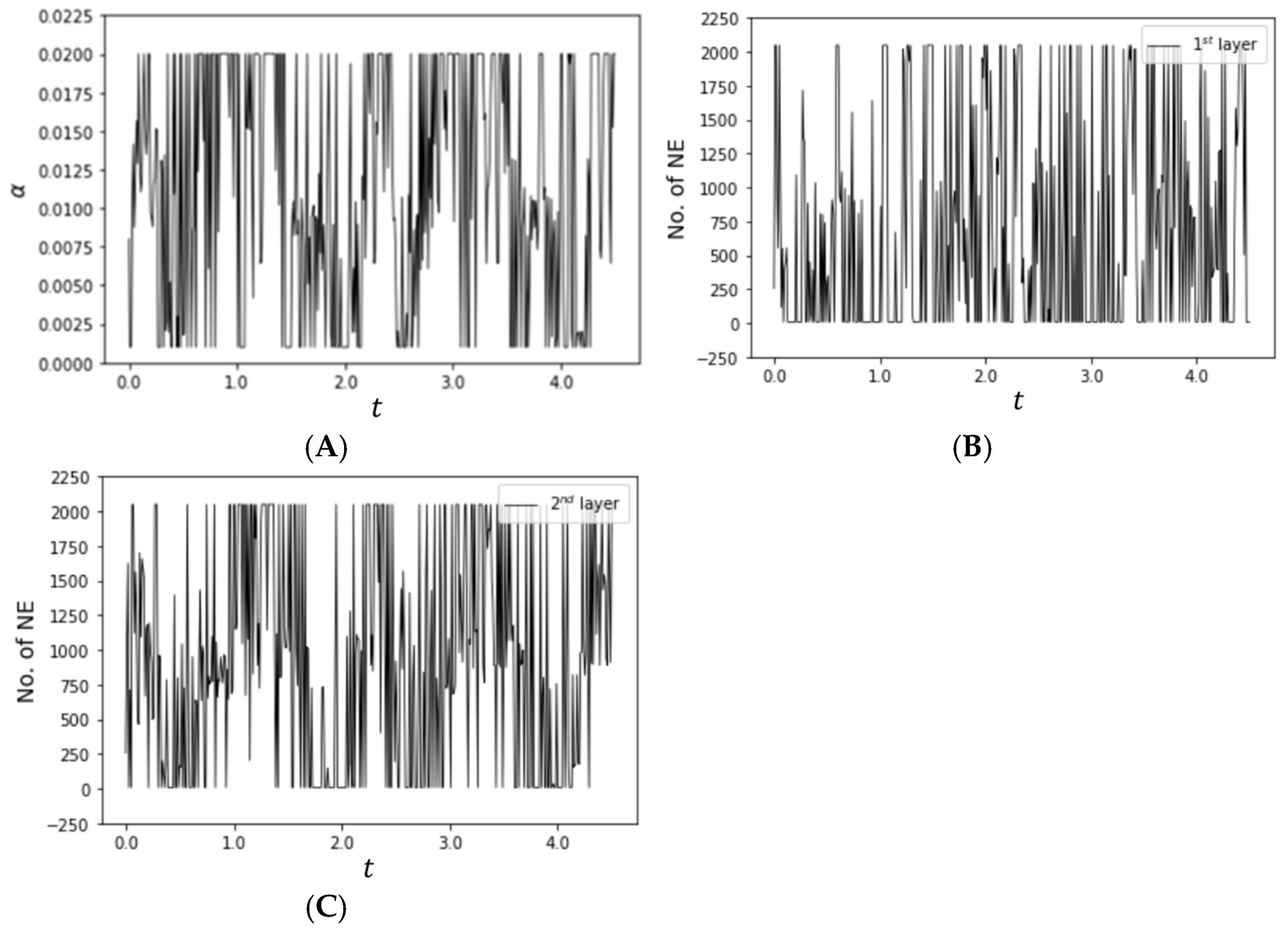
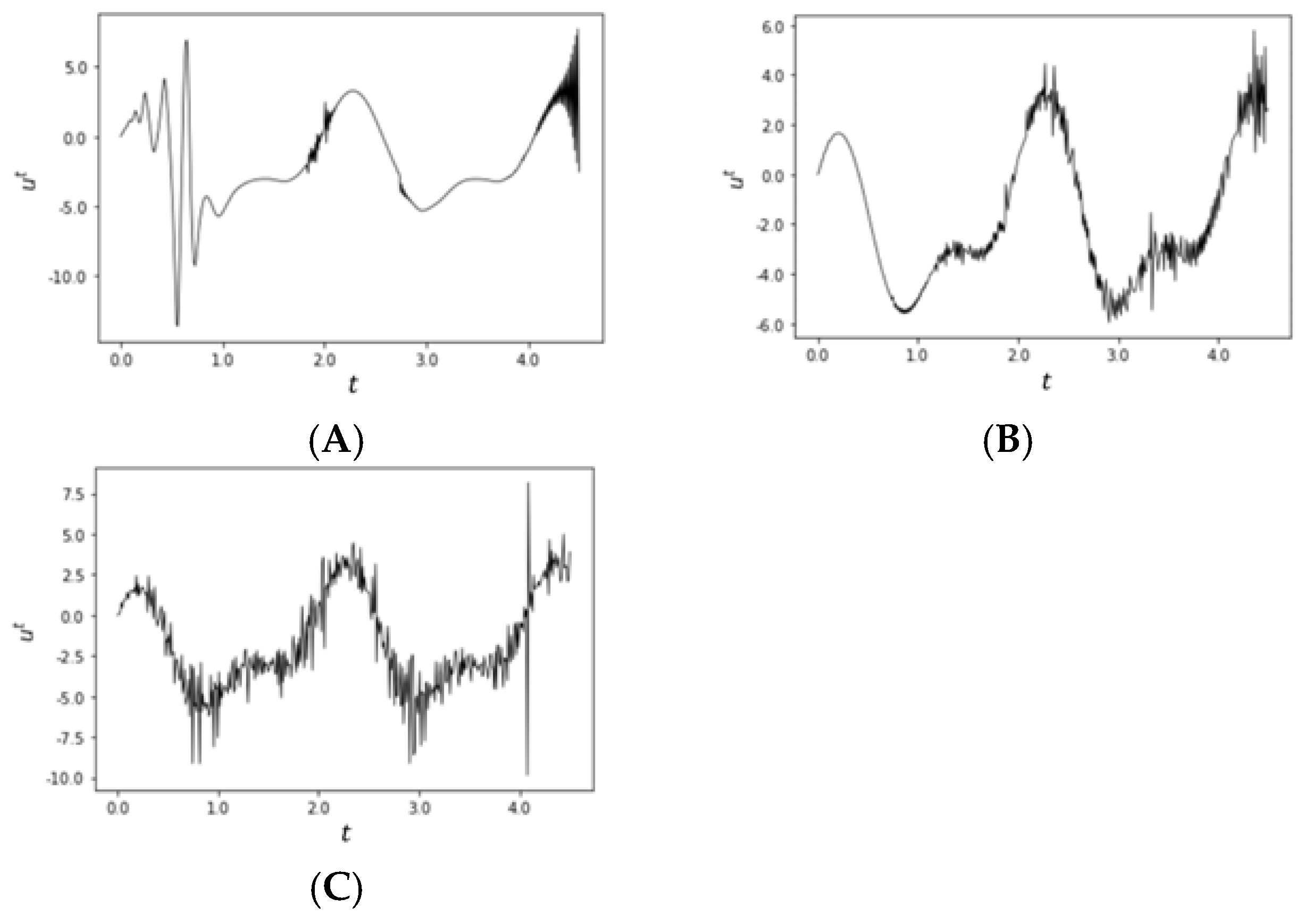
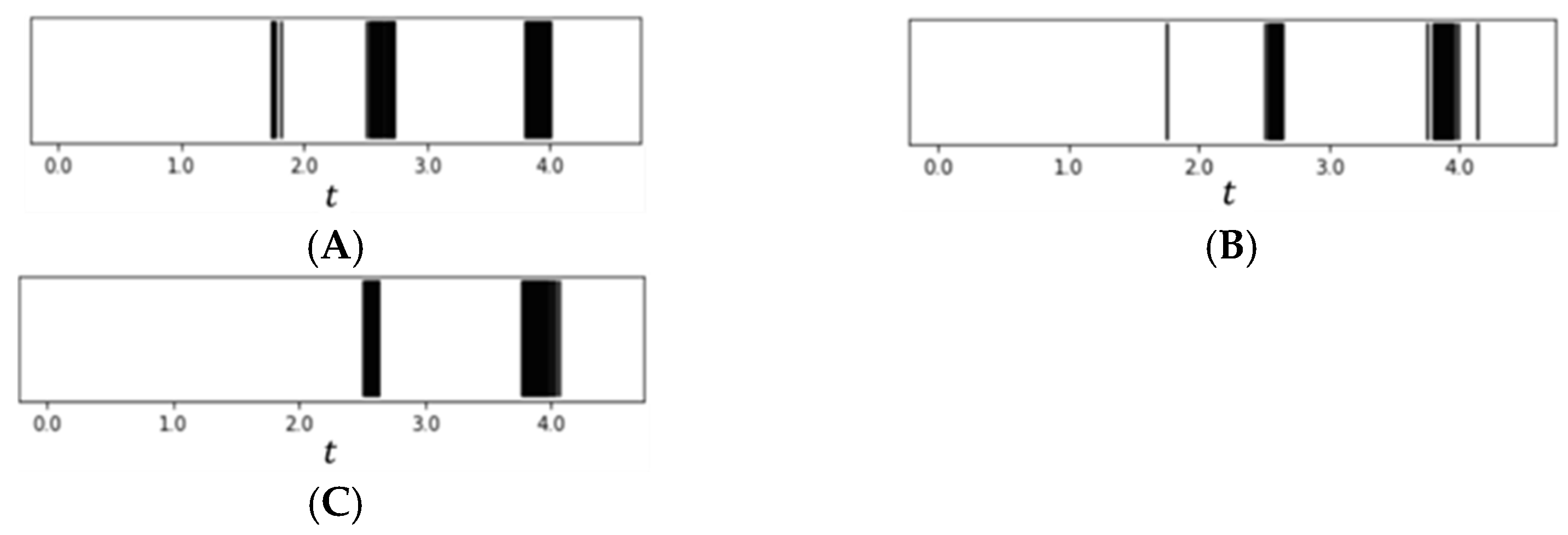
4. Simulation Results and Discussion
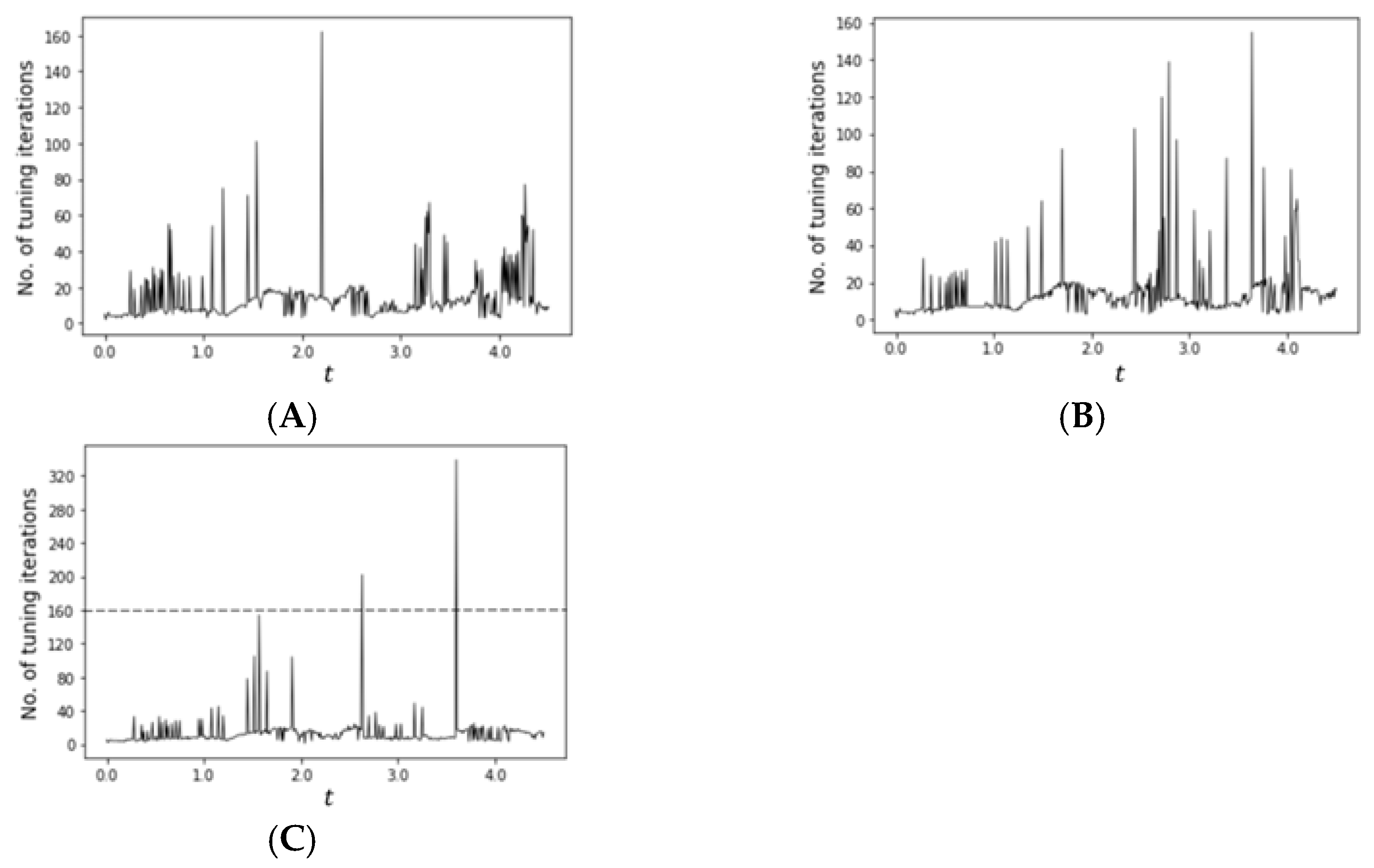

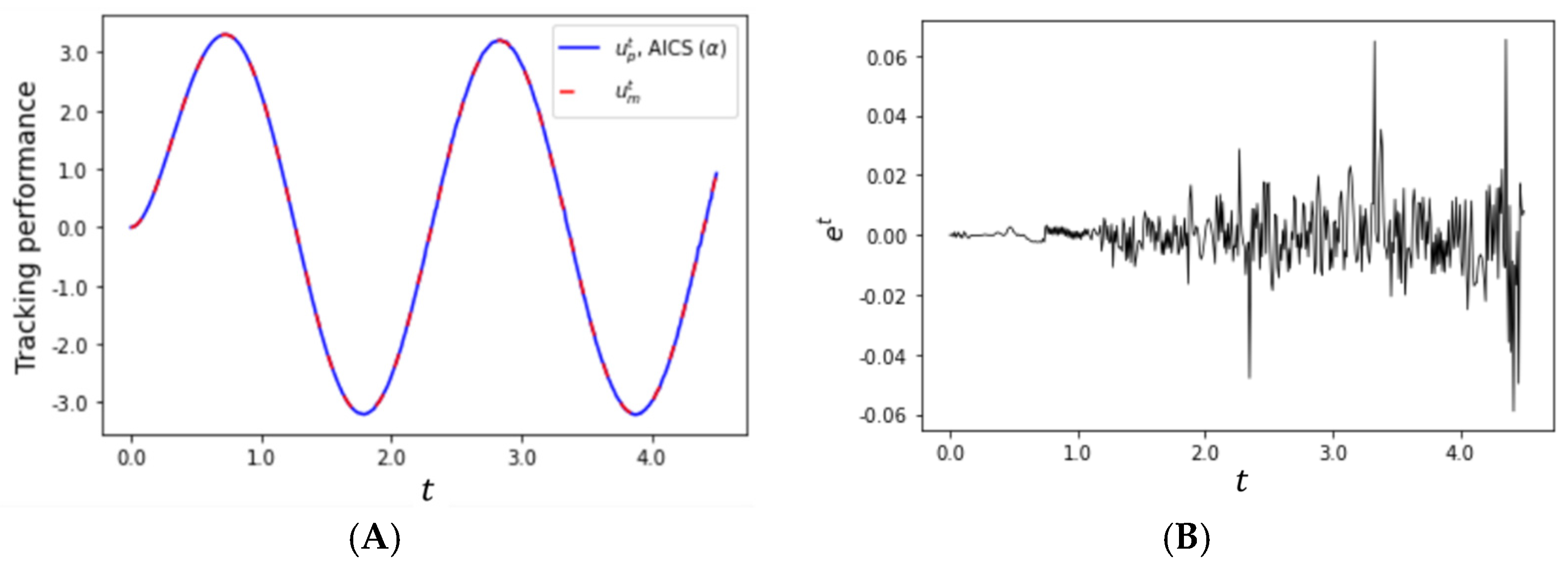

5. Conclusions
6. Future Study
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duanyai, W.; Song, W.K.; Konghuayrob, P.; Parnichkun, M. Event-triggered model reference adaptive control system design for SISO plants using meta-learning-based physics-informed neural networks without labeled data and transfer learning. Int. J. Adapt. Control Signal Process. 2024, 38, 1442–1456. [Google Scholar] [CrossRef]
- Antsaklis, P.J. Intelligent Control. Wiley Encyclopedia of Electrical and Electronics Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1999; pp. 493–505. [Google Scholar]
- Jagannathan, S.; Lewis, F.L.T. Identification of nonlinear dynamical systems using multilayered neural networks. Automatica 1996, 32, 1707–1712. [Google Scholar] [CrossRef]
- Kwan, C.M.; Lewis, F.L.; Dawson, D.M. Robust neural-network control of rigid-link electrically driven robots. IEEE Trans. Neural Netw. 1998, 9, 581–588. [Google Scholar] [CrossRef] [PubMed]
- Lewis, F.L.; Liu, K.; Yesildirek, A. Neural net robot controller with guaranteed tracking performance. IEEE Trans. Neural Netw. 1995, 6, 703–715. [Google Scholar] [CrossRef] [PubMed]
- Lewis, F.L.; Yesildirek, A.; Kai, L. Multilayer neural-net robot controller with guaranteed tracking performance. IEEE Trans. Neural Netw. 1996, 7, 388–399. [Google Scholar] [CrossRef]
- Yeşildirek, A.; Lewis, F.L. Feedback linearization using neural networks. Automatica 1995, 31, 1659–1664. [Google Scholar] [CrossRef]
- Yu, S.-H.; Annaswamy, A.M. Stable neural controllers for nonlinear dynamic systems. Automatica 1998, 34, 641–650. [Google Scholar] [CrossRef]
- Gu, F.; Yin, H.; Ghaoui, L.E.; Arcak, M.; Seiler, P.J.; Jin, M. Recurrent Neural Network Controllers Synthesis with Stability Guarantees for Partially Observed Systems; Association for the Advancement of Artificial Intelligence (AAAI): Washington, DC, USA, 2022; pp. 5385–5394. [Google Scholar]
- Widrow, B.; Walach, E. Adaptive Inverse Control: A Signal Processing Approach; Wiley-IEEE Press: Hoboken, NJ, USA, 2007. [Google Scholar]
- Nahas, E.P.; Henson, M.A.; Seborg, D.E. Nonlinear internal model control strategy for neural network models. Comput. Chem. Eng. 1992, 16, 1039–1057. [Google Scholar] [CrossRef]
- Hunt, K.J.; Sbarbaro, D.; Żbikowski, R.; Gawthrop, P.J. Neural networks for control systems—A survey. Automatica 1992, 28, 1083–1112. [Google Scholar] [CrossRef]
- Narendra, K.S.; Parthasarathy, K. Identification and control of dynamical systems using neural networks. IEEE Trans. Neural Netw. 1990, 1, 4–27. [Google Scholar] [CrossRef]
- Wang, D.; Liu, D.; Zhang, Q.; Zhao, D. Data-based adaptive critic designs for nonlinear robust optimal control with uncertain dynamics. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 1544–1555. [Google Scholar] [CrossRef]
- Jin, L.; Nikiforuk, P.N.; Gupta, M.M. Direct adaptive output tracking control using multilayered neural networks. J. Eng. Technol. 1993, 140, 393–398. [Google Scholar] [CrossRef]
- Jin, L.; Nikiforuk, P.N.; Gupta, M.M. Fast neural learning and control of discrete-time nonlinear systems. IEEE Trans. Syst. Man Cybern. 1995, 25, 478–488. [Google Scholar] [CrossRef]
- Levin, A.U.; Narenda, K.S. Control of nonlinear dynamical systems using neural networks. II. Observability, identification, and control. IEEE Trans. Neural Netw. 1996, 7, 40–42. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning, an Introduction, 2nd ed.; The MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef]
- Shen, Y.; Tobia, M.J.; Sommer, T.; Obermayer, K. Risk-sensitive reinforcement learning. Neural Comput 2014, 26, 1298–1328. [Google Scholar] [CrossRef][Green Version]
- Chen, H.; Liu, C. Safe and sample-efficient reinforcement learning for clustered dynamic environments. IEEE Control Syst. Lett. 2022, 6, 1928–1933. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhao, P.; Hovakimyan, N. Safe and efficient reinforcement learning using disturbance-observer-based control barrier functions. In Proceedings of the 5th Annual Learning for Dynamics and Control Conference, Philadelphia, PA, USA, 14–16 June 2023; PMLR 211: New York, NY, USA, 2023; pp. 104–115. Available online: https://proceedings.mlr.press/v211/cheng23a.html (accessed on 3 August 2025).
- Wachi, A.; Hashimoto, W.; Shen, X.; Hashimoto, K. Safe exploration in reinforcement learning: A generalized formulation and algorithms. In Proceedings of the 37th International Conference on Neural Information Processing Systems, New Orleans, LA, USA; 2024. [Google Scholar]
- Du, H.; Hao, B.; Zhao, J.; Zhang, J.; Wang, Q.; Yuan, Q. A path planning approach for mobile robots using short and safe Q-learning. PLoS ONE 2022, 17, e0275100. [Google Scholar] [CrossRef]
- Xu, H.; Zhan, X.; Zhu, X. Constraints Penalized Q-Learning for Safe Offline Reinforcement Learning; Association for the Advancement of Artificial Intelligence (AAAI): Washington, DC, USA, 2022; pp. 8753–8760. [Google Scholar]
- Ge, Y.; Zhu, F.; Ling, X.; Liu, Q. Safe Q-learning method based on constrained markov decision processes. IEEE Access 2019, 7, 165007–165017. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Dong, S.; Li, Z. Local extreme learning machines and domain decomposition for solving linear and nonlinear partial differential equations. Comput. Methods Appl. Mech. Eng. 2021, 387, 114129. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Kharazmi, E.; Karniadakis, G.E. Conservative physics-informed neural networks on discrete domains for conservation laws: Applications to forward and inverse problems. Comput. Methods Appl. Mech. Eng. 2020, 365, 113028. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, Y.; Sun, H. Physics-guided convolutional neural network (PhyCNN) for data-driven seismic response modeling. Eng. Struct. 2020, 215, 110704. [Google Scholar] [CrossRef]
- Zhu, Y.; Zabaras, N.; Koutsourelakis, P.-S.; Perdikaris, P. Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. J. Comput. Phys. 2019, 394, 56–81. [Google Scholar] [CrossRef]
- Sun, L.; Wang, J.-X. Physics-constrained bayesian neural network for fluid flow reconstruction with sparse and noisy data. Theor. Appl. Mech. Lett. 2020, 10, 161–169. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, X.; Yan, S.; Ren, Z. A Preliminary study on the resolution of electro-thermal multi-physics coupling problem using physics-informed neural network (PINN). Algorithms 2022, 15, 53. [Google Scholar] [CrossRef]
- Amini Niaki, S.; Haghighat, E.; Campbell, T.; Poursartip, A.; Vaziri, R. Physics-informed neural network for modelling the thermochemical curing process of composite-tool systems during manufacture. Comput. Methods Appl. Mech. Eng. 2021, 384, 113959. [Google Scholar] [CrossRef]
- Robinson, H.; Pawar, S.; Rasheed, A.; San, O. Physics guided neural networks for modelling of non-linear dynamics. Neural Netw. 2022, 154, 333–345. [Google Scholar] [CrossRef]
- Hochreiter, S.; Younger, A.S.; Conwell, P.R. Learning to learn using gradient descent. In Proceeding of the Artificial Neural Networks-ICANN 2001, Vienna, Austria, 21–25 August 2001. [Google Scholar]
- Younger, A.S.; Hochreiter, S.; Conwell, P.R. Meta-Learning with Backpropagation; IEEE: Washington, DC, USA, 2001; pp. 2001–2006. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017. [Google Scholar]
- Liu, X.; Zhang, X.; Peng, W.; Zhou, W.; Yao, W. A novel meta-learning initialization method for physics-informed neural networks. Neural Comput. Appl. 2022, 34, 14511–14534. [Google Scholar] [CrossRef]
- Psaros, A.F.; Kawaguchi, K.; Karniadakis, G.E. Meta-learning PINN loss functions. J. Comput. Phys. 2022, 458, 111121. [Google Scholar] [CrossRef]
- Penwarden, M.; Zhe, S.; Narayan, A.; Kirby, R.M. A metalearning approach for Physics-informed neural networks (PINNs): Application to parameterized PDEs. J. Comput. Phys. 2023, 477, 111912. [Google Scholar] [CrossRef]
- Nicodemus, J.; Kneifl, J.; Fehr, J.; Unger, B. Physics-informed neural networks-based model predictive control for multi-link manipulators. IFAC-PapersOnline 2022, 55, 331–336. [Google Scholar] [CrossRef]
- Gokhale, G.; Claessens, B.; Develder, C. Physics informed neural networks for control oriented thermal modeling of buildings. Appl. Energy 2022, 314, 118852. [Google Scholar] [CrossRef]
- García-Cervera, C.J.; Kessler, M.; Periago, F. Control of partial differential equations via physics-informed neural networks. J. Optim. Theory Appl. 2022, 196, 391–414. [Google Scholar] [CrossRef]
- Shi, G.; Azizzadenesheli, K.; O’Connell, M.; Chung, S.-J.; Yue, Y. Meta-adaptive nonlinear control: Theory and algorithms. In Proceedings of the 35th International Conference on Neural Information Processing Systems 34, Vancouver, BC, Canada, 6–14 December 2021; Available online: https://proceedings.neurips.cc/paper_files/paper/2021/hash/52fc2aee802efbad698503d28ebd3a1f-Abstract.html (accessed on 3 August 2025).
- Richards, S.M.; Azizan, N.; Slotine, J.-J.; Pavone, M. Adaptive-control-oriented meta-learning for nonlinear systems. Robotics: Science and Systems. arXiv 2021, arXiv:2103.04490. [Google Scholar] [CrossRef]
- Nagabandi, A.; Clavera, I.; Liu, S.; Fearing, R.S.; Abbeel, P.; Levine, S.; Finn, C. Learning to Adapt in Dynamic, Real-World Environments through Meta-Reinforcement Learning. In Proceedings of the 2nd Workshop on Meta-Learning, Montreal, QC, Canada, 8 December 2018. [Google Scholar] [CrossRef]
- Belkhale, S.; Li, R.; Kahn, G.; McAllister, R.; Calandra, R.; Levine, S. Model-based meta-reinforcement learning for flight with suspended payloads. IEEE Robot. Autom. Lett. 2021, 6, 1471–1478. [Google Scholar] [CrossRef]
- Penwarden, M.; Jagtap, A.D.; Zhe, S.; Karniadakis, G.E.; Kirby, R.M. A unified scalable framework for causal sweeping strategies for physics-informed neural networks (PINNs) and their temporal decompositions. J. Comput. Phys. 2023, 493, 112464. [Google Scholar] [CrossRef]
- Masood, A. Automated Machine Learning: Hyperparameter Optimization, Neural Architecture Search, and Algorithm Selection with Cloud Platforms; Packt Publishing Limited: Birmingham, UK, 2023. [Google Scholar]
- Kushner, H.J. A new method of locating the maximum point of an arbitrary multipeak curve in the presence of noise. J. Fluids Eng. 1964, 86, 97–106. [Google Scholar] [CrossRef]
- Zhilinskas, A.G. Single-step Bayesian search method for an extremum of functions of a single variable. J. Cybermetics Syst. Anal. 1975, 11, 160–166. [Google Scholar] [CrossRef]
- Močkus, J. On Bayesian Methods for Seeking the Extremum; Springer: Berlin/Heidelberg, Germany, 1975; pp. 400–404. [Google Scholar]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient global optimization of expensive black-box functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. In Proceedings of the Advances in Neural Information Processing Systems 25, Lake Tahoe, NV, USA, 3–6 December 2012; Available online: https://proceedings.neurips.cc/paper/2012/hash/05311655a15b75fab86956663e1819cd-Abstract.html (accessed on 3 August 2025).
- Salemi, P.; Nelson, B.L.; Staum, J. Discrete Optimization via Simulation Using Gaussian Markov Random Fields; IEEE: Georgia, GA, USA, 2014; pp. 3809–3820. [Google Scholar]
- Mehdad, E.; Kleijnen, J.P.C. Efficient global optimisation for black-box simulation via sequential intrinsic Kriging. J. Oper. Res. Soc. 2018, 69, 1725–1737. [Google Scholar] [CrossRef]
- Booker, A.J.; Dennis, J.J.E.; Frank, P.D.; Serafini, D.B.; Torczon, V.; Trosset, M.W. A rigorous framework for optimization of expensive functions by surrogates. J. Struct. Multidiscip. Optim. 1999, 17, 1–13. [Google Scholar] [CrossRef]
- Regis, R.G.; Shoemaker, C.A. Constrained global optimization of expensive black box functions using radial basis functions. J. Glob. Optim. 2016, 31, 153–171. [Google Scholar] [CrossRef]
- Regis, R.G.; Shoemaker, C.A. Improved strategies for radial basis function methods for global optimization. J. Glob. Optim. 2006, 37, 113–135. [Google Scholar] [CrossRef]
- Regis, R.G.; Shoemaker, C.A. Parallel radial basis function methods for the global optimization of expensive functions. Eur. J. Oper. Res. 2007, 182, 514–535. [Google Scholar] [CrossRef]
- Audet, C.; Denni, J.; Moore, D.; Booker, A.; Frank, P. A surrogate-model-based method for constrained optimization. In Proceedings of the 8th Symposium on Multidisciplinary Analysis and Optimization, Long Beach, CA, USA, 6–8 September 2000. [Google Scholar]
- Mahendran, N.; Wang, Z.; Hamze, F.; Freitas, N.D. Adaptive MCMC with Bayesian optimization. In Proceedings of the Fifteenth International Conference on Artificial Intelligence and Statistics, Proceedings of Machine Learning Research; Canary Island, Spain, 21–23 April 2021, Available online: https://proceedings.mlr.press/v22/mahendran12.html (accessed on 3 August 2025).
- Meeds, E.; Welling, M. GPS-ABC: Gaussian process surrogate approximate Bayesian computation. In Proceedings of the Thirtieth Conference on Uncertainty in Artificial Intelligence, Quebec City, QC, Canada, 23–27 July 2014. [Google Scholar]
- Genton, M.G. Classes of kernels for machine learning: A statistics perspective. J. Mach. Learn. Res. 2001, 2, 299–312. [Google Scholar]
- Sollich, P.; Urry, M.; Coti, C. Kernels and learning curves for Gaussian process regression on random graphs. In Proceedings of the Advances in Neural Information Processing Systems 22, Vancouver, BC, Canada, 7–10 December 2009; Available online: https://proceedings.neurips.cc/paper/2009/hash/92cc227532d17e56e07902b254dfad10-Abstract.html (accessed on 3 August 2025).
- Wilson, A.; Adams, R. Gaussian Process Kernels for Pattern Discovery and Extrapolation. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2021; PMLR: New York, NY, USA, 2013; Volume 28, pp. 1067–1075. Available online: https://proceedings.mlr.press/v28/wilson13.html (accessed on 3 August 2025).
- Duvenaud, D.; Lloyd, J.; Grosse, R.; Tenenbaum, J.; Zoubin, G. Structure discovery in nonparametric regression through compositional kernel search. In Proceedings of the 30th International Conference on Machine Learning, Proceedings of Machine Learning Research; Atlanta, GA, USA, 16–21 June 2023, Available online: https://proceedings.mlr.press/v28/duvenaud13.html (accessed on 3 August 2025).
- Roman, I.; Santana, R.; Mendiburu, A.; Lozano, J.A. An experimental study in adaptive kernel selection for Bayesian optimization. IEEE Access 2019, 7, 184294–184302. [Google Scholar] [CrossRef]
- Couckuyt, I.; Deschrijver, D.; Dhaene, T. Fast calculation of multiobjective probability of improvement and expected improvement criteria for Pareto optimization. J. Glob. Optim. 2013, 60, 575–594. [Google Scholar] [CrossRef]
- Chapelle, O.; Li, L. An Empirical Evaluation of Thompson Sampling. Curran Associates. In Proceedings of the Advances in Neural Information Processing Systems 24, Granada, Spain, 12–17 December 2011; Available online: https://proceedings.neurips.cc/paper/2011/hash/e53a0a2978c28872a4505bdb51db06dc-Abstract.html (accessed on 3 August 2025).
- Duanyai, W.; Song, W.K.; Chitthamlerd, T.; Kumar, G. Meta-learning-based physics-informed neural network: Numerical simulations of initial value problems of nonlinear dynamical systems without labeled data and correlation analyses. J. Nonlinear Model. Anal. 2024, 6, 485–513. [Google Scholar] [CrossRef]
- Nocedal, J. Updating quasi-Newton matrices with limited storage. Math. Comput. 1980, 35, 773–782. [Google Scholar] [CrossRef]
- Byrd, R.H.; Nocedal, J.; Schnabel, R.B. Representations of quasi-Newton matrices and their use in limited memory methods. Math. Program. 1994, 63, 129–156. [Google Scholar] [CrossRef]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Duanyai, W. A Comparision of the Controllability of Model Reference Adaptive Control and Intelligent Control Systems for a Nonlinear SISO Plant; King Mongkut Institute of Technology Ladkrabang: Bangkok, Thailand, 2024. [Google Scholar]


| MTR | Target Hyperparameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NE (First Hidden Layer) | NE (Second Hidden Layer) | |||||||||
| Min. V | Int. V | Max. V | Min. V | Int. V | Max. V | Min. V | Int. V | Max. V | ||
| Scenario 1 | 0.01 | 8 | 256 | |||||||
| Scenario 2 | 5 | 0.001 | 0.001 | 0.02 | 8 | 256 | ||||
| Scenario 3 | 20 | 0.001 | 0.001 | 0.02 | 8 | 256 | 2048 | 8 | 256 | 2048 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duanyai, W.; Song, W.K.; Ka, M.-H.; Lee, D.-W.; Dissanayaka, S. Novel Adaptive Intelligent Control System Design. Electronics 2025, 14, 3157. https://doi.org/10.3390/electronics14153157
Duanyai W, Song WK, Ka M-H, Lee D-W, Dissanayaka S. Novel Adaptive Intelligent Control System Design. Electronics. 2025; 14(15):3157. https://doi.org/10.3390/electronics14153157
Chicago/Turabian StyleDuanyai, Worrawat, Weon Keun Song, Min-Ho Ka, Dong-Wook Lee, and Supun Dissanayaka. 2025. "Novel Adaptive Intelligent Control System Design" Electronics 14, no. 15: 3157. https://doi.org/10.3390/electronics14153157
APA StyleDuanyai, W., Song, W. K., Ka, M.-H., Lee, D.-W., & Dissanayaka, S. (2025). Novel Adaptive Intelligent Control System Design. Electronics, 14(15), 3157. https://doi.org/10.3390/electronics14153157






