Parameter Identification Method of Grid-Forming Static Var Generator Based on Trajectory Sensitivity and Proximal Policy Optimization Algorithm
Abstract
1. Introduction
2. Control Method and Trajectory Sensitivity Analysis of GFM-SVGs
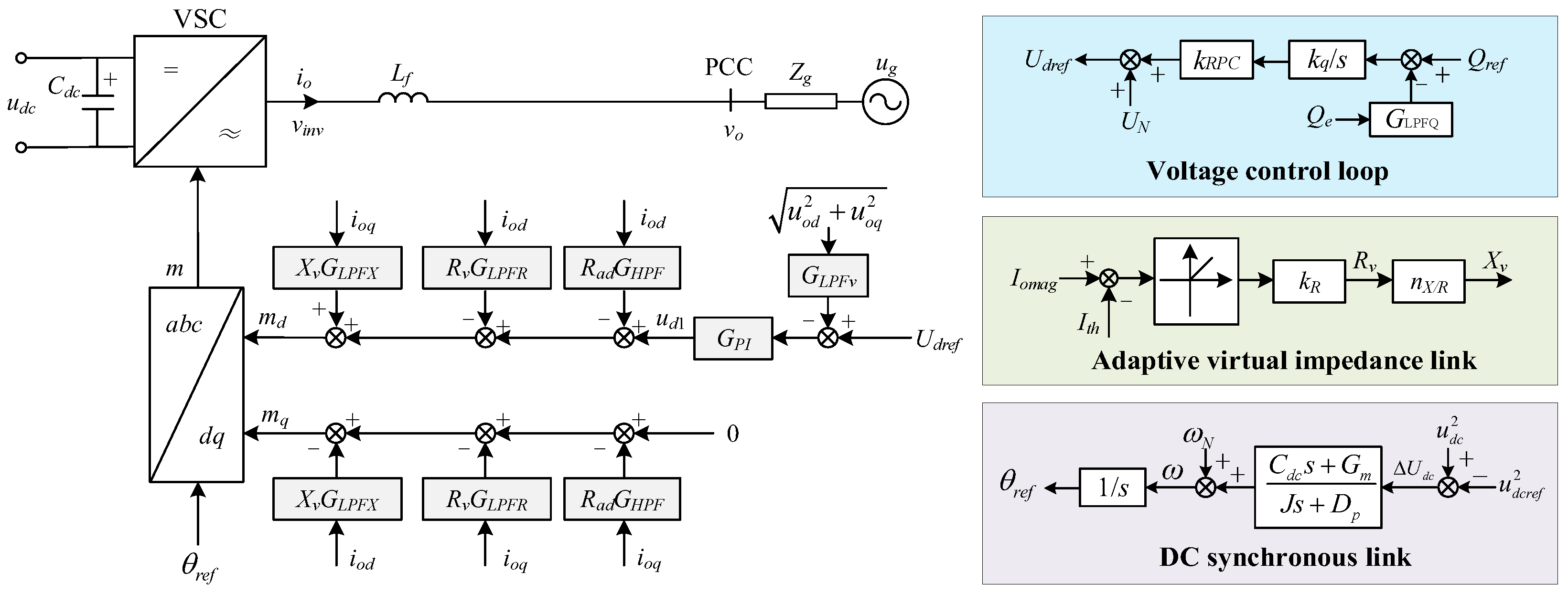
2.1. Control Method of GFM-SVGs
2.2. Parameter Selection Method of GFM-SVG Based on Trajectory Sensitivity
3. Parameter Identification Method Based on PPO Algorithm for GFM-SVG
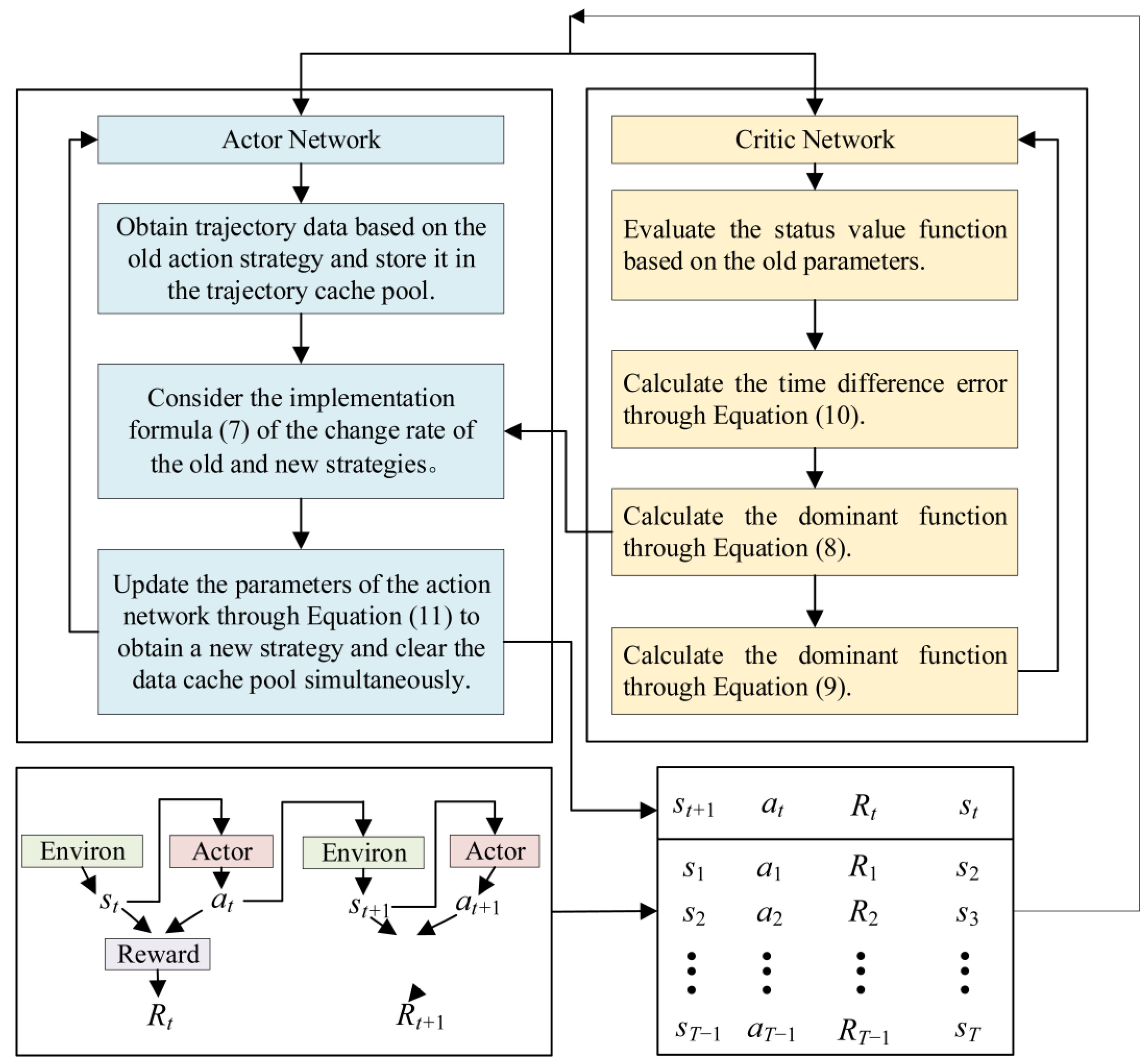
3.1. PPO Algorithm
3.2. Parameter Identification of GFM-SVG Based on PPO Algorithm
4. Simulation Example
4.1. Key Parameters Selection Based on Trajectory Sensitivity Analysis
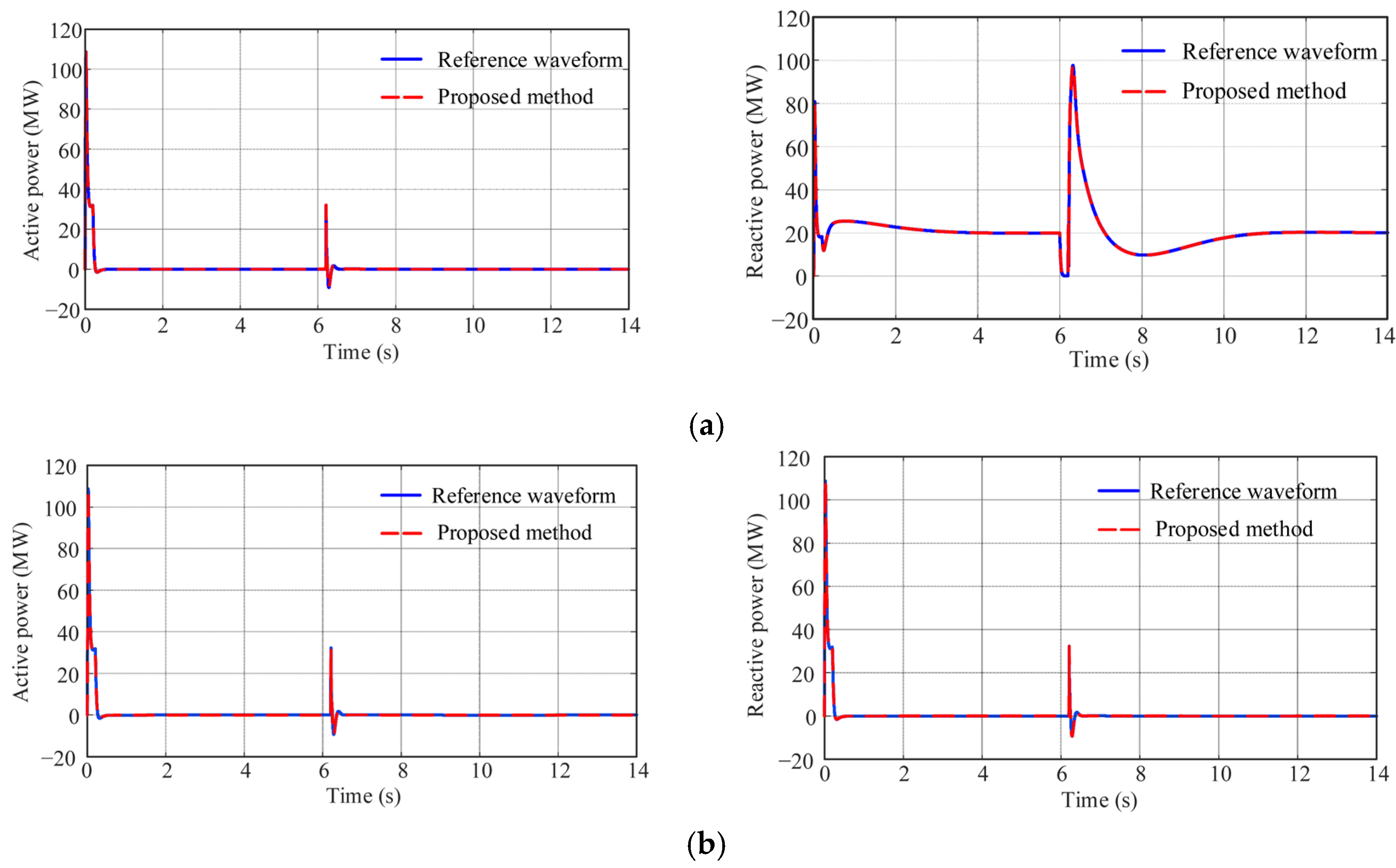
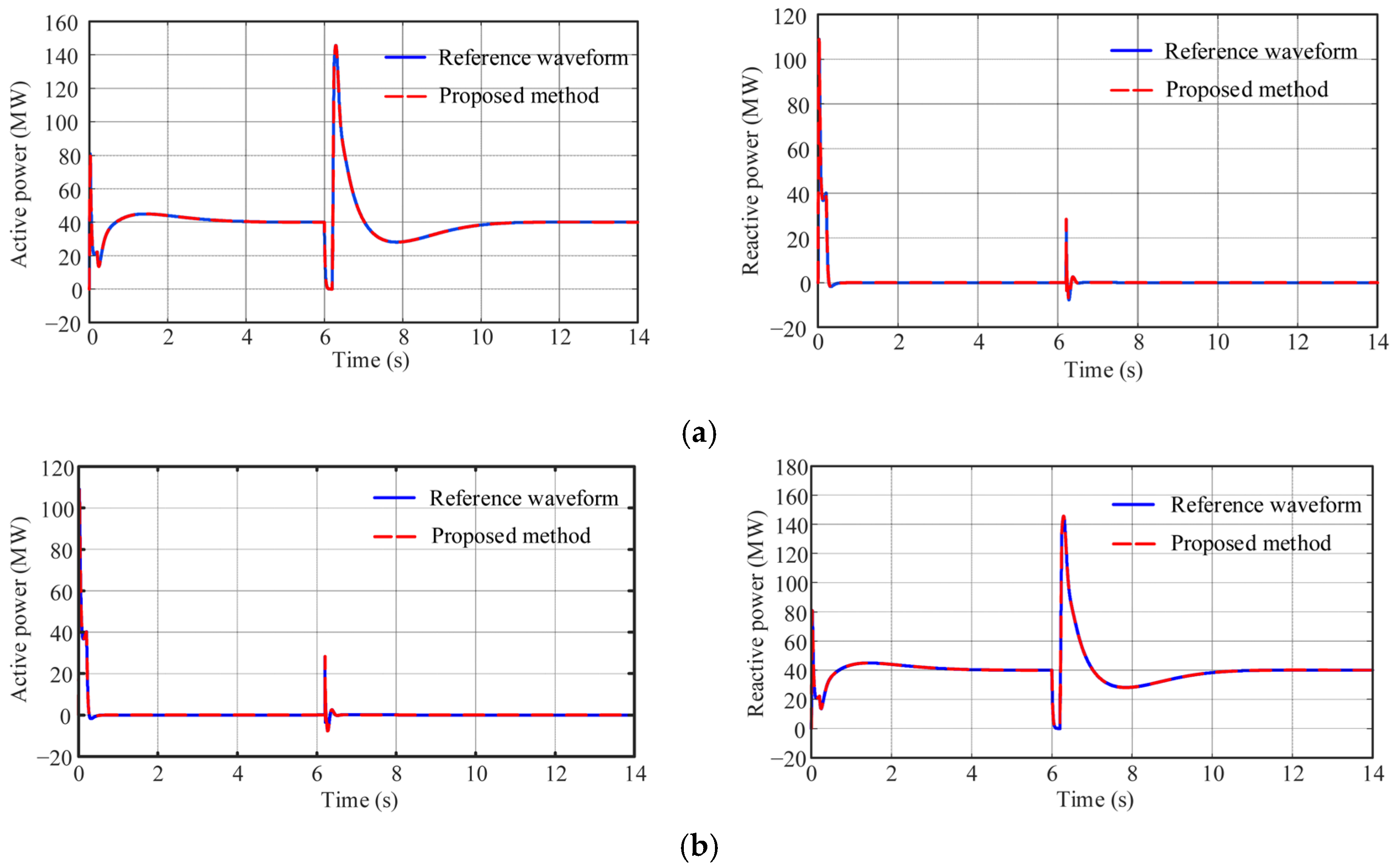
4.2. Validation of the Parameter Identification Results for GFM-SVGs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GFM-SVG | Grid-forming static var generator |
| PPO | Proximal policy optimization |
| SVC | Static var compensator |
| RTDS | Real-time digital simulation system |
| PSO | Particle swarm optimization |
| DC | Direct current |
| AC | Alternating current |
References
- Zhang, X.; Liu, J. Distributed Power, Energy Storage Planning, and Power Tracking Studies for Distribution Networks. Electronics 2025, 14, 2833. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, T.; Gao, S.; Chen, Y.; Chen, W.; Zhou, X. Conceptualization and application prospect of digital twin system in hydroelectric unit. Proc. CSEE 2025, 45, 4526–4542. [Google Scholar]
- Wang, Y.; Wang, X.; Liao, J.; Su, M.; Liu, Y. Probabilistic small-signal stability assessment and cooperative control for interconnected microgrids via back-to-back converters. J. Mod. Power Syst. Clean Energy 2025, 13, 552–563. [Google Scholar] [CrossRef]
- Markovic, U.; Stanojev, O.; Aristidou, P.; Vrettos, E.; Callaway, D.; Hug, G. Understanding small-signal stability of low-inertia systems. IEEE Trans. Power Syst 2021, 36, 3997–4017. [Google Scholar] [CrossRef]
- Ratnam, K.S.; Palanisamy, K.; Yang, G. Future low-inertia power systems: Requirements, issues, and solutions—A review. Renew. Sustain. Energy Rev. 2020, 124, 109773. [Google Scholar] [CrossRef]
- Hosseinzadeh, N.; Aziz, A.; Mahmud, A.; Gargoom, A.; Rabbani, M. Voltage stability of power systems with renewable-energy inverter-based generators: A review. Electronics 2021, 10, 115. [Google Scholar] [CrossRef]
- Tuo, M.; Li, X. Security-constrained unit commitment considering locational frequency stability in low-inertia power grids. IEEE Trans. Power Syst. 2022, 38, 4134–4147. [Google Scholar] [CrossRef]
- Gomis-Bellmunt, O.; Tavakoli, S.D.; Lacerda, V.A.; Prieto-Araujo, E. Grid-forming loads: Can the loads be in charge of forming the grid in modern power systems? IEEE Trans. Smart Grid 2023, 14, 1042–1055. [Google Scholar] [CrossRef]
- Gao, H.; Huang, Z.; Diao, R.; Zhang, J.; Hou, B.; Wu, C.; Sun, F.; Lan, T. A machine learning-based SVG parameter identification framework using hardware-in-the-loop testbed. IEEE Trans. Power Syst. 2024, 39, 6849–6860. [Google Scholar] [CrossRef]
- Dahat, A.; Dhabale, A. Coordinated robust damping control for hybrid SVC/SSSC to enhance power system stability in large-scale systems. IEEE Trans. Ind. Appl. 2024, 60, 1589–1598. [Google Scholar] [CrossRef]
- Rosso, R.; Wang, X.; Liserre, M.; Lu, X.; Engelken, S. Grid-forming converters: Control approaches, grid-synchronization, and future trends—A review. IEEE Open J. Ind. Appl. 2021, 2, 93–109. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Yang, Y.; Kim, K.A.; Rodriguez, J. Power electronics technology for large-scale renewable energy generation. Proc. IEEE 2023, 111, 335–355. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, H.; Song, X.; Zhang, H.; Zhang, Y.; Chen, J.; Liu, H. Analysis of influence of grid-following and grid-forming static var generators on high-frequency resonance in doubly fed induction generator-based wind farms. Electronics 2024, 13, 3879. [Google Scholar] [CrossRef]
- Zhou, Z.; Mastoi, M.S.; Wang, D.; Haris, M. Control strategy of DFIG and SVG cooperating to regulate grid voltage of wind power integration point. Electr. Power Syst. Res. 2023, 214, 108862. [Google Scholar] [CrossRef]
- Li, X.; Zheng, Z.; Meng, J.; Wang, Q. Robust estimation of lithium battery state of charge with random missing current measurement data. Electronics 2024, 13, 4436. [Google Scholar] [CrossRef]
- Xia, T.; Ma, J.; Huang, H.; Peng, Y.; Xiao, X.; Chen, H.; Guo, R. Parameter identification of SVG controller based on RTDS hardware-in-loop test. Power Syst. Prot. Control 2020, 48, 110–116. [Google Scholar]
- Cao, B.; Yu, C.; Shuai, Y.; Xiaolin, Z.; Qi, W.; Liqiang, W.; Yongfei, Z. SVG model parameter test method based on controller hardware-in-loop. Low Volt. Appar. 2021, 6, 63. [Google Scholar]
- Guo, Q.; Sun, H.; Gao, L.; Xi, M.; Nie, Y.; Song, R. Research on intelligent identification method of SVG model parameters considering the random characteristics of wind farm. Proc. CSEE 2020, 40, 7950–7958. [Google Scholar]
- Zhai, B.; Ou, K.; Wang, Y.; Cao, T.; Dai, H.; Zheng, Z. Parameter identification of PMSG-based wind turbine based on sensitivity analysis and improved gray wolf optimization. Energies 2024, 17, 4361. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X. Small-signal modeling and controller parameters tuning of grid-forming VSCs with adaptive virtual impedance-based current limitation. IEEE Trans. Power Electron. 2021, 37, 7185–7199. [Google Scholar] [CrossRef]
- Li, D.; Wang, T.; Pan, W.; Ding, X.; Gong, J. A comprehensive review of improving power quality using active power filters. Electr. Power Syst. Res. 2021, 199, 107389. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, C.; Zhu, L.; Zhang, G.; Li, X.; Chen, Y. Comprehensive modeling and parameter identification of wind farms based on wide-area measurement systems. J. Mod. Power Syst. Clean Energy 2016, 4, 383–393. [Google Scholar] [CrossRef]
- Gu, Y.; Cheng, Y.; Chen, C.L.P.; Wang, X. Proximal policy optimization with policy feedback. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 4600–4610. [Google Scholar] [CrossRef]
- An, H.; Wang, L. Robust topology generation of Internet of Things based on PPO algorithm using discrete action space. IEEE Trans. Ind. Inform. 2023, 20, 5406–5414. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, P.; Xie, H.; Lu, X.; Wu, X.; Liu, Z. Graph attention network based deep reinforcement learning for voltage/var control of topologically variable power system. J. Mod. Power Syst. Clean Energy 2024, 13, 215–227. [Google Scholar] [CrossRef]
- Wu, P.; Chen, C.; Lai, D.; Zhong, J.; Bie, Z. Real-time optimal power flow method via safe deep reinforcement learning based on primal-dual and prior knowledge guidance. IEEE Trans. Power Syst. 2024, 40, 597–611. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Duan, J.; Shi, D.; Benidris, M. A deep reinforcement learning-based multi-agent framework to enhance power system resilience using shunt resources. IEEE Trans. Power Syst. 2021, 36, 5525–5536. [Google Scholar] [CrossRef]
- Jin, J.; Xu, Y. Optimal policy characterization enhanced actor-critic approach for electric vehicle charging scheduling in a power distribution network. IEEE Trans. Smart Grid 2020, 12, 1416–1428. [Google Scholar] [CrossRef]
- Song, Y.; Chen, Y.; Yu, Z.; Huang, S.; Shen, C. CloudPSS: A high-performance power system simulator based on cloud computing. Energy Rep. 2020, 6, 1611–1618. [Google Scholar] [CrossRef]


| Variable | Parameter | Variable | Parameter |
|---|---|---|---|
| kp | 5 | 100π | |
| ki | 0.2 | kR | 10 |
| 20π | nx/r | 5 | |
| 100π | kq | 0.2 | |
| J | 0.0254648 | 100π | |
| kRPC | 0.1 | Dp | 59.685 |
| Gm | 0.5 | 20π |
| Variable | Parameter | Variable | Parameter |
|---|---|---|---|
| kp | 47.079 | 1.761 | |
| ki | 7.714 | kR | 79.495 |
| 0.257 | nx/r | 193.949 | |
| 0.593 | kq | 192.855 | |
| J | 80.811 | 1.665 | |
| kRPC | 488.197 | Dp | 25.838 |
| Gm | 3121.849 | 3.063 |
| Variable | Typical Value | PPO (Error) | PSO (Error) |
|---|---|---|---|
| kp | 5 | 5.0094 (0.188%) | 5.7826 (15.652%) |
| J | 0.0254648 | 0.0255 (0.138%) | 0.0280 (9.957%) |
| kRPC | 0.1 | 0.0998 (0.200%) | 0.1273 (27.300%) |
| Gm | 0.5 | 0.5012 (0.240%) | 0.5170 (3.400%) |
| kR | 10 | 10.0079 (0.079%) | 9.4101 (5.899%) |
| nx/r | 5 | 4.9879 (0.242%) | 5.1343 (2.686%) |
| kq | 0.2 | 0.1997 (0.150%) | 0.1598 (20.100%) |
| Dp | 59.685 | 59.7018 (0.028%) | 70.0462 (17.355%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, Y.; Shi, P.; Bai, J.; Wang, X.; Shao, Z.; Cao, T.; Guan, X.; Zheng, Z. Parameter Identification Method of Grid-Forming Static Var Generator Based on Trajectory Sensitivity and Proximal Policy Optimization Algorithm. Electronics 2025, 14, 3119. https://doi.org/10.3390/electronics14153119
Teng Y, Shi P, Bai J, Wang X, Shao Z, Cao T, Guan X, Zheng Z. Parameter Identification Method of Grid-Forming Static Var Generator Based on Trajectory Sensitivity and Proximal Policy Optimization Algorithm. Electronics. 2025; 14(15):3119. https://doi.org/10.3390/electronics14153119
Chicago/Turabian StyleTeng, Yufei, Peng Shi, Jiayu Bai, Xi Wang, Ziyuan Shao, Tian Cao, Xianglian Guan, and Zongsheng Zheng. 2025. "Parameter Identification Method of Grid-Forming Static Var Generator Based on Trajectory Sensitivity and Proximal Policy Optimization Algorithm" Electronics 14, no. 15: 3119. https://doi.org/10.3390/electronics14153119
APA StyleTeng, Y., Shi, P., Bai, J., Wang, X., Shao, Z., Cao, T., Guan, X., & Zheng, Z. (2025). Parameter Identification Method of Grid-Forming Static Var Generator Based on Trajectory Sensitivity and Proximal Policy Optimization Algorithm. Electronics, 14(15), 3119. https://doi.org/10.3390/electronics14153119







