Abstract
Effective energy management in Low Earth Orbit satellites is critical, as inefficient energy management can significantly affect mission objectives. The dynamic and harsh space environment further complicates the development of effective energy management strategies. To address these challenges, we propose a Deep Reinforcement Learning approach using Deep-Q Network to develop an adaptive energy management framework for Low Earth Orbit satellites. Compared to traditional techniques, the proposed solution autonomously learns from environmental interaction, offering robustness to uncertainty and online adaptability. It adjusts to changing conditions without manual retraining, making it well-suited for handling modeling uncertainties and non-stationary dynamics typical of space operations. Training is conducted using a realistic satellite electric power system model with accurate component parameters and single-orbit power profiles derived from real space missions. Numerical simulations validate the controller performance across diverse scenarios, including multi-orbit settings, demonstrating superior adaptability and efficiency compared to conventional Maximum Power Point Tracking methods.
1. Introduction
Low Earth Orbit (LEO) satellites operate at altitudes ranging from 160 km to 2000 km [1,2,3]. This orbital regime presents a unique balance of benefits, costs, and constraints. This balance makes LEO satellites suitable for a range of applications, including Earth observation, satellite communication, and scientific research [1,2,3]. The proximity to Earth allows for high image resolutions, high bandwidth and low latency communication, reduced per-satellite launch costs, and increased satellite accessibility (for crew and servicing) [4]. However, the limited field of view, combined with high orbital speeds, necessitates a large number of satellites to achieve continuous Earth coverage. Deploying a large number of LEO satellites per application increases launch costs, which can be mitigated by constraining satellite dimensions and mass.
The limitations on size and mass, along with the necessity of deploying large constellations for specific applications (e.g., communication), affect the design of LEO satellite Electrical Power Systems (EPSs): (i) the onboard battery pack must be small and lightweight to fit the available space, but it must also be capable of storing an appropriate amount of energy during sunlight and delivering it to the load during each eclipse period, in accordance with the space mission specifications [5,6]; (ii) to operate within a constellation, each satellite can require additional antennas for inter-satellite communication, reducing available space onboard and increasing energy and power consumption [4]. In practice, managing power efficiently during frequent transitions in and out of Earth’s shadow is a key design challenge in LEO satellite EPSs, necessitating careful battery management.
1.1. Typical Approaches for Satellite EPSs
Satellite EPSs are responsible for regulating, managing, and distributing the power generated by Solar Arrays (SAs) and stored in battery packs throughout the mission and across all operational modes [7]. Its principal components include the SAs, SA drive assembly, battery packs, bus voltage regulator, load switching, fuses, distribution harness, and battery charge and discharge regulators [8]. Figure 1 shows the main functionality of a satellite EPS. Those pertinent to this paper’s scope are the power source, energy storage, and power control and regulation, since they are involved in the onboard energy management processes.

Figure 1.
Functional breakdown of a satellite EPS.
Power source and energy storage functions are implemented using SAs and battery packs, respectively. SAs are composed of numerous Photo Voltaic (PV) cells stacked in series-parallel connections to obtain the desired voltage and current [9]. Similarly, battery packs are built using series-parallel combinations of rechargeable electrochemical cells [10].
Power regulation and control functions are achieved through a typical nested control architecture with analog (for faster inner loops in power converters) and/or digital (for slower outer loops in power management systems) implementation [11]. Such functions are required since the SA, the battery, and the loads are not operated at the same constant voltage during the space mission [8]. At the beginning of its operational life, a SA typically delivers a higher output voltage due to optimal efficiency and minimal degradation. A similar effect is observed immediately after an eclipse, when the SA re-emerges from Earth’s shadow and its panels are suddenly re-exposed to direct sunlight. In contrast, the battery pack exhibits a lower output voltage while discharging energy to power onboard satellite systems. This is because, as the stored energy depletes, internal resistance increases, leading to a progressive voltage drop. Conversely, during the charging phase, particularly when the solar array is sunlit and generating power, the battery voltage tends to rise, reflecting the inflow of current. Thus, appropriate power regulation and control are essential to comply with the voltages of different power components, and deliver power to the loads within specified limits throughout the space mission [12].
There exist two typical power regulation and control techniques: Direct Energy Transfer (DTE) and Peak Power Tracking (PPT) [13]. In DTE, the solar power is directly supplied to the battery pack and load without regulation units in between. In PPT, a DC/DC power conversion chain connects the SA with the battery pack and the load. However, additional control loops can be necessary to achieve the desired power performance requirements, such as a supervisor activating appropriate control laws based on the current operational mode [8,14].
1.2. Motivation and Contribution
Three approaches can be identified in the literature for energy management in LEO satellite EPSs: (i) separating load- and line-regulation design [15], e.g., as with standard linearized techniques; (ii) separating power and energy management design [16]; (iii) unifying the design via advanced model-based techniques using, e.g., optimization as in [17], where an optimal battery charging profile is attained by minimizing an objective function that considers the recharging time, power dissipation, and variations in the battery’s internal temperature. Unfortunately, even in the latter case where robust methods can be applied, for instance, to address cell heterogeneity causing early battery degradation, only slight deviations from the nominal values of a limited set of parameters can be effectively managed. Conversely, data-driven and model-free approaches can effectively handle these aspects and offer a number of advantages over the current state-of-the-art [18].
Deep Reinforcement Learning (DRL)-based solutions [19,20,21] adapt well to changing environments and provide robustness against system uncertainties [22,23,24]. Their technological maturity is highlighted in several works that address different applications. For example, Ref. [25] offers a good perspective in smart buildings with an in-depth literature analysis on the topic; Refs. [26,27] showcase their use in vehicular technologies, where the former uses a soft actor–critic DRL algorithm in order to effectively allocate the power between the electric motor and the internal combustion engine of a hybrid bus during the drive, and the latter uses a confidence-aware DRL-based strategy to improve the driving range of electric vehicles; Ref. [28] demonstrates how to achieve microgrid real-time management by formulating this problem as a Markov Decision Process (MDP) and solving it via the Proximal Policy Optimization (PPO) algorithm (a policy-based DRL algorithm with continuous state and action spaces); and Ref. [29] adopts a variant of the Deep Deterministic Policy Gradient (DDPG) algorithm for energy management in cognitive radio networks, a type of wireless communication system that improves spectrum utilization by allowing unlicensed users to opportunistically access unused licensed spectrum bands.
In general, DRL-based solutions employ Neural Networks (NNs) to formulate control policies, enabling Reinforcement Learning (RL) to scale to high-dimensional, continuous state and action spaces and to handle system nonlinearities. In contrast to the high computational costs required for their training, and, more importantly, compared to model-based techniques [18], only limited memory and computational resources are usually required to execute the resultant trained DRL agent online.
In this paper, we employ a DRL-based approach for energy management in LEO satellite EPSs. Among the various alternatives, including machine learning methods such as supervised learning, Long Short-Term Memory (LSTM)- and Convolutional Neural Network (CNN)-based approaches, as well as more specialized DRL approaches like actor–critic algorithms such as Twin-Delayed Deep Deterministic (TD3) and Soft Actor–Critic (SAC), this work adopts an adaptive control framework based on the Deep-Q Network (DQN) algorithm [30], presenting its core elements: the state space, the action space, and the reward function. Indeed, among the available options, the DQN algorithm proves to be better suited for the specific application at hand.
In particular, with respect to supervised learning methods, such as LSTM- or CNN-based approaches, it provides
- Sequential decision-making: The energy management task involves sequential decision-making under uncertainty and dynamic environmental conditions (e.g., varying solar exposure and power profiles). As a DRL technique, DQN is well-suited for such problems where the goal is to learn optimal policies over time, rather than static mappings between input and output as in supervised learning [20,31].
- Lack of labeled data: Supervised learning approaches (including LSTM- or CNN-based solutions) require large, labeled datasets representing optimal energy management decisions. Such datasets are typically unavailable or infeasible to generate at scale for highly dynamic satellite environments [32]. In contrast, DQN-based agents learn through interaction with a simulated environment, making it more flexible and scalable for this context [33].
- Online adaptability and robustness: DQN-trained agents can also adapt to new operating conditions without requiring manual relabeling or retraining, offering robustness to modeling uncertainties and non-stationary environments, both of which are common in space operations [34].
Further, with respect to more complex DRL techniques, like actor–critic methods, it offers
- Simplicity and robustness: DQN offers a simpler architecture and training pipeline, while actor–critic methods often require more complex coordination between actor and critic networks and additional hyperparameter tuning [25,30].
- Discrete action space suitability: The energy management problem for LEO satellite EPSs can be effectively modeled using a discrete action space, as shown in Section 3, making DQN particularly well-suited to this setting without requiring the complexities of continuous control methods. This design choice allows achieving a good trade-off between expressiveness and implementability, which is critical for embedded systems aboard LEO satellites with limited computational and memory resources [6,32].
- Computational efficiency: DQN is lightweight in both training and inference, which is a crucial advantage when targeting real-time deployment aboard resource-constrained satellite platforms [34]. Methods like TD3 and SAC generally involve a higher computational overhead and memory consumption [20,21].
- Demonstrated effectiveness: Despite its relative simplicity, as reported in Section 4, the proposed DQN-based solution achieved very competitive results in extensive simulation studies, providing good adaptability and performance across multiple operational scenarios.
Thus, the proposed DQN-controller/agent is trained by considering an EPS (acting as environment in RL terms) with realistic component specifications, a specific single-orbit power profile to be met, and changing initial battery State of Charges (SoCs). The trained DQN agent is then validated by taking into account scenarios with different single-orbit power profiles, and by altering the starting SoC over a wider range than during the training phase. All the power profiles used for training and validation have been derived from real space missions, see [14,17,35].
Then, to further assess the robustness and generalization capabilities of the trained DQN agent and verify its applicability to a more realistic operational setting, a multi-orbit validation scenario is also examined. Finally, a comparative study with the Maximum Power Point Tracking (MPPT) control technique is provided in order to highlight the benefits of the proposed solution over widely used approaches.
1.3. Paper Organization and Notation
The rest of the paper is organized as follows. Section 2 describes the EPS environment realized with a PPT unregulated bus architecture, including the SA, power conversion, and battery models. Section 3 presents the implementation of the EPS controller within the proposed DQN-based framework. Section 4 includes simulation studies showing the effectiveness of the proposed solution. Section 5 concludes the paper.
The notation used in this paper is as follows. and indicate, respectively, the sets of non-negative real and natural numbers. Sets are denoted with capital letters in calligraphy, for example , while matrices and vectors are written in bold letters. The prime symbol (′) is the transpose operator. Finally, indicates the discrete-time step, while continuous-time dependencies in variables of interest are omitted for readability throughout the paper.
2. The EPS Environment
The EPS LEO satellite analyzed in this paper adopts the PPT unregulated bus EPS architecture [36]. Figure 2 illustrates the interaction between the controller (the “EPS agent”, responsible for selecting the duty cycle) and the “EPS environment”, which is based on the PPT architecture. The key components of this environment are the payloads (acting as loads), a battery, PV panels, and a DC-DC buck power converter.

Figure 2.
Illustration of the interaction between the EPS environment, based on the PPT architecture, and the RL control agent.
The output voltage of the battery (), which varies between upper and lower limits based on whether the battery is being charged or discharged, is directly correlated with the bus voltage. There is an increase in voltage when charging, and a reduction in voltage during discharging.
The PV panels are connected to the bus by means of the DC-DC converter, and supply power according to the solar irradiance () and panel temperature (). When available, the battery stores extra energy and provides electricity when PV generation is insufficient, such as during eclipse phases when the power generated by the PV panels () is zero.
The EPS controller plays a crucial role by ensuring that the satellite receives the required power while also managing the charging of the battery. The power generated by the PV (), the battery power (), and the required payload (load) power () must satisfy the instantaneous power balance
where , and and are the voltage and the current of the battery, respectively. During the eclipse phase, when , the battery becomes the only power source for the satellite, supplying all the necessary power to the payloads (). In this case, the DC-DC power converter is inactive. During sunlight, the system faces the challenge of balancing the power demand of the payloads with the need to charge the battery. When the payload demand exceeds the power supplied by the PV, the battery assists the PV in providing additional power.
The following subsections provide a detailed explanation of the EPS elements. In particular, the PV is modeled using CTJ30 space-grade solar cells manufactured by CESI [37], capturing irradiance-dependent I-V characteristics and temperature effects. The battery model is based on MP176065 Li-ion cells [38]. Mission power profiles used for training and validation were derived from existing LEO satellite datasets and published EPS studies [14,17,35], capturing realistic payload demand patterns and orbital transitions, including sunlight and eclipse phases.
2.1. Photovoltaic Panel
PV panels provide electrical power during sunlight and are disconnected from the electrical subsystem during eclipse phases. For simplicity, the PV is modeled as a single panel connected to a DC-DC converter. This panel consists of PV cells connected in series and PV cells connected in parallel, supplying the necessary voltage and current. The PV panel generates electrical power based on environmental conditions, with solar irradiance and temperature serving as external inputs that vary throughout the satellite mission.
Figure 3 depicts the equivalent circuit of a solar cell under steady-state conditions [39,40]. The series resistor represents the material’s internal resistance to current flow, caused by its inherent resistivity.
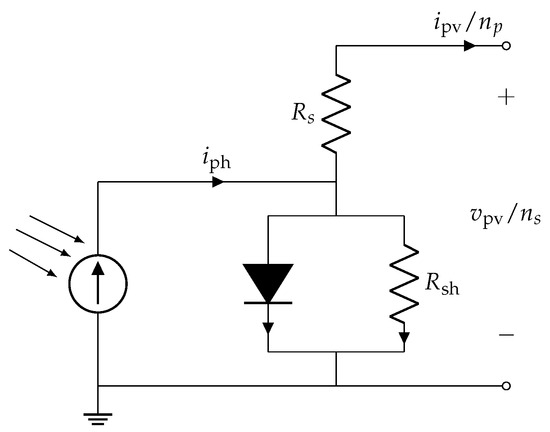
Figure 3.
An equivalent circuit for a single solar cell.
The shunt resistor accounts for leakage current across the junction, and it is influenced by factors such as junction depth, impurities, and contact resistance. In an ideal PV cell, there would be no series losses or leakage current, which would correspond to a short circuit for and an open circuit for .
From a modeling perspective, the total current supplied by the parallel-connected PV cells, denoted as , is a function of the sum of the voltages across the series-connected cells, denoted as , and can be expressed as
with K the Boltzmann constant, n the diode ideality factor, q the electron charge, the diode saturation current, the temperature on the PV panel which is considered as an input together with the irradiance , and the photo-generated current. The diode ideality factor n, the series resistance and the shunt resistance can be obtained from the maximum power point values, while the photo-generated current and the diode saturation current can be expressed using standard parameters available from the cell datasheet, i.e., the short circuit current and the open circuit voltage [17]. For any pair of temperature and irradiance, it is straightforward to see that, given the voltage , there exists a single value for the current that satisfies (2). In order to keep the computational burden low, (2) is replaced by a map where the PV model takes the terminal voltage as an input and provides the current as an output, which is subsequently used as an input in the battery model.
Figure 4 shows the characteristic of the panel under different conditions. The upper curves correspond to constant irradiance with increasing temperature, while the lower curves represent constant temperature with increasing irradiance. In the plots, the short circuit operating point A (, ), the open circuit operating point B (, ), and the maximum power operating point C, at rated temperature and irradiance (, ), are highlighted. The maximum power available increases with irradiance but decreases with temperature.

Figure 4.
PV cell current for increasing temperature {−80, −50, −25, 0, 25, 50, 80} °C in blue, orange, green, brown, red, violet, and cyan solid lines, respectively, at constant irradiance (left); and for increasing irradiance , 400, 600, 800, 1000, 1200, in blue, orange, green, brown, red, violet, and cyan lines, respectively, at constant temperature Tpv = 25 °C (right).
2.2. DC-DC Converter
In the following, the averaged DC-DC converter model is adopted, as battery dynamics evolve over time scales at least one order of magnitude larger. The battery voltage is determined by the payload, while the buck converter determines the operating point of the PV panel (i.e., the value of ) through the duty cycle d, with
and where depends on the constraint on the maximum voltage of the PV panel, i.e., .
During the sunlight phase, at steady-state, the buck DC-DC power converter sets the panel voltage as
while, during the eclipse phase (), the power converter does not operate.
2.3. Battery Model
The battery model considered in this work is based on the equivalent circuit shown in Figure 5. By applying the Kirchhoff laws to the EPS equivalent electric circuit of Figure 6, and adding the dynamic equation of the SoC, it follows
where the battery voltage is the output and the battery current is the input, considered positive during discharging and negative during charging. The voltage v on the internal battery capacitor and are the state variables. The model parameters are as follows: the internal resistance , the capacity Q, the resistance R, and the capacitance C of the equivalent branch for representing the relaxation phenomenon of the battery.
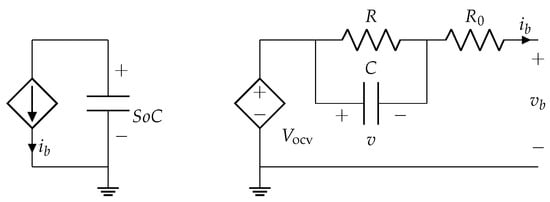
Figure 5.
Battery equivalent electric circuit.

Figure 6.
Equivalent circuit of the considered EPS architecture.
The open circuit voltage of the EPS equivalent electric circuit is a nonlinear function of SoC and changes under varying conditions, i.e., the charge/discharge current and the temperature [41,42]. The battery model adopted in this paper is derived from the MP176065 lithium-ion cell specifications [38]. During discharging, is actually lower than during charging for the same , therefore an averaged behavior is actually considered [35]. The resulting map, , is reported in Figure 7. In the following, the power at the battery’s terminals is assumed negative during charging.

Figure 7.
Cell voltage as a function of [35], achieved via the single-capacitor model (5c).
Still, by considering the EPS equivalent electrical circuit of Figure 6, the current can be written as follows
where is the payload current and the current is the output of the PV model. By applying the constraint on the duty cycle and using (6) in (3), one obtains
where , and in particular, equal to zero during the eclipse phase.
2.4. Payload Power Profiles
The payload power varies depending on the mission’s operational mode [6,7]. Figure 8 shows the payload power profiles for five different operational modes, as derived in [14,17,35] from real space missions. At each time instant, the payload current is obtained as
where is the output of the battery model (5). Since the DC bus voltage is determined by the battery voltage, and by considering (4) and (6), it follows
Then, the instantaneous power equilibrium condition (1) is satisfied.

Figure 8.
Payload power profiles for five space missions’ operational modes.
2.5. Controller
This system uses a RL-based controller that acts on the duty cycle d of the DC-DC converter, depending on the battery voltage and current , the solar irradiance and temperature , the PV current , and the payload power profile . In particular, is used to determine the current SoC, while , , , and are needed to calculate the SoC reference profile used as input to the RL controller, as seen in Figure 2.
The proposed RL-based controller regulates d, allowing the PV panels to provide the needed power while adjusting the battery current to meet the mission power requirements.
3. The Proposed DQN-Based Framework for LEO Satellite EPSs
3.1. Brief on Reinforcement Learning and DQN Algorithm
RL is an interdisciplinary field of machine learning and optimal control focusing on how an agent (controller) can learn an effective control strategy (referred to as “policy”) via episodic interactions with its own environment (plant), see [20,33,43]. At each step of these learning episodes, the RL agent receives a representation of the environment state and selects an action based on this information and the current policy. When the action is executed, the environment changes its state and produces a scalar reward signal that will be returned to the agent, together with the representation for the next state, allowing it to improve its current policy.
MDPs offer the mathematical framework for learning through agent–environment interactions [33]. A MDP is a tuple , with being the environment state space (and its generic state), the action space (and its generic action), and the reward function (and r the reward signal). is the state transition probability function and provides the probability that the environment enters the state when the action is executed in . The agent’s policy maps states into actions and defines its whole control strategy. In a given episode, the agent interacts with its own environment in this way: at each discrete-time step (with indicating the final time step of a learning episode), the agent observes the environment state , and then chooses the action . Following its execution, the agent obtains a reward signal , and the environment changes to a new state .
To evaluate the performance of a given policy , the so-called action-value function is introduced [33]
with being the discount factor and the expectation operator for the policy . The optimal policy maximizes Equation (10), and the related optimal action-value function fulfills the Bellman equation [33]
It is typically not feasible to solve the Bellman Equation (11) exactly for real-world complex systems with large state spaces [20,31]. Furthermore, their MDP formulation cannot be precisely defined. Thanks to their model-free nature and capability of handling large-scale problems, RL-based approaches can be used to compute approximate optimal action-value functions and policies in case of complex systems [33]. They fall into one of two primary categories: value function methods (e.g., DQN) and policy-based methods (e.g., actor–critic-based algorithm); see [20,31].
As shown in the following subsection, EPS systems are characterized by continuous state variables and discrete control variables, making value function solutions a suitable choice [20,31]. This paper uses the DQN algorithm [30]: it is part of the Deep Reinforcement Learning sub-field, and uses NNs to approximate value functions. This allows for scaling to high-dimensional state spaces and addressing system non-linearity [31].
The DQN algorithm employees two neural networks (that is, the behavior NN and the target NN) and an experience replay buffer to stabilize the learning process. In every training episode, all transitions are produced using the -greedy method, which is adopted to achieve a balance between exploration and exploitation [30]. These transitions are saved into the replay buffer and utilized to train the behavior and the target NNs. In order to minimize data correlation, a random subset of transitions is selected from the experience replay buffer to form a mini-batch. Following the training phase, the resultant behavior NN becomes the estimated optimal action-value , and is used to compute the estimated optimal policy during testing.
3.2. Designing State Space, Action Space, and Reward Function
In the following, the DQN framework for energy management in LEO satellite EPSs is presented. The satellite EPS system described in the previous section acts as the environment. Within a given orbit, learning takes place only during the sunlight phase, as the DC/DC power converter duty cycle (controller output) is only active during this phase.
State space: The measured battery SoC and panel current are used to form the state vector of the agent’s environment as follows:
where and are, respectively, the battery SoC and PV panel current measured at the orbit discrete-time step , with and being the duration, expressed in time steps, of the sunlight phase. Furthermore, the SoC reference profile, say , is designed in such a way that its starting and ending values during the current orbit are the same. This implies that the SoC reference value when the satellite exits the sunlight region () is equal to , where is the SoC variation corresponding to the energy required by the satellite throughout the entire eclipse phase. This value depends on the addressed satellite operational mode [7]. In summary, is defined as follows:
Note that, similar to the other components of the proposed DQN-based framework, the SoC reference value is calculated exclusively during the sunlight phase, when the DQN agent is active.
Action space: The scalar control action is the discretized duty cycle d of the DC/DC power converter. In other words, the control action is chosen from the discrete action space
where is the step-size used to discretize the interval between the duty cycle bounds and .
Reward function: In the context of RL, and thus in the proposed DQN-based framework, the optimization problem is not formulated in terms of an explicit objective function with separate constraints, as is typically done in traditional optimal control problems [31,33]. Instead, the goal of RL is to learn a policy that maximizes the expected cumulative reward, which is defined through the action-value function, see (10). In the presented formulation, task-specific objectives, such as tracking a reference SoC profile, and system constraints, such as soft or hard limits on the SoC, are all embedded within the reward function. More specifically, the reward function is defined with two basic purposes: (i) tracking the SoC reference profile (13) during the sunlight phase despite the different battery SoC values at the beginning of each orbit and the satellite operational modes, resulting in different onboard power requirements; (ii) satisfying the battery constraints in terms of SoC to avoid battery deterioration and extend its lifespan [8].
In this paper, the tracking performance metrics are defined as the absolute difference between the current and reference SoC values. There are two types of constraints: hard and soft constraints [22]. Hard constraints cause training episodes to end with negative rewards, while soft constraints result in lesser negative rewards without their premature termination. Therefore, the following reward function is used for energy management in LEO satellite EPSs (computed only when )
where , , and represent the coefficients applied to the metrics of tracking performance, the violations of soft constraints, and the violations of hard constraints, respectively. These coefficients can change over time, as tracking inaccuracies may become less favorable as the training episode progresses. Equation (15) incorporates the subsequent Boolean functions for the violations pertaining to soft and hard constraints.
where, e.g., is the minimum value allowed by the soft constraint for the battery SoC.
4. Numerical Simulations and Results
This section shows the training methodology of the presented DQN-based framework for the LEO satellite EPSs, and illustrates the performance validation of the resulting trained DQN agent. Space mission power profiles are used for both training and validation to verify its applicability to real-world scenarios and confirm its generalization capabilities (i.e., adaptability to environmental conditions different from those used in training [23]). Finally, the performance of the resulting DQN policy is also assessed against that of a MPPT controller [44,45,46], thus elucidating the comparative advantages and potential enhancements offered by the developed approach. The validation campaign focused on assessing control performance; while eclipse phases and irradiance variability were accurately modeled, long-term uncertainties, e.g., solar panel degradation, battery aging, and thermal fluctuations, were not included. These factors will be incorporated as part of planned enhancements aimed at improving model fidelity and extending the framework applicability to long-duration missions.
4.1. Simulation Set-Up and Parameter Configuration
The EPS system shown in Section 2 serves as the environment for the proposed DQN-based framework. To begin with, its battery model is characterized by the following key-parameters: the internal resistor , and the RC branch with capacitance and resistor . The battery system is designed with two parallel and eight series-connected lithium-ion MP176065 cells, where each cell has a capacity of , thus resulting in . In conjunction with the battery, the PV panel is a critical component and comprises parallel and series-connected PV cells. The CESI CTJ30 cell datasheet [37] provided the specifications for the photovoltaic PV panel. The I-V characteristics of the panel under varying irradiance and temperature are reported in Figure 4.
The payload power profiles for the considered five operational modes are depicted in Figure 8. To obtain the SoC reference profile (13), it is necessary to calculate . This computation has to consider the payload power profile of the addressed operational mode during the eclipse phase, as well as the bus voltage. In this study, the LEO satellite’s orbit has a period of 5400 , with sunlight exposure and eclipse durations of 3600 and 1800 . The action sampling time for the DQN agent is 10 , and thus the above time quantities, expressed in time steps, become , , and . The step-size for the action space (14) is set to , with and .
As for the reward function (15), we have the following constant weighting factors: , , and . Moreover, the thresholds of the soft and hard constraint violations are as follows: , , , and . The discount factor is set to .
The dimensions of the replay buffer and mini-batch in the DQN algorithm are set to 10,000 and 64, respectively [30]. The behavior and target fully connected NNs have the same structure with two input neurons, two hidden layers of 256 neurons, and an output layer of 18 neurons. The total number of learnable parameters is 71,186.
4.2. The Learning Process
During training, an exponentially decaying -greedy mechanism is employed to balance exploration and exploitation, a strategy widely adopted in DQN implementations [22,30]. At each time step, the learning agent selects either a random action (exploration, with probability ) or the best action based on the currently estimated action-value function (exploitation, with probability ). The exploration probability is computed using the following formula
where
- is the initial (maximum) exploration probability,
- is the final (minimum) exploration probability,
- is the exponential decay rate,
- is the current step number, incremented after each action.
This expression enables the exponential decay of from its maximum to minimum value over time, thus ensuring a smooth transition from high exploration at the beginning of training to increased exploitation as learning progresses. In this study, the parameters are defined as follows: , , and . Moreover, at the start of each training episode, the initial battery SoC is chosen from the range of .
A fine-tuning strategy was employed to address the complex learning process of the system at hand. This method enhances transfer learning by adjusting the parameters of a pre-trained model with additional data specific to the targeted task [22,47]. This entails reactivating certain layers, or potentially all layers, of the pre-trained models, allowing for additional training and adjustment to the specific task at hand. Throughout this stage, it is also feasible to adjust specific hyperparameters and initiate the exploration process anew to enhance performance.
Both pre-training and fine-tuning phases involved 20,000 episodes, each spanning a single orbit. As for the fine-training, the same setup of the pre-training was used, with the sole exception of the exploration probability , which was set again to its maximum value . This adjustment facilitated a fresh exploration phase while leveraging pre-training knowledge.
4.3. Performance Validation and Generalization Capabilities of the Trained DQN Agent
The performance validation of the trained DQN agent was initially conducted by employing the same scenario used during training. Figure 9 illustrates the detailed results of a specific validation episode, spanning a single orbit and in operational mode M1. In particular, during the eclipse phase, the cumulative reward remains constant with each time step yielding a reward value of zero. This confirms that, as per design, the eclipse phase has not been factored into the reward definition (15). However, during the eclipse phase, the PV panels do not produce current, resulting in a higher battery discharge rate (and positive current) to meet the power demands of the payload. The learning and application of actions occur exclusively during the satellite’s sunlight exposure phase, as the DC/DC converter between the battery and the solar array is active only during this period. Thus, the duty cycle value during the eclipse phase is irrelevant and is not propagated from the controller to the converter. More importantly, during the whole episode, the error between the SoC reference and its actual value always remains at an approximate order of magnitude of , and the SoC never violates its constraints. Thus, the trained DQN agent demonstrates its ability to effectively follow a predefined SoC profile, even in the face of initial uncertainties regarding the starting SoC value.

Figure 9.
The results are obtained for a single orbit under operational mode M1. The first row sequentially displays the achieved SoC with its dashed-line reference, the battery current, and the payload’s current demand. The second row presents the current supplied by the PV panels, the battery voltage, and the requested duty cycle. The final row illustrates the reward signal, the cumulative reward, and the irradiance profile. In all subplots, the eclipse period of the orbit is highlighted in blue.
To further highlight the performance of the trained DQN agent, Figure 10 reports the episodic cumulative rewards and a histogram representing their distribution over 1000 episodes, still for the operational mode M1. In this validation exercise, the initial SoC values were varied within the same range used during the training phase. The observed mean and standard deviation of the cumulative rewards are and , respectively, with the median positioned at . This regularity in cumulative reward metrics shows how consistently the agent performs throughout episodes.

Figure 10.
The histogram representation (bottom) of rewards accumulated (top) by the trained DQN agent, evaluated over 1000 episodes using the same training scenario.
Finally, a validation exercise was conducted to assess the adaptability of the DQN agent trained in operating mode M1 to the five modes shown in Figure 8. Moreover, the initial battery SoC value was chosen over a wider range, i.e., . Figure 11 shows the cumulative rewards and corresponding histogram for the trained DQN agent across 1000 episodes encompassing all the operational modes of Figure 8, which were randomly selected. Notably, the histogram reveals five distinct peaks, each corresponding to a particular operational mode, with a mean cumulative reward of , a standard deviation of , and a median of . Despite reduced performance, the DQN agent was shown to be resilient to environmental conditions different from the ones used in training by tracking the SoC reference and fulfilling the SoC constraints.

Figure 11.
The histogram representation (bottom) of rewards accumulated (top) by the trained DQN agent, evaluated over 1000 episodes for the five operational modes shown in Figure 8.
4.4. A Comparison with MPPT Control Technique
To assess the effectiveness of our trained DQN policy, we compared it to an MPPT controller using the same training scenario to ensure consistency between evaluations. The MPPT approach is a widely used control technique for PV systems, and aims to maximize the power extracted from PV panels by dynamically adjusting the operating point to track the Maximum Power Point (MPP). This approach is critical for PV-based energy systems, as the MPP, where the product of current and voltage is at its maximum, is not constant, and varies with external conditions such as irradiance and temperature. For instance, as irradiance increases, the MPP generally moves to higher current values, while voltage remains relatively stable. Conversely, as temperature rises, the MPP shifts slightly, reducing the output voltage due to increased semiconductor conductivity in the solar cells, which decreases the voltage at the MPP. Consequently, an effective MPPT control algorithm is required to continuously adjust the duty cycle to maximize power extraction and manage fluctuations in irradiance and variations in temperature.
More specifically, the comparative analysis was performed with the Lookup Table-based MPPT algorithm, selected among classical methods as outlined in [48]. This approach was chosen due to its structural affinity with our proposed control strategy, which employs proportional duty cycle adjustment based on real-time measurements. The Lookup Table MPPT baseline was specifically optimized under the same environmental and system conditions used to validate the DQN agent, including identical irradiance profiles and payload demands. This allowed for a consistent one-to-one comparison focused on control adaptability and energy tracking performance.
Assuming a constant temperature in this study, the MPP shift is attributed only to variations in the irradiance profile. Figure 12 illustrates the performance of the EPS under MPPT control during a representative episode of the nominal mission M1.

Figure 12.
The results are obtained for a single orbit under operational mode M1 by using the MPPT controller. The first row sequentially displays the achieved SoC with its dashed-line reference, the battery current, and the payload’s current demand. The second row presents the current supplied by the PV panels, the battery voltage, and the requested duty cycle. The final row illustrates the reward signal, the cumulative reward, and the irradiance profile. In all subplots, the eclipse period of the orbit is highlighted in blue.
The duty cycle profile exhibits oscillatory behavior, alternating between the value corresponding to the maximum power point (which, for this level of irradiance, is ) and the minimum duty cycle value, . It is noteworthy that during periods of slowly varying irradiance, such as the onset of sunlight, fluctuations in the optimal operating point are minimized, allowing the duty cycle to remain close to . The rapid oscillations in the duty cycle lead to a corresponding change in the PV panel current, cycling from non-zero values to zero, which impacts the stability of the power output.
The superiority of our proposed DQN-based policy is evident when examining the SoC profile. Under the MPPT controller, the SoC profile exhibits a more pronounced ripple effect and struggles to follow the initial SoC trajectory accurately. In contrast, our policy demonstrates better adherence to the SoC reference profile, achieving smoother performance with minimal deviation. This improvement is quantitatively reflected in the cumulative reward values: the MPPT controller yields a cumulative reward of approximately for Mission M1, whereas our DQN policy achieves a significantly better cumulative reward of (see Figure 9), indicating enhanced alignment with the mission objectives. The higher cumulative reward for our policy correlates directly with improved single-step rewards, suggesting a consistent advantage over the MPPT approach.
Additional information about the MPPT controller’s performance is provided in Figure 13, which displays the cumulative rewards and their histogram representation for 1000 episodes and the five operational modes of Figure 8. In this case, the mean and standard deviation of the cumulative rewards are and , respectively, with the median located at , confirming the superiority of the proposed approach in terms of SoC reference-tracking performance.

Figure 13.
Cumulative rewards and their histogram representation of the MPPT controller over 1000 episodes.
4.5. Multi-Orbit Scenario
To further assess the robustness and generalization capabilities of the trained DQN agent, we examined a multi-orbit scenario. Our goal was to determine if the resultant DQN policy, trained for a single orbit, could consistently guarantee SoC tracking performance and constraint satisfaction throughout periodic orbits.
The findings of this test, shown in Figure 14, confirm the periodicity of all variables involved over consecutive orbits. Specifically, the SoC at the beginning and end of each orbit constantly returns to the same value, indicating that the control strategy preserves the battery energy balance across multiple orbits. This fact highlights the DQN policy capability to maintain a sustainable energy profile supporting long-term operational requirements.

Figure 14.
The graph illustrates the results for five orbits under operational mode M1. The first row sequentially displays the achieved SoC, the battery current, and the payload’s current demand. The second row presents the current supplied by the PV panels, the battery voltage, and the requested duty cycle. The final row illustrates the reward signal, the cumulative reward, and the irradiance profile.
During each sunlight phase, a slight deviation in the SoC from its initial value can be observed; however, this deviation is effectively corrected by the control actions taken by the DQN policy, which actively tracks the reference . This corrective control action ensures that the system remains within operational constraints, supporting the goal of a balanced SoC throughout the mission.
Moreover, the instantaneous reward profile achieved during each orbit also exhibits periodicity, mirroring the values obtained in the single-orbit simulation. This consistency in reward across orbits underscores the effectiveness of the trained policy in optimizing performance metrics continuously, even under the recurring variations in solar exposure due to orbital dynamics. These results corroborate the tracking performance and energy management consistency of the proposed approach even in a multi-orbit setting, indicating its suitability for a realistic operational scenario.
Remark 1.
The proposed DQN-based framework for LEO satellite EPSs has been designed with real-time deployment in mind, particularly considering the limited computational and memory resources of embedded satellite systems [6]. Notably, the training of the DQN agent can be performed offline on ground-based infrastructure. Once trained, the onboard inference phase (i.e., the action selection during flight) requires only a forward pass through a relatively small NN. This computation is lightweight and compatible with the capabilities of modern space-grade onboard computers, especially in light of recent advancements in radiation-tolerant processors and embedded artificial intelligence accelerators [32]. Although the presented approach has not yet been validated on actual satellite avionics, its computational efficiency and compact policy representation make it a strong candidate for future in-orbit implementation. The trained control policy can be implemented onboard and executed efficiently, enabling fast decision-making with minimal latency and low memory usage.
5. Conclusions and Outlook
This paper presented a DRL approach using DQN to develop an adaptive energy management framework for LEO satellites. The definition of its core elements (i.e., the state space, the action space, and the reward function) was presented and thoroughly discussed. In particular, the reward function aimed to ensure accurate tracking of a reference battery SoC profile during sunlight phases, accounting for varying initial SoC and changing satellite operational modes, which imposed different power demands. Additionally, the resulting DQN agent was trained to meet the final SoC constraint at the end of each orbit, mitigating premature battery degradation and extending the satellite operational lifespan.
The trained DQN controller proved to effectively handle system uncertainties and complex operational scenarios encompassing varying initial battery SoC and multi-orbit operations. Numerical simulations demonstrated its adaptability and performance across diverse mission power profiles derived from real missions. A comparative analysis with Lookup Table-based MPPT techniques also highlighted the superiority of the proposed solution. While alternative MPPT techniques like perturb and observe, incremental conductance, or intelligent hybrid variants might exhibit differentiated behavior under more dynamic conditions, their implementation and evaluation were considered beyond the scope of this work. Therefore, a broader benchmarking with multiple MPPT algorithms can be identified as a direction for future investigation, especially to generalize the findings across a wider spectrum of control paradigms and mission profiles. In the future, we also plan to extend the presented framework to address energy management in diverse space mission scenarios, such as satellite constellations and more complex multi-orbit profiles. Finally, we acknowledge that further profiling and hardware-in-the-loop validation are necessary to fully assess the deployment feasibility of the proposed solution on specific satellite platforms and onboard computing architectures.
Author Contributions
Conceptualization, S.B., E.M., M.T. and V.M.; methodology, S.B., E.M. and M.T.; software, S.B. and E.M.; validation, S.B., E.M. and M.T.; investigation, S.B. and E.M.; writing—original draft preparation, S.B., E.M., M.T. and V.M.; writing—review and editing, S.B., E.M., M.T. and V.M.; visualization, S.B., E.M., M.T. and V.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to confidentiality concerns.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript (This term indicates all apparatus requiring power supply, including satellite platform equipment and payload. It corresponds to the number of actions performed during a given learning episode):
| CNN | Convolutional Neural Network |
| DDPG | Deep Deterministic Policy Gradient |
| DQN | Deep-Q Network |
| DRL | Deep Reinforcement Learning |
| DTE | Direct Energy Transfer |
| EPS | Electrical Power System |
| LEO | Low Earth Orbit |
| LSTM | Long Short-Term Memory |
| MDP | Markov Decision Process |
| MPP | Maximum Power Point |
| MPPT | Maximum Power Point Tracking |
| NN | Neural Network |
| PPO | Proximal Policy Optimization |
| PPT | Peak Power Tracking |
| PV | Photo Voltaic |
| RL | Reinforcement Learning |
| SA | Solar Array |
| SAC | Soft Actor–Critic |
| SoC | State of Charge |
| TD3 | Twin-Delayed Deep Deterministic |
References
- Capannolo, A.; Silvestrini, S.; Colagrossi, A.; Pesce, V. Chapter Four-Orbital dynamics. In Modern Spacecraft Guidance, Navigation, and Control; Pesce, V., Colagrossi, A., Silvestrini, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2023; pp. 131–206. [Google Scholar]
- Low Earth Orbit (LEO) Satellite Feasibility Report; Technical report; Washington State Department of Commerce: Washington, DC, USA, 2023.
- Jung, J.; Sy, N.V.; Lee, D.; Joe, S.; Hwang, J.; Kim, B. A Single Motor-Driven Focusing Mechanism with Flexure Hinges for Small Satellite Optical Systems. Appl. Sci. 2020, 10, 7087. [Google Scholar] [CrossRef]
- Yang, Y.; Mao, Y.; Ren, X.; Jia, X.; Sun, B. Demand and key technology for a LEO constellation as augmentation of satellite navigation systems. Satell. Navig. 2024, 5, 11. [Google Scholar] [CrossRef]
- Knap, V.; Vestergaard, L.K.; Stroe, D.I. A Review of Battery Technology in CubeSats and Small Satellite Solutions. Energies 2020, 13, 4097. [Google Scholar] [CrossRef]
- Tipaldi, M.; Legendre, C.; Koopmann, O.; Ferraguto, M.; Wenker, R.; D’Angelo, G. Development strategies for the satellite flight software on-board Meteosat Third Generation. Acta Astronaut. 2018, 145, 482–491. [Google Scholar] [CrossRef]
- Nardone, V.; Santone, A.; Tipaldi, M.; Liuzza, D.; Glielmo, L. Model checking techniques applied to satellite operational mode management. IEEE Syst. J. 2018, 13, 1018–1029. [Google Scholar] [CrossRef]
- Zoppi, M.; Tipaldi, M.; Di Cerbo, A. Cross-model verification of the electrical power subsystem in space projects. Measurement 2018, 122, 473–483. [Google Scholar] [CrossRef]
- Faria, R.P.; Gouvêa, C.P.; Vilela de Castro, J.C.; Rocha, R. Design and implementation of a photovoltaic system for artificial satellites with regulated DC bus. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 676–681. [Google Scholar]
- Mokhtar, M.A.; ElTohamy, H.A.F.; Elhalwagy Yehia, Z.; Mohamed, E.H. Developing a novel battery management algorithm with energy budget calculation for low Earth orbit (LEO) spacecraft. Aerosp. Syst. 2024, 7, 143–157. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimović, D. Fundamentals of Power Electronics, 3rd ed.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Patel, M.R. Spacecraft Power Systems; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Mostacciuolo, E.; Baccari, S.; Sagnelli, S.; Iannelli, L.; Vasca, F. An Optimization Approach for Electrical Power System Supervision and Sizing in Low Earth Orbit Satellites. IEEE Access 2024, 12, 151864–151875. [Google Scholar] [CrossRef]
- Mostacciuolo, E.; Iannelli, L.; Sagnelli, S.; Vasca, F.; Luisi, R.; Stanzione, V. Modeling and power management of a LEO small satellite electrical power system. In Proceedings of the 2018 European Control Conference (ECC), Limassol, Cyprus, 12–15 June 2018; pp. 2738–2743. [Google Scholar]
- Yaqoob, M.; Lashab, A.; Vasquez, J.C.; Guerrero, J.M.; Orchard, M.E.; Bintoudi, A.D. A Comprehensive Review on Small Satellite Microgrids. IEEE Trans. Power Electron. 2022, 37, 12741–12762. [Google Scholar] [CrossRef]
- Khan, O.; Moursi, M.E.; Zeineldin, H.; Khadkikar, V.; Al Hosani, M. Comprehensive design and control methodology for DC-powered satellite electrical subsystem based on PV and battery. IET Renew. Power Gener. 2020, 14, 2202–2210. [Google Scholar] [CrossRef]
- Mostacciuolo, E.; Vasca, F.; Baccari, S.; Iannelli, L.; Sagnelli, S.; Luisi, R.; Stanzione, V. An optimization strategy for battery charging in small satellites. In Proceedings of the 2019 European Space Power Conference, Juan-les-Pins, France, 30 September–4 October 2019; pp. 1–8. [Google Scholar]
- Maddalena, E.T.; Lian, Y.; Jones, C.N. Data-driven methods for building control—A review and promising future directions. Control Eng. Pract. 2020, 95, 104211. [Google Scholar] [CrossRef]
- Yaghoubi, E.; Yaghoubi, E.; Khamees, A.; Razmi, D.; Lu, T. A systematic review and meta-analysis of machine learning, deep learning, and ensemble learning approaches in predicting EV charging behavior. Eng. Appl. Artif. Intell. 2024, 135, 108789. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep Reinforcement Learning: A Brief Survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, N.D.; Nahavandi, S. Deep Reinforcement Learning for Multiagent Systems: A Review of Challenges, Solutions, and Applications. IEEE Trans. Cybern. 2020, 50, 3826–3839. [Google Scholar] [CrossRef]
- Baccari, S.; Tipaldi, M.; Mariani, V. Deep Reinforcement Learning for Cell Balancing in Electric Vehicles with Dynamic Reconfigurable Batteries. IEEE Trans. Intell. Veh. 2024, 9, 6450–6461. [Google Scholar] [CrossRef]
- Joshi, A.; Tipaldi, M.; Glielmo, L. Multi-agent reinforcement learning for decentralized control of shared battery energy storage system in residential community. Sustain. Energy Grids Netw. 2025, 41, 101627. [Google Scholar] [CrossRef]
- Brescia, E.; Pio Savastio, L.; Di Nardo, M.; Leonardo Cascella, G.; Cupertino, F. Accuracy of Online Estimation Methods of Stator Resistance and Rotor Flux Linkage in PMSMs. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 4941–4955. [Google Scholar] [CrossRef]
- Yu, L.; Qin, S.; Zhang, M.; Shen, C.; Jiang, T.; Guan, X. A Review of Deep Reinforcement Learning for Smart Building Energy Management. IEEE Internet Things J. 2021, 8, 12046–12063. [Google Scholar] [CrossRef]
- Wu, J.; Wei, Z.; Li, W.; Wang, Y.; Li, Y.; Sauer, D.U. Battery Thermal- and Health-Constrained Energy Management for Hybrid Electric Bus Based on Soft Actor-Critic DRL Algorithm. IEEE Trans. Ind. Inform. 2021, 17, 3751–3761. [Google Scholar] [CrossRef]
- Wu, J.; Huang, C.; He, H.; Huang, H. Confidence-aware reinforcement learning for energy management of electrified vehicles. Renew. Sustain. Energy Rev. 2024, 191, 114154. [Google Scholar] [CrossRef]
- Guo, C.; Wang, X.; Zheng, Y.; Zhang, F. Real-time optimal energy management of microgrid with uncertainties based on deep reinforcement learning. Energy 2022, 238, 121873. [Google Scholar] [CrossRef]
- Zheng, K.; Jia, X.; Chi, K.; Liu, X. DDPG-Based Joint Time and Energy Management in Ambient Backscatter-Assisted Hybrid Underlay CRNs. IEEE Trans. Commun. 2023, 71, 441–456. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Bertsekas, D. Reinforcement Learning and Optimal Control; Athena Scientific: Nashua, NH, USA, 2019. [Google Scholar]
- Furano, G.; Meoni, G.; Dunne, A.; Moloney, D.; Ferlet-Cavrois, V.; Tavoularis, A.; Byrne, J.; Buckley, L.; Psarakis, M.; Voss, K.O.; et al. Towards the Use of Artificial Intelligence on the Edge in Space Systems: Challenges and Opportunities. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 44–56. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Tipaldi, M.; Iervolino, R.; Massenio, P.R. Reinforcement learning in spacecraft control applications: Advances, prospects, and challenges. Annu. Rev. Control 2022, 54, 1–23. [Google Scholar] [CrossRef]
- Baccari, S.; Vasca, F.; Mostacciuolo, E.; Iannelli, L.; Sagnelli, S.; Luisi, R.; Stanzione, V. A characterization system for LEO satellites batteries. In Proceedings of the 2019 European Space Power Conference (ESPC), Juan-les-Pins, France, 30 September–4 October 2019; pp. 1–6. [Google Scholar]
- Edpuganti, A.; Khadkikar, V.; Moursi, M.S.E.; Zeineldin, H.; Al-Sayari, N.; Al Hosani, K. A Comprehensive Review on CubeSat Electrical Power System Architectures. IEEE Trans. Power Electron. 2022, 37, 3161–3177. [Google Scholar] [CrossRef]
- Triple-Junction Solar Cell for Space Applications (CTJ30). 2020. Available online: https://www.cesi.it/app/uploads/2020/03/Datasheet-CTJ30-1.pdf (accessed on 13 July 2025).
- MP 176065 Rechargeble Li-on Prismatic Cell. Available online: https://docs.rs-online.com/32de/0900766b8056b890.pdf (accessed on 13 July 2025).
- Jalil, M.F.; Khatoon, S.; Nasiruddin, I.; Bansal, R. Review of PV array modelling, configuration and MPPT techniques. Int. J. Model. Simul. 2022, 42, 533–550. [Google Scholar] [CrossRef]
- Chaibi, Y.; Salhi, M.; El-Jouni, A.; Essadki, A. A new method to extract the equivalent circuit parameters of a photovoltaic panel. Sol. Energy 2018, 163, 376–386. [Google Scholar] [CrossRef]
- Farmann, A.; Sauer, D.U. A study on the dependency of the open-circuit voltage on temperature and actual aging state of lithium-ion batteries. J. Power Sources 2017, 347, 1–13. [Google Scholar] [CrossRef]
- Mostacciuolo, E.; Iannelli, L.; Baccari, S.; Vasca, F. An interlaced co-estimation technique for batteries. In Proceedings of the 2023 31st Mediterranean Conference on Control and Automation (MED), Limassol, Cyprus, 26–29 June 2023; pp. 73–78. [Google Scholar]
- Joshi, A.; Tipaldi, M.; Glielmo, L. A belief-based multi-agent reinforcement learning approach for electric vehicle coordination in a residential community. Sustain. Energy Grids Netw. 2025, 43, 101790. [Google Scholar] [CrossRef]
- Subudhi, B.; Pradhan, R. A comparative study on maximum power point tracking techniques for photovoltaic power systems. IEEE Trans. Sustain. Energy 2012, 4, 89–98. [Google Scholar] [CrossRef]
- Schirone, L.; Granello, P.; Massaioli, S.; Ferrara, M.; Pellitteri, F. An Approach for Maximum Power Point Tracking in Satellite Photovoltaic Arrays. In Proceedings of the 2024 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Ischia, Italy, 19–21 June 2024; IEEE: New York, NY, USA, 2024; pp. 788–793. [Google Scholar]
- Balal, A.; Murshed, M. Implementation and comparison of Perturb and Observe, and Fuzzy Logic Control on Maximum Power Point Tracking (MPPT) for a Small Satellite. J. Soft Comput. Decis. Support Syst. 2021, 8, 14–18. [Google Scholar]
- Mason, K.; Grijalva, S. A review of reinforcement learning for autonomous building energy management. Comput. Electr. Eng. 2019, 78, 300–312. [Google Scholar] [CrossRef]
- Bollipo, R.B.; Mikkili, S.; Bonthagorla, P.K. Hybrid, optimal, intelligent and classical PV MPPT techniques: A review. CSEE J. Power Energy Syst. 2021, 7, 9–33. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).