Graph Convolution-Based Decoupling and Consistency-Driven Fusion for Multimodal Emotion Recognition

Abstract

Multimodal emotion recognition (MER) is essential for understanding human emotions from diverse sources such as speech, text, and video. However, modality heterogeneity and inconsistent expression pose challenges for effective feature fusion. To address this, we propose a novel MER framework combining a Dynamic Weighted Graph Convolutional Network (DW-GCN) for feature disentanglement and a Cross-Attention Consistency-Gated Fusion (CACG-Fusion) module for robust integration. DW-GCN models complex inter-modal relationships, enabling the extraction of both common and private features. The CACG-Fusion module subsequently enhances classification performance through dynamic alignment of cross-modal cues, employing attention-based coordination and consistency-preserving gating mechanisms to optimize feature integration. Experiments on the CMU-MOSI and CMU-MOSEI datasets demonstrate that our method achieves state-of-the-art performance, significantly improving the $AC{C}_7$, $AC{C}_2$, and $F1$ scores.

1. Introduction

Speech emotion recognition (SER) is a critical technology designed to identify emotional states from human speech. It plays a pivotal role in human–computer interaction, speech synthesis, and intent detection. By enabling machines to understand speakers’ emotions, it enhances robotic empathy expression, adaptive interaction behaviors, and context-aware decision-making in intelligent systems. However, speech alone often fails to fully capture the complexity of human emotional expressions. This limitation is particularly evident when emotions are conveyed implicitly or sarcastically. Such cases make accurate recognition challenging with single-modality data.

Multimodal emotion recognition (MER) integrates speech, text, and visual information to overcome these limitations. It significantly enhances emotion recognition accuracy and robustness. With growing demand for sophisticated human–computer interactions and emotional intelligence, MER has diverse applications. For instance, in automotive safety, MER systems assess driver emotions to anticipate hazards. In healthcare, they aid professionals in analyzing patients’ emotional states for improved diagnoses. These systems also enhance customer service through real-time emotion detection. Additionally, they support children with autism in developing social and emotional skills.

Deep learning and attention mechanisms have notably driven MER progress. Cross-modal attention mechanisms enable effective modeling of inter-modal interactions. Traditional MER methods typically fall into two categories: multimodal feature fusion strategies and cross-modal attention mechanisms. Nevertheless, critical challenges persist. First, inherent modality heterogeneity complicates effective feature fusion. This includes differences in data types, sampling rates, and expression forms. Second, human emotional expressions exhibit inherent complexity and diversity. This leads to varying contributions from each modality. Expression inconsistencies occur when the spoken language contradicts emotional states. These inconsistencies further complicate recognition.

To overcome these challenges, researchers introduced multimodal feature decoupling strategies. These separate modality-specific features from modality-invariant ones. This mitigates modality heterogeneity’s negative impact. However, existing decoupling methods often rely on simplistic network architectures, which fail to model deep, dynamic inter-modal relationships adequately. Furthermore, feature fusion after decoupling is frequently superficial. Common techniques like concatenation or weighted summation neglect crucial aspects. They particularly overlook feature consistency and discrepancies.

In this paper, we propose a novel multimodal feature decoupling approach based on a Dynamic Weighted Graph Convolutional Network (DW-GCN). DW-GCN is designed to deeply capture the complex and dynamic interactions various modalities. It effectively extracts both modality-shared common features and modality-specific private features across modalities. Specifically, we construct fully connected graphs with dynamically updated edge weights between modality feature nodes. This dynamic modeling enables precise representation of inter-modal relationships, providing richer and more discriminative common features compared to conventional static graph convolutional approaches.

The key contributions are summarized as follows:

• We introduce a novel Dynamic Weighted Graph Convolutional Network (DW-GCN) for multimodal feature decoupling, explicitly modeling dynamic and complex inter-modal relationships to extract robust common and private features.
• We propose the Cross-Attention Consistency-Gated Fusion (CACG-Fusion) module, effectively handling modality inconsistencies by adaptively integrating modality-specific and modality-invariant features through a novel gating mechanism.
• We conduct experiments on the widely used multimodal emotion recognition datasets MOSI and MOSEI. Our model achieves improvements of up to 2.5% and 1.0% in $AC{C}_7$, respectively, compared to existing state-of-the-art approaches.

2. Related Works

2.1. Multimodal Emotion Recognition

Multimodal emotion recognition (MER) aims to infer genuine human emotional states by effectively integrating multiple modalities, such as visual (facial expressions), textual (spoken words or transcriptions), and acoustic (vocal intonations and prosodic variations) signals. Due to the complexity and heterogeneity inherent to multimodal data—manifesting in different feature scales, temporal alignments, and semantic expressions—efficient fusion strategies are critical yet challenging. These strategies play a crucial role in multimodal modeling and are primarily categorized into feature-level fusion, decision-level fusion, model-level fusion, and hybrid-level fusion. Each category attempts to exploit multimodal complementarity differently, balancing between computational complexity, interpretability, and interaction depth to achieve optimal performance.

Feature-level fusion (early fusion) directly integrates raw or processed features from different modalities into a unified representation before feeding them into subsequent classifiers or predictors. This fusion paradigm leverages low-level interactions among modalities early in the modeling pipeline, theoretically preserving more comprehensive multimodal information. For example, Wu et al. [1] developed a parallel convolutional neural network framework that simultaneously processes multi-scale sEMG signals, concatenating these feature representations directly at the input stage for emotion recognition. More advanced approaches, such as the Tensor Fusion Network (TFN) proposed by Zadeh et al. [2], explicitly model high-order multimodal interactions through tensor outer products. Despite their effectiveness, early fusion methods face significant challenges due to inherent feature heterogeneity, requiring normalization or embedding into common latent spaces. Furthermore, concatenating or tensor fusion often results in high-dimensional and sparse data representations, potentially increasing model complexity and the risk of overfitting, thus necessitating regularization or low-rank approximations like low-rank multimodal fusion (LMF), introduced by Liu et al. [3], and hierarchical strategies such as the Hierarchical Feature Fusion Network (HFFN) by Mai et al. [4].

Decision-level fusion (late fusion) combines predictions or decisions generated independently by unimodal classifiers into a final inference. This strategy allows each modality to utilize specialized models optimized for their data characteristics, enhancing flexibility and interpretability. For instance, Chen et al. [5] employed ensemble methods that aggregated modality-specific classifiers’ decisions, showing effectiveness in leveraging each modality’s distinct strengths. Similarly, tensor-based decision-level fusion approaches, such as TFN, view unimodal embeddings as distilled decisions, fusing them via tensor products. Despite its conceptual simplicity and ease of implementation, decision-level fusion limits explicit interaction between modalities, potentially overlooking valuable fine-grained inter-modal correlations available at earlier stages. Additionally, training independent classifiers for each modality can be computationally intensive, requiring extensive hyperparameter tuning and validation. Consequently, decision-level fusion is typically preferred when interpretability and flexibility outweigh the demand for fine-grained multimodal interactions.

Model-level fusion employs specialized neural network architectures that explicitly model multimodal interactions within intermediate representations. Unlike simpler fusion strategies, it leverages deep learning techniques, such as attention mechanisms or transformer-based architectures, to capture rich cross-modal semantic alignments. Prominent examples include the MulT proposed by Tsai et al. [6], which applies cross-modal transformers to explicitly attend one modality’s features using another modality’s context. Additionally, MAG (Multimodal Adaptation Gate), introduced by Rahman et al. [7], effectively integrates non-linguistic cues into pretrained language models like BERT through adaptive gating. These methods significantly enhance the semantic alignment and dynamic interactions across modalities, thus generally achieving superior recognition performance. However, these advanced architectures also entail increased model complexity, computational resources, and sensitivity to data quality and quantity, posing additional challenges in optimization and generalization.

Hybrid-level fusion integrates early, decision-level, and model-level fusion strategies within a unified framework, aiming to exploit their complementary strengths. Sebastian and Pierucci [8] combined early fusion of speech and text features with late fusion of modality-specific decisions, achieving improved emotion recognition accuracy. Wu et al. [9] proposed a dual-branch model that simultaneously handled time-synchronous and time-asynchronous multimodal inputs, effectively capturing both immediate and delayed emotional cues across modalities. Wang et al. [10] further advanced hybrid fusion with the MTAF model, explicitly integrating initial multimodal representations through early fusion and subsequently refining them using a transformer-based model-level fusion mechanism. While hybrid approaches enable sophisticated interactions between modalities and generally enhance MER performance, they also increase model complexity and training challenges, necessitating careful design and optimization strategies.

2.2. Multimodal Feature Decoupling

Multimodal feature decoupling is an important direction in current research on multimodal emotion recognition. Although traditional MER methods can integrate multimodal information and infer emotions through modal fusion strategies at different levels, there are limitations in handling heterogeneous modal data. To overcome these challenges, researchers have recently leaned towards using feature representation learning methods to extract common features and private features from different modalities. This approach aims to achieve more effective multimodal feature fusion and emotion recognition by learning shared information and unique features between modalities.

Hazarika et al. [11] proposed the MISA model using simple feedforward neural networks with private and common parameters as private and common feature extractors and carrying out decoupling through similarity loss and orthogonalization loss, projecting each modality feature into modality-invariant and modality-specific subspaces to address heterogeneity between modal features. Yang et al. [12] introduced FDMER using two perceptron layers and a GeLu activation function as public and private feature encoders and incorporating a modality discriminator to further constrain the decoupling process. In the feature fusion process, a more complex cross-modal attention mechanism is used for fusion. Li et al. [13] presented DF-ERC, achieving decoupling at both modality and sentence levels to enhance emotion recognition tasks. These methods based on multimodal feature decoupling not only improve the performance of multimodal emotion recognition but also provide new ideas and approaches for the effective integration and utilization of cross-modal information.

Recent advancements have introduced novel architectural designs and quantitative evaluation frameworks. Shou et al. [14] developed the BSSM model that leverages 1D convolutional operations and positional encoding mechanisms, employing an extensive mamba architecture to deconstruct multimodal features. The model further incorporates a probability-guided fusion strategy to enhance inter-modal information consistency. Concurrently, Fu et al. [15] proposed the FDR-MSA framework, which effectively decouples multimodal data features through perceptron-based modules and GeLU activation functions for extracting shared/private characteristics. The framework innovatively employs the Hilbert–Schmidt independence criterion (HSIC) to quantitatively assess the independence between private representations. In parallel developments, Li et al. [16] devised a disentangled Mamba network with a Temporally Slack Reconstruction Mechanism (DMA-TSM), which decouples raw multimodal features into modality-common and modality-private components through temporal relaxation constraints, significantly reducing feature-level redundancy.

Multimodal feature decoupling has demonstrated significant potential in advancing multimodal speech emotion recognition. By deeply disentangling the commonality and uniqueness of emotional characteristics, this methodology enhances feature diversity and effectiveness in emotion-related tasks. It not only improves the recognition accuracy in multimodal emotion analysis but also drives technological progress in cross-modal information integration. In practical applications, such decoupling strategies enhance the interpretability of deep learning models, rendering their decision-making processes more transparent. With its widespread adoption and demonstrated efficacy in speech emotion recognition, this paradigm has garnered increasing attention across diverse research domains. As evidenced in studies [17,18], multimodal feature decoupling approaches have achieved notable success in fields beyond emotion recognition, inspiring researchers to adopt similar disentanglement strategies for model design and optimization in other contexts.

However, multimodal feature decoupling methods still confront several critical challenges. First, existing approaches predominantly emphasize complex optimization constraints to refine the extraction of common and private features. For instance, they employ orthogonal loss [11] or Hilbert-Schmidt independence criterion (HSIC) loss [15] to regulate similarity between private and common features or integrate adversarial discriminators with contrastive learning losses to amplify their distinctiveness. Despite these efforts, the architectural innovation of feature encoders remains under-explored. Most methods continue to rely on simplistic encoder architectures—such as linear layers or 1D convolutional networks—which inadequately capture the intricate patterns of common features, consequently imposing performance bottlenecks. Second, existing fusion mechanisms struggle to comprehensively address information interaction and complementarity across modalities in real-world scenarios characterized by diverse human emotional expressions. After extracting common and private features, current approaches typically resort to elementary fusion strategies (e.g., concatenation, summation, voting) or marginally enhanced attention mechanisms to aggregate features for final classification. These methods fail to systematically evaluate the context-dependent contributions of common and private features to emotion classification, particularly under varying environmental conditions or expression modalities. Such limitations hinder the generalization capability and operational robustness of models in practical deployments.

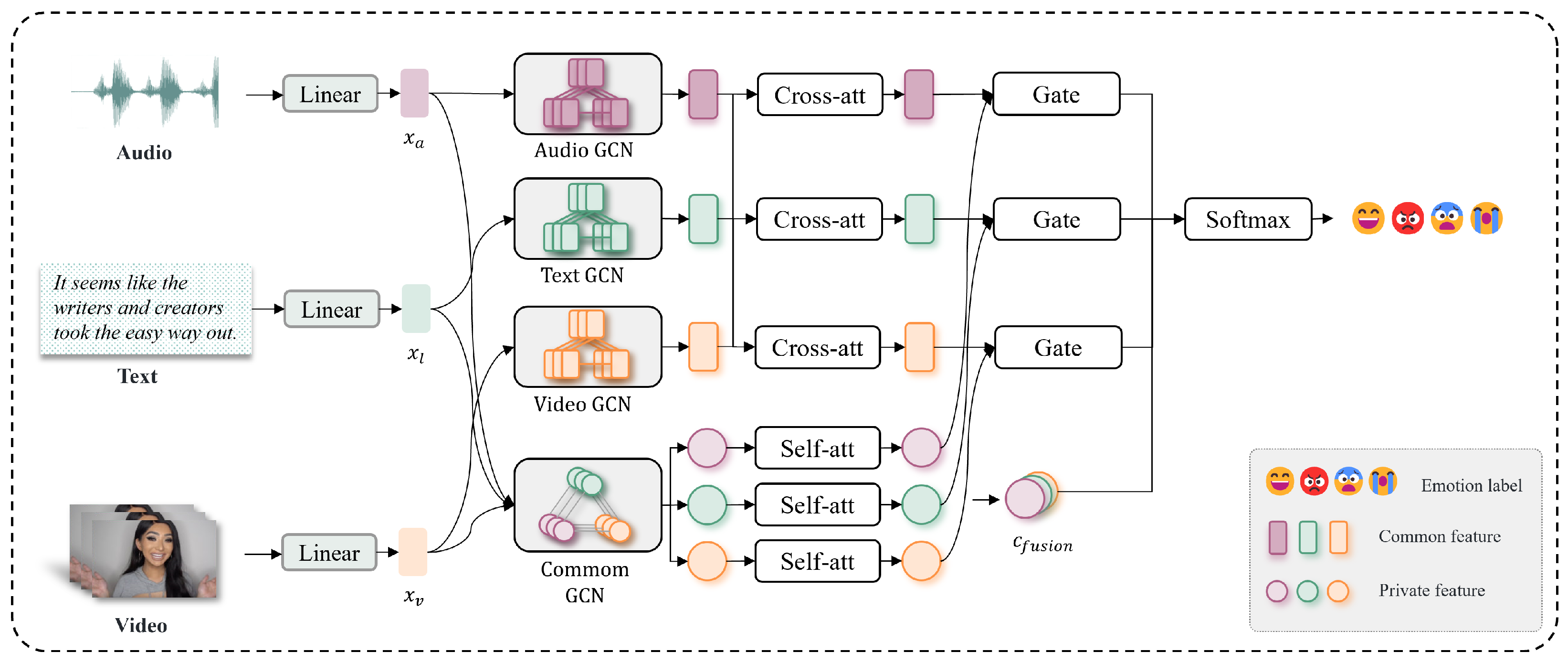
3. Methods

As illustrated in Figure 1, the proposed multimodal feature disentanglement framework comprises three key components: multimodal feature extraction, multimodal feature disentanglement based on Dynamic Edge-Weighted Graph Convolutional Networks, and Consistency-driven multimodal feature fusion.

3.1. Multimodal Feature Extraction

We employ the multimodal feature extraction strategy introduced by MISA [11] on the CMU-MOSI [19] and CMU-MOSEI [20] datasets. The feature extraction procedure involves three modalities: text, video, and audio.

3.1.1. Text Features

The textual modality utilizes the BERT-base-uncased model [21] to extract textual embeddings of dimension 768:

$${\tilde{x}}_l=\mathrm{BERT}\left(\mathrm{input}\right)\in {\mathbb{R}}^{T_l\times 768}$$

(1)

where $T_l$ denotes the length of the text sequence, and ${\tilde{x}}_l$ represents the extracted textual features.

3.1.2. Video Features

The visual modality employs the Facet facial behavior analysis tool, extracting 47-dimensional and 35-dimensional features from the MOSI and MOSEI datasets, respectively, and denoted as ${\tilde{x}}_v$.

3.1.3. Audio Features

Audio features are extracted using the COVAREP acoustic analysis toolkit, resulting in 74-dimensional low-level features including MFCC, VUV, pitch, and glottal parameters, denoted as ${\tilde{x}}_a$.

3.1.4. Unified Feature Representation

To achieve dimensional consistency, we apply modality-specific linear transformations:

$$\begin{array}{c}\hfill x_l=W_l{\tilde{x}}_l+b_l\\ \hfill x_v=W_v{\tilde{x}}_v+b_v\\ \hfill x_a=W_a{\tilde{x}}_a+b_a\end{array}$$

(2)

where $W_l,W_v$, and $W_a$ are projection matrices, mapping all features into a unified latent space with dimension $d=46$:

$$x_l,x_v,x_a\in {\mathbb{R}}^{T\times d}$$

(3)

3.2. DW-GCN for Multimodal Feature Disentanglement

To effectively disentangle modality-shared and modality-specific features in multimodal emotion recognition, we adopt two types of graph convolutional networks (GCNs) with different structures. For private feature learning, we utilize a fixed intra-modal graph where each modality (e.g., audio) is treated as multiple nodes and edges are fully connected without dynamic weighting. In contrast, for common feature extraction, we propose DW-GCN, where each modality is treated as a single node, and the graph is fully connected with dynamically learned edge weights. This allows for the adaptive modeling of inter-modality relationships, which is essential for capturing shared semantic information across modalities.

Theoretically, DW-GCN is motivated by two key principles: (1) Multimodal information correlation can be inferred via feature similarity, and (2) the strength of cross-modal message passing should be learned rather than fixed. We employ a learnable function (FC) to map similarity to edge weights. This mechanism is aligned with attention-based relational modeling in GATs and transformers, where softmax-based normalization enhances stability and interpretability.

Furthermore, from an information-theoretic viewpoint, higher similarity between two modalities suggests potential redundancy or complementarity, which justifies allocating stronger edge weights for their mutual influence. DW-GCN thus enables adaptive information fusion, where strongly correlated modalities exert more influence during graph propagation, leading to the enhanced representation of common semantic cues.

3.2.1. Private Feature Extraction

To capture modality-specific characteristics, each modality is processed using an independent GCN. Taking the audio modality as an example, we treat its segmented features across time as nodes in a fully connected graph. The graph structure is fixed and designed to emphasize intra-modal patterns without introducing inter-modal influence. Formally, given input features $x_m$ for modality $m\in \{l,v,a\}$, we compute its private features as follows:

$$\begin{array}{c}\hfill s_l={\mathrm{GCN}}_l\left(x_l\right)\\ \hfill s_v={\mathrm{GCN}}_v\left(x_v\right)\\ \hfill s_a={\mathrm{GCN}}_a\left(x_a\right)\end{array}$$

(4)

where $s_l,s_v$, and $s_a\in {\mathbb{R}}^{T\times d}$ are modality-specific private features.

3.2.2. Common Feature Extraction

To model shared information among modalities, we construct a fully connected graph where each modality (text, audio, and video) is treated as a single node. The edges between nodes are assigned dynamic weights, which are learned from the similarity of modality features. This structure forms our DW-GCN, which enables the network to adaptively emphasize stronger modality correlations and suppress irrelevant ones.

First, we stack modality inputs as follows:

$$X_{common}=[x_l,x_v,x_a]\in {\mathbb{R}}^{3\times T\times d}$$

(5)

For each modality pair, we compute dynamic edge weights using a learnable function. These weights are conditioned on feature similarity and normalized via softmax to ensure effective information flow:

$$w_{ij}=\mathrm{softmax}\left(\mathrm{FC}\left([x_i\parallel x_j]\right)\right)$$

(6)

where $[·\parallel ·]$ denotes concatenation, $\mathrm{FC}$ denotes a Fully Connected Layer with fixed input dimension $2d$ and output dimension 1. Softmax ensures normalized weights over edges.

We then construct the adjacency matrix with zero self-connections, focusing exclusively on cross-modal interactions:

$$W_{ij}=\left\{\begin{array}{cc}{w}_{ij},\hfill & i\ne j\hfill \\ 0,\hfill & i=j\hfill \end{array}\right.$$

(7)

where $W\in {\mathbb{R}}^{3\times 3}$ stores the dynamic edge weights between each pair of modality nodes, and self-connections are set to zero.

Finally, the GCN operates on this graph to extract shared features, adaptively enhancing important cross-modal connections:

$$C={\mathrm{GCN}}_{common}(X_{common},W)$$

(8)

where $C=[c_l,c_v,c_a]$ denotes the common features extracted for each modality node.

3.2.3. Decoupling Losses

To better regulate the learning of common and private features, we design the following three loss functions, each serving a distinct purpose in the feature disentanglement process:

(1) Orthogonality Loss: To encourage the common and private features within each modality to capture diverse information and reduce redundancy, we introduce orthogonality loss. This loss penalizes the cosine similarity between the common and private features, forcing them to be as orthogonal as possible in the feature space. By doing so, it ensures that the common features focus on information shared across modalities, while the private features capture modality-specific aspects, which is crucial for effective multimodal feature disentanglement:

$${\mathcal{L}}_{ort}=\sum _{m\in \{l,v,a\}}\cos (s_m,c_m)$$

(9)

where m represents one of the modalities (audio, text, or video), and cos denotes cosine similarity. A lower ${\mathcal{L}}_{ort}$ value indicates better separation between common and private features.

(2) Reconstruction Loss: To ensure that the disentangled features (common and private) can fully represent the original input, we introduce reconstruction loss. By concatenating the common and private features of each modality and feeding them into a decoder, we aim to reconstruct the original modality features. This loss constrains the feature disentanglement process so that no essential information is lost, maintaining the completeness of the original data representation:

$${\mathcal{L}}_{recon}=\parallel x_l-x_l^{rec}{\parallel }_2^2+\parallel x_v-x_v^{rec}{\parallel }_2^2+{\parallel x_a-x_a^{rec}\parallel }_2^2$$

(10)

The reconstructed features are obtained by concatenating the common and private features and feeding them into decoder:

$$x_m^{rec}={\mathrm{Decoder}}_m\left([s_m,c_m]\right)$$

(11)

(3) Cycle-Consistency Loss: To further enhance the stability and robustness of the private features, we add a cycle-consistency loss. After reconstructing the pseudo-modality features, we pass them through the private feature extractor and require the resulting features to remain close to the original private features. This constraint ensures that modality-specific information is preserved throughout the reconstruction and re-encoding process, validating the effectiveness of the feature disentanglement:

$${\mathcal{L}}_{cycle}=\parallel s_l-s_l^{rec}{\parallel }_2^2+\parallel s_v-s_v^{rec}{\parallel }_2^2+{\parallel s_a-s_a^{rec}\parallel }_2^2$$

(12)

where $s_l^{rec}$ is obtained by passing $x_l^{rec}$ through the private feature extractor:

$$s_l^{rec}={\mathrm{GCN}}_m\left(x_l^{rec}\right)$$

(13)

The final decoupling loss integrates all three components to jointly guide the feature disentanglement process:

$${\mathcal{L}}_{decouple}={\mathcal{L}}_{ort}+{\mathcal{L}}_{recon}+{\mathcal{L}}_{cycle}$$

(14)

3.3. Cross-Attention Consistency-Gated Fusion (CACG-Fusion)

To effectively integrate shared and private features, we propose a Cross-Attention Consistency-Gated Fusion (CACG-Fusion) mechanism. This fusion module dynamically adjusts the contribution of each feature based on their internal consistency and inter-modal relationships. It consists of three stages: enhancing shared features via self-attention, enriching private features via cross-attention, and finally, performing consistency-gated fusion.

The motivation behind this module is to enforce semantic agreement between modality-specific and shared features. We hypothesize that when these two types of features are consistent in meaning, they reinforce each other; otherwise, the model should downweight their fusion to avoid conflict.

Mathematically, we define the consistency gate as a sigmoid-activated gating function, where the input is the element-wise sum of shared and private projections. This gate $z_m$ captures a soft alignment score between two representations. If $c_m^{att}$ and $h_m^{proj}$ are similar, the sigmoid will output values close to 1, allowing more of the common representations to pass. Conversely, dissimilar features will shift the gate toward 0, preferring private features.

This gating strategy is inspired by the Information Bottleneck principle, which suggests that retaining only task-relevant and non-contradictory information improves robustness. By fusing only consistent signals, CACG-Fusion suppresses modality noise and preserves essential multimodal evidence.

3.3.1. Self-Attention on Common Features

To enhance the expressiveness and contextual dependencies within each shared feature, we apply self-attention to each modality’s common representation. This allows the model to capture temporal dependencies and refine feature quality.

For each modality $m\in \{l,v,a\}$,

$$c_m^{att}=\mathrm{SelfAttention}\left(c_m\right)$$

(15)

The refined features are then concatenated to form a global common representation:

$$c_{fusion}=\mathrm{Concat}(c_l^{att},c_v^{att},c_a^{att})$$

(16)

3.3.2. Cross-Attention on Private Features

We enhance private features by modeling cross-modal interactions through cross-attention. This allows each modality to selectively attend to relevant information from the others, enriching the private representation with complementary context.

For example, for the language modality,

$$\begin{array}{c}\hfill h_l^a=\mathrm{CrossAttention}(s_l,s_a,s_a)\\ \hfill h_l^v=\mathrm{CrossAttention}(s_l,s_v,s_v)\end{array}$$

(17)

The outputs are concatenated and projected as follows:

$$h_m^{proj}=\mathrm{FC}\left([h_m^a\parallel h_m^v]\right),m\in \{l,v,a\}$$

(18)

3.3.3. Consistency-Gated Fusion

To adaptively combine shared and private features, we introduce a consistency gate that reflects their agreement. The gate dynamically controls the fusion weight based on the similarity between the two types of features.

The gate is computed as

$$z_m=\sigma (W_g(c_m^{att}\oplus h_m^{proj})+b_g)$$

(19)

where ⊕ is the element-wise addition, and $\sigma$ is the sigmoid function.

The final fused feature is as follows:

$${\widehat{z}}_m=z_m\odot c_m^{att}+(1-z_m)\odot h_m^{proj}$$

(20)

We concatenate all fused features and the global common representation:

$$h_{final}=\mathrm{Concat}({\widehat{z}}_l,{\widehat{z}}_v,{\widehat{z}}_a,c_{fusion})$$

(21)

3.3.4. Classification Layer

Finally, we predict sentiment labels using a linear layer followed by softmax:

$$y=\mathrm{Softmax}(W_{out}{h}_{final}+b_{out})$$

(22)

4. Datasets and Metrics

4.1. Datasets

We adopt two widely used multimodal datasets, CMU-MOSI [19] and CMU-MOSEI [20], for evaluation in our experiments. These datasets provide rich annotations across multiple modalities and are well-suited for both sentiment intensity and categorical emotion analysis. Detailed statistics and descriptions are provided below

Table 1. Comparison between CMU-MOSI and CMU-MOSEI datasets.

Attribute	CMU-MOSI [19]	CMU-MOSEI [20]
Number of Speakers	89	1000
Number of Sentences	2199	23,453
Total Duration	50 h	65 h
Continuous Emotion Labels	[−3,3]	[−3,3]
Discrete Emotion Labels	-	Happiness, Sadness, Anger, Fear, Disgust, Surprise

.

4.1.1. CMU-MOSI

The CMU-MOSI (Multi-modal Opinion-level Sentiment Intensity) dataset [19] is constructed by Carnegie Mellon University and focuses on sentiment intensity analysis from multi-modal YouTube monologue video clips. Comprising 2199 annotated video segments, the standard partition allocates 1284 samples for training, 229 for validation, and 686 for testing. The dataset contains 89 distinct speakers (41 female and 48 male) covering topics such as product reviews, movie reviews, and personal opinions, reflecting real-world emotional expressions. It includes video, audio, and corresponding text transcriptions, enabling researchers to analyze features from visual, auditory, and linguistic modalities. The detailed distribution of samples per sentiment polarity is shown in

Table 2. Sample distribution across sentiment polarities in CMU-MOSI.

Sentiment Polarity	−3	−2	−1	0	+1	+2	+3
Number of Samples	80	385	404	403	379	463	85

.

4.1.2. CMU-MOSEI

The CMU-MOSEI (Multimodal Opinion Sentiment and Emotion Intensity) dataset [20] expands significantly upon MOSI, with data sourced similarly from YouTube monologues but covering a broader range of topics, including reviews, debates, and interviews. It involves 1000 speakers and provides multimodal data (video, audio, and text) for comprehensive sentiment analysis. The dataset is partitioned into 16,326 training samples, 1871 validation samples, and 4659 testing samples according to its predetermined data split. Each segment is annotated for both sentiment intensity (ranging from [−3, 3]) and categorical emotions (anger, disgust, fear, happiness, sadness, and surprise), as detailed in

Table 3. Sample distribution across emotion categories in CMU-MOSEI.

Emotion	Anger	Disgust	Fear	Happiness	Sadness	Surprise
Number of Samples	4600	3755	1803	10,752	5601	2055

.

4.2. Metrics

To evaluate the performance of our multimodal emotion recognition model, we adopt two commonly used classification metrics: accuracy (ACC) and F1 score. These metrics provide a comprehensive understanding of the model’s ability to correctly classify emotional categories.

Accuracy (ACC) measures the proportion of correctly classified samples over the total number of samples. It reflects the overall effectiveness of the model across all classes. The formula is as follows:

$$ACC={\displaystyle \frac{{\sum }_{i=1}^{C}T{P}_i}{{\sum }_{i=1}^C{N}_i}}$$

(23)

where C is the total number of classes, $T{P}_i$ is the number of correctly predicted samples in class i, and $N_i$ is the total number of samples in class i.

The F1 score balances precision and recall for classification evaluation, particularly valuable in multi-class scenarios. In sentiment analysis, these metrics quantify a model’s ability to distinguish emotional categories (e.g., positive/negative/neutral). The macro-averaged F1 score is computed as follows:

$$F1={\displaystyle \frac{1}{C}}\sum _{i=1}^C{\displaystyle \frac{2·{\mathrm{Precision}}_i·{\mathrm{Recall}}_i}{{\mathrm{Precision}}_i+{\mathrm{Recall}}_i}}$$

(24)

where Precision (${\mathrm{Precision}}_i={\displaystyle \frac{{\mathrm{TP}}_i}{{\mathrm{TP}}_i+{\mathrm{FP}}_i}}$) measures how many predictions for class i are correct, with ${\mathrm{FP}}_i$ (false positives) being samples that are not in i but predicted as i. Recall (${\mathrm{Recall}}_i={\displaystyle \frac{{\mathrm{TP}}_i}{{\mathrm{TP}}_i+{\mathrm{FN}}_i}}$) measures how many true class i samples are captured, with ${\mathrm{FN}}_i$ (false negatives) being samples in i but predicted as other classes.

Following the calculation methods from prior studies [11,22], we report $AC{C}_7$ (full seven-class accuracy on CMU-MOSEI and CMU-MOSI datasets) and $AC{C}_2$ (binary accuracy with merged categories: negative class $[-3,0)$ and non-negative class $[0,3]$), alongside macro-averaged F1 scores. All results use macro-averaged metrics unless otherwise stated, ensuring balanced evaluations across emotion categories.

5. Experience and Results

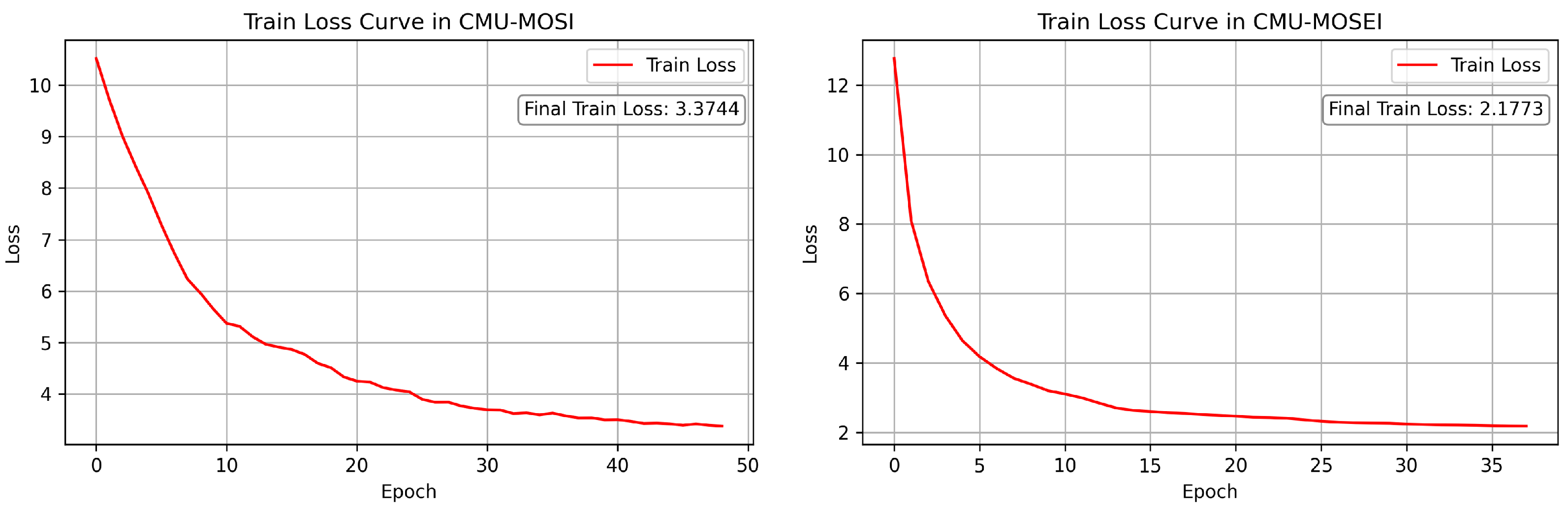
5.1. Experimental Setup

The experiments were conducted on a high-performance workstation equipped with an NVIDIA RTX 4090 GPU (24 GB VRAM, NVIDIA Corporation, Santa Clara, CA, USA) using the PyTorch 2.0 framework. Training leveraged the Adam optimizer with a batch size of 16 and an initial learning rate of 0.0001. Model training proceeded for 50 epochs on the CMU-MOSI dataset (requiring approximately 0.5 h per run) and 37 epochs on the larger CMU-MOSEI dataset (requiring approximately 2 h per run). Early stopping with patience set to 10 epochs was implemented to prevent overfitting. Textual features were extracted using the pretrained BERT-base-uncased model, which underwent fine-tuning during the training process. Detailed hyperparameter configurations specific to each dataset, including dropout rates, gradient clipping thresholds, and weight decay coefficients, are comprehensively documented in

Table 4. Training parameters on MOSI and MOSEI datasets.

Parameter	MOSI	MOSEI
$NumberofSamples$	1284	16,326
$TextFeatureDimension$	768	768
$AudioFeatureDimension$	5	74
$VisualFeatureDimension$	20	35
$InitialLearningRate$	0.0001	0.0001
$BatchSize$	16	16
$EarlyStoppingPatience$	5	5
$Attdropout$	0.3	0.4
$Outputdropout$	0.5	0.5
$Weightdecay$	0.005	0.001

.

5.2. Baseline

To evaluate the effectiveness of our proposed method, we compare it with a series of representative multimodal emotion recognition approaches. These baselines cover various modeling paradigms, including early fusion, attention mechanisms, feature disentanglement, and graph-based methods.

Table 5. Comparison of baseline methods.

Methods	Text Features	Audio Features	Video Features	Feature Extraction
MARN [23]	GloVe.840B.200d	12 MFCCs	-	LSTM
MFN [24]	GloVe.840B.300d	12 MFCCs	35 AUs	LSTM
CIA [25]	-	-	-	Dense
ICCN [26]	BERT-Base	74 features	35 AUs	conv1d, LSTM, CNN
RAVEN [27]	GloVe.840B.300d	74 features	35 AUs	LSTM
PMR [28]	GloVe.840B.300d	74 features	35 AUs	Transformer
MulT [6]	GloVe.840B.300d	12 MFCCs	35 AUs	LSTM, transformer
MISA [11]	GloVe or Bert-base	74 features	35 AUs	Bert, LSTM, and transformer
FDMER [12]	Bert-base	74 features	35 AUs	Transformer
DMD [22]	Bert-base	74 features	35 AUs	conv1d

and

Table 6. Comparison of feature disentanglement methods.

Methods	Common/Private Feature Extraction	Common/Private Feature Fusion
MISA [11]	Feed-forward neural layers	Self-attention
FDMER [12]	Two-layer perceptrons	Cross-attention
DMD [22]	conv1d	Cross-attention

summarize the key similarities and differences among the baseline methods regarding their input features, extraction models, and strategies for handling common and private feature representations.

It is noteworthy that almost all these baselines employ similar primitive feature extraction approaches. For text, GloVe or BERT embeddings are typically used. Audio features are mainly extracted as Mel-frequency cepstral coefficients (MFCCs) or low-level descriptors such as the 74-dimensional feature set provided by the COVAREP toolkit. For video, features such as Action Units (AUs), temporal frequencies, or dimensional descriptors are mostly extracted using the Facet toolkit. These pre-extracted features form the input for subsequent multimodal modeling.

Among the listed methods, the first seven (MARN, MFN, CIA, ICCN, RAVEN, PMR, and MulT), as shown in Table 5, are based on modality fusion strategies. These approaches primarily focus on bridging the heterogeneity gap across modalities and improving the overall performance of multimodal emotion recognition by exploring effective fusion mechanisms.

In contrast, the last three methods (MISA, FDMER, and DMD), as shown in Table 6, represent research on feature disentanglement for multimodal emotion recognition. They are mainly dedicated to investigating the role of both modality-invariant (common) and modality-specific (private) representations in emotion classification. As summarized in the table, previous feature disentanglement works typically adopt relatively simple modules for extracting common and private features, while the fusion of these features is mostly realized through attention-based mechanisms, such as self-attention or cross-attention. This reflects a trend in the field towards the finer-grained modeling of both shared and unique aspects of multimodal emotion expressions:

• Multi-Attention Recurrent Network (MARN) [23]: MARN employs recurrent neural networks with multiple attention mechanisms to capture dynamic interactions between modalities over time.
• Memory Fusion Network (MFN) [24]: MFN utilizes memory attention mechanisms within LSTM structures to model intra-modal dynamics and inter-modal dependencies in sequential data.
• Context-Aware Interactive Attention (CIA) [25]: CIA integrates context-aware interactive attention by employing inter-modal reconstruction and BiGRU to fuse multimodal contextual clues effectively.
• Interaction Canonical Correlation Network (ICCN) [26]: ICCN leverages Deep Canonical Correlation Analysis to learn correlated embeddings across text, audio, and video modalities.
• Recurrent Attended Variation Embedding Network (RAVEN) [27]: RAVEN dynamically adjusts word embeddings using nonverbal behaviors, capturing fine-grained multimodal interactions.
• Progressive Modality Reinforcement (PMR) [28]: PMR progressively incorporates multimodal information through layered cross-modal interaction units, effectively capturing hierarchical multimodal interactions.
• Multimodal Transformer (MulT) [6]: MulT applies directional pairwise cross-modal attention mechanisms within the transformer framework, effectively modeling long-range dependencies without explicit alignment.
• Modality-Invariant and -Specific Representations (MISAs) [11]: MISA introduces a disentanglement framework that projects each modality into two subspaces: a modality-invariant space capturing shared semantic content and a modality-specific space retaining unique characteristics of each modality. The model incorporates distribution similarity constraints, orthogonality loss, and reconstruction loss to enhance the separation of common and private features. By explicitly modeling modality-specific variations and common semantics, MISA mitigates the effects of modality heterogeneity and supports more robust multimodal fusion.
• Feature Disentangled Multimodal Emotion Recognition (FDMER) [12]: FDMER explicitly constructs private and common encoders for each modality. A modality discriminator is employed to adversarially supervise the separation of modality-specific and modality-invariant representations. The private encoder learns distinct features, while the common encoder learns to generate representations that are indistinguishable across modalities. Additionally, FDMER introduces cross-modal attention mechanisms to integrate the disentangled features for emotion recognition, promoting both feature complementarity and independence.
• Decoupled Multimodal Distilling (DMD) [22]: DMD introduces a graph-based decoupling and distillation framework that separately encodes modality-invariant and modality-specific features. It employs two parallel graph distillation units to propagate knowledge across modalities—one for shared representations and another for private ones. These graphs are dynamically constructed based on inter-modal similarities, enabling adaptive and fine-grained feature transfer. This method enhances both the discriminative power and independence of disentangled features across modalities.

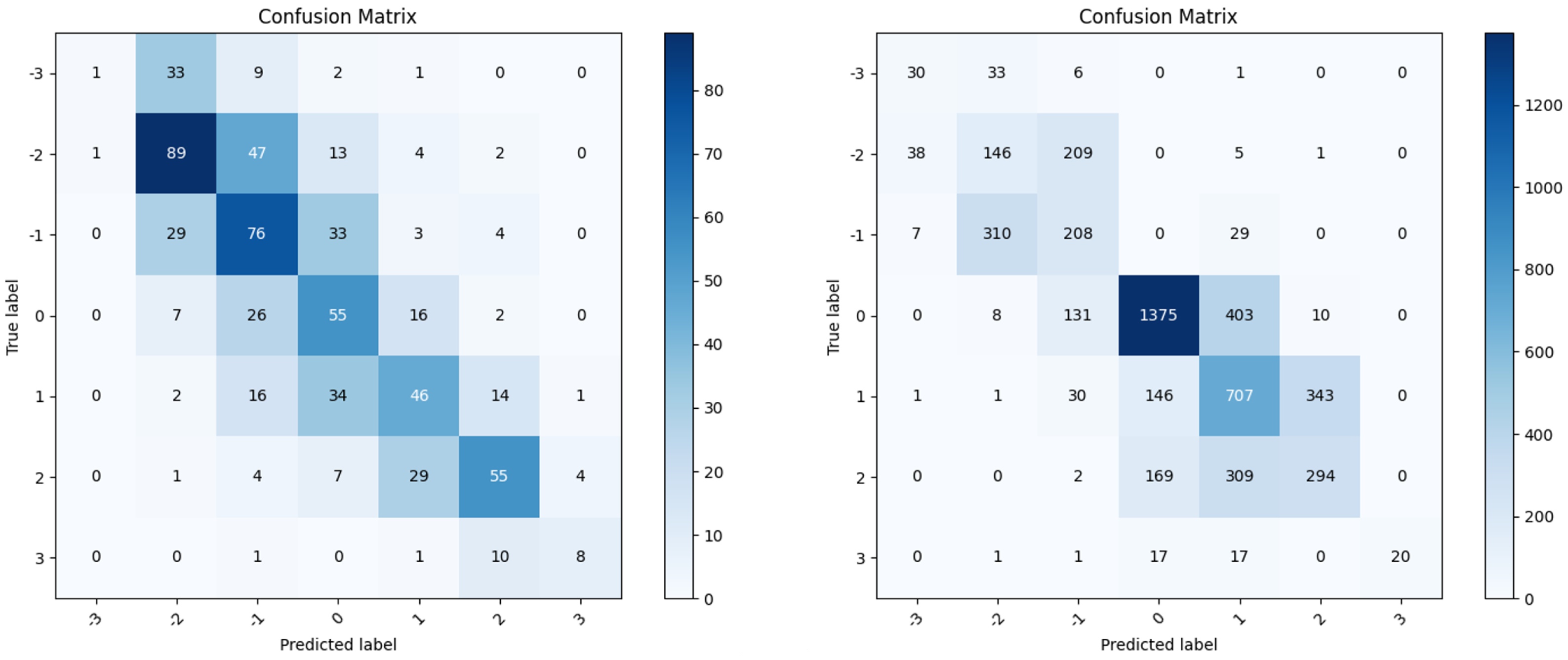
5.3. Results and Analysis

To comprehensively evaluate the effectiveness of our proposed framework, we conduct extensive experiments on two benchmark datasets—CMU-MOSI and CMU-MOSEI. The analysis is organized into three parts: overall performance comparison with existing state-of-the-art methods, ablation studies to assess the contribution of each module, and loss curve analysis to demonstrate the training stability and convergence behavior of our model. Through both quantitative and qualitative evaluations, we aim to validate the robustness, accuracy, and generalization capability of our multimodal emotion recognition approach.

5.3.1. Overall Performance

We begin our evaluation by reporting the overall classification results on both datasets, highlighting the performance gains brought by our proposed method. In particular, we compare with a wide range of representative baselines that employ various multimodal fusion and feature disentanglement strategies. This section focuses on demonstrating how our model outperforms existing methods across multiple metrics, offering deeper insight into its effectiveness in real-world multimodal emotion recognition tasks.

As shown in

Table 7. Performance on the MOSI dataset.

Methods	ACC7	ACC2	F1
TFN [2]	32.1	73.9	73.4
MARN [23]	34.7	77.1	77.0
MFN [24]	34.1	77.4	77.3
MFM [29]	36.2	78.1	78.1
CIA [25]	38.9	79.8	79.1
ICCN [26]	39.0	83.0	83.0
MulT [6]	40.0	83.0	82.8
MISA [11]	42.3	83.4	83.6
FDMER [12]	44.1	84.6	84.7
DMD [22]	45.6	86.0	86.0
OURS	48.1	86.6	86.2

, our method achieves the best performance on all three metrics ($AC{C}_7$, $AC{C}_2$, and $F1$) in the MOSI dataset, reaching 48.1%, 86.6%, and 86.2%, respectively. Compared to the current state-of-the-art multimodal disentanglement method DMD [22] (45.6%, 86.0%, and 86.0%), our model improves $AC{C}_7$ by 2.5% and $AC{C}_2$ and $F1$ by 0.6% and 0.2%, respectively, demonstrating more accurate emotion classification capabilities. Furthermore, compared to FDMER [12] (44.1%, 84.6%, and 84.7%) and MISA [11] (42.3%, 83.4%, and 83.6%), our $AC{C}_7$ improves by 4.0% and 5.8%, $AC{C}_2$ by 2% and 3.2%, and $F1$ by 1.5% and 2.6%, respectively, verifying that our method better models the interactions among multimodal features.

Furthermore, our model leverages a Dynamic Weighted Graph Convolutional Network (DW-GCN) for extracting both common and private multimodal features, while methods like MISA, DMD, and FDMER only utilize simple feed-forward layers, 1D convolution, or two-layer perceptrons. Although these conventional architectures can learn intra-modal representations, they are limited in capturing dynamic cross-modal interactions.

Our proposed DW-GCN dynamically adjusts edge weights based on inter-modal correlations in real-time, allowing it to better adapt to evolving feature interactions and more accurately model shared representations. This dynamic feature modeling mechanism not only enhances feature expressiveness but also improves adaptability and generalization in multimodal fusion. Notably, DMD introduces a Graph Distillation Unit (GD-Unit) to enhance feature communication via cross-modal knowledge distillation. However, even without using knowledge distillation, our method outperforms DMD, highlighting the effectiveness of DW-GCN in capturing dynamic inter-modal relationships and its superiority in multimodal emotion recognition tasks.

As shown in

Table 8. Performance on the MOSEI dataset.

Methods	ACC7	ACC2	F1
RAVEN [27]	50.0	79.1	79.5
CIA [25]	50.1	80.4	78.2
TFN [2]	50.2	82.5	82.1
MFM [29]	51.3	84.4	84.3
ICCN [26]	51.6	84.2	84.2
MulT [6]	51.8	82.5	82.3
MISA [11]	52.2	85.5	85.3
PMR [28]	52.5	83.3	82.6
FDMER [12]	54.1	86.1	85.8
DMD [22]	54.5	86.6	86.6
OURS	55.5	86.9	87.2

, our method also achieves the best results on the MOSEI dataset, with $AC{C}_7$, $AC{C}_2$, and $F1$ reaching 55.5%, 86.9%, and 87.2%, respectively—surpassing the previous SOTA DMD [22] by 1.0%, 0.3%, and 0.6%. Compared with FDMER [12] and MISA [11], our model improves $AC{C}_7$ by 1.4% and 2.3%, $AC{C}_2$ by 0.8% and 1.4%, and $F1$ by 1.4% and 1.9%, respectively, further validating the robustness and generalization capability of our proposed method.

Figure 2 displays the confusion matrices of our model on the MOSI and MOSEI datasets. Both datasets use seven classes (−3, −2, −1, 0, 1, 2, and 3). The horizontal axis is labeled x, and the vertical axis is labeled y. The number in cell (x, y) represents the number of samples from class x that are classified as class y. The darker the color, the more accurate the classification for that class. On the MOSI dataset, the model’s classification performance is weakest for the −3 class, often misclassifying it as −2. Conversely, the −2 and −1 classes exhibit relatively better classification performance. Additionally, the model seems to struggle with the 3 class, likely due to the scarcity of training data for this class. On the MOSEI dataset, there is a slight improvement in the model’s ability to handle the −3 class compared to MOSI, although misclassifications as −2 still occur. Notably, the model performs well in classifying the 0 and 1 classes. However, similarly to MOSI, the performance of the 3 class is compromised, likely due to the limited amount of training data available for this class.

Figure 3 illustrates the training loss curves of our proposed method. On the left, the curve for the MOSI dataset shows a drop to 3.3744 after 57 epochs. On the right, the MOSEI curve reaches 2.1773 after 38 epochs.

The MOSEI dataset presents more diverse emotional expressions and complex modal interactions. Although existing methods like PMR [28], MulT [6], and ICCN [26] perform reasonably well, their modeling strategies rely mainly on temporal cues, cross-modal attention, or shallow fusion schemes, which limit performance due to their inability to handle modality inconsistency effectively. In contrast, our DW-GCN-based approach performs the precise disentanglement of multimodal features and significantly enhances the modeling of shared representations. This demonstrates that our method performs reliably not only on smaller datasets like MOSI but also on larger, more challenging benchmarks like MOSEI, proving its robustness and wide applicability in multimodal emotion recognition tasks.

5.3.2. Ablation Studies

To verify the effectiveness of our proposed multimodal feature disentanglement and fusion strategy, we conduct ablation experiments. This helps isolate the contributions of key components and validate their necessity in the overall framework. We set up three ablation experiments to analyze specific aspects of our model.The reasons for these settings are as follows:

• “only conv1d”: This setting aims to examine the effect of using simple convolutional feature extractors compared to graph-based modeling. By comparing it to the full model, we can evaluate the benefit of GCNs in capturing inter-modality relationships and improving feature disentanglement.
• “wo.dynamic-weight”: This ablation is designed to verify the effect of dynamic edge weighting on adaptively modeling the semantic relationships between modalities and enhancing the extraction of shared features.
• “wo.consistency-gate”: This setting is used to test whether the consistency gate mechanism improves the integration of common and private features, thereby enhancing overall model performance.

As shown in

Table 9. Ablation study on the MOSI dataset.

Methods	ACC7	ACC2	F1
only-conv1d	45.8	84.6	84.6
wo.dynamic-weight	45.7	84.9	84.9
wo.consistency-gate	47.0	85.7	85.7
ours	48.1	86.6	86.2

, the model using only 1D convolution for extracting common and private features achieves 45.8% ($AC{C}_7$), 84.6% ($AC{C}_2$), and 84.6% ($F1$), which are 2.3%, 2.0%, and 1.6% lower than the complete model, respectively. This indicates that 1D convolution is insufficient for modeling inter-modal interactions and can only capture intra-modal information, thus failing to effectively extract common features. The model using only graph convolution performs slightly better ($AC{C}_7$ improves by 0.1%, $AC{C}_2$ improves by 0.3%, and $F1$ improves by 0.3%), but it still falls short of the complete model, showing that graph convolution alone lacks the capacity to finely model private features.

Furthermore, when we remove the consistency-gated fusion mechanism (while retaining self-attention for private features and cross-attention for common features), the performance drops to 47.0%, 85.7%, and 85.7% on $AC{C}_7$, $AC{C}_2$, and $F1$, respectively—down by 1.1%, 0.9%, and 0.5%. This demonstrates that consistency-gated fusion plays a crucial role in dynamically adjusting the integration of multimodal information, mitigating modality conflicts, and enhancing emotion classification. The full model consistently outperforms all ablated variants, confirming the synergy between feature disentanglement, dynamic modeling, and consistency-aware fusion, which jointly improve multimodal emotion recognition performance.

As presented in

Table 10. Ablation study on the MOSEI dataset.

Methods	ACC7	ACC2	F1
only-conv1d	51.1	84.1	84.2
wo.dynamic-weight	51.2	84.7	84.5
wo.consistency-gate	52.0	85.1	85.0
ours	55.5	86.9	87.2

, the ablation trends on the MOSEI dataset are consistent with those observed on MOSI. The model using only 1D convolution achieves 51.1%, 84.1%, and 84.2% for $AC{C}_7$, $AC{C}_2$, and $F1$, respectively—significantly lower than the complete model by 4.4%, 2.8%, and 3.0%. This suggests that 1D convolution struggles to model inter-modal dynamics effectively in larger, more complex datasets. The graph convolution-only variant reaches 51.2%, 84.7%, and 84.5%, but it still underperforms compared to the full model, indicating that graph-based methods, while helpful, require the complementary fine-grained modeling of private features.

When the consistency-gated mechanism is removed, performance drops to 52.0%, 85.1%, and 85.0%, respectively, which is 3.5%, 1.8%, and 2.2% below the full model. This again confirms the key role of consistency gating in harmonizing multimodal fusion. The gains of the full model are more pronounced on the MOSEI dataset, further validating the effectiveness of our proposed disentanglement and fusion strategy in large-scale settings.

In summary, the ablation results demonstrate the following: (1) Using only 1D convolution or graph convolution for feature extraction cannot achieve the same performance as the full model—combining graph convolution with dynamic weighting significantly improves both common and private feature modeling. (2) Removing the consistency-gated fusion mechanism leads to lower performance than the full model but still outperforms individual extraction modules, confirming its importance in resolving modality inconsistencies. (3) The complete model consistently achieves the best performance across all metrics, verifying the effectiveness of our design in enhancing multimodal emotion recognition.

6. Conclusions

We presented a novel feature disentanglement framework for multimodal speech emotion recognition and validated its effectiveness through experiments on multiple benchmark datasets. The results demonstrate that the proposed method achieves state-of-the-art performance on both the CMU-MOSI and CMU-MOSEI datasets, achieving improvements on all key evaluation metrics, including $AC{C}_7$, $AC{C}_2$, and $F1$.

In contrast to existing approaches that often rely on simple linear layers or 1D convolutions, we introduce a Dynamic Weighted Graph Convolutional Network (DW-GCN) as the multimodal feature extractor. DW-GCN enables more effective modeling of the complex and dynamic interactions between modalities, leading to more robust and discriminative common and private feature representations. Furthermore, we propose a Cross-Attention Consistency-Gated Fusion (CACG-Fusion) module, which incorporates cross-modal attention and a consistency-aware gating mechanism to explicitly reconcile the alignment and discrepancy between common and private modality features. This design enhances both the accuracy of feature fusion and the generalization capability of the model.

To further assess the effectiveness of each module, we conducted extensive ablation studies. The results show that models using only 1D convolution for feature extraction perform significantly worse than our DW-GCN-based approach. Moreover, removing the dynamic weighting mechanism from DW-GCN results in a slight performance drop, confirming the importance of dynamic edge modeling in feature disentanglement. In addition, eliminating the consistency-gated fusion module leads to a substantial performance decline, highlighting its critical role in mitigating modality conflicts and improving fusion quality.

Overall, the experimental results confirm the effectiveness of combining DW-GCN, common–private feature modeling, and consistency-gated fusion. The proposed framework not only achieves excellent empirical performance but also provides new insights and perspectives for future research on feature disentanglement and modality integration in multimodal learning.