Abstract
With the increasing scale of low Earth orbit (LEO) satellite networks, leveraging non−terrestrial networks (NTNs) to complement terrestrial networks (TNs) has become a critical issue. In this paper, we investigate the issue of handover satellite selection between multiple terrestrial terminal groups (TTGs). To support effective handover decision-making, we propose a long short-term memory (LSTM)-network-based traffic prediction mechanism based on historical traffic data. Building on these predictions, we formulate the handover strategy as a Markov Decision Process (MDP) and propose an attention-enhanced rainbow-DQN-based joint traffic prediction and handover design framework (ARTHF) by jointly considering the satellite switching frequency, communication quality, and satellite load. Simulation results demonstrate that our approach significantly outperforms existing methods in terms of the handover efficiency, service quality, and load balancing across satellites.
Keywords:
LEO satellite network; traffic prediction; LSTM; handover strategy; attention; rainbow DQN 1. Introduction
Non−terrestrial network (NTN) communication is pivotal for overcoming the coverage limitations of terrestrial networks (TNs), ensuring reliable and seamless connectivity under challenging conditions and enabling global communication in sixth−generation (6G) wireless systems [1,2]. Low Earth orbit (LEO) satellites, with their extensive coverage, reduced latency, and cost−effective deployment [3], have emerged as a cornerstone for addressing the constraints of traditional infrastructure, facilitating efficient global connectivity [4]. However, the rapid movement of LEO satellites results in limited coverage time for terrestrial terminal groups (TTGs), presenting challenges in providing continuous service. Thus, designing effective handover policies is crucial to maintain high−quality service in dynamic satellite networks.
In recent years, numerous studies have investigated handover strategies. In [5], the authors proposed a strategy based on the distance between satellites and TTGs, selecting the nearest satellite for handover. By comprehensively evaluating the signal−to− interference−plus−noise ratio (SINR), bandwidth utilization, transmission delay, packet loss rate, and monetary cost, the authors of [6] proposed a service−adaptive multi−criteria vertical handover algorithm that reduces the dropping probability and enhances the overall system throughput. Furthermore, the authors of [7] proposed a multi−metric handover method that uses the Floyd algorithm to identify the shortest path in a dynamic graph, effectively reducing the total handover delay and avoiding unnecessary handovers. Nevertheless, these methods primarily considered network conditions at the moment of decision−making.
As an emerging deep learning technique, deep reinforcement learning (DRL) facilitates the maximization of cumulative rewards through repeated trial−and−error interactions, making it especially suitable for long−term optimization problems. In [8], the authors introduced a satellite handover strategy based on multi−agent Q−learning, aiming to minimize the average satellite handovers while satisfying the load constraints of each satellite. In [9], a centralized−training−and−distributed−execution scheme based on deep Q−networks (DQNs) was proposed, where environmental parameters were trained by a training node in the backhaul network and are distributed to TTGs for independent handover decisions. Additionally, the authors of [10] addressed the freshness of information and proposed an age−oriented satellite handover strategy based on dueling−double−deep−Q−learning (D3QN) to minimize the long−term peak age of information. However, these approaches failed to accurately model the communication traffic demands of TTGs, which could result in a large number of TTGs simultaneously accessing a previously underloaded satellite, causing network load imbalances and degrading quality of service (QoS).
Traffic prediction utilizes historical traffic data and advanced algorithms to forecast communication demands, establishing a robust foundation for subsequent decision −making [11]. Early studies relied on simple learning methods, such as linear regression [12] and support vector regression (SVR) [13], for traffic prediction. With the advent of neural networks, their superior generalization ability and predictive accuracy have made deep learning the dominant choice for modern traffic prediction methods. The authors of [14] addressed wireless traffic forecasting with an attention−enhanced deep residual convolutional neural network (CNN). On the other hand, the authors of [15] reformulated traffic prediction as a classification task, using CNNs to assign traffic in fixed time intervals to predefined categories, and thus, improve the accuracy. As a step further, to capture temporal dependencies, the authors of [16] employed gated recurrent units (GRUs) to achieve precise traffic forecasts. Nevertheless, the aforementioned methods often fail to adequately capture long−range temporal dependencies in complex, highly variable traffic patterns, particularly in satellite communication systems characterized by fluctuating user activity, recurring usage patterns, and periodic application demands [17].
In this paper, we address the critical challenge of generating effective handover policies for TTGs in a satellite−to−ground communication system, where TTGs remain stationary while LEO satellites continuously orbit the Earth, necessitating robust solutions for seamless connectivity and load balancing in NTNs. We propose the Attention−Enhanced Rainbow DQN−based Joint Traffic Prediction and Handover Design Framework (ARTHF), which combines advanced traffic forecasting with intelligent handover decision−making to enhance the performance of LEO satellite networks. The main contributions in this paper are summarized as follows:
- We propose a traffic prediction module based on long short−term memory (LSTM) networks, which accurately forecasts TTG traffic demands by leveraging historical traffic data, thereby enabling proactive and reliable handover decisions.
- We model the handover decision problem as a Markov Decision Process (MDP) and solve it using an attention−enhanced rainbow DQN, which optimizes handover policies by jointly considering satellite switching frequency, communication quality, and load distribution.
- We validate the proposed framework through extensive simulations using a realistic LEO satellite constellation model. The results show that the proposed ARTHF effectively reduces handover frequency, enhances service quality, and achieves a fair load distribution among the satellites.
2. System Model and Problem Formulation
2.1. System Model
We investigate the issue of handover selection for numerous TTGs in satellite−to−ground communication, as illustrated in Figure 1. As depicted, the system comprises K static TTGs on the ground, each requiring continuous communication services. Above them, a constellation of LEO satellites continuously orbits. For each TTG, there is always one ‘serving satellite’ providing active communication, while several other satellites are visible and available for a potential handover, forming a dynamic set of choices.
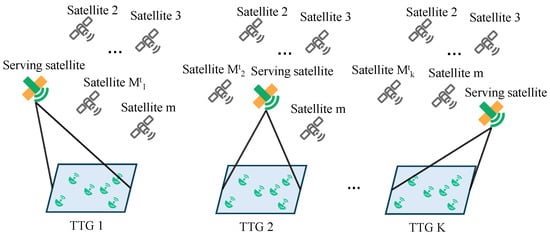
Figure 1.
An illustration of LEO satellite−to−ground communication system with handover selection for multiple TTGs.
All satellites are assumed to operate at the same altitude, denoted as , and maintain a constant speed . Each TTG is simultaneously covered by multiple satellites at any given time. However, due to the relative motion between the satellites and the TTGs, the visibility time of each satellite to a specific TTG is limited. When a satellite can no longer cover TTG k due to its movement, the satellite network broadcasts system information to configure a set of visible satellites for the TTG, enabling a seamless handover and sustained communication. For TTG k, the number of visible satellites at time slot t is denoted as , with each satellite indexed by . The service status for TTG k at time slot t is represented by the vector , where is a binary variable indicating whether satellite m is serving TTG k at time slot t, defined as
Note that different TTGs may have distinct resource requirements, such as throughput and latency. To effectively model these varying demands, we introduce a normalized resource demand weight for each TTG, ranging from 0 to 1. The sum of the weights of all TTGs accessing a particular satellite indicates the satellite’s load state. We assume each TTG periodically retrieves load information for its visible satellites from the System Information Block (SIB) broadcast. The load of the visible satellites for TTG k is represented as
where denotes the sum of the normalized demand weights of all the TTGs accessing satellite m.
We assume that TTG k accurately determines its location via Global Navigation Satellite System (GNSS) services, denoted as , where and denote its fixed horizontal coordinates. Additionally, TTG k can obtain the position and velocity of its visible satellites at time slot t from the broadcast ephemeris [18], denoted as , where , and and are the satellite’s time−varying horizontal coordinates. Using this information, TTG k can calculate the distance to satellite m, expressed as
With this distance, the elevation angle , defined as the angle between the horizontal plane and the line connecting satellite m and TTG k, can be calculated using
Subsequently, satellite m’s remaining cover time for TTG k can be derived from a geometric relationship denoted as
where denotes the radius of the Earth, and represents the minimum visible elevation angle.
2.2. Communication Model
The channel quality between LEO satellites and TTGs varies rapidly due to their relative movement, making it a crucial factor in determining handover policies. Given the significant distance between them, which leads to relatively slow spatial signal variations, we primarily focus on large−scale fading (LSF). According to document [19] proposed by the International Telecommunication Union Radio Communications Sector (ITU−R), the LSF in satellite−to−ground communication mainly comprises four parts, i.e., free−space path loss, rain attenuation, ionospheric attenuation, and shadowing, expressed as
where , , , and represent the free−space path loss, rain attenuation, ionospheric attenuation, and shadowing from satellite m to TTG k at time slot t, respectively.
The free−space path loss is calculated by
where denotes the carrier frequency.
The rain attenuation, accounting for the rainfall rate, elevation angle, frequency, and polarization, is computed based on the ITU−R P.837 [20] using
where represents the rain absorption coefficient, calculated by
where k and are coefficients dependent on the frequency and polarization, respectively, and represents the polarization−adjusted rainfall rate. Additionally, represents the effective path length of the signal through the rain region, expressed as
where denotes the projected length of the rain region along the signal propagation direction, calculated by
where represents the height of the isotherm.
Ionospheric attenuation primarily arises from two components: absorption loss and scintillation loss, expressed as
where and represent the ionospheric absorption loss and ionospheric scintillation loss, respectively, from satellite m to TTG k at time slot t. The absorption loss primarily results from the interaction between the signal and electrons in the ionospheric D and E layers, expressed as
where and represent the starting and ending heights of the ionospheric D and E layers, respectively, while and denote the height−dependent electron density and ionospheric absorption coefficient, respectively. Ionospheric scintillation loss arises from the irregular structure of the electron density in the ionospheric F layer. According to ITU−RP.618 [19], its probability density function can be expressed as
where and represent the mean and standard deviation of the scintillation attenuation, respectively.
As for the shadowing, we model it as a log−normal distribution with a mean of 0 and a variance of , which is related to the satellite elevation angle and can be found in TR38.811 [21].
Therefore, the expected power of the signal received by TTG k from satellite m is denoted as
where and represent the received and transmitted signal power at TTG k and satellite m, respectively. Consequently, the signal−to−noise ratio (SNR) at the receiver of TTG k is
where denotes the power of additive white Gaussian noise (AWGN).
2.3. Problem Formulation
In this paper, we focus on selecting optimal handover satellites for TTGs. Since each handover of TTG k to satellite m introduces a signaling overhead and increases the risk of transmission interruptions, we propose a cost function to quantify the handover cost defined as
where is a positive constant.
Additionally, to enhance the QoS for TTGs and encourage connections to satellites with a better link quality, we consider the SNR between TTGs and satellites. Furthermore, to achieve load balancing between satellites while comprehensively considering the current and future traffic demands of terminals, we define a load cost as
where represents the current load of the TTG, denotes the predicted load of the TTG, and is the prediction weight.
By integrating these factors, the problem of handover selection can be formulated as
where denotes the set of handover strategies across all TTGs and slots, and and are weighting coefficients that balance the contributions of the SNR and load cost, respectively.
3. Proposed Joint Traffic Prediction and Handover Design Framework
We propose a unified framework that combines traffic prediction and a handover policy design for LEO satellite networks. As shown in Figure 2, the workflow begins with traffic forecasting using an LSTM network, followed by satellite load computation based on the predicted TTG traffic. This information, along with the satellite status, forms the MDP state space, which is then used by an attention−enhanced rainbow DQN to derive optimal handover policies.

Figure 2.
An illustration of the workflow of the proposed ARTHF.
3.1. LSTM−Enabled Traffic Prediction
LSTM networks, with their ability to model sequential data and capture long−term dependencies, are well−suited for predicting TTG traffic demand, enabling optimized satellite communication performance. To leverage LSTM for traffic prediction, we model the historical traffic data of each TTG as a time series with dimensions , where denotes the number of historical time slots used for prediction, and represents the number of channels for each TTG’s traffic data. As illustrated in Figure 3, data from each TTG is processed independently by a two−layer stacked LSTM architecture. Within this architecture, the first LSTM layer sequentially processes the input feature vector for each time slot t, leveraging its previous hidden state to generate current hidden states . These outputs are then fed into the second LSTM layer, which further refines them to produce . Once all inputs have been processed by the stacked LSTM layers, the final hidden states from the second LSTM layer are stacked and passed through a series of fully connected layers with ReLU activation to generate traffic predictions for each TTG.
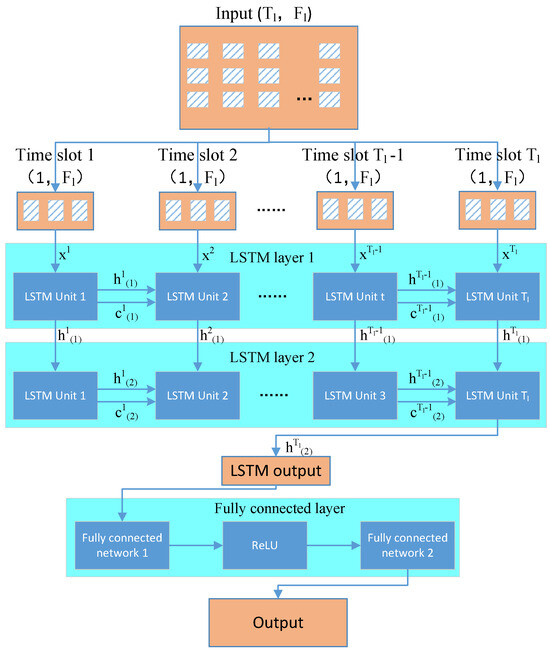
Figure 3.
An illustration of the detailed architecture of the stacked LSTM network for time series traffic prediction.
Each LSTM layer employs forget, input, and output gates to regulate the information flow, maintaining a memory cell that selectively retains or discards information to capture temporal dependencies. For each time slot t in the first layer, the LSTM processes the input feature vector and the previous hidden state . First, the forget gate discards irrelevant information from the previous cell state , expressed as
where is the forget gate’s weight matrix, is its bias vector, and denotes the sigmoid function. The input gate then decides what new information to store, which is calculated by
where is the input gate’s weight matrix, and is the bias vector. Concurrently, a candidate cell state is computed using
where is the candidate state’s weight matrix, and is its bias vector. Then, the cell state is updated using
combining retained and new information. Finally, the output gate produces the hidden state
where , with as the output gate’s weight matrix and as its bias vector. The second LSTM layer applies identical gated operations with its own weight matrices and bias vectors to produce its hidden state .
3.2. MDP Framework for Satellite Handover
Based on the system model established in Section 2, we formulate the problem as an MDP, where each TTG is considered an agent that makes decisions based on the state information and selects optimal actions. An MDP is typically defined as a tuple that describes the agent’s sequential decision−making process. The following discussion provides a detailed explanation of these components:
- State space : The state space for each TTG is constructed based on the current link status and the load conditions derived from the predicted traffic. For TTG k, each state is represented as a matrix , where each row corresponds to one of the visible satellites. The seven columns capture the satellite’s service status , elevation angle , distance , remaining service time , SNR , normalized demand weight , and computed load information . Notably, the load information is obtained by combining the predicted traffic demand from Section 3.1 with the real−time satellite state through Equation (18), enabling each TTG to make decisions that are both adaptive and anticipatory.
- Action space : The action space defines the handover decisions available to the TTG in each time slot. Each action specifies the satellite selected by the TTG for handover.
- Reward function : The reward function quantifies the immediate reward given by the environment after the TTGs take action in state . This reward comprehensively considers the handover cost, the coverage quality of the TTG, and the load balancing between satellites, which is expressed as
- Discount factor : This determines the weight of future rewards relative to immediate rewards, with . A higher value places greater emphasis on long−term rewards.
3.3. Attention−Enhanced Rainbow DQN
To address the satellite handover problem formulated as an MDP, we propose the attention−enhanced rainbow DQN, a reinforcement learning framework that integrates a self−attention mechanism with the dueling architecture of a rainbow DQN, which dynamically selects the optimal satellite for handover from a variable set of visible satellites.
The model input is obtained by zero−padding to form , where represents the maximum number of visible satellites for TTG k. As shown in Figure 4, the proposed attention−enhanced rainbow DQN architecture integrates a self−attention mechanism with a dueling network structure to process satellite data and estimate Q−values. The input is passed through a series of layers, including a self−attention module, fully connected layers, and the dueling architecture, ultimately producing selection probabilities for handover decisions. This structure effectively captures inter−satellite dependencies and adapts to varying numbers of visible satellites. In particular, the self−attention layer captures contextual relationships between satellites and adapts dynamically to changes in . For satellite m, the feature vector is projected into query, key, and value vectors, which are expressed as
where , , and are learnable matrices, and the output dimension is denoted as D. Then, the attention score is calculated by
where is a scaling factor to stabilize the gradients. The output vector for satellite m is
constituting the m-th column of matrix , where each row captures the inter−satellite dependencies and global contextual information.
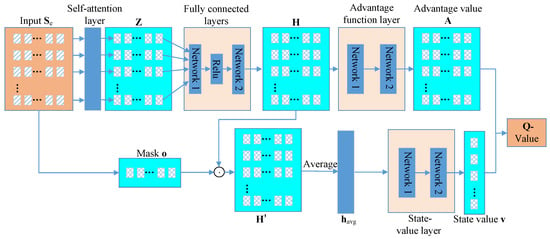
Figure 4.
An illustration of the detailed architecture of the attention−enhanced rainbow DQN for handover decision generation.
The matrix then passes through several fully connected layers with ReLU activations, each processing rows independently to preserve the matrix structure, thereby producing and extracting higher−level features via nonlinear transformations. A mask identifies valid satellites, defined as
yielding and retaining valid satellite features.
The dueling architecture, a core component of a rainbow DQN, then estimates the Q−value distributions across two branches. For the state−value branch, the valid features in are averaged, denoted as
and processed through a fully connected layer to obtain the state value . In parallel, the advantage branch processes with a similar fully connected structure to generate the advantage values , where each row represents the advantage distribution corresponding to satellite m.
Finally, the network combines the state value and the output of the advantage value to obtain the Q−value estimation matrix . The Q−value distribution for satellite m is computed as
By applying the softmax function to each row of , the network derives the selection probability distribution , where each row indicates the likelihood of selecting satellite m for each TTG.
4. Numerical Results
4.1. Simulation Settings
To evaluate the effectiveness of the proposed ARTHF in addressing the handover problem, we conducted simulations in an idle−mode TTG handover scenario within a large−scale satellite network. The simulations were performed using a custom−built platform developed with Satellite Tool Kit (STK) 12.2 and Python 3.8. To ensure realism and reliability, satellite radio frequency (RF) and TTG parameters were configured in accordance with the NTN RF system specifications outlined in 3GPP TR 38.821. Specifically, the Ka−band (20 GHz) was adopted in the simulation, as is commonly used in LEO satellite systems, such as Starlink, to support high−bandwidth data transmission. For the satellite RF parameters, a system bandwidth of 400 MHz was configured, along with a wave Effective Isotropic Radiated Power (EIRP) density of 4 dBW/MHz. The satellites were equipped with directional antennas, featuring a maximum gain of 38.5 dBi and a 3 dB Half−power Beamwidth (HPBW) of 1.7647°. The satellite beam diameter was set as 20 km, with an antenna equivalent aperture of 0.25 m. A minimum communication elevation angle of 40° was maintained. For the user RF parameters, the frequency was also set to 20 GHz. The TTGs were likewise equipped with directional antennas, which featured a receiver gain of 39.7 dBi. The antenna noise temperature for the TTGs was 150 K, and the noise factor was 1.2 dB.
The simulation modeled a typical large−scale LEO satellite constellation, based on the design of SpaceX’s Starlink, consisting of multiple sub−constellations, as outlined in Table 1. The TTGs were arranged in a grid, scaled to a 25 km grid size, with the traffic distribution derived from the Milan traffic dataset [22] due to its realistic representation of temporal traffic variations, which are critical for assessing handover strategies in dynamic satellite networks, enabling the simulation of diverse traffic conditions, including high- and low−demand periods. Within each 15 s interval (three time slots), the dataset captured dynamic traffic patterns that ranged from peak loads to lower loads that reflected realistic user demand fluctuations. The simulation platform generated link relationship data at each time slot, where each slot lasted 5 s. Traffic data for each TTG, sourced from the Milan dataset, was updated every three slots (15 s). To align with this granularity, the handover trigger interval was also set as three slots, and traffic conditions were adjusted accordingly.

Table 1.
Constellation structure parameters.
The ARTHF integrates two neural network modules. The LSTM−based traffic predictor adopts a two−layer stacked architecture that processes historical data with dimensions [, ], representing three time steps and three feature channels per TTG. Each LSTM layer comprises three units, followed by fully connected layers (128, 64, 32, 1) with ReLU activations to generate traffic predictions. The attention−enhanced rainbow DQN for handover decision−making accepts a zero−padded input state matrix . The model includes a self−attention layer, followed by three fully connected layers (256, 128, 64), and adopts a dueling architecture that separates the state−value and advantage streams. The resulting Q−values guide the action selection process. Both networks are trained with a learning rate of 0.001 and a discount factor for 1000 episodes.
4.2. Performance Discussion
To assess the performance of the proposed ARTHF, we compared it with the following methods: (1) a classic rainbow DQN algorithm incorporating traffic prediction, denoted as ‘rainbow DQN + traffic prediction’; (2) an attention−enhanced rainbow DQN algorithm operating under fixed traffic conditions (i.e., without traffic prediction), denoted as ‘attention−enhanced rainbow DQN’; and (3) a classic rainbow DQN algorithm under fixed traffic conditions, denoted as ‘rainbow DQN’. These methods were selected to isolate and evaluate the individual contributions of the traffic prediction and attention mechanisms, while also providing fair comparisons against both traditional and advanced DRL−based handover strategies. For the algorithms without traffic prediction, the lack of insight into TTG traffic variations leads to the adoption of a greedy approach for load−balancing rewards. Specifically, these algorithms encourage all TTGs to select the satellite with the currently lowest load, without considering the real traffic demands of the TTGs in the reward design.
Figure 5 shows the average number of handovers per slot for each algorithm. The different algorithms evaluated and presented in the figure’s legend are the ’attention−enhanced rainbow DQN’; the ’rainbow DQN’; the ’ARTHF (attention−enhanced rainbow DQN + traffic prediction)’, which is our proposed framework; and the ’rainbow DQN + traffic prediction’. The attention−enhanced rainbow DQN significantly reduces the handover frequency compared with the classic rainbow DQN, which struggles with varying numbers of candidate satellites due to fixed input structures. This leads to positional bias and unbalanced training, where satellites later in the input are undervalued. By introducing a self−attention layer, the improved architecture captures inter−satellite relationships and eliminates positional bias, enabling more accurate and stable handover decisions. Notably, the ARTHF performs similarly to its non−predictive counterpart in terms of handover frequency, indicating that traffic prediction does not compromise handover stability and instead improves other performance aspects. Thanks to the Milan dataset’s inclusion of both peak and off−peak traffic scenarios, the framework’s robustness across fluctuating demand levels is well validated, consistently achieving lower handover frequency compared with the baseline methods and demonstrating its efficiency and stability in diverse network loads.
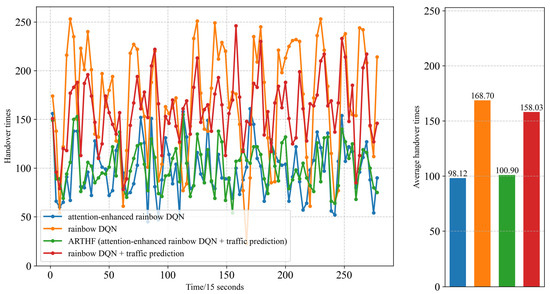
Figure 5.
Handover times over time and average handover times.
To evaluate the load−balancing performance, we used Jain’s index [23] and the satellite peak load as key metrics. Jain’s index is a widely used measure of fairness, ranging from 0 (worst) to 1 (perfect fairness), indicating how evenly traffic is distributed across satellites. As shown in Figure 6, the attention−enhanced algorithms consistently achieved significantly higher Jain’s fairness indices compared with the classic DQN architecture, highlighting the limitations of the traditional approach in managing constrained candidate satellites. By incorporating the traffic prediction, the improved architecture further increased the Jain’s fairness index, though the improvement was modest, demonstrating that anticipating future demand promotes a more equitable distribution of network load. Figure 7 illustrates the peak load experienced by each satellite at each time slot, providing a clear visualization of the congestion risk. The prediction−driven algorithm significantly reduced the satellite peak loads compared with its non−predictive counterpart, indicating a lower likelihood of system congestion. In particular, under high−load conditions, the ARTHF leverages traffic forecasts to proactively assign TTGs with high expected demand to underutilized satellites. This predictive load−balancing strategy mitigates congestion and enhances the overall fairness, as evidenced by the improved Jain’s index and reduced peak loads.
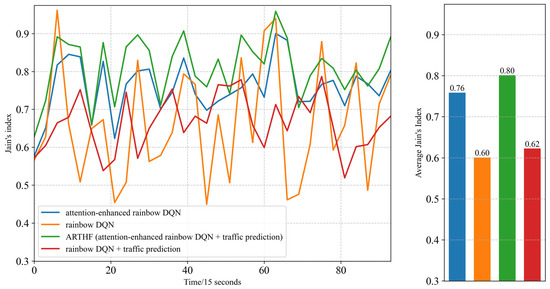
Figure 6.
Jain’s index over time and average Jain’s index.
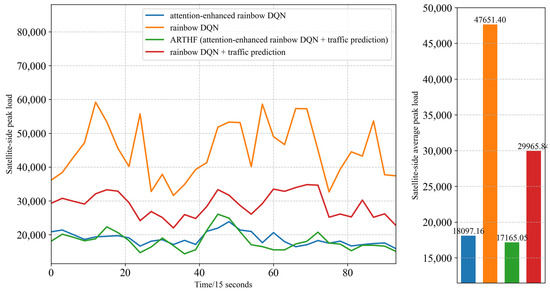
Figure 7.
Peak load over time and average maximum peak load.
The communication quality was evaluated using the average SNR across all TTGs, as shown in Figure 8. The prediction−driven algorithms demonstrated a significant increase in the average SNR compared with both its non−predictive counterparts, highlighting a core advantage of traffic forecasting. By anticipating future traffic demands, the algorithm enables differentiated handover strategies. TTGs with predicted high future demand can be assigned to satellites prioritized for load capacity, even if the instantaneous SNR is slightly compromised. Conversely, TTGs with a lower predicted demand can be allocated to satellites offering optimal signal quality without significantly impacting the overall network load. This flexibility allows the system to better optimize the overall communication quality. Notably, in low−load scenarios, the ARTHF framework naturally prioritizes the signal strength, selecting satellites with an optimal SNR and thereby ensuring a robust performance under varying traffic conditions.
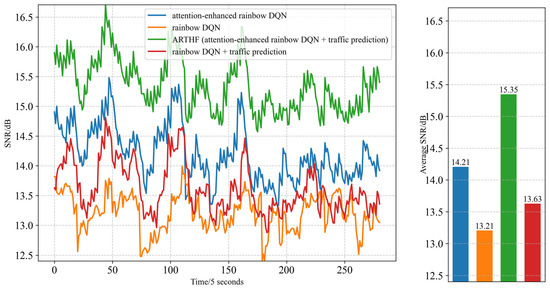
Figure 8.
SNR over time and average SNR.
In summary, the simulation results clearly demonstrate the superior performance of the ARTHF in optimizing handover decisions for LEO satellite networks. By integrating LSTM−based traffic prediction with an attention−enhanced rainbow DQN, the framework enables proactive load balancing and alleviates congestion under high−load conditions, as reflected in the improved Jain’s fairness index and reduced peak loads shown in Figure 6 and Figure 7. It also preserves high communication quality in low−load scenarios, as indicated by the enhanced SNR in Figure 8, while consistently achieving lower handover frequencies across diverse traffic scenarios, as illustrated in Figure 5. These findings, supported by the realistic and dynamic traffic patterns of the Milan dataset, highlight the robustness and adaptability of ARTHF for practical use in dynamic satellite−to−ground communication systems.
5. Conclusions
In this study, we addressed the critical challenge of handover selection in large−scale LEO satellite−to−ground networks involving numerous TTGs. To adapt to dynamic traffic patterns, we incorporated an LSTM−based traffic prediction model using historical data, enabling proactive and informed decision−making. The handover problem was formulated as an MDP, and we propose an attention−enhanced rainbow DQN algorithm that jointly considers the satellite switching frequency, communication quality, and satellite load. The proposed ARTHF features a flexible architecture applicable to various constellation configurations and traffic scenarios, as reflected in the Milan dataset’s diverse traffic patterns. Extensive simulations consistently demonstrated ARTHF’s significant superiority over the baseline methods, where it achieved substantial improvements in load balancing, improved communication quality, and reduced handover frequency. These compelling results affirm ARTHF’s robustness, efficiency, and practical effectiveness in ensuring seamless and optimized connectivity within dynamic satellite network systems.
Author Contributions
Conceptualization, D.F. and J.L.; methodology, S.Z.; software, Z.Y.; validation, D.F., J.L., M.Z. and S.Z.; formal analysis, Z.Y. and M.Z.; investigation, D.F.; resources, D.F.; data curation, J.L.; writing—original draft preparation, J.L.; writing—review and editing, J.L.; visualization, J.L.; supervision, J.L.; project administration, M.Z.; funding acquisition, M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Beijing Natural Science Foundation−Haidian Originat Innovation Joint Fund, grant number L232002.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LEO | Low Earth orbit |
| NTN | Non−terrestrial network |
| TN | Terrestrial network |
| TTG | Terrestrial terminal group |
| LSTM | Long short-term memory |
| MDP | Markov Decision Process |
| DQN | Deep Q network |
| D3QN | Dueling-double-deep-Q-learning network |
| ARTHF | Attention-enhanced rainbow-DQN-based joint traffic prediction and handover design framework |
| 6G | Sixth−generation |
| SINR | Signal−to− interference −plus−noise ratio |
| DRL | Deep reinforcement learning |
| QoS | Quality of service |
| SVR | Support vector regression |
| CNN | Convolutional neural network |
| GRU | Gated recurrent unit |
| SIB | System information block |
| GNSS | Global navigation satellite system |
| LSF | Large−scale fading |
| ITU−R | International telecommunication union radio communications sector |
| AWGN | Additive white Gaussian noise |
| STK | Satellite tool kit |
| RF | Radio frequency |
| EIRP | Effective isotropic radiated power |
| HPBW | Half−power beamwidth |
References
- Yaacoub, E.; Alouini, M.S. A key 6G challenge and opportunity—Connecting the base of the pyramid: A survey on rural connectivity. Proc. IEEE 2020, 108, 533–582. [Google Scholar] [CrossRef]
- Kodheli, O.; Lagunas, E.; Maturo, N.; Sharma, S.K.; Shankar, B.; Montoya, J.F.M.; Duncan, J.C.M.; Spano, D.; Chatzinotas, S.; Kisseleff, S.; et al. Satellite communications in the new space era: A survey and future challenges. IEEE Commun. Surv. Tutor. 2020, 23, 70–109. [Google Scholar] [CrossRef]
- Yang, Z.; Zeng, M.; Fei, Z. Attention-Enhanced Rainbow DQN for Cell Reselection in Satellite Communication Networks. In Proceedings of the 2024 16th International Conference on Wireless Communications and Signal Processing (WCSP), Hefei, China, 24–26 October 2024; pp. 999–1005. [Google Scholar]
- De Sanctis, M.; Cianca, E.; Araniti, G.; Bisio, I.; Prasad, R. Satellite communications supporting internet of remote things. IEEE Internet Things J. 2015, 3, 113–123. [Google Scholar] [CrossRef]
- Sun, T.; Shi, L. Load balancing and carrier-to-noise ratio based handover algorithm for LEO satellite network. In Proceedings of the 2023 IEEE 11th International Conference on Information, Communication and Networks (ICICN), Xi’an, China, 17–20 August 2023; pp. 207–211. [Google Scholar]
- Chen, J.; Wei, Z.; Wang, Y.; Sang, L.; Yang, D. A service-adaptive multi-criteria vertical handoff algorithm in heterogeneous wireless networks. In Proceedings of the 2012 IEEE 23rd International Symposium on Personal, Indoor and Mobile Radio Communications-(PIMRC), Sydney, Australia, 9–12 September 2012; pp. 899–904. [Google Scholar]
- Dai, C.Q.; Liu, Y.; Fu, S.; Wu, J.; Chen, Q. Dynamic handover in satellite-terrestrial integrated networks. In Proceedings of the 2019 IEEE Globecom Workshops (GC Wkshps), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- He, S.; Wang, T.; Wang, S. Load-aware satellite handover strategy based on multi-agent reinforcement learning. In Proceedings of the GLOBECOM 2020-2020 IEEE Global Communications Conference, Taipei, China, 7–11 December 2020; pp. 1–6. [Google Scholar]
- Cao, Y.; Lien, S.Y.; Liang, Y.C. Deep reinforcement learning for multi-user access control in non-terrestrial networks. IEEE Trans. Commun. 2020, 69, 1605–1619. [Google Scholar] [CrossRef]
- Cai, Y.; Wu, S.; Luo, J.; Jiao, J.; Zhang, N.; Zhang, Q. Age-oriented access control in GEO/LEO heterogeneous network for marine IoRT: A deep reinforcement learning approach. IEEE Internet Things J. 2022, 9, 24919–24932. [Google Scholar] [CrossRef]
- Agyapong, P.K.; Iwamura, M.; Staehle, D.; Kiess, W.; Benjebbour, A. Design considerations for a 5G network architecture. IEEE Commun. Mag. 2014, 52, 65–75. [Google Scholar] [CrossRef]
- Sun, H.; Liu, H.X.; Xiao, H.; Ran, B. Short Term Traffic Forecasting Using the Local Linear Regression Model 2002. Available online: https://escholarship.org/uc/item/540301xx (accessed on 1 March 2025).
- Sapankevych, N.I.; Sankar, R. Time series prediction using support vector machines: A survey. IEEE Comput. Intell. Mag. 2009, 4, 24–38. [Google Scholar] [CrossRef]
- Li, M.; Wang, Y.; Wang, Z.; Zheng, H. A deep learning method based on an attention mechanism for wireless network traffic prediction. Ad Hoc Netw. 2020, 107, 102258. [Google Scholar] [CrossRef]
- Ko, T.; Raza, S.M.; Binh, D.T.; Kim, M.; Choo, H. Network prediction with traffic gradient classification using convolutional neural networks. In Proceedings of the 2020 14th International Conference on Ubiquitous Information Management and Communication (IMCOM), Taichung, China, 3–5 January 2020; pp. 1–4. [Google Scholar]
- Yu, L.; Li, M.; Jin, W.; Guo, Y.; Wang, Q.; Yan, F.; Li, P. STEP: A spatio-temporal fine-granular user traffic prediction system for cellular networks. IEEE Trans. Mob. Comput. 2020, 20, 3453–3466. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, Y.; Lu, S. A Dynamic Spatio-Temporal Traffic Prediction Model Applicable to Low Earth Orbit Satellite Constellations. Electronics 2025, 14, 1052. [Google Scholar] [CrossRef]
- Li, J.; Wang, D.; Liu, L.; Wang, B.; Sun, C. Satellite ephemeris broadcasting architecture for 5G integrated leo satellite internet. In Proceedings of the 2022 IEEE 22nd International Conference on Communication Technology (ICCT), Nanjing, China, 11–14 November 2022; pp. 1437–1441. [Google Scholar]
- Propagation Data and Prediction Methods Required for the Design of Earth-Space Telecommunication Systems; Technical Report, 3rd Generation Partnership Project (3GPP). 2023. Available online: https://www.itu.int/dms_pubrec/itu-r/rec/p/R-REC-P.618-12-201507-S!!PDF-E.pdf (accessed on 1 July 2025).
- Characteristics of Precipitation for Propagation Modelling; Technical Report, 3rd Generation Partnership Project (3GPP). 2017. Available online: https://www.itu.int/rec/R-REC-P.837/en (accessed on 1 July 2025).
- TR 38.811: Study on New Radio (NR) to Support Non-Terrestrial Networks; Technical Report TR 38.811, 3rd Generation Partnership Project (3GPP). 2018. Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3234 (accessed on 1 July 2025).
- Villani, F.; Civico, R.; Pucci, S.; Pizzimenti, L.; Nappi, R.; De Martini, P.M. A database of the coseismic effects following the 30 October 2016 Norcia earthquake in Central Italy. Sci. Data 2018, 5, 53. [Google Scholar] [CrossRef] [PubMed]
- Jain, R.K.; Chiu, D.M.W.; Hawe, W.R. A Quantitative Measure of Fairness and Discrimination; Eastern Research Laboratory, Digital Equipment Corporation: Hudson, MA, USA, 1984; Volume 21, pp. 2022–2023. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).