Maximization of Average Achievable Rate for NOMA-UAV Dual-User Communication System Assisted by RIS

Abstract

Non-orthogonal multiple access (NOMA) technology can effectively improve spectrum efficiency, unmanned aerial vehicle (UAV) communication has the advantage of flexible deployment, and reconfigurable intelligent surface (RIS) can intelligently control the wireless transmission environment. Traditional communication systems have problems such as limited coverage and low spectrum efficiency in complex scenarios. However, a key challenge in deploying RIS-assisted NOMA-UAV communication systems lies in how to jointly optimize the UAV flight trajectory, power allocation strategy, and RIS phase offset to achieve the maximum average achievable rate for users. The non-convex nature of the optimization complicates the problem, making it challenging to find an efficient solution. Based on this, this paper presents a RIS-assisted NOMA-UAV communication system consisting of one UAV, one RIS, and two ground users. To achieve the maximum average rate for users, the UAV flight trajectory, power allocation strategy, and RIS phase offset are jointly optimized. For the non-convex problem, we decompose it into three sub-problems based on its inherent structural characteristics and use an alternating iterative approach to gradually converge to a feasible solution. The simulation results demonstrate that the proposed scheme offers significant advantages in the application scenario. Compared to other benchmark schemes, it delivers superior performance improvements to the communication system and offers higher practical value.

1. Introduction

RIS technology provides a new performance optimization opportunity for sixth-generation communication systems, thanks to its low cost and intelligent ability to reconstruct the wireless propagation environment. As such, it is considered a key technology with significant development potential. Specifically, RIS consists of electromagnetic units and a programmable patch array. Each unit intelligently controls the phase shift and accurately reflects the incident electromagnetic waves [1]. RIS offers an economical and effective solution for controlling the radio propagation environment while avoiding additional power consumption and the costly deployment of communication devices, thereby enhancing the system’s achievable rate [2].

With its rapid deployment capabilities, spatial mobility, and reliable line-of-sight transmission, UAV communication offers an effective solution for optimizing wireless communication standards [3]. In [4], the author focuses on utilizing UAV cooperative operations to extend communication time and proposes two strategies to maximize system throughput. The UAV relay’s flight trajectory and the power output between the sender node and the UAV relay are jointly optimized.

Due to its high spectrum efficiency and large-scale access capabilities, NOMA is regarded as an advanced multiple access technology to address challenges in future wireless communication networks [5]. The core concept of NOMA involves leveraging users’ varying channel conditions to improve spectrum efficiency and ensure fairness. The concept aims to promote spectrum resource sharing among users. These two communication technologies are complementary and can be integrated to meet the challenging demands of 6G cellular networks [6].

Leveraging the unique advantages of UAVs in communication and the technological potential of RIS and NOMA, their integration has become a major research direction. In [7], the author considers a multi-user communication system where UAVs provide services to a large number of ground users by using NOMA as a flying base station. They formulated the maximum and minimum rate optimization problem and proposed a path tracking method to address it. In the RIS-assisted UAV communication scenario, reference [8] proposes a strategy to jointly optimize the RIS phase, UAV time-slot power allocation, and flight trajectory by developing a three-terminal system model, effectively improving the average achievable data rate for ground users. In literature [9], a RIS-assisted UAV communication model is developed, and the trajectory and RIS beam are jointly optimized. The Successive Convex Approximation (SCA) approach is employed to iteratively solve the non-convex problem. Subsequently, using the optimal phase shift, a sub-optimal trajectory solution is derived to enhance the average rate. In [10], the author proposes a hybrid aviation full-duplex relay protocol, utilizing a UAV equipped with RIS in decode-and-forward mode, integrated with NOMA technology to enhance the frequency resource efficiency of information transmission between the base station and multiple users.

Additionally, many studies focus on the NOMA-UAV cooperative system based on RIS. In [11], the author proposes a RIS-assisted UAV NOMA-based crisis communication infrastructure. Multiple RISs form an intelligent link. Users transmit data through the nearest RIS, with same-side users employing NOMA for transmission. In [12], the author develops a UAV-RIS-assisted communication system. By combining NOMA with imperfect successive interference cancellation (SIC) and jointly optimizing the three-dimensional UAV trajectory, power allocation, and RIS phase shift, a two-step method is proposed to maximize system throughput and adapt to both users and UAV mobility scenarios. In [13], the author proposes a novel scheme to optimize the NOMA-based multi-UAV network with RIS. The focus is on the association between ground user equipment and UAVs, UAV power distribution, and RIS reactive beamforming. The goal is to enhance the frequency resource efficiency of the system, assuming imperfect continuous interference cancellation. In [14], the author focuses on a RIS-assisted multi-UAV network scenario. The research goal is to minimize the system’s total power expenditure while ensuring the minimum data rate threshold for users and the smallest safe spacing between drones. The joint optimal configuration problem is solved using the SCA algorithm and maximum ratio transmission technique. In [15], a UAV-RIS cooperative mobile edge computing framework is developed, and a dedicated NOMA-based task offloading protocol is introduced. The UAV performs both relay and computing functions, enabling ground users to offload tasks to remote access points via RIS.

In [16], the author thoroughly investigates the UAV communication scenario assisted by RIS. The research focuses on maximizing the total data throughput of all participants by collaboratively refining the RIS beamforming weight vector, the drone’s spatial flight trajectory, and the energy distribution strategy. Within a downlink NOMA-UAV network, a UAV equipped with a single antenna is connected to a pair of users, each with a single antenna, with the assistance of RIS. The incoming signal is reconfigured via RIS and then forwarded to the users. The issue of enhancing total throughput in RIS-aided NOMA-based UAV communication systems is addressed, and a practical, efficient algorithm is proposed to obtain a suboptimal solution to the original problem [17].

In [18], this work investigates the synergistic optimization of a multi-RIS-assisted satellite-UAV-terrestrial integrated network and reshapes the transmission path in UAVs equipped with RIS to account for obstacles and dynamic environments. For the RIS-UAV hybrid optimization framework, ref. [19] proposes broadcasting data to ground devices using the NOMA protocol and maximizing the total rate of the vehicular network framework under the constraints of rate, battery, and coordination. In [20], the author investigates the RIS-assisted UAV-NOMA data collection network, where RIS enhances channel controllability, reduces interference, and adapts to UAV dual-mode switching scenarios. In [21], the NOMA network with a single UAV and RIS is studied. For scenarios involving a temporary base station and two users, the full-path outage probability and time-averaged channel capacity under the Nakagami-m channel are evaluated, with selection combining and maximum ratio combining techniques applied. The performance of both perfect and imperfect NOMA schemes based on SIC is analyzed. In [22], this paper investigates the NOMA millimeter-wave network in multi-UAV base station and distributed RIS scenarios, jointly optimizing beamforming, phase shifts, power, and three-dimensional layout to maximize system energy efficiency under imperfect SIC. In [23], the author investigates the optimization of power-utilization efficiency in the uplink NOMA system. The UAV equipped with RIS for anti-eavesdropping is used to jointly optimize power, coefficients, and three-dimensional layout, subject to rate and safe flight constraints. Additionally, in the high-frequency band, the channels of RIS and UAV are often sparse, meaning most propagation paths cannot effectively transmit signals, making the modeling of channel sparsity particularly important. In [24], the author propose a sparse adaptive channel estimation approach with a dynamic-threshold mechanism. By focusing exclusively on the columns of the measurement matrix that are above the threshold, this approach effectively minimizes computational complexity and subsequently decreases the number of required inner-product calculations. The comparison of related literature is shown in

Table 1. Summary of some contributions of existing papers.

Reference	Application Scene	Solution Method
[8]	RIS-assisted UAV communication system	Joint design iterative optimization
[9]	New RIS-assisted UAV communication system	Closed phase shift solution, SCA
[10]	Hybrid air full-duplex relay mode	Riemann gradient method
[11]	STAR-RIS-assisted UAV	LRCPPO algorithm
[12]	RIS-assisted multi-UAV communication system	Double deep Q network
[13]	RIS combined with NOMA multi-UAV	Quadratic programming, SCA
[15]	RIS mobile edge computing framework	Semidefinite relaxation, SCA
[16]	STAR-RIS-assisted UAV	Joint design iterative optimization
[17]	STAR-RIS assisted NOMA-UAV network	Joint optimization algorithm
[19]	T-RIS assisted UAV	D3RL framework
[20]	Aerial RIS-assisted wireless network	MADDPG method
[21]	RIS-assisted UAV communication system	Diversity combining techniques
[23]	STAR-RIS-assisted UAV	Double deep Q network, SCA

.

The RIS-assisted NOMA-UAV scheme has garnered increasing attention in the context above. In this paper, the NOMA communication mode is introduced for the RIS-assisted UAV, with the number of users increased to two. The effects of RIS phase, UAV power allocation, and UAV trajectory optimization on system performance are further examined. The core objective of this study is to optimize the RIS phase, UAV power allocation, and trajectory design in the RIS-assisted NOMA-UAV system to maximize the system’s average reachability. We model the RIS phase, UAV power allocation, and trajectory, and propose an optimization scheme to enhance the system’s overall performance. The principal outcomes of this research are presented below.

•

We design a RIS-assisted NOMA-UAV communication system. Unlike the scheme in reference [17], which optimizes the UAV’s hovering position, our algorithm addresses the system performance optimization problem by optimizing the UAV’s trajectory. Optimizing the drone’s position improves communication coverage, but this method has spatial limitations. In contrast, the trajectory optimization algorithm is more flexible, enabling a wider coverage area and more stable signal transmission. However, UAV trajectory optimization increases the complexity of the modeling, making the optimization problem more challenging to solve.

•

We divide the problem into three manageable sub-problems—RIS phase optimization, UAV trajectory optimization, and power optimization and solve it using alternating iterative optimization. We compare our proposed scheme with four benchmark algorithms. As the number of RIS array elements increases, the optimization performance of our proposed scheme (OT&OP&OW) improves slightly. When the UAV transmission power increases, OT&OP&OW improves significantly. The results of all optimization algorithms outperform the random phase curve (T&OP), and our proposed schemes outperform the other benchmark algorithms.

Notation: Some symbols are given here. $∥·∥$ represents Euclidean norm. $\left|·\right|$ denotes amplitude, ${\left(·\right)}^H$ denotes complex conjugate matrix, and ${\left(·\right)}^T$ denotes taking matrix transpose. $\mathbb{CN}(*,{*}^2)$ represents the circular symmetric complex Gaussian distribution with mean * and variance ${*}^2$. And $\widetilde{·}$ indicates that this is a random component. Angle $\left(·\right)$ denotes taking phase.

2. System Model

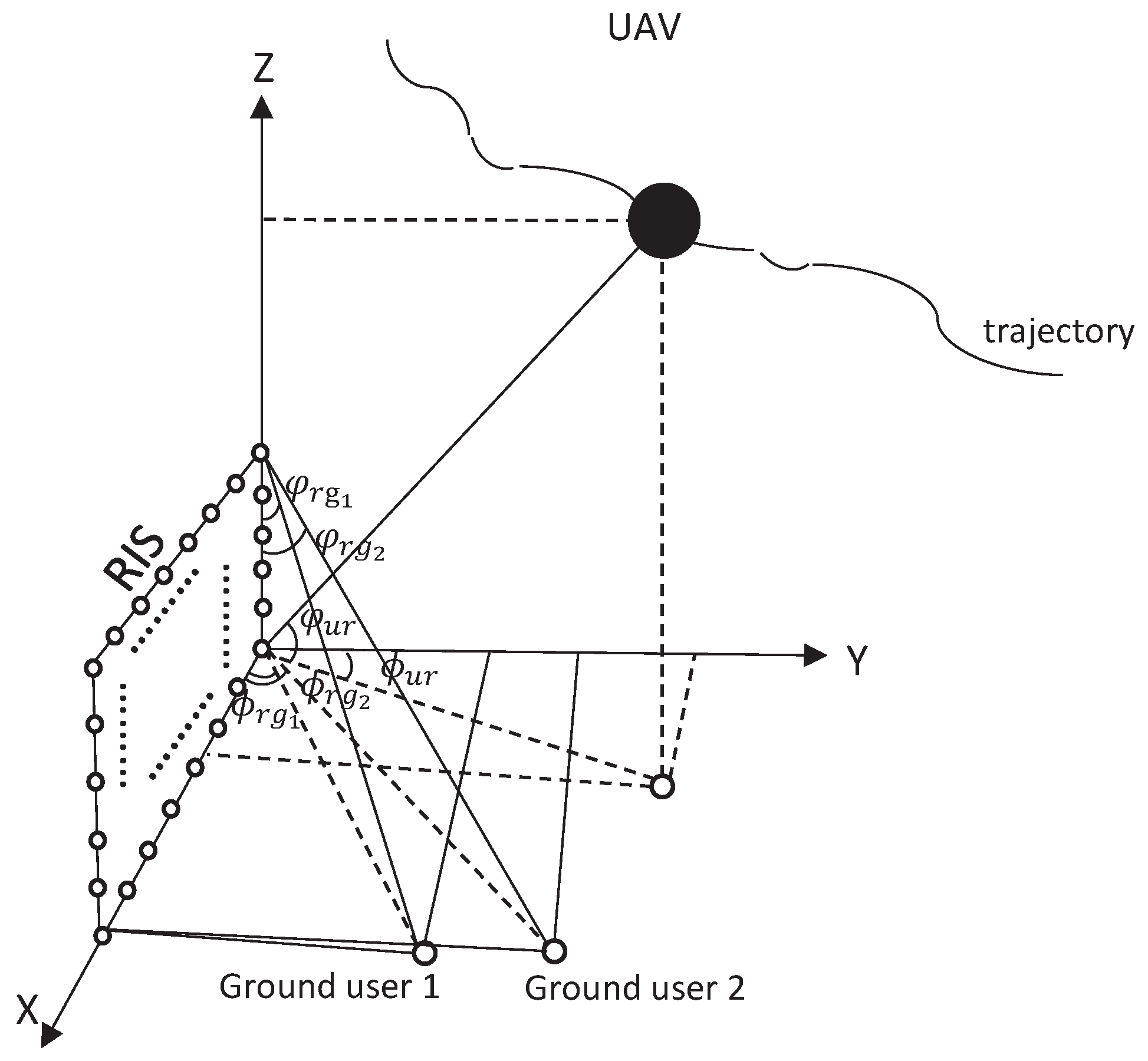
This paper discusses a RIS-assisted NOMA-UAV communication system architecture. The system consists of a UAV in flight, a RIS deployed on a wall, and two ground terminal users utilizing NOMA communication. The UAV maintains a line-of-sight (LoS) wireless connection with the RIS installed on the building’s side wall to ensure stable signal propagation. Even if the wireless connection between the UAV and the terrestrial user is interrupted, the system can still use RIS to enable effective signal reception by the ground user. All nodes involved in the communication process are positioned in a three-dimensional rectangular coordinate system, as shown in Figure 1. The location of the User 1 is set to $L_{G1}={[x_{G1},y_{G1}]}^T$, and the location of the User 2 is set to $L_{G2}={[x_{G2},y_{G2}]}^T$. The complete flight path of the UAV is expanded in the X-Y-Z three-dimensional coordinate system. During the whole flight cycle, the flight height of UAV remains unchanged, which is $Z_{UAV}$ [9]. In addition, the height of RIS is set to $Z_{RIS}$, the location of the RIS is set to $L_R={[x_R,y_R]}^T$. The maximum speed during flight is limited to $V_{max}$. The UAV’s flight cycle is denoted as J, which is divided into K time intervals, each of duration $\delta$. The UAV can cover a maximum distance in a single time interval, as calculated by $D=V_m\delta$. Based on this, the position of the UAV at time k can be represented by $Q\left[k\right]={[x_U\left[k\right],y_U\left[k\right]]}^T$, $k\in \{1,2,\dots ,K\}$. To better align with the actual flight trajectory, the UAV follows the constraints outlined below.

$$\begin{array}{cc}\hfill & {∥q[k+1]-q\left[k\right]∥}^2\le D^2,k\in \{1,2,\dots ,K-1\}\hfill \end{array}$$

(1a)

$$\begin{array}{cc}\hfill & {∥q\left[K\right]-q_e∥}^2\le D^2,\hfill \end{array}$$

(1b)

$$\begin{array}{cc}\hfill & q\left[1\right]=q_s.\hfill \end{array}$$

(1c)

Here $q_s$ and $q_e$ denote the UAV’s starting and terminal points. The constraint achieves a high-precision dynamic approximation of the real flight trajectory by discretizing the continuous path into a series of differential segments.

The RIS is assumed to consist of a uniform planar array with $M=M_x\times M_z$ elements. $\Theta \left[k\right]=diag\{e^{j{\theta }_{(0,0)}\left[k\right]},\dots ,e^{j{\theta }_{(m,n)}\left[k\right]},\dots ,e^{j{\theta }_{(M_x-1,M_z-1)}\left[k\right]}\}$ is defined as a diagonal phase matrix, where ${\theta }_{(m,n)}\left[k\right]\in [0,2\pi ),k\in \{1,2,\dots ,K\},m\in \{0,1,\dots ,M_x\},n\in \{0,1,\dots ,M_z\}$ denotes the stage value of the $(m,n)$th reflection unit in the k slot.

$h_{u{g}_1}$ and $h_{u{g}_2}$ are set as the direct links from UAV to ground User 1 and User 2, respectively. Although the direct signal from the transmitting source to the receiver may be blocked by obstacles, some signals can bypass these obstructions through reflection or scattering. These signals will experience attenuation or interference during propagation. A commonly used model to describe this phenomenon is Rayleigh fading. The values of $h_{u{g}_2}\left[k\right]$ and $h_{u{g}_1}\left[k\right]$ in the kth time slot can get

$$h_{u{g}_1}\left[k\right]=\sqrt{c_0{d}_{u{g}_1}^{-\alpha }\left[k\right]}{\tilde{h}}_1,$$

(2)

$$h_{u{g}_2}\left[k\right]=\sqrt{c_0{d}_{u{g}_2}^{-\alpha }\left[k\right]}{\tilde{h}}_2,$$

(3)

$d_{u{g}_1}\left[k\right]=\sqrt{Z_{UAV}^2+{∥q\left[k\right]-L_{G1}∥}^2}$ and $d_{u{g}_2}\left[k\right]=\sqrt{Z_{UAV}^2+{∥q\left[k\right]-L_{G2}∥}^2}$ are the distance from UAV to User 1 and User 2 respectively. The $c_0$ is the path loss, and $\alpha$ is the path loss index of UAV-user. ${\tilde{h}}_1$$\sim \mathbb{CN}(0,1)$ and ${\tilde{h}}_2$$\sim \mathbb{CN}(0,1)$. Assuming that the channel between UAV and RIS is a LoS channel and is set to $h_{ur}$, the value of $h_{ur}\left[k\right]$ at the kth time slot can obtain

$$\begin{array}{cc}\hfill h_{ur}\left[k\right]=\sqrt{c_0{d}_{ur}^{-\kappa }\left[k\right]}& \{1,\dots ,e^{-j{\displaystyle \frac{2\pi }{\lambda }}d{\chi }_{ur}^{(m,n)}\left[k\right]}\hfill \\ \hfill & ,\dots ,e^{-j{\displaystyle \frac{2\pi }{\lambda }}d{\chi }_{ur}^{(M_x-1,M_z-1)}\left[k\right]}{\}}^T,\hfill \end{array}$$

(4)

the d represents the interval between the antennas, $\lambda$ represents the wavelength, $\kappa$ is the signal loss index of the UAV-RIS, and $d_{ur}\left[k\right]=\sqrt{{(Z_{UAV}-Z_{RIS})}^2+{∥q\left[k\right]-L_R∥}^2}$ is the distance of the UAV-RIS in the time slot. ${\chi }_{ur}^{(m,n)}\left[k\right]=msin{\varphi }_{ur}\left[k\right]cos{\phi }_{ur}\left[k\right]+nsin{\phi }_{ur}\left[k\right]$, $sin{\varphi }_{ur}\left[k\right]cos{\phi }_{ur}\left[k\right]={\displaystyle \frac{x_R-x_U\left[k\right]}{d_{ur}\left[k\right]}}$, $sin{\phi }_{ur}\left[k\right]={\displaystyle \frac{Z_{UAV}-Z_{RIS}}{d_{ur}\left[k\right]}}$, ${\varphi }_{ur}\left[k\right]$ and ${\phi }_{ur}\left[k\right]$ respectively denote the azimuth and pitch angle of the signal from UAV to RIS within time slot k.

We define the distance between the user and the RIS as the distance from the user to the first array element of the RIS [25]. The channel between RIS users is modeled using Rician fading effect. Unlike Rayleigh fading, the Rician model accounts for the reflected signals from the RIS, denoted as $h_{r{g}_1}$ and $h_{r{g}_2}$. Then $h_{r{g}_1}$ and $h_{r{g}_2}$ can get

$$\begin{array}{cc}\hfill h_{r{g}_1}=& \sqrt{c_0{d}_{r{g}_1}^{-\tau }}\left(\sqrt{{\displaystyle \frac{\sigma }{1+\sigma }}}{h}_{r{g}_1}^{LOS}+\sqrt{{\displaystyle \frac{1}{1+\sigma }}}{h}_{r{g}_1}^{NLOS}\right),\hfill \end{array}$$

(5)

$$\begin{array}{c}\hfill h_{r{g}_1}^{LOS}={\left\{1,\dots ,e^{-j{\displaystyle \frac{2\pi }{\lambda }}d{\chi }_{r{g}_1}^{(m,n)}\left[k\right]},\dots ,e^{-j{\displaystyle \frac{2\pi }{\lambda }}d{\chi }_{r{g}_1}^{(M_x-1,M_z-1)}\left[k\right]}\right\}}^T,\end{array}$$

(6)

$$\begin{array}{cc}\hfill h_{r{g}_2}=& \sqrt{c_0{d}_{r{g}_2}^{-\tau }}\left(\sqrt{{\displaystyle \frac{\sigma }{1+\sigma }}}{h}_{r{g}_2}^{LOS}+\sqrt{{\displaystyle \frac{1}{1+\sigma }}}{h}_{r{g}_2}^{NLOS}\right),\hfill \end{array}$$

(7)

$$\begin{array}{c}\hfill h_{r{g}_2}^{LOS}={\left\{1,\dots ,e^{-j{\displaystyle \frac{2\pi }{\lambda }}d{\chi }_{r{g}_2}^{(m,n)}\left[k\right]},\dots ,e^{-j{\displaystyle \frac{2\pi }{\lambda }}d{\chi }_{r{g}_2}^{(M_x-1,M_z-1)}\left[k\right]}\right\}}^T,\end{array}$$

(8)

we define parameters $d_{r{g}_1}=\sqrt{Z_{RIS}^2+{∥L_R-L_{G1}∥}^2}$ and $d_{r{g}_2}=\sqrt{Z_{RIS}^2+{∥L_R-W_{G2}∥}^2}$ as the distances from the RIS to User 1 and User 2, which facilitates subsequent performance analysis. $h_{r{g}_1}^{NLOS}$$\sim \mathbb{CN}(0,1)$ and $h_{r{g}_2}^{NLOS}$$\sim \mathbb{CN}(0,1)$ represent the circular symmetric complex Gaussian distribution. $\sigma$ is the Rician factor; $\tau$ is the path loss index corresponding to RIS-ground users. And ${\chi }_{r{g}_1}^{(m,n)}\left[k\right]=mcos{\varphi }_{r{g}_1}sin{\phi }_{r{g}_1}+ncos{\phi }_{r{g}_1}$, where $cos{\varphi }_{r{g}_1}sin{\phi }_{r{g}_1}={\displaystyle \frac{x_R-x_{G1}}{d_{r{g}_1}}}$, $cos{\phi }_{r{g}_1}={\displaystyle \frac{Z_{RIS}}{d_{r{g}_1}}}$, ${\varphi }_{r{g}_1}$ and ${\phi }_{r{g}_1}$ signify the horizontal and vertical directions, respectively, of the signal being transmitted from the RIS-ground User 1. Similarly, ${\chi }_{r{g}_2}^{(m,n)}\left[k\right]=mcos{\varphi }_{r{g}_2}sin{\phi }_{r{g}_2}+ncos{\phi }_{r{g}_2}$, where $cos{\varphi }_{r{g}_2}sin{\phi }_{r{g}_2}={\displaystyle \frac{x_R-x_{G2}}{d_{r{g}_2}}}$, $cos{\phi }_{r{g}_2}={\displaystyle \frac{Z_{RIS}}{d_{r{g}_2}}}$, ${\varphi }_{r{g}_2}$ and ${\phi }_{r{g}_2}$ represent the horizontal and vertical directions, respectively, of the signal transmitted from the RIS to ground-based User 2. To facilitate subsequent calculations, we transform $h_{r{g}_1}$ and $h_{r{g}_2}$ into

$$\begin{array}{cc}\hfill h_{r{g}_1}=& [\left|h_{r{g}_1,(0,0)}\right|e^{j{\eta }_1(0,0)},\dots ,\left|h_{r{g}_1,(m,n)}\right|e^{j{\eta }_1(m,n)}\hfill \\ \hfill & ,\dots ,\left|h_{r{g}_1,(M_x-1,M_z-1)}\right|e^{j{\eta }_1(M_x-1,M_z-1)}{]}^T,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill h_{r{g}_2}=& [\left|h_{r{g}_2,(0,0)}\right|e^{j{\eta }_2(0,0)},\dots ,\left|h_{r{g}_2,(m,n)}\right|e^{j{\eta }_2(m,n)}\hfill \\ \hfill & ,\dots ,\left|h_{r{g}_2,(M_x-1,M_z-1)}\right|e^{j{\eta }_2(M_x-1,M_z-1)}{]}^T.\hfill \end{array}$$

(10)

The amplitude and phase are decoupled to simplify the calculation. Where $\left|h_{r{g}_1,(m,n)}\right|$ and $\left|h_{r{g}_2,(m,n)}\right|$ represent the amplitude of each element $(m,n)$ of $h_{r{g}_1}$ and $h_{r{g}_2}$ respectively, and ${\eta }_1(m,n)$ and ${\eta }_2(m,n)$ represent the phase of each element (m,n) of $h_{r{g}_1}$ and $h_{r{g}_2}$ respectively.

We assume that the signals in the system take the form of linear combinations, with each signal affected by different noises and disturbances. The signal in the system can be expressed as: $y=H*s+n$, where y is the received signal, H is the channel matrix, s is the transmitted signal, and n is the noise. To ensure successful decoding, when the signal-to-noise ratio (SNR) of the received signal exceeds the decoding threshold, the receiver can recover the target signal. The residual interference in subsequent signal processing can be significantly reduced by reconstructing and eliminating the interference component. This expresses it as:

$$\begin{array}{c}\hfill SN{R}_{target}\ge SN{R}_{threshold},\end{array}$$

(11)

where $SN{R}_{target}$ is the target SNR of the current signal, and $SN{R}_{threshold}$ is the minimum SNR required for successful decoding. To minimize the influence of the signal on subsequent processing after decoding, the interference power must be minimized. This can be quantified by the interference-to-noise ratio (INR) of each signal, we can get:

$$\begin{array}{c}\hfill INR={\displaystyle \frac{P_{interference}}{P_{noise}}}\to min,\end{array}$$

(12)

Next, we sort the signal intensities and determine the decoding order. After decoding the interference signal, perfect SIC can be achieved by minimizing the interference power.

In the NOMA system, ground users employ SIC to decode their signals. To streamline the analysis, we posit the sequence of decoding [26]. We first regard the signal of User 2 as noise to decode the signal of User 1, and then remove it from the superimposed signal. Then you need to meet the following constraints.

$$\begin{array}{c}\hfill H_2\left[k\right]\ge H_1\left[k\right],\end{array}$$

(13)

$$\begin{array}{c}\hfill p_2\left[k\right]\le p_1\left[k\right],\end{array}$$

(14)

$p_1\left[k\right]$ and $p_2\left[k\right]$ are the power allocated by the UAV to User 1 and User 2 for transmission in k time slots, respectively. $H_1\left[k\right]={∥h_{u{g}_1}\left[k\right]+h_{r{g}_1}^H{\Theta }_1\left[k\right]h_{ur}\left[k\right]∥}^2$ and $H_2\left[k\right]={∥h_{u{g}_2}\left[k\right]+h_{r{g}_2}^H{\Theta }_2\left[k\right]h_{ur}\left[k\right]∥}^2$ represent the joint channel vectors of UAV to ground User 1 and ground User 2 at the kth time slot, respectively.

Then the average achievable rates of User 1 and User 2 take the form of

$$R_1\left[k\right]={log}_2\left(1+{\displaystyle \frac{p_1\left[k\right]H_1\left[k\right]}{p_2\left[k\right]H_1\left[k\right]+{\xi }^2}}\right).$$

(15)

$$R_2\left[k\right]={log}_2\left(1+{\displaystyle \frac{p_2\left[k\right]H_2\left[k\right]}{{\xi }^2}}\right).$$

(16)

Then we can obtain the average achievable rate

$$\overline{R}={\displaystyle \frac{1}{K}}\sum _{k=1}^K(R_1\left[k\right]+R_2\left[k\right]).$$

(17)

3. Problem Formulation

After the expression of $\overline{R}$ is obtained, we aim to jointly optimize UAV power allocation, RIS phase, and UAV flight trajectory to maximize the average achievable rate, subject to the constraints on UAV flight trajectory and NOMA decoding sequence. We use $Q\triangleq \left\{q\right[k],k\in 1,2,\dots ,K\}$ to represent the UAV trajectory, ${\Phi }_{1,2}\triangleq \{{\Theta }_{1,2}\left[k\right],k\in 1,2,\dots ,K\}$ to represent the RIS phase, and $P_{1,2}\triangleq \{p_{1,2}\left[k\right],k\in 1,2,\dots ,K\}$ to represent the UAV transmission power. Therefore, we can express the optimization problem as

$$\begin{array}{cc}\hfill \mathrm{P}\left(1\right):& \underset{P,\Phi ,Q}{max}\overline{R}\hfill \\ \hfill s.t.& 0\le {\theta }_{(m,n)}\left[k\right]\le 2\pi ,\forall m,n,k\hfill \\ \hfill & {∥q[k+1]-q\left[k\right]∥}^2\le D^2,k\in \{1,2,\dots ,K-1\}\hfill \\ \hfill & {∥q\left[K\right]-q_e∥}^2\le D^2,\hfill \\ \hfill & q\left[1\right]=q_s,\hfill \\ \hfill & H_2\left[k\right]\ge H_1\left[k\right],\hfill \\ \hfill & p_2\left[k\right]\le p_1\left[k\right],\hfill \\ \hfill & p_2\left[k\right]+p_1\left[k\right]\le P_{max},\hfill \\ \hfill & p_2\left[k\right]\ge 0,k\in \{1,2,\dots ,K\},\hfill \end{array}$$

(18)

4. Proposed Algorithm

In the previous section, we derive the optimization problem. Due to the presence of coupling variables and non-convex constraints, problem $\mathrm{P}\left(1\right)$ presents a significant challenge. Therefore, we dissect the problem into three distinct sub-problems: the optimization of RIS phase shifts, UAV transmission power, and UAV flight trajectories.

4.1. RIS Phase Shift Optimization

When we fix the UAV power $P_{1,2}$ and UAV flight trajectory Q, we can rewrite $H_1\left[k\right]$ as

$$h_{r{g}_1}^H{\Theta }_1\left[k\right]h_{ur}\left[k\right]={\displaystyle \frac{{\displaystyle \sqrt{c_0}\sum _{m=0}^{M_x-1}\sum _{n=0}^{M_z-1}\left|h_{r{g}_1,(m,n)}\right|e^{j{\beta }_{1(m,n)}\left[k\right]}}}{d_{ur}^{\frac{\kappa }{2}}\left[k\right]}},$$

(19)

and through the integration of phase can be drawn ${\beta }_{1(m,n)}\left[k\right]={\theta }_{1(m,n)}\left[k\right]-{\eta }_{1(m,n)}-{\displaystyle \frac{2\pi }{\lambda }}d{\chi }_{ur}^{(m,n)}\left[k\right]$. According to [27], the equivalent maximum channel gain is achieved when the phases of $h_{u{g}_1}$ and $h_{r{g}_1}^H{\Theta }_1\left[k\right]h_{ur}\left[k\right]$ are aligned. Then we can derive it from

$${\theta }_{1(m,n)}\left[k\right]=arg\left({\tilde{h}}_1\right)\left[k\right]+{\eta }_{1(m,n)}+{\displaystyle \frac{2\pi }{\lambda }}d{\chi }_{ur}^{(m,n)}\left[k\right],$$

(20)

Using the same method, we can express the $H_2\left[k\right]$ as

$$h_{r{g}_2}^H{\Theta }_2\left[k\right]h_{ur}\left[k\right]={\displaystyle \frac{{\displaystyle \sqrt{c_0}\sum _{m=0}^{M_x-1}\sum _{n=0}^{M_z-1}\left|h_{r{g}_2,(m,n)}\right|e^{j{\beta }_{2(m,n)}\left[k\right]}}}{d_{ur}^{\frac{\kappa }{2}}\left[k\right]}},$$

(21)

where ${\beta }_{2(m,n)}\left[k\right]={\theta }_{2(m,n)}\left[k\right]-{\eta }_{2(m,n)}-{\displaystyle \frac{2\pi }{\lambda }}d{\chi }_{ur}^{(m,n)}\left[k\right]$. We align the phase of RIS to User 1. According to the literature [28], we align the RIS phase with User 1, as the positions of User 1 and User 2 differ, resulting in a phase difference. So we make ${\theta }_{1(m,n)}\left[k\right]={\theta }_{2(m,n)}\left[k\right]$ and put ${\theta }_{1(m,n)}\left[k\right]$ into ${\beta }_{2(m,n)}\left[k\right]$, we can get

$${\beta }_{2(m,n)}\left[k\right]=arg\left({\tilde{h}}_1\right)\left[k\right]+{\eta }_{1(m,n)}-{\eta }_{2(m,n)},$$

(22)

Because of mathematical formulae $\left|e^{j\theta }\right|=1$, we can rewrite $H_1$ and $H_2$ as

$$H_1\left[k\right]={\left({\displaystyle \frac{\sqrt{c_0}\left|{\tilde{h}}_1\right|}{d_{u{g}_1}^{\frac{\alpha }{2}}\left[k\right]}}+{\displaystyle \frac{{\displaystyle \sqrt{c_0}\sum _{m=0}^{M_x-1}\sum _{n=0}^{M_z-1}\left|h_{r{g}_1,(m,n)}\right|}}{d_{ur}^{\frac{\kappa }{2}}\left[k\right]}}\right)}^2,$$

(23)

$$H_2\left[k\right]={\left({\displaystyle \frac{\sqrt{c_0}\left|{\tilde{h}}_2\right|}{d_{u{g}_2}^{\frac{\alpha }{2}}\left[k\right]}}+{\displaystyle \frac{{\displaystyle \sqrt{c_0}\sum _{m=0}^{M_x-1}\sum _{n=0}^{M_z-1}\left|h_{r{g}_2,(m,n)}\right|}}{d_{ur}^{\frac{\kappa }{2}}\left[k\right]}}\right)}^2.$$

(24)

RIS can be equipped with high-precision phase control modules (e.g., varactor diodes) that independently adjust the phase of each reflection unit. In this paper, an alternating iterative iterative solution method is employed to ensure smooth and continuous phase adjustment, while the UAV’s continuity constraints are incorporated to prevent system instability. Therefore, continuous-phase operation is feasible.

Quantization phase shifts introduce errors that affect the accuracy, stability, and complexity of the optimization problem, particularly at lower quantization levels (e.g., 2-bit and 4-bit), where larger quantization errors can degrade convergence speed and algorithm accuracy. Additionally, lower quantization levels reduce the signal-to-noise ratio and increase the bit error rate, potentially limiting the achievable transmission rate.

This section focuses on UAV trajectory optimization. Following this, we will address the UAV power allocation problem.

4.2. UAV Trajectory Optimization

By fixing the RIS phase shift ${\Phi }_{1,2}$ and the UAV power $P_{1,2}$, there is only one variable Q. Then we can get

$$\begin{array}{cc}\hfill \mathrm{P}\left(2\right):& \underset{Q}{max}{\displaystyle \frac{1}{K}}\sum _{k=1}^K(R_1\left[k\right]+R_2\left[k\right])\hfill \\ \hfill s.t.& {∥q[k+1]-q\left[k\right]∥}^2\le D^2,k\in \{1,2,\dots ,K-1\},\hfill \\ \hfill & {∥q\left[K\right]-q_e∥}^2\le D^2,\hfill \\ \hfill & q\left[1\right]=q_s,\hfill \\ \hfill & H_2\left[k\right]\ge H_1\left[k\right],\hfill \end{array}$$

both $R_1\left[k\right]$ and $R_2\left[k\right]$ are nonconvex, we will deal with them separately and transform them into convex functions. Expand Formulas (23) and (24) to get

$$H_1^{\prime }\left[k\right]={\displaystyle \frac{A}{d_{u{g}_1}^{\alpha }\left[k\right]}}+{\displaystyle \frac{B}{d_{u{g}_1}^{\frac{\alpha }{2}}\left[k\right]d_{ur}^{\frac{\kappa }{2}}\left[k\right]}}+{\displaystyle \frac{C}{d_{ur}^{\kappa }\left[k\right]}},$$

(25)

$$H_2^{\prime }\left[k\right]={\displaystyle \frac{D}{d_{u{g}_2}^{\alpha }\left[k\right]}}+{\displaystyle \frac{E}{d_{u{g}_2}^{\frac{\alpha }{2}}\left[k\right]d_{ur}^{\frac{\kappa }{2}}\left[k\right]}}+{\displaystyle \frac{F}{d_{ur}^{\kappa }\left[k\right]}},$$

(26)

where ${\displaystyle A=c_0{\left|{\tilde{h}}_1\right|}^2, B=2c_0\sum _{m=0}^{M_x-1}\sum _{n=0}^{M_z-1}\left|h_{r{g}_1,(m,n)}\right|, C=c_0\sum _{m=0}^{M_x-1}\sum _{n=0}^{M_z-1}{\left|h_{r{g}_1,(m,n)}\right|}^2}$, $D=c_0{\left|{\tilde{h}}_2\right|}^2$, ${\displaystyle E=2c_0\sum _{m=0}^{M_x-1}\sum _{n=0}^{M_z-1}\left|h_{r{g}_2,(m,n)}\right|}$, ${\displaystyle F=c_0\sum _{m=0}^{M_x-1}\sum _{n=0}^{M_z-1}{\left|h_{r{g}_2,(m,n)}\right|}^2}$. In order to relax the constraints, we introduce the relaxation variables ${\mathit{u}}_{\mathbf{1}}\triangleq \left\{u_1\left[k\right]\right\},k\in \{1,2,\dots ,K\}$, ${\mathit{u}}_{\mathbf{2}}\triangleq \left\{u_2\left[k\right]\right\},$ $k\in \{1,2,\dots ,K\}$ and ${\mathit{v}}_{\mathbf{1}}\triangleq \left\{v_1\left[k\right]\right\},k\in \{1,2,\dots ,K\}$ to strike a balance between the constraint strictness and the problem’s solvability.

$$\begin{array}{c}\hfill v_1\left[k\right]\ge \sqrt{{(Z_{UAV}-Z_{RIS})}^2+{∥q\left[k\right]-L_R∥}^2},\end{array}$$

(27)

$$\begin{array}{c}\hfill u_1\left[k\right]\ge \sqrt{Z_{UAV}^2+{∥q\left[k\right]-L_{G1}∥}^2},\end{array}$$

(28)

$$\begin{array}{c}\hfill u_2\left[k\right]\ge \sqrt{Z_{UAV}^2+{∥q\left[k\right]-L_{G2}∥}^2},\end{array}$$

(29)

Substituting Formulas (27)–(29) into Formulas (25) and (26), we can get

$$H_1^{\prime }\left[k\right]={\displaystyle \frac{A}{u_1^{\alpha }\left[k\right]}}+{\displaystyle \frac{B}{u_1^{\frac{\alpha }{2}}\left[k\right]v_1^{\frac{\kappa }{2}}\left[k\right]}}+{\displaystyle \frac{C}{v_1^{\kappa }\left[k\right]}},$$

(30)

$$H_2^{\prime }\left[k\right]={\displaystyle \frac{D}{u_2^{\alpha }\left[k\right]}}+{\displaystyle \frac{E}{u_2^{\frac{\alpha }{2}}\left[k\right]v_1^{\frac{\kappa }{2}}\left[k\right]}}+{\displaystyle \frac{F}{v_1^{\kappa }\left[k\right]}},$$

(31)

$$R_1^{\prime }\left[k\right]={log}_2\left(1+{\displaystyle \frac{p_1\left[k\right]}{p_2\left[k\right]+\frac{{\xi }^2}{H_1^{\prime }\left[k\right]}}}\right).$$

(32)

$$R_2^{\prime }\left[k\right]={log}_2\left(1+{\displaystyle \frac{p_2\left[k\right]H_2^{\prime }\left[k\right]}{{\xi }^2}}\right).$$

(33)

Taylor approximation is a technique used to approximate a function by utilizing its derivative information at a specific point. Let $f\left(x\right)$ have all derivatives of order at a point $x_0$, then the Taylor expansion of $f\left(x\right)$ at that point is: $f\left(x\right)=f\left(x\right)+f^{\prime }\left(x_0\right)$$(x-x_0)+{\displaystyle \frac{f^{\prime \prime }\left(x_0\right)}{2!}}{(x-x_0)}^2+\dots +{\displaystyle \frac{f^{\left(n\right)}\left(x_0\right)}{n!}}{(x-x_0)}^n$. This expansion approximates the function value by progressively incorporating higher-order derivatives. In practical applications, the Taylor series is typically truncated to obtain an approximation. The accuracy of the Taylor expansion relies on the local linearization assumption and the differentiability of the function. In this paper, each iteration requires calculating only the gradient at the current point, with the expansion truncated to a single term.

Next, we obtain the first-order Taylor series of $H_1^{\prime }\left[k\right],H_2^{\prime }\left[k\right],R_1^{\prime }\left[k\right],R_2^{\prime }\left[k\right],u_1^2\left[k\right],u_2^2\left[k\right]$ and $v_1^2\left[k\right]$ for fixed points ${\mathit{u}}_{\mathbf{1}}^{\left(\mathbf{0}\right)}={\left\{u_1^{\left(0\right)}\left[k\right]\right\}}_{k=1}^K,{\mathit{u}}_{\mathbf{2}}^{\left(\mathbf{0}\right)}={\left\{u_2^{\left(0\right)}\left[k\right]\right\}}_{k=1}^K$ and ${\mathit{v}}_{\mathbf{1}}^{\left(\mathbf{0}\right)}={\left\{v_1^{\left(0\right)}\left[k\right]\right\}}_{k=1}^K$, respectively. That is, we calculate the first-order partial derivatives of $u_1\left[k\right]$,$u_2\left[k\right]$ and $v_1\left[k\right]$ for (32) and (33). Then we can get

$$\begin{array}{cc}\hfill R_1^{\prime }\left[k\right]\ge {log}_2{A}_0\left[k\right]+& {\displaystyle \frac{B_0\left[k\right]}{A_0\left[k\right]ln2}}(u_1\left[k\right]-u_1^{\left(0\right)}\left[k\right])\hfill \\ \hfill & +{\displaystyle \frac{C_0\left[k\right]}{A_0\left[k\right]ln2}}(v_1\left[k\right]-v_1^{\left(0\right)}\left[k\right]),\hfill \end{array}$$

(34)

$$\begin{array}{c}\hfill -u_1^2\left[k\right]\le {\left(u_1^{\left(0\right)}\right)}^2\left[k\right]-2u_1^{\left(0\right)}{u}_1\left[k\right]\end{array},$$

(35)

$$\begin{array}{c}\hfill -u_2^2\left[k\right]\le {\left(u_2^{\left(0\right)}\right)}^2\left[k\right]-2u_2^{\left(0\right)}{u}_2\left[k\right]\end{array},$$

(36)

$$\begin{array}{c}\hfill -v_1^2\left[k\right]\le {\left(v_1^{\left(0\right)}\right)}^2\left[k\right]-2v_1^{\left(0\right)}{v}_1\left[k\right]\end{array},$$

(37)

$$\begin{array}{cc}\hfill R_2^{\prime }\left[k\right]\ge {log}_2{A}_1\left[k\right]+& {\displaystyle \frac{B_1\left[k\right]}{A_1\left[k\right]ln2}}(u_2\left[k\right]-u_2^{\left(0\right)}\left[k\right])\hfill \\ \hfill & +{\displaystyle \frac{C_1\left[k\right]}{A_1\left[k\right]ln2}}(v_1\left[k\right]-v_1^{\left(0\right)}\left[k\right]),\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill H_1^{\prime }\left[k\right]\ge & \left({\displaystyle \frac{A}{{\left(u_1^{\left(0\right)}\right)}^{\alpha }\left[k\right]}}+{\displaystyle \frac{B}{{\left(u_1^{\left(0\right)}\right)}^{\frac{\alpha }{2}}\left[k\right]{\left(v_1^{\left(0\right)}\right)}^{\frac{\kappa }{2}}\left[k\right]}}+{\displaystyle \frac{C}{{\left(v_1^{\left(0\right)}\right)}^{\kappa }\left[k\right]}}\right)\hfill \\ \hfill & +L_1^{\left(0\right)}\left(u_1\left[k\right]-u_1^{\left(0\right)}\left[k\right]\right)+J_1^{\left(0\right)}\left(v_1\left[k\right]-v_1^{\left(0\right)}\left[k\right]\right)\hfill \\ \hfill & =t_1\left[k\right],\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill H_2^{\prime }\left[k\right]\ge & \left({\displaystyle \frac{A}{{\left(u_2^{\left(0\right)}\right)}^{\alpha }\left[k\right]}}+{\displaystyle \frac{B}{{\left(u_2^{\left(0\right)}\right)}^{\frac{\alpha }{2}}\left[k\right]{\left(v_1^{\left(0\right)}\right)}^{\frac{\kappa }{2}}\left[k\right]}}+{\displaystyle \frac{C}{{\left(v_1^{\left(0\right)}\right)}^{\kappa }\left[k\right]}}\right)\hfill \\ \hfill & +L_2^{\left(0\right)}\left(u_2\left[k\right]-u_2^{\left(0\right)}\left[k\right]\right)+J_2^{\left(0\right)}\left(v_1\left[k\right]-v_1^{\left(0\right)}\left[k\right]\right)\hfill \\ \hfill & =t_2\left[k\right],\hfill \end{array}$$

(40)

where $A_0\left[k\right]={log}_2\left(1+{\displaystyle \frac{p_1\left[k\right]}{p_2\left[k\right]+\frac{{\xi }^2}{H_1^{\prime \left(0\right)}\left[k\right]}}}\right)$, $B_0\left[k\right]={\displaystyle \frac{p_1\left[k\right]H_1^{\prime \left(0\right)}\left[k\right]}{{(p_2\left[k\right]H_1^{\prime \left(0\right)}\left[k\right]+{\xi }^2)}^2}}\left({\displaystyle \frac{-\alpha A}{{\left(u_1^{\left(0\right)}\right)}^{\alpha +1}\left[k\right]}}+{\displaystyle \frac{-\frac{\alpha }{2}B}{{\left(u_1^{\left(0\right)}\right)}^{\frac{\alpha }{2}+1}\left[k\right]{\left(v_1^{\left(0\right)}\right)}^{\frac{\kappa }{2}}\left[k\right]}}\right)$, $C_0\left[k\right]={\displaystyle \frac{p_1\left[k\right]H_1^{\prime \left(0\right)}\left[k\right]}{{(p_2\left[k\right]H_1^{\prime \left(0\right)}\left[k\right]+{\xi }^2)}^2}}\left({\displaystyle \frac{-\kappa C}{{\left(v_1^{\left(0\right)}\right)}^{\kappa +1}\left[k\right]}}+{\displaystyle \frac{-\frac{\kappa }{2}B}{{\left(u_1^{\left(0\right)}\right)}^{\frac{\alpha }{2}}\left[k\right]{\left(v_1^{\left(0\right)}\right)}^{\frac{\kappa }{2}+1}\left[k\right]}}\right)$, $A_1\left[k\right]={log}_2\left(1+{\displaystyle \frac{p_2\left[k\right]H_2^{\prime \left(0\right)}\left[k\right]}{{\xi }^2}}\right)$, $B_1\left[k\right]={\displaystyle \frac{p_2\left[k\right]}{{\xi }^2}}\left({\displaystyle \frac{-\alpha D}{{\left(u_2^{\left(0\right)}\right)}^{\alpha +1}\left[k\right]}}+{\displaystyle \frac{-\frac{\alpha }{2}E}{{\left(u_2^{\left(0\right)}\right)}^{\frac{\alpha }{2}+1}\left[k\right]{\left(v_1^{\left(0\right)}\right)}^{\frac{\kappa }{2}}\left[k\right]}}\right)$, $C_1\left[k\right]={\displaystyle \frac{p_2\left[k\right]}{{\xi }^2}}\left({\displaystyle \frac{-\kappa F}{{\left(v_1^{\left(0\right)}\right)}^{\kappa +1}\left[k\right]}}+{\displaystyle \frac{-\frac{\kappa }{2}E}{{\left(u_2^{\left(0\right)}\right)}^{\frac{\alpha }{2}}\left[k\right]{\left(v_1^{\left(0\right)}\right)}^{\frac{\kappa }{2}+1}\left[k\right]}}\right)$, $L_1^{\left(0\right)}=({\displaystyle \frac{-\alpha A}{{\left(u_1^{\left(0\right)}\right)}^{\alpha +1}\left[k\right]}}+{\displaystyle \frac{-\frac{\alpha }{2}B}{{\left(u_1^{\left(0\right)}\right)}^{\frac{\alpha }{2}+1}\left[k\right]{\left(v_1^{\left(0\right)}\right)}^{\frac{\kappa }{2}}\left[k\right]}}$, $J_1^{\left(0\right)}={\displaystyle \frac{-\kappa C}{{\left(v_1^{\left(0\right)}\right)}^{\kappa +1}\left[k\right]}}+{\displaystyle \frac{-\frac{\kappa }{2}B}{{\left(u_1^{\left(0\right)}\right)}^{\frac{\alpha }{2}}\left[k\right]{\left(v_1^{\left(0\right)}\right)}^{\frac{\kappa }{2}+1}\left[k\right]}}$, $L_2^{\left(0\right)}={\displaystyle \frac{-\alpha D}{{\left(u_2^{\left(0\right)}\right)}^{\alpha +1}\left[k\right]}}+{\displaystyle \frac{-\frac{\alpha }{2}E}{{\left(u_2^{\left(0\right)}\right)}^{\frac{\alpha }{2}+1}\left[k\right]{\left(v_1^{\left(0\right)}\right)}^{\frac{\kappa }{2}}\left[k\right]}}$, $J_2^{\left(0\right)}={\displaystyle \frac{-\kappa F}{{\left(v_1^{\left(0\right)}\right)}^{\kappa +1}\left[k\right]}}+{\displaystyle \frac{-\frac{\kappa }{2}E}{{\left(u_2^{\left(0\right)}\right)}^{\frac{\alpha }{2}}\left[k\right]{\left(v_1^{\left(0\right)}\right)}^{\frac{\kappa }{2}+1}\left[k\right]}}$. To simplify the equation, symbols are used in place of complex terms.

Finally, we can conclude that the optimization problem $\mathrm{P}\left(2\right)$ of UAV trajectory can be rewritten as

$$\begin{array}{cc}\hfill \mathrm{P}\left(3\right):\underset{Q,u1,u2,v1}{max}& {\displaystyle \frac{1}{K}}\sum _{k=1}^K\left(R_1^{″}\left[k\right]+R_2^{″}\left[k\right]\right)\hfill \\ \hfill s.t.& Z_{UAV}^2+{∥q\left[k\right]-L_{G1}∥}^2+{\left(u_1^{\left(0\right)}\right)}^2\left[k\right]\hfill \\ \hfill & -2\left(u_1^{\left(0\right)}\right)\left[k\right]u_1\left[k\right]\le 0,\forall k,\hfill \\ \hfill & Z_{UAV}^2+{∥q\left[k\right]-L_{G2}∥}^2+{\left(u_2^{\left(0\right)}\right)}^2\left[k\right]\hfill \\ \hfill & -2\left(u_2^{\left(0\right)}\right)\left[k\right]u_2\left[k\right]\le 0,\forall k,\hfill \\ \hfill & {(Z_{UAV}-Z_{RIS})}^2+{∥q\left[k\right]-L_R∥}^2+{\left(v_1^{\left(0\right)}\right)}^2\left[k\right]\hfill \\ \hfill & -2\left(v_1^{\left(0\right)}\right)\left[k\right]v_1\left[k\right]\le 0,\forall k,\hfill \\ \hfill & {∥q[k+1]-q\left[k\right]∥}^2\le D^2,k\in \{1,2,\dots ,K-1\}\hfill \\ \hfill & {∥q\left[K\right]-q_e∥}^2\le D^2,\hfill \\ \hfill & q\left[1\right]=q_s,\hfill \\ \hfill & t_2\left[k\right]\ge t_1\left[k\right],\hfill \end{array}$$

where $R_1^{″}\left[k\right]={\displaystyle \frac{B_0\left[k\right]}{A_0\left[k\right]ln2}}{u}_1\left[k\right]+{\displaystyle \frac{C_0\left[k\right]}{A_0\left[k\right]ln2}}{v}_1\left[k\right]$, $R_2^{″}\left[k\right]={\displaystyle \frac{B_1\left[k\right]}{A_1\left[k\right]ln2}}{u}_2\left[k\right]+{\displaystyle \frac{C_1\left[k\right]}{A_1\left[k\right]ln2}}{v}_1\left[k\right]$. Finally, problem $\mathrm{P}\left(3\right)$ has the property of convexity. Based on this property, mature standard optimization solvers, such as CVX [29], can efficiently solve this problem.

4.3. UAV Power Allocation Optimization

When we fix RIS Phase Shift ${\Phi }_{1,2}$ and UAV flight trajectory Q. In order to facilitate the distinction, the following uses $R_a\left[k\right]$ instead of $R_1\left[k\right]$, $R_b\left[k\right]$ instead of $R_2\left[k\right]$. We can rewrite problem $\mathrm{P}\left(1\right)$ as

$$\begin{array}{cc}\hfill \mathrm{P}\left(4\right):& \underset{P_{1,2}}{max}{\displaystyle \frac{1}{K}}\sum _{k=1}^K(R_a\left[k\right]+R_b\left[k\right])\hfill \\ \hfill s.t.& p_2\left[k\right]\le p_1\left[k\right],k\in \{1,2,\dots ,K\},\hfill \\ \hfill & p_2\left[k\right]+p_1\left[k\right]\le P_{max},k\in \{1,2,\dots ,K\},\hfill \\ \hfill & p_2\left[k\right]\ge 0,k\in \{1,2,\dots ,K\},\hfill \end{array}$$

The consequence of adding two functions with convexity is still a convex-type function [30]. The non-convex component of problem $\mathrm{P}\left(4\right)$ is $R_a\left[k\right]$, which primarily transforms $R_a\left[k\right]$ into a convex function. Based on the properties of logarithms, the division of logarithms with the same base can be rewritten as the difference of two logarithms. Convert $R_a\left[k\right]$ into

$$\begin{array}{cc}\hfill R_a\left[k\right]=& {log}_2\left(1+{\displaystyle \frac{p_1\left[k\right]H_1\left[k\right]}{p_2\left[k\right]H_1\left[k\right]+{\xi }^2}}\right)\hfill \\ \hfill =& {log}_2\left({\displaystyle \frac{p_1\left[k\right]H_1\left[k\right]+p_2\left[k\right]H_1\left[k\right]+{\xi }^2}{p_2\left[k\right]H_1\left[k\right]+{\xi }^2}}\right)\hfill \\ \hfill =& {log}_2\left((p_1\left[k\right]+p_2\left[k\right])+{\displaystyle \frac{{\xi }^2}{H_1\left[k\right]}}\right)\hfill \\ \hfill & -{log}_2\left(p_2\left[k\right]+{\displaystyle \frac{{\xi }^2}{H_1\left[k\right]}}\right).\hfill \end{array}$$

(41)

The latter term of the above equation is expanded by the first-order Taylor expansion at the fixed point ${\mathit{p}}_{\mathbf{2}}^{\left(\mathbf{0}\right)}\triangleq \left\{p_2^{\left(0\right)}\left[k\right]\right\},k\in \{1,2,\dots ,K\}$, while the former term remains unchanged. We can get

$$\begin{array}{cc}\hfill R_a\left[k\right]\ge R_a^{\prime }\left[k\right]=& {log}_2\left((p_1\left[k\right]+p_2\left[k\right])+{\displaystyle \frac{{\xi }^2}{H_1\left[k\right]}}\right)\hfill \\ \hfill & +R_a^{″}\left[k\right],\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill R_a^{″}\left[k\right]=& -{log}_2\left(p_2^{\left(0\right)}\left[k\right]+{\displaystyle \frac{{\xi }^2}{H_1\left[k\right]}}\right)\hfill \\ \hfill & -{\displaystyle \frac{1}{ln2(p_2^{\left(0\right)}\left[k\right]+\frac{{\xi }^2}{H_1\left[k\right]})}}\left(p_2\left[k\right]-p_2^{\left(0\right)}\left[k\right]\right),\hfill \end{array}$$

(43)

we can solve $R_b\left[k\right]$ directly. We can rewrite problem $\mathrm{P}\left(4\right)$ as

$$\begin{array}{cc}\hfill \mathrm{P}\left(5\right):& \underset{P_{1,2}}{max}{\displaystyle \frac{1}{K}}\sum _{k=1}^K(R_a^{\prime }\left[k\right]+R_b\left[k\right])\hfill \\ \hfill s.t.& p_2\left[k\right]\le p_1\left[k\right],k\in \{1,2,\dots ,K\},\hfill \\ \hfill & p_2\left[k\right]+p_1\left[k\right]\le P_{max},k\in \{1,2,\dots ,K\},\hfill \\ \hfill & p_2\left[k\right]\ge 0,k\in \{1,2,\dots ,K\}.\hfill \end{array}$$

Since problem $\mathrm{P}\left(5\right)$ features a linear objective function coupled with linear inequality constraints, its convexity can be easily proven. Thus, the transformed problem $\mathrm{P}\left(5\right)$ can be solved by using the CVX [29] tool.

5. Overall Algorithm

We summarize the algorithm presented in the previous section and perform alternating iterations. In this algorithm, the results from the previous iteration are used as the starting estimate for the succeeding iteration, and the pseudo-code for the alternating iteration of the three sub-problems is provided in Algorithm 1. In the forthcoming convergence analysis, we will demonstrate that the average achievable rate obtained in each iteration of Algorithm 1 for solving problem $\mathrm{P}\left(1\right)$ will not decrease compared to the previous iteration, meaning it will not decrease as the number of iterations increases. The algorithm flow chart is shown in Appendix A.

Algorithm 1 Solve problem $\mathrm{P}\left(1\right)$ by alternating iterative algorithm.

1: Initialize: set the number of iterations $i=0$, give the initial value $P_1^{\left[0\right]}$,$P_2^{\left[0\right]}$,$Q^{\left[0\right]}$,${\Phi }_1^{\left[0\right]}$,${\Phi }_2^{\left[0\right]}$,$u_1^{\left[0\right]}$,$u_2^{\left[0\right]}$,$v_1^{\left[0\right]}$, and then solve the initial ${\overline{R}}^{\left[0\right]}$ by (17) through the above initial value. 2: while ture 3: Set the number of iterations $i=i+1$; 4: After fixation of $P_1^{[i-1]}$, $P_2^{[i-1]}$,${\Phi }_1^{[i-1]}$ and ${\Phi }_2^{[i-1]}$, update $(Q^{\left[i\right]},u_1^{\left[i\right]},u_2^{\left[i\right]},v_1^{\left[i\right]})$ by addressing problem $\mathrm{P}\left(3\right)$; 5: Update ${\Phi }_1^{\left[i\right]}$ and ${\Phi }_2^{\left[i\right]}$ by addressing Formulas (20) and (22); 6: Using the $Q^{\left[i\right]}$,${\Phi }_1^{\left[i\right]}$ and ${\Phi }_2^{\left[i\right]}$ of the previous iteration, update $P_1^{\left[i\right]}$ and $P_2^{\left[i\right]}$ by addressing problem $\mathrm{P}\left(5\right)$; 7: Combined with $(P_1^{\left[i\right]},P_2^{\left[i\right]},{\Phi }_1^{\left[i\right]},{\Phi }_2^{\left[i\right]},Q^{\left[i\right]},u_1^{\left[i\right]},u_2^{\left[i\right]},v_1^{\left[i\right]})$, calculate ${\overline{R}}^{\left[i\right]}$ according to (17); 8: if${\displaystyle \frac{{\overline{R}}^{\left[i\right]}-{\overline{R}}^{[i-1]}}{{\overline{R}}^{\left[i\right]}}}<ϵ$  then 9:    break; 10: end if 11: return the optimal solutions $P_1^{\left[i\right]},P_2^{\left[i\right]},{\Phi }_1^{\left[i\right]},{\Phi }_2^{\left[i\right]},Q^{\left[i\right]}$.

Convergence and Complexity Analysis

The target value after iteration using Algorithm 1 is always increasing or not decreasing, and then converges back to a bounded value [31]. Assuming that the average achievable rate based on Q, ${\Phi }_{1,2}$ and $P_{1,2}$ is denoted by $f\left(Q^i,{\Phi }_{1,2}^i,P_{1,2}^i\right)$, since the optimized phase shift does not change the transmit power and trajectory, $f\left(Q^i,{\Phi }_{1,2}^i,P_{1,2}^i\right)\le f\left(Q^i,{\Phi }_{1,2}^{i+1},P_{1,2}^i\right)$ holds when the phase is optimal. Since $Q^{i+1}$ is the optimal solution obtained by using ${\Phi }_{1,2}^{i+1}$ and $P_{1,2}^i$ to solve the problem $\mathrm{P}\left(3\right)$, $f\left(Q^i,{\Phi }_{1,2}^{i+1},P_{1,2}^i\right)\le f\left(Q^{i+1},{\Phi }_{1,2}^{i+1},P_{1,2}^i\right)$ holds. Since $P_{1,2}^{i+1}$ is the optimal solution obtained by solving the problem $\mathrm{P}\left(5\right)$ with the help of $Q^{i+1}$ and ${\Phi }_{1,2}^{i+1}$, it can be determined that the inequality $f\left(Q^{i+1},{\Phi }_{1,2}^{i+1},P_{1,2}^i\right)\le f\left(Q^{i+1},{\Phi }_{1,2}^{i+1},P_{1,2}^{i+1}\right)$ holds.

Algorithm 1 is monotonic, meaning that its output does not decrease in each iteration. In other words, the output either remains unchanged or increases in each iteration, ensuring that the algorithm does not diverge in an unfavorable direction. Specifically, monotonicity guarantees that the algorithm consistently progresses in a predictable direction without exhibiting erratic or unstable fluctuations. The monotonicity of the algorithm is directly linked to its convergence. By analyzing the update rules and constraints, we observe that after sufficient iterations, the output of Algorithm 1 will approach a stable value, ultimately converging to a finite value. Therefore, Algorithm 1 is convergent.

The complexity of the proposed algorithm is described as follows. According to [32], the complexity of RIS phase optimization is $\mathcal{O}\left(iM\right)$, the complexity of UAV trajectory optimization is $\mathcal{O}\left(i{J}^{3.5}\right)$, and the complexity of UAV power allocation optimization is $\mathcal{O}\left(i{Y}^{3.5}\right)$. M denotes the number of array elements, $MJ$ represents the total flight cycle, and Y indicates the quantity of users, while i is the number of iterations. Therefore, the algorithm has an overall complexity of $\mathcal{O}\left(i(M+J^{3.5}+Y^{3.5})\right)$.

6. Numerical Results

The following are the settings for the simulation parameters. The ground users is located at $L_{G1}={[800,70]}^T$ and $L_{G2}={[700,70]}^T$, respectively. And the RIS is positioned at $L_R={[500,0]}^T$, with the RIS standing at a height of $Z_{RIS}=40$ m. For the UAV, its flight altitude remains constant at $Z_{UAV}=80$ m, starting from the position $q_s={[0,20]}^T$ and concluding its journey at $q_e={[1000,20]}^T$. The parameter settings are as follows: In the current configuration, both the ground users and the UAV each have one antenna. The Rician factor is $\sigma =3$ dB. The remaining parameter settings are $V_m=30$ m/s, $c_0=-20$ dB, $J=K=300$, $\delta =1$ s, $\alpha =3.5$, $\kappa =2$, $\tau =2.8$, $d={\displaystyle \frac{\lambda }{2}}$, $P_{max}=100$ mw, ${\xi }^2=-80$ dBm. For Algorithm 1, the threshold value of $ϵ$ is established at ${10}^{-4}$. We set the maximum number of iterations to 20.

We demonstrate the simulation findings acquired through implementing our devised algorithm (abbreviated as OT&OP&OW). For the purpose of comparative analysis, we introduce three additional benchmark algorithms. The trajectory optimization design that also optimizes phase shifts (abbreviated as OT&OP), aiming to find the optimal trajectory while considering phase-shift optimization. The initial trajectory design that optimizes phase shifts (abbreviated as T&OP), aiming to enhance signal performance through phase adjustment. The power optimization design with optimized phase shifts (abbreviated as OW&OP), which focuses on optimizing power allocation while adjusting phase shifts. The initial trajectory design based on random phase (abbreviated as T&RP), where the phase values are randomly assigned. If the duration is sufficiently long, the UAV follows the initially planned trajectory. However, if the available time is limited, the UAV will deviate from the set trajectory and proceed directly to the endpoint at maximum speed.

Initial feasible solutions for the OT&OP&OW, OT&OP, and OW&OP algorithms are generated using the T&RP algorithm. These initial solutions act as a starting point for further optimization. During the flight cycle, the initial power values for these algorithms are randomly generated, with the condition that the power of $P_1$ exceeds that of $P_2$.

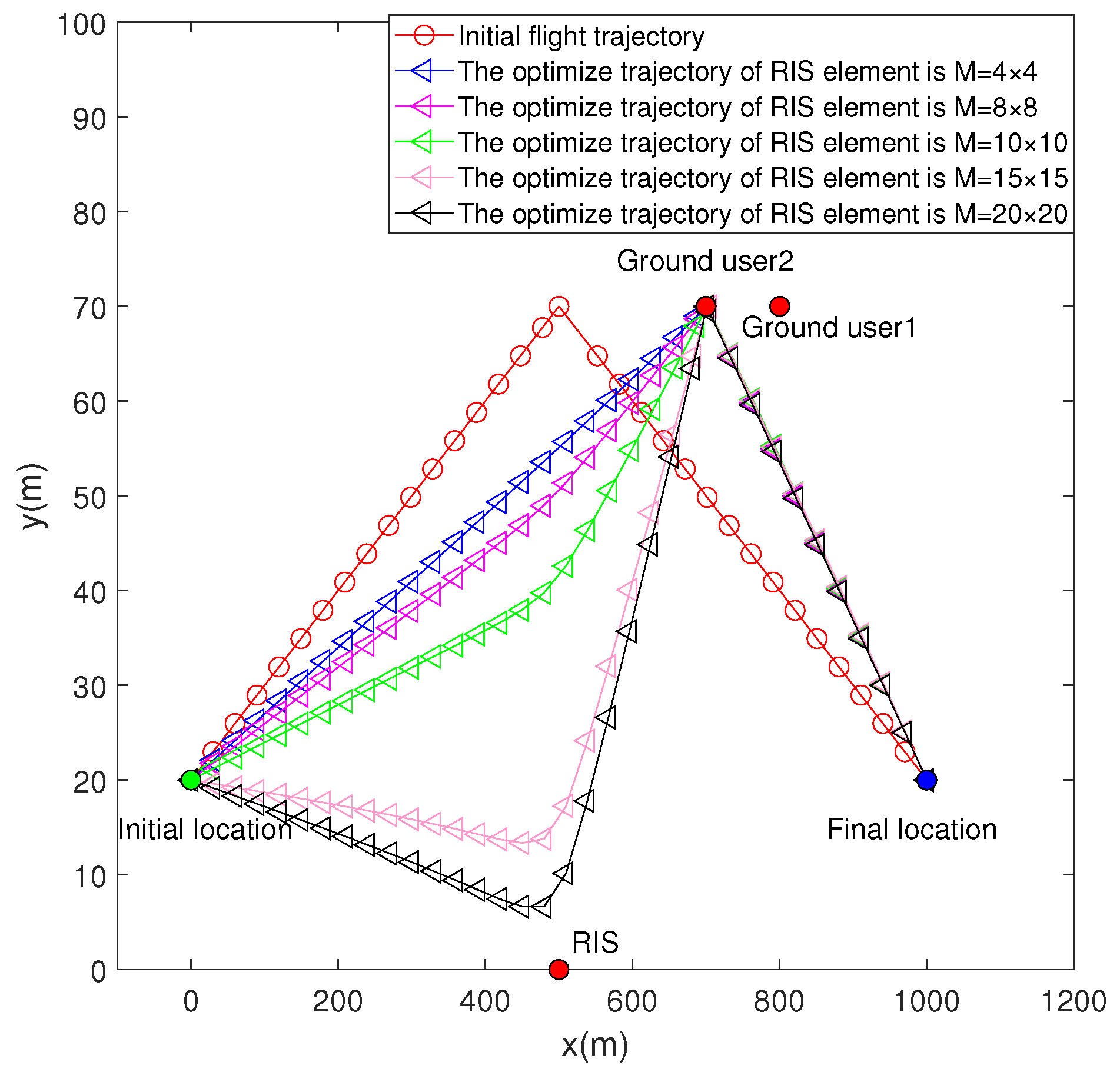
In Figure 2, we look at the UAV’s initial trajectory and optimized trajectories, with number of array elements M varying. This helps us see how M impacts the UAV’s flight path. The UAV initially chooses to hover over User 2 to achieve the maximum average rate and flies directly to User 2. As the quantity of RIS array elements rises, the UAV’s trajectory bends and gradually shifts towards the RIS position in the middle. When the RIS array elements are sufficient, the UAV will hover between RIS and User 2.

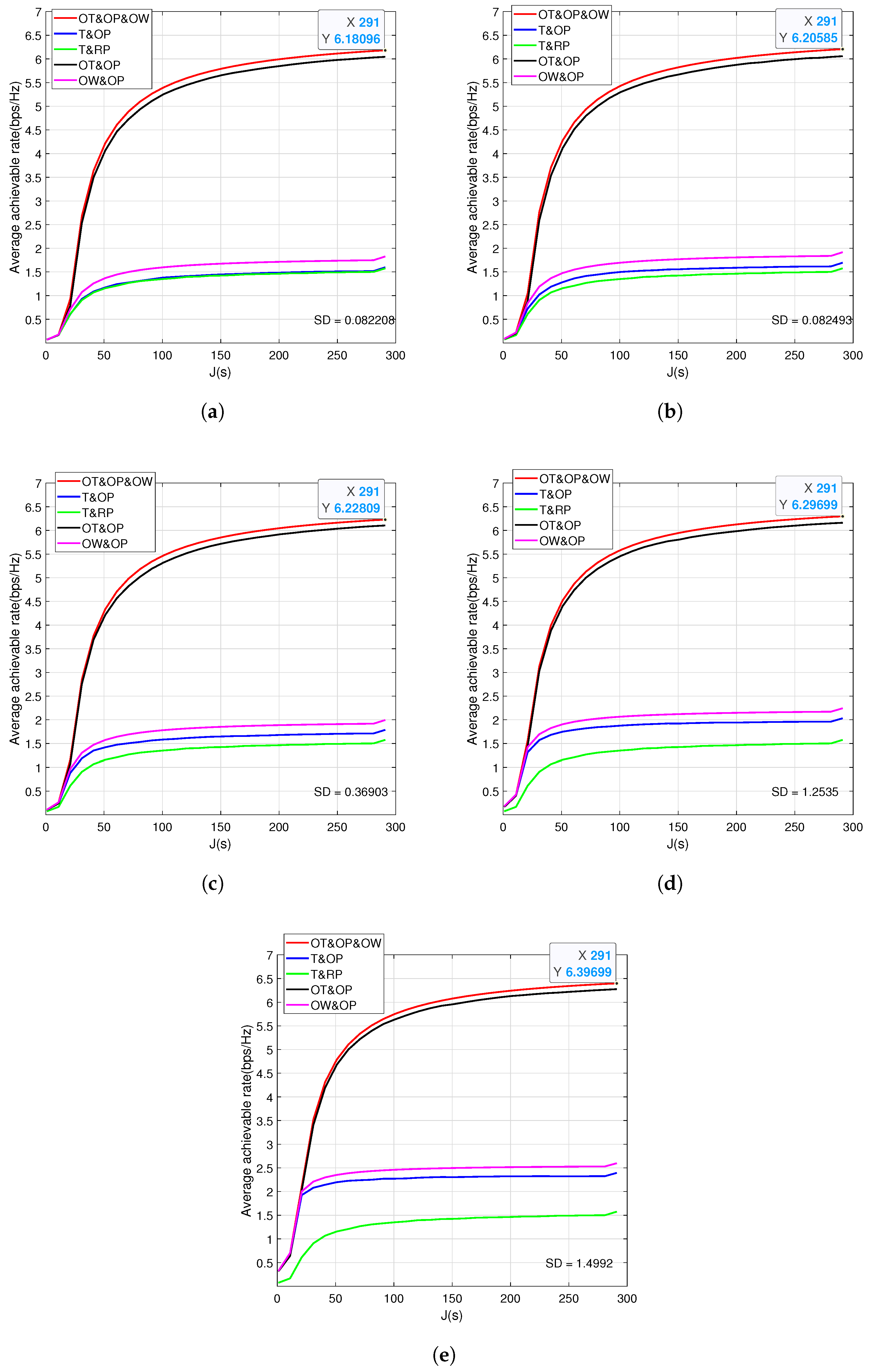
In Figure 3, we illustrate the bearing of different RIS array elements on the average achievable rate under the same maximum transmit power. We use the standard deviation (denoted as SD) as a measure of data dispersion. As RIS array elements increases, the degree of dispersion also increases. As the number of RIS array elements increases, the overall optimization effect shows minimal improvement. However, the blue and pink curves reveal a significant increase in phase optimization as the number of RIS elements grows. Combined with Figure 2, since the UAV trajectory is not close to the RIS, the impact of adding more RIS array elements on the overall performance is minimal. However, it can be concluded that even with a small number of RIS array elements, our scheme effectively improves the system’s average achievable rate, in contrast to relying on a large number of elements.

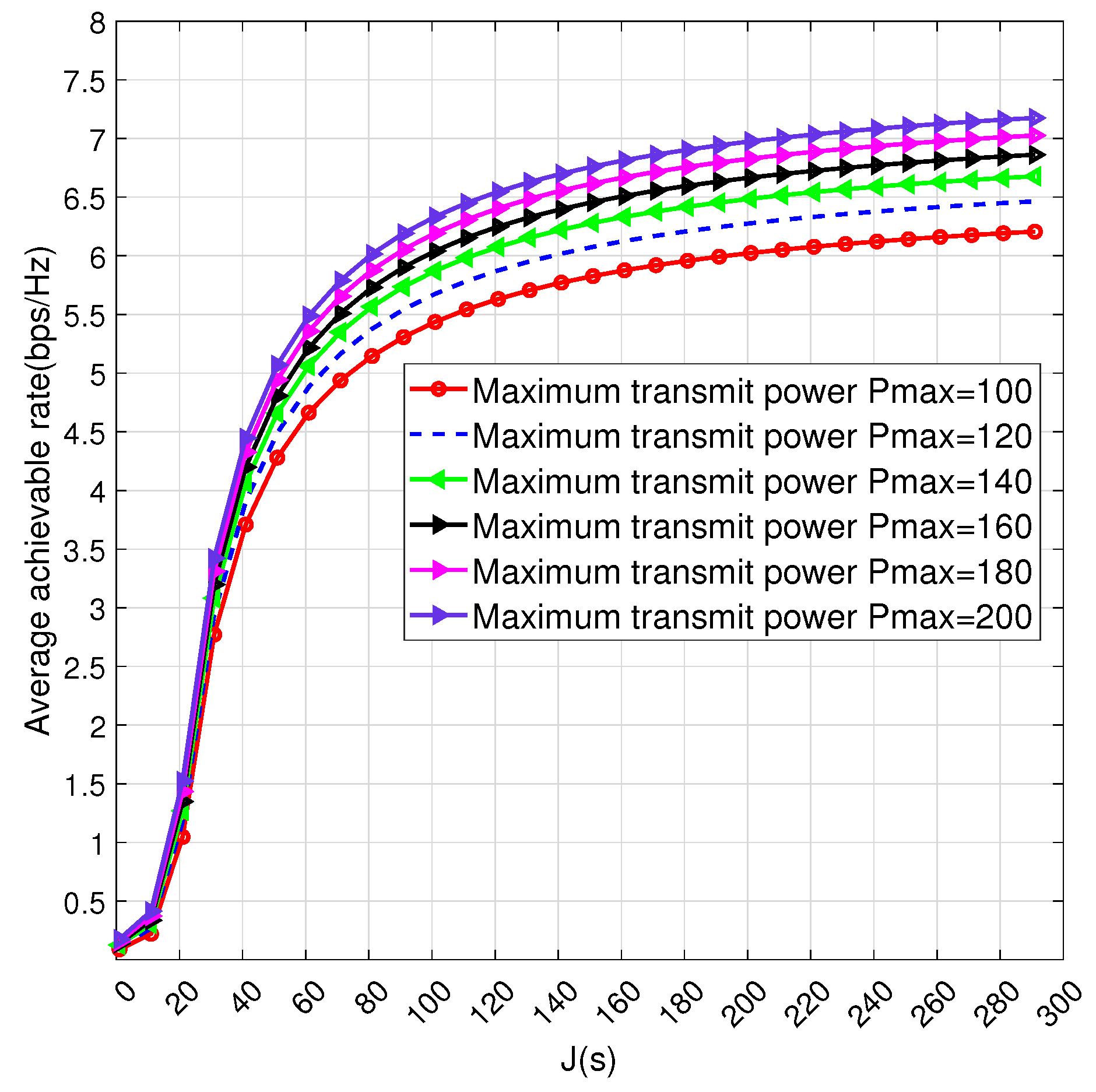
In Figure 4, we give the influence of different peak transmission power $P_{max}$ on the average achievable rate under the same RIS array elements M. It can be inferred that as $P_{max}$ increases, the mean achievable throughput also increases significantly. Since the UAV’s flight trajectory hovered over User 2, increasing $P_{max}$ had a minimal impact on overall optimization. This suggests that increasing $P_{max}$ yields a better optimization effect compared to increasing the RIS array elements. Considering the RIS layout and installation cost, the choice of increasing $P_{max}$ is a better choice.

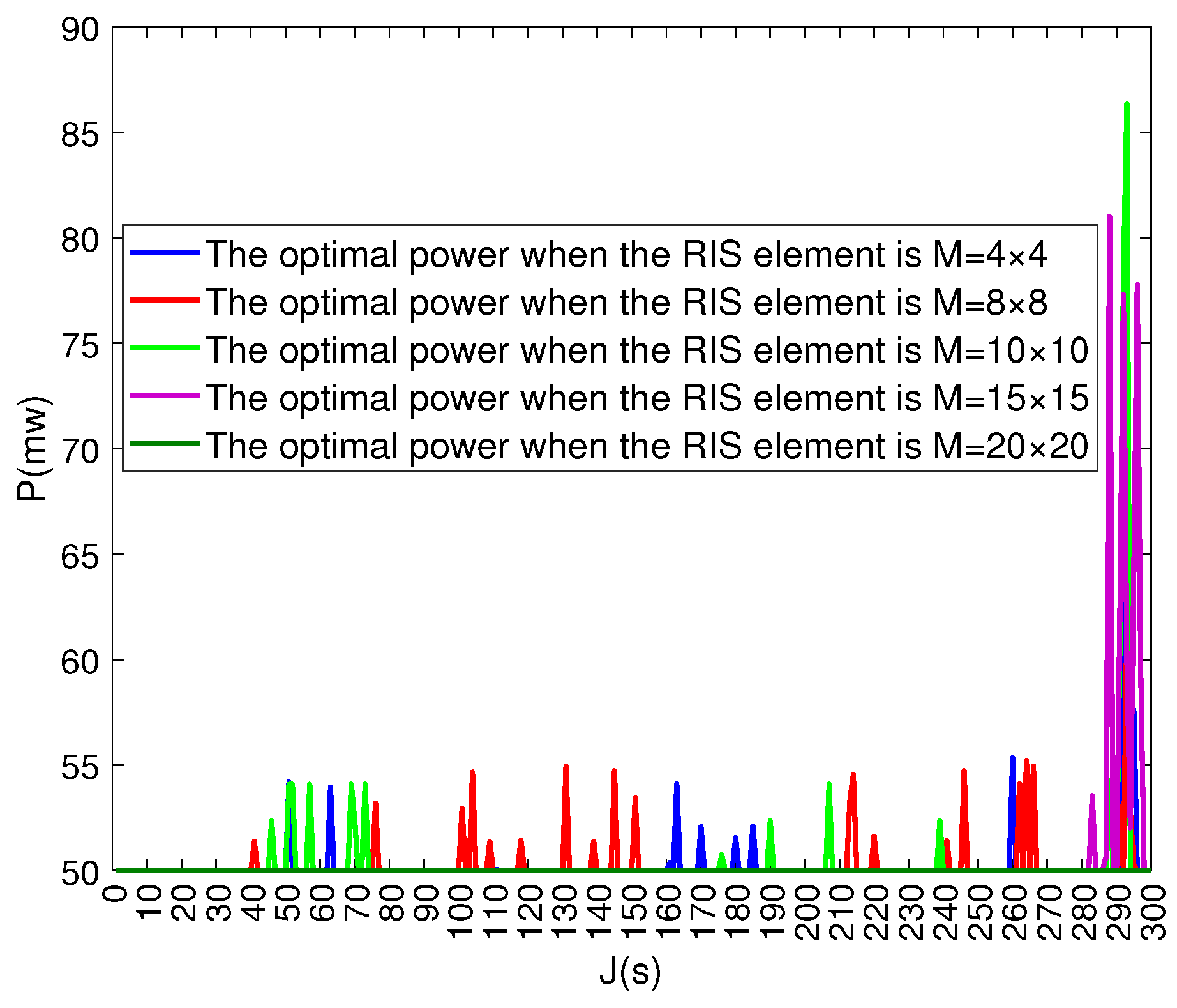
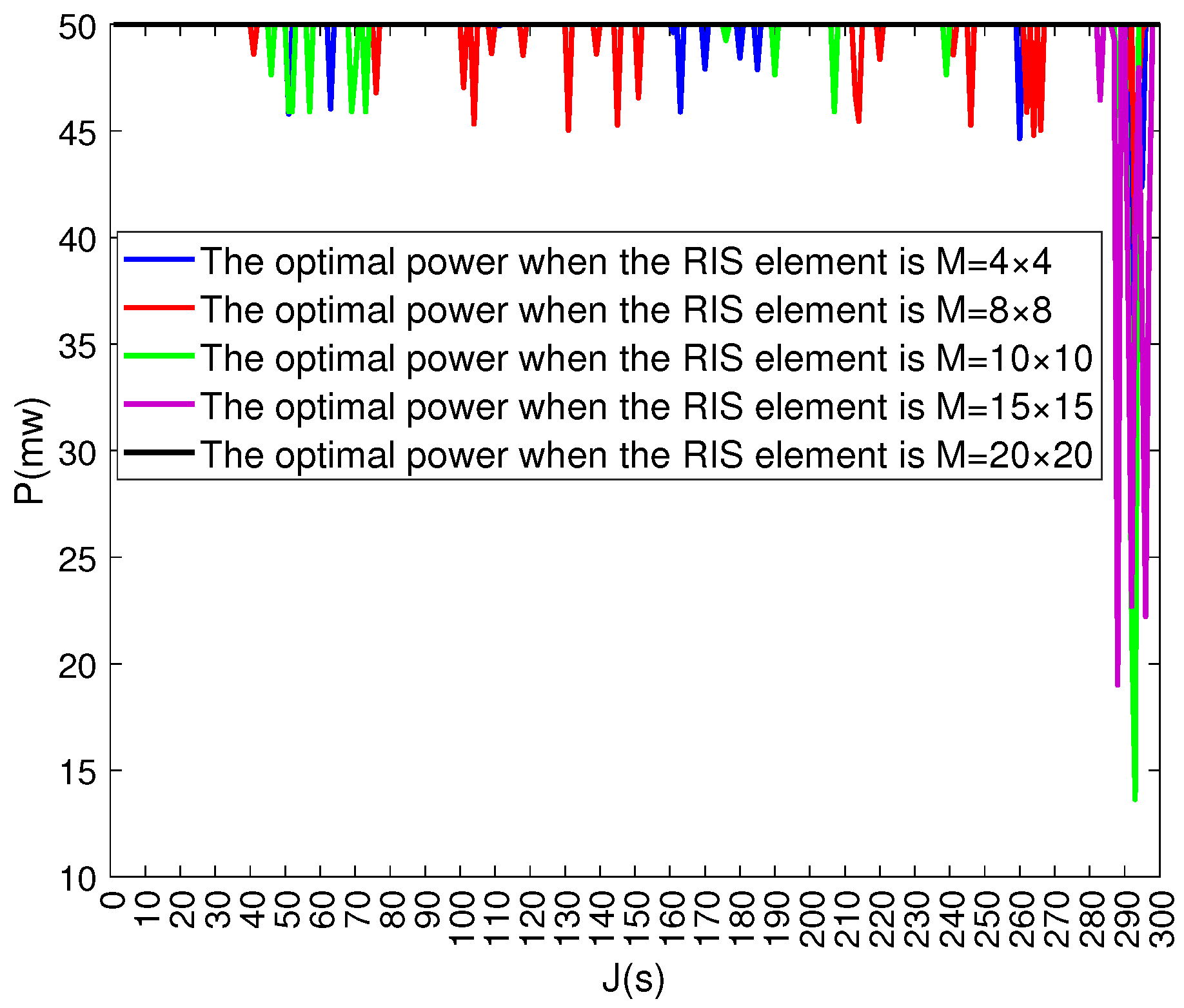
Figure 5 and Figure 6 are in the same $P_{max}$, the influence of different M on the mean achievable throughput. It can be observed that both $P_1$ and $P_2$ fluctuate around 50 mW, while 50 mW remains stable without fluctuation. The power allocated to both components satisfies the constraints. The maximum average achievable rate is obtained based on atransmission power allocation during the flight. As the number of RIS array elements increases, the fluctuation becomes smaller. When the RIS array element is $M=20\times 20$, the power allocated to both users is 50 mw, and the UAV trajectory is closer to the RIS. At certain times, the UAV allocates more power to User 1 and less to User 2 to ensure both users achieve a higher communication rate.

7. Conclusions

This paper investigates the RIS-assisted NOMA-UAV communication system. To maximize the average achievable rate, we break down the optimization into three sub-problems: optimizing the UAV trajectory, configuring the RIS phase shifts, and allocating power among users. The outcomes generated by the simulation indicate the proficiency of the presented optimization algorithm. Reasonable increase of RIS array elements and maximum transmission power can achieve better optimization results. This paper analyzes the NOMA-UAV communication system with RIS assistance. However, during the optimization process, we assume ideal conditions by neglecting interference and noise, which could cause deviations in practical applications. Furthermore, the computational complexity of the system model may increase in large-scale user or multi-UAV scenarios. Future research should explore more realistic channel models or focus on reducing algorithmic complexity to improve practical applicability.