Abstract
In the deep integration process between digital infrastructure and new economic forms, structural imbalance between the evolution rate of cloud storage technology and the growth rate of data-sharing demands has caused systemic security vulnerabilities such as blurred data sovereignty boundaries and nonlinear surges in privacy leakage risks. Existing academic research indicates current proxy re-encryption schemes remain insufficient for cloud access control scenarios characterized by diversified user requirements and personalized permission management, thus failing to fulfill the security needs of emerging computing paradigms. To resolve these issues, a revocable attribute-based proxy re-encryption scheme supporting policy-hiding is proposed. Data owners encrypt data and upload it to the blockchain while concealing attribute values within attribute-based encryption access policies, effectively preventing sensitive information leaks and achieving fine-grained secure data sharing. Simultaneously, proxy re-encryption technology enables verifiable outsourcing of complex computations. Furthermore, the SM3 (SM3 Cryptographic Hash Algorithm) hash function is embedded in user private key generation, and key updates are executed using fresh random factors to revoke malicious users. Ultimately, the scheme proves indistinguishability under chosen-plaintext attacks for specific access structures in the standard model. Experimental simulations confirm that compared with existing schemes, this solution delivers higher execution efficiency in both encryption/decryption and revocation phases.
1. Introduction
As information technology becomes deeply integrated into all sectors of society, digital platforms and network connectivity have evolved into unremovable components of modern life. Cloud computing has extended its reach to critical domains such as healthcare, education and training, and transportation, delivering substantial efficiency gains across society.The swift advancement of cloud computing technology has fueled industrial demand for enhanced computational capabilities, streamlined workflows, and strict cost governance. This trend drives massive data migration to cloud infrastructures. However, this shift creates security vulnerabilities stemming from data sovereignty transfer. When data custody moves from enclosed on-premises environments to third-party platforms, security threat models undergo radical transformation. In response, academia and industry focus on pioneering cryptographic access control mechanisms. Critical approaches include the following: Granular authorization via functional encryption for precise data-access policies. Dynamic privilege management through proxy re-encryption enabling real-time permission updates without data decryption. Distributed trust frameworks using access control encryption ensuring multi-stakeholder consensus in cross-domain verification.
Proxy re-encryption (PRE) [1] overcomes limitations of traditional functional encryption in dynamic authority management by securely delegating ciphertext access rights through semi-trusted proxies. This process maintains zero-knowledge keys and end-to-end confidentiality while supporting fine-grained temporary authorization and cross-domain collaboration. Although evolving multi-hop and bidirectional features enhance flexibility, their associated risks render unidirectional single-hop schemes preferable [2]. Traditional “one-to-one” modes [3,4] are superseded by attribute-based PRE (AB-PRE), significantly optimizing one-to-many authorization efficiency and dynamic privacy protection in cloud environments. Conditional proxy re-encryption (CPRE) addresses heterogeneous scenarios by implementing predicate-bound, fine-grained transfer authorization through conditional triggers. Responding to deficiencies in CPA security models, the Honest Re-encryption Attack (HRA) security model was proposed, driving advances in attribute-based HRA schemes, threshold proxy mechanisms, and key privacy protection solutions. Current challenges focus on integrating attribute-based/identity-based mechanisms for dynamic access control, which requires blockchain integration to support real-time policy updates with on-chain verification while systematically mitigating sensitive information leakage risks in permission validation via attribute obfuscation, differential privacy, and secure multi-party computation.
Proxy re-encryption (PRE) technology in cloud environments demonstrates significant advantages in fine-grained permission management by combining identity-based and attribute-based encryption. However, when confronting dynamic access control requirements—such as real-time responses to user behavior characteristics, authentication states, and environmental variables—existing blockchain-based PRE solutions exhibit deficiencies in dynamic policy updating and on-chain verification. This necessitates mechanisms supporting real-time adjustment of access policies. Consequently, privacy protection mechanisms must be integrated during access control processes. These should systematically mitigate sensitive information leakage risks during permission verification through cryptographic techniques, including differential privacy and secure multi-party computation.
This paper addresses uncontrolled proxy authority boundaries in cross-domain ciphertext sharing scenarios by constructing an attribute-conditional functional proxy re-encryption scheme based on broadcast conditional proxy re-encryption. Targeting inherent limitations of traditional identity-based access models in fine-grained permission allocation and multi-dimensional attribute adaptation, we propose an attribute-based access control functional proxy re-encryption scheme. This framework allows access policies to be defined according to multiple user attributes, providing flexible authorization that triggers decryption only when user attributes fully satisfy access policies. A formal security verification framework supports the scheme’s security argumentation. Theoretical derivations and experimental results demonstrate precise constraints on proxy key conversion privileges and receiver decryption permissions.
To achieve secure data sharing, this paper proposes an Attribute-Based Revocable Access Control Function Proxy Re-Encryption scheme. The contributions are as follows:
- (1)
- The scheme uses attribute-based encryption to achieve fine-grained data access control. Each user attribute consists of an attribute name index and attribute value. By hiding attribute values and not transmitting them with ciphertext, access policy hiding is achieved to protect sensitive user information.
- (2)
- The scheme combines attribute-based encryption and proxy re-encryption, achieving fine-grained one-to-many encryption and secure ciphertext conversion. This resolves the limitations of immutable access policies and low decryption efficiency in attribute-based encryption. Verification algorithms are incorporated during the re-encryption phase to ensure ciphertext verifiability.
- (3)
- When revoking a user in this scheme, a private key is generated for the user using the SM3 hash function, and a random factor corresponding to the new version number is generated. The revocation of malicious user access permissions is completed when updating the keys of unreleased users.
- (4)
- The scheme resists collusion attacks from semi-trusted third parties and users. Security-wise, based on the decisional q-parallel Bilinear Diffie-Hellman hardness assumption, the scheme is proven to satisfy indistinguishability under chosen-plaintext attacks for specific access structures in the standard model. Performance analysis shows higher efficiency in encryption/decryption, revocation, and file download phases.
2. Related Work
Matt Blaze et al. first proposed the concept of Proxy Re-Encryption (PRE) in 1998 [1]. In the PRE cryptosystem, a semi-trusted proxy can convert ciphertext encrypted by the message owner into ciphertext decryptable by users without leaking information. However, it still has limitations in secure information sharing, failing to consider sensitive information protection and fine-grained access control of data.
To meet the requirements of multi-user scenarios, identity-based broadcast proxy re-encryption (IB-BPRE) is proposed. A data owner can generate a re-encryption key for an authorized user set, and the proxy uses this key to transform the data owner’s ciphertext into a re-encrypted ciphertext under the identity set of authorized users. Only users belonging to the authorized set can successfully decrypt this ciphertext to obtain the data; even if other users collude, they cannot access the content within the ciphertext [5]. The availability of PRE relies on the proxy honestly performing re-encryption operations. However, in practice, the proxy may generate incorrect re-encrypted ciphertexts to save local storage space and computational resources. To address the issue of untrusted proxies returning erroneous ciphertexts, Ohata et al. [6] introduced the concept of re-encryption verifiability, proposing a verifiable proxy re-encryption scheme to achieve correctness verification of re-encrypted ciphertexts. However, the verification phase in this scheme requires joint participation of the data owner and authorized users, leading to wastage of computational and communication resources. Additionally, it fails to resolve situations where the proxy is maliciously held accountable despite honestly converting ciphertexts. To tackle this problem, Ge et al. [7] introduced the concept of fairness based on verifiability, proposing a verifiable and fair attribute-based PRE scheme. This scheme utilizes the commitment concept, generating additional commitments for data and random numbers in the initial ciphertext through message-locked encryption technology to ensure re-encryption verifiability and fairness. Building on the ideas from [7], Sun et al. [8] and Jing et al. [9] proposed verifiable and fair schemes. However, in the correctness verification of re-encrypted ciphertexts in schemes [7,8,9], transmitting the original ciphertext and re-encryption key incurs additional communication overhead and risks leakage of the re-encryption key; moreover, if the proxy provides incorrect original ciphertexts or re-encryption keys, the scheme fails to satisfy verifiability. Furthermore, generating additional commitments during ciphertext generation increases computational costs.
Although the aforementioned schemes satisfy multi-user scenarios and verify re-encrypted ciphertexts, they also introduce additional computational overhead. In Attribute-based Proxy Re-Encryption (ABPRE) [10], a semi-trusted proxy server can convert ciphertext to generate new ciphertext, thereby solving problems such as immutable access policies, single data-sharing modes, and low efficiency in attribute-based encryption. Li et al. [11] proposed an ABPRE blockchain data-sharing scheme supporting policy hiding, achieving the distributed storage of ciphertext on the blockchain. Cui et al. [12] proposed an ABPRE scheme with partially hidden policies in 2018, implementing partial policy hiding in prime-order groups. In 2019, Feng et al. [13] proposed a CP-ABPRE scheme supporting outsourced computation in the cloud, which not only resists collusion attacks but also reduces user computational overhead through outsourced data computation. Zhai et al. [14] proposed a blockchain-based ABPRE data-sharing scheme using a dual-chain structure (ciphertext chain and index chain), achieving secure data storage and user decryption authorization. Subsequently, Liu et al. [10] proposed a multi-authority CP-ABE combined with PRE scheme for cloud storage; the proposed multi-authority CP-ABPRE scheme has five characteristics: unidirectionality, controllability, verifiability, non-interactivity, and repeatability. However, while these schemes achieve fine-grained data sharing, they cannot revoke malicious users. Yang et al. [15] proposed a dynamically updatable ABPRE scheme in the cloud in 2022, which revokes malicious users by updating user sets and attributes. Nevertheless, PRE consumes significant resources during ciphertext conversion, and malicious proxies may generate incorrect re-encrypted ciphertext during re-encryption operations, failing to achieve ciphertext verifiability in data sharing. To address this, Ge et al. proposed a Verifiable and Fair VF-ABPRE scheme, which not only achieves ciphertext verifiability but also ensures transaction fairness between users and cloud servers. Subsequently, they further proposed [16,17] an ABPRE-DR scheme with direct revocation mechanism, empowering cloud servers to directly revoke users from the original sharing set, significantly improving revocation efficiency.Furthermore, Yu et al. [18] introduced Chameleon Hash Functions into blockchain to update user attributes, thereby achieving user revocation and fine-grained access control. In Guo et al.’s [19] scheme, Chameleon Hash Functions are leveraged to generate user private keys without the need for key distribution, enabling the revocation of malicious users through updates to the attribute set and keys. Yan et al. [17] employed Chameleon Hash Functions to generate private keys for users; by updating the keys of non-revoked users, they completed the revocation of access permissions for malicious users. Currently, proposed revocable ABPRE schemes exhibit significant advantages but face security risks in practical applications, such as malicious insiders, key leakage, and collusion attacks, and suffer from issues such as sender repudiation and receiver framing. Particularly when revoked users collude, they combine attributes to attempt to satisfy updated access structures. Moreover, if revoked keys inadvertently leak information about non-revoked keys, the revocation becomes invalid.
Simultaneously, revocation mechanisms demonstrate broad applicability and critical importance, serving scenarios such as facial recognition template update protection, dynamic access control in vehicular networks, and malicious user key revocation in cloud computing. Zhang et al. [20] proposed an Identity-Based Broadcast Proxy Re-Encryption (IB-BPRE) scheme for data sharing in Vehicular Ad-hoc Networks (VANETs). Through pseudo-identity dynamic updates, Lagrange interpolation polynomial re-encryption, and constant-overhead decryption mechanisms, it resolved challenges including high encryption burdens for multi-receiver dynamic groups, historical data access difficulties for new members, and vehicle privacy leakage. However, it lacks expressive power for attribute-based complex policies, and its revocation targets entire identities/pseudo-identities rather than specific access permission attributes. Luo et al. [21] addressed key security vulnerabilities and insufficient template integrity in prior schemes by introducing a Chaos-based Index-of-Minimum (C-IoM) hashing scheme with chaotic random seed generation algorithms and sliding window selection mechanisms. Nevertheless, their authorization lacks complex user/environment-based attribute policies, hindering extension to fine-grained permission revocation in data sharing. Dai et al. [22] devised an LWE-based publicly traceable and revocable proxy re-encryption scheme integrating inner-product functional proxy re-encryption with dynamic vector revocation mechanisms. This tackled issues including piracy decryption risks from key abuse in traditional proxy re-encryption and inefficient user permission revocation. Yet it remains constrained by bounded user limitations and requires support for unbounded identity management. Consequently, for fine-grained attribute-specific data sharing in dynamic environments (e.g., cloud computing, IoT) and real-time revocation of user permissions meeting specific attribute conditions, Attribute-Based Revocable Proxy Re-Encryption (AB-RPRE) schemes incorporating Attribute-Based Encryption (ABE) principles emerge as the optimal choice. They deeply integrate user attributes, data access policies, and efficient proxy re-encryption capabilities, enabling flexible fine-grained access control while precisely and efficiently revoking decryption permissions for users with designated attributes. This overcomes traditional schemes’ limitations in policy expression and revocation precision.
In summary, existing schemes exhibit respective strengths in data sharing. While generally supporting unidirectionality, non-interactivity, and controllability, they show deficiencies in malicious user revocation, sensitive information protection, and fine-grained permission management. Within practical large-scale deployments, computational overhead and fine-grained access control limitations constrain their applicability. Against this backdrop, Attribute-Based Revocable Proxy Re-Encryption schemes offer superior solutions for enhanced security revocation and fine-grained access control.
3. Preliminaries
3.1. Elliptic Curve Discrete Logarithm Problem (ECDLP)
Elliptic Curve Cryptography (ECC) is built upon a public-key cryptosystem based on elliptic curves over finite fields. The elliptic curve defined over the finite field is given by the following equation: , where . The group G consists of points on the elliptic curve and the point at infinity O. Let and be points on . The group operations are defined as follows: (1) ; (2) ; (3) ; (4) If such that , then and , where
Definition 1.
(Elliptic Curve Discrete Logarithm Problem (ECDLP)) Let E be an elliptic curve defined over a finite field . Given a base point and its scalar multiple , if there exists a non-trivial integer satisfying , solve for the integer k.
Under the hardness assumption of ECDLP, for any probabilistic polynomial-time algorithm , its success probability in solving for is a negligible function . That is, for all sufficiently large security parameters , holds, where is any polynomial function. This implies that cannot break ECDLP with non-negligible advantage in polynomial time.
3.2. Provable Security
The theory of provable security played a crucial role in cryptography, providing a theoretical foundation for designing and analyzing encryption algorithms and protocols with robust security. This ensured that cryptographic designs were endowed with rigorous security guarantees, susceptibility to attacks was reduced, trust in security was enhanced, and the advancement of cryptographic technology was promoted. The provable security of cryptographic schemes generally involved the following components: First, formal definitions of the security objectives of the scheme were established. Second, adversarial models were constructed based on the attacker’s capabilities. Subsequently, the security of the scheme was formally defined, that is, its resistance against specified adversarial goals. Finally, reduction theory was employed to demonstrate the security of the cryptographic scheme within the defined security model. The fundamental concept utilized a proof-by-contradiction approach, reducing the security of the cryptographic scheme to a computational problem believed to be infeasible to solve within polynomial time. However, it is widely acknowledged that such difficult problems are unsolvable within polynomial time; consequently, no adversary capable of breaking the cryptographic scheme within polynomial time could exist. A critically important concept here is indistinguishability, which is commonly used to characterize the security of cryptographic schemes under certain adversarial models. Specifically, indistinguishability defines the adversary’s inability to differentiate between two distinct scenarios, formally defined as follows:
Definition 2.
(Indistinguishability) For any algorithm (called a distinguisher) that could interact with system X or system Y and produce a binary output (0 or 1), its distinguishing advantage under the security parameter λ satisfied (2)
If the above condition was satisfied, systems X and Y were said to be (computationally) indistinguishable. Here, represented a negligible function, asymptotically smaller than any inverse polynomial function.
Within provable security theory, two prevalent models are frequently employed: the random oracle model and the standard model. The random oracle model, an idealized, completely random, and unpredictable function, offered a simplified means of introducing randomness and streamlined the security analysis, facilitating easier design and assessment of cryptographic algorithms or protocols. The standard model, conversely, operated without reliance on an idealized random oracle and was considered more realistic. Consequently, security proofs achieved in this model were generally regarded as more rigorous and trustworthy. However, establishing such proofs within the standard model often presented greater difficulty and potentially necessitated more sophisticated techniques and methodologies.
Through provable security theory, strict mathematical proofs could be constructed, ensuring that designed cryptographic schemes satisfied specified security properties under defined adversarial models. This furnished cryptography research and practice with a powerful toolkit and methodology, supporting the design and analysis of increasingly secure and reliable encryption algorithms and protocols.
3.3. Formal Definition of Access Control Function Proxy Re-Encryption
The formal definition of the ACFPRE scheme is as follows: Let the key space comprise public keys, private keys, and re-encryption keys, where an empty key existed. The plaintext space X and the functional space constituted the input and output domains of the algorithms. The scheme was composed of the following six probabilistic polynomial-time (PPT) algorithms:
- Setup: The system was initialized. The parameter was accepted. Public parameters were generated. The master secret key was retained.
- KeyGen: Keys were generated. Public-private key pairs , , , were generated.
- Encrypt: The encryption algorithm was executed. The ciphertext was output.
- ReKeyGen: The re-encryption key was generated. The data owner’s private key and public key were utilized. A re-encryption key with the embedded function was generated.
- ReEncrypt: The re-encryption algorithm was executed. The proxy employed the re-encryption key . The ciphertext C was re-encrypted into a new ciphertext .
- Decrypt: The decryption algorithm was executed. The data user’s private key was utilized to decrypt the ciphertext . The functional output value was obtained.
Decryption Correctness: For any valid ciphertext C, re-encryption key , and user private key , with respect to the data user, if Equation (3) held, then the ACFPRE scheme was said to be correct.
3.4. Security Model for Access Control Function Proxy Re-Encryption
For the security model of Access Control Function Proxy Re-Encryption (ACFPRE), the game-based CPA security definition is provided below. It must be noted that before the game commenced, the adversary ’s selection of messages and had to be restricted such that Equation (4) was satisfied. This ensured that messages and were of equal length, .
- Initialization: The challenger executed Setup.
- Phase 1: The adversary initiated queries to the challenger .
- KeyGen was executed. The private key query set was initialized. The re-encryption key query set was initialized. The challenge user was recorded.
- Phase 2: The adversary could repeatedly perform operations from Phase 1.
- Challenge: The adversary initiated a challenge to the challenger .was executed. was selected.
- Encrypt was executed.
- Guess: The adversary output a guess for .was executed. If , 1 was returned; otherwise, 0 was returned.: If or , ⊥ was output.was updated. The private key was output.: If and , ⊥ was output.was updated. The re-encryption key was output.
4. Scheme Design
In this section, an attribute-based access control proxy re-encryption scheme was proposed, and its security proof was provided.
4.1. System Architecture
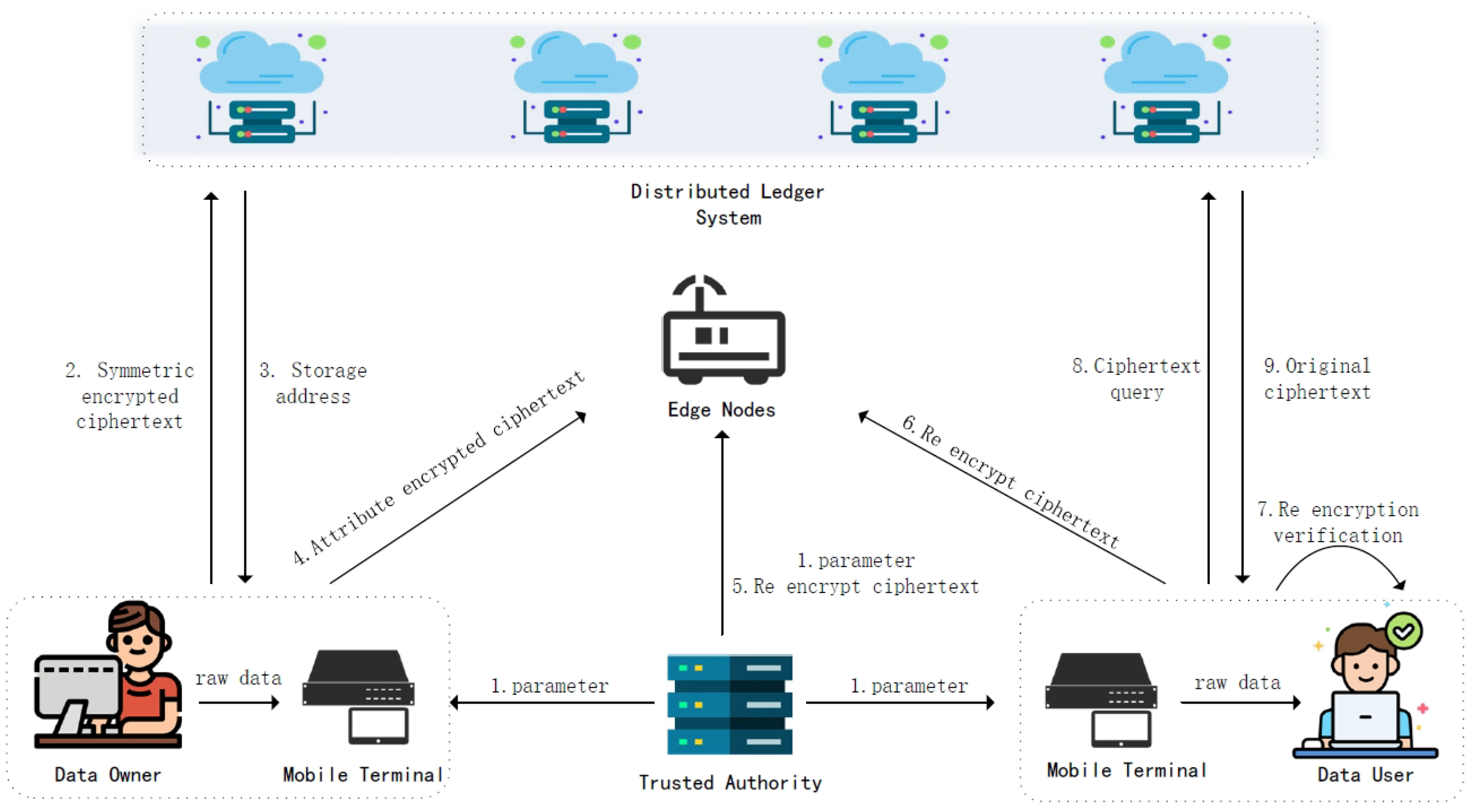
Figure 1 illustrates the overall framework of the scheme, comprising five core components: Data Owner, Distributed Ledger System, Trusted Authority, Edge Nodes, and Data User: (1) Data Owner: The data owner performs multi-layer encryption operations. It encrypts data and hosts it on the distributed ledger system. It simultaneously constructs proxy re-encryption keys and broadcasts them to the blockchain network. (2) Distributed Ledger System: Provides distributed storage services using Merkle–Patricia tree structures for verifiable storage of data fingerprint chains. Records storage information of ciphertext resources and maintains data provenance chains through smart contract mechanisms. Periodically executes full-node consensus verification for data integrity validation modules to ensure immutability of storage replicas. (3) Trusted Authority: Manages the full lifecycle of keys and can perform revocation operations on users. (4) Edge Nodes: Responsible for storing ciphertext and performing re-encryption computations. (5) Data User: Obtains ciphertext from edge nodes and performs verification operations. If verification passes, decrypts the ciphertext to recover the key, then locates and retrieves the original ciphertext via blockchain; terminates access if anomalies are detected.
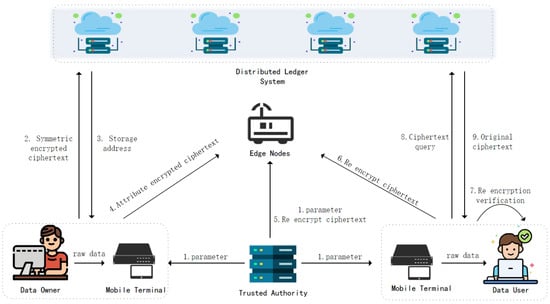
Figure 1.
Secure data-sharing model.
4.2. Attribute-Based Access Control Function Proxy Re-Encryption Definition
An attribute-based access control function proxy re-encryption scheme consists of seven PPT algorithms as shown in Figure 2: System Initialization, Encryption Key Generation, Encryption Algorithm, Re-encryption Key Generation, Re-encryption Algorithm, Decryption Algorithm, and Revocation Algorithm.
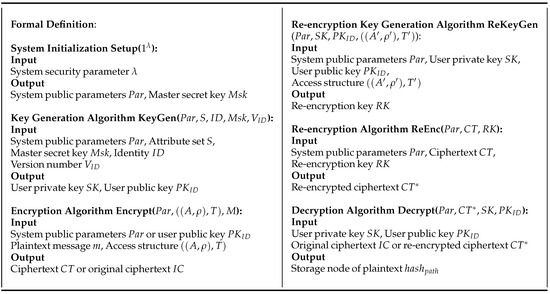
Figure 2.
Formal definition of Attribute-Based Access Control Function Proxy Re-Encryption.
(1) In the Encryption Algorithm Encrypt(), the ciphertext is associated with the access structure ; hence, this is an ACFPRE scheme. (2) Correctness: If the data owner satisfies the access policy , they satisfy Equation (5).
4.3. Security Model for Attribute-Based Access Control Function Proxy Re-Encryption
The interactive attack experiment involves two entities: (1) The adversary possesses probabilistic polynomial-time (PPT) computational capability and can adaptively initiate oracle queries such as key generation (KeyGen), re-encryption key generation (ReKeyGen), re-encryption (ReEnc), and decryption (Dec), aiming to compromise the scheme’s chosen-ciphertext security (SEL-HRA). (2) The challenger simulates the cryptographic system logic, initializes public parameters, maintains key states, and responds to the adversary’s queries according to security rules. Its core task is to construct a reduction proof based on the adversary’s attack behavior, anchoring the scheme’s security to fundamental mathematical problems. Details are illustrated in Figure 3.

Figure 3.
Security model for Attribute-Based Access Control Function Proxy Re-Encryption.
Definition 3.
Formal Definition of Security Advantage: In the indistinguishability SEL-HRA (Selective Honest Re-encryption Attack) security experiment, the adversary participates in the final decision by outputting a guess . If and only if , the challenger outputs decision result 1, indicating successfully breaks the scheme; otherwise it outputs 0. The computational advantage of the adversary is defined as follows:
where λ is the security parameter, and U denotes the set of oracles accessible to the adversary. If for any probabilistic polynomial-time (PPT) adversary , its advantage satisfies ( is a negligible function), then the ACFPRE scheme can be proven to possess adaptive security under the SEL-HRA model. This definition strictly characterizes the scheme’s resistance to key leakage and re-encryption attacks by quantifying the deviation of the adversary’s guess from randomness.
4.4. Scheme Process
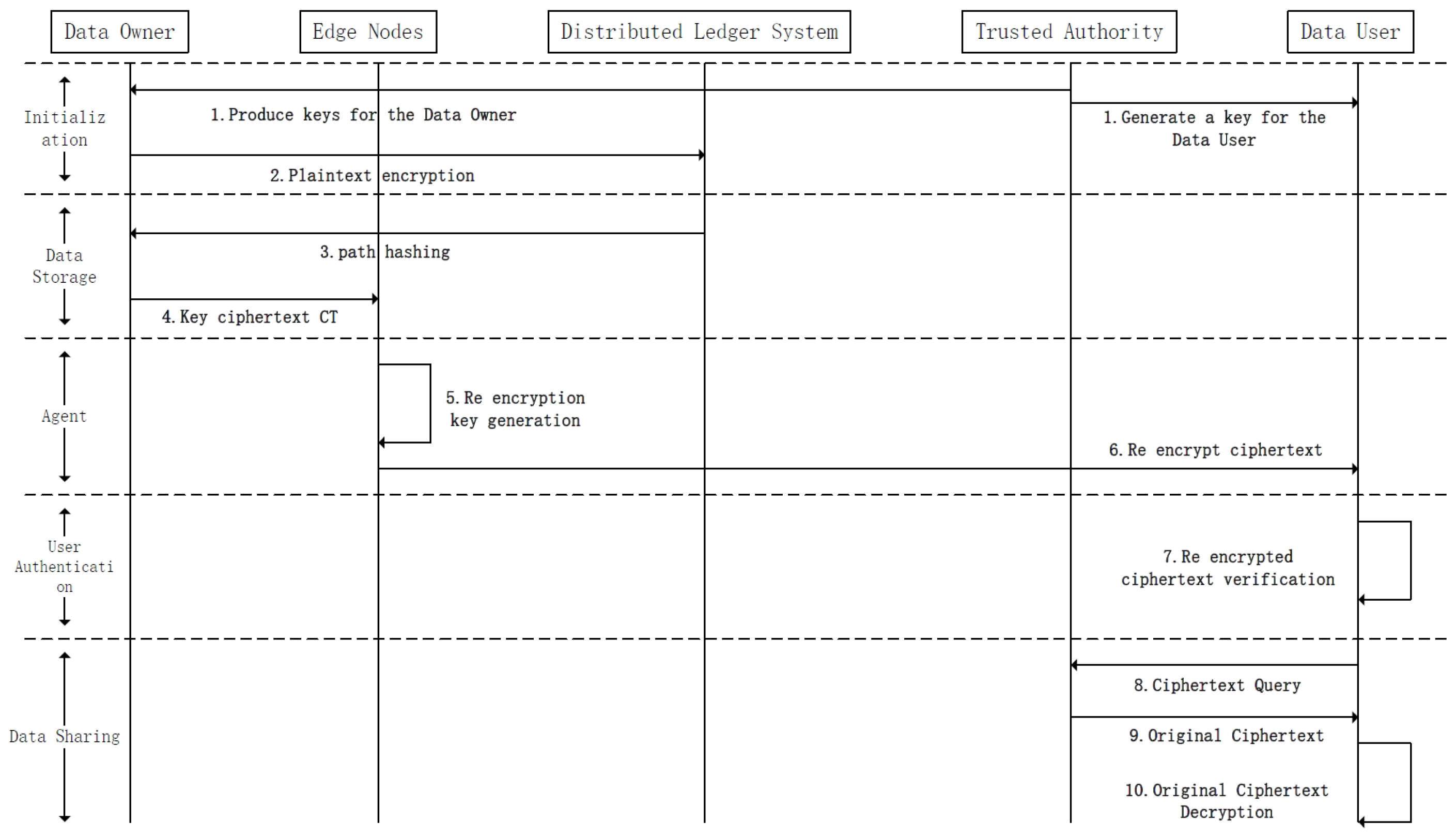
The data-sharing scheme is divided into five stages, as shown in the Figure 4.
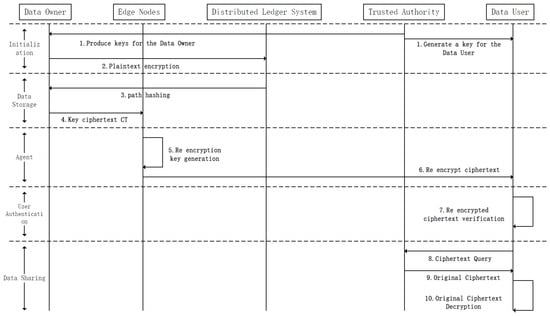
Figure 4.
Data sharing process.
4.5. Scheme Description
- System Setup Algorithm. Setup: represented the system security parameter. Bilinear group parameters were generated: Bilinear groups of large prime order p were selected, where constituted a computable bilinear map. Generators were chosen. For the universal attribute set U, for each attribute , was randomly selected, and the attribute public key component was computed. The master secret key was randomly selected, and the master public key was computed. An encoding function was defined for ciphertext conversion. The public parameters included collision-resistant hash functions , , and a discrete logarithm-based trapdoor hash function . The trusted authority published the system parameters , while the master secret key was securely stored.
- Key Generation Algorithm. KeyGen: The data owner’s attribute set was defined as , where each attribute consisted of an index set and a value set . The trusted authority executed the following: secret parameters and a version control factor were randomly selected. A trapdoor key was generated by combining the user identifier ID and key version number :where represented a cryptographic hash function. Bilinear pairing parameters were computed as follows:For each attribute index , the following was generated as follows:Based on the attribute verification tuple , where denoted the version identifier and , the user private key component was computed as follows:This process ensured dynamic binding between the private key and attribute values, supporting key revocation and update mechanisms based on version numbers.
- Encryption Algorithm. Encrypt or Encrypt: For the original message , the data owner utilized the key for encryption, obtaining the initial ciphertext . For the critical message , the data owner selected the corresponding access structure to encrypt M. Subsequently, the data owner randomly selected a vector , where represented the secret value to be shared, and were random numbers used to conceal r. The value was computed. The data owner selected , then computed the initial ciphertext components: , , , , , . The final ciphertext was generated as .
- Re-Encryption Key Generation Algorithm. ReKeyGen: The re-encryption authority selected a new access structure , where was an matrix and was an injective function mapping each row of to an attribute name. was chosen, and along with the master-key-related term were computed. was encoded as . A ciphertext was generated by encrypting under the new policy:where components satisfied the following:Blinding was applied to the original private key attribute components:The re-encryption key was output as follows:This algorithm achieved dynamic updating of the access control function through the policy-binding matrix , and the blinding of key components ensured the security of the original private key.
- Re-Encryption Algorithm. ReEnc: The re-encryption key and the original ciphertext were input. If the ciphertext was marked as non-re-encryptable (i.e., permission had been revoked or expired), or if the attribute set S failed to satisfy the original access structure , the termination symbol ⊥ was output. Otherwise, a valid attribute index set was determined. Lagrange coefficients were selected such thatwhere denoted the t-th row vector of matrix A. The re-encrypted ciphertext component was synthesized using bilinear pairing operations:where represented the attribute public key component; was derived from the re-encryption key ; was an original ciphertext component; was the system public key; and the numerator part was computed via the blinded private key and attribute parameters, while the denominator part verified proxy authority legitimacy. The re-encrypted ciphertext decryptable by the target user was constructed:where were the LSSS matrix and labeling function of the new access policy; and preserved the original encryption random number s and ciphertext core; and contained the blinded factor encrypted in the re-encryption key.
- Decryption Algorithm. Decrypt or Decrypt: Blinding factor extraction: Decryption was performed on the non-re-encrypted ciphertext , and was decoded. The verification parameter was computed as follows:If held, the proxy re-encryption computation was deemed correct (true was output). Otherwise, the process was terminated (⊥ was output). For the re-encrypted ciphertext ,where satisfied ;The blockchain smart contract was accessed via to retrieve the original encrypted data IC. The session key k was utilized to execute the following:The original plaintext data was recovered.
- Revocation Algorithm. Revocation: For non-revoked users , the trusted proxy distributed a new random factor . The attribute set of remained unchanged (), and was maintained. During revocation, only required updates to the key and . Additionally, the trusted proxy selected a random factor to update F, resulting in , whereThe data owner executed the key update operation using parameters generated by the trusted proxy:Non-revoked data users accessed original data using the updated and . For revoked data users, the trusted proxy updated the attribute set . In the updated , since the random factor was not distributed to data users by the trusted proxy, key updates were impossible and access to original data was prevented. The revocation of data owners was thereby completed by the trusted proxy.
4.6. Security Proof
4.6.1. Correctness Analysis
First verifies the correctness of decrypting the non-re-encrypted ciphertext component , as follows:
. was obtained by decoding , i.e., .
Secondly, when the data user satisfied the access policy , it simultaneously satisfied . The decryption algorithm was executed. The correctness of the decryption process for the re-encrypted ciphertext was verified, as detailed below:
4.6.2. Security Analysis
Theorem 1.
Under the assumption that the decisional q-parallel BDHE problem is hard, the adaptive attack advantage of any probabilistic polynomial-time (PPT) adversary against a chosen access policy satisfies
This conclusion demonstrates that the scheme achieves indistinguishability security against selectively chosen access structures in the standard model. The adversary cannot gain significant cracking advantages through policy selection.
Proof.
If a probabilistic polynomial-time (PPT) adversary breaks the scheme with advantage
In the CPA game, there exists an algorithm capable of breaking the decisional q-parallel BDHE assumption with non-negligible advantage. Specifically, the challenger simulates ’s attack process, directly reducing the adversary’s advantage to the intractability of the q-parallel BDHE problem:
This reduction rigorously proves that if the q-parallel BDHE assumption holds, the scheme satisfies IND-sAS-CPA security in the standard model. The adversary’s success probability is suppressed within the negligible function range.
The game is executed according to the following simulated algorithms (Sim.Init, Sim.Setup, Sim.KeyGen, Sim.ReKeyGen):
Sim.Init: issues a challenge request for access structure to , where the sharing matrix .
Sim.Setup: initializes the key storage structure. An empty private key list and a public key list are generated, with their index domain covering the attribute set .
Sim.KeyGen: Queries are generated by regarding attribute sets that do not match the access policy . selects random factors . When , , resulting in a vector . Additionally, all x satisfying were identified where , such that held for each. Under the current version Ver, selected and output user identity-related public keys . Private keys generated via the discrete logarithm-based trapdoor hash function were , . injected the generated private key into and public key into , then returned to . If the attribute set S satisfied access policy (i.e., ), randomly selected and terminated the security game. This operation severed the adversary’s advantage accumulation path through policy constraints, ensuring the rigor of the reduction proof.
Sim.ReKeyGen: Queries for required re-encryption keys were issued by to via attribute set S and access policy . The adversary selected attribute set S. When S satisfied access structures and (i.e., and ), then output any value from and terminated the game. Otherwise, executed algorithm , selected random factor , and computed and . was encoded as , then was encrypted under to obtain . were computed, where . The re-encryption key was output and sent to .
Challenge: Equal-length messages and were submitted by to . was randomly selected by . Ciphertext was generated and returned to . This process tested the adversary’s cracking capability through message indistinguishability, constructing the core verification link for security reduction.
Guess: After output guess value , challenger determined the result as follows: (1) Successful guess: If , inferred (i.e., ), indicating successfully associated ciphertext with message . (2) Failed guess: If , determined to be a random element in (i.e., ). The adversary could not obtain effective informational correlation. Security quantification: The adversary ’s cracking advantage was defined as
If and only if the decisional q-parallel BDHE assumption holds, there exists a negligible function such that
This conclusion rigorously proves the scheme’s adaptive security in the standard model by reducing ’s advantage to the intractability of the q-parallel BDHE problem.
If output result , then , indicating could not obtain related to . According to the security model’s guessing, . The challenger ’s advantage could be derived as follows:
Theoretical analysis shows the adversary ’s attack advantage satisfies
The challenger ’s reduction advantage for cracking the q-parallel BDHE problem is
Based on the intractability of the decisional q-parallel Bilinear Diffie–Hellman assumption, the scheme satisfies IND-sAS-CPA security under the adaptive chosen attribute set attack model. This contradictory relationship proves the existential conclusion: If the assumption holds, the adversary’s advantage must be negligible. □
5. Efficiency Analysis
5.1. Theoretical Analysis
As shown in the Table 1, the scheme proposed in this paper is compared with other data-sharing schemes in functional features. The scheme in [11] supports policy hiding, which effectively protects users’ private information by hiding sensitive attribute values; while schemes [10,13,15] additionally support verification of re-encrypted ciphertexts on the basis of ABPRE. This achieves one-time encryption with multiple sharing, and the verifiability of ciphertexts effectively prevents collusion attacks from semi-trusted proxies and malicious users. Furthermore, the re-encrypted ciphertext embeds the original ciphertext generated by the encoding function, making the verification process controllable.

Table 1.
Functional comparison with other related schemes.
The scheme proposed in this paper not only inherits the advantage of verifiable re-encrypted ciphertexts from schemes [10,13,15,17], but also possesses the characteristics of attribute revocation and collusion attack resistance from scheme [11]. Additionally, our scheme satisfies indistinguishability against chosen-plaintext attacks under specific access structures.
The distributed storage of data on the blockchain in scheme [11] ensures message integrity during data sharing. This paper chooses to store encrypted data on the blockchain, effectively avoiding repeated uploading of identical ciphertexts and reducing the workload of data owners. Although schemes in [15,17] both implement user revocation, the methods they use differ. This paper adopts a more efficient revocation method by constructing private keys using SM3 and updating keys to revoke malicious users.
Analysis of the results in Table 2 indicates that the Ge2023 scheme [16] exhibits constrained storage efficiency in large-scale scenarios due to its public parameter size scaling linearly with attribute quantity. In contrast, the proposed scheme adopted a fixed-length parameter design, achieving minimized storage occupation for public parameters while enhancing adaptability to scalability requirements in extensive IoT environments. As attribute counts in user access structures increased, all storage overhead metrics in schemes [10,11,13,15,17] demonstrated linear growth patterns. The proposed scheme maintained lower overhead across all dimensions compared to existing solutions, concurrently reducing key compromise risks. In summary, substantially reduced storage occupation was achieved by the proposed solution relative to alternative data-sharing approaches.

Table 2.
Storage space comparison of related schemes.
As detailed in Table 3, computational overhead is compared across four dimensions: key generation, data encryption, re-encryption key generation, and auxiliary operations. The proposed scheme achieves functional enhancements while maintaining superior computational efficiency in all four aspects compared to existing solutions.

Table 3.
Comparison of computational costs for related schemes.
5.2. Experimental Analysis
To evaluate the performance of the proposed scheme, four schemes were executed on a 12th Gen Intel(R) Core(TM) i5-12500H CPU operating at 3.10 GHz within the PyCharm 2023.1.4 (Professional Edition) environment. Experimental results are presented in Table 4.

Table 4.
Computation time of cryptographic operations.
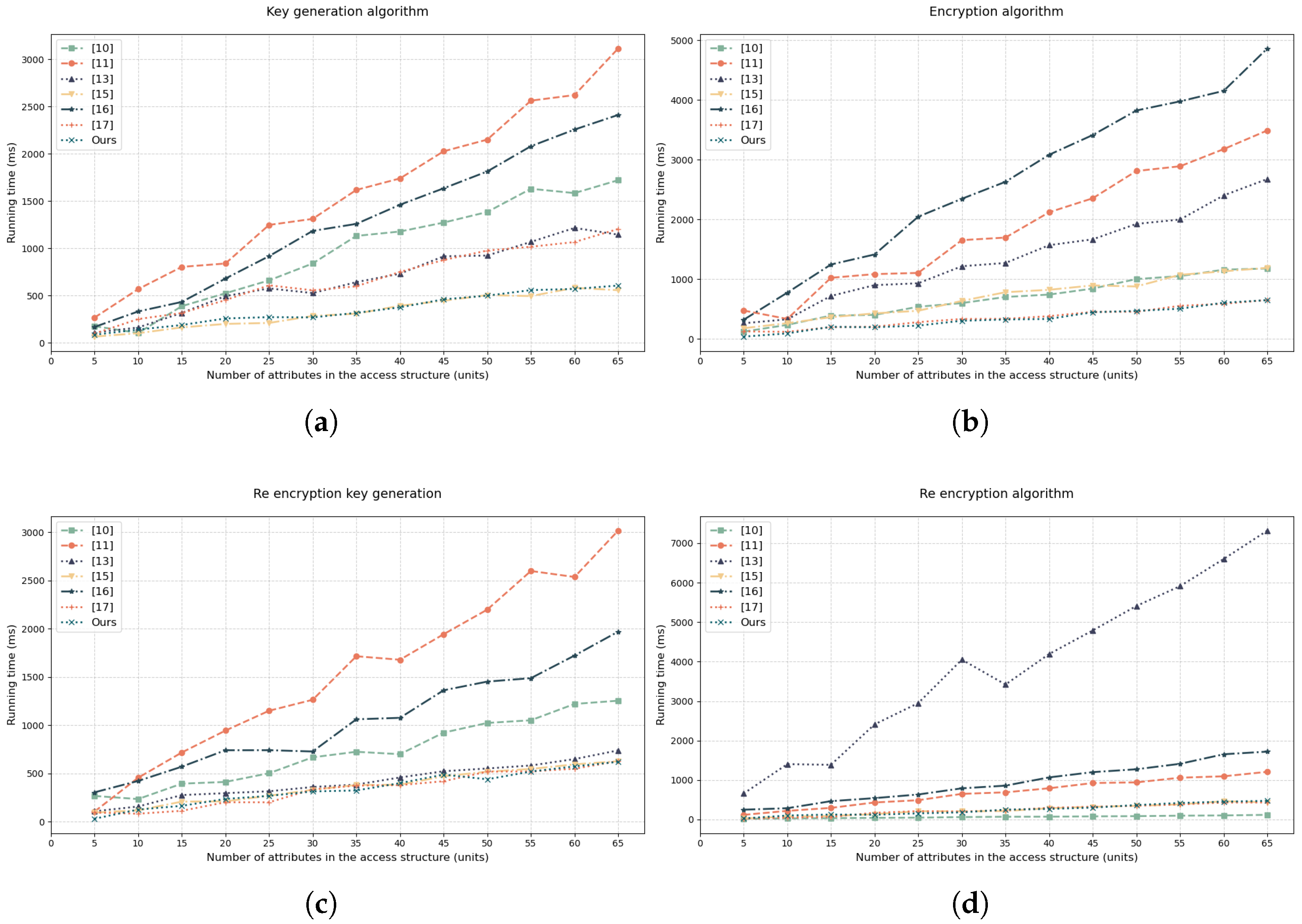
Time consumption during four critical phases—key generation, encryption, re-encryption key generation, and re-encryption—was comparatively analyzed against schemes from [10,11,13,15,16,17]. Experimental comparisons are visualized in Figure 5. This paper selects the number of attributes in the access structure as the independent variable, taking the average value after 50 experiments in each phase.
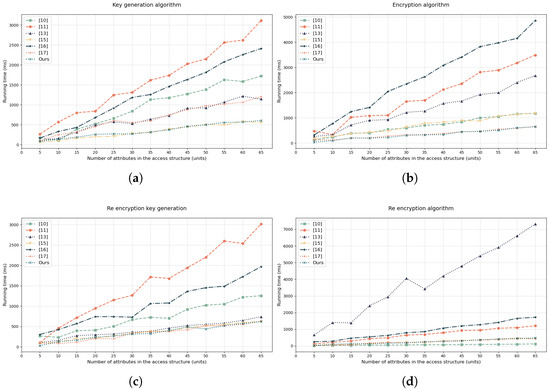
Figure 5.
Comparative analysis of time consumption for Attribute-Based PRE Schemes [10,11,13,15,16,17].
According to Figure 5a, this study demonstrates that in key generation scenarios, the algorithm’s execution time increases significantly with the number of attributes in the access structure; all seven schemes exhibit an upward trend, with scheme [11] showing the highest computational overhead (reaching 2800 ms at 60 attributes). Our scheme maintains optimal efficiency throughout, requiring only 600 ms under identical conditions, closely approaching the suboptimal scheme [17]; particularly beyond 20 attributes, performance disparities accelerate, highlighting our solution’s effectiveness in curbing the time-increase slope through algorithmic optimizations. Figure 5b shows that key generation time for all schemes exhibits a monotonically increasing trend with attribute growth; Scheme [16] demonstrates the most significant time overhead escalation, while our solution maintains efficiency leadership with execution time significantly lower than most algorithms and the flattest growth curve aligned with scheme [17].
Curve trend analysis based on Figure 5c indicates execution time for all re-encryption key generation schemes increases monotonically with attribute count; scheme [11] consistently exhibits the highest curve position, while our solution maintains the lowest trajectory with significantly flatter growth slope; performance gaps markedly widen beyond 20 attributes. Analysis of Figure 5d demonstrates all schemes show monotonically increasing execution time yet divergent growth patterns: scheme [13,16] display drastic nonlinear acceleration, while scheme [11,15] maintain gradual increases; our solution shows the shallowest growth slope, confining incremental cost to millisecond-level increases—starkly contrasting Ge2023’s thousands-of-milliseconds surge.
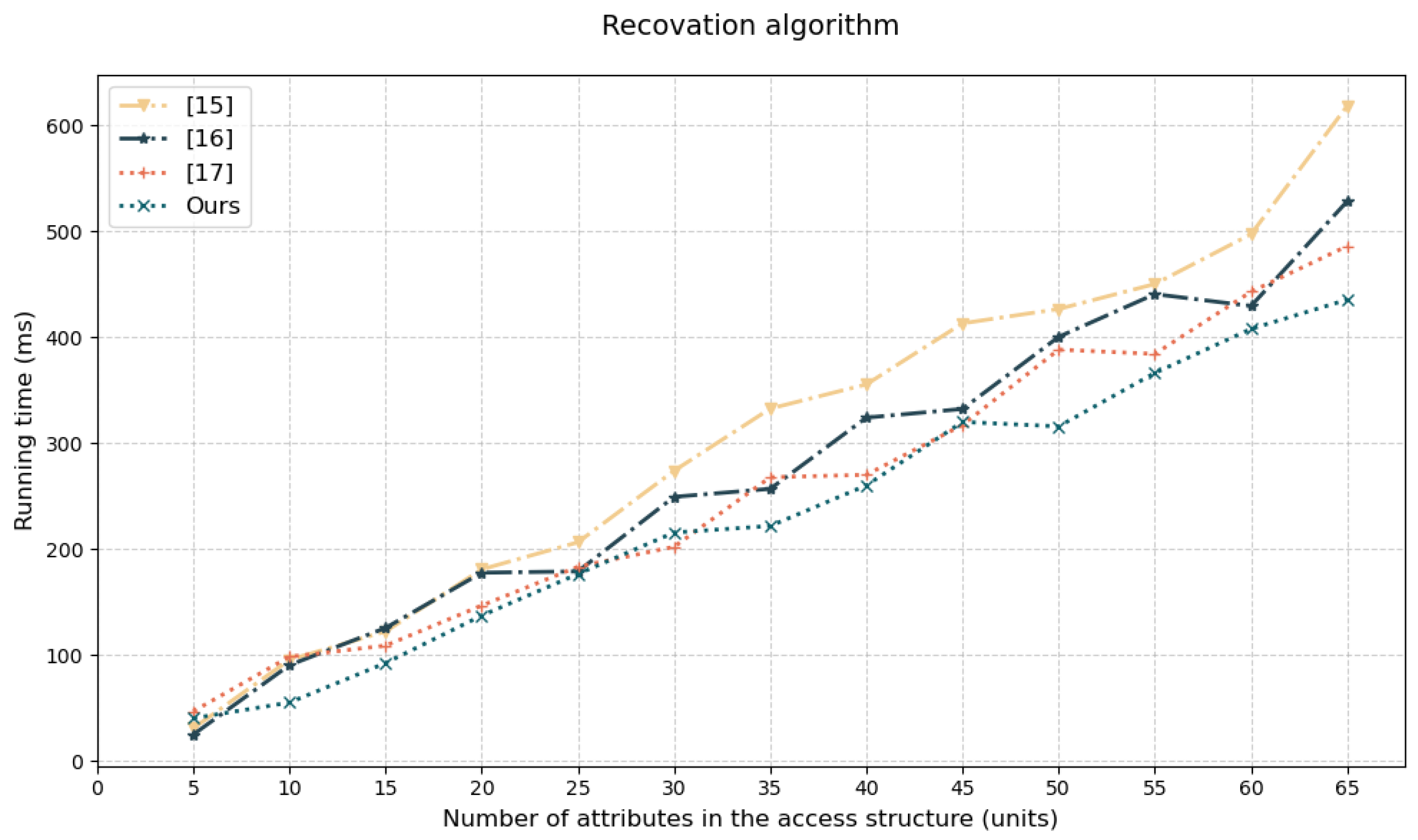
These results confirm our design effectively suppresses nonlinear time-cost expansion through algorithmic optimizations, establishing critical foundations for large-scale re-encryption deployment. Curve trend analysis of Figure 6 shows that execution time for scheme [15,16,17] and our scheme increases monotonically with attributes;scheme [15] shows highest curve position indicating lowest efficiency; scheme [16,17] exhibit mid-tier performance with scheme [16] slope steepening; our solution maintains lowest trajectory, validating our revocation algorithm suppresses computational burden expansion and enables efficient re-encryption deployment. During the revocation process, the trusted authority executes the revocation algorithm to generate random factors for non-revoked users. This process only requires performing key update computations, and the update involves only one exponentiation operation. When the number of attributes in the access structure is 50, the time consumed is approximately 324 ms.
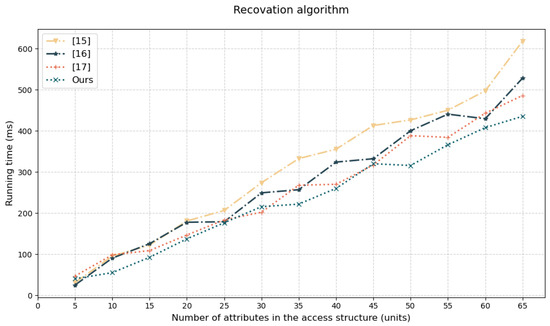
Figure 6.
Revocation efficiency [15,16,17].
6. Conclusions
To address proxy authority boundary violations in cross-domain ciphertext sharing, this work constructs an Attribute-Based Access Control Proxy Re-Encryption scheme. Targeting limitations in traditional identity-based models for fine-grained permission allocation and multi-dimensional attribute adaptation, the scheme enables access policy definition based on multiple user attributes. It provides flexible authorization that restricts data access exclusively to users satisfying specific attribute conditions. A formal security model with comprehensive proofs is established. Theoretical and experimental results demonstrate effective control over proxy/receiver permissions, featuring shorter key generation latency and compact keys. This resolves proxy permission overreach and receiver permission diffusion issues.
Author Contributions
Conceptualization, G.Z.; methodology, G.Z.; validation, G.Z.; formal analysis, G.Z.; visualization, G.Z.; supervision, C.P. and W.T.; funding acquisition, C.P. and W.T.; writing—original draft preparation, G.Z.; writing—review and editing, C.P. and W.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 62272124, No. 62361010), the Open Fund of Advanced Cryptography and System Security Key Laboratory of Sichuan Province (No. SKLACSS-202414),and the Major Scientific and Technological Special Project of Guizhou Province (No. [2024]014).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
No conflict of interest exists in the submission of this manuscript, and the manuscript is approved by all authors for publication. I would like to declare on behalf of my co-authors that the work described was original research that has not been published previously, and not under consideration for publication elsewhere, in whole or in part. All the authors listed have approved the manuscript that is enclosed.
References
- Matt, B.; Gerrit, B.; Martin, S. Divertible protocols and atomic proxy cryptography. In Advances in Cryptology—EUROCRYPT’98; Springer: Berlin/Heidelberg, Germany, 1998; pp. 127–144. [Google Scholar]
- Elena, K. Proxy Re-encryption from Lattices. In Proceedings of the 17th International Conference on Practice and Theory in Public-Key Cryptography, Buenos Aires, Argentina, 26–28 March 2014; pp. 77–94. [Google Scholar]
- Dutta, P.; Susilo, W.; Duong, D.H.; Baek, J.; Roy, P.S. Identity-based unidirectional proxy re-encryption and re-signature in standard model: Lattice-based constructions. J. Internet Serv. Inf. Secur. 2020, 10, 1–22. [Google Scholar]
- Dutta, P.; Susilo, W.; Duong, D.H.; Roy, P.S. Collusion-resistant identity-based proxy re-encryption: Lattice-based constructions in standard model. Theor. Comput. Sci. 2021, 871, 16–29. [Google Scholar] [CrossRef]
- Deng, H.; Qin, Z. Identity-Based Encryption Transformation for Flexible Sharing of Encrypted Data in Public Cloud. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3168–3180. [Google Scholar] [CrossRef]
- Ohata, S.; Kawai, Y. Re-Encryption Verifiability: How to Detect Malicious Activities of a Proxy in Proxy Re-Encryption. In Topics in Cryptology—CT-RSA 2015; Springer International Publishing: Berlin, Germany, 2015; Volume 9048, pp. 410–428. [Google Scholar]
- Ge, C.; Susilo, W. A Verifiable and Fair Attribute-Based Proxy Re-Encryption Scheme for Data Sharing in Clouds. IEEE Trans. Dependable Secur. Comput. 2022, 19, 2907–2919. [Google Scholar] [CrossRef]
- Sun, J.; Xu, G. Verifiable, Fair and Privacy-Preserving Broadcast Authorization for Flexible Data Sharing in Clouds. IEEE Trans. Inf. Forensics Secur. 2023, 18, 683–698. [Google Scholar] [CrossRef]
- Jiang, L.; Alazab, M. Secure Task Distribution With Verifiable Re-Encryption in Mobile-Crowdsensing-Assisted Emergency IoT System. IEEE Internet Things J. 2024, 11, 3896–3908. [Google Scholar] [CrossRef]
- Liu, S.; Guo, Y. Multi-authority based CP-ABE proxy re-encryption scheme for cloud computing. Chin. J. Netw. Inf. Secur. 2022, 8, 176–188. [Google Scholar]
- Li, X.; Zhang, X.; Gao, J.; Xiang, D. Blockchain data sharing scheme supporting attribute and proxy re-encryption. J. Xidian Univ. 2022, 49, 1–16. [Google Scholar]
- Cui, H.; Deng, R. An efficient and expressive ciphertext-policy attribute-based encryption scheme with partially hidden access structures. Comput. Netw. 2018, 133, 157–165. [Google Scholar] [CrossRef]
- Feng, C.; Luo, W.; Qin, Z.; Yuan, D.; Zou, L. Attribute-based proxy re-encryption scheme with multiple features. J. Commun. 2019, 40, 13. [Google Scholar]
- Zhai, P.; Tong, T. Blockchain-Based Attribute Proxy Re-Encryption Data Sharing Scheme. Comput. Eng. Appl. 2023, 69, 270–279. [Google Scholar]
- Yang, G.; Guo, R.; Zhuang, C.; Wang, X. Dynamically updatable attribute based proxy re-encryption scheme in cloud. J. Cyber Secur. 2022, 7, 43–55. [Google Scholar]
- Ge, C.; Susilo, W.; Liu, Z.; Baek, J.; Luo, X.; Fang, L. On maximizing the sum secret key rate for reconfigurable intelligent surface-assisted multiuser systems. IEEE Trans. Dependable Secur. Comput. 2024, 21, 949–960. [Google Scholar] [CrossRef]
- Yan, Y.; Zheng, D.; Wang, Y. Fine-grained data sharing scheme based on revocable proxy re-encryption. J. Front. Comput. Sci. Technol. 2024, 19, 1945–1957. [Google Scholar]
- Yu, G.; Zha, X. Enabling attribute revocation for fine-grained access control in blockchain-IoT systems. IEEE Trans. Eng. Manag. 2020, 67, 1213–1230. [Google Scholar] [CrossRef]
- Guo, R.; Yang, G. An efficient and revocable attribute-based encryption scheme in the cloud-assisted IoMT system. IEEE Internet Things J. 2021, 8, 8949–8963. [Google Scholar] [CrossRef]
- Zhang, J.; Su, S. Identity-Based Broadcast Proxy Re-Encryption for Flexible Data Sharing in VANETs. IEEE Trans. Inf. Forensics Secur. 2023, 18, 4830–4842. [Google Scholar] [CrossRef]
- Luo, F.; Wang, H. Public Trace-and-Revoke Proxy Re-Encryption for Secure Data Sharing in Clouds. IEEE Trans. Inf. Forensics Secur. 2024, 19, 2919–2934. [Google Scholar] [CrossRef]
- Dai, W.; Li, B. Chaos-Based Index-of-Min Hashing Scheme for Cancellable Biometrics Security. IEEE Trans. Inf. Forensics Secur. 2024, 19, 8982–8997. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).