A m-RGA Scheduling Algorithm Based on High-Performance Switch System and Simulation Application

Abstract

High-speed switching chips are key components of network core devices in the high-performance computing paradigm, and their scheduling algorithm performance directly influences the throughput, latency, and fairness within the system. However, traditional scheduling algorithms often encounter issues such as high implementation complexity and high communication overhead when dealing with bursty traffic. To addressing the issue of bottlenecks in high-speed switching chip scheduling, we propose a low-complexity and high-performance scheduling algorithm called m-RGA, where m represents a priority mechanism. First, by monitoring the historical service time and load level of the VOQs at the port, the priority of the VOQs is dynamically adjusted to enhance the efficient matching and fair allocation of port resources. Additionally, we prove that an algorithm achieving a 2× speedup under a constant traffic model can simultaneously guarantee throughput and latency, making this algorithm theoretically as excellent as any maximum matching algorithm. Through simulation, we demonstrate that m-RGA outperforms Highest Rank First (HRF) arbitration in terms of latency under non-uniform and bursty traffic patterns.

1. Introduction

With the transformation of data generation methods in data centers in recent years, artificial intelligence (AI) has increasingly become one of the core driving forces for the development of computationally intensive tasks and High-Performance Computing (HPC) [1,2]. Simultaneously, the scale of data has shown exponential growth [3] far exceeding the processing capabilities of traditional linear expansion, posing higher requirements for computing architectures and communication networks. HPC is a computing paradigm that combines multiple computing nodes (typically high-performance servers) into a cluster and enables them to work collaboratively to complete large-scale and complex tasks [4]. Communication bottlenecks may lead to high latency and increased idle time of nodes, resulting in reduced overall resource utilization [2].

As one of the core components of HPC interconnection networks, high-speed switches must be capable of providing extremely low latency and high bandwidth to support data transmission performance in any communication mode [5]. Therefore, although expansion can be achieved by increasing the number of ports in the switching structure, the problems of excessive expansion in terms of cost, power consumption, and congestion are also obvious [6]. Recent studies have shown that adopting scalable low-latency switching structures such as crossbar switches has become one of the mainstream directions. This structure not only has the advantages of strong parallelism and low latency but also makes it easy to achieve efficient resource utilization through scheduling algorithms, consequently becoming an important interconnection technology route in current HPC and AI data centers [7].

Switch types mainly include Output Queued (OQ) [8] and Input Queued (IQ) [9] switches. OQ switches are difficult to implement in high-speed traffic because they requires a speedup by a factor of N hardware support (such as memory bandwidth and switch rate). Thus, IQ switches are the preferred solution for high-speed systems due to their low speedup requirement (speedup of 1) and hardware scalability. However, the performance of IQ switches is highly dependent on the optimization of scheduling algorithms. Achieving efficient packet transmission in complex traffic scenarios remains a critical and unresolved challenge, especially with increasing port counts and stringent low-latency requirements.

Although some scheduling algorithms for IQ switches exhibit strong scheduling capabilities, several challenges remain that hinder their effectiveness in dynamic traffic scenarios. For instance, certain algorithms fail to efficiently utilize switching resources in bursty traffic under high-load conditions, leading to issues such as many-to-one port contention and port matching synchronization failures. Consequently, the design of iteration scheduling algorithms that offer high throughput, low complexity, and adaptability to dynamic traffic patterns remains a critical research focus in the field of IQ switches.

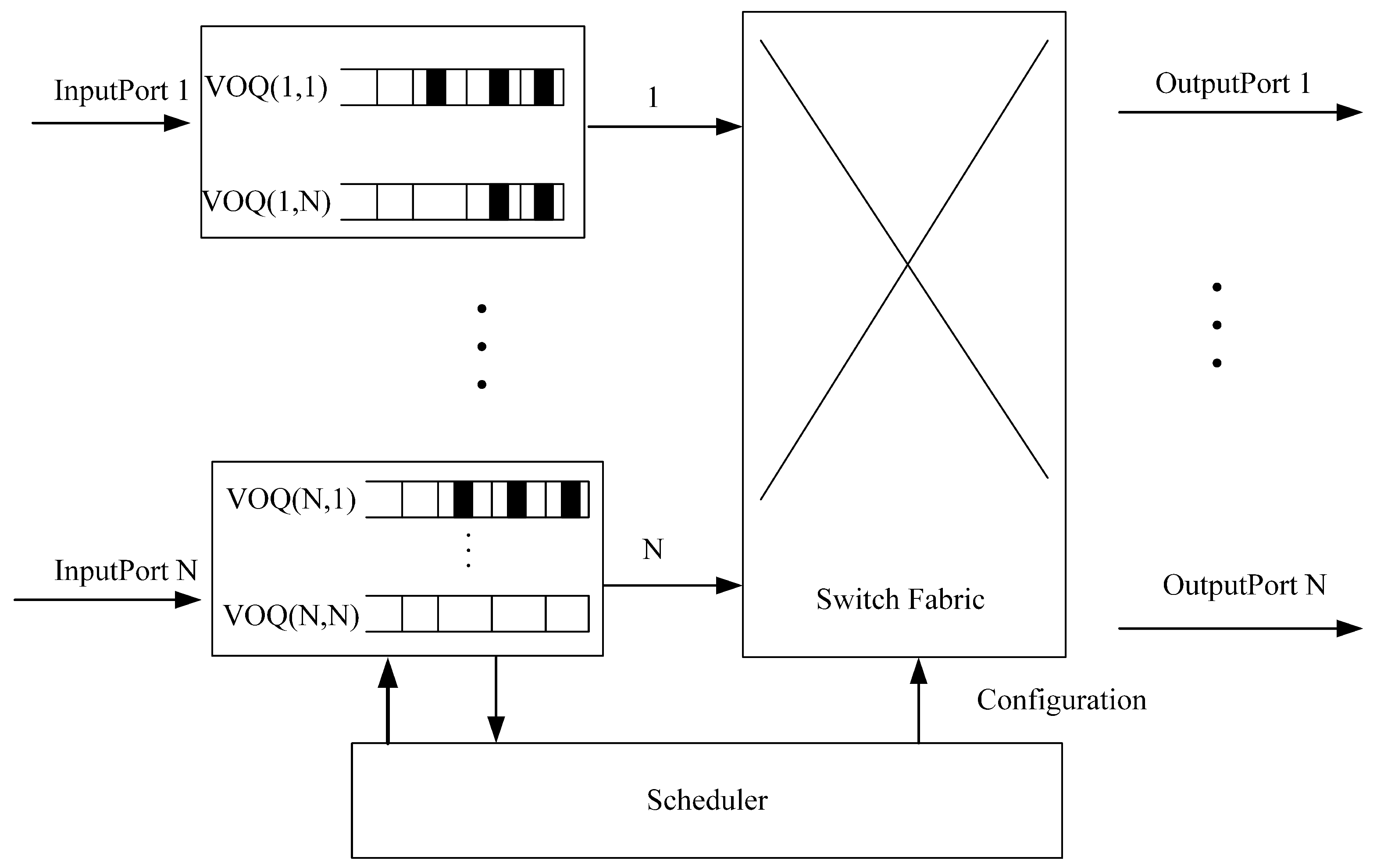
To solve the above problems, we propose a new dynamic adaptive priority iteration scheduling algorithm for single bit request, which we call m-RGA. Figure 1 illustrates an N × N centrally-scheduled input-queued switch, where N represents the number of ports of the switch. The rest of this paper is organized as follows: the next section discusses several iterative algorithms and summarizes the existing problems involving these algorithms; in Section 3, we introduce the proposed m-RGA algorithms with examples; in Section 4, the performance of the proposed algorithms is evaluated and compared with existing schemes; Section 5 presents the conclusions of this paper; finally, Appendix A includes the stability proof of m-RGA, which proves that the 2-speedup algorithm of m-RGA can satisfy the requirement of stability in the execution process under constant traffic.

2. Related Work

In order to solve the problem of head of line blocking [10] caused by FIFO in IQ switch, the VOQ structure was introduced. In the input buffer structure, multiple VOQ buffers are set at the input port according to the destination port. If the number of ports is N, then the number of VOQs in the input bus will also be N, while the total number of queues at the input port will be $N^2$. In the switch fabric, the throughput of the switch unit is improved by providing buffer; however, this also increases the crossbar hardware structure and scheduling ability.

The introduction of the VOQ structure in the last three decades has led to many algorithms being produced, all of which belong to the category of iterative scheduling algorithms. These algorithms differ from others in the information sent in the request phase as well as in the arbitration mechanisms used in the rest phases and in the grant and accept phases. Due to the use of massively parallel processing, a set of widely accepted iterative scheduling algorithms are used to compute matches in an iterative manner, causing the scheduling decision to consider whether or not the VOQ of the input port is occupied. In general, each iterative scheduling algorithm consists of three steps, with only unmatched inputs and outputs considered. In the request phase, if an input has a cell waiting for the VOQ of a output, then the input port will send a request to that output. In the grant phase, each output port, if it receives multiple requests sent from different input ports, will select one of them, after which the output tells the input whether or not its request has been granted. In the accept phase, if the input receives more than one grant, it receives one of them. The following are practical examples of multiple iterative scheduling algorithms.

PIM [11] adopts multi-round iteration; each iteration includes three phases: request, grant and accept. Inputs and outputs request and respond randomly based on their current state. However, the need for random matching in each iteration leads to poor fairness, while random arbitration leads to higher hardware costs. iSLIP [12] uses a fixed pointer and a sliding window mechanism to ensure that the input and output ports are fairly selected. Although iSLIP is beneficial in uniform traffic scenarios, it does not consider port weights, and its performance is poor under nonuniform and bursty traffic characteristics. Although the queue length of VOQ is considered as a weight in iLQF [13], its actual length is transmitted as communication overhead in the control phase, which increases the communication overhead. In addition, iLQF uses the queue length as a weight, ignoring the waiting time of the head of the cell. This can easily cause the port to become blocked for a long time, which is not conducive to the fairness of the port. DRRM [14] follows the same method on the arbitration pointers of input and output ports, and both approaches adopt the polling method. The input and output ports in DRRM have less contention, which can reduce the communication and time cost in the scheduling process; however, it is less sensitive to VOQ with more packets buffered in the queue. Similarly, GA [15] is similar to DRRM, and is not suitable for use in other scenarios.

SRR [16], RR/LQF [17], and HRF [11] adopt the longest VOQ length and preferred input/output pair, and all share the same core calculation formula (1). SRR uses the longest VOQ length at the input port for matching, while RR/LQF uses the longest VOQ length at both the input and output ports for arbitration. When multiple ports have VOQs of the same length, the former two methods adopt the polling method. HRF proposes a highest rank first method. This can provide a higher matching probability than the strategy only relying on the longest queue length, resulting in improved scheduling performance. Although HRF outperforms the other two algorithms, its performance degrades as the load increases. This degradation is primarily due to the additional overhead introduced by queue length calculation and sorting during the scheduling process, which increases the waiting time of cells at the input ports and adversely affects overall transmission efficiency. Moreover, all three algorithms require sorting based on queue lengths, resulting in high time complexity, which is unfavorable for efficient scheduling in high-speed switching scenarios under heavy load conditions. In contrast, $\Pi$-RGA [18] introduces the earliest activation time as its priority, demonstrating good performance under extremely high-load traffic. However, its performance significantly deteriorates under other traffic patterns and its complex priority management mechanism makes it difficult to implement efficiently in high-speed switching environments. In the following, we summarize the key limitations of traditional iteration scheduling algorithms:

The first such limitation involves multiple iterations. To improve throughput during scheduling, it is desirable to maximize port matching through multiple iterations, that is, to reach a state in which no input or output remains unnecessarily idle. However, introducing multiple iterations increases the time duration of the control phase, which in turn extends the queuing delay of cells in the buffer and increases overall latency.

A second limitation concerns multi-bit communication overhead. In iterative scheduling algorithms, communication overhead primarily arises from the three phases, namely, request, grant, and accept. Among these, the request phase incurs the highest cost. While the grant and accept phases typically involve only a single-bit exchange per output or input port, the request phase can be more demanding; for example, in the request phase of iLQF, each input port sends a weight value based on the corresponding VOQ length, resulting in a time complexity of O(N). This significantly increases the overhead of the transmission process. A key objective is to reduce this overhead to O(1) in order to simplify the transfer control phase.

The third limitation consists of stability and fairness requirements. In addition to high throughput and low latency, scheduling algorithms must also ensure stability and fairness. The switching chip should remain stable under dynamic load conditions and guarantee that each non-empty VOQ has a fair opportunity to be served. This implies that as long as there is at least one cell ready for transmission and the corresponding VOQ is non-empty, the scheduling algorithm should avoid starvation and ensure timely servicing of all ports.

3. m-RGA Scheduling Algorithm

This paper proposes a dynamic adaptive priority iterative scheduling algorithm called m-RGA (where m is a priority matching scheme) which has good adaptive ability and stably matches as many ports as possible. In Equation (1), $\mathit{i}$, $\mathit{j}$, $\mathit{t}$, $\mathit{N}$ represent the input port i, output port $\mathit{j}$, current time slot $\mathit{t}$, and number of ports $\mathit{N}$. The formula shows that after $\mathit{N}$ time slots, each output port will be answered once by input port $\mathit{i}$ in a round-robin fashion. This form reflects the fact that in actual scheduling, $\mathit{N}$ output ports corresponding to input port $\mathit{i}$ will be matched uniformly one time, which is a reaction phenomenon of global polling pointers. In the grant phase of the actual scheduling, output port $\mathit{j}$ will respond to input port i according to the time slot and Equation (1). Therefore, if output port $\mathit{j}$ receives the request signal sent by VOQij, it will respond to the VOQ first. Similarly, in the accept phase, input port $\mathit{i}$ preferentially looks for the grant signal from output port $\mathit{j}$ to respond; note that the request–grant and accept3 phases occur in the same time slot. At the same time, during the response process, the arbitration response of the port will be affected by other scheduling priority mechanisms such as the queue length and the wait time of the first cell, which are in the form of local polling pointers.

$$j=(i+t)modN$$

(1)

m-RGA takes into account both the queue length and the historical service time of the queue, then dynamically adjusts the scheduling priority according to the port load in order to adapt to different traffic scenarios. Based on this, global and local polling pointers are introduced. Under the condition of maintaining stable matching, new connection possibilities are tried periodically by releasing connections in order to gradually increase the number of matches and improve the throughput. For time t, input port $\mathit{i}$ is preferred to be served in the previous timeslot. For transmission port $\mathit{j}$, if the last timeslot is in the matching state, then it continues to determine whether the port meets the priority service mechanism. If the condition is satisfied, the request sent by the VOQ is changed from a strong request to a weak request. In the scheduling phase, input port $\mathit{i}$ records a historical service time counter P containing N VOQs, which is used to store the timeslot in which each VOQ is actually transmitted. $\mathit{N}$ counters SC(i,j) are recorded at output port j to detect queue lengths in real time in VOQs with the same destination port j but different input port i, where $i,j\in \{0,\dots ,N-1\}$. The detailed operation of the algorithm at time slot t is summarized as follows.

For requests (Figure 2), at a time slot t, input port $\mathit{i}$ has the priority to determine whether or not the port was in the matching state in the previous time slot. Initially, each port is a strong request ($\mathit{R}$ = 2), representing the highest priority. If it is in the matching state, it continues to determine whether the matched output port meets the $\mathit{j}$ value in Equation (1). If the condition is met, the request is changed to a weak request ($\mathit{R}$ = 1), which means that output port $\mathit{j}$ has already completed a response, and it can respond to other ports. If not, it will continue to set the request to a strong request ($\mathit{R}$ = 2) and to look for the port that meets this condition. When the earliest historical service time $\mathit{P}$ of VOQ $\mathit{A}$ is greater than the threshold $\mathit{A}$ (where $\mathit{A}$ represents the maximum delay of arbitration response), the VOQ’s $\mathit{R}$ is set to 2 and the packets in the queue are preferentially responded to (the VOQ will also send a strong request signal). When another input port $\mathit{k}$ is not connected but there are non-empty VOQs in the input port k at the same time, VOQs will also send weak request signals. VOQs that are not empty will not participate in further operations; in this case, we set the value of $\mathit{R}$ to 0, indicating the lowest priority ($\mathit{R}$ = 0).

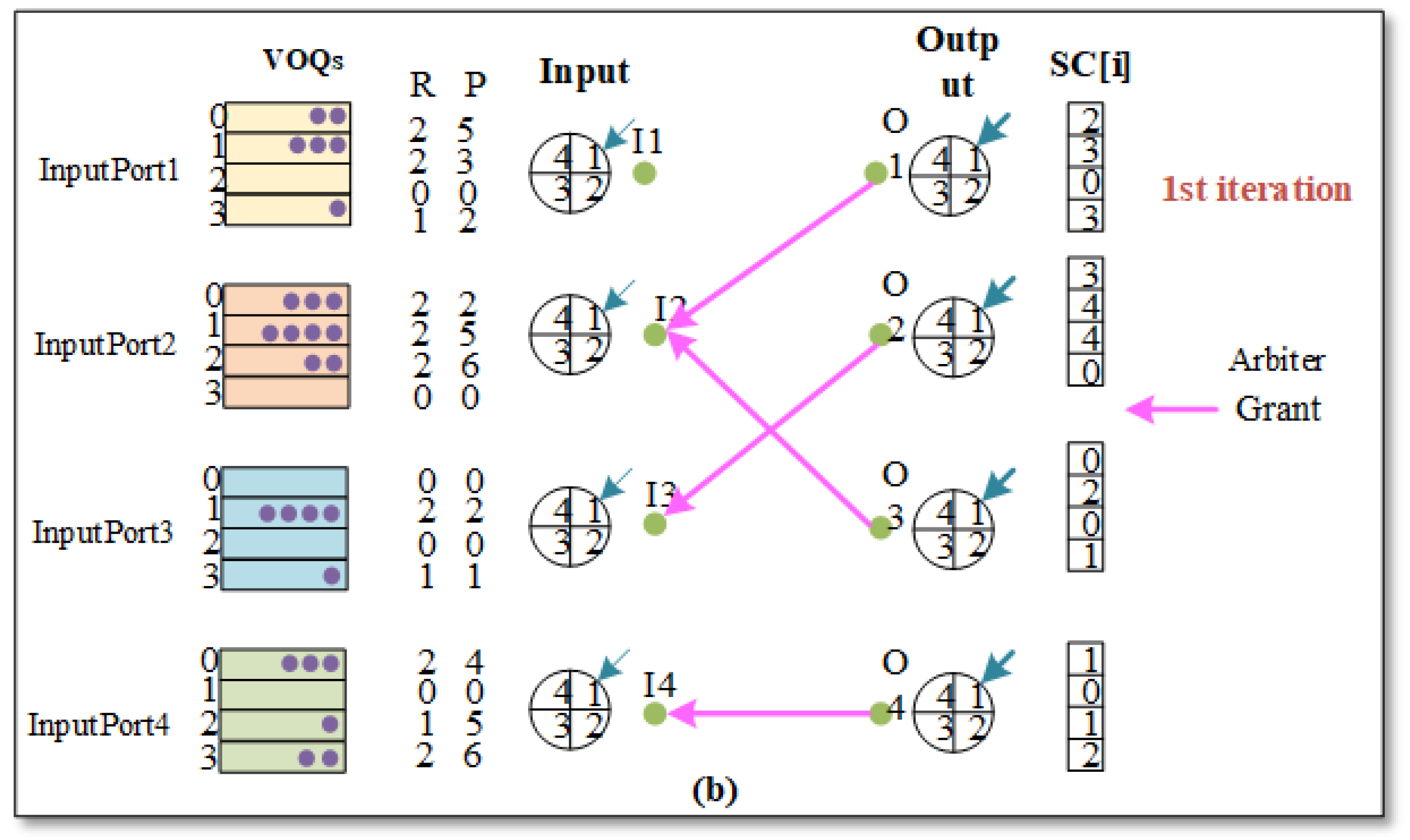
For the grant phase (Figure 3), if output j receives a VOQ request in more than one input port, then output port j selects SC(i,j) based on the strength of the request. SC(i,j) is used to represent the actual length of VOQs under the same output port. If SC(i,j) > 0, then output j is assigned to the VOQ with the largest SC(i,j). When a strong request has higher priority than a weak request, $i,j\in \{0,\dots ,N-1\}$.

For the accept phase (Figure 4), if input i receives multiple grant signals from output m, then according to the strong and weak grant signals in input i, the p value of the oldest historical load VOQ in the strong grant signal is preferred. If p > 0, then input port i preferentially selects the port with the largest P, input i is assigned to this output port j, and the value of p is changed to this time slot value in order to complete the port matching, where $i,j\in \{0,\dots ,N-1\}$. When the in-port match is successful, the VOQ status during the participation in the arbitration is recorded. When a packet is transmitted out of the VOQ, we modify the historical load time of the VOQ to 0 at this time. When the queue length of a non-empty VOQ becomes empty during transmission, we disconnect and record the connection of the VOQ at this time. Figure 3 shows the whole process of this scheduling in a time slot. Here, we only outline the core idea and significance of this research.

It is important to point out that A represents the maximum delay of arbitration response when a VOQ in the input port has not been matched and cannot transmit the data packet. This value is generally used for the change of the request signal in the request phase. When the earliest historical service time P of VOQ A is greater than the threshold A (in general, we set it as 50), the priority of the request signal of the VOQ is forced to change from weak to strong. At this time, the VOQ has a large probability of being selected and transmitting data packets in this time slot.

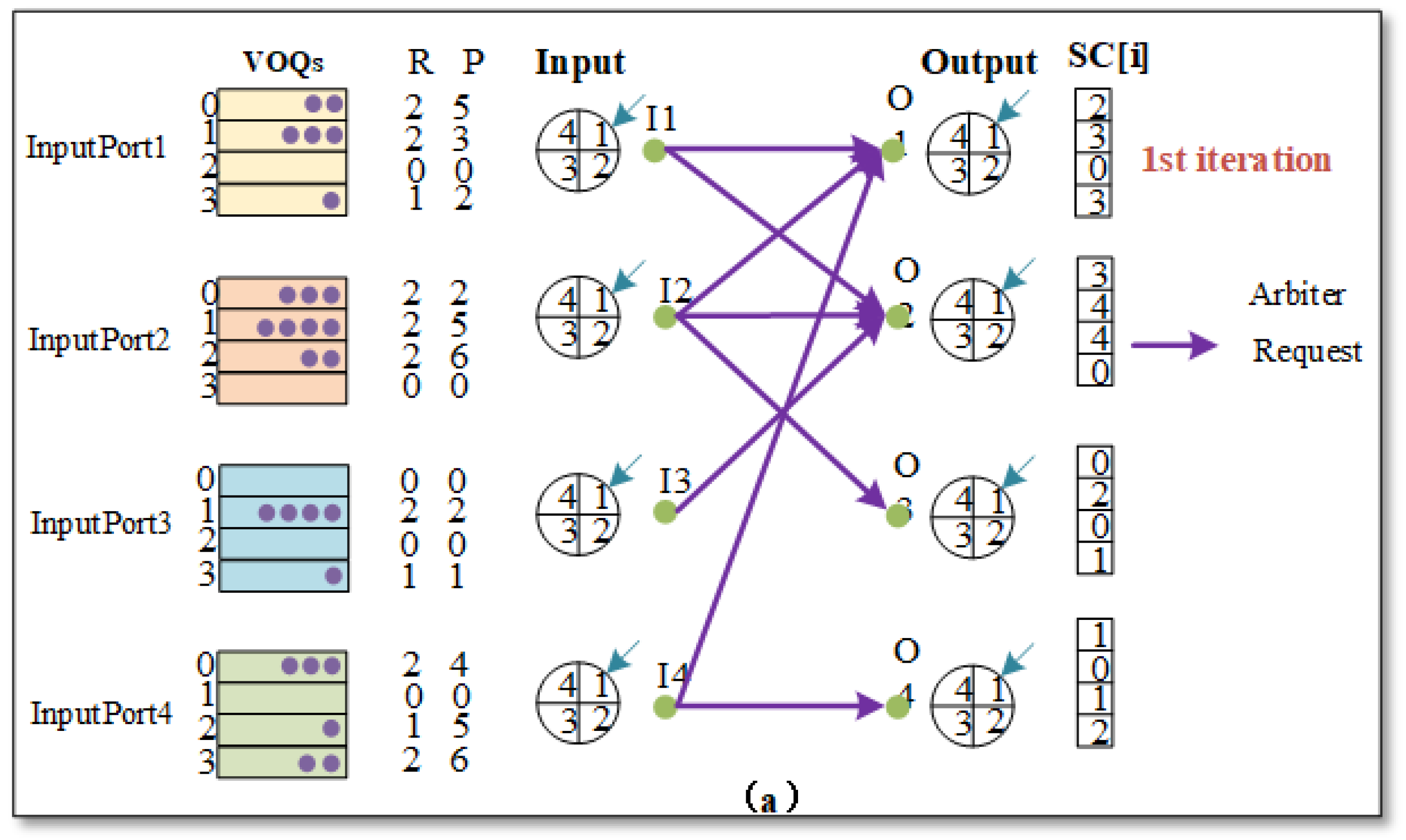
In Figure 2, we provide a detailed example to explain the working mechanism of the m-RGA algorithm. Note that only the example analysis of strong signals is shown in Figure 2. The figure shows the state (R, P, SC[i]) of all VOQs in a 4 × 4 input-queued switch chip in a given time slot. At this time, all of the input and output ports are idle; meanwhile, output port 1 satisfies Equation (1). Its matching input port is input port 2, and output port 2 satisfies input port 3 in Equation (1). We take input port 2 as an example to analyze the overall flow of m-RGA scheduling. In the request phase, at this time the non-empty VOQs in input port 2 send request signals to O1, O2, and O3 in the output ports. In the grant phase (Figure 3), the received request signals for O1 are all strong request signals and satisfy Equation (1); thus, O1 sends grant signals to input port I2, O2 sends grant signals to I3, O3 sends grant signals to I2, and O4 sends grant signals to I4. In the accept phase (Figure 4), I2 receives the grant signals sent by both O1 and O3. At this time, I2 chooses to grant O3 according to the P value of the corresponding position, sends the accept signal, and completes the scheduling process one time. The pointer is then changed to the next position that matches the output port.

3.1. Analysis of Key Technologies

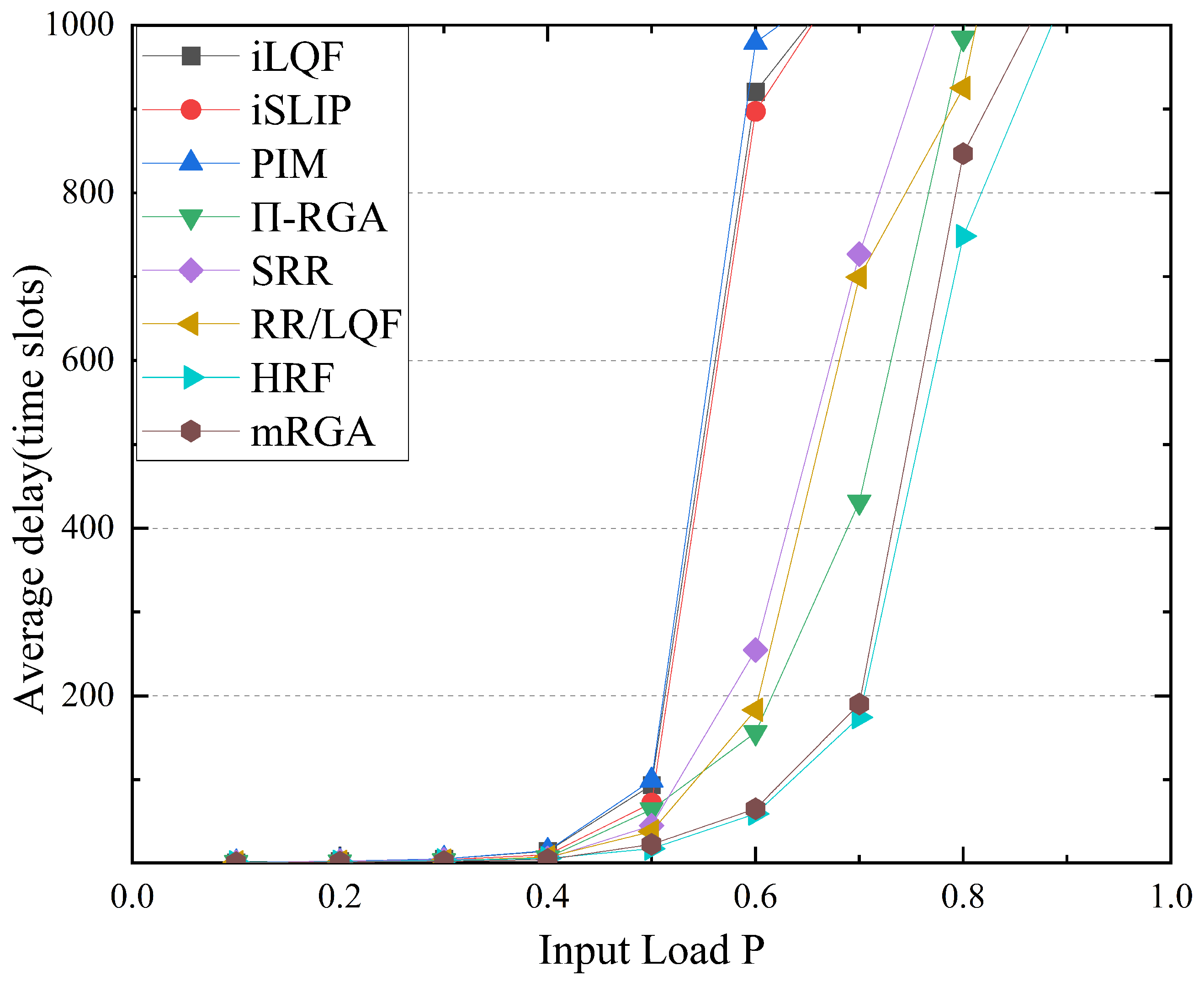
m-RGA reduces the time step size of multiple iterations in the every timeslot, and reduces the communication overhead from O(N) to O(1). In addition, for the case where there may be idle ports in a single iteration of m-RGA, global and local pointers are introduced to enhance the probability of port matching. At the same time, the queue length and historical service time of VOQs were recorded by preferentially retrieving the matched ports in the last time slot. On the premise of stable matching, the matching fluctuation was reduced and the fairness of service ports was increased. The results show that the proposed algorithm can achieve better performance under different traffic models. Below, we summarize the advantages of m-RGA.

First, m-RGA provides low communication overhead with single-iteration and single-bit requests. The m-RGA algorithm achieves port matching using only a single iteration per timeslot, thereby decreasing scheduling phase and minimizing latency. Despite the use of just one iteration, m-RGA delivers high throughput across diverse traffic conditions thanks to its tailored matching mechanism and dynamic responsiveness to port load variations. In addition, it operates using only a single-bit request per input port, significantly lowering communication overhead and achieving a favorable tradeoff between scheduling efficiency and implementation complexity.

Second, m-RGA incorporates both strong and weak request mechanisms in a dual request mechanism, providing enhanced port utilization and matching stability. Strong requests allow matched ports to be re-used based on the results from the previous timeslot, maintaining existing matches and reducing redundant computation. Concurrently, weak requests increase the opportunities for new matches by avoiding direct contention with strong requests. This allows previously unmatched ports to compete more effectively based on port load, thereby improving the overall matching probability, enhancing throughput, and maintaining stable switching performance.

Third, m-RGA introduces scalable matching with global and local polling pointers. To steadily increase the number of input-output port matching, m-RGA employs both global and local polling pointer mechanisms. In a single iteration, some VOQs may fail to form point-to-point connections due to port contention. The global polling pointer periodically releases previously matched ports by clearing existing connections at each time slot, enabling re-matching and preventing the algorithm from converging to suboptimal local solutions. This promotes progressive optimization of matching quality and enhances system throughput. Simultaneously, the local polling pointer, in conjunction with historical service time constraints, disconnects point-to-point connections if a VOQ exceeds a predefined service delay threshold. These VOQs are then prioritized in subsequent scheduling, effectively mitigating starvation. Together, the global and local pointer mechanisms improve matching flexibility and fairness, enabling the algorithm to maintain stability and adaptability under various traffic patterns.

Fourth, m-RGA employs simplified hardware implementation in the form of a lightweight hardware structure consisting of a set of state counters at both input and output ports. In combination with the use of global and local pointers to guide efficient matching, these counters and control mechanisms are straightforward to implement on existing hardware platforms, allowing the algorithm to be practically deployed with minimal hardware overhead.

3.2. Time Complexity of m-RGA

In this paper, each non-empty VOQ only has two conditions when sending a request signal: strong request signals or weak request signals. In fact, the m-RGA algorithm does not sort the two kinds of signals; in the grant phase, the Arbiter component chooses according to the request signal that is sent, and the request signal at this time will not exceed N (where N is the number of ports). In the grant phase, the actual operation sequence of the Arbiter component is as follows: (1) the Arbiter receives the request signal and judges the priority of the request signal (strong request is greater than weak request); (2) the Arbiter determines whether the relationship between the input port i, output port j, and time slot t of Equation (1) is satisfied according to the strong request priority; if it is satisfied, the input port i is given priority; (3) if Equation (1) is not satisfied, the Arbiter selects which input port i to grant priority to based on the value in each SC[i]. The arbiter in each port performs the above steps.

Therefore, returning to the time complexity of m-RGA, the choice of strong and weak request signals is actually only $O\left(1\right)$. However, a schedule contains three phases (request, grant, and acknowledge), in which only the grant phase needs to make the most response to the request signal, which is $O\left(N^2\right)$. As the number of grant signals in the acknowledge phase will be further reduced ($O\left(N\right)$ at most), we only consider the ordering of SC[i] in the grant phase. However, SC[i] actually detects the length of each VOQ. Commonly used sorting algorithms such as quicksort run in $O(nlogn)$ time; in practice, however, the ranking process can be greatly simplified due to the property of input-queued switches that any input port receives and sends at most one packet per time slot.

Specifically, the ranked list can be stored in a balanced binary search tree. When a new packet arrives at ${\mathrm{VOQ}}_{ij}$, its queue size is increased by one, while the other VOQs remain unchanged; then, the new ranking of ${\mathrm{VOQ}}_{ij}$ becomes higher or remains the same. The time complexity of finding a new rank in a binary tree is $O(logn)$. The same procedure can also be used for packet departure processing. Therefore, the overall time complexity of m-RGA is reduced to $O(logn)$. In summary, the time complexity of the m-RGA algorithm is $O(logn)$ due to the use of balanced binary search tree to maintain and update the queue. This shows that the algorithm has a significant advantage in efficiency, especially when dealing with large-scale data exchange.

3.3. Pseudocode Description of the m-RGA Algorithm

This subsection explains the pseudocode of m-RGA (Algorithm 1). During the request phase, each nonempty ${\mathrm{VOQ}}_{ij}$ sends a strong or weak request signal as appropriate. In the grant phase, the Arbiter component selects the strong/weak grant signal according to the strong/weak request signal and the longest $\mathrm{SC}\left[k\right]$. In the accept phase, the Input Arbiter selects the final result based on the size of $\mathrm{actTime}\left[i\right]\left[j\right]$ of the grant signal.

• $SC\left[i\right]\left[j\right]$: Length of the k-th VOQ in output port.
• $actTime\left[i\right]\left[j\right]$: Last activated time of VOQ ${}_{i,j}$.
• A: Activation time threshold for VOQ ${}_{i,j}$.
• $\mathrm{Arbiter}\left[j\right]$: The j-th arbiter in the output port.
• $\mathrm{input}\_\mathrm{Arbiter}\left[i\right]$: The i-th arbiter in the input port.
• $busy\left[i\right]\left[j\right]$: A Boolean indicating whether VOQ ${}_{i,j}$ was successfully matched in the last timeslot.

Algorithm 1: m-RGA Algorithm

3.4. Comparative Analysis of Algorithm Performance

In this chapter, we technically compare our newly proposed m-RGA algorithm with the performance of previously introduced algorithms. The summary results are recorded in

Table 1. Comparison of m-RGA with other algorithms.

Scheduling Algorithm	Number of Iterations	Request Type	Input/Output Arbiter	Time Complexity
iSLIP	Multiple iterations	Multiple SBR	Local Round Robin	$O\left(1\right)$
PIM	Multiple iterations	Multiple SBRS	Random Selection	$O(NlogN)$
iLQF	Multiple iterations	Multiple MBR	Longest VOQ	$O(N^{2}logN)$
$\Pi$-RGA	Single iteration	Multiple MBRS	Dynamic priority matching	$O(logN)$
SRR	Single iteration	Single SBR	Global Round Robin and longest VOQ (input only)	$O(logN)$
RR/LQF	Single iteration	Single SBR	Global Round Robin and longest VOQ	$O(logN)$
HRF	Single iteration	Multiple SBRS	Global Round Robin and Highest Rank	$O(logN)$
m-RGA	Single iteration	Multiple SBRS	Global and Loacl Round Robin	$O(logN)$

. The m-RGA algorithm combines global and local polling mechanisms to ensure that the matching is stable, and gradually provides fairness for other ports to obtain the priority. Because each port of m-RGA only sorts the state counters into strong and weak signals, the time complexity of m-RGA is O(logN). In this chapter, m-RGA, SRR, RR/LQF, and HRF all belong to the category of single-iteration scheduling algorithms. These algorithms are compared and the differences are summarized in Table 1. In addition, although we have summarized the complexity of the other algorithms in Table 1, this does not fully represent their overall complexity; for example $\Pi$-RGA and HRF are actually difficult to implement during execution due to their high complexity. In addition, both iSLIP and iLQF can have single and multiple iterations; only their single-iteration cases are summarized in Table 1.

To accurately represent the earliest activation time in $\Pi$-RGA, it is necessary to use Multi Bit Request (MBRS) to store these timestamps and transmit multiple MBRS in the control link. Because only the earliest activation time and state counter are used, $\Pi$-RGA is only suitable for transmission in non-uniform traffic scenarios. In high load and uniform traffic scenarios, the priority differentiation of each port is low, as the activation time of all VOQs is very close. However, SRR, RR/LQF, HRF, and m-RGA all adopt preferential input–output pairs, that is, global polling. Both SRR and RR/LQF use the longest VOQ; SRR uses the longest VOQ at the input, while RR/LQF uses the longest VOQ at the input and output ports, then uses a polling method in cases with more than one VOQ. HRF proposes a highest VOQ rank-first approach, which has more matching possibilities than just using the longest VOQ. Our m-RGA absorbs the advantages of $\Pi$-RGA by only sending a Single Bit Request (SBR) when the VOQ is not empty, which improves the poor performance of $\Pi$-RGA in uniform traffic scenarios. In addition, m-RGA introduces global and local polling methods to modify the shortcomings of $\Pi$-RGA in uniform traffic scenarios.

The design of the m-RGA algorithm is actually based on the limitations of the traditional scheduling algorithm, that is, multiple iterations and multi-bit communication overhead. In the design of traditional scheduling algorithm, it generally takes $O\left(logN\right)$ iterations to complete the maximum matching of ports (when no input or output is unnecessary idle, the rate maximum matching is achieved), and the most influence on the number of communication overhead bits in the scheduling process is the comparison of queue lengths in the request phase. The m-RGA algorithm only needs one or two iterations, that is, the corresponding matching between ports can be completed, and the level is reduced to $O\left(1\right)$. In addition, because only 2 bits of the priority of the request signal need to be transmitted in the request phase, the time delay in the communication process is greatly reduced compared to using the queue length as the priority, as in the iLQF algorithm, and the communication overhead in this phase is also $O\left(1\right)$ level.

For the other counters (SC[i], R, and P), the design itself is related to the state of VOQ and the Arbiter component; thus, a group of VOQ strong and weak priority counters, a group of oldest activation time counters, and a group of VOQ queue length counters need to be added. These counters and state variables are very convenient and simple when implemented in existing hardware.

4. Performance Analysis

This section describes the design and testing of m-RGA. The simulation experiment used OMNeT++5.5.1 and was run on a Windows computer with Intel(R) Core(TM) i5-10210U CPU and 12GB RAM. We analyzed the performance of the new algorithm through simulation and compared it with other classical iterative scheduling algorithms such as PIM, iSLIP, iLQF, SRR, RR/LQF, HRF, and $\Pi$-RGA. In Figure 5, Figure 6 and Figure 7 we consider three classical traffic patterns, namely, uniform, bursty, and hotspot traffic. Although we set the size of the switch to N = 32 in the simulation, the results also hold for other sizes. Finally, each data point in the figure is the result of running ${10}^5$ timeslots, where the initial 5 × ${10}^3$ timeslots are the warm-up phase and the threshold of its historical load is 50. The horizontal axis represents the input load p and the vertical axis represents the average queuing delay of data packets.

4.1. Uniform Traffic

In the uniform traffic model, during each time slot, a packet arrives at each input port with a probability p (i.e., the input load) and the destination output port is selected uniformly at random.

In Figure 5, the performance ratios of the PIM, iLQF, and $\Pi$-RGA algorithms are still significantly different from those of SRR, iSLIP, RR/LQF, and m-RGA and weaker than those of HRF. When the input load is at low or medium level, the gap between SRR, RR/LQF, and m-RGA is not very large. This is because the number of non-empty VOQs in the matching state is not large and the activation time is mostly in the same time slot. In this case, Equation (1) can be used to directly obtain the matching result. When the input load p = 0.7, in m-RGA the data packet can wait an average of 99.168 timeslots to complete the scheduling; however, in this case the data packet needs 213.83 timeslots to complete. The former is about two times less than the latter, while in the $\Pi$-RGA algorithm, the data packet needs 732.87 time slots to complete; thus, m-RGA is about more than seven times as large. When the input load p > 0.7, the delay performance of $\Pi$-RGA becomes sluggish, which may be because its activation time is in effect as the load increases. When the input load p > 0.8, m-RGA performs better than SRR and RR/LQF. This is because in the uniform traffic pattern, when choosing VOQ, all arbiters consider not only the historical service time but also its load strength, which is more convenient for distinguishing priorities and generating request signals with different strengths. In summary, this prioritization mechanism is significantly more complex than the preferred formula calculation, meaning that its performance increases dramatically.

4.2. Burst Traffic

The bursty traffic follows the ON/OFF traffic model, which is modeled by a two-state Markov process. In the ON state, a packet arrival is generated for each time slot. In the OFF state, no packet arrives. Packets of the same burst have the same destination port, and the destination ports of each burst are uniformly distributed. Given the average input load p and burst size s, the state transition probability from OFF to ON is p/[s(1-p)] and the state transition probability from ON to OFF is 1/s. During our simulation, we set the burst size s = 30 packets.

In Figure 6, the performance of $\Pi$-RGA and m-RGA algorithm is significantly better than that of HRF algorithm. When the input load p > 0.7, the average queuing delay of HRF algorithm increases sharply, while that of $\Pi$-RGA and m-RGA algorithm increases significantly after input load p > 0.8. m-RGA only uses the VOQ queue length in the output accept phase and only transmits single-bit information of strong and weak signals in the communication phase. This is different from HRF, which sorts the VOQ queue length first and then encodes it, which increases extra computational overhead and delay consumption. m-RGA is more responsive to historical response/activation time and load intensity in the same time slot. This is because in our implementation we use the queue length and activation time considerations of VOQ, meaning that it consumes less time than HRF. The performance of the m-RGA algorithm is also better than that of the $\Pi$-RGA algorithm, which is because m-RGA uses only a single bit of communication overhead in the request and prioritizes serving the last timeslot to match the port, while $\Pi$-RGA uses multi-bit communication overhead in the control phase. As a result, m-RGA shows reduced delay consumption in the transmission process.

4.3. Hotspot Traffic

In Figure 7, the performance of $\Pi$-RGA and m-RGA algorithms is significantly better than that of HRF algorithm. When input load p > 0.7, the average queuing delay of the HRF algorithm increases sharply, while that of the $\Pi$-RGA and m-RGA algorithms increases significantly after input load p > 0.8. According to the characteristics of hotspot traffic, a VOQ will continue to receive data packets, and when the VOQ is responded multiple times it will seriously affect the queuing time of other VOQs. Therefore, we introduce the historical activation time to provide port fairness; as the VOQ load continues to rise, the priority of other VOQs will also increase.

4.4. Fairness Analysis

Table 2. The fairness of the m-RGA algorithm under high load ($p\ge 80$) conditions.

Input Load P (%)	Bursty Traffic (%)	Hotspot Traffic (%)
80%	97.21%	98.32%
85%	97.64%	98.42%
90%	98.92%	98.20%
95%	96.57%	97.68%

shows the fairness of the m-RGA algorithm under high load ($p\ge 80$) conditions under the burst traffic and hotspot traffic models. As shown in the table, the fairness performance of m-RGA can remain above 97% even in high-load traffic scenarios. This is related to the increase of the priority input–output pairs in Equation (1). When the port is not in a matching state and the port load is high, the port will preferentially execute this formula. Additionally, when the historical load of VOQ is greater than 50, the VOQ that has not been in a “hungry” state will also be matched.

5. Future Prospects

First, in the traffic patterns used in our experiments, we have mainly discussed the ideal case of the m-RGA algorithm under uniform, uniform bursty, and hotspot traffic scenarios. However, in actual hardware implementations bursts will also be generated for different types of traffic scenarios, including extreme scenarios. In this study, we were limited by the specific time frame and available hardware resources; thus, there are some intended use cases that have not yet been fully covered or explored in depth. Our experiments focused on key scenarios that can effectively demonstrate the core advantages of the m-RGA algorithm. This means that despite our encouraging results in these critical scenarios, we have not yet fully evaluated other possible application scenarios, especially those requiring higher flexibility or adaptation to more complex network dynamics.

Second, the m-RGA algorithm relies on the ordering of queue length and the ordering of the oldest activation time in the parameter settings, which requires the information of each VOQ to be precisely maintained. This mechanism requires careful consideration during parameter setting. Particularly in dynamic network environments, it is crucial to ensure that the ranking can accurately reflect the actual queue state changes.

Third, concerning the sensitivity of hardware constraints, this precise parameter setting of the m-RGA algorithm is an important consideration for modern high-speed switches that seek high performance and low latency. In hardware implementation, it will occupy more resources, which limits its application in resource-first environments.

Future work will be devoted to further expanding the application scope of m-RGA algorithm, including but not limited to developing more elaborate parameter adjustment mechanisms, exploring performance under different traffic patterns, and optimizing the performance of the algorithm for different hardware configurations. We look forward to addressing the current limitations in subsequent research and continuously improving the applicability and efficiency of m-RGA algorithm.

6. Conclusions

In this paper, we propose a new single-iteration scheduling algorithm which reduces the limitations of the traditional iterative algorithm and limits the number of iterations and the overhead of the request phase to a single and single bit. To ensure high throughput and low delay, the VOQ priority is dynamically adjusted according to the historical service time and load degree of the VOQ in the port, meaning that each VOQ has a chance to be served and the starvation problem caused by some VOQs not being served for a long time is avoided. Second, we provide a time complexity analysis of the proposed m-RGA algorithm and list it together with other algorithms to compare the number of iterations, request type, input/output arbitration, and time complexity. Third, we discuss the shortcomings of the m-RGA algorithm, specifically its sensitivity to traffic patterns, parameter settings, and hardware limitations. We show that an algorithm that achieves a speedup of 2 under a constant traffic model can achieve both throughput and delay performance, which makes the algorithm as good as any maximum matching algorithm in a theoretical sense. Simulation results show that the proposed algorithm can achieve high throughput under both uniform and non-uniform traffic patterns.