Abstract
Creating high-fidelity digital twins (DTs) for Industry 4.0 applications, it is fundamentally reliant on the accurate 3D modeling of physical assets, a task complicated by the inherent imperfections of real-world point cloud data. This paper addresses the challenge of reconstructing accurate, watertight, and topologically sound 3D meshes from sparse, noisy, and incomplete point clouds acquired in complex industrial environments. We introduce a robust two-stage completion-to-reconstruction framework, C2R3D-Net, that systematically tackles this problem. The methodology first employs a pretrained, self-supervised point cloud completion network to infer a dense and structurally coherent geometric representation from degraded inputs. Subsequently, a novel adaptive surface reconstruction network generates the final high-fidelity mesh. This network features a hybrid encoder (FKAConv-LSA-DC), which integrates fixed-kernel and deformable convolutions with local self-attention to robustly capture both coarse geometry and fine details, and a boundary-aware multi-head interpolation decoder, which explicitly models sharp edges and thin structures to preserve geometric fidelity. Comprehensive experiments on the large-scale synthetic ShapeNet benchmark demonstrate state-of-the-art performance across all standard metrics. Crucially, we validate the framework’s strong zero-shot generalization capability by deploying the model—trained exclusively on synthetic data—to reconstruct complex assets from a custom-collected industrial dataset without any additional fine-tuning. The results confirm the method’s suitability as a robust and scalable approach for 3D asset modeling, a critical enabling step for creating high-fidelity DTs in demanding, unseen industrial settings.
1. Introduction
The fourth industrial revolution, or Industry 4.0, is catalyzing a paradigm shift in manufacturing, driven by the integration of cyber–physical systems, the Internet of Things (IoT), and data-driven analytics [1,2,3,4]. Central to this transformation is the concept of the digital twin (DT), a high-fidelity virtual representation of a physical asset, process, or system that serves as its dynamic digital counterpart. By mirroring the entire life cycle of industrial entities, DTs unlock transformative capabilities in predictive maintenance, process optimization, and virtual commissioning [5,6,7,8]. However, the efficacy of these advanced applications is fundamentally contingent on the accuracy and fidelity of the underlying 3D geometric model, which serves as the digital foundation for the physical asset. This foundational challenge of creating high-fidelity models from imperfect point cloud data, acquired via LiDAR or photogrammetry, has therefore become a critical bottleneck [9].
The efficacy of a DT is fundamentally contingent on the accuracy and fidelity of its underlying 3D model. Point cloud data, acquired via LiDAR scanning or photogrammetry, has emerged as the primary modality for capturing the complex geometries of as-is industrial environments [10,11]. However, raw point clouds are inherently imperfect, suffering from significant data degradation due to occlusions, non-uniform sampling densities, sensor noise, and the intricate nature of industrial machinery [12]. These challenges give rise to incomplete and ambiguous geometric representations, which severely impede the direct generation of accurate, watertight, and topologically sound 3D meshes, which are required for robust DT applications [13,14,15].
Current methodologies for 3D surface reconstruction from point clouds, while having progressed significantly, still face critical limitations in the demanding context of industrial settings [16,17,18]. Traditional geometric approaches often falter in the presence of noise and sparsity, struggling to preserve sharp features, thin structures, and complex topologies characteristic of industrial components. While learning-based methods, particularly those employing implicit neural representations, have demonstrated superior robustness, they often presuppose relatively clean and complete input data [19]. Although many prior works adopt two-stage pipelines, their ultimate performance is highly contingent upon the output quality of the initial completion network [20]. More crucially, traditional reconstruction networks employed in the second stage frequently exhibit limited robustness when processing the inevitably imperfect point clouds generated during completion. These networks typically assume clean and complete inputs, making them prone to losing fine-grained structures or amplifying residual noise, artifacts, and geometric inconsistencies inherited from the completion phase. Such deficiencies ultimately compromise the fidelity and reliability of the resulting DT models.
Furthermore, the reliance on extensive annotated datasets for training remains a major bottleneck for practical deployment [21,22]. In real-world industrial scenarios, acquiring and manually labeling high-quality data for every new asset, environment, or configuration is often infeasible due to prohibitive cost and time requirements. Therefore, developing models with strong zero-shot capabilities has emerged as a problem of paramount importance. In this work, the term zero-shot 3D reconstruction refers to the capability of a model to accurately reconstruct 3D surfaces of previously unseen objects or scenes without any additional fine-tuning or retraining on target domain data. Specifically, it denotes transferring geometric priors learned exclusively from synthetic datasets to real-world industrial scans, thereby bridging the domain gap purely through inherent model generalization.
To address these pressing challenges, this paper introduces C2R3D-Net, a robust two-stage framework specifically designed to generate high-fidelity 3D surface meshes that form the geometric foundation for industrial digital twin (DT) applications. The proposed approach systematically decomposes the reconstruction task into two sequential components: self-supervised point cloud completion and adaptive, boundary-aware surface reconstruction. In the first stage, we leverage a pretrained, Transformer-based network, FMPNet [23], to infer a complete and structurally coherent point cloud representation from partial inputs, thereby effectively mitigating data degradation without the need for manual annotations.
The core contribution of this work lies in the second stage: a novel surface reconstruction network engineered for high-fidelity modeling of complex industrial geometries. Its innovations include the following:
- An enhanced encoder architecture, FKAConv-LSA-DC, that dynamically fuses fixed-kernel and deformable convolutions with a local self-attention mechanism. This hybrid design robustly captures both global structural context and fine-grained, adaptive local features, demonstrating superior performance on irregular and topologically complex shapes.
- A boundary-aware multi-head interpolation decoder that explicitly modulates attention weights based on proximity to geometric boundaries. This mechanism significantly enhances reconstruction fidelity for sharp edges, thin structures, and other challenging surface features where conventional methods typically fail.
- A comprehensive validation that demonstrates the framework’s strong zero-shot, cross-domain performance. Our model, trained solely on the ShapeNet synthetic benchmark, successfully reconstructs complex, unseen industrial assets from real-world scans without any fine-tuning, outperforming leading approaches and confirming its practical deployability.
This paper is structured as follows: Section 2 reviews related work in point cloud completion and surface reconstruction, identifying the research gaps our work addresses. Section 3 details the proposed methodology, including the architecture of our adaptive reconstruction network. Section 4 presents a comprehensive experimental evaluation, including quantitative and qualitative results, comparisons with state-of-the-art methods, and an in-depth ablation study. Finally, Section 5 discusses the implications and limitations of our findings, and Section 6 concludes this paper with a summary of its contributions and avenues for future research.
2. Related Work
This section provides a narrative review of seminal and contemporary works in point cloud completion and surface reconstruction. We categorize existing methods based on their underlying technical paradigms to situate our contributions and identify the key research gaps that this paper addresses. Relevant studies were identified through targeted keyword searches in major scientific databases.
2.1. Self-Supervised Point Cloud Completion Methods
In recent years, self-supervised learning (SSL) has become a dominant approach for representation learning in 3D point cloud domains [24]. By formulating pretext tasks based on intrinsic geometric patterns, SSL methods eliminate the need for costly manual annotations and enable efficient large-scale training [25]. This section reviews several representative strategies and clarifies the data provenance adopted in this work.
One notable line of research focuses on masked point or patch reconstruction. Inspired by masked language modeling in natural language processing, Point-BERT [26] introduced masked modeling to point clouds by recovering discrete point tokens within masked regions using a discrete variational autoencoder (dVAE). Building on this foundation, Point-MAE [27] employed an asymmetric encoder–decoder architecture to reconstruct point patches under high masking ratios. Point-M2AE [28] further enhanced this paradigm by integrating multi-scale masking with a hierarchical Transformer, allowing progressive decoding and coarse-to-fine representation learning.
Recent work has also leveraged cross-modal supervision or large-scale scene data. ULIP [29] learns unified embeddings for point clouds, images, and language by distilling knowledge from pretrained vision–language models, thus enhancing 3D understanding without explicit 3D labels. Occupancy-MAE [30], targeting large-scale outdoor LiDAR datasets, reformulated the reconstruction objective by predicting voxel-level occupancy instead of raw coordinates, leading to more robust performance in sparse environments.
In our prior work [23], we proposed a feature-masked pyramid network (FMPNet) that learns to complete sparse or occluded point clouds through a Transformer-based self-supervised pipeline. The model encodes multi-scale geometric features and decodes complete shapes using a hierarchical folding mechanism. Extensive experiments validated the effectiveness of this method in recovering semantically and structurally consistent 3D shapes across synthetic and real-world datasets.
In this study, we directly use the completed point clouds generated by FMPNet [23] as the input to our surface reconstruction pipeline. We focus exclusively on the downstream task of mesh generation from completed point clouds and do not revisit the completion process in detail.
2.2. Surface Reconstruction
Surface reconstruction from point clouds is a core problem in 3D vision and graphics, with critical applications in DT systems and industrial-scale modeling. Existing methods fall into four main categories: surface-based interpolation, surface-based approximation, volume-based interpolation, and volume-based approximation. This section presents a structured review of these paradigms, emphasizing representative techniques, their strengths, and their inherent limitations.
2.2.1. Surface-Based Interpolation Methods
Surface-based interpolation methods construct triangular meshes directly by connecting locally adjacent points in the point cloud. A representative example is the Ball Pivoting Algorithm (BPA) [31], which simulates a virtual ball pivoting across points to form triangle faces. The BPA is computationally efficient and yields satisfactory results on uniformly sampled, noise-free data. However, its performance degrades severely in the presence of noise, occlusions, or irregular point density. The method is highly sensitive to the choice of ball radius and cannot reliably handle complex topologies such as multiple holes or thin branches, often failing to generate manifold or watertight meshes.
Recent improvements have sought to increase robustness against such limitations. For instance, IER-Meshing [32] employs a learned intrinsic–extrinsic ratio (IER) to assess whether point pairs lie on a continuous surface. It constructs candidate triangles from k-nearest neighbor graphs and uses a neural network to predict the ratio between Euclidean and geodesic distances. Triangles with high surface continuity likelihood are retained. While IER-Meshing improves robustness to noise, it still struggles to guarantee manifoldness and complete watertightness under real-world scanning artifacts.
2.2.2. Surface-Based Approximation Methods
Surface-based approximation methods reconstruct surfaces by fitting parameterized local patches or deforming template meshes to approximate the underlying geometry. These methods are capable of capturing complex surface details and typically do not require ground-truth meshes during training.
Delaunay triangulation-based reconstruction [33] offers a classical geometric approach by establishing neighborhood connections through Delaunay complexes. It constructs a triangulated surface by selecting a subset of simplices from the Delaunay triangulation that best matches the sampled surface in terms of local geometry and topology. This method effectively handles non-uniform sampling and adapts to local curvature, making it a robust alternative to grid-based interpolation. However, the method lacks explicit constraints to ensure global smoothness or watertightness, and it may generate non-manifold artifacts in sparse or noisy regions.
DSE-Meshing [34] further improves local surface fidelity by projecting neighborhoods via logarithmic maps and applying Delaunay triangulation in the projected space. The resulting local patches are then aligned and merged in 3D to form a global surface. While this learning-based approach adapts well to fine-scale geometry and topological variations, it still does not guarantee closed or manifold surfaces due to potential inconsistencies in patch integration.
2.2.3. Volume-Based Interpolation Methods
Volume-based interpolation techniques partition the 3D space (e.g., into voxels or tetrahedra) and derive surface boundaries based on occupancy or visibility labeling. These methods naturally produce watertight and manifold surfaces and are robust to topological complexity and missing data.
The -shapes algorithm [35] constructs Delaunay tetrahedralizations and retains those with a circumsphere radius below a threshold . The boundary of retained tetrahedra approximates the object’s surface. Although intuitive and effective on clean data, -shapes are highly sensitive to parameter tuning and data resolution.
Graph-cut-based labeling methods [36] provide more robust alternatives. They formulate surface reconstruction as an energy minimization problem over a 3D Delaunay graph, labeling each tetrahedron as inside or outside based on visibility and smoothness priors. Recent extensions, such as DGNN [37], use graph neural networks to estimate per-tetrahedron occupancy, improving adaptability to real-world data while preserving surface watertightness and manifoldness.
2.2.4. Volume-Based Approximation Methods
Volume-based approximation has emerged as the dominant paradigm for point cloud surface reconstruction, wherein surfaces are represented implicitly via continuous fields such as signed distance functions (SDFs) or occupancy fields, often parameterized by neural networks to capture complex geometry from sparse and noisy inputs. A classical method in this category is Screened Poisson Surface Reconstruction (SPSR) [38], which solves a Poisson equation over the gradient field induced by oriented points to generate smooth, watertight meshes. However, its reliance on clean normals often leads to oversmoothing of fine structures.
To overcome such limitations, learning-based implicit representations have been introduced. DeepSDF [18] learns continuous SDFs conditioned on latent codes, enabling expressive shape modeling across categories, though at the cost of requiring per-instance optimization and ground-truth SDF supervision. ConvONet [17] addresses scalability by combining convolutional encoders with implicit decoders, utilizing 3D CNNs to capture local spatial priors, but remains limited by voxel discretization and memory usage. SAP [39] reformulates the problem as predicting a set of oriented points, which are then converted into an implicit field via a differentiable Poisson solver, yielding accurate and efficient reconstructions by integrating geometric priors in an end-to-end manner. POCO [40] proposes a point-based convolutional architecture that leverages local geometric features and attention mechanisms to predict occupancy values at arbitrary query locations. By avoiding voxelization, it offers improved adaptability to varying point densities and has demonstrated competitive performance in detail preservation and topological consistency on standard benchmarks.
In summary, surface reconstruction has undergone a significant transition from explicit mesh-based methods to learning-driven implicit modeling paradigms. Classical techniques based on surface interpolation and approximation offer computational efficiency and intuitive formulations yet often struggle with noisy inputs and complex topologies. In contrast, recent advances in volumetric representations—particularly those employing implicit neural fields—demonstrate superior robustness and generalization, enabling high-fidelity surface recovery under real-world sensing conditions. This evolution reflects a broader trend from deterministic geometry-based pipelines toward data-driven, flexible frameworks that are better suited for handling incomplete, irregular, and cluttered point clouds. The comparative analysis of representative methods across interpolation-based and volumetric approaches further underscores how learning-based designs enhance adaptability, accuracy, and structural integrity in surface reconstruction tasks.
Table 1 summarizes representative surface reconstruction methods across all categories, highlighting their core principles, strengths, limitations, and references for ease of comparison.

Table 1.
Summary of surface reconstruction methods.
2.3. Research Gaps
Despite significant progress in point cloud completion and surface reconstruction, several critical challenges remain unresolved, particularly in the context of DT modeling for complex industrial environments.
Firstly, most existing surface reconstruction methods inherently rely on the assumption of surface smoothness, which severely limits their capacity to accurately recover sharp boundaries, thin structures, and intricate topologies frequently encountered in industrial components.
Secondly, contemporary reconstruction frameworks exhibit limited adaptability when processing non-uniform, sparse, or noisy point clouds, conditions that are ubiquitous in real-world scanning scenarios. Although attention-based mechanisms and convolutional architectures have demonstrated promise, their ability to robustly capture highly variable local geometric patterns remains insufficient.
Thirdly, the majority of widely adopted two-stage frameworks lack explicit coupling strategies between the completion and reconstruction phases. In most existing methods, the optimization objectives of the completion networks are limited to standalone output metrics (e.g., Chamfer Distance), without considering whether the predicted point clouds are inherently well-suited for downstream surface generation. Reconstruction networks, in turn, are seldom tailored to leverage the specific characteristics of completion outputs. As a result, structural inconsistencies introduced during completion often propagate unmitigated into the reconstruction stage. Consequently, the lack of end-to-end training prevents reconstruction losses from directly influencing completion learning dynamics, ultimately constraining the achievable fidelity on complex industrial geometries.
Finally, the majority of learning-based reconstruction methods necessitate extensive annotated datasets to achieve competitive performance. This reliance significantly impedes scalability and generalization to previously unseen environments. Of particular concern is the lack of zero-shot reconstruction capabilities, wherein models are expected to extrapolate to novel industrial shapes without additional fine-tuning. This gap is especially critical for practical deployment in industrial scenarios, where acquiring comprehensive labeled data is often prohibitively expensive, time-consuming, or altogether infeasible.
3. Methods
We now describe the proposed two-stage pipeline as C2R3D-Net (Completion-to-Reconstruction 3D Network). This architecture first leverages a pretrained completion backbone to infer dense and structurally coherent point clouds from sparse inputs, and subsequently reconstructs high-fidelity 3D meshes via a novel adaptive reconstruction module.
Figure 1 provides an overview of C2R3D-Net. As illustrated, the framework comprises two main stages: a point cloud completion module and a surface reconstruction module. The first stage employs a Transformer-based encoder–decoder architecture to predict dense and semantically consistent point clouds from incomplete observations. The second stage reconstructs high-fidelity meshes by learning an implicit occupancy field through boundary-aware interpolation.
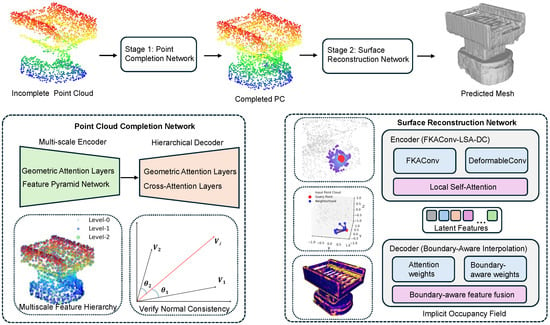
Figure 1.
Overview of C2R3D-Net, the proposed completion-to-reconstruction framework. The pipeline comprises two sequential stages. First, the point cloud completion module leverages FMPNet to generate dense and structurally consistent point clouds from incomplete inputs. Second, the surface reconstruction module employs a multi-scale encoder integrating FKAConv, Deformable Convolution, and Local Self-Attention to extract hierarchical geometric features, followed by a boundary-aware multi-head interpolation decoder that predicts implicit occupancy fields and reconstructs high-fidelity 3D meshes. Notably, in the surface reconstruction network, the three images on the left (from top to bottom) illustrate the operations of DeformableConv, Local Self-Attention, and boundary-aware weights, respectively.
3.1. Point Completion via FMPNet
In this work, we adopt the published FMPNet [23] as the point cloud completion backbone. The model was originally proposed for self-supervised 3D shape completion in industrial DT scenarios, demonstrating strong performance under severe occlusion and structural incompleteness. We do not modify or retrain this component; instead, we directly integrate it into our reconstruction pipeline as a fixed, frozen module.
FMPNet is a Transformer-based point cloud completion network that leverages a feature pyramid network (FPN) integrated with geometric attention layers to model hierarchical geometric priors. Its architecture consists of two main components: (i) a multi-scale encoder that utilizes stacked geometric attention layers to progressively extract local and global features from partial inputs; and (ii) a decoder that employs cross-attention mechanisms to fuse these multi-scale features and generate a dense, complete point cloud.
Notably, FMPNet’s training is guided by a comprehensive multi-objective loss function without requiring ground-truth labels. This loss combines a shape reconstruction loss and a shape matching loss (both based on Chamfer Distance), a latent space alignment loss, and a manifoldness constraint that promotes surface smoothness through normal vector consistency.
In contrast to prior works that treat completion and reconstruction as fully independent stages, our approach incorporates explicit priors in the completion phase to improve downstream surface quality. Specifically, the latent space alignment loss constrains the completed point clouds to reside in a globally consistent shape embedding, thereby reducing distributional discrepancies that could hinder subsequent reconstruction. Simultaneously, the manifoldness constraint enforces local normal coherence, encouraging the completion network to produce smooth and geometrically plausible surfaces. Together, these mechanisms serve as a form of prior coupling that effectively enhances the compatibility of the completion outputs with the reconstruction module.
In our system, FMPNet processes the input partial point cloud and produces a completed version with 3000 points and associated normals. These outputs are subsequently consumed by our mesh reconstruction module, as described in Section 3.2.
3.2. Adaptive Point-to-Mesh Reconstruction Method
To reconstruct accurate and high-fidelity 3D surfaces from incomplete point clouds in DT applications, we propose an adaptive reconstruction pipeline based on point-wise convolutional encoding and boundary-aware occupancy interpolation. To improve conceptual clarity, Figure 2 presents an intuitive example of occupancy-based interpolation. This illustration shows how sparse point observations are transformed into a continuous occupancy field, which is then thresholded to extract coherent surface boundaries.
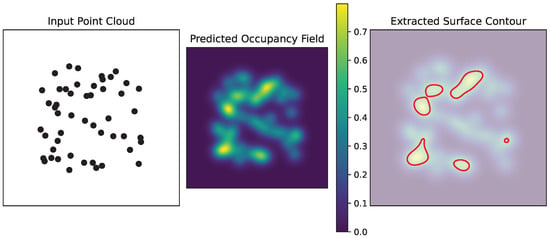
Figure 2.
Conceptual illustration of occupancy-based interpolation. Left: Incomplete input point cloud exhibiting sparsity and missing regions. Center: Predicted occupancy field, where higher intensity indicates a greater probability of occupancy. Right: Extracted contour corresponding to the 0.5 occupancy threshold, delineating the reconstructed surface boundary.
As illustrated across Figure 3 and Figure 4, the pipeline comprises three primary stages: (1) local feature encoding using a self-attention enhanced network, (2) boundary-aware multi-head interpolation for per-point occupancy prediction, and (3) mesh extraction via isosurface reconstruction.
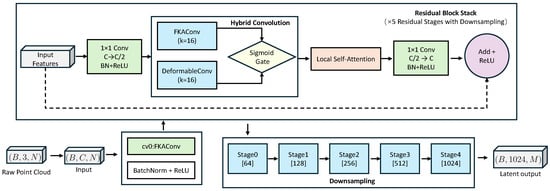
Figure 3.
Overview of the proposed encoder architecture based on stacked residual blocks. Starting from raw point cloud input , the input features are first processed by an initial convolutional layer (cv0) followed by batch normalization and ReLU activation. The resulting features are then passed through a stack of five residual blocks, each containing a hybrid convolution module that adaptively fuses Deformable Convolution and FKAConv via a learnable sigmoid gate. This is followed by local self-attention and a 1 × 1 convolution to restore channel dimensions. A shortcut connection and optional max pooling are applied before the residual addition and ReLU activation. The output is a latent representation of shape , progressively downsampled across stages.
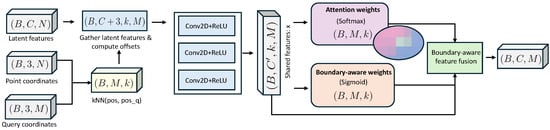
Figure 4.
Illustration of the boundary-aware multi-head interpolation decoder. Latent features are aggregated via k-NN and fused with geometric offsets. Attention weights (Softmax) are rescaled by learned boundary-aware modulation weights (Sigmoid) to enhance sensitivity near structural boundaries.
Building upon this conceptual foundation, the proposed design enables robust geometric reconstruction under sparse, noisy, and structurally complex industrial settings.
3.2.1. Local Self-Attention Encoder with Adaptive Deformable Convolution (FKAConv-LSA-DC)
As shown in Figure 3, we propose an enhanced encoder architecture that integrates a Deformable Convolution (DeformableConv) module with a Local Self-Attention (LSA) mechanism to improve geometric representation learning under irregular and non-manifold structures. Unlike fixed-kernel approaches such as FKAConv, our DeformableConv dynamically adapts its receptive fields by learning spatially adaptive kernel weights based on local feature variations. This enables more flexible and context-aware aggregation of neighborhood features, which is critical for capturing fine-grained geometric cues in complex industrial point clouds.
To further balance structural rigidity and adaptive flexibility, we design a hybrid convolutional module that fuses the outputs of FKAConv [41] and DeformableConv via a learnable sigmoid-based gating function. This dynamic fusion strategy allows the network to selectively leverage the strengths of both convolution types depending on local geometric context, thereby enhancing robustness across sparse, noisy, or topologically diverse regions.
To realize this adaptive behavior, we introduce a spatially aware kernel weighting strategy that computes dynamic attention scores based on feature contrasts within each local neighborhood. Given input features and corresponding neighbor indices, the kernel weights are computed as
where the concatenation of center–neighbor feature differences explicitly encodes local structural variations. The multi-layer perceptron (MLP) then maps these variations to a set of kernel scores , enabling the network to dynamically adjust the contribution of each convolutional basis during aggregation. This formulation allows the model to emphasize critical geometric cues such as curvature, sharp edges, and occluded regions.
We then perform a weighted summation over the adaptive kernel responses, leading to the output:
where denotes the i-th learnable convolution kernel, and K is the number of kernel bases. This formulation enables the model to flexibly select and blend multiple local filters based on the surrounding geometry.
To further enhance robustness and generalization, we propose a hybrid convolutional mechanism that adaptively combines the advantages of both fixed and deformable convolutions. This is achieved through a gated fusion strategy:
where is a learnable scalar and denotes the sigmoid function. This formulation allows the network to learn an optimal balance between the structural stability of FKAConv and the adaptability of DeformableConv. As a result, the hybrid module can effectively capture both coarse global geometry and fine-grained local deformations, which is critical for high-quality surface reconstruction in industrial DT applications.
Subsequently, the Local Self-Attention (LSA) module refines the convolutional features, capturing local contextual dependencies and enhancing sensitivity to structural variations. Given feature maps , the attention-enhanced representation is computed as
where , , are derived from shared convolutional layers and denotes linear projection. This dual integration of DeformableConv and LSA not only ensures high adaptability to geometric irregularities but also preserves long-range structural coherency.
Finally, global max pooling aggregates the enriched features into a compact latent embedding, which encodes both global context and local detail essential for accurate mesh reconstruction.
3.2.2. Boundary-Aware Multi-Head Interpolation Decoder
To reconstruct a continuous implicit occupancy field from the latent representation, we design a boundary-aware multi-head interpolation decoder that enhances geometric fidelity near structural discontinuities. As illustrated in Figure 4, our decoder integrates boundary-sensitive weighting directly into the attention computation, allowing for improved prediction around thin structures, occluded surfaces, and sharp edges—regions where conventional interpolation often fails.
Given a query point , we first retrieve its K nearest neighbors from the encoded point set using a fast k-NN search. For each neighbor, a relative embedding is computed by concatenating its latent feature with the geometric offset :
where the MLP consists of three shared convolutional layers with ReLU activations. This operation encodes both appearance and spatial context within each local neighborhood.
A shared multi-head attention mechanism is then applied to compute the importance of each neighbor. To improve discrimination near topological boundaries, we augment the attention weights with a learned boundary-aware modulation. For each head h, the attention score is computed as
where , are learnable parameters for head h, denotes the sigmoid function, and is a trainable scalar initialized to 1.0. The boundary-aware term amplifies the contribution of neighbors that lie on or near geometric boundaries, improving occupancy estimation in critical regions.
The final interpolated feature for the query point is obtained by aggregating over all heads and neighbors:
where is a lightweight decoder comprising three convolutional layers. The scalar output denotes the predicted occupancy at .
By densely sampling query points within a bounding volume and decoding their occupancy scores, we construct a volumetric occupancy field. The target surface is then extracted as the 0.5-level isosurface via Marching Cubes. The resulting mesh preserves both global structure and local geometric detail, even under sparse or noisy inputs, owing to the boundary-aware attention mechanism that guides feature interpolation in semantically challenging regions.
Beyond improving reconstruction fidelity, the architectural choices in our reconstruction network are also designed to enhance zero-shot generalization capability. Specifically, the hybrid encoder combining fixed-kernel and deformable convolutions allows the model to adaptively capture both coarse and fine-grained geometric patterns across a diverse range of shapes. The Local Self-Attention module further enables the network to model long-range dependencies, which is critical for transferring learned priors from synthetic training data to unseen real-world objects. In addition, the boundary-aware multi-head interpolation decoder improves robustness in reconstructing sharp edges and thin structures, even when input distributions differ significantly from those observed during training. Collectively, these components contribute to the framework’s strong performance under cross-domain and zero-shot evaluation settings, making it a practical solution for diverse industrial reconstruction scenarios.
4. Experiments
4.1. Datasets and Preprocessing
To rigorously evaluate the effectiveness of C2R3D-Net, the proposed completion-to-reconstruction framework, we conduct comprehensive experiments on two representative datasets: the large-scale synthetic benchmark ShapeNet [42], and a custom-collected industrial workshop dataset representing real-world manufacturing scenarios. All experiments were conducted on a workstation running Ubuntu 22.04 via Windows Subsystem for Linux (WSL), equipped with an Nvidia RTX 4070 Laptop GPU (NVIDIA Corporation, Santa Clara, CA, USA), an Intel Core i9-13980HX CPU (Intel Corporation, Santa Clara, CA, USA), and 48 GB of RAM. The implementation was developed in Python 3.13.2 using the PyTorch 1.8.1 (Meta AI, Menlo Park, CA, USA)+cu111 deep learning framework.
4.1.1. ShapeNet Benchmark Dataset
The ShapeNet dataset [42] provides a broad repository of 3D CAD models covering a wide range of categories and geometric complexities. It has been widely adopted in shape completion and reconstruction tasks due to its clean surfaces and controlled annotation environment.
In this study, we follow the preprocessing pipeline from [43], adopting a subset containing 13 object categories with standard train/validation splits and a test set of 8500 samples. Each ground-truth mesh is uniformly sampled to generate dense point clouds. During training, we randomly sample 3000 points per epoch from each mesh surface and apply Gaussian noise with zero mean and a standard deviation of 0.05. This simulates realistic sensor imperfections and enhances model robustness to input degradation. All point clouds are normalized into a unit sphere to ensure consistent scale and centroid alignment across samples. All point clouds were generated by uniform surface sampling of the CAD meshes to produce synthetic data rather than being obtained from LiDAR scanning or photogrammetric reconstruction.
4.1.2. Industrial Workshop Dataset
To assess the model’s zero-shot generalization capability under practical conditions, the industrial workshop dataset was collected from real manufacturing environments and includes key smart factory modules such as AGV systems, robotic workcells, machine tools, and inspection stations. The point clouds were acquired using a Leica RTC360 3D laser scanner (Leica Geosystems AG, Heerbrugg, Switzerland), which provides high-accuracy long-range measurements with a ranging precision of 1 mm + 10 ppm, and no photogrammetric methods were used. The scanner was mounted on a tripod to ensure stability during acquisition. Raw point cloud data were exported in PTS format and subsequently downsampled to a fixed resolution (3000 points per sample) for preprocessing and normalization prior to reconstruction. These scenes span logistics, machining, assembly, and quality control domains, featuring diverse spatial layouts, materials, and occlusion patterns. Importantly, this dataset was used exclusively for testing and evaluation. The reconstruction network was trained solely on the ShapeNet dataset and was never trained, fine-tuned, or otherwise exposed to any samples from this industrial dataset, making our evaluation a strict test of zero-shot, cross-domain transfer.
4.2. Data Normalization and Augmentation
To ensure consistent scale alignment and to mitigate the influence of heterogeneous sensing modalities, all point clouds—including both the incomplete inputs and the corresponding ground-truth targets—are normalized into a canonical unit sphere centered at the origin. This preprocessing step enforces scale invariance and facilitates stable convergence across diverse object categories and acquisition scenarios.
During the training phase, we employ a comprehensive suite of data augmentation strategies to enhance the model’s generalization capability and robustness against input perturbations. Specifically, each point cloud is subjected to randomized rigid transformations, including uniform rotations around the principal axes and random mirror reflections. These transformations effectively simulate diverse viewing angles and symmetries commonly encountered in practical scanning environments.
Additionally, to emulate real-world sensor noise and to promote resilience against surface irregularities, isotropic Gaussian noise with zero mean and a standard deviation of is independently added to each point coordinate. This perturbation strategy ensures that the network learns to distinguish true geometric structures from stochastic variations. The combination of rigorous normalization and diverse augmentation not only stabilizes the optimization process but also significantly improves the reconstruction fidelity under challenging and noisy input conditions.
To enable a unified and reproducible processing pipeline, all point clouds undergo controlled resampling prior to ingestion by the completion and reconstruction modules. Specifically, for the point cloud completion phase leveraging FMPNet, each incomplete input sample is uniformly downsampled or upsampled to a fixed cardinality of 3000 points. This standardized resolution not only aligns with the architectural requirements of FMPNet but also ensures consistent representation density across diverse object categories and occlusion patterns. By imposing a fixed input size, the network is encouraged to learn robust completion priors that are invariant to variations in sampling density.
For the subsequent 3D reconstruction stage, the output produced by FMPNet—namely, the completed point cloud comprising 3000 points—is directly consumed by our reconstruction network without additional resampling or preprocessing. This design choice allows the reconstruction module to fully exploit the semantically enriched and geometrically coherent point distributions generated by the completion backbone. As a result, the end-to-end system maintains a seamless transition between completion and reconstruction, thereby minimizing information loss and preserving fine-grained geometric details essential for high-fidelity mesh generation.
4.3. Stage 1: Point Cloud Completion via FMPNet
High-quality 3D reconstruction begins with complete and structurally consistent point cloud inputs. However, in real industrial acquisitions, data are frequently degraded by occlusions and sensor limitations. To address this issue, we adopt the previously published FMPNet as the first key stage of C2R3D-Net.
FMPNet is a self-supervised point cloud completion network that leverages multi-scale feature extraction and attention mechanisms to reconstruct complete geometry from single, incomplete observations. Its effectiveness was thoroughly validated on both the public 3D-EPN benchmark [44] and a custom industrial dataset. In the published work, FMPNet achieved an average CD- of on the 3D-EPN dataset, outperforming multiple supervised and unsupervised baseline methods.
In this study, we directly utilize the pretrained FMPNet model without additional retraining. Its primary role is to transform sparse, degraded input point clouds into dense, high-quality outputs containing 3000 points, which serve as the input for subsequent surface reconstruction. Figure 5 illustrates the outstanding completion results achieved by FMPNet on both synthetic and real-world industrial data. The model successfully recovers complex geometric structures while maintaining smooth surface continuity. For detailed architecture descriptions, training protocols, and comprehensive evaluation, we refer the reader to our previous publication.
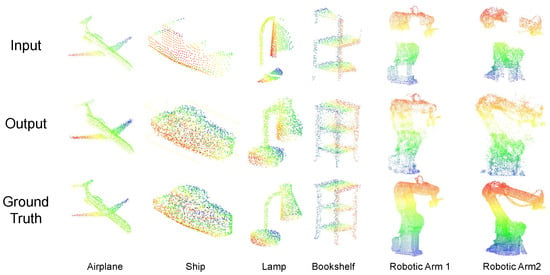
Figure 5.
Visualization of point cloud completion results obtained using FMPNet. The left panel illustrates completions on the 3D-EPN dataset, and the right panel presents completions generated from the self-collected industrial dataset. These dense point clouds are subsequently utilized as inputs to the reconstruction network.
4.4. Stage 2: 3D Surface Reconstruction
This section presents a comprehensive evaluation of the proposed C2R3D-Net reconstruction pipeline. We assess its effectiveness across both in-domain synthetic benchmarks and out-of-domain real-world industrial scenarios. All experiments leverage the completed point clouds generated by FMPNet as inputs to the reconstruction module. We report quantitative metrics and qualitative results to demonstrate the method’s accuracy, robustness, and capacity for cross-domain generalization.
4.4.1. Quantitative Evaluation
The reconstruction experiments were conducted using consistent hyperparameter settings to ensure comparability. Table 2 summarizes the key configuration parameters, including input resolution, latent feature dimensionality, and training schedule. These settings were selected based on preliminary experiments balancing computational efficiency and reconstruction fidelity.

Table 2.
Experimental configuration for 3D reconstruction.
To rigorously assess reconstruction accuracy in a controlled setting, we first evaluated C2R3D-Net on the ShapeNet dataset, which provides clean, well-annotated ground-truth meshes across diverse object categories. Reconstruction quality was measured using four widely adopted metrics: Chamfer Distance (CD), F-Score, Intersection-over-Union (IoU), and Normal Consistency (NC). Table 3 reports per-category results.

Table 3.
Quantitative reconstruction results across ShapeNet categories. Lower CD and higher F-Score, IoU, and NC indicate better performance.
C2R3D-Net consistently achieved low Chamfer Distances and high F-Scores, demonstrating its ability to recover both global structure and fine-grained surface detail. For context, Table 4 compares our results to state-of-the-art baselines.

Table 4.
Quantitative comparison with state-of-the-art methods. Higher IoU, NC, FS and lower CD indicate better performance.
4.4.2. Qualitative Evaluation on ShapeNet
In addition to quantitative metrics, qualitative visualization is crucial for understanding how effectively the reconstruction network preserves both global topology and fine-scale geometric details. Figure 6 depicts representative examples selected from diverse ShapeNet categories, including airplanes, chairs, lamps, and vessels. Each example compares the incomplete input point clouds to the final reconstructed meshes produced by C2R3D-Net.

Figure 6.
Qualitative reconstruction results on ShapeNet objects. Top: Input partial point clouds. Bottom: Reconstructed meshes produced by the proposed method.
Across all categories, the reconstructed surfaces exhibit high fidelity to the ground-truth shapes. Thin structural elements such as airplane wings, lamp arms, and chair backrests are consistently recovered, demonstrating the model’s capacity to integrate local and global geometric cues. Even under severe occlusions and sparsity, the framework produces smooth, watertight meshes without introducing spurious artifacts or oversmoothing critical details.
In particular, objects with high intra-class variability, such as chairs and lamps, pose significant challenges for generalization. Despite this, C2R3D-Net consistently reconstructs salient features—such as chair legs and lamp bases—without relying on category-specific supervision, underscoring its strong representation learning capabilities.
These visual results complement the quantitative evidence presented earlier and validate that the model not only minimizes distance-based error metrics but also recovers visually convincing, structurally coherent meshes. The observations highlight the framework’s suitability for downstream tasks requiring high-resolution 3D models, such as simulation, inspection, and interaction.
4.4.3. Zero-Shot Evaluation on Real-World Industrial Data
To rigorously assess cross-domain generalization, we conducted a strict zero-shot evaluation on our self-collected industrial dataset. The reconstruction network, trained exclusively on synthetic ShapeNet data, was directly applied to reconstruct complex assets acquired under real-world manufacturing conditions. This scenario constitutes a demanding test of the model’s capacity to transfer learned geometric priors without any fine-tuning or domain-specific adaptation.
While quantitative evaluation on ShapeNet primarily measures in-domain performance, the ultimate test of practical utility lies in assessing robustness to domain shift and unseen structural variability. We therefore performed zero-shot reconstruction on the subset of industrial samples for which approximate reference meshes were available. Table 5 reports the quantitative metrics from this synthetic-to-real evaluation. Despite the substantial challenges posed by occlusion, clutter, heterogeneous surface reflectance, and non-uniform sampling densities, the method consistently achieved performance trends comparable to those observed on synthetic benchmarks. Notably, F-Score and Normal Consistency values remained high, confirming that the learned representations can generalize effectively beyond the source domain.

Table 5.
Quantitative reconstruction results on the self-collected industrial dataset subset. Lower Chamfer Distance (CD) and higher IoU, F-Score, and Normal Consistency (NC) indicate better performance. On average, inference of a single object required approximately 13.2 s.
These results underscore that the completion-to-reconstruction pipeline maintains strong geometric fidelity under realistic industrial conditions. The comparatively lower IoU scores are primarily attributed to severe incompleteness of input scans and the partial nature of available reference models, which inherently reduce volumetric overlap even when surface reconstruction succeeds visually. Nonetheless, the consistently low Chamfer Distance and robust F-Score metrics indicate that the reconstructed meshes closely approximate the target geometries in both local detail and overall topology.
For transparency, we emphasize that the remaining samples in the dataset could not be quantitatively evaluated due to the absence of fully verified ground-truth meshes. Future work will prioritize expanding this annotated subset to enable broader analysis and more rigorous benchmarking across diverse industrial asset types and acquisition conditions.
Figure 7 further provides compelling qualitative evidence of the model’s zero-shot reconstruction capability. The visual results illustrate that even when faced with assets fundamentally different in geometry and scale from the training data (e.g., large-scale robotic systems, material handling equipment, and inspection workstations), the model successfully reconstructs high-fidelity surfaces while preserving critical structural features such as support struts and recessed cavities.
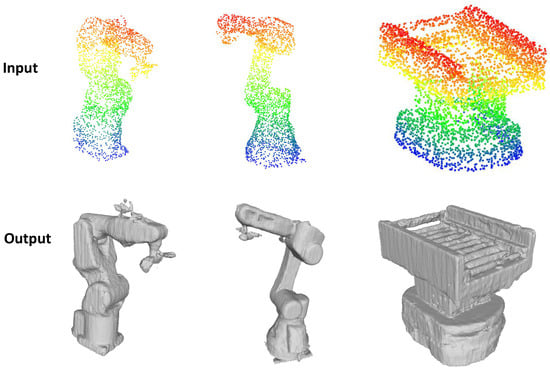
Figure 7.
Qualitative reconstruction results on the self-collected industrial dataset. Top: Incomplete input point clouds. Bottom: Reconstructed mesh surfaces generated by our method.
These qualitative observations reinforce the quantitative findings and validate the framework’s capacity to generalize learned geometric priors to complex, unseen scenarios without any retraining. The combination of boundary-aware attention and adaptive interpolation in the reconstruction network plays a pivotal role in achieving this robustness, enabling fine-scale detail recovery without sacrificing global shape coherence.
Overall, this strict zero-shot evaluation highlights the practical viability of C2R3D-Net for real-world industrial deployment, where the ability to produce accurate, watertight meshes without labor-intensive fine-tuning can significantly accelerate digital twin development pipelines. Such out-of-the-box performance is essential for applications in simulation, monitoring, predictive maintenance, and interactive visualization.
4.5. Ablation Study
To systematically validate the contributions of each proposed component in our reconstruction framework, we conduct a comprehensive ablation study on the ShapeNet benchmark dataset. Specifically, we evaluate the impact of the Adaptive Deformable Convolution (DC), the Local Self-Attention (LSA), and the boundary-aware multi-head interpolation decoder. By selectively removing these modules, we quantitatively assess their individual and joint effects on reconstruction accuracy.
4.5.1. Experimental Configurations
We define the following four configurations for comparison:
- Full Model: Encoder equipped with FKAConv, Deformable Convolution (DC), and Local Self-Attention (LSA); decoder incorporating boundary-aware weighting (BA).
- No DC: Encoder without Deformable Convolution; retains FKAConv and LSA.
- No LSA: Encoder without Local Self-Attention; retains FKAConv and DC.
- No-BA Decoder: Decoder without boundary-aware weighting (i.e., removing the modulation term in Equation (6)).
All configurations are trained and evaluated under identical conditions for fair comparison. We employ four widely adopted metrics to comprehensively assess reconstruction performance: Chamfer Distance (L1), Normal Consistency, Intersection-over-Union (IoU), and F-Score.
4.5.2. Quantitative Results
Table 6 presents the quantitative results of each configuration. The Full Model consistently achieves the best performance across all metrics, demonstrating the importance of integrating both encoder and decoder enhancements.

Table 6.
Quantitative results of the ablation study. Lower Chamfer Distance and higher Normal Consistency, IoU, and F-Score indicate better performance.
The results presented in Table 6 and illustrated in Figure 8 reveal several important insights regarding the contributions of individual components within the proposed reconstruction pipeline. Removing either the Deformable Convolution or the Local Self-Attention module leads to a noticeable degradation in performance across all evaluation metrics, underscoring their complementary roles in capturing fine-grained geometric features and maintaining structural consistency. In particular, the exclusion of the Local Self-Attention mechanism results in a substantial reduction in F-Score, exceeding 8%, which highlights its critical importance for modeling long-range dependencies and preserving global shape coherence. Furthermore, the absence of the boundary-aware weighting in the decoder yields the most pronounced decline in Intersection-over-Union and Normal Consistency, demonstrating that this mechanism is essential for accurately reconstructing thin structures, sharp edges, and other boundary-sensitive regions. As shown in Figure 8, the comparative bar charts provide a clear visual summary of these trends, facilitating an intuitive understanding of how each module impacts reconstruction quality. Collectively, these findings confirm that the integration of adaptive convolution, self-attention, and boundary-aware interpolation is indispensable for achieving high-fidelity surface reconstruction, especially in scenarios characterized by sparse or noisy point cloud inputs. Overall, the ablation study demonstrates that each component contributes distinct and synergistic benefits, and their combination is crucial to realizing state-of-the-art reconstruction performance.
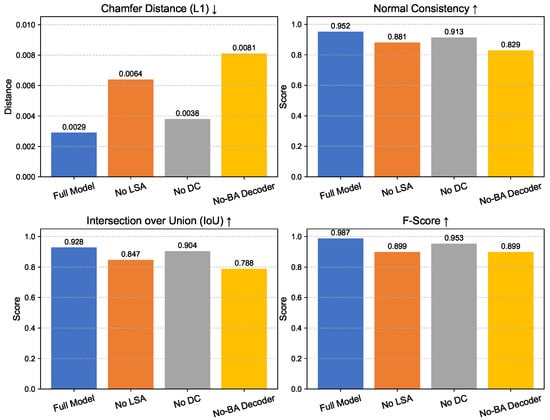
Figure 8.
Comparative bar charts illustrating the results of the ablation study across four evaluation metrics. Each subfigure shows the impact of removing individual components on Chamfer Distance (↓ indicates lower is better), Normal Consistency, Intersection over Union (IoU), and F-Score (↑ indicates higher is better).
5. Discussion
5.1. Summary of Key Advantages and Contributions
C2R3D-Net, the proposed completion-to-reconstruction framework, provides a robust pipeline for generating high-fidelity 3D meshes from sparse and incomplete point clouds, addressing a fundamental requirement in industrial DT applications. Empirical results and ablation studies underscore its main strengths while identifying areas for further investigation.
A key advantage lies in its modular, two-stage design, which systematically decouples shape completion and surface reconstruction. The initial stage employs a pretrained, self-supervised completion network (FMPNet) to infer complete geometry from partial data without manual annotations. This produces dense and coherent point clouds that facilitate effective surface generation from degraded industrial scans.
The reconstruction network’s core innovation is its hybrid, adaptive architecture. The FKAConv-LSA-DC encoder combines fixed-kernel and deformable convolutions to balance structural stability with flexibility, enabling the capture of both coarse shapes and fine details. The integration of Local Self-Attention further improves contextual modeling and long-range consistency. Ablation results confirm that removing either component significantly degrades reconstruction accuracy.
The boundary-aware multi-head interpolation decoder also contributes substantially to performance, particularly in recovering sharp edges, thin structures, and other complex features. By modulating attention weights near geometric boundaries, it improves fidelity where conventional interpolation often fails. This is evidenced by the most pronounced performance decline in IoU and Normal Consistency when the boundary-aware module is removed. Finally, quantitative comparisons against methods such as POCO and ConvONet show that C2R3D-Net achieves consistently competitive or superior results across standard benchmarks.
5.2. Zero-Shot Generalization and Practical Implications
A key finding of this work, validated by our experiments, is the framework’s remarkable effectiveness in a zero-shot, synthetic-to-real setting. Unlike many prior studies that rely on extensive fine-tuning or domain adaptation, our model was trained exclusively on the ShapeNet synthetic dataset and evaluated directly on complex, real-world industrial scans without any additional supervision. This has significant implications for the practical adoption of DT technologies. Specifically, it demonstrates the feasibility of leveraging large, publicly available synthetic datasets to train reconstruction models, thereby bypassing the costly and often impractical process of collecting and annotating large-scale data from proprietary industrial environments. The architectural choices in our reconstruction network, particularly the hybrid encoder and the boundary-aware decoder, appear crucial for learning robust geometric representations that generalize beyond the source domain. This successful transfer highlights the potential of C2R3D-Net as a scalable and deployable solution for high-fidelity 3D modeling in diverse industrial contexts.
5.3. Limitations and Future Work
Despite demonstrating strong empirical performance, the proposed framework exhibits several notable limitations that merit careful consideration, particularly with respect to deployment in diverse industrial scenarios.
First, the reconstruction quality is fundamentally dependent on the effectiveness of the initial completion stage. As a two-stage architecture, C2R3D-Net relies on FMPNet to produce geometrically coherent and artifact-free point clouds. In situations where the completion network fails to accurately infer missing geometry—due to severe occlusion, highly noisy input data, or distributional shift—resulting errors propagate unmitigated into the final reconstructed mesh. This dependency represents a critical vulnerability, as there is currently no corrective mechanism within the pipeline to recover from such upstream inaccuracies.
Second, the computational cost associated with the cascaded design presents practical constraints. The combination of a transformer-based completion network and an adaptive reconstruction module incurs substantial inference time and memory consumption. Empirically, the average time required to reconstruct a single object is approximately 13.2 s on an NVIDIA RTX 4070 GPU, a latency that may be prohibitive for applications requiring near-real-time processing or high-throughput operation. Furthermore, reliance on high-end hardware limits applicability in resource-constrained environments such as embedded industrial controllers or edge computing devices.
A notable limitation of the presented zero-shot generalization claims arises from the restricted diversity of the custom industrial dataset used in this study. Although the dataset encompasses representative manufacturing scenarios—including robotic arms, automated guided vehicles (AGVs), and other large-scale mechanical assemblies—it does not capture the full spectrum of variability observed across industrial domains. In particular, the framework’s performance has not been assessed on assets characterized by fine-grained geometric features, such as those encountered in electronic component manufacturing, nor on settings with distinct material properties and acquisition artifacts prevalent in aerospace applications. Accordingly, while the empirical results demonstrate promising cross-domain transfer within the tested scope, extrapolation to substantially different operational contexts should be approached with caution. Comprehensive validation across a broader range of industrial conditions will be essential to substantiate the framework’s general applicability and reliability.
Fourth, the design choice of producing a fixed-density point cloud comprising 3000 points in the completion stage may not be optimal for all target geometries. While this uniform representation facilitates consistent downstream processing, it imposes limitations when reconstructing objects with either extremely simple surfaces, where excessive sampling may be redundant, or highly intricate structures, where a higher point density could be necessary to capture fine details accurately. Future iterations of the framework could explore adaptive mechanisms that dynamically adjust point cloud resolution in response to the complexity of the observed geometry.
Fifth, the evaluation framework, while comprehensive in its use of standard geometric metrics (e.g., Chamfer Distance, IoU), relies exclusively on quantitative analysis. These metrics are invaluable for measuring geometric fidelity but may not fully correlate with the perceptual quality or functional suitability of the reconstructed models as judged by human experts. For instance, a mesh might achieve a low Chamfer Distance yet contain small, topologically incorrect artifacts that render it unsuitable for specific engineering simulations (e.g., CFD or FEA) or downstream manufacturing tasks. The absence of perceptual metrics or formal subjective evaluations by industrial stakeholders constitutes a limitation in assessing the framework’s practical utility.
Finally, while this study focused on demonstrating the feasibility and effectiveness of zero-shot cross-domain generalization, it is acknowledged that supervised fine-tuning could further improve reconstruction fidelity in specific industrial domains. A systematic comparison between the presented zero-shot configuration and fine-tuned variants would help quantify the associated trade-offs and provide valuable insights into the cost-benefit balance of adopting lightweight adaptation strategies. Conducting such evaluations remains an important direction for future research. At the same time, the core motivation of this work is to address practical scenarios where acquiring and annotating sufficient high-quality 3D data is often infeasible due to prohibitive costs, operational constraints, or limited asset accessibility.
Addressing these limitations will constitute a valuable foundation for advancing this line of work. Possible avenues include the development of end-to-end trainable architectures that allow reconstruction losses to inform the completion stage, strategies for lightweight model distillation and acceleration to improve runtime efficiency, and extensive validation on broader industrial datasets. Crucially, future studies should also incorporate more application-centric evaluation methodologies. This could involve computational perceptual metrics designed for 3D shapes or, more impactfully, formal subjective studies with domain experts to assess the usability of reconstructed models for specific downstream tasks.
6. Conclusions
To provide a consolidated overview of the framework’s performance, Table 7 summarizes the key quantitative results across both synthetic and real-world datasets.

Table 7.
Summary of reconstruction performance across synthetic (ShapeNet) and real-world industrial datasets. Arrows indicate the desirable direction of each metric: ↓ for lower is better (Chamfer Distance), and ↑ for higher is better (F-Score, IoU, and Normal Consistency).
In this paper, we have presented C2R3D-Net, a two-stage framework for generating high-fidelity 3D meshes from sparse and incomplete point clouds, specifically targeting the challenges of industrial digital twin applications. The proposed approach systematically decouples the reconstruction task into self-supervised point cloud completion and adaptive surface reconstruction. The initial stage leverages a pretrained completion network (FMPNet) to infer dense and coherent geometry from partial inputs, while the reconstruction network combines a hybrid FKAConv-LSA-DC encoder and a boundary-aware multi-head interpolation decoder to recover fine-grained surface details and preserve complex structural features.
Comprehensive experiments on the ShapeNet benchmark and a custom industrial dataset validate the framework’s capacity to achieve strong reconstruction performance and notable zero-shot generalization without additional fine-tuning. The results demonstrate that it is feasible to train effective reconstruction models solely on synthetic data and deploy them directly in industrial scenarios, significantly reducing the need for large-scale proprietary datasets. Ablation studies further highlight the contributions of each architectural component, particularly the role of boundary-aware interpolation in recovering thin structures and sharp edges.
Despite these strengths, the framework presents several limitations that warrant consideration. Its performance remains inherently dependent on the accuracy of the completion stage, with errors and artifacts propagating directly into the reconstructed mesh. The cascaded architecture incurs substantial computational costs, with an average inference time of approximately 13.2 s per object, which may limit applicability in real-time or resource-constrained environments. Moreover, while the approach shows promising results on selected industrial assets, its generalization across domains with markedly different scales, materials, or topologies requires further validation. Finally, the use of a fixed-cardinality point cloud output from the completion network may not be optimal for objects of widely varying geometric complexity.
Future work will focus on addressing these challenges by exploring end-to-end optimization strategies that enable joint learning across stages, developing adaptive point density mechanisms, and extending evaluation to more diverse industrial datasets. Additionally, optimizing runtime efficiency through model compression and acceleration will be critical for facilitating deployment in time-sensitive and embedded applications. Moreover, integrating perceptual evaluation metrics and expert-based assessments will be prioritized to enrich the validation framework and ensure that reconstructed models meet application-specific quality standards.
In summary, this work contributes a practical and extensible framework for high-fidelity 3D reconstruction of industrial assets from imperfect data, offering a foundation for advancing digital twin technologies in complex manufacturing environments.
Author Contributions
Conceptualization, Y.X. and B.H.S.A.; methodology, Y.X., H.Z. and B.H.S.A.; resources, B.H.S.A., H.Z. and Y.X.; writing—original draft preparation, B.H.S.A. and Y.X.; writing—review and editing, B.H.S.A. and Y.X.; supervision, B.H.S.A.; visualization, B.H.S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tao, F.; Zhang, H.; Zhang, C. Advancements and challenges of digital twins in industry. Nat. Comput. Sci. 2024, 4, 169–177. [Google Scholar] [CrossRef]
- Kritzinger, W.; Karner, M.; Traar, G.; Henjes, J.; Sihn, W. Digital Twin in manufacturing: A categorical literature review and classification. Ifac-PapersOnline 2018, 51, 1016–1022. [Google Scholar] [CrossRef]
- Leng, J.; Zhu, X.; Huang, Z.; Li, X.; Zheng, P.; Zhou, X.; Mourtzis, D.; Wang, B.; Qi, Q.; Shao, H.; et al. Unlocking the power of industrial artificial intelligence towards Industry 5.0: Insights, pathways, and challenges. J. Manuf. Syst. 2024, 73, 349–363. [Google Scholar] [CrossRef]
- Sarkar, B.D.; Shardeo, V.; Dwivedi, A.; Pamucar, D. Digital transition from industry 4.0 to industry 5.0 in smart manufacturing: A framework for sustainable future. Technol. Soc. 2024, 78, 102649. [Google Scholar] [CrossRef]
- Tao, F.; Xiao, B.; Qi, Q.; Cheng, J.; Ji, P. Digital twin modeling. J. Manuf. Syst. 2022, 64, 372–389. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, C.; Kevin, I.; Wang, K.; Huang, H.; Xu, X. Digital Twin-driven smart manufacturing: Connotation, reference model, applications and research issues. Robot. Comput. Integr. Manuf. 2020, 61, 101837. [Google Scholar] [CrossRef]
- Jin, L.; Zhai, X.; Wang, K.; Zhang, K.; Wu, D.; Nazir, A.; Jiang, J.; Liao, W.H. Big data, machine learning, and digital twin assisted additive manufacturing: A review. Mater. Des. 2024, 244, 113086. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, J.; Wang, P.; Law, J.; Calinescu, R.; Mihaylova, L. A deep learning-enhanced Digital Twin framework for improving safety and reliability in human–robot collaborative manufacturing. Robot. Comput.-Integr. Manuf. 2024, 85, 102608. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Liu, A.; Zhang, J.; Zhang, J. Ontology of 3D virtual modeling in digital twin: A review, analysis and thinking. J. Intell. Manuf. 2025, 36, 95–145. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Li, Y.; Xiao, Z.; Li, J.; Shen, T. Integrating vision and laser point cloud data for shield tunnel digital twin modeling. Autom. Constr. 2024, 157, 105180. [Google Scholar] [CrossRef]
- Zhu, Q.; Fan, L.; Weng, N. Advancements in point cloud data augmentation for deep learning: A survey. Pattern Recognit. 2024, 153, 110532. [Google Scholar] [CrossRef]
- Xiao, A.; Zhang, X.; Shao, L.; Lu, S. A survey of label-efficient deep learning for 3d point clouds. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 9139–9160. [Google Scholar] [CrossRef]
- Sulzer, R.; Marlet, R.; Vallet, B.; Landrieu, L. A survey and benchmark of automatic surface reconstruction from point clouds. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 47, 2000–2019. [Google Scholar] [CrossRef]
- Wu, J.; Wyman, O.; Tang, Y.; Pasini, D.; Wang, W. Multi-view 3D reconstruction based on deep learning: A survey and comparison of methods. Neurocomputing 2024, 582, 127553. [Google Scholar] [CrossRef]
- Mescheder, L.; Oechsle, M.; Niemeyer, M.; Nowozin, S.; Geiger, A. Occupancy networks: Learning 3d reconstruction in function space. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 4460–4470. [Google Scholar]
- Peng, S.; Niemeyer, M.; Mescheder, L.; Pollefeys, M.; Geiger, A. Convolutional occupancy networks. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part III 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 523–540. [Google Scholar]
- Park, J.J.; Florence, P.; Straub, J.; Newcombe, R.; Lovegrove, S. Deepsdf: Learning continuous signed distance functions for shape representation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 165–174. [Google Scholar]
- Shen, L.; Pauly, J.; Xing, L. NeRP: Implicit neural representation learning with prior embedding for sparsely sampled image reconstruction. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 770–782. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Y.; Nan, L.; Zhu, X.X. Parametric Point Cloud Completion for Polygonal Surface Reconstruction. In Proceedings of the Computer Vision and Pattern Recognition Conference (CVPR), Nashville, TN, USA, 11–15 June 2025; pp. 11749–11758. [Google Scholar]
- Zhao, Z.; Alzubaidi, L.; Zhang, J.; Duan, Y.; Gu, Y. A comparison review of transfer learning and self-supervised learning: Definitions, applications, advantages and limitations. Expert Syst. Appl. 2024, 242, 122807. [Google Scholar] [CrossRef]
- Gui, J.; Chen, T.; Zhang, J.; Cao, Q.; Sun, Z.; Luo, H.; Tao, D. A survey on self-supervised learning: Algorithms, applications, and future trends. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 9052–9071. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Zhu, H.; Honarvar Shakibaei Asli, B. A Self-Supervised Point Cloud Completion Method for Digital Twin Smart Factory Scenario Construction. Electronics 2025, 14, 1934. [Google Scholar] [CrossRef]
- Fu, K.; Gao, P.; Liu, S.; Qu, L.; Gao, L.; Wang, M. Pos-bert: Point cloud one-stage bert pre-training. Expert Syst. Appl. 2024, 240, 122563. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, F.; Hou, Z.; Mian, L.; Wang, Z.; Zhang, J.; Tang, J. Self-supervised learning: Generative or contrastive. IEEE Trans. Knowl. Data Eng. 2021, 35, 857–876. [Google Scholar] [CrossRef]
- Yu, X.; Tang, L.; Rao, Y.; Huang, T.; Zhou, J.; Lu, J. Point-bert: Pre-training 3d point cloud transformers with masked point modeling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 19313–19322. [Google Scholar]
- Pang, Y.; Wang, W.; Tay, F.E.; Liu, W.; Tian, Y.; Yuan, L. Masked autoencoders for point cloud self-supervised learning. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 604–621. [Google Scholar]
- Zhang, R.; Guo, Z.; Gao, P.; Fang, R.; Zhao, B.; Wang, D.; Qiao, Y.; Li, H. Point-m2ae: Multi-scale masked autoencoders for hierarchical point cloud pre-training. Adv. Neural Inf. Process. Syst. 2022, 35, 27061–27074. [Google Scholar]
- Xue, L.; Gao, M.; Xing, C.; Martín-Martín, R.; Wu, J.; Xiong, C.; Xu, R.; Niebles, J.C.; Savarese, S. Ulip: Learning a unified representation of language, images, and point clouds for 3d understanding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 1179–1189. [Google Scholar]
- Min, C.; Xiao, L.; Zhao, D.; Nie, Y.; Dai, B. Occupancy-mae: Self-supervised pre-training large-scale lidar point clouds with masked occupancy autoencoders. IEEE Trans. Intell. Veh. 2023, 9, 5150–5162. [Google Scholar] [CrossRef]
- Bernardini, F.; Mittleman, J.; Rushmeier, H.; Silva, C.; Taubin, G. The ball-pivoting algorithm for surface reconstruction. IEEE Trans. Vis. Comput. Graph. 2002, 5, 349–359. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, X.; Su, H. Meshing point clouds with predicted intrinsic-extrinsic ratio guidance. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part VIII 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 68–84. [Google Scholar]
- Cazals, F.; Giesen, J. Delaunay triangulation based surface reconstruction. In Effective Computational Geometry for Curves and Surfaces; Springer: Berlin/Heidelberg, Germany, 2006; pp. 231–276. [Google Scholar]
- Rakotosaona, M.J.; Guerrero, P.; Aigerman, N.; Mitra, N.J.; Ovsjanikov, M. Learning delaunay surface elements for mesh reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021; pp. 22–31. [Google Scholar]
- Bernardini, F.; Bajaj, C.L. Sampling and Reconstructing Manifolds Using Alpha-Shapes. In Proceedings of the 9th Canadian Conference on Computational Geometry (CCCG’97), Kingston, ON, Canada, 11–14 August 1997; pp. 193–198. [Google Scholar]
- Labatut, P.; Pons, J.P.; Keriven, R. Robust and efficient surface reconstruction from range data. In Proceedings of the Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2009; Volume 28, pp. 2275–2290. [Google Scholar]
- Sulzer, R.; Landrieu, L.; Marlet, R.; Vallet, B. Scalable Surface Reconstruction with Delaunay-Graph Neural Networks. In Proceedings of the Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2021; Volume 40, pp. 157–167. [Google Scholar]
- Kazhdan, M.; Hoppe, H. Screened poisson surface reconstruction. ACM Trans. Graph. (ToG) 2013, 32, 1–13. [Google Scholar] [CrossRef]
- Peng, S.; Jiang, C.; Liao, Y.; Niemeyer, M.; Pollefeys, M.; Geiger, A. Shape as points: A differentiable poisson solver. Adv. Neural Inf. Process. Syst. 2021, 34, 13032–13044. [Google Scholar]
- Boulch, A.; Marlet, R. Poco: Point convolution for surface reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; pp. 6302–6314. [Google Scholar]
- Boulch, A.; Puy, G.; Marlet, R. FKAConv: Feature-kernel alignment for point cloud convolution. In Proceedings of the Asian Conference on Computer Vision, Kyoto, Japan, 30 November–4 December 2020. [Google Scholar]
- Chang, A.X.; Funkhouser, T.; Guibas, L.; Hanrahan, P.; Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H.; et al. Shapenet: An information-rich 3d model repository. arXiv 2015, arXiv:1512.03012. [Google Scholar]
- Choy, C.B.; Xu, D.; Gwak, J.; Chen, K.; Savarese, S. 3d-r2n2: A unified approach for single and multi-view 3d object reconstruction. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part VIII 14. Springer: Berlin/Heidelberg, Germany, 2016; pp. 628–644. [Google Scholar]
- Dai, A.; Ruizhongtai Qi, C.; Nießner, M. Shape completion using 3d-encoder-predictor cnns and shape synthesis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5868–5877. [Google Scholar]
- Lionar, S.; Emtsev, D.; Svilarkovic, D.; Peng, S. Dynamic plane convolutional occupancy networks. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2021; pp. 1829–1838. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).