DPAO-PFL: Dynamic Parameter-Aware Optimization via Continual Learning for Personalized Federated Learning
Abstract
1. Introduction
1.1. Motivation
1.2. Designs and Contributions
- By integrating online importance estimation and path integral sensitivity scoring, we designed a task-agnostic dynamic regularization mechanism. Importance weights were updated with an event-triggered mechanism (loss stabilization period), thereby effectively reducing communication and computational overheads.
- We propose DPAO-PFL, a dual-dimension optimized adaptive PFL method, which leverages parameter decomposition and an Elastic Weight Consolidation strategy based on CL. This approach effectively decouples the adaptation to specific client needs from the retention of global shared knowledge.
- We performed an extensive evaluation of the proposed method using publicly available federated learning benchmark datasets. The experimental results indicate that DPAO-PFL surpasses existing state-of-the-art methods in both performance and stability while exhibiting strong robustness to hyperparameters.
2. Related Work
2.1. Federated Learning
2.2. Continuous Iterative
3. Preliminaries
3.1. Parameter Decomposition
3.2. Parameter Importance Score
3.3. Problem Formulation
4. Methods
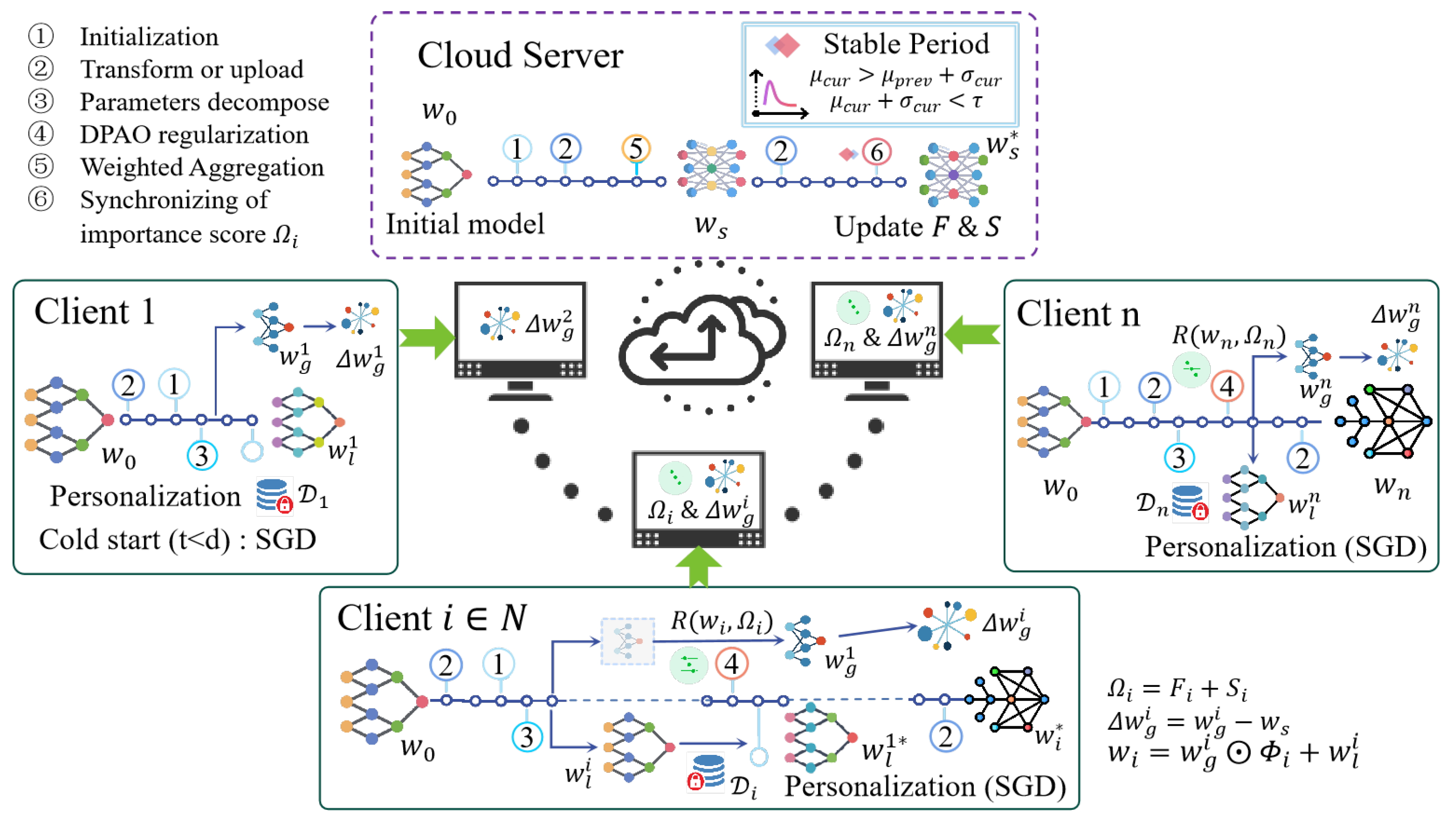
4.1. Architecture Overview
| Algorithm 1: PFL with adaptive parameter decomposition (run on the server). |
 |
4.2. Adaptive Parameters Descomposition (APD)
4.3. Dynamic Parameter-Aware Regularization (DPAO)
| Algorithm 2: DPAO: Dynamic Parameter-Aware Optimization regularization. |
 |
5. Results
5.1. Experiment Setup
5.1.1. Dataset
5.1.2. Baselines
5.1.3. Implementation Details
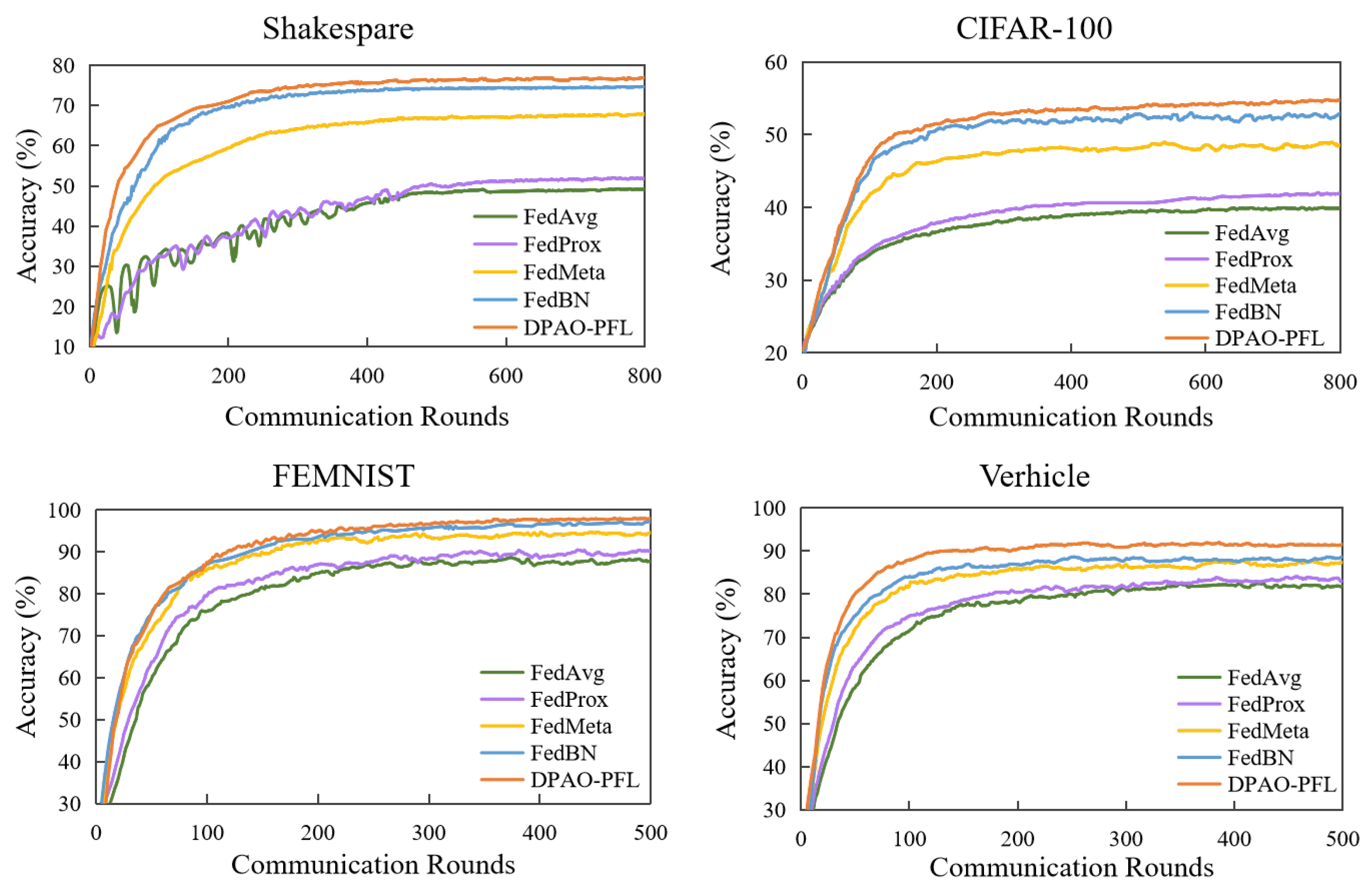
5.2. Performance Comparison
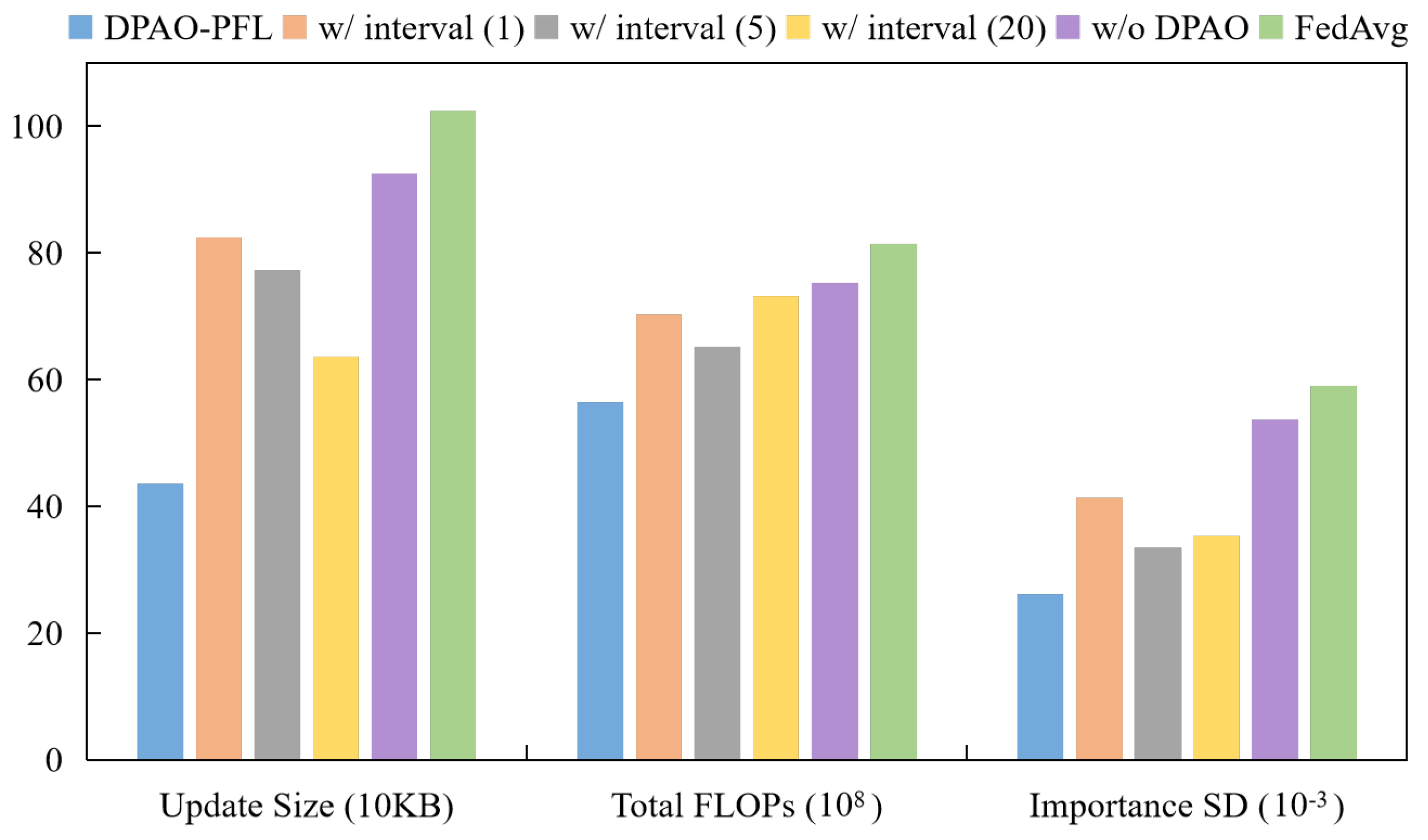
5.3. Ablation Studies
5.4. Communication and Overhead
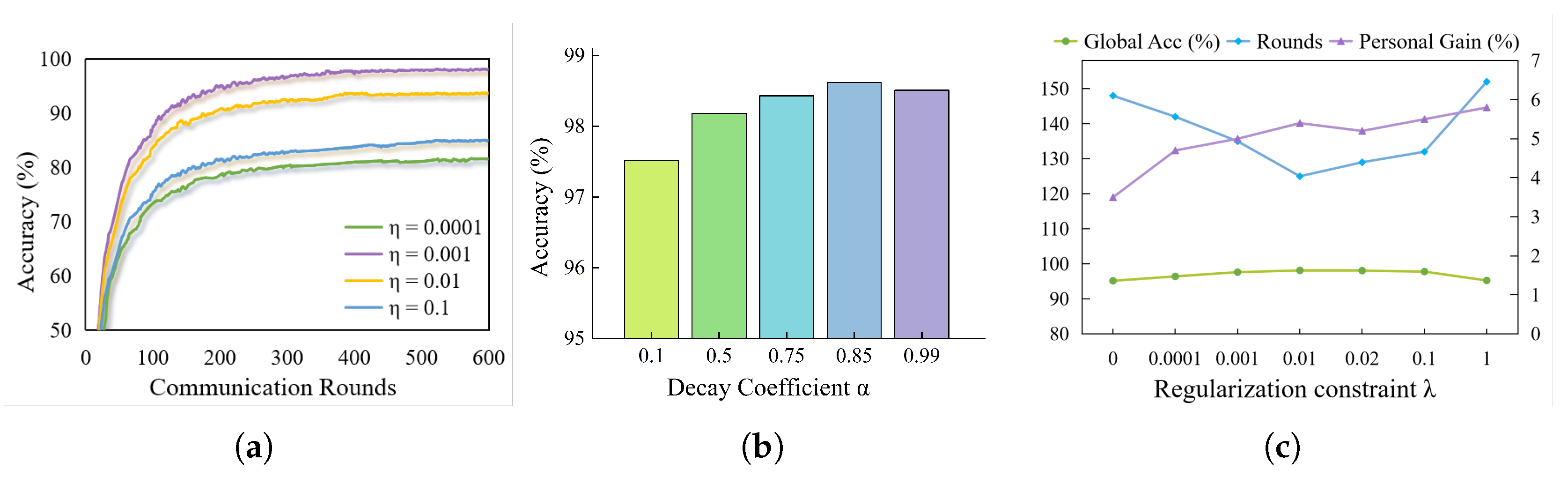
5.5. Hyperarameter Study
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Panduman, Y.Y.F.; Funabiki, N.; Fajrianti, E.D.; Fang, S.; Sukaridhoto, S. A survey of AI techniques in IoT applications with use case investigations in the smart environmental monitoring and analytics in real-time IoT platform. Information 2024, 15, 153. [Google Scholar] [CrossRef]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the Artificial Intelligence and Statistics, PMLR, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Li, Q.; Diao, Y.; Chen, Q.; He, B. Federated learning on non-iid data silos: An experimental study. In Proceedings of the 2022 IEEE 38th International Conference on Data Engineering (ICDE), Kuala Lumpur, Malaysia, 9–12 May 2022; pp. 965–978. [Google Scholar]
- Javeed, D.; Saeed, M.S.; Kumar, P.; Jolfaei, A.; Islam, S.; Islam, A.N. Federated learning-based personalized recommendation systems: An overview on security and privacy challenges. IEEE Trans. Consum. Electron. 2023, 70, 2618–2627. [Google Scholar] [CrossRef]
- Li, Y.; Wen, G. Research and Practice of Financial Credit Risk Management Based on Federated Learning. Eng. Lett. 2023, 31, 271. [Google Scholar]
- Liu, X.; Zhao, J.; Li, J.; Cao, B.; Lv, Z. Federated neural architecture search for medical data security. IEEE Trans. Ind. Inform. 2022, 18, 5628–5636. [Google Scholar] [CrossRef]
- Li, T.; Sahu, A.K.; Talwalkar, A.; Smith, V. Federated learning: Challenges, methods, and future directions. IEEE Signal Process. Mag. 2020, 37, 50–60. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, M.; Lai, L.; Suda, N.; Civin, D.; Chandra, V. Federated learning with non-iid data. arXiv 2018, arXiv:1806.00582. [Google Scholar] [CrossRef]
- Li, X.; Huang, K.; Yang, W.; Wang, S.; Zhang, Z. On the convergence of fedavg on non-iid data. arXiv 2019, arXiv:1907.02189. [Google Scholar]
- Tan, A.Z.; Yu, H.; Cui, L.; Yang, Q. Towards personalized federated learning. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 9587–9603. [Google Scholar] [CrossRef] [PubMed]
- Fallah, A.; Mokhtari, A.; Ozdaglar, A. Personalized federated learning with theoretical guarantees: A model-agnostic meta-learning approach. Adv. Neural Inf. Process. Syst. 2020, 33, 3557–3568. [Google Scholar]
- Zhang, J.; Guo, S.; Ma, X.; Wang, H.; Xu, W.; Wu, F. Parameterized knowledge transfer for personalized federated learning. Adv. Neural Inf. Process. Syst. 2021, 34, 10092–10104. [Google Scholar]
- Karimireddy, S.P.; Kale, S.; Mohri, M.; Reddi, S.; Stich, S.; Suresh, A.T. Scaffold: Stochastic controlled averaging for federated learning. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 5132–5143. [Google Scholar]
- Yoon, J.; Kim, S.; Yang, E.; Hwang, S.J. Scalable and Order-robust Continual Learning with Additive Parameter Decomposition. arXiv 2019, arXiv:1902.09432. [Google Scholar]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated machine learning: Concept and applications. ACM Trans. Intell. Syst. Technol. (TIST) 2019, 10, 1–19. [Google Scholar] [CrossRef]
- Kairouz, P.; McMahan, H.B.; Avent, B.; Bellet, A.; Bennis, M.; Bhagoji, A.N.; Bonawitz, K.; Charles, Z.; Cormode, G.; Cummings, R.; et al. Advances and open problems in federated learning. Found. Trends® Mach. Learn. 2021, 14, 1–210. [Google Scholar] [CrossRef]
- Wu, W.; He, L.; Lin, W.; Mao, R.; Maple, C.; Jarvis, S. SAFA: A semi-asynchronous protocol for fast federated learning with low overhead. IEEE Trans. Comput. 2020, 70, 655–668. [Google Scholar] [CrossRef]
- Lin, Y.; Han, S.; Mao, H.; Wang, Y.; Dally, W.J. Deep gradient compression: Reducing the communication bandwidth for distributed training. arXiv 2017, arXiv:1712.01887. [Google Scholar]
- Reddi, S.; Charles, Z.; Zaheer, M.; Garrett, Z.; Rush, K.; Konečnỳ, J.; Kumar, S.; McMahan, H.B. Adaptive federated optimization. arXiv 2020, arXiv:2003.00295. [Google Scholar]
- Mansour, Y.; Mohri, M.; Ro, J.; Suresh, A.T. Three approaches for personalization with applications to federated learning. arXiv 2020, arXiv:2002.10619. [Google Scholar]
- Ghosh, A.; Chung, J.; Yin, D.; Ramchandran, K. An efficient framework for clustered federated learning. Adv. Neural Inf. Process. Syst. 2020, 33, 19586–19597. [Google Scholar] [CrossRef]
- Yu, S.L.; Liu, Q.; Wang, F.; Yu, Y.; Chen, E. Federated News Recommendation with Fine-grained Interpolation and Dynamic Clustering. In Proceedings of the CIKM’23: 32nd ACM International Conference on Information and Knowledge Management, Birmingham, UK, 21–25 October 2023; pp. 3073–3082. [Google Scholar] [CrossRef]
- Hahn, S.J.; Jeong, M.; Lee, J. Connecting Low-Loss Subspace for Personalized Federated Learning. In Proceedings of the KDD’22: Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 505–515. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, X.; Su, H.; Zhu, J. A Comprehensive Survey of Continual Learning: Theory, Method and Application. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 5362–5383. [Google Scholar] [CrossRef] [PubMed]
- Parisi, G.I.; Kemker, R.; Part, J.L.; Kanan, C.; Wermter, S. Continual lifelong learning with neural networks: A review. Neural Netw. 2019, 113, 54–71. [Google Scholar] [CrossRef] [PubMed]
- Shoham, N.; Avidor, T.; Keren, A.; Israel, N.; Benditkis, D.; Mor-Yosef, L.; Zeitak, I. Overcoming Forgetting in Federated Learning on Non-IID Data. arXiv 2019, arXiv:1910.07796. [Google Scholar]
- Yao, X.; Sun, L. Continual Local Training For Better Initialization Of Federated Models. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 25–28 October 2020; pp. 1736–1740. [Google Scholar] [CrossRef]
- Li, D.; Wang, J. FedMD: Heterogenous Federated Learning via Model Distillation. arXiv 2019, arXiv:1910.03581. [Google Scholar]
- Yang, X.; Yu, H.; Gao, X.; Wang, H.; Zhang, J.; Li, T. Federated Continual Learning via Knowledge Fusion: A Survey. IEEE Trans. Knowl. Data Eng. 2024, 36, 3832–3850. [Google Scholar] [CrossRef]
- Criado, M.F.; Casado, F.E.; Iglesias, R.; Regueiro, C.V.; Barro, S. Non-IID data and Continual Learning processes in Federated Learning: A long road ahead. Inf. Fusion 2022, 88, 263–280. [Google Scholar] [CrossRef]
- Yoon, J.; Jeong, W.; Lee, G.; Yang, E.; Hwang, S.J. Federated Continual Learning with Weighted Inter-client Transfer. In Proceedings of the 38th International Conference on Machine Learning, Virtual Event, 18–24 July 2021; Meila, M., Zhang, T., Eds.; Proceedings of Machine Learning Research. PMLR: New York, NY, USA, 2021; Volume 139, pp. 12073–12086. [Google Scholar]
- Zuo, X.; Luopan, Y.; Han, R.; Zhang, Q.; Liu, C.H.; Wang, G.; Chen, L.Y. FedViT: Federated continual learning of vision transformer at edge. Future Gener. Comput. Syst. 2024, 154, 1–15. [Google Scholar] [CrossRef]
- Zhang, P.; Yang, X.; Chen, Z. Neural network gain scheduling design for large envelope curve flight control law. J. Beijing Univ. Aeronaut. Astronaut. 2005, 31, 604–608. [Google Scholar]
- Pascanu, R.; Bengio, Y. Revisiting natural gradient for deep networks. arXiv 2013, arXiv:1301.3584. [Google Scholar]
- Kirkpatrick, J.; Pascanu, R.; Rabinowitz, N.; Veness, J.; Desjardins, G.; Rusu, A.A.; Milan, K.; Quan, J.; Ramalho, T.; Grabska-Barwinska, A.; et al. Overcoming catastrophic forgetting in neural networks. Proc. Natl. Acad. Sci. USA 2017, 114, 3521–3526. [Google Scholar] [CrossRef] [PubMed]
- Chaudhry, A.; Dokania, P.K.; Ajanthan, T.; Torr, P.H. Riemannian walk for incremental learning: Understanding forgetting and intransigence. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 532–547. [Google Scholar]
- Zenke, F.; Poole, B.; Ganguli, S. Continual learning through synaptic intelligence. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 3987–3995. [Google Scholar]
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of the COMPSTAT’2010: 19th International Conference on Computational Statistics, Paris, France, 22–27 August 2010; Keynote, Invited and Contributed Papers. Springer: Berlin/Heidelberg, Germany, 2010; pp. 177–186. [Google Scholar]
- Alex, K. Learning Multiple Layers of Features from Tiny Images. Toronto, ON, Canada, 8 April 2009; Volume 2. Available online: https://api.semanticscholar.org/CorpusID:18268744 (accessed on 20 July 2025).
- Caldas, S.; Duddu, S.M.K.; Wu, P.; Li, T.; Konečnỳ, J.; McMahan, H.B.; Smith, V.; Talwalkar, A. Leaf: A benchmark for federated settings. arXiv 2018, arXiv:1812.01097. [Google Scholar]
- Smith, V.; Chiang, C.K.; Sanjabi, M.; Talwalkar, A.S. Federated multi-task learning. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Sivaraman, S.; Trivedi, M.M. Looking at vehicles on the road: A survey of vision-based vehicle detection, tracking, and behavior analysis. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1773–1795. [Google Scholar] [CrossRef]
- Aslan, Ö.; Zhang, X.; Schuurmans, D. Convex deep learning via normalized kernels. In Proceedings of the Annual Conference on Neural Information Processing Systems 2014, Montreal, QC, Canada, 8–13 December 2014; Volume 27. [Google Scholar]
- Cohen, G.; Afshar, S.; Tapson, J.; Van Schaik, A. EMNIST: Extending MNIST to handwritten letters. In Proceedings of the 2017 international joint conference on neural networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 2921–2926. [Google Scholar]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. Proc. Mach. Learn. Syst. 2020, 2, 429–450. [Google Scholar]
- Chen, F.; Luo, M.; Dong, Z.; Li, Z.; He, X. Federated meta-learning with fast convergence and efficient communication. arXiv 2018, arXiv:1802.07876. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 1126–1135. [Google Scholar]
- Li, X.; Jiang, M.; Zhang, X.; Kamp, M.; Dou, Q. Fedbn: Federated learning on non-iid features via local batch normalization. arXiv 2021, arXiv:2102.07623. [Google Scholar]
- Hsu, T.M.H.; Qi, H.; Brown, M. Measuring the effects of non-identical data distribution for federated visual classification. arXiv 2019, arXiv:1909.06335. [Google Scholar]
- Li, M.; Zhang, T.; Chen, Y.; Smola, A.J. Efficient mini-batch training for stochastic optimization. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 661–670. [Google Scholar]


| Symbol | Meaning |
|---|---|
| Index and total number of clients. | |
| t | Communication round index. |
| Number of local training epochs and local batch size per client. | |
| w | Full model parameter vector. |
| Global shared parameter subvector (communicated). | |
| Local personalized parameter subvector (retained on client). | |
| Parameters of the network layer | |
| Multiplicative transfer vector for layer k. | |
| Collection of all layer transfer vectors . | |
| Expected local loss of client i under parameters w. | |
| Fisher information estimate for client i at round t. | |
| Path-integral sensitivity score for client i at round t. | |
| Regularization strength (forgetting coefficient) at round t. | |
| Indicator for “stable” periods, and “peak” periods in loss fluctuation. | |
| Update increment of parameter between aggregations. |
| Dataset | Model | Partition | Devices | Samples | Samples/Device | |
|---|---|---|---|---|---|---|
| Mean | Standard | |||||
| FEMNIST [40] | CNN | Writters | 1100 | 245,337 | 223 | 83 |
| Shakespeare [40] | LSTM | Roles | 523 | 1,378,095 | 2635 | 2800 |
| CIFAR-100 [39] | ResNet18 | Labels | 100 | 60,000 | 600 | 300 |
| Vehicle [41] | SVM | Sensors | 23 | 43,698 | 1899 | 349 |
| Methods | Communication Rounds | Convergence | ||
|---|---|---|---|---|
| 60% | 80% | 90% | Accuracy | |
| FedAvg | 51 | 139 | − | 88.73 ± 3.24% |
| APD | 38 | 81 | 165 | 93.37 ± 2.32% |
| DPAO | 35 | 76 | 148 | 95.16 ± 1.39% |
| interval(1) | 45 | 95 | 173 | 96.50 ± 1.71% |
| interval(5) | 53 | 105 | 161 | 95.82 ± 1.89% |
| interval(20) | 62 | 127 | 182 | 95.33 ± 2.16% |
| DPAO-PFL | 26 | 62 | 125 | 98.12 ± 0.58% |
| Methods | ||||
|---|---|---|---|---|
| CIFAR-100 | ||||
| FedAvg | 24.37% | 39.83% | 32.51% | 27.69% |
| FedProx | 25.19% | 41.75% | 35.34% | 28.13% |
| FedMeta | 33.82% | 48.63% | 43.12% | 36.27% |
| DPAO-PFL | 37.25% | 53.24% | 47.19% | 42.61% |
| FEMNIST | ||||
| FedAvg | 53.28% | 78.73% | 83.12% | 89.36% |
| FedProx | 54.63% | 79.45% | 84.05% | 90.27% |
| FedMeta | 68.10% | 94.39% | 97.53% | 97.61% |
| DPAO-PFL | 72.50% | 98.12% | 98.62% | 98.59% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Gao, Y.; Li, X.; Jia, J. DPAO-PFL: Dynamic Parameter-Aware Optimization via Continual Learning for Personalized Federated Learning. Electronics 2025, 14, 2945. https://doi.org/10.3390/electronics14152945
Tang J, Gao Y, Li X, Jia J. DPAO-PFL: Dynamic Parameter-Aware Optimization via Continual Learning for Personalized Federated Learning. Electronics. 2025; 14(15):2945. https://doi.org/10.3390/electronics14152945
Chicago/Turabian StyleTang, Jialu, Yali Gao, Xiaoyong Li, and Jia Jia. 2025. "DPAO-PFL: Dynamic Parameter-Aware Optimization via Continual Learning for Personalized Federated Learning" Electronics 14, no. 15: 2945. https://doi.org/10.3390/electronics14152945
APA StyleTang, J., Gao, Y., Li, X., & Jia, J. (2025). DPAO-PFL: Dynamic Parameter-Aware Optimization via Continual Learning for Personalized Federated Learning. Electronics, 14(15), 2945. https://doi.org/10.3390/electronics14152945







