UDirEar: Heading Direction Tracking with Commercial UWB Earbud by Interaural Distance Calibration
Abstract
1. Introduction
- We propose UDirEar, a heading direction tracking system that relies solely on UWB sensors embedded in wireless earbuds. Because it uses a COTS UWB device, it operates only on high-level UWB information such as distance and direction without access to the amplitude or phase of the CIR.
- We present an EKF model that exploits the interaural distance for heading direction tracking with both ears. Rather than estimating heading directly from sensor distance and direction, this model infers heading indirectly through sensor placement. By inserting an EKF model between raw measurements and final tracking, UDirEar reduces performance degradation due to sensor error and defines the EKF model explicitly around the constant interaural distance.
- We experimentally evaluate UDirEar’s performance against existing methods. We further analyze how factors such as target distance, elapsed time, EKF calibration, and NLoS conditions impact accuracy. We compare results across different scenarios and explain the reasons behind any observed performance changes.
2. Related Work
3. Technical Background
3.1. UWB Primer
3.2. UWB Positioning Using Ranging and AoA
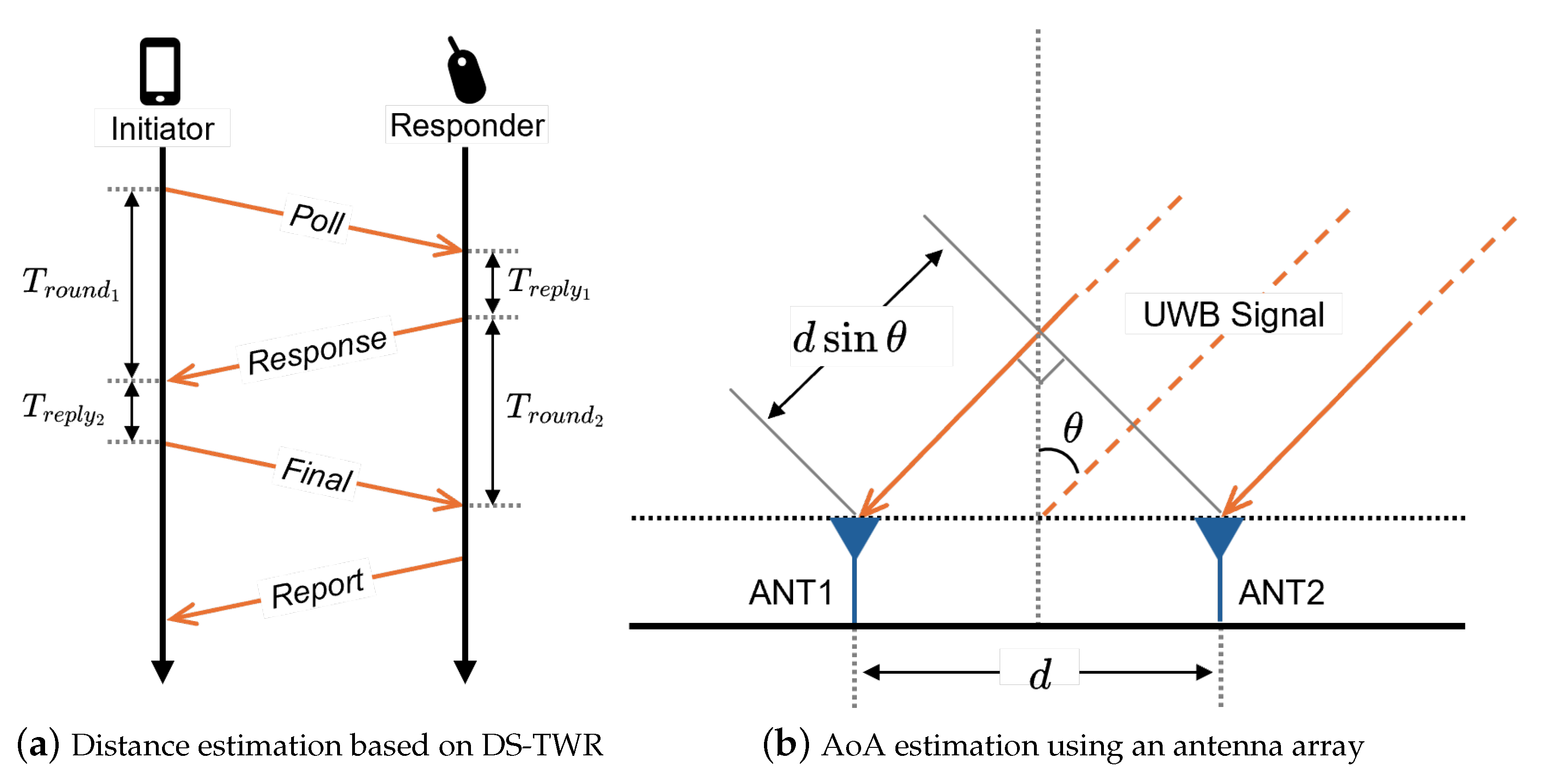
3.2.1. ToF-Based Ranging
3.2.2. AoA Estimation
3.2.3. Three-Dimensional Positioning Capabilities of COTS UWB Devices
3.3. Error Correction Using Extended Kalman Filter
4. Methods
4.1. Heading Direction Basic Model
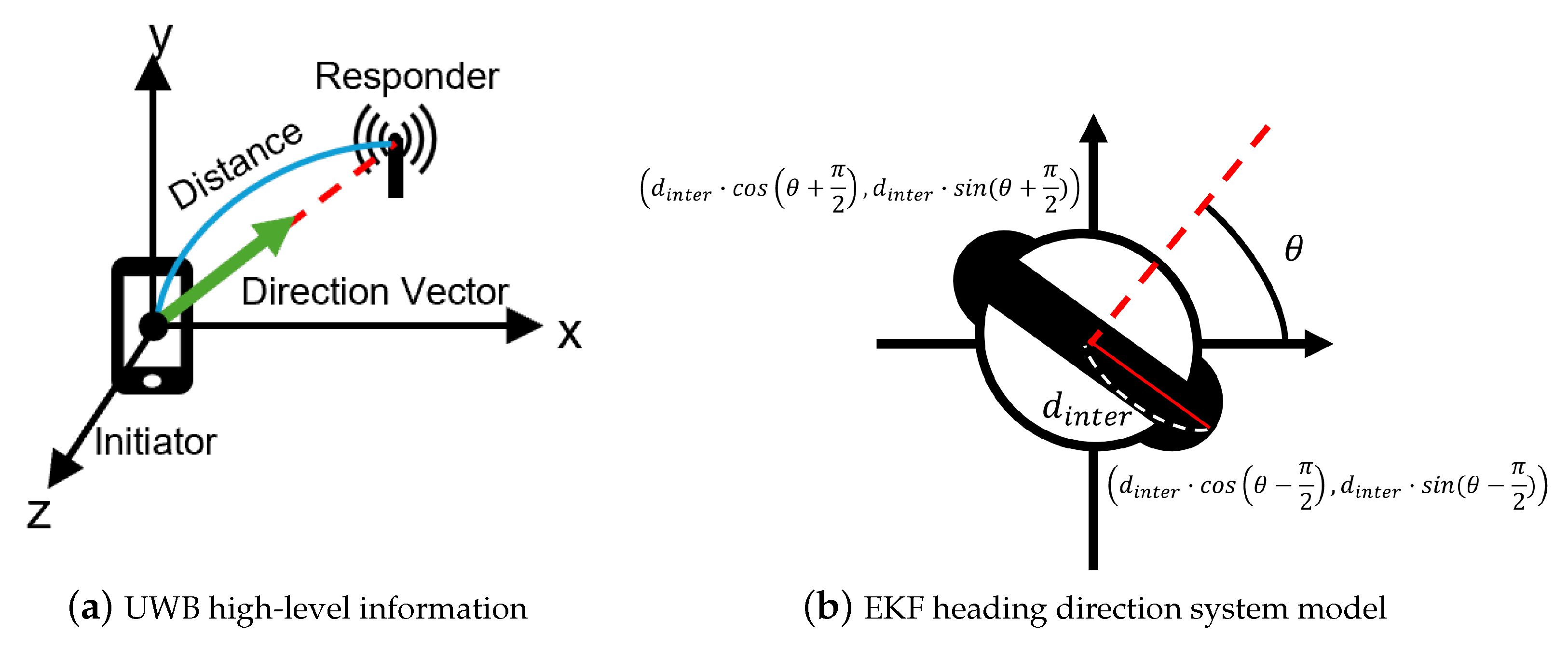
4.1.1. UWB Coordination System
4.1.2. Heading Direction Model
4.2. EKF-Based Correction of Roto-Translational Interference
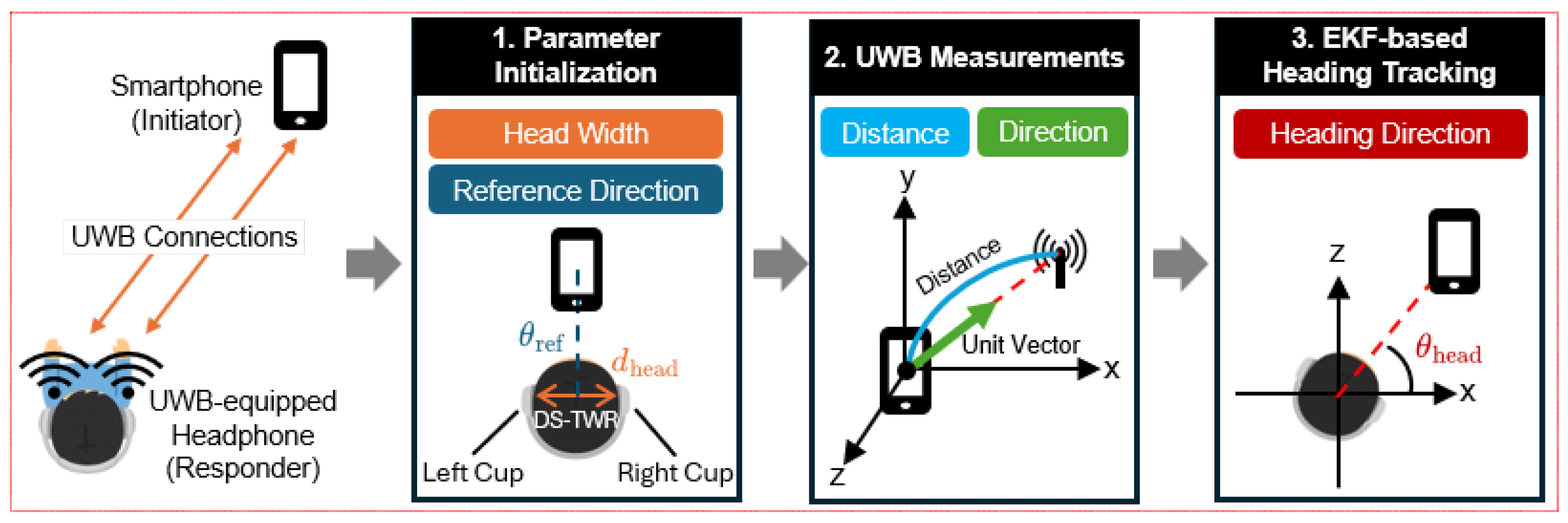
4.3. System Overview
4.4. EKF-Based Heading Tracking
| Algorithm 1 Algorithm of EKF-based heading direction tracking |
|
5. Results
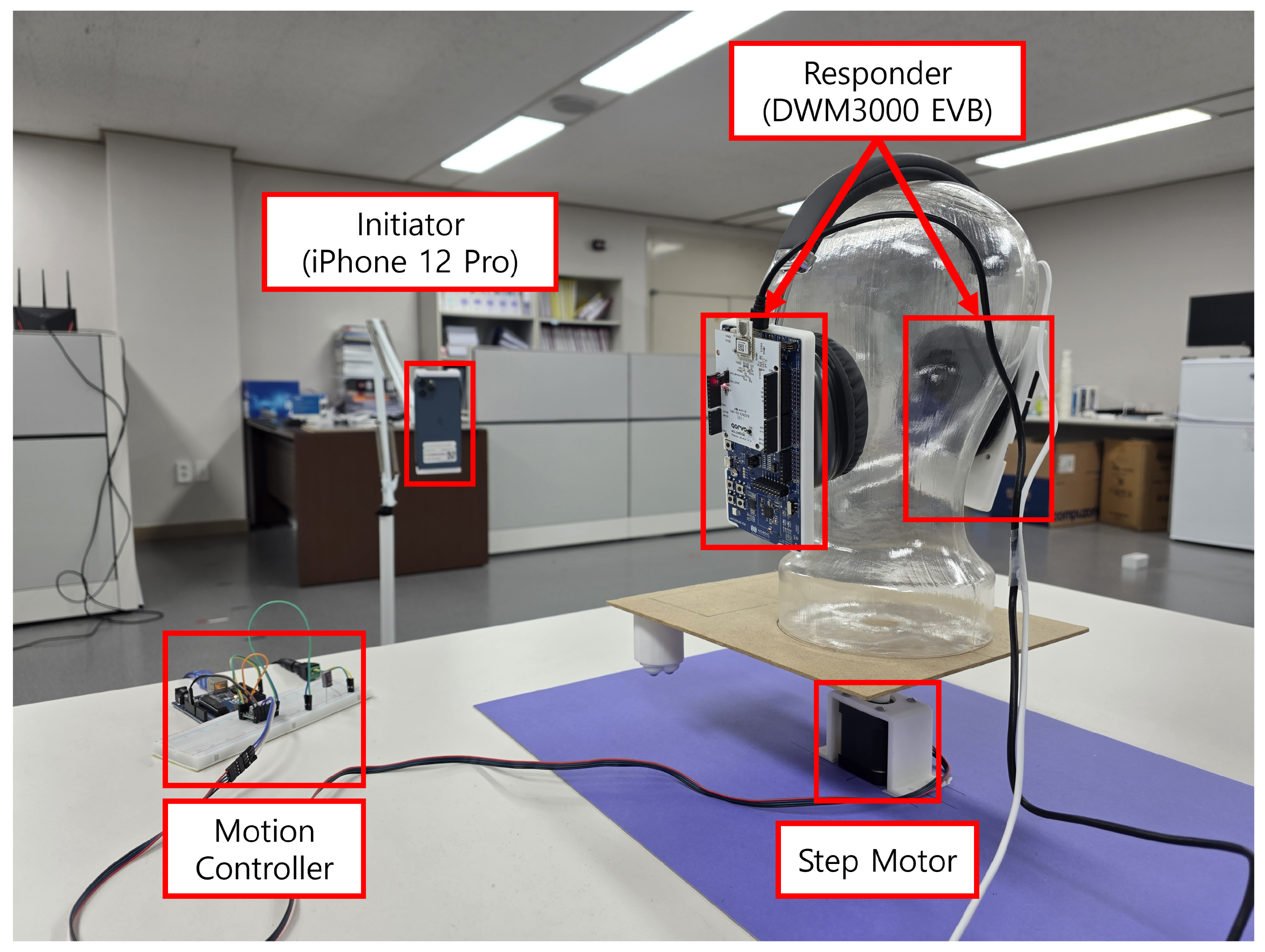
5.1. Experimental Setup
- Ground Truth: The angular trajectory pre-programmed into the dummy head.
- Metric: The mean absolute error (MAE) between the predefined trajectory and estimated heading.
5.2. Experimental Results
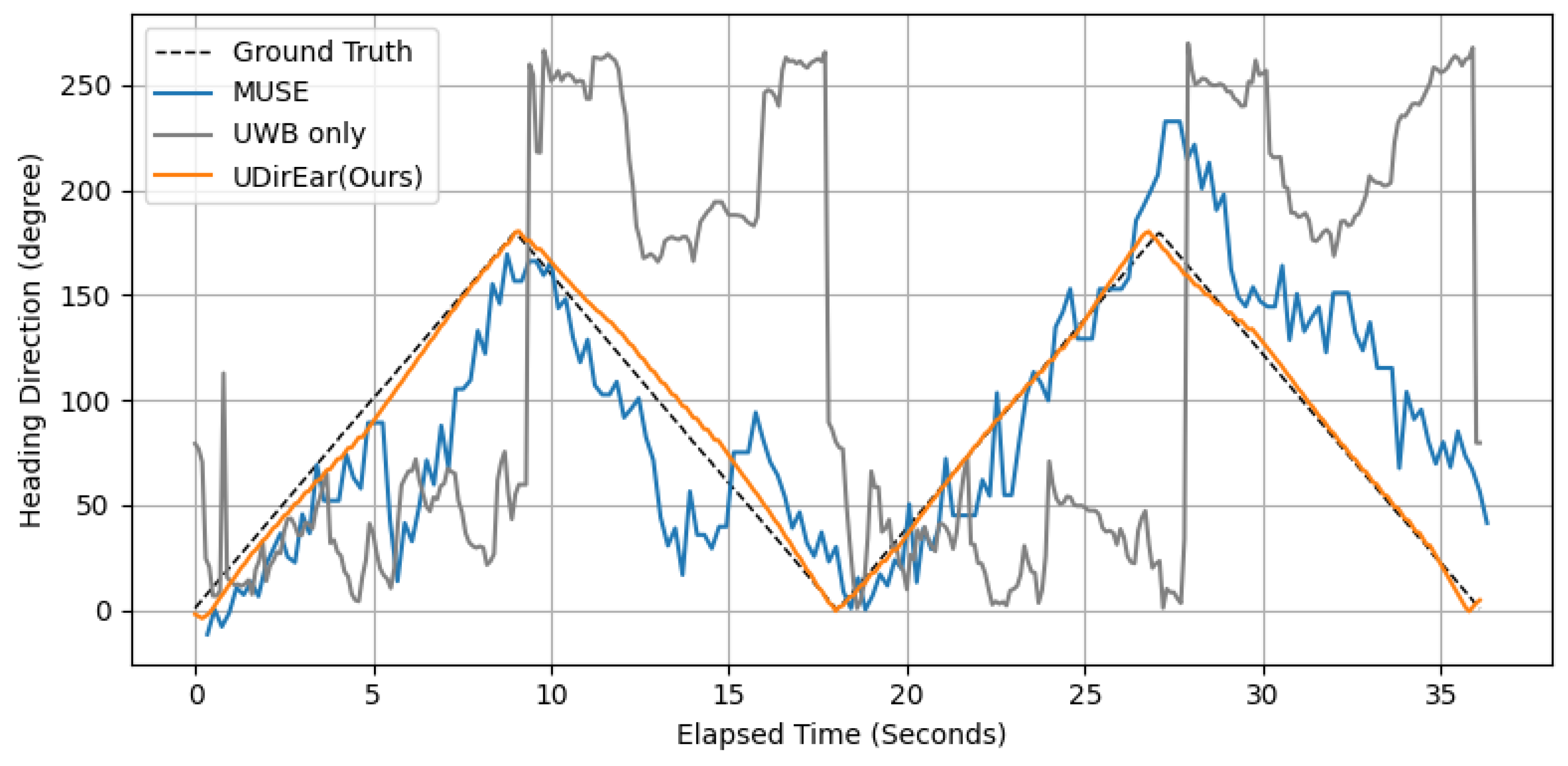
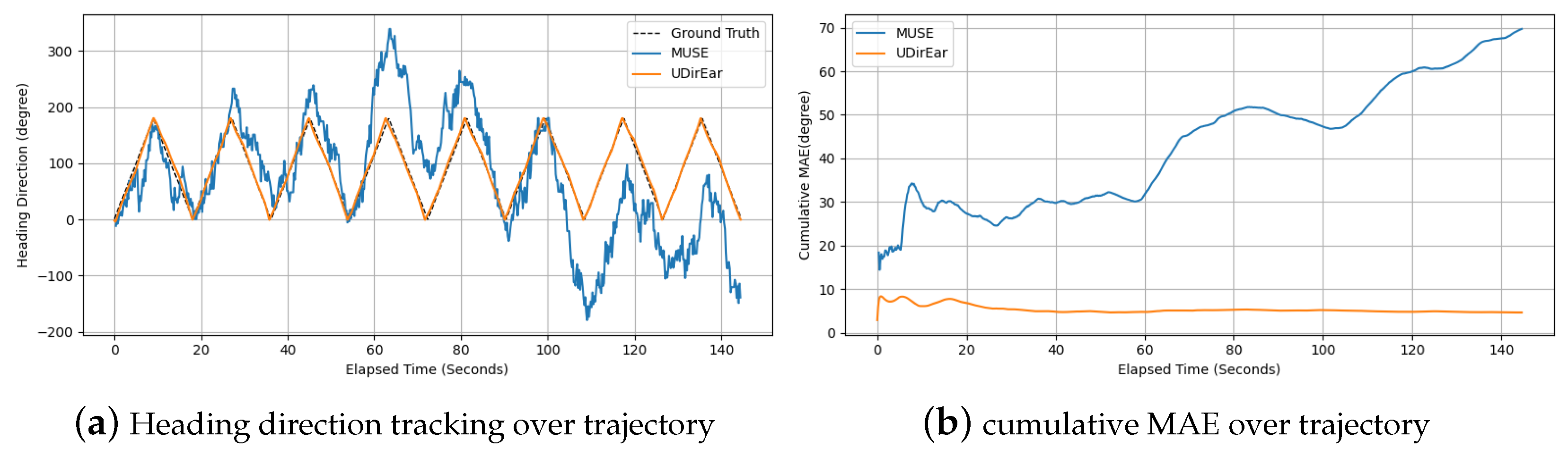
5.2.1. Comparison Between Baseline and UDirEar
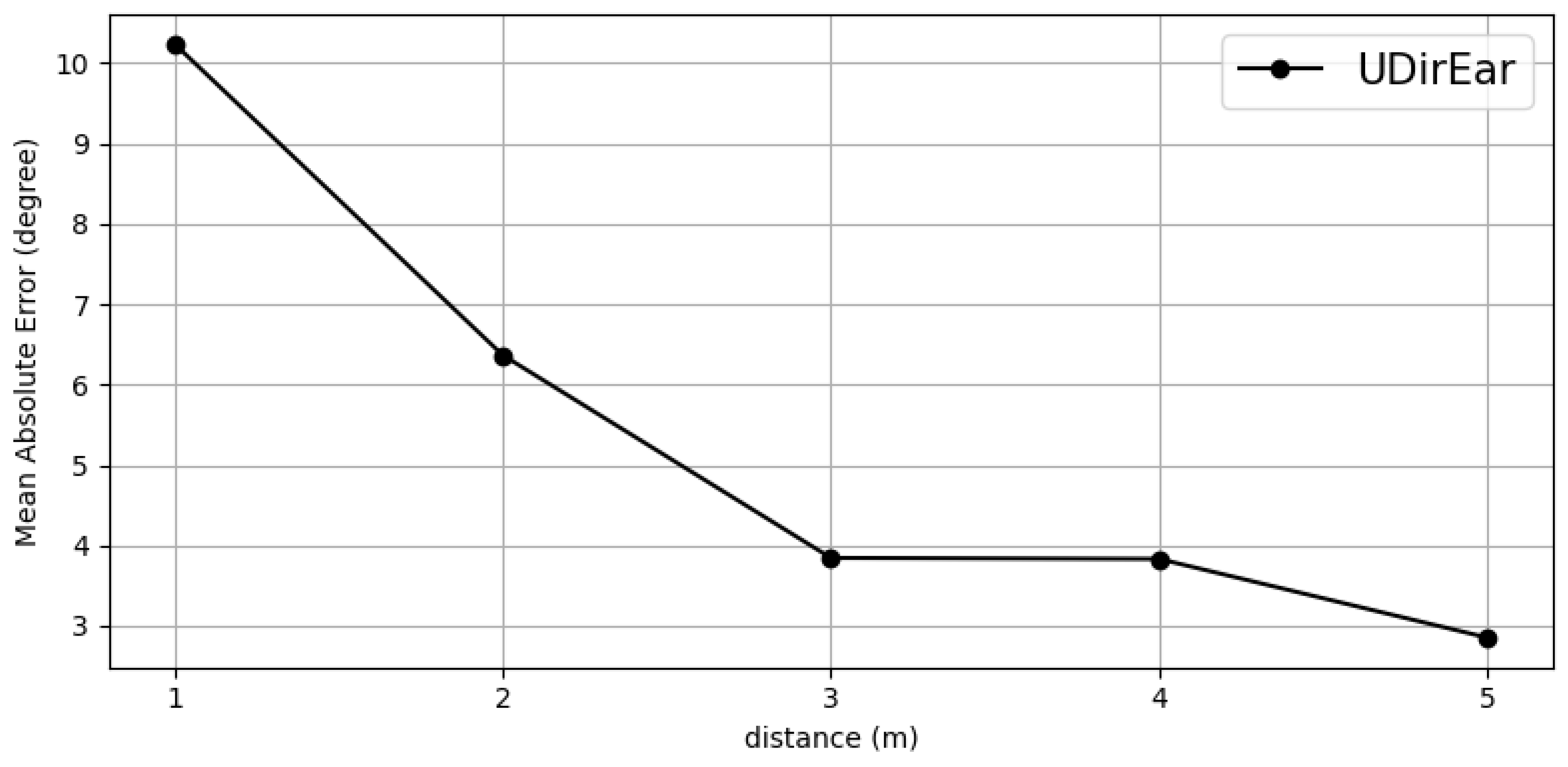
5.2.2. Effect of Distance Between Dummy Head and Initiator
5.2.3. Effect of Elapsed Time
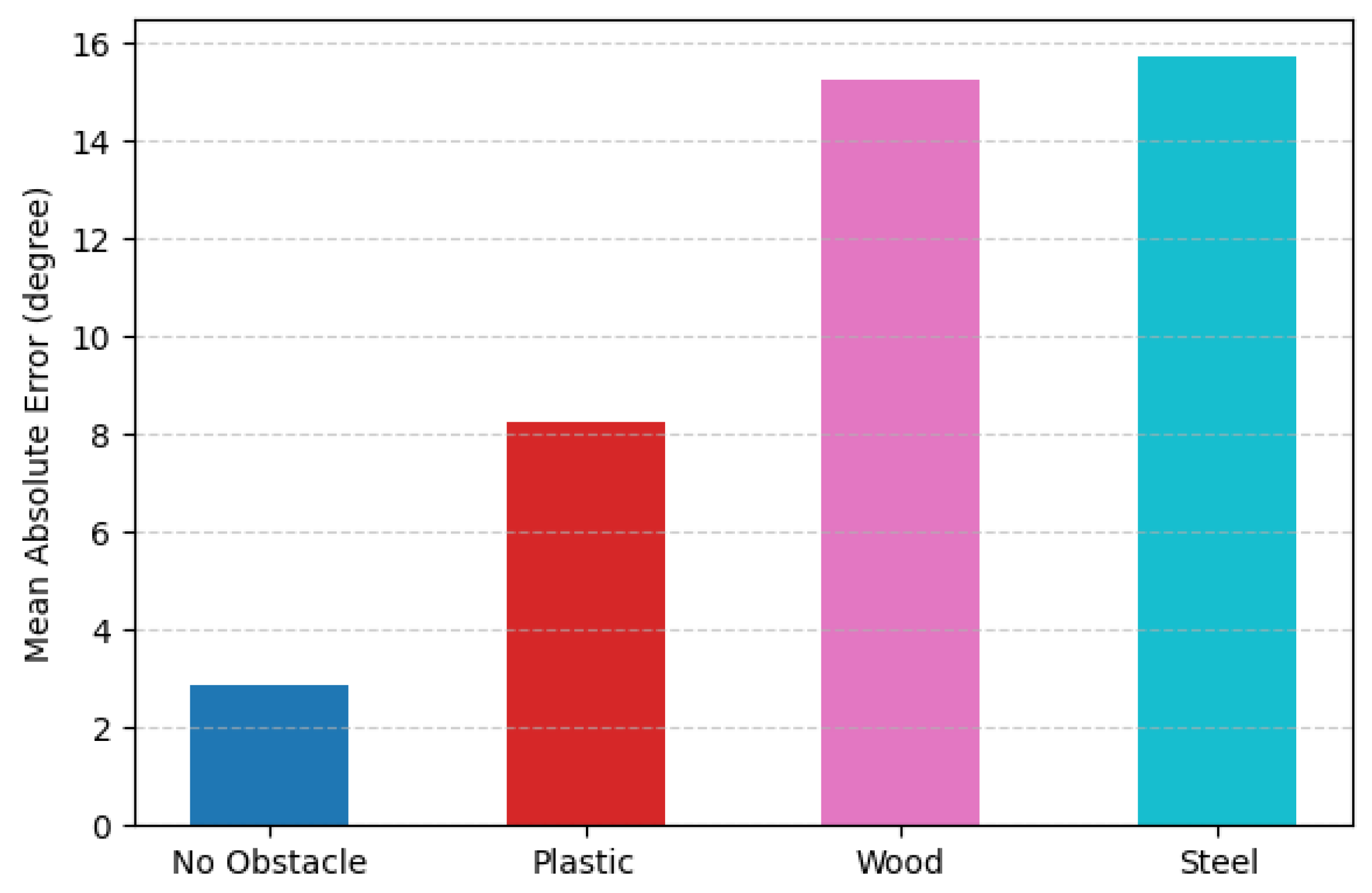
5.2.4. Effect of NLoS by Occlusion
6. Discussion
6.1. IMU-Enhanced Initiator Initialization and Tracking
6.2. Fine-Grained Practical Head Movement Tracking
6.3. Heading Direction Application in Daily Life
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- LaValle, S.M.; Yershova, A.; Katsev, M.; Antonov, M. Head tracking for the Oculus Rift. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 187–194. [Google Scholar] [CrossRef]
- Banaszczyk, A.; Lysakowski, M.; Nowicki, M.R.; Skrzypczynski, P.; Tadeja, S.K. How Accurate is the Positioning in VR? Using Motion Capture and Robotics to Compare Positioning Capabilities of Popular VR Headsets. In Proceedings of the 2024 IEEE International Symposium on Mixed and Augmented Reality Adjunct (ISMAR-Adjunct), Bellevue, WA, USA, 21–25 October 2024; pp. 79–86. [Google Scholar] [CrossRef]
- Vox, J.P.; Weber, A.; Wolf, K.I.; Izdebski, K.; Schüler, T.; König, P.; Wallhoff, F.; Friemert, D. An Evaluation of Motion Trackers with Virtual Reality Sensor Technology in Comparison to a Marker-Based Motion Capture System Based on Joint Angles for Ergonomic Risk Assessment. Sensors 2021, 21, 3145. [Google Scholar] [CrossRef]
- Cutolo, F.; Mamone, V.; Carbonaro, N.; Ferrari, V.; Tognetti, A. Ambiguity-Free Optical–Inertial Tracking for Augmented Reality Headsets. Sensors 2020, 20, 1444. [Google Scholar] [CrossRef]
- Franček, P.; Jambrošić, K.; Horvat, M.; Planinec, V. The Performance of Inertial Measurement Unit Sensors on Various Hardware Platforms for Binaural Head-Tracking Applications. Sensors 2023, 23, 872. [Google Scholar] [CrossRef]
- Hoang, M.L.; Carratù, M.; Paciello, V.; Pietrosanto, A. Fusion Filters between the No Motion No Integration Technique and Kalman Filter in Noise Optimization on a 6DoF Drone for Orientation Tracking. Sensors 2023, 23, 5603. [Google Scholar] [CrossRef]
- Kuti, J.; Piricz, T.; Galambos, P. A Robust Method for Validating Orientation Sensors Using a Robot Arm as a High-Precision Reference. Sensors 2024, 24, 8179. [Google Scholar] [CrossRef]
- Hu, L.; Tang, Y.; Zhou, Z.; Pan, W. Reinforcement Learning for Orientation Estimation Using Inertial Sensors with Performance Guarantee. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 10243–10249. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Lin, A.; Kumar, M.; Yang, T.H.; Ramanan, D.; Tulsiani, S. Cameras as Rays: Pose Estimation via Ray Diffusion. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- de Medeiros Esper, I.; Smolkin, O.; Manko, M.; Popov, A.; From, P.J.; Mason, A. Evaluation of RGB-D Multi-Camera Pose Estimation for 3D Reconstruction. Appl. Sci. 2022, 12, 4134. [Google Scholar] [CrossRef]
- Chen, F.; Wu, Y.; Liao, T.; Zeng, H.; Ouyang, S.; Guan, J. GMIW-Pose: Camera Pose Estimation via Global Matching and Iterative Weighted Eight-Point Algorithm. Electronics 2023, 12, 4689. [Google Scholar] [CrossRef]
- Yen-Chen, L.; Florence, P.; Barron, J.T.; Rodriguez, A.; Isola, P.; Lin, T.Y. iNeRF: Inverting Neural Radiance Fields for Pose Estimation. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; IEEE Press: Piscataway, NJ, USA, 2021; pp. 1323–1330. [Google Scholar] [CrossRef]
- Li, J.; Liu, K.; Wu, J. Ego-Body Pose Estimation via Ego-Head Pose Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 17142–17151. [Google Scholar]
- Wu, M.Y.; Ting, P.W.; Tang, Y.H.; Chou, E.T.; Fu, L.C. Hand pose estimation in object-interaction based on deep learning for virtual reality applications. J. Vis. Commun. Image Represent. 2020, 70, 102802. [Google Scholar] [CrossRef]
- Mao, W.; He, J.; Qiu, L. CAT: High-precision acoustic motion tracking. In Proceedings of the MobiCom’16: 22nd Annual International Conference on Mobile Computing and Networking, New York, NY, USA, 3–7 October 2016; pp. 69–81. [Google Scholar] [CrossRef]
- Yang, Z.; Wei, Y.L.; Shen, S.; Choudhury, R.R. Ear-AR: Indoor acoustic augmented reality on earphones. In Proceedings of the MobiCom’20: 26th Annual International Conference on Mobile Computing and Networking, London, UK, 21–25 September 2020. [Google Scholar] [CrossRef]
- Hu, J.; Jiang, H.; Liu, D.; Xiao, Z.; Zhang, Q.; Liu, J.; Dustdar, S. Combining IMU With Acoustics for Head Motion Tracking Leveraging Wireless Earphone. IEEE Trans. Mob. Comput. 2024, 23, 6835–6847. [Google Scholar] [CrossRef]
- Zhou, H.; Lu, T.; Liu, Y.; Zhang, S.; Liu, R.; Gowda, M. One Ring to Rule Them All: An Open Source Smartring Platform for Finger Motion Analytics and Healthcare Applications. In Proceedings of the IoTDI’23: 8th ACM/IEEE Conference on Internet of Things Design and Implementation, San Antonio, TX, USA, 9–12 May 2023; pp. 27–38. [Google Scholar] [CrossRef]
- Zhou, P.; Li, M.; Shen, G. Use it free: Instantly knowing your phone attitude. In Proceedings of the MobiCom’14: 20th Annual International Conference on Mobile Computing and Networking, Maui, HI, USA, 7–11 September 2014; pp. 605–616. [Google Scholar] [CrossRef]
- Kumar, A.; Pundlik, S.; Peli, E.; Luo, G. Comparison of Visual SLAM and IMU in Tracking Head Movement Outdoors. Behav. Res. Methods 2023, 55, 2787–2799. [Google Scholar] [CrossRef]
- Ferlini, A.; Montanari, A.; Grammenos, A.; Harle, R.; Mascolo, C. Enabling In-Ear Magnetic Sensing: Automatic and User Transparent Magnetometer Calibration. In Proceedings of the 2021 IEEE International Conference on Pervasive Computing and Communications (PerCom), Kassel, Germany, 22–26 March 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Ferlini, A.; Montanari, A.; Mascolo, C.; Harle, R. Head Motion Tracking Through in-Ear Wearables. In Proceedings of the EarComp’19: 1st International Workshop on Earable Computing, London, UK, 9 September 2020; pp. 8–13. [Google Scholar] [CrossRef]
- Hinterstoisser, S.; Lepetit, V.; Ilic, S.; Fua, P.; Navab, N. Dominant orientation templates for real-time detection of texture-less objects. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 2257–2264. [Google Scholar] [CrossRef]
- Shi, Y.; Yu, X.; Campbell, D.; Li, H. Where Am I Looking At? Joint Location and Orientation Estimation by Cross-View Matching. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 4063–4071. [Google Scholar] [CrossRef]
- Sundermeyer, M.; Marton, Z.C.; Durner, M.; Brucker, M.; Triebel, R. Implicit 3D Orientation Learning for 6D Object Detection from RGB Images. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Zhao, Y.; Görne, L.; Yuen, I.M.; Cao, D.; Sullman, M.; Auger, D.; Lv, C.; Wang, H.; Matthias, R.; Skrypchuk, L.; et al. An Orientation Sensor-Based Head Tracking System for Driver Behaviour Monitoring. Sensors 2017, 17, 2692. [Google Scholar] [CrossRef]
- Xie, X.; Shin, K.G.; Yousefi, H.; He, S. Wireless CSI-based head tracking in the driver seat. In Proceedings of the CoNEXT’18: 14th International Conference on Emerging Networking Experiments and Technologies, Heraklion, Greece, 4–7 December 2018; pp. 112–125. [Google Scholar] [CrossRef]
- Cao, G.; Yuan, K.; Xiong, J.; Yang, P.; Yan, Y.; Zhou, H.; Li, X.Y. EarphoneTrack: Involving earphones into the ecosystem of acoustic motion tracking. In Proceedings of the SenSys’20: 18th Conference on Embedded Networked Sensor Systems, Virtual Event, Japan, 16–19 November 2020; pp. 95–108. [Google Scholar] [CrossRef]
- Wang, A.; Gollakota, S. MilliSonic: Pushing the Limits of Acoustic Motion Tracking. In Proceedings of the CHI’19: 2019 CHI Conference on Human Factors in Computing Systems, Glasgow, UK, 4–9 May 2019; pp. 1–11. [Google Scholar] [CrossRef]
- Wang, Y.; Ding, J.; Chatterjee, I.; Salemi Parizi, F.; Zhuang, Y.; Yan, Y.; Patel, S.; Shi, Y. FaceOri: Tracking Head Position and Orientation Using Ultrasonic Ranging on Earphones. In Proceedings of the CHI’22: 2022 CHI Conference on Human Factors in Computing Systems, New Orleans, LA, USA, 29 April–5 May 2022. [Google Scholar] [CrossRef]
- Ge, L.; Zhang, Q.; Zhang, J.; Chen, H. EHTrack: Earphone-Based Head Tracking via Only Acoustic Signals. IEEE Internet Things J. 2024, 11, 4063–4075. [Google Scholar] [CrossRef]
- Hu, J.; Jiang, H.; Xiao, Z.; Chen, S.; Dustdar, S.; Liu, J. HeadTrack: Real-Time Human–Computer Interaction via Wireless Earphones. IEEE J. Sel. Areas Commun. 2024, 42, 990–1002. [Google Scholar] [CrossRef]
- Venkatnarayan, R.H.; Shahzad, M.; Yun, S.; Vlachou, C.; Kim, K.H. Leveraging Polarization of WiFi Signals to Simultaneously Track Multiple People. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2022, 4, 1–24. [Google Scholar] [CrossRef]
- Wang, H.; Sen, S.; Elgohary, A.; Farid, M.; Youssef, M.; Choudhury, R.R. No need to war-drive: Unsupervised indoor localization. In Proceedings of the MobiSys’12: 10th International Conference on Mobile Systems, Applications, and Services, Ambleside, UK, 25–29 June 2012; pp. 197–210. [Google Scholar] [CrossRef]
- Jiang, C.; He, Y.; Zheng, X.; Liu, Y. OmniTrack: Orientation-Aware RFID Tracking With Centimeter-Level Accuracy. IEEE Trans. Mob. Comput. 2021, 20, 634–646. [Google Scholar] [CrossRef]
- Wei, T.; Zhang, X. Gyro in the air: Tracking 3D orientation of batteryless internet-of-things. In Proceedings of the MobiCom’16: 22nd Annual International Conference on Mobile Computing and Networking, New York, NY, USA, 3–7 October 2016; pp. 55–68. [Google Scholar] [CrossRef]
- Apple Inc. Apple iPhone 14—Specifications. 2022. Available online: https://www.apple.com/iphone-14/specs (accessed on 30 May 2025).
- Apple Inc. Apple iPhone 15—Specifications. 2023. Available online: https://www.apple.com/iphone-15/specs (accessed on 30 May 2025).
- Apple Inc. Apple iPhone 16—Specifications. 2024. Available online: https://www.apple.com/iphone-16/specs (accessed on 30 May 2025).
- Samsung Electronics. Samsung Galaxy S25 Ultra—Specifications. 2025. Available online: https://www.samsung.com/us/smartphones/galaxy-s25-ultra (accessed on 30 May 2025).
- Samsung China Semiconductor Co., Ltd.; Samsung Electronics Co., Ltd. Method and Apparatus for Controlling Wireless Headphones and Headphone System. CN117041792A, November 2023. Available online: https://patents.google.com/patent/CN117041792A/en (accessed on 16 June 2025).
- Arun, A.; Saruwatari, S.; Shah, S.; Bharadia, D. XRLoc: Accurate UWB Localization to Realize XR Deployments. In Proceedings of the SenSys’23: 21st ACM Conference on Embedded Networked Sensor Systems, Istanbul, Turkiye, 12–17 November 2024; pp. 459–473. [Google Scholar] [CrossRef]
- Cao, Y.; Dhekne, A.; Ammar, M. ViSig: Automatic Interpretation of Visual Body Signals Using On-Body Sensors. In Proceedings of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies; Association for Computing Machinery: New York, NY, USA, 2023; Volume 7, pp. 1–27. [Google Scholar] [CrossRef]
- Kempke, B.; Pannuto, P.; Dutta, P. Harmonium: Asymmetric, Bandstitched UWB for Fast, Accurate, and Robust Indoor Localization. In Proceedings of the 2016 15th ACM/IEEE International Conference on Information Processing in Sensor Networks (IPSN), Vienna, Austria, 11–14 April 2016; pp. 1–12. [Google Scholar] [CrossRef]
- Feng, D.; Wang, C.; He, C.; Zhuang, Y.; Xia, X.G. Kalman-Filter-Based Integration of IMU and UWB for High-Accuracy Indoor Positioning and Navigation. IEEE Internet Things J. 2020, 7, 3133–3146. [Google Scholar] [CrossRef]
- Gowda, M.; Dhekne, A.; Shen, S.; Choudhury, R.R.; Yang, L.; Golwalkar, S.; Essanian, A. Bringing IoT to Sports Analytics. In Proceedings of the 14th USENIX Symposium on Networked Systems Design and Implementation (NSDI 17), Boston, MA, USA, 27–29 March 2017; pp. 499–513. [Google Scholar]
- Cao, Y.; Dhekne, A.; Ammar, M. ITrackU: Tracking a pen-like instrument via UWB-IMU fusion. In Proceedings of the MobiSys’21; 19th Annual International Conference on Mobile Systems, Applications, and Services, Virtual Event, WI, USA, 24 June–2 July 2021; pp. 453–466. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J. FusionTrack: Towards Accurate Device-free Acoustic Motion Tracking with Signal Fusion. ACM Trans. Sens. Netw. 2024, 20, 1–30. [Google Scholar] [CrossRef]
- Xu, C.; Zheng, X.; Ren, Z.; Liu, L.; Ma, H. UHead: Driver Attention Monitoring System Using UWB Radar. Proc. ACM Interact. Mob. Wearable Ubiquitou Technol. 2024, 8, 1–28. [Google Scholar] [CrossRef]
- Zhou, H.; Yuan, K.; Gowda, M.; Qiu, L.; Xiong, J. Rethinking Orientation Estimation with Smartphone-equipped Ultra-wideband Chips. In Proceedings of the ACM MobiCom’24: 30th Annual International Conference on Mobile Computing and Networking, Washington, DC, USA, 18–22 November 2024; pp. 1045–1059. [Google Scholar] [CrossRef]
- Cao, Y.; Dhekne, A.; Ammar, M. UTrack3D: 3D Tracking Using Ultra-wideband (UWB) Radios. In Proceedings of theMOBISYS’24: 22nd Annual International Conference on Mobile Systems, Applications and Services, Tokyo, Japan, 3–7 June 2024; pp. 345–358. [Google Scholar] [CrossRef]
- IEEE Std 802.15.4-2020; Revision of IEEE Std 802.15.4-2015, IEEE Standard for Low-Rate Wireless Networks. IEEE: New York, NY, USA, 2020; pp. 1–800. [CrossRef]
- Apple Inc. Apple Watch Series 10—Specifications. 2024. Available online: https://www.apple.com/apple-watch-series-10 (accessed on 30 May 2025).
- Google Inc. Google Pixel Watch 3—Specifications. 2024. Available online: https://store.google.com/gb/product/pixel_watch_3_specs (accessed on 30 May 2025).
- Apple Inc. Nearby Interaction API. Available online: https://developer.apple.com/documentation/nearbyinteraction (accessed on 30 May 2025).
- Google Inc. Android Ultra-Wideband (UWB) API. Available online: https://developer.android.com/develop/connectivity/uwb (accessed on 30 May 2025).
- Neirynck, D.; Luk, E.; McLaughlin, M. An alternative double-sided two-way ranging method. In Proceedings of the 2016 13th Workshop on Positioning, Navigation and Communications (WPNC), Bremen, Germany, 19–20 October 2016; pp. 1–4. [Google Scholar]
- Montañez, O.J.; Suárez, M.J.; Fernández, E.A. Application of Data Sensor Fusion Using Extended Kalman Filter Algorithm for Identification and Tracking of Moving Targets from LiDAR–Radar Data. Remote Sens. 2023, 15, 3396. [Google Scholar] [CrossRef]
- Yin, Y.; Zhang, J.; Guo, M.; Ning, X.; Wang, Y.; Lu, J. Sensor Fusion of GNSS and IMU Data for Robust Localization via Smoothed Error State Kalman Filter. Sensors 2023, 23, 3676. [Google Scholar] [CrossRef] [PubMed]
- Deng, Z.A.; Hu, Y.; Yu, J.; Na, Z. Extended Kalman Filter for Real Time Indoor Localization by Fusing WiFi and Smartphone Inertial Sensors. Micromachines 2015, 6, 523–543. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; Technical Report TR 95-041; University of North Carolina at Chapel Hill: Chapel Hill, NC, USA, 2006. [Google Scholar]
- Ribeiro, M.I. Kalman and Extended Kalman Filters: Concept, Derivation and Properties; Technical Report; Institute for Systems and Robotics, Instituto Superior Técnico, Universidade de Lisboa: Lisboa, Portugal, 2004. [Google Scholar]
- Zhang, F.; Chang, Z.; Xiong, J.; Ma, J.; Ni, J.; Zhang, W.; Jin, B.; Zhang, D. Embracing Consumer-level UWB-equipped Devices for Fine-grained Wireless Sensing. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2022, 6, 1–27. [Google Scholar] [CrossRef]
- Heuring, J.; Murray, D. Modeling and copying human head movements. IEEE Trans. Robot. Autom. 1999, 15, 1095–1108. [Google Scholar] [CrossRef]
- Bai, J.; He, X.; Jiang, Y.; Zhang, T.; Bao, M. Rotating One’s Head Modulates the Perceived Velocity of Motion Aftereffect. Multisensory Res. 2020, 33, 189–212. [Google Scholar] [CrossRef]
- Shen, S.; Gowda, M.; Roy Choudhury, R. Closing the Gaps in Inertial Motion Tracking. In Proceedings of the MobiCom’18: 24th Annual International Conference on Mobile Computing and Networking, New Delhi, India, 29 October–2 November 2018; pp. 429–444. [Google Scholar] [CrossRef]
- Awinic Technology Co., Ltd. DW1000 User Manual. 2021. Available online: https://www.sunnywale.com/uploadfile/2021/1230/DW1000%20User%20Manual_Awin.pdf (accessed on 10 June 2025).
- Shah, S.; Chaiwong, K.; Kovavisaruch, L.O.; Kaemarungsi, K.; Demeechai, T. Antenna Delay Calibration of UWB Nodes. IEEE Access 2021, 9, 63294–63305. [Google Scholar] [CrossRef]
- Preter, A.D.; Goysens, G.; Anthonis, J.; Swevers, J.; Pipeleers, G. Range Bias Modeling and Autocalibration of an UWB Positioning System. In Proceedings of the 2019 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Pisa, Italy, 30 September–3 October 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Han, S.; Jang, B.J. Extending the Coverage of IEEE 802.15.4z HRP UWB Ranging. Sensors 2025, 25, 3058. [Google Scholar] [CrossRef]
| Symbol | Description |
|---|---|
| a | state vector at step k |
| control input at step k | |
| process model’s noise vector at step k | |
| error covariance at step k | |
| process model’s noise covariance at step k | |
| sensor value’s noise covariance at step k | |
| residual noise covariance at step k | |
| A | state transition matrix |
| H | observation matrix |
| Kalman gain at step k | |
| sensor value at step k |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.; Nam, Y.; Kim, J.; Suh, Y.-J. UDirEar: Heading Direction Tracking with Commercial UWB Earbud by Interaural Distance Calibration. Electronics 2025, 14, 2940. https://doi.org/10.3390/electronics14152940
Kim M, Nam Y, Kim J, Suh Y-J. UDirEar: Heading Direction Tracking with Commercial UWB Earbud by Interaural Distance Calibration. Electronics. 2025; 14(15):2940. https://doi.org/10.3390/electronics14152940
Chicago/Turabian StyleKim, Minseok, Younho Nam, Jinyou Kim, and Young-Joo Suh. 2025. "UDirEar: Heading Direction Tracking with Commercial UWB Earbud by Interaural Distance Calibration" Electronics 14, no. 15: 2940. https://doi.org/10.3390/electronics14152940
APA StyleKim, M., Nam, Y., Kim, J., & Suh, Y.-J. (2025). UDirEar: Heading Direction Tracking with Commercial UWB Earbud by Interaural Distance Calibration. Electronics, 14(15), 2940. https://doi.org/10.3390/electronics14152940







