Nonlinear Observer-Based Distributed Adaptive Fault-Tolerant Control for Vehicle Platoon with Actuator Faults, Saturation, and External Disturbances
Abstract
1. Introduction
- Unlike disturbance observers presented in [21,22,23], which requires prior knowledge about the upper bounds of external disturbances, this paper proposes a novel nonlinear observer capable of directly estimating external disturbances without the need to know the upper bounds of disturbances, which makes the proposed approach more general and extends its applicability to a broader range of practical vehicle platoons.
- A novel nonlinear observer-based distributed adaptive fault-tolerant control strategy based on the proposed nonlinear observer-adaptive updating mechanism, RBFNN, and the ESP is designed for the vehicle platoon to effectively address actuator faults, saturation, and external disturbances and achieve the platoon control objectives.
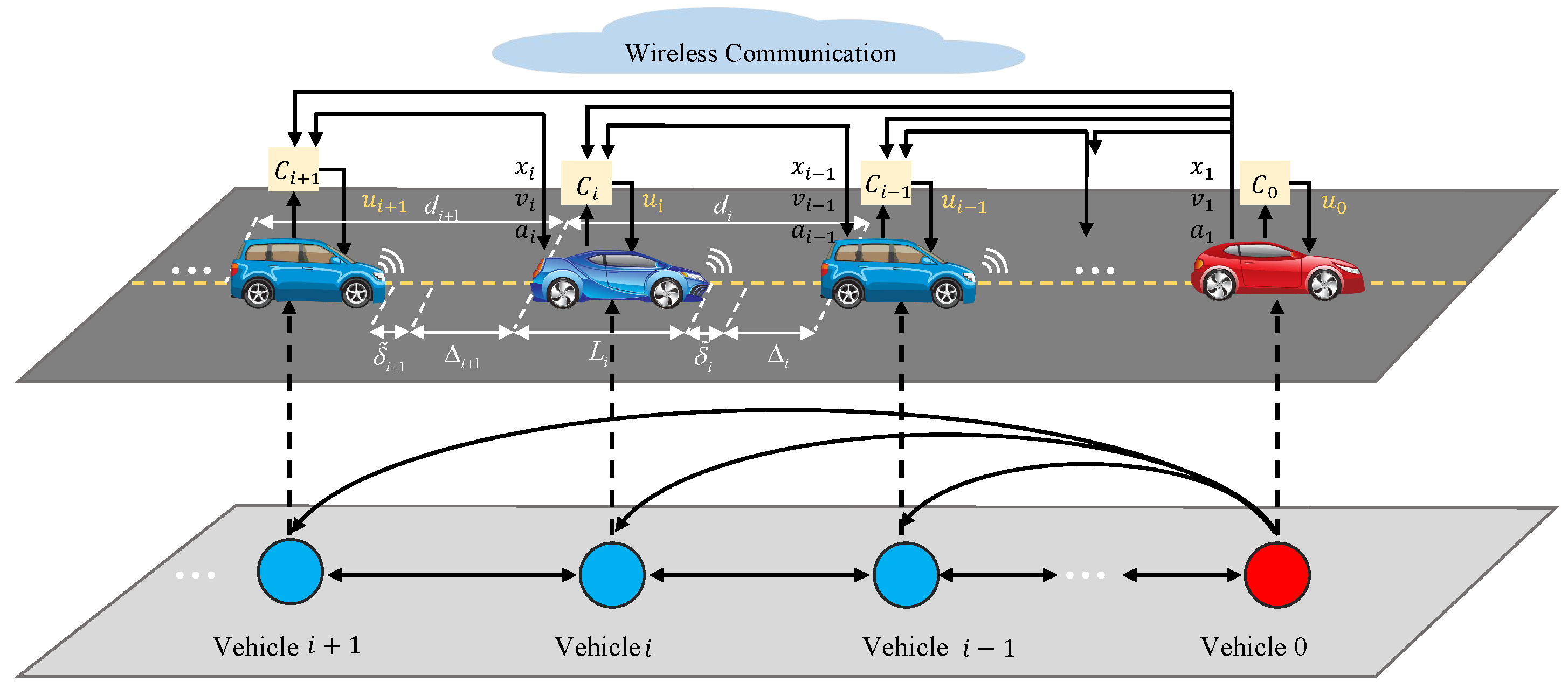
2. Problem Formulation
2.1. Vehicle Dynamics Modeling
2.2. RBFNN
2.3. Platoon Control Problem Formulation
- Internal stability [36]: Each vehicle keeps the predetermined spacing from the preceding vehicle and achieves velocity synchronization with the leader vehicle.
- String stability [37]: The platoon is regarded to be string stable, if
- Traffic flow stability [38]: This requires that the gradient is positive, that is,where and P denote the traffic flow rate and traffic density, respectively.
3. Nonlinear Observer-Based Distributed Adaptive Fault-Tolerant Control Design
3.1. Nonlinear Observer
3.2. Nonlinear Observer-Based Distributed Adaptive Fault-Tolerant Control Design
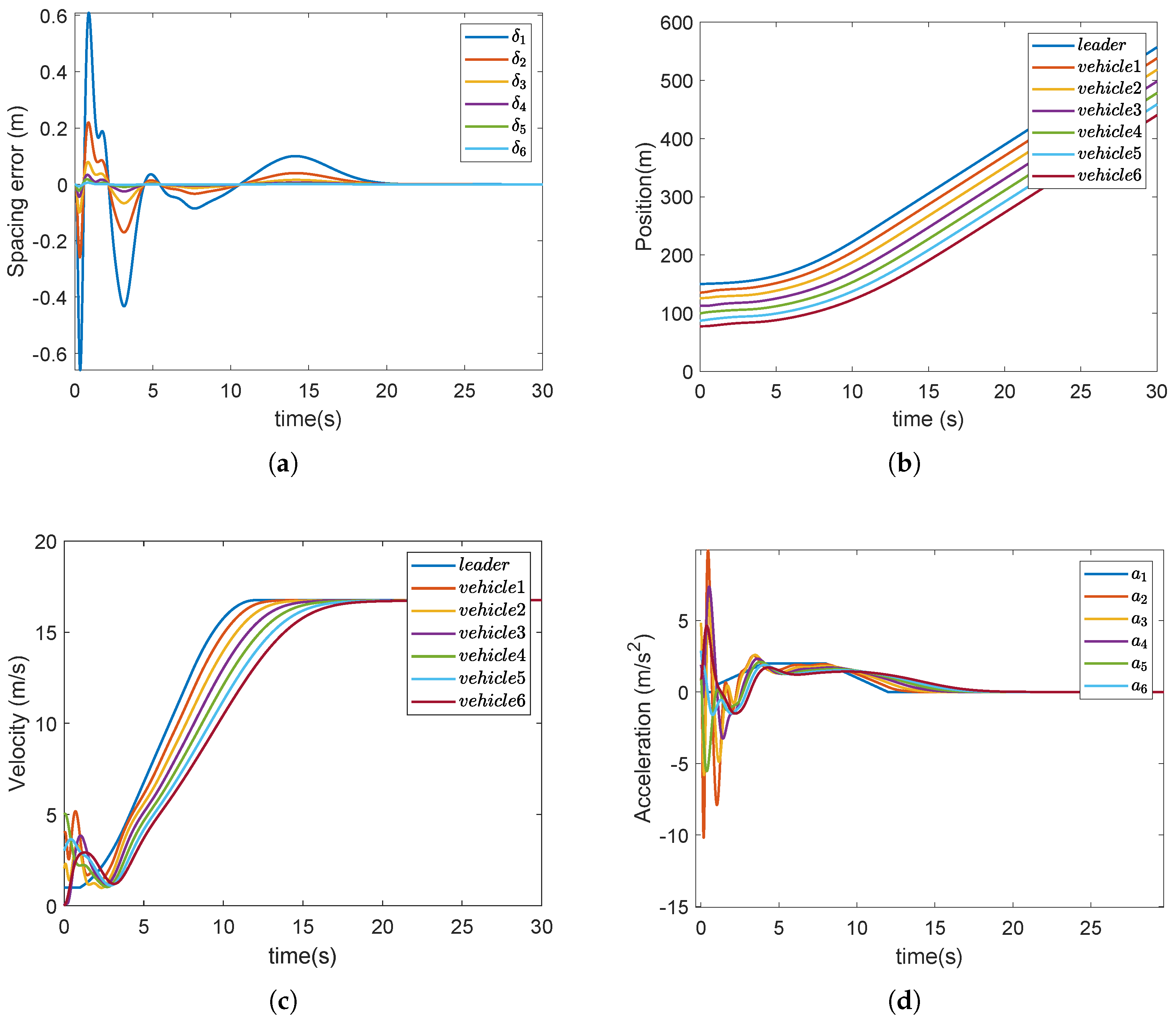
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ISEs | Initial Spacing Errors |
| EPS | Exponential Spacing Policy |
| GEF | Gaussian Error Function |
| RBFNN | Radial Basis Function Neural Network |
References
- Li, X.; Shi, P.; Wang, Y.; Wang, S. Cooperative tracking control of heterogeneous mixed-order multiagent systems with higher-order nonlinear dynamics. IEEE Trans. Cybern. 2020, 52, 5498–5507. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Liang, H.; Li, J.; Lv, Z. Connected automated vehicle platoon control with input saturation and variable time headway strategy. IEEE Trans. Intell. Transp. Syst. 2020, 22, 4929–4940. [Google Scholar] [CrossRef]
- Qiang, Z.; Dai, L.; Chen, B.; Xia, Y. Distributed model predictive control for heterogeneous vehicle platoon with inter-vehicular spacing constraints. IEEE Trans. Intell. Transp. Syst. 2022, 24, 3339–3351. [Google Scholar] [CrossRef]
- Hu, M.; Li, C.; Bian, Y.; Zhang, H.; Qin, Z.; Xu, B. Fuel economy-oriented vehicle platoon control using economic model predictive control. IEEE Trans. Intell. Transp. Syst. 2022, 23, 20836–20849. [Google Scholar] [CrossRef]
- Xu, Z.; Jiao, X. Robust control of connected cruise vehicle platoon with uncertain human driving reaction time. IEEE Trans. Intell. Veh. 2021, 7, 368–376. [Google Scholar] [CrossRef]
- Kwon, J.; Chwa, D. Adaptive bidirectional platoon control using a coupled sliding mode control method. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2040–2048. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Y.; Zhu, H.; Hua, W.; Huang, G.; Yu, S.; Li, S.E.; Gao, X. Joint sliding-mode controller and observer for vehicle platoon subject to disturbance and acceleration failure of neighboring vehicles. IEEE Trans. Intell. Veh. 2022, 8, 2345–2357. [Google Scholar] [CrossRef]
- Li, X.; Shi, P.; Wang, Y. Distributed cooperative adaptive tracking control for heterogeneous systems with hybrid nonlinear dynamics. Nonlinear Dyn. 2019, 95, 2131–2141. [Google Scholar] [CrossRef]
- Zheng, Y.; Xu, M.; Wu, S.; Wang, S. Development of connected and automated vehicle platoons with combined spacing policy. IEEE Trans. Intell. Transp. Syst. 2022, 24, 596–614. [Google Scholar] [CrossRef]
- Mattas, K.; Albano, G.; Donà, R.; He, Y.; Ciuffo, B. On the relationship between traffic hysteresis and string stability of vehicle platoons. Transp. Res. Part B Methodol. 2023, 174, 102785. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, J.; Wang, Z.; Yan, H.; Zhang, C. Distributed adaptive event-triggered control and stability analysis for vehicular platoon. IEEE Trans. Intell. Transp. Syst. 2020, 22, 1627–1638. [Google Scholar] [CrossRef]
- Wang, J.; Luo, X.; Wang, L.; Zuo, Z.; Guan, X. Integral sliding mode control using a disturbance observer for vehicle platoons. IEEE Trans. Ind. Electron. 2019, 67, 6639–6648. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, Y.; Qu, X.; Li, S.; Ran, B. Developing platooning systems of connected and automated vehicles with guaranteed stability and robustness against degradation due to communication disruption. Transp. Res. Part Emerg. Technol. 2024, 168, 104768. [Google Scholar] [CrossRef]
- Kianfar, R.; Falcone, P.; Fredriksson, J. A control matching model predictive control approach to string stable vehicle platooning. Control Eng. Pract. 2015, 45, 163–173. [Google Scholar] [CrossRef]
- Lin, Y.; Tiwari, A.; Fabien, B.; Devasia, S. Constant-spacing connected platoons with robustness to communication delays. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3370–3382. [Google Scholar] [CrossRef]
- Chehardoli, H.; Ghasemi, A. Adaptive centralized/decentralized control and identification of 1-D heterogeneous vehicular platoons based on constant time headway policy. IEEE Trans. Intell. Transp. Syst. 2018, 19, 3376–3386. [Google Scholar] [CrossRef]
- Herman, I.; Knorn, S.; Ahlén, A. Disturbance scaling in bidirectional vehicle platoons with different asymmetry in position and velocity coupling. Automatica 2017, 82, 13–20. [Google Scholar] [CrossRef]
- Xu, L.; Zhuang, W.; Yin, G.; Bian, C.; Wu, H. Modeling and robust control of heterogeneous vehicle platoons on curved roads subject to disturbances and delays. IEEE Trans. Veh. Technol. 2019, 68, 11551–11564. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Li, X.; Liang, Y. Distributed consensus tracking control based on state and disturbance observations for mixed-order multi-agent mechanical systems. J. Frankl. Inst. 2023, 360, 943–963. [Google Scholar] [CrossRef]
- Guo, G.; Li, P.; Hao, L.Y. Adaptive fault-tolerant control of platoons with guaranteed traffic flow stability. IEEE Trans. Veh. Technol. 2020, 69, 6916–6927. [Google Scholar] [CrossRef]
- Wang, J.; Luo, X.; Yan, J.; Guan, X. Distributed integrated sliding mode control for vehicle platoons based on disturbance observer and multi power reaching law. IEEE Trans. Intell. Transp. Syst. 2020, 23, 3366–3376. [Google Scholar] [CrossRef]
- Boo, J.; Chwa, D. Integral sliding mode control-based robust bidirectional platoon control of vehicles with the unknown acceleration and mismatched disturbance. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10881–10894. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, Y.; Guo, G. Prescribed-time control of vehicular platoons based on a disturbance observer. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3789–3793. [Google Scholar] [CrossRef]
- Afifa, R.; Ali, S.; Pervaiz, M.; Iqbal, J. Adaptive backstepping integral sliding mode control of a mimo separately excited DC motor. Robotics 2023, 12, 105. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, B.; Yuan, J. Decentralized adaptive fault tolerant control for a class of interconnected systems with nonlinear multisource disturbances. J. Frankl. Inst. 2018, 355, 4493–4514. [Google Scholar] [CrossRef]
- Awan, Z.S.; Ali, K.; Iqbal, J.; Mehmood, A. Adaptive backstepping based sensor and actuator fault tolerant control of a manipulator. J. Electr. Eng. Technol. 2019, 14, 2497–2504. [Google Scholar] [CrossRef]
- Wang, L.; Bian, Y.; Cao, D.; Qin, H.; Hu, M. Hierarchical Safe Control of Heterogeneous Connected Vehicle Systems Using Adaptive Fault-Tolerant Control. IEEE Trans. Veh. Technol. 2024, 73, 14313–14325. [Google Scholar] [CrossRef]
- An, J.; Cao, L.; Wang, Y.; Khan Jadoon, A.; Wang, S. Adaptive Fault-Tolerant Optimized Platoon Cloud Tracking Control for Heterogeneous Vehicles via Dual Learning Mechanism. IEEE Trans. Autom. Sci. Eng. 2025, 22, 4382–4393. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Y. Adaptive fuzzy predefined-time fault-tolerant control for third-order heterogeneous vehicular platoon systems. Int. J. Robust Nonlinear Control 2023, 33, 4422–4437. [Google Scholar] [CrossRef]
- Yan, S.; Gu, Z.; Park, J.H.; Xie, X.; Sun, W. Distributed cooperative voltage control of networked islanded microgrid via proportional-integral observer. IEEE Trans. Smart Grid 2024, 15, 5981–5991. [Google Scholar] [CrossRef]
- Yan, S.; Gu, Z.; Park, J.H.; Xie, X. A delay-kernel-dependent approach to saturated control of linear systems with mixed delays. Automatica 2023, 152, 110984. [Google Scholar] [CrossRef]
- Wu, Z.; Sun, J.; Hong, S. RBFNN-based adaptive event-triggered control for heterogeneous vehicle platoon consensus. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18761–18773. [Google Scholar] [CrossRef]
- Ren, B.; Ge, S.S.; Su, C.Y.; Lee, T.H. Adaptive neural control for a class of uncertain nonlinear systems in pure-feedback form with hysteresis input. IEEE Trans. Syst. Man, Cybern. Part B (Cybern.) 2008, 39, 431–443. [Google Scholar]
- Wang, Y.; Shi, P.; Li, X. Event-Triggered Observation-Based Control of Nonlinear Mixed-Order Multiagent Systems Under Input Saturation. IEEE Syst. J. 2024, 18, 1392–1401. [Google Scholar] [CrossRef]
- Yan, S.; Ding, L.; Cai, Y. Memory-based attack-tolerant TS fuzzy control of networked artificial pancreas system subject to false data injection attacks. Fuzzy Sets Syst. 2025, 518, 109486. [Google Scholar] [CrossRef]
- Feng, S.; Zhang, Y.; Li, S.E.; Cao, Z.; Liu, H.X.; Li, L. String stability for vehicular platoon control: Definitions and analysis methods. Annu. Rev. Control 2019, 47, 81–97. [Google Scholar] [CrossRef]
- Besselink, B.; Johansson, K.H. String stability and a delay-based spacing policy for vehicle platoons subject to disturbances. IEEE Trans. Autom. Control 2017, 62, 4376–4391. [Google Scholar] [CrossRef]
- Guo, G.; Li, P.; Hao, L.Y. A new quadratic spacing policy and adaptive fault-tolerant platooning with actuator saturation. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1200–1212. [Google Scholar] [CrossRef]
- Guo, X.; Wang, J.; Liao, F.; Teo, R.S.H. CNN-based distributed adaptive control for vehicle-following platoon with input saturation. IEEE Trans. Intell. Transp. Syst. 2017, 19, 3121–3132. [Google Scholar] [CrossRef]
- Pan, C.; Chen, Y.; Liu, Y.; Ali, I.; He, W. Distributed finite-time fault-tolerant control for heterogeneous vehicular platoon with saturation. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21259–21273. [Google Scholar] [CrossRef]
- Jin, I.G.; Orosz, G. Optimal control of connected vehicle systems with communication delay and driver reaction time. IEEE Trans. Intell. Transp. Syst. 2016, 18, 2056–2070. [Google Scholar] [CrossRef]
- Chen, M.; Tao, G. Adaptive Fault-Tolerant Control of Uncertain Nonlinear Large-Scale Systems With Unknown Dead Zone. IEEE Trans. Cybern. 2016, 46, 1851–1862. [Google Scholar] [CrossRef] [PubMed]


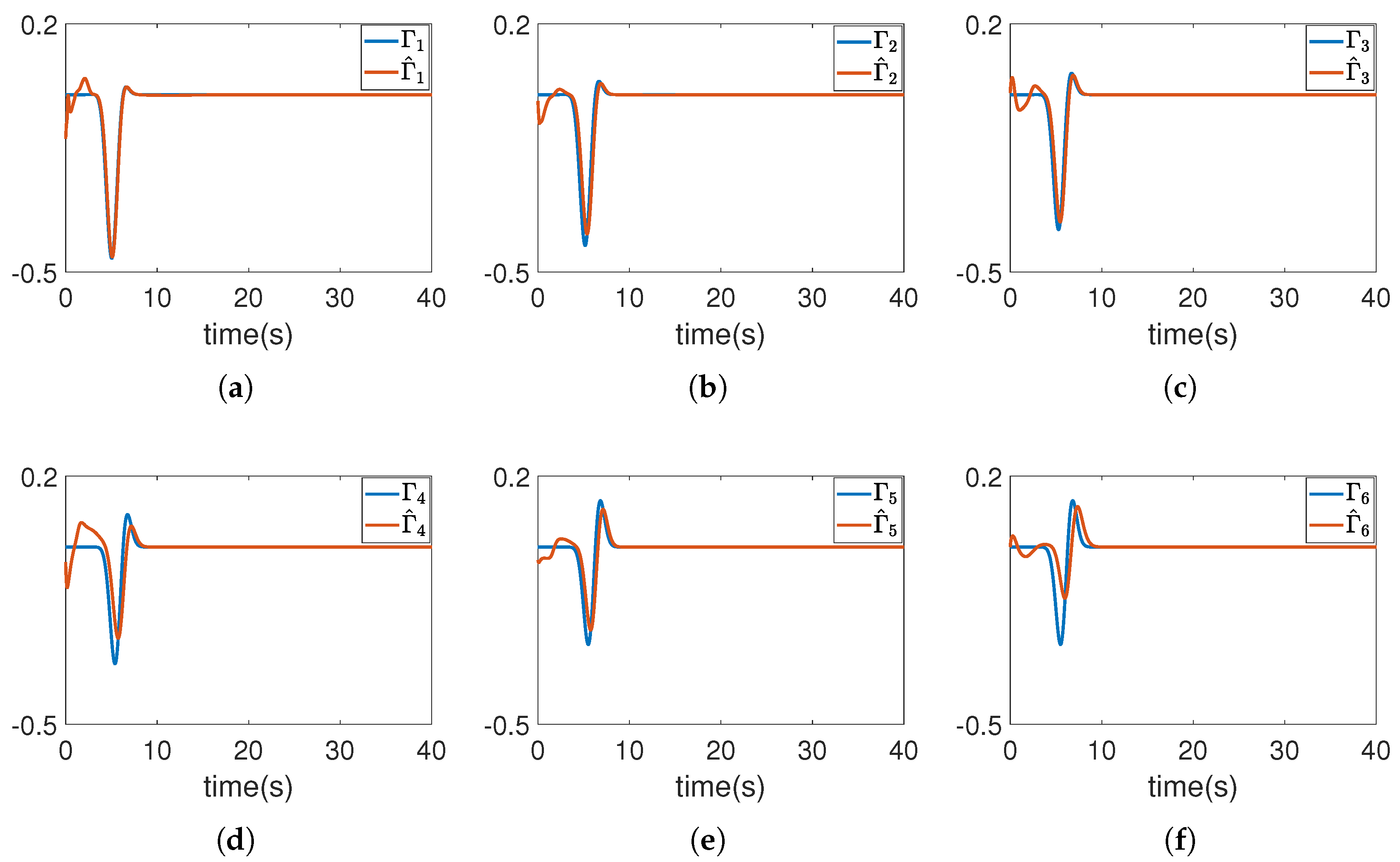
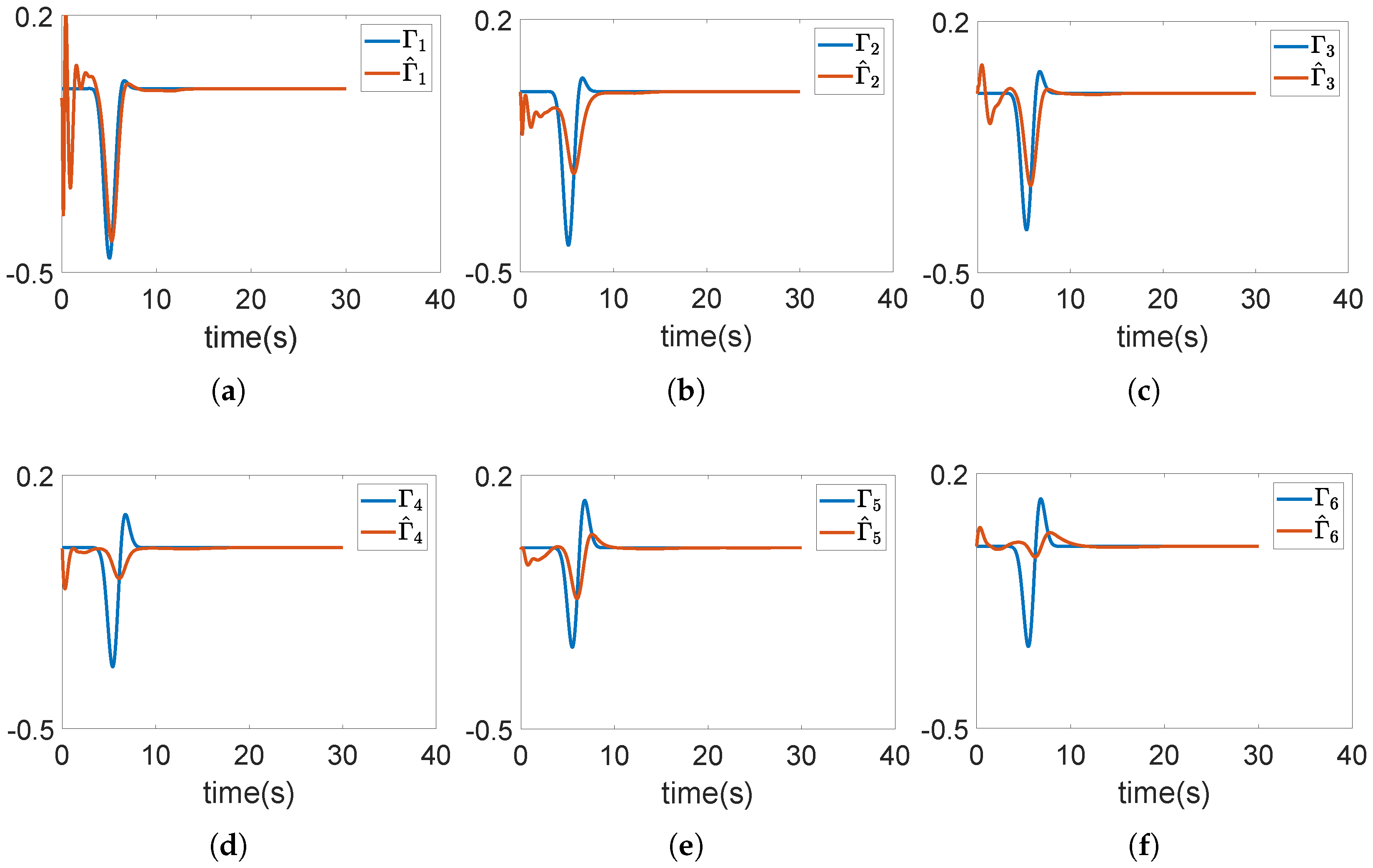
| Nonlinear Observer-Based Sliding Mode Controller | Disturbance Observer-Based Sliding Mode Controller | |
|---|---|---|
| Overshoot of | 0.0558 | 0.1317 |
| 0.0041 | 0.0071 |
| Nonlinear Observer | Disturbance Observer | |
|---|---|---|
| Overshoot of | 0.0915 | 0.1260 |
| 0.0220 | 0.0398 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, A.; Wang, Y.; Li, X.; Zhan, X.; Yang, M.; Ding, Y. Nonlinear Observer-Based Distributed Adaptive Fault-Tolerant Control for Vehicle Platoon with Actuator Faults, Saturation, and External Disturbances. Electronics 2025, 14, 2879. https://doi.org/10.3390/electronics14142879
Tong A, Wang Y, Li X, Zhan X, Yang M, Ding Y. Nonlinear Observer-Based Distributed Adaptive Fault-Tolerant Control for Vehicle Platoon with Actuator Faults, Saturation, and External Disturbances. Electronics. 2025; 14(14):2879. https://doi.org/10.3390/electronics14142879
Chicago/Turabian StyleTong, Anqing, Yiguang Wang, Xiaojie Li, Xiaoyan Zhan, Minghao Yang, and Yunpeng Ding. 2025. "Nonlinear Observer-Based Distributed Adaptive Fault-Tolerant Control for Vehicle Platoon with Actuator Faults, Saturation, and External Disturbances" Electronics 14, no. 14: 2879. https://doi.org/10.3390/electronics14142879
APA StyleTong, A., Wang, Y., Li, X., Zhan, X., Yang, M., & Ding, Y. (2025). Nonlinear Observer-Based Distributed Adaptive Fault-Tolerant Control for Vehicle Platoon with Actuator Faults, Saturation, and External Disturbances. Electronics, 14(14), 2879. https://doi.org/10.3390/electronics14142879





