Intelligent Diagnosis Method for Early Weak Faults Based on Wave Intercorrelation–Convolutional Neural Networks

Abstract

Rolling bearings are widely used in rotating machinery, and their health status is crucial for the safe operation of the equipment. The research on relevant fault diagnosis algorithms is a hot topic in the field. As a leading deep learning paradigm, Convolutional Neural Networks (CNNs) have demonstrated remarkable effectiveness in bearing fault diagnosis. However, conventional CNNs encounter significant limitations in accurately identifying and classifying early-stage bearing faults, primarily due to two challenges: (1) the diagnostic accuracy is highly susceptible to variations in the input signal length and segmentation strategies and (2) incipient faults are characterized by extremely low signal-to-noise ratios (SNRs), which obscure fault signatures. To address these challenges, we propose a Waveform Intersection-CNN (WI-CNN)-based intelligent diagnosis method for early faults. This approach integrates Gramian Angular Field theory to construct high-resolution fault signatures, enabling the CNN-based diagnosis of incipient bearing faults. Validation using the Case Western Reserve University dataset demonstrates an average diagnostic accuracy exceeding 98%. Furthermore, we established a custom test platform to develop a hybrid diagnosis strategy for 10 distinct fault types. Comparative studies against two conventional CNN diagnostic methods confirm that our approach delivers superior diagnostic precision, a faster iteration speed, and enhanced algorithmic robustness. The empirical findings demonstrate that the model achieves an accuracy of 99.67% during training and 98.167% in the testing phase. Crucially, the proposed method offers exceptional simplicity, computational efficiency, and practical applicability, facilitating its widespread implementation.

1. Introduction

As pivotal supporting elements in rotating machinery, bearings play a critical role in determining the operational safety and service life of the equipment through their physical state. Industrial data show that bearing failures caused by continuous wear on the mating surfaces account for 30–45% of the total failures of rotating machinery [1]. Among them, early minor damages (such as pitting or cracks of less than 0.5 mm) are difficult to detect under strong background noise (SNR often lower than −5 dB), becoming a core challenge in fault diagnosis [2]. At its core, machinery fault diagnosis can be framed as a pattern recognition challenge centered around identifying distinct equipment states. Traditional methods rely on a three-stage framework of “preprocessing-feature extraction-classification” [3]. Time-domain statistics (skewness and peak factor), frequency-domain spectral analysis (FFT and envelope spectrum), and time–frequency domain methods (wavelet transform and Hilbert–Huang transform) all have bottlenecks of insufficient feature significance in weak fault scenarios [4].

Classical methods (short-time Fourier, wavelet packet decomposition, etc.) face the contradiction of not being able to achieve both time–frequency resolution in low-signal-to-noise-ratio environments [5]. The synchronous compression transform (SST) improves energy focusing by redistributing operators [6,7,8], but its feature enhancement intensity is positively correlated with the signal amplitude (correlation coefficient > 0.82) [9], resulting in the suppression of weak impact components in strong-interference backgrounds. The random resonance (SR) technology converts environmental noise energy into fault feature enhancement energy by constructing a bistable potential well nonlinear system in the bearing experiments, achieving a signal-to-noise ratio gain of >12 dB [10]. However, the output signal of SR has problems of non-stationary enhancement and feature redundancy [11], requiring further optimization in combination with physical characteristics.

Owing to their exceptional capacity for automatic feature extraction, convolutional neural networks (CNN) have emerged as the dominant approach for fault diagnosis in industrial applications. For example, the study by Feng [12] proposes a hybrid architecture that integrates one-dimensional convolutional neural networks with long short-term memory (LSTM) units to enable end-to-end fault pattern recognition. Ishida [13] proposes a lightweight fault diagnosis framework based on one-dimensional CNN, which processes the features extracted by CNNs through correlation alignment (CORAL) to minimize the domain shift and does not require any historical labeled data for the target domain of fault diagnosis. Nevertheless, the performance of one-dimensional CNNs deteriorates significantly in the presence of noise, rendering them ineffective for detecting incipient faults with low signal-to-noise ratios. Sun [14], Cai [15], and Deshmukh [16] convert vibration signals into two-dimensional images through a Gram angle field (GAF), Markov transition field (MTF), and short-time Fourier transform (STFT). Subsequently, CNNs are used to utilize the useful information in the images and identify faults. While convolutional neural networks (CNNs) have revolutionized two-dimensional image analysis, their performance falters in weak signal scenarios. This shortcoming arises from their heavy dependence on discriminative features, which are often scarce or corrupted in low-SNR environments. Specifically, CNNs exhibit a limited capacity for extracting subtle features and tend to focus on superficial patterns, leading to misclassifications during early fault diagnosis.

In order to further improve the two-dimensional image recognition ability of CNNs, Sinitsin [17] proposes a new fault diagnosis method that can handle different types of data simultaneously. This model combines MLP for the numerical input and a CNN for HHT images. The experimental findings indicate that the proposed hybrid model exhibits a superior performance compared to standalone CNN and MLP implementations. Based on fault cycles and the rotational frequency of the shaft under different fault types, Ruan [18] determines the size of the CNN input. The envelope of the decaying acceleration signal is fitted with an exponential function and the length of the signal within different decay rates defines the size of the CNN kernel. Its diagnostic effect has higher accuracy than the baseline CNN. To eliminate noise interference, Zhang [19] first decomposed the raw signal into multiple modes via EMD. The retained modes were then Fourier-transformed, followed by the application of Gaussian window functions to refine the signal. Ultimately, the preprocessed one-dimensional vibration data were converted into a two-dimensional image and fed into the CNN.

This study carried out research on data preprocessing, data division, and the design of the CNN’s internal structure, demonstrating an excellent performance in fault diagnosis. Nevertheless, no specific design was made regarding the conversion of 2D images, with data partitioning only relying on the fault cycle—this approach lacks sufficient physical meaning. In addition, the signal-to-noise ratios of the bearings’ early fault signals are extremely low, such that straightforward data preprocessing is unable to produce the desired effects.

Against the aforementioned issues, this paper puts forward a method that utilizes wave peak cross-correlation sliding sampling to strengthen the significance of early fault features. Furthermore, it combines the random resonance theory, GAF theory, and CNNs to achieve the intelligent diagnosis of early weak faults.

2. The Proposed Wave Intercorrelation Function Fault Diagnosis Method

The framework of the proposed method, depicted in Figure 1, comprises three components. The first component centers on data preprocessing, during which a particle-swarm-optimization-driven adaptive stochastic resonance (ASR) denoising strategy is proposed. This strategy efficiently elevates the signal-to-noise ratio of incipient weak fault signals. In the second component, the emphasis lies in data augmentation and resampling. Herein, a resampling scheme is presented, which ascertains the partitioning of data segments according to the wave peak positions via the cross-analysis of fault signals, thus effectively strengthening the fault features. The third part focuses on intelligent fault identification. In this phase, the data segments with enhanced features are employed as sources to construct Gramian Angular Field data samples, which are then integrated with a Convolutional Neural Network (CNN) for intelligent fault detection.

2.1. Data Preprocessing

The accuracy of CNN-based intelligent diagnosis is significantly affected by the characteristics of the source signal. Since the feature signals of incipient faults are extremely faint and may even be buried in noise, this presents a significant challenge for CNNs in diagnosing and classifying early-stage faults. This paper puts forward an ASR-based preprocessing method for the CNN front-end.

2.1.1. Stochastic Resonance

The model investigated in this paper is an underdamped second-order SR model, and its mathematical model is presented as Equation (1).

$${\displaystyle \frac{d^{2}x(t)}{d{t}^2}}=-{\displaystyle \frac{dU(x)}{dx}}-\gamma {\displaystyle \frac{dx(t)}{dt}}+Y(t)$$

(1)

In this equation, $x(t)$ denotes the output signal post-stochastic resonance, while $\gamma$ represents the damping factor. The observed signal is defined as $Y(t)=S(t)+N(t)$, where the fault signal takes the form $S(t)=A\cos (2\pi ft+\phi )$ and the strong noise component $N(t)=\sqrt{2D}\xi (t)$ models the noise masking the fault signal. Statistically, $〈N(t)〉=0$, $〈N(t)N(t^{\prime })〉=2D\delta (t-t^{\prime })$, with D characterizing the noise intensity and $\xi (t)$ denoting Gaussian white noise. The symmetric bistable potential $U(x)$ is mathematically defined as:

$$U(x)=-{\displaystyle \frac{a}{2}}{x}^2+{\displaystyle \frac{b}{4}}{x}^4$$

(2)

with a and b denoting the positive and actual potential parameters, respectively.

Figure 2 illustrates the bistable SR behavior under diverse parameter settings. The potential wells are situated at $x_m=\pm \sqrt{a/b}$ and the height of the potential barrier is given by $a^2/(4b)$. When the inflection point of the potential function coincides with its extremum, the system’s critical amplitude is derived as $A_c=\sqrt{{\displaystyle \frac{4a^3}{27b}}}$. With noise and the fault signal acting on the nonlinear system concurrently and attaining parameter-matching conditions, even if $A\le A_C$, the mass point can still traverse the potential barrier and oscillate between the two potential wells at frequency $\omega$. When the frequencies of the fault signal and output signal coincide, there is an effective boost in the SNR of the source signal.

Within the stochastic resonance system, the signal-to-noise ratio is mathematically formulated as

$$SNR={\displaystyle \frac{a{A}^2\sqrt{2\mathrm{a}}}{4\mathrm{b}{D}^2}}\exp (-{\displaystyle \frac{a^2}{4bD}}){[1-{\displaystyle \frac{2a^2{A}^2\exp (-\frac{a^2}{2bD})}{4ab{D}^2\exp (-\frac{a^2}{2bD})+2b{D}^2{\pi }^2{\Omega }^2}}]}^{-1}$$

(3)

2.1.2. Adaptive Stochastic Resonance

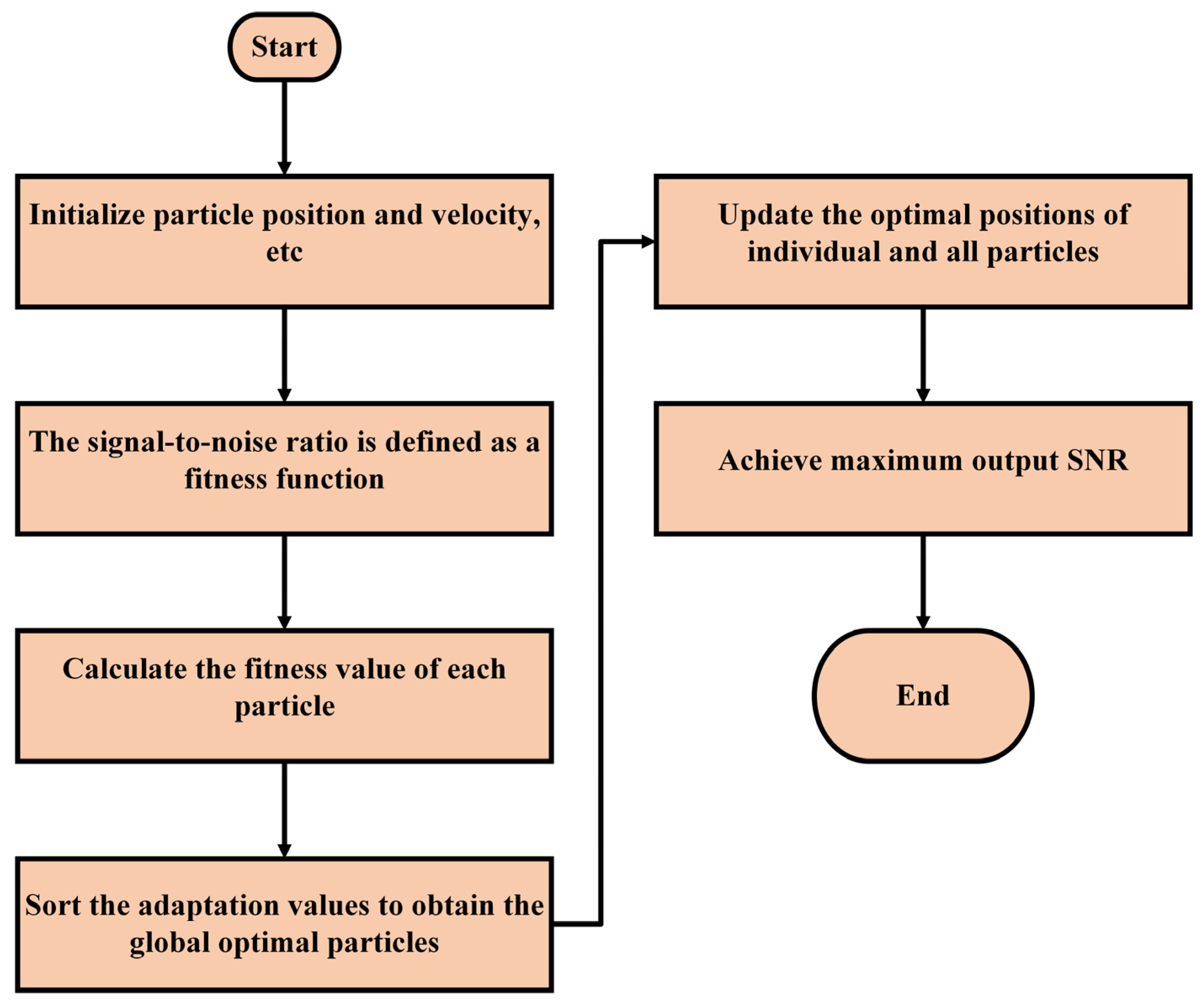
Due to the significant differences in the output signal-to-noise ratios of stochastic resonance systems under different parameters, if the optimal parameters are calculated one by one, it will take too much time, resulting in low economic efficiency and low algorithm efficiency. As shown in Figure 3 (in this paper, the particle swarm optimization algorithm is adopted, with the signal-to-noise ratio as the fitness function to find the optimal parameters, which significantly improves the calculation efficiency), the flowchart of ASR is shown in Figure 4. Where $A$ = 0.1, $\Omega$ = 0.005, and D = 0.3, the optimal parameters a and b are to be found to determine the maximum signal-to-noise ratio of the stochastic resonance system.

2.2. Data Division Using Wave Intercorrelation Function

Practically, acceleration sensors typically perform continuous sampling at a constant frequency. However, when training a CNN with acceleration signals, one must segment the original data into individual samples. During sample division, a common practice is to resample the original signal using a fixed-sized window, yet the window dimensions might be unsuitable. The data divided in this way are disorderly and the correlation between data points is low. As a result, when input into a CNN, it may not be possible to accurately perform fault classification. Thus, this paper employs the wave intercorrelation coefficient for data division, aiming to ascertain the division positions and window dimensions.

2.2.1. Data Division by Intercorrelation

During fault signal segmentation, longer data segments inherently encapsulate more information. However, overly extended segments diminish the number of resultant training and validation subsets for CNNs. Given CNNs’ inherent demand for substantial training data, this can counteract the model performance. During partitioning, segments should retain sufficient contextual information while avoiding an undue reduction in training samples. Thus, the optimizing segment length is pivotal for CNN-based diagnostic tasks.

CNNs retrieve fault signal features via a sequence of convolutional and pooling operations, subsequently categorizing these features. Thus, the greater the correlation of signals segmented from the same fault, the more alike the features retrieved by CNNs will be, and the more precise the fault classification will become. The correlation between two data segments can be ascertained via the intercorrelation function, an indicator of how well the two segments match at relative positions. The calculation formula of the intercorrelation coefficient is presented in Equation (10). In this paper, the intercorrelation coefficients between data under different division windows are calculated to determine the optimal division window.

Since the peak positions and intercorrelation functions of different fault signals vary, the size of the division window for different fault signals is also different. Therefore, in this paper, the optimal division window for all fault signals is determined. First, the shortest data segment containing complete information is calculated according to the following formula. The interval for searching for peaks in the data segment should be at least 1.5 $L_{\min }$, and to ensure that the CNN has sufficient training data, the maximum interval is 2.5 $L_{\min }$. In this study, cross-correlation analyses are performed between all segmented data segments and the initial segment. The maximum cross-correlation value is determined and, subsequently, an average is computed. The data point demonstrating the highest average within the interval of 1.5 $L_{\min }$ to 2.5 $L_{\min }$ is designated as the segmentation window.

$$\begin{array}{l}\overline{X}={\displaystyle \frac{{\displaystyle \sum _{i=1}^n{X}_i}}{n}}\\ \overline{Y}={\displaystyle \frac{{\displaystyle \sum _{i=1}^n{Y}_i}}{n}}\\ r={\displaystyle \frac{{\displaystyle \sum _{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}}{\sqrt{{\displaystyle \sum _{i=1}^n{(X_i-\overline{X})}^2}}\sqrt{{\displaystyle \sum _{i=1}^n{(Y_i-\overline{Y})}^2}}}}\end{array}$$

(4)

$$L_{\min }=f_s/n\ast 60$$

where $f_s$ represents the sampling frequency and $n$ represents the rotational speed.

2.2.2. Peak Gramian Angular Field

Common CNN architectures typically accommodate 1D or 2D signal inputs. Given CNNs’ inherent sensitivity to image-like structures, this study casts fault signals into Gramian Angular Field (GAF) representations as the CNN input. GAF transforms time-series data into 2D imagery by leveraging polar coordinates. As each element in the GAF matrix is dictated by the distance and angular relationship between a target point and its reference, this approach preserves strong temporal correlations inherent in the data. Suppose the fault signal is $X=(x_1,x_2,x_3,\dots ,x_N)$, the Gramian Angular Field is then defined as follows:

$$G=X^{T}X=\left[\begin{array}{cccc}〈x_1,x_1〉& 〈x_1,x_2〉& \dots & 〈x_1,x_N〉\\ 〈x_2,x_1〉& 〈x_2,x_2〉& \dots & 〈x_2,x_N〉\\ \dots & \dots & \dots & \dots \\ 〈x_N,x_1〉& 〈x_N,x_2〉& \dots & 〈x_N,x_N〉\end{array}\right]$$

(5)

Calculation Steps of Gramian Angular Field

First, the time-series data are normalized to the range of [0,1] according to Equation (6):

$${\tilde{x}}_i={\displaystyle \frac{x_i-\min (x)}{\max (x)-\min (x)}}$$

(6)

Next, the normalized data values are converted to a polar coordinate form, following the formulation presented in Equation (7):

$${\varphi }_i=\arccos {\tilde{x}}_i$$

(7)

$$r_i={\displaystyle \frac{t_i}{N}}$$

(8)

Here, $t_i$ denotes the timestamp corresponding to the data point $x_i$ and $N$ stands for the total count of time points within the time-series data.

To quantify the degree of angular correlation, the GAF matrix employs a distinctive inner product formulation in Equation (9), where the “inner product” between two time-series instances denotes the cosine of the sum of their polar angles derived by first transforming these instances into polar coordinates. Subsequently, Equation (9) is re-expressed as Equation (10).

$$〈x_1,x_2〉=\cos ({\varphi }_1+{\varphi }_2)$$

(9)

$$GAF=\left[\begin{array}{cccc}\cos ({\varphi }_1+{\varphi }_1)& \cos ({\varphi }_1+{\varphi }_2)& \dots & \cos ({\varphi }_1+{\varphi }_N)\\ \cos ({\varphi }_2+{\varphi }_1)& \cos ({\varphi }_2+{\varphi }_2)& \dots & \cos ({\varphi }_2+{\varphi }_N)\\ \dots & \dots & \dots & \dots \\ \cos ({\varphi }_N+{\varphi }_1)& \cos ({\varphi }_N+{\varphi }_2)& \dots & \cos ({\varphi }_N+{\varphi }_N)\end{array}\right]$$

(10)

From the GAF matrix, it is observable that the values in each row and column of the matrix are associated with the sequence of the data points, and this also corresponds to the time series. When dividing the data, it is often divided at equal intervals for a whole segment of data, which makes the order of each segment of data disorderly. There will be great differences when each segment of the data is converted into GAF and it is difficult for the CNN to classify after feature extraction. Thus, the data are partitioned, starting from each peak of the fault signal, ensuring that the sequence length of each data segment is approximately identical. As depicted in Figure 5, the data undergo division according to peak positions and are, subsequently, converted into a Gramian Angular Field.

2.3. GAF-CNN

Convolutional neural networks (CNNs) have higher recognition accuracy for two-dimensional images than for one-dimensional signals. Therefore, the conversion of the fault signal into a two-dimensional Gramian Angular Field (GAF) is carried out. The fault diagnosis steps of the GAF-CNN are as follows:

• Segment the collected vibration signals. Following the GAF encoding method, each signal segment is transformed into a two-dimensional image, and these images are then divided into a training set and a validation set.
• By inputting the feature maps into the built CNN model and optimizing its parameters, the model gains the ability to extract relevant details from image features and acquire different categories of fault information.
• Through a Softmax classifier, a mapping correlation between the information and the respective fault types is constructed to derive the outcomes of fault diagnosis.

The proposed CNN architecture incorporates two convolutional layers coupled with two pooling layers. To mitigate feature dimensionality from convolutional outputs, streamline network parameters, and curb overfitting, the pooling layer employs max-pooling. Each convolutional layer is followed by a ReLU activation function adopted in this study to introduce nonlinearity. The last part of the network architecture includes a fully connected layer along with an output layer. As shown in Figure 6, the sizes of the convolution kernels for the first layer and the second layer are 8 × 12 and 4 × 6, respectively. The padding method for each layer’s input matrix is 0 padding. Using a 64-core CPU workstation, the training time is set to 600 s.

3. Method Validation

With the aim of evaluating how the proposed bearing fault diagnosis model performs, it is applied to the bearing fault dataset of Case Western Reserve University. The primary types of bearing faults include inner race defects, rolling element defects, and outer race defects. Given that all these faults are fundamentally based on the rotational frequency and their fault characteristics exhibit similar patterns, they can be diagnosed using a single category of methods. As most current fault diagnosis approaches based on deep learning rely on data simulated in laboratories, there remains a discrepancy between them and actual real-world conditions. To tackle this problem, this paper intends to gather data from a physically constructed bearing fault test bench and feed them into the proposed model for fault diagnosis purposes.

3.1. Rationality Validation Based on Case Western Reserve University Bearing Fault Data

The experimental data employed for validation are derived from the bearing test bench at Case Western Reserve University. The SKF bearings utilized in this experiment feature faults that were processed via electrical discharge machining. Included in the experimental data are vibration signals from normal conditions, as well as vibration data for three fault categories (inner race, rolling element, and outer race faults) under different fault magnitudes, where the fault sizes measure 0.2 mm, 0.3 mm, and 0.5 mm, respectively. In total, 10 distinct bearing health conditions exist. A sampling frequency of 12 kHz is adopted and the rotational speed is 1730 (r/min).

As shown in

Table 1. Dataset description of Western Reserve University.

Fault Type	Fault Size (mm)	Classification Label
Normal	-	0
Inner Race Fault	0.2	1
Inner Race Fault	0.3	2
Inner Race Fault	0.5	3
Rolling Element Fault	0.2	4
Rolling Element Fault	0.3	5
Rolling Element Fault	0.5	6
Outer Race Fault	0.2	7
Outer Race Fault	0.3	8
Outer Race Fault	0.5	9

, each dataset represents a bearing health condition, containing a total of 1000 samples. Of these, 800 samples are chosen as the training dataset, and 200 as the validation set. In total, the proposed model processes ten datasets; each contains one normal state and three fault types, and a respective label is assigned to every dataset.

3.2. Fault Classification

With the aim of enhancing the signal-to-noise ratio of weak fault signals, the initial step involves inputting the original fault signals into ASR. According to Equation (10), the minimum complete period of the bearing $L_{\min }$ is calculated. Between 1.5 $L_{\min }$ and 2.5 $L_{\min }$, the window size is determined according to the intercorrelation coefficient between the data segments. The window sizes of bearings with different health conditions are shown in

Table 2. Window sizes for each fault division.

Fault Type	Fault Size (mm)	Window Size
Normal	-	950
Inner Race Fault	0.2	849
Inner Race Fault	0.3	849
Inner Race Fault	0.5	834
Rolling Element Fault	0.2	860
Rolling Element Fault	0.3	950
Rolling Element Fault	0.5	883
Outer Race Fault	0.2	810
Outer Race Fault	0.3	912
Outer Race Fault	0.5	801

.

As shown in Figure 7, after the original signals of the normal condition and three fault types with a fault size of 0.2 mm are processed by ASR, the peak positions are found according to the calculated window size and data segments are divided. The segmented data segments are transformed into two-dimensional images via GAF and then fed into the CNN for fault diagnosis.

To verify the diagnostic accuracy of the proposed method, a comparison was made of the diagnostic accuracy rates of three distinct methods when input into a CNN. Compared to conventional time–frequency domain analysis methods, the CNN does not require the provision of amplitude-based threshold criteria. Instead, it intelligently learns from training datasets to train a diagnostic model, thereby achieving fault classification. The first one is to perform no data preprocessing, fix the window size at 1000 for data division and conversion into GAF, and input the two-dimensional GAF into the CNN for fault classification (CNN). The second one takes the peak as the starting point, determines the division window size by the intercorrelation coefficient, converts it into GAF, and inputs it into the CNN for classification (Peak_CNN). The third one performs ASR for data preprocessing before the second method to enhance the signal-to-noise ratio, and then uses the second method for fault classification (ASR_Peak_CNN). We input the three methods into a CNN system with the same parameters for 100 training iterations. The outcomes of the training are illustrated in the figure. Regarding the training set, the third method achieves a 100% accuracy rate. Although the second method can also reach 100%, the third method requires fewer iterations to reach 100% and less time. The training curve of the third method is more stable, while the training curve of the second method fluctuates greatly, indicating that the third method has better robustness. The first method without any processing has the lowest accuracy rate, only reaching about 90%. In terms of the validation set, the training curve of the third method is basically higher than that of the first and second methods in each iteration round, and finally, it is about 6% higher than the second method.

The CNN training graph only represents a random single training run and the accuracy is not precise. To enhance the persuasiveness of the experimental data, we have performed 10 training runs for each of the three methods. This allows us to derive the maximum, minimum, and average accuracy rates for both the training set and validation set, which are then subjected to comparison. As shown in

Table 3. Fault classification results of three models (Western Reserve University dataset).

Diagnostic Method	Training Set			Validation Set
	Max	Min	Avg.	Max	Min	Avg.
Normal	91.406	85.406	89.538	88.5	85.5	86.8
Wave Intercorrelation	100	97.656	99.062	95	88.5	92.9
ASR_Wave Intercorrelation	100	99.218	99.688	98	96	96.9

, it can be intuitively seen that in terms of the training set, three has better diagnostic performance than two and one. Although both the second and third methods can reach up to 100% at maximum, and the average rate only differs by 0.626%, it can be seen from the training graph (Figure 8) that the three requires fewer iterations to reach 100% and is more stable, which indicates that three needs less training time and has more advantages in practical applications. The maximum accuracy rate of the validation set for one only reaches 91.406%, having a large gap from two and three. In terms of the more important validation set, the average values of two and three differ by 4%. For two, the gap between the maximum and minimum values stands at 6.5%, whereas this figure is merely 2% for three. It can be inferred from this that system three for fault diagnosis possesses better robustness.

To characterize the clustering behavior, t-SNE—which inherently preserves local structural relationships—indicates that spatially adjacent data points in a high-dimensional space tend to retain their proximity in low-dimensional embedding. The clustering results for the three methods are visualized in Figure 9. The visualization shows that fault labels from the conventional CNN are highly clustered, with significant label overlap between training and test partitions, yielding a suboptimal clustering performance. In contrast, the proposed method exhibits a prominent clustering effect, marked by well-separated labels and sharply defined boundaries. The wave intercorrelation method demonstrates an intermediate clustering performance relative to these two extremes.

To move beyond the mere validation of the algorithm through accuracy metrics, this study additionally quantified precision, recall, and F1 scores across training and test partitions to evaluate the diagnostic performance of the CNN. The results demonstrate that the precision, recall, and F1 scores of the proposed method—across both partitions—are significantly superior to those of the other two methods, with detailed comparative results presented in

Table 4. Fault classification results of three models (performance measurement).

Diagnostic Methods	Training Set Accuracy Rate	Test Set Accuracy Rate	Training Set Recall Rate	Test Set Recall Rate	Training Set F1 Score	Test Set F1 Score
CNN	0.578	0.661	0.525	0.531	0.612	0.589
WI-CNN	0.997	0.942	0.964	0.941	0.983	0.942
ASR-WI-CNN	0.993	0.968	0.992	0.972	0.995	0.967

.

3.3. Early Weak Fault Diagnosis Experiment

3.3.1. Experimental Device

To validate the practical applicability of the proposed model, fault signals were acquired from a custom-built experimental platform, and these real-world signals were fed into the model for fault identification. The experimental setup serves for data acquisition, incorporating a test-bench controller capable of regulating the shaft’s speed, acceleration, and other operational parameters. Among the two bearings installed on the test bench, one is defect-free, while the other functions as the test bearing. An acceleration sensor of the CT1010LC model is mounted on the bearing housing, with vibration acceleration data acquired using an NI acquisition card.

3.3.2. Data Description

Data signals are captured via the acceleration sensor, with a sampling frequency of 12 kHz and a rotational speed of 2000 (r/min). Ten different health-state bearings are introduced for the bearing on the input shaft, including a normal state, outer-ring pitting, ball pitting, inner-ring pitting, inner-and-outer-ring pitting, and cage fracture. The bearing selected is the 6202-model bearing from the SKF Company, and the fault is processed by an electric discharge. Bearing an early-stage fault refers to the initial stage of bearing damage, where the damage has just formed or is very minor, and has not yet significantly compromised the normal operation of the equipment. Generally, based on established engineering experience, a fault size of less than 1 mm is defined as an early-stage fault. For such faults, conventional spectral analysis methods are difficult to detect. Figure 10 shows the bearing with inner-and-outer-ring faults.

(a)

Early fault diagnosis results

For the experimental setup, 70% of the data collected under respective operating conditions were allocated to the training phase, with the remaining 30% reserved for testing. The CNN model was then subjected to 100 training epochs in this configuration. The accuracy outcomes are presented in the table.

Table 5. Introduction of measured bearing dataset.

Health Condition	Fault Size (mm)	Training Dataset	Validation Dataset	Classification Label
Normal	-	140	60	0
Inner-ring pitting	0.2	140	60	1
Inner-ring pitting	0.4	140	60	2
Inner-ring pitting	0.7	140	60	3
Inner-and-outer-ring pitting	0.2	140	60	4
Inner-and-outer-ring pitting	0.4	140	60	5
Inner-and-outer-ring pitting	0.7	140	60	6
Outer-ring pitting	0.2	140	60	7
Outer-ring pitting	0.4	140	60	8
Outer-ring pitting	0.7	140	60	9

reveals that for the measured data, the training set achieves an accuracy rate of 99.8%, while the test set reaches 98.31%. When the original CNN is used for diagnosis, the training set achieves an accuracy rate of 95.75%, while the test set reaches 86.32%.

The confusion matrix is shown in Figure 11. It can be seen that in the test set of the original CNN, each fault has classification errors, and the maximum number of classification errors reaches 16, while the maximum number of classification errors in SR_GAF_CNN is only 5, and most errors only have 1–2 confusions. In terms of the test set, only three fault classifications in SR_GAF_CNN are confused, while only one fault in the CNN is not confused, and there is a large gap in the accuracy rate.

To conduct a more thorough comparison of the feature extraction performance, t-SNE is utilized to visualize features extracted by all methods. As illustrated in

Table 6. Classification results based on measured bearing signals.

Method	Training Set Accuracy	Validation Set Accuracy
CNN	95.75%	86.32%
ASR_GAF_CNN	99.8%	98.31%

and Figure 12, the fault classification boundaries of the SR_GAF_CNN are highly distinguishable, whereas in the conventional CNN, multiple faults are intermingled, leading to a suboptimal clustering performance. Figure 13 illustrates the CNN training curves associated with the two methods. Across nearly every iteration epoch, both in the training partition and test partition, the classification accuracy of the SR_GAF_CNN is significantly superior to that of the conventional CNN. Additionally, the training curve of the SR_GAF_CNN exhibits greater smoothness, requiring fewer iterations to reach a stable state. This indicates that the proposed method requires a shorter convergence time while demonstrating enhanced generalization robustness.

(b)

Diagnosis results under cross-speed and variable operating conditions

For the purpose of verifying how the proposed method performs in terms of its diagnostic accuracy across different data sources, data gathered at 12 kHz and 2000 r/min were employed to train the CNN. Experimental data with the rotational speed increased to 2400 r/min and decreased to 1600 r/min were then diagnosed separately. The training results are shown in Figure 13. When the speed was reduced to 1800 r/min, the diagnostic accuracy of the CNN method dropped to only 25%, while the proposed method achieved up to 54% (Figure 14a). At the increased speed of 2200 r/min (Figure 14b), the proposed method attained a diagnostic accuracy of 68%, significantly outperforming the CNN method’s 32%. These findings indicate that the proposed method demonstrates greater robustness against system variations, offering valuable implications for facilitating cross-domain fault diagnosis.

4. Conclusions

In traditional CNN systems, data are usually divided with a fixed window when partitioning data. However, different faults have different characteristics, so the length of the partitioned data should also vary. In this study, a novel framework for the early detection of incipient weak bearing faults is proposed, leveraging the WI-CNN model. Specifically, the proposed approach sequentially preprocesses the raw signal, partitions it according to wave peaks and intercorrelation coefficients, and transforms the data into GAF representations for the CNN input. This method can divide the corresponding optimal signal length for different fault signals. After processing the dataset from Case Western Reserve University, the validation set achieves an average accuracy of 99.688%, with its maximum accuracy reaching 98%. Moreover, on the self-built test-bed, the validation set also has an accuracy rate of 98.31%. Compared with the ordinary CNN system, the accuracy rate has been significantly improved.

Contrasted against the conventional CNN model, the proposed framework demonstrates three salient merits: Firstly, it achieves superior classification accuracy across training and test partitions. Additionally, its accelerated convergence rate effectively shortens the training duration. Finally, the model exhibits enhanced generalization robustness compared to its conventional counterpart.

However, the proposed model has its own limitations: optimally partitioning data for each signal may require a large amount of computation, the internal structure of the CNN has not been designed, and the size of the CNN convolutional kernels and the number of convolutional layers can be optimized according to the input size. Future research can further improve the internal structure of the CNN.