Hierarchical Deep Reinforcement Learning-Based Path Planning with Underlying High-Order Control Lyapunov Function—Control Barrier Function—Quadratic Programming Collision Avoidance Path Tracking Control of Lane-Changing Maneuvers for Autonomous Vehicles
Abstract
1. Introduction
- This paper introduces a novel low-level controller based on the combined High-Order Control Lyapunov Function (HOCLF) and High-Order Control Barrier Function (HOCBF) framework, specifically designed for on-road vehicle dynamic models. This controller enables accurate path tracking under normal conditions and ensures effective collision avoidance in the presence of obstacles.
- Inspired by human driving collision avoidance behavior, we propose a hierarchical control framework that combines a high-level DDQN decision-making agent and low-level optimization-based control. This control framework enables the system to autonomously select appropriate lane-level strategies for collision avoidance.
- The DDQN agent observes the surrounding traffic environment and determines high-level lane-change actions (e.g., idle—meaning no lane change; left lane change; and right lane change). These discrete decisions are then translated into reference tracking formulation and executed by the HOCLF-HOCBF-QP controller.
- This hierarchical architecture takes advantage of both the learning-based approach and the optimization-based approach. The DRL-based high-level planner enables flexible decision-making in various traffic scenarios, while the optimization-based low-level controller adds hard safety constraints through HOCBFs, preventing unsafe behavior.
2. Methodology
2.1. Single-Track Lateral Vehicle Dynamic Model
2.2. Control Lyapunov Functions and Control Barrier Functions
2.2.1. Preliminary
2.2.2. HOCLF and HOCBF Definition
2.2.3. HOCLF and HOCBF Design
2.2.4. HOCLF-HOCBF-QP Formulation
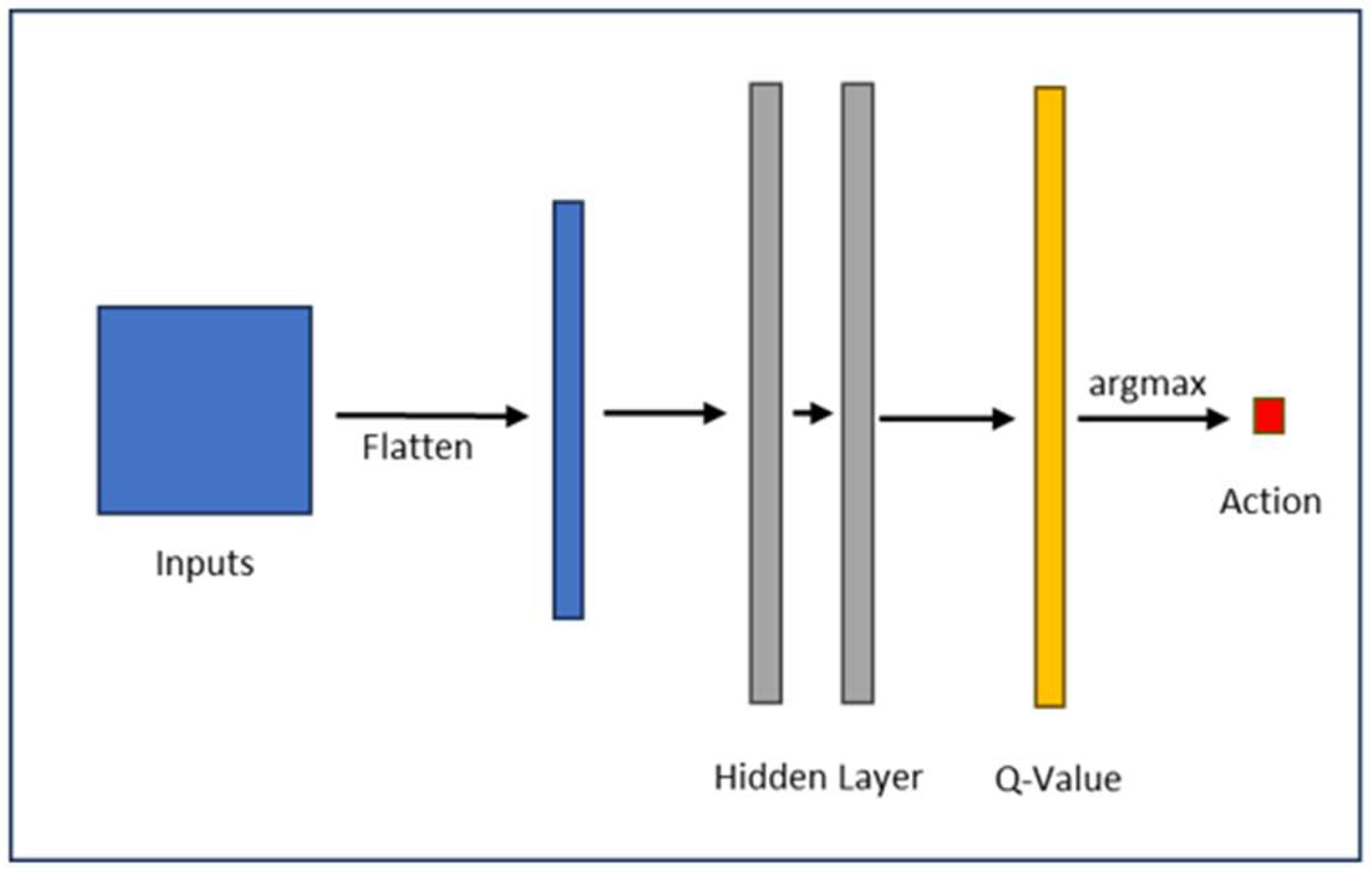
2.3. Deep-Reinforcement-Learning
| Algorithm 1: Hierarchical DDQN algorithm flowchart |
| 1: Initialize high-level DDQN agent |
| 2: Initialize low-level HOCLF-HOCBF-QP controller |
| 3: for each episode do |
| 4: Initialize and reset traffic environment |
| 5: for t = 1 to T do |
| 6: With probability select a random high-level action |
| 7: Otherwise select high-level action |
| 8: for each low-level control steps do |
| 9: Reset target tracking point according to current states and |
| 10: Reset obstacle list according to current states |
| 11: Calculate optimal control using HOCLF-HOCBF-QP |
| 12: Execute for a control step |
| 13: end for |
| 14: Calculate reward and record next state |
| 15: Store transition (, , , ) in replay buffer |
| 16: if t mod training frequency == 0 then |
| 17: Sample random minibatch of transitions (, , , )) from D |
| 18: Set |
| 19: for non-terminal |
| 20: or for terminal |
| 21: Perform a gradient descent step to update |
| 22: Every N steps reset = |
| 23: end if |
| 24: Set = |
| 25: end for |
| 26: end for |
3. Results
3.1. CLF-CBF-Based Optimization Controller
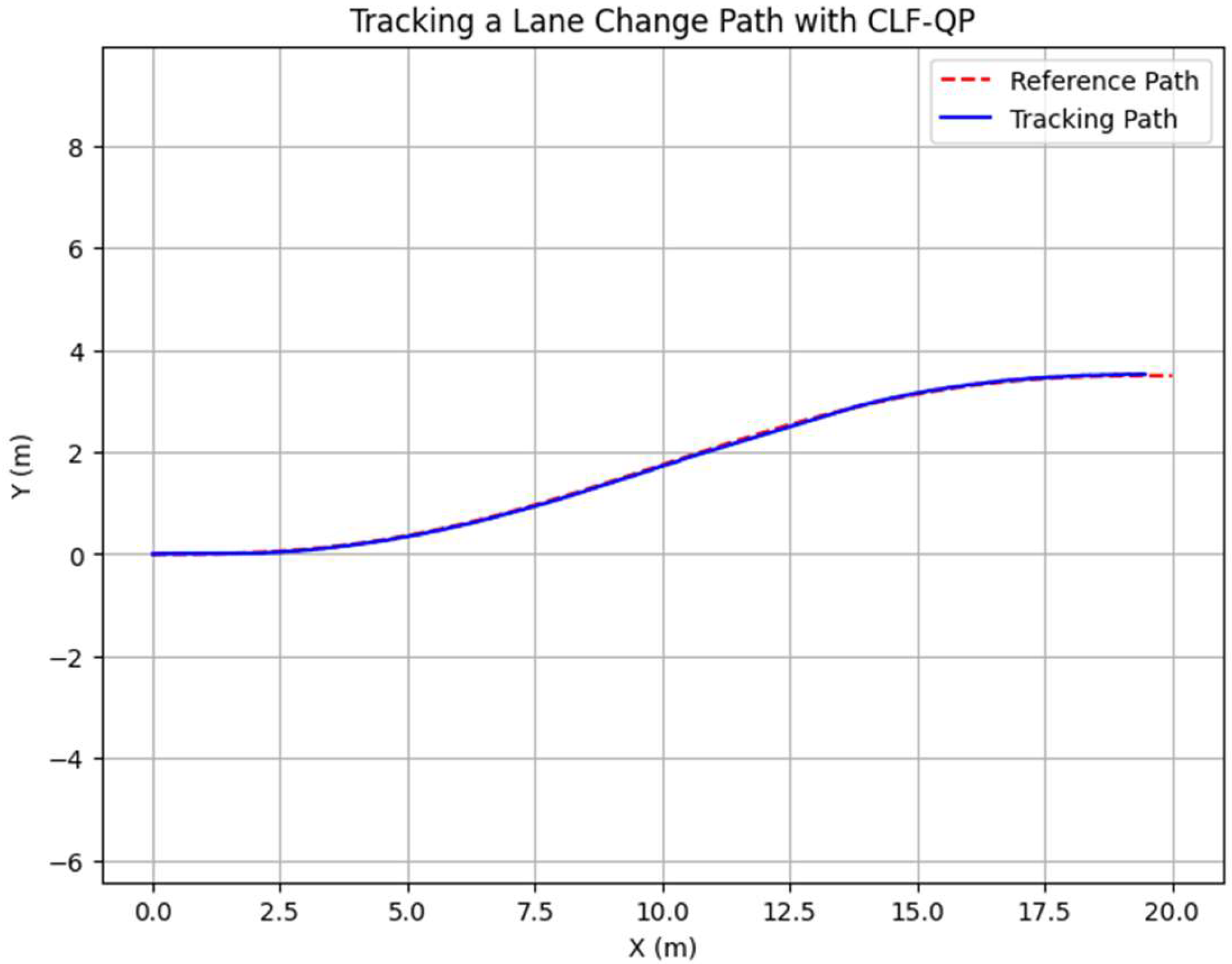
3.1.1. CLF-Based Path Tracking Controller
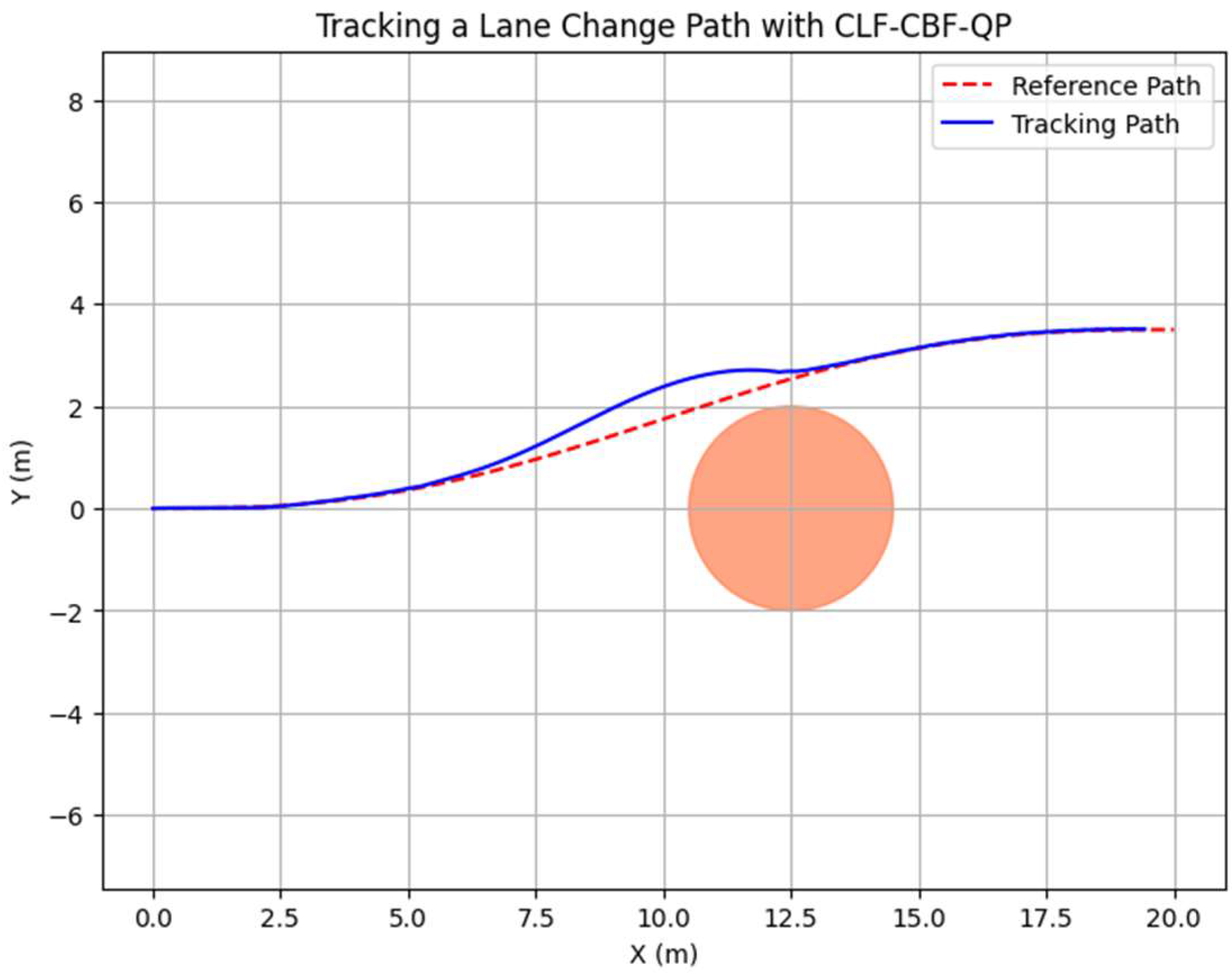
3.1.2. CLF-CBF-Based Autonomous Driving Controller for Static Obstacle
3.1.3. CLF-CBF-Based Autonomous Driving Controller for Dynamic Obstacle
3.2. Hybrid DRL and CLF-CBF-Based Controller
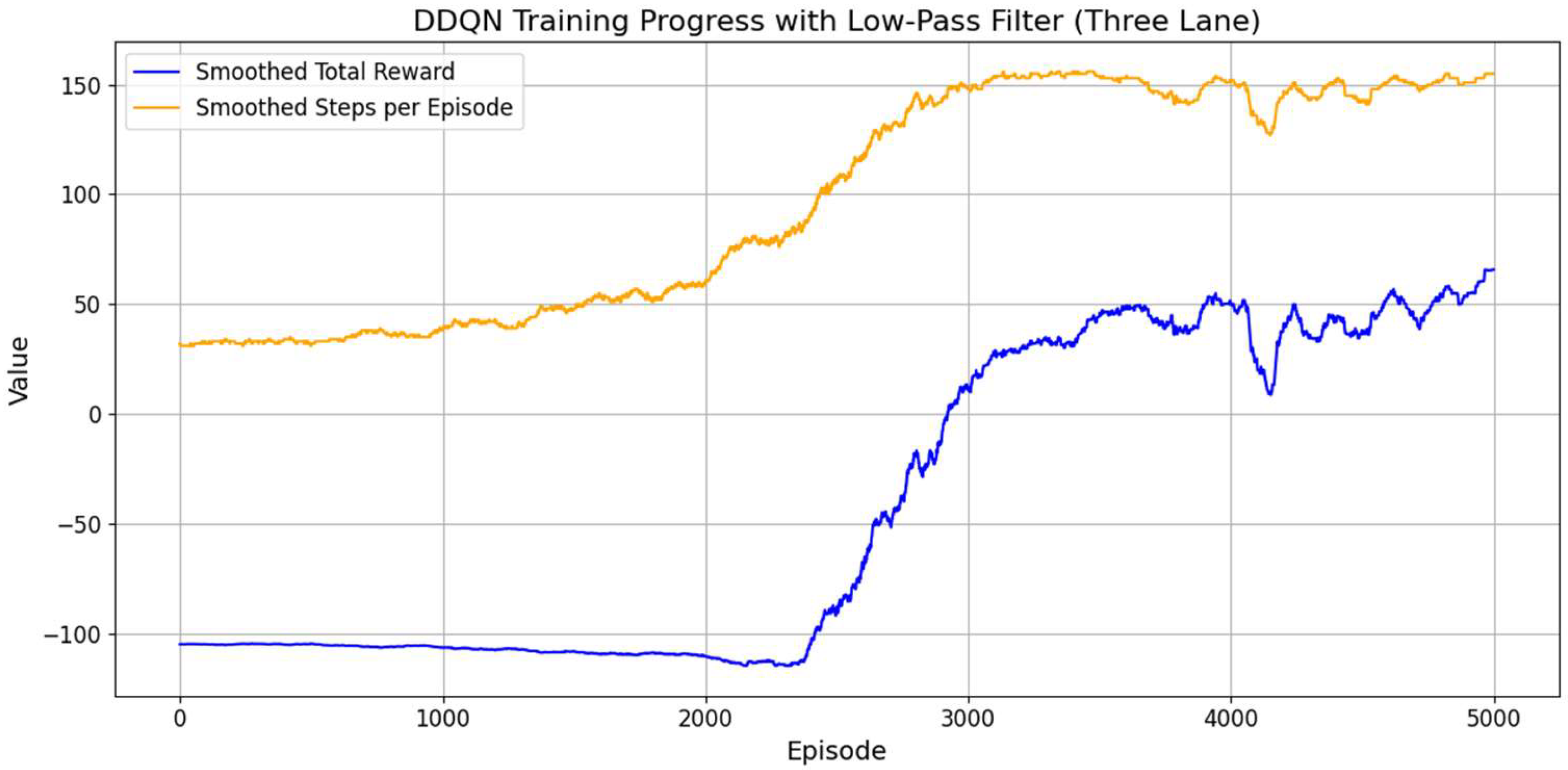
3.2.1. DRL High-Level Decision-Making Agent
3.2.2. Hybrid DRL and CLF-CBF Controller
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wen, B.; Gelbal, S.; Aksun-Guvenc, B.; Guvenc, L. Localization and Perception for Control and Decision Making of a Low Speed Autonomous Shuttle in a Campus Pilot Deployment. arXiv 2018, arXiv:2407.00820. [Google Scholar] [CrossRef]
- Gelbal, S.Y.; Guvenc, B.A.; Guvenc, L. SmartShuttle: A unified, scalable and replicable approach to connected and automated driving in a smart city. In Proceedings of the 2nd International Workshop on Science of Smart City Operations and Platforms Engineering, in SCOPE ’17, Pittsburgh, PA, USA, 18–21 April 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 57–62. [Google Scholar] [CrossRef]
- “Autonomous Road Vehicle Path Planning and Tracking Control | IEEE eBooks | IEEE Xplore”. Available online: https://ieeexplore.ieee.org/book/9645932 (accessed on 24 October 2023).
- Ararat, O.; Aksun-Guvenc, B. Development of a Collision Avoidance Algorithm Using Elastic Band Theory. IFAC Proc. Vol. 2008, 41, 8520–8525. [Google Scholar] [CrossRef]
- Ames, A.D.; Grizzle, J.W.; Tabuada, P. Control barrier function based quadratic programs with application to adaptive cruise control. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; pp. 6271–6278. [Google Scholar] [CrossRef]
- Ames, A.D.; Xu, X.; Grizzle, J.W.; Tabuada, P. Control Barrier Function Based Quadratic Programs for Safety Critical Systems. IEEE Trans. Autom. Control. 2017, 62, 3861–3876. [Google Scholar] [CrossRef]
- Ames, A.D.; Coogan, S.; Egerstedt, M.; Notomista, G.; Sreenath, K.; Tabuada, P. Control Barrier Functions: Theory and Applications. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 3420–3431. [Google Scholar] [CrossRef]
- Wang, L.; Ames, A.D.; Egerstedt, M. Safety Barrier Certificates for Collisions-Free Multirobot Systems. IEEE Trans. Robot. 2017, 33, 661–674. [Google Scholar] [CrossRef]
- Desai, M.; Ghaffari, A. CLF-CBF Based Quadratic Programs for Safe Motion Control of Nonholonomic Mobile Robots in Presence of Moving Obstacles. In Proceedings of the 2022 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Sapporo, Japan, 11–15 July 2022; pp. 16–21. [Google Scholar] [CrossRef]
- Reis, M.F.; Andrade, G.A.; Aguiar, A.P. Safe Autonomous Multi-vehicle Navigation Using Path Following Control and Spline-Based Barrier Functions. In Robot 2023: Sixth Iberian Robotics Conference; Marques, L., Santos, C., Lima, J.L., Tardioli, D., Ferre, M., Eds.; Springer: Cham, Switzerland, 2024; pp. 297–309. [Google Scholar] [CrossRef]
- Yang, G.; Vang, B.; Serlin, Z.; Belta, C.; Tron, R. Sampling-based Motion Planning via Control Barrier Functions. In Proceedings of the 2019 3rd International Conference on Automation, Control and Robots, Prague, Czech Republic, 11–13 October 2019; pp. 22–29. [Google Scholar] [CrossRef]
- Li, Y.; Peng, Z.; Liu, L.; Wang, H.; Gu, N.; Wang, A.; Wang, D. Safety-Critical Path Planning of Autonomous Surface Vehicles Based on Rapidly-Exploring Random Tree Algorithm and High Order Control Barrier Functions. In Proceedings of the 2023 8th International Conference on Automation, Control and Robotics Engineering (CACRE), Guangzhou, China, 13–15 July 2023; pp. 203–208. [Google Scholar] [CrossRef]
- He, S.; Zeng, J.; Zhang, B.; Sreenath, K. Rule-Based Safety-Critical Control Design using Control Barrier Functions with Application to Autonomous Lane Change. arXiv 2021, arXiv:2103.12382. [Google Scholar] [CrossRef]
- Liu, M.; Kolmanovsky, I.; Tseng, H.E.; Huang, S.; Filev, D.; Girard, A. Potential Game-Based Decision-Making for Autonomous Driving. arXiv 2023, arXiv:2201.06157. [Google Scholar] [CrossRef]
- Jabbari, F.; Samsami, R.; Arefi, M.M. A Novel Online Safe Reinforcement Learning with Control Barrier Function Technique for Autonomous vehicles. In Proceedings of the 2024 10th International Conference on Control, Instrumentation and Automation (ICCIA), Kashan, Iran, 5–7 November 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, X.; Liu, X.; Zhang, M. Autonomous Vehicle Lane-Change Control Based on Model Predictive Control with Control Barrier Function. In Proceedings of the 2024 IEEE 13th Data Driven Control and Learning Systems Conference (DDCLS), Kaifeng, China, 17–19 May 2024; pp. 1267–1272. [Google Scholar] [CrossRef]
- Thirugnanam, A.; Zeng, J.; Sreenath, K. Safety-Critical Control and Planning for Obstacle Avoidance between Polytopes with Control Barrier Functions. arXiv 2022, arXiv:2109.12313. [Google Scholar] [CrossRef]
- Xiao, W.; Belta, C. High-Order Control Barrier Functions. IEEE Trans. Autom. Control. 2022, 67, 3655–3662. [Google Scholar] [CrossRef]
- Chriat, A.E.; Sun, C. High-Order Control Lyapunov–Barrier Functions for Real-Time Optimal Control of Constrained Non-Affine Systems. Mathematics 2024, 12, 24. [Google Scholar] [CrossRef]
- Wang, H.; Tota, A.; Aksun-Guvenc, B.; Guvenc, L. Real time implementation of socially acceptable collision avoidance of a low speed autonomous shuttle using the elastic band method. Mechatronics 2018, 50, 341–355. [Google Scholar] [CrossRef]
- Lu, S.; Xu, R.; Li, Z.; Wang, B.; Zhao, Z. Lunar Rover Collaborated Path Planning with Artificial Potential Field-Based Heuristic on Deep Reinforcement Learning. Aerospace 2024, 11, 253. [Google Scholar] [CrossRef]
- Morsali, M.; Frisk, E.; Åslund, J. Spatio-Temporal Planning in Multi-Vehicle Scenarios for Autonomous Vehicle Using Support Vector Machines. IEEE Trans. Intell. Veh. 2021, 6, 611–621. [Google Scholar] [CrossRef]
- Zhu, S. Path Planning and Robust Control of Autonomous Vehicles. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2020. Available online: https://www.proquest.com/docview/2612075055/abstract/73982D6BAE3D419APQ/1 (accessed on 24 October 2023).
- Chen, G.; Yao, J.; Gao, Z.; Gao, Z.; Zhao, X.; Xu, N.; Hua, M. Emergency Obstacle Avoidance Trajectory Planning Method of Intelligent Vehicles Based on Improved Hybrid A*. SAE Int. J. Veh. Dyn. Stab. NVH 2023, 8, 3–19. [Google Scholar] [CrossRef]
- Kiran, B.R.; Sobh, I.; Talpaert, V.; Mannion, P.; Al Sallab, A.A.; Yogamani, S.; Perez, P. Deep Reinforcement Learning for Autonomous Driving: A Survey. IEEE Trans. Intell. Transp. Syst. 2022, 23, 4909–4926. [Google Scholar] [CrossRef]
- Ye, F.; Zhang, S.; Wang, P.; Chan, C.-Y. A Survey of Deep Reinforcement Learning Algorithms for Motion Planning and Control of Autonomous Vehicles. In Proceedings of the 2021 IEEE Intelligent Vehicles Symposium (IV), Nagoya, Japan, 11–17 July 2021; pp. 1073–1080. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhao, H. A Survey of Deep RL and IL for Autonomous Driving Policy Learning. IEEE Trans. Intell. Transp. Syst. 2022, 23, 14043–14065. [Google Scholar] [CrossRef]
- Kendall, A.; Hawke, J.; Janz, D.; Mazur, P.; Reda, D.; Allen, J.-M.; Lam, V.-D.; Bewley, A.; Shah, A. Learning to Drive in a Day. arXiv 2018, arXiv:1807.00412. [Google Scholar] [CrossRef]
- Yurtsever, E.; Capito, L.; Redmill, K.; Ozguner, U. Integrating Deep Reinforcement Learning with Model-based Path Planners for Automated Driving. arXiv 2020, arXiv:2002.00434. [Google Scholar] [CrossRef]
- Aksjonov, A.; Kyrki, V. A Safety-Critical Decision-Making and Control Framework Combining Machine-Learning-Based and Rule-Based Algorithms. SAE Int. J. Veh. Dyn. Stab. NVH 2023, 7, 287–299. [Google Scholar] [CrossRef]
- “Deep Reinforcement-Learning-Based Driving Policy for Autonomous Road Vehicles—Makantasis—2020—IET Intelligent Transport Systems—Wiley Online Library”. Available online: https://ietresearch.onlinelibrary.wiley.com/doi/full/10.1049/iet-its.2019.0249 (accessed on 24 October 2023).
- Merola, F.; Falchi, F.; Gennaro, C.; Di Benedetto, M. Reinforced Damage Minimization in Critical Events for Self-driving Vehicles. In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications, Lisbon, Portugal, 19–21 February 2023; pp. 258–266. [Google Scholar] [CrossRef]
- Nageshrao, S.; Tseng, H.E.; Filev, D. Autonomous Highway Driving using Deep Reinforcement Learning. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 2326–2331. [Google Scholar] [CrossRef]
- Peng, B.; Sun, Q.; Li, S.E.; Kum, D.; Yin, Y.; Wei, J.; Gu, T. End-to-End Autonomous Driving Through Dueling Double Deep Q-Network. Automot. Innov. 2021, 4, 328–337. [Google Scholar] [CrossRef]
- Cao, Z.; Biyik, E.; Wang, W.; Raventos, A.; Gaidon, A.; Rosman, G.; Sadigh, D. Reinforcement Learning based Control of Imitative Policies for Near-Accident Driving. arXiv 2020, arXiv:2007.00178. [Google Scholar] [CrossRef]
- Jaritz, M.; de Charette, R.; Toromanoff, M.; Perot, E.; Nashashibi, F. End-to-End Race Driving with Deep Reinforcement Learning. arXiv 2018, arXiv:1807.02371. [Google Scholar] [CrossRef]
- Ashwin, S.H.; Raj, R.N. Deep reinforcement learning for autonomous vehicles: Lane keep and overtaking scenarios with collision avoidance. Int. J. Inf. Tecnol. 2023, 15, 3541–3553. [Google Scholar] [CrossRef]
- Muzahid, A.J.M.; Kamarulzaman, S.F.; Rahman, M.A.; Alenezi, A.H. Deep Reinforcement Learning-Based Driving Strategy for Avoidance of Chain Collisions and Its Safety Efficiency Analysis in Autonomous Vehicles. IEEE Access 2022, 10, 43303–43319. [Google Scholar] [CrossRef]
- Dinh, L.; Quang, P.T.A.; Leguay, J. Towards Safe Load Balancing based on Control Barrier Functions and Deep Reinforcement Learning. arXiv 2024, arXiv:2401.05525. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, F.; Aksun-Guvenc, B. Collision Avoidance in Autonomous Vehicles Using the Control Lyapunov Function–Control Barrier Function–Quadratic Programming Approach with Deep Reinforcement Learning Decision-Making. Electronics 2025, 14, 557. [Google Scholar] [CrossRef]
- Chen, H.; Cao, X.; Guvenc, L.; Aksun-Guvenc, B. Deep-Reinforcement-Learning-Based Collision Avoidance of Autonomous Driving System for Vulnerable Road User Safety. Electronics 2024, 13, 1952. [Google Scholar] [CrossRef]
- Wong, K.; Stölzle, M.; Xiao, W.; Santina, C.D.; Rus, D.; Zardini, G. Contact-Aware Safety in Soft Robots Using High-Order Control Barrier and Lyapunov Functions. arXiv 2025, arXiv:2505.03841. [Google Scholar] [CrossRef]
- Watkins, C.J.C.H.; Dayan, P. Q-learning. Mach Learn 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- van Hasselt, H.; Guez, A.; Silver, D. Deep Reinforcement Learning with Double Q-learning. arXiv 2015, arXiv:1509.06461. [Google Scholar] [CrossRef]
- Wang, Z.; Schaul, T.; Hessel, M.; van Hasselt, H.; Lanctot, M.; de Freitas, N. Dueling Network Architectures for Deep Reinforcement Learning. arXiv 2016, arXiv:1511.06581. [Google Scholar] [CrossRef]
- Williams, R.J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 1992, 8, 229–256. [Google Scholar] [CrossRef]
- Sutton, R.S.; McAllester, D.; Singh, S.; Mansour, Y. Policy Gradient Methods for Reinforcement Learning with Function Approximation. In Advances in Neural Information Processing Systems; MIT Press: Boston, MA, USA, 1999; Available online: https://proceedings.neurips.cc/paper_files/paper/1999/hash/464d828b85b0bed98e80ade0a5c43b0f-Abstract.html (accessed on 5 November 2024).
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.P.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous Methods for Deep Reinforcement Learning. arXiv 2016, arXiv:1602.01783. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2019, arXiv:1509.02971. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. arXiv 2018, arXiv:1801.01290. [Google Scholar] [CrossRef]
- Fujimoto, S.; van Hoof, H.; Meger, D. Addressing Function Approximation Error in Actor-Critic Methods. arXiv 2018, arXiv:1802.09477. [Google Scholar] [CrossRef]
- Leurent, E. An Environment for Autonomous Driving Decision-Making; Python. May 2018. Available online: https://github.com/eleurent/highway-env (accessed on 14 June 2025).
- Zhao, H.; Guo, Y.; Liu, Y.; Jin, J. Multirobot unknown environment exploration and obstacle avoidance based on a Voronoi diagram and reinforcement learning. Expert Syst. Appl. 2025, 264, 125900. [Google Scholar] [CrossRef]
- Zhao, H.; Guo, Y.; Li, X.; Liu, Y.; Jin, J. Hierarchical Control Framework for Path Planning of Mobile Robots in Dynamic Environments Through Global Guidance and Reinforcement Learning. IEEE Internet Things J. 2025, 12, 309–333. [Google Scholar] [CrossRef]






| Symbol | Parameter |
|---|---|
| Earth-fixed frame coordinate | |
| Vehicle-fixed frame coordinate | |
| Center-of-gravity (CG) velocity | |
| m | Mass |
| Yaw moment of inertia | |
| Side-slip angle | |
| Yaw angle | |
| r | Yaw rate |
| Yaw disturbance moment | |
| Front and rear wheel steer angle | |
| Front and rear tire slip angle | |
| Front and rear tire cornering stiffness | |
| Distance between CG and front and rear axle | |
| Front and rear axle velocity | |
| Front and rear lateral tire force |
| Symbol | Parameter |
|---|---|
| State | |
| Action | |
| Immediate reward | |
| Target-network’s parameter | |
| Online-network’s parameter | |
| Discount for future reward |
| Symbol | Parameter | Value |
|---|---|---|
| Center-of-gravity (CG) velocity | 5 m/s | |
| m | Mass | 3000 kg |
| Yaw moment of inertia | 5.113 × 103 kg m2 | |
| Front tire cornering stiffness | 3 × 105 N/rad | |
| Rear tire cornering stiffness | 3 × 105 N/rad | |
| Distance between CG and front axle | 2 m | |
| Distance between CG and rear axle | 2 m | |
| Maximum allowed front wheel steer angle | 0.7 rad | |
| Minimum allowed front wheel steer angle | −0.7 rad |
| Hyperparameter | Value |
|---|---|
| Replay buffer size | 100,000 |
| Mini-batch size | 64 |
| Learning rate | 0.001 |
| Target network update frequency | Every 100 steps |
| Exploration strategy (ε decay) | 1.0 → 0.05 over 200,000 steps |
| Discount factor (γ) | 0.99 |
| Optimizer | Adam |
| Loss function | Mean Squared Error (MSE) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Aksun-Guvenc, B. Hierarchical Deep Reinforcement Learning-Based Path Planning with Underlying High-Order Control Lyapunov Function—Control Barrier Function—Quadratic Programming Collision Avoidance Path Tracking Control of Lane-Changing Maneuvers for Autonomous Vehicles. Electronics 2025, 14, 2776. https://doi.org/10.3390/electronics14142776
Chen H, Aksun-Guvenc B. Hierarchical Deep Reinforcement Learning-Based Path Planning with Underlying High-Order Control Lyapunov Function—Control Barrier Function—Quadratic Programming Collision Avoidance Path Tracking Control of Lane-Changing Maneuvers for Autonomous Vehicles. Electronics. 2025; 14(14):2776. https://doi.org/10.3390/electronics14142776
Chicago/Turabian StyleChen, Haochong, and Bilin Aksun-Guvenc. 2025. "Hierarchical Deep Reinforcement Learning-Based Path Planning with Underlying High-Order Control Lyapunov Function—Control Barrier Function—Quadratic Programming Collision Avoidance Path Tracking Control of Lane-Changing Maneuvers for Autonomous Vehicles" Electronics 14, no. 14: 2776. https://doi.org/10.3390/electronics14142776
APA StyleChen, H., & Aksun-Guvenc, B. (2025). Hierarchical Deep Reinforcement Learning-Based Path Planning with Underlying High-Order Control Lyapunov Function—Control Barrier Function—Quadratic Programming Collision Avoidance Path Tracking Control of Lane-Changing Maneuvers for Autonomous Vehicles. Electronics, 14(14), 2776. https://doi.org/10.3390/electronics14142776






