A Lightweight Multi-Angle Feature Fusion CNN for Bearing Fault Diagnosis
Abstract
1. Introduction
- A lightweight multi-angle feature fusion convolutional module (LMAF module), referred to as the main branch, was designed to enable multi-scale local receptive field feature extraction from vibration signals, effectively reducing both the number of parameters and the overall computational complexity.
- A lightweight channel attention mechanism, ECA, was introduced as an auxiliary branch to effectively enhance the adaptive weighting capability of the feature channels while avoiding complex matrix multiplication and high-dimensional computations.
- The proposal of an end-to-end feature extraction and classification framework combining lightweight yet robust features with global average pooling and a fully connected classifier. The proposed method achieved superior performance in fault diagnosis tasks and demonstrated significant advantages over traditional CNN or Transformer methods.
2. Bearing Fault Diagnosis Method Based on LMAFCNN
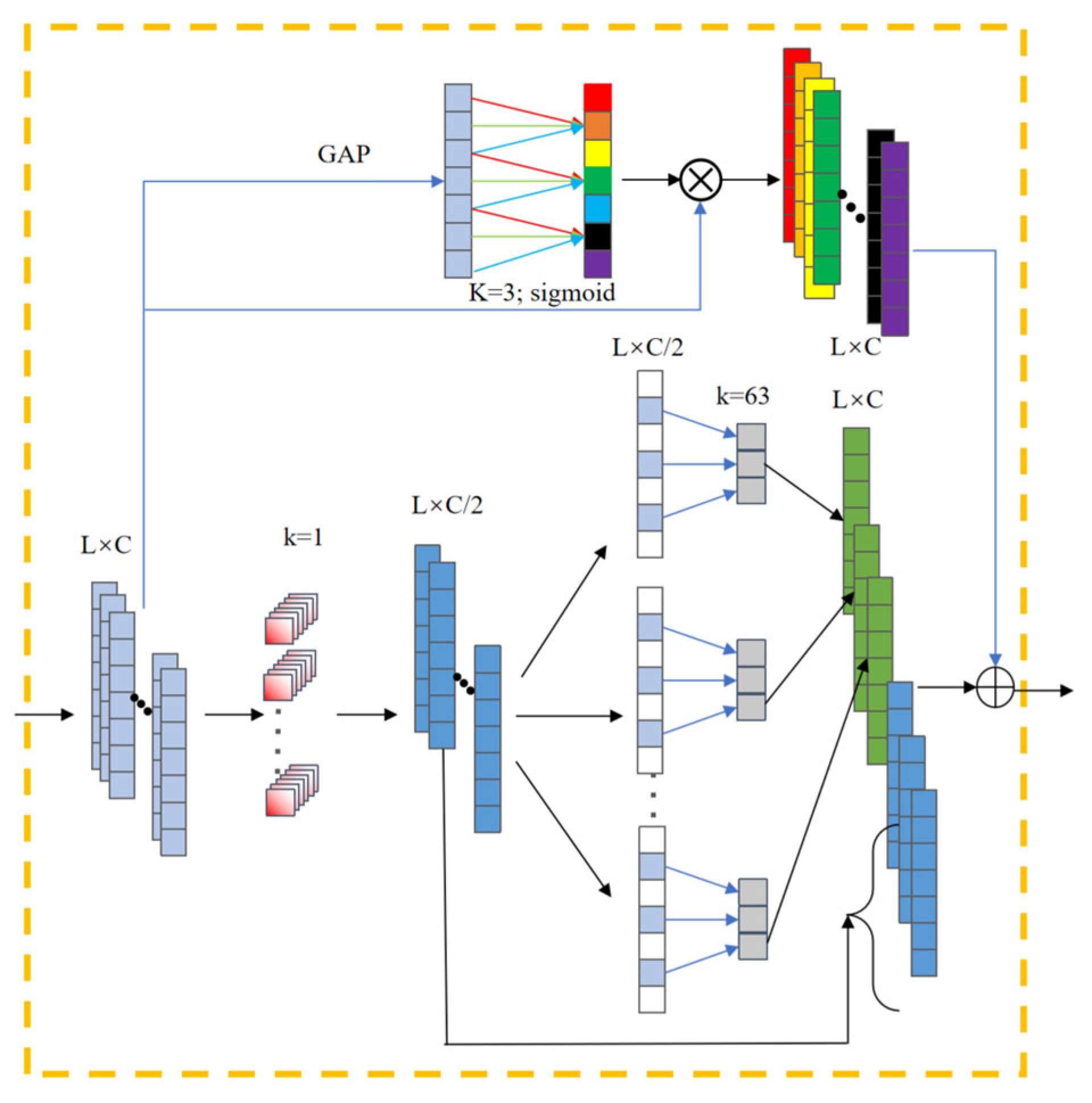
2.1. LMAF Module
2.1.1. Pointwise Convolution
2.1.2. Channel-Wise Dilated Convolution with Large-Kernels
2.1.3. ECA Channel Attention Module
2.1.4. Output of the LMAF Layer
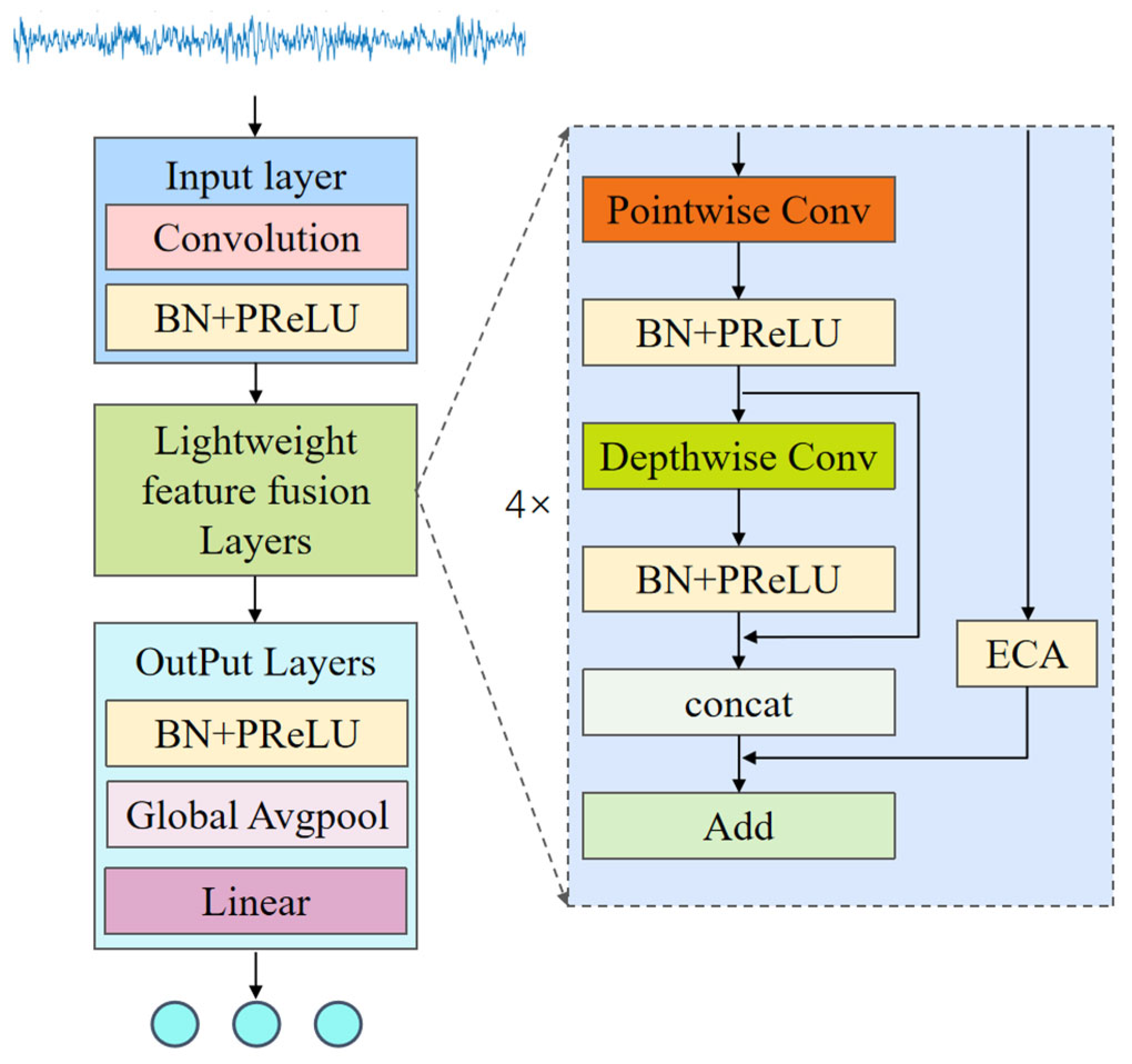
2.2. Overall Framework of LMAFCNN
- Input preprocessing: First, the raw vibration signals are processed through a wide-kernel convolutional layer to achieve data compression and channel expansion, laying the foundation for subsequent multi-angle feature extraction.
- Feature learning core: Subsequently, the signals pass through multiple stacked LMAF modules, which constitute the core of the network and are responsible for learning deep features from multiple angles.
- Classification Output: Finally, the learned features are aggregated using a GAP layer, and fault diagnosis is performed using a fully connected (FC) layer and a softmax layer. The final output is a probability vector , where C denotes the number of fault categories. Each element represents the predicted probability that the input sample belongs to class i. Specifically, the final output is computed aswhere is the input feature map and FC is the fully connected layer projecting to the number of fault categories. Softmax converts the output of the FC layer into a probability distribution over the C fault categories, ensuring that the predicted probabilities sum to 1.
2.3. Fault Diagnosis Process Based on LMAFCNN
- Data collection and sample division: To ensure data independence and prevent information leakage, non-overlapping sliding window technology was used to divide the dataset into samples, generating mutually independent training, validation, and testing samples.
- Lightweight model design and training: The model was trained using the LMAFCNN architecture, which integrates lightweight modules, including large-kernel channel-wise dilated convolutions and ECA. The best model on the validation set was selected as the final diagnostic model.
- Fault diagnosis and result visualization: Test set data were input into the trained diagnostic model, and the diagnostic results were systematically analyzed and visualized in multiple dimensions through various technical means, such as confusion matrices and feature visualization.
3. Experimental Results and Analysis
3.1. Data Description
3.1.1. PU Bearing Failure Dataset
3.1.2. Harbin Institute of Technology (HIT) Aviation Intershaft Bearing Dataset
3.2. Experimental Setup
3.3. Analysis of the Experimental Results for the PU Dataset
3.3.1. Results of Different Models
3.3.2. Model Complexity Experiments
3.3.3. Feature Visualization and Classification Performance Comparison Analysis
3.4. Model Generalization Experiments
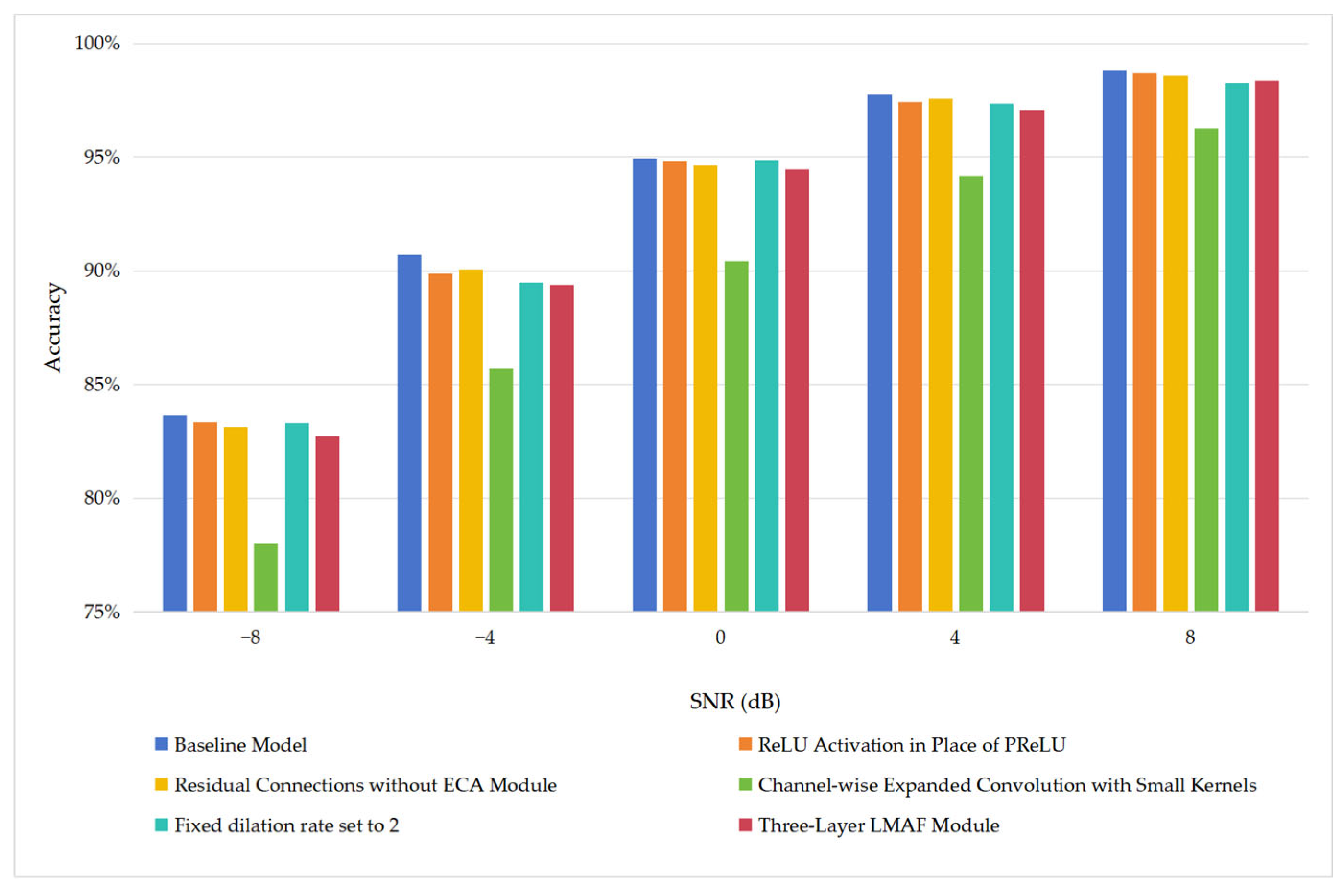
3.5. Ablation Experiment
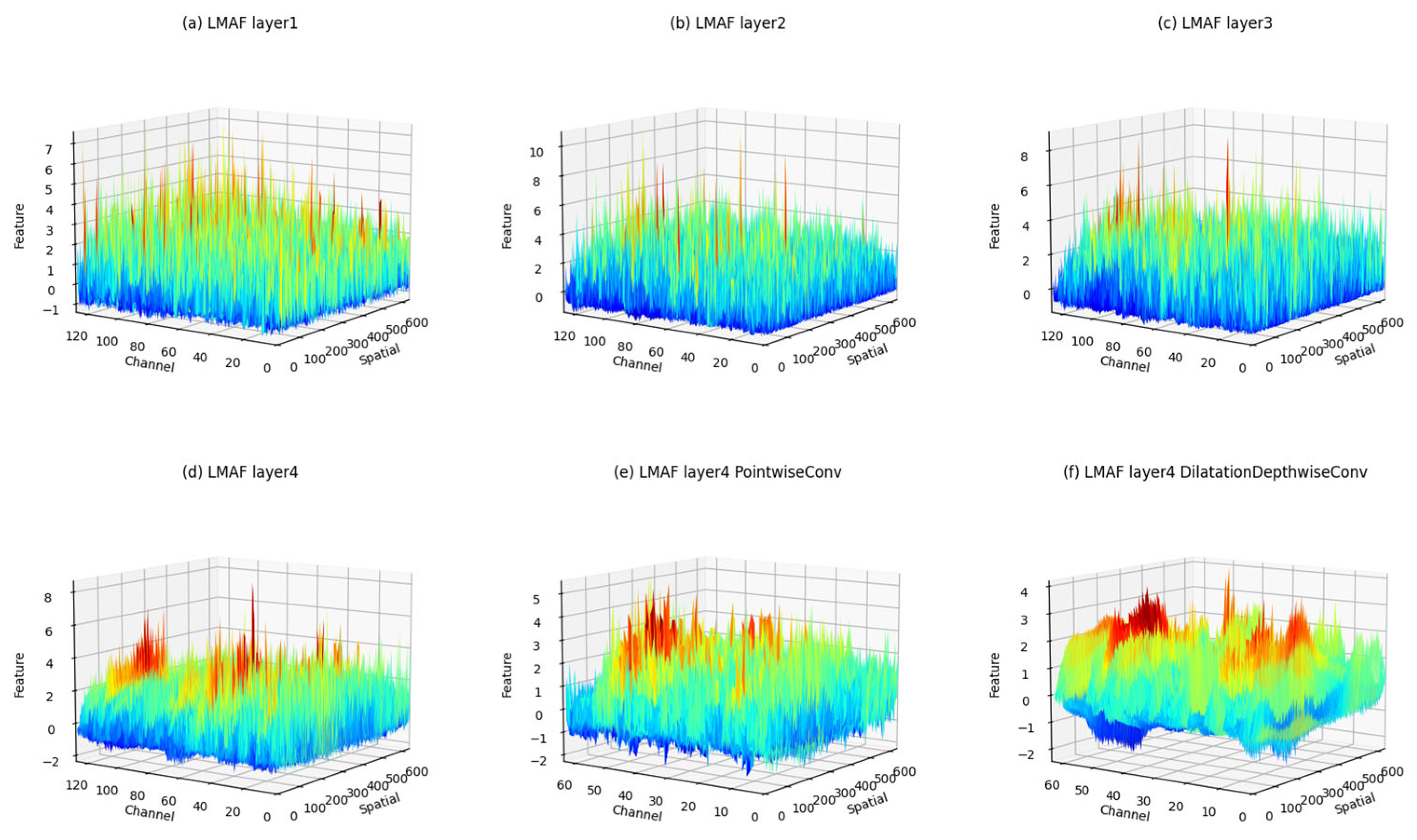
3.6. Model Interpretability Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumar, S.; Mukherjee, D.; Guchhait, P.K.; Banerjee, R.; Srivastava, A.K.; Vishwakarma, D.N.; Saket, R.K. A Comprehensive Review of Condition Based Prognostic Maintenance (CBPM) for Induction Motor. IEEE Access 2019, 7, 90690–90704. [Google Scholar] [CrossRef]
- Wei, Z.; Xu, Y.; Nolan, J.P. An alternative bearing fault detection strategy for vibrating screen bearings. J. Vib. Control 2023, 30, 4304–4316. [Google Scholar] [CrossRef]
- Barai, V.; Ramteke, S.M.; Dhanalkotwar, V.; Nagmote, Y.; Shende, S.; Deshmukh, D. Bearing fault diagnosis using signal processing and machine learning techniques: A review. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Nagpur, India, 26–28 May 2022; p. 012034. [Google Scholar]
- Jiang, D.; He, C.; Chen, Z.; Zhao, J. Are Novel Deep Learning Methods Effective for Fault Diagnosis? IEEE Trans. Reliab. 2024, 1–15. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, W.; Huang, J.; Ma, X. A comprehensive review of deep learning-based fault diagnosis approaches for rolling bearings: Advancements and challenges. AIP Adv. 2025, 15, 020702. [Google Scholar] [CrossRef]
- Zhu, Z.; Lei, Y.; Qi, G.; Chai, Y.; Mazur, N.; An, Y.; Huang, X. A review of the application of deep learning in intelligent fault diagnosis of rotating machinery. Measurement 2023, 206, 112346. [Google Scholar] [CrossRef]
- Ko, J.H.; Yin, C. A review of artificial intelligence application for machining surface quality prediction: From key factors to model development. J. Intell. Manuf. 2025. [Google Scholar] [CrossRef]
- Wu, M.; Arshad, M.H.; Saxena, K.K.; Qian, J.; Reynaerts, D. Profile prediction in ECM using machine learning. Procedia CIRP 2022, 113, 410–416. [Google Scholar] [CrossRef]
- Chung, J.; Shen, B.; Kong, Z.J. Anomaly detection in additive manufacturing processes using supervised classification with imbalanced sensor data based on generative adversarial network. J. Intell. Manuf. 2024, 35, 2387–2406. [Google Scholar] [CrossRef]
- Gong, L.; Pang, C.; Wang, G.; Shi, N. Lightweight Bearing Fault Diagnosis Method Based on Improved Residual Network. Electronics 2024, 13, 3749. [Google Scholar] [CrossRef]
- Zhang, G.; Xu, J.; Huang, X.; Li, Z. A Novel Two-Dimensional Quad-Stable Stochastic Resonance System for Bearing Fault Detection. Fluct. Noise Lett. 2023, 23, 2450017. [Google Scholar] [CrossRef]
- Gong, W.; Wang, Y.; Zhang, M.; Mihankhah, E.; Chen, H.; Wang, D. A Fast Anomaly Diagnosis Approach Based on Modified CNN and Multisensor Data Fusion. IEEE Trans. Ind. Electron. 2022, 69, 13636–13646. [Google Scholar] [CrossRef]
- Li, X.; Chen, Y.; Liu, Y. A novel convolutional neural network with global perception for bearing fault diagnosis. Eng. Appl. Artif. Intell. 2025, 143, 109986. [Google Scholar] [CrossRef]
- Zheng, X.; Hu, Q.; Li, C.; Zhao, S. An Enhanced Dual-Channel-Omni-Scale 1DCNN for Fault Diagnosis. In Proceedings of the Chinese Conference on Pattern Recognition and Computer Vision (PRCV), Urumqi, China, 18–20 October 2024; pp. 152–166. [Google Scholar]
- Janssens, O.; Slavkovikj, V.; Vervisch, B.; Stockman, K.; Loccufier, M.; Verstockt, S.; Van de Walle, R.; Van Hoecke, S. Convolutional Neural Network Based Fault Detection for Rotating Machinery. J. Sound Vib. 2016, 377, 331–345. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, G.; Li, C.; Chen, Y.; Zhang, Z. A New Deep Learning Model for Fault Diagnosis with Good Anti-Noise and Domain Adaptation Ability on Raw Vibration Signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef]
- Zhao, M.; Zhong, S.; Fu, X.; Tang, B.; Pecht, M. Deep Residual Shrinkage Networks for Fault Diagnosis. IEEE Trans. Ind. Inf. 2020, 16, 4681–4690. [Google Scholar] [CrossRef]
- Wang, C.; Li, X.; Yuan, P.; Su, K.; Xie, Z.; Wang, J. An integrated approach for mechanical fault diagnosis using maximum mean square discrepancy representation and CNN-based mixed information fusion. Struct. Health Monit. 2024, 14759217241279996. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Peng, D.; Qin, Y. Understanding and Learning Discriminant Features based on Multiattention 1DCNN for Wheelset Bearing Fault Diagnosis. IEEE Trans. Ind. Inf. 2020, 16, 5735–5745. [Google Scholar] [CrossRef]
- Fang, H.; Deng, J.; Zhao, B.; Shi, Y.; Zhou, J.; Shao, S. LEFE-Net: A Lightweight Efficient Feature Extraction Network with Strong Robustness for Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Zhao, Z.; Jiao, Y. A Fault Diagnosis Method for Rotating Machinery Based on CNN with Mixed Information. IEEE Trans. Ind. Inf. 2023, 19, 9091–9101. [Google Scholar] [CrossRef]
- Jin, T.; Yan, C.; Chen, C.; Yang, Z.; Tian, H.; Guo, J. New domain adaptation method in shallow and deep layers of the CNN for bearing fault diagnosis under different working conditions. Int. J. Adv. Manuf. Technol. 2023, 124, 3701–3712. [Google Scholar] [CrossRef]
- Li, S.; Jiang, Q.; Xu, Y.; Feng, K.; Wang, Y.; Sun, B.; Yan, X.; Sheng, X.; Zhang, K.; Ni, Q. Digital twin-driven focal modulation-based convolutional network for intelligent fault diagnosis. Reliab. Eng. Syst. Saf. 2023, 240, 109590. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, H.; Li, H. A rotating machinery fault diagnosis method based on multi-sensor fusion and ECA-CNN. IEEE Access 2023, 11, 106443–106455. [Google Scholar] [CrossRef]
- Chen, G.; Song, W.; Shao, W.; Sun, H.; Qing, X. Damage presence, localization and quantification of aircraft structure based on end-to-end deep learning framework. IEEE Trans. Instrum. Meas. 2025, 74, 1–15. [Google Scholar] [CrossRef]
- Hu, B.; Liu, J.; Xu, Y. A novel multi-scale convolutional neural network incorporating multiple attention mechanisms for bearing fault diagnosis. Measurement 2025, 242, 115927. [Google Scholar] [CrossRef]
- Yan, H.; Si, X.; Liang, J.; Duan, J.; Shi, T. Unsupervised Learning for Machinery Adaptive Fault Detection Using Wide-Deep Convolutional Autoencoder with Kernelized Attention Mechanism. Sensors 2024, 24, 8053. [Google Scholar] [CrossRef]
- Yan, S.; Shao, H.; Wang, J.; Zheng, X.; Liu, B. LiConvFormer: A lightweight fault diagnosis framework using separable multiscale convolution and broadcast self-attention. Expert Syst. Appl. 2024, 237, 121338. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Yao, J.; Li, M.; Gao, Z. Multi-sensor fusion fault diagnosis method of wind turbine bearing based on adaptive convergent viewable neural networks. Reliab. Eng. Syst. Saf. 2024, 245, 109980. [Google Scholar] [CrossRef]
- Xu, H.; Wang, X.; Huang, J.; Zhang, F.; Chu, F. Semi-supervised multi-sensor information fusion tailored graph embedded low-rank tensor learning machine under extremely low labeled rate. Inf. Fusion 2024, 105, 102222. [Google Scholar] [CrossRef]
- Mitra, S.; Koley, C. Real-time robust bearing fault detection using scattergram-driven hybrid CNN-SVM. Electr. Eng. 2024, 106, 3615–3625. [Google Scholar] [CrossRef]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Ding, X.; Zhang, X.; Han, J.; Ding, G. Scaling up your kernels to 31x31: Revisiting large kernel design in cnns. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 11963–11975. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient channel attention for deep convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11534–11542. [Google Scholar]
- Lin, M.; Chen, Q.; Yan, S. Network in network. arXiv 2013, arXiv:1312.4400. [Google Scholar]
- Wang, P.; Chen, P.; Yuan, Y.; Liu, D.; Huang, Z.; Hou, X.; Cottrell, G. Understanding Convolution for Semantic Segmentation. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 1451–1460. [Google Scholar]
- Lessmeier, C.; Kimotho, J.K.; Zimmer, D.; Sextro, W. Condition monitoring of bearing damage in electromechanical drive systems by using motor current signals of electric motors: A benchmark data set for data-driven classification. In Proceedings of the PHM Society European Conference, Bilbao, Spain, 5–8 July 2016. [Google Scholar]
- Hou, L.; Yi, H.; Jin, Y.; Gui, M.; Sui, L.; Zhang, J.; Chen, Y. Inter-shaft bearing fault diagnosis based on aero-engine system: A benchmarking dataset study. J. Dyn. Monit. Diagn. 2023, 2, 228–242. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.-C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]










| Module | Main Branch | Sub-Branch | Convolution Kernel Size/Stride | Number of Output Channels |
|---|---|---|---|---|
| DownSample Conv | Conv1d | - | 16/4 | 128 |
| LMAF Layer1 (expansion rate = 1) LMAF Layer2 (expansion rate = 2) LMAF Layer3 (expansion rate = 5) LMAF Layer4 (expansion rate = 1) | Pointwise Conv1d | ECA | 1/1 | 64 |
| Dilatation DepthwiseConv1d | 63/1 | 64 | ||
| Concat | - | 128 | ||
| Add | - | 128 | ||
| GAP | GAP | - | - | 128 |
| Linear | Linear | - | - | 3 |
| Fault Type | Label | Bearing Code | Damage Method | Damage Level | Training/Validation/Test Set |
|---|---|---|---|---|---|
| Inner ring | 0 | KI01 | EDM | 1 | 1440/180/180 |
| KI05 | electric engraver | 1 | |||
| KI07 | electric engraver | 2 | |||
| Outer ring | 1 | KA01 | EDM | 1 | |
| KA05 | electric engraver | 1 | 1440/180/180 | ||
| KA07 | drilling | 1 | |||
| Health | 2 | K002 | - | - | 1440/180/180 |
| Fault Type | Label | Bearing Code | Damage Method | Damage Level | Training/Validation/Test Set |
|---|---|---|---|---|---|
| Inner ring | 0 | KI14, KI17, KI21 KI16 | fatigue: potting | 1 | 1440/180/180 |
| fatigue: potting | 3 | ||||
| KI18 | fatigue: potting | 2 | |||
| Outer ring | 1 | KA04, KA22, KA16 | fatigue: potting | 1 | 1440/180/180 |
| fatigue: potting | 2 | ||||
| KA30, KA15 | Plastic deform: indentations | 1 | |||
| Health | 2 | K001 | - | - | 1440/180/180 |
| Fault Type | Label | Fault Depth | Fault Length | Training/Validation/Test Set |
|---|---|---|---|---|
| Inner ring | 0 | 0.5 | 0.5, 1.0 | 1600/200/200 |
| Health | 1 | 0 | 0 | 1600/200/200 |
| Outer ring | 2 | 0.5 | 0.5 | 1600/200/200 |
| Dataset | Model | SNR (dB) | ||||||
|---|---|---|---|---|---|---|---|---|
| −10 | −8 | −4 | 0 | 4 | 8 | None | ||
| Artificial damage | WDCNN | 65.85% | 72.52% | 80.09% | 85.46% | 88.48% | 90.35% | 91.63% |
| MA1DCNN | 71.87% | 77.67% | 85.33% | 90.02% | 93.17% | 95.41% | 97.63% | |
| DRSN_CW | 65.46% | 69.91% | 80.04% | 86.57% | 90.44% | 92.96% | 95.41% | |
| ResNet18 | 69.78% | 74.57% | 82.54% | 86.81% | 91.07% | 94.37% | 97.89% | |
| MobileNetV2 | 67.46% | 73.93% | 82.04% | 87.43% | 90.83% | 93.35% | 96.20% | |
| LiConvFormer | 73.85% | 78.63% | 85.76% | 90.19% | 92.61% | 94.61% | 97.15% | |
| MIXCNN2 | 77.35% | 82.06% | 88.44% | 93.59% | 96.65% | 98.35% | 99.35% | |
| LMAFCNN | 78.91% | 83.65% | 90.72% | 94.93% | 97.74% | 98.83% | 99.50% | |
| Natural injury | WDCNN | 91.39% | 94.89% | 98.39% | 99.50% | 99.87% | 99.98% | 99.98% |
| MA1DCNN | 96.37% | 97.70% | 99.41% | 99.89% | 100.00% | 100.00% | 100.00% | |
| DRSN_CW | 92.81% | 95.76% | 98.39% | 99.54% | 99.93% | 100.00% | 100.00% | |
| ResNet18 | 91.13% | 93.78% | 97.85% | 99.57% | 99.96% | 100.00% | 100.00% | |
| MobileNetV2 | 91.46% | 94.65% | 98.04% | 99.63% | 99.96% | 100.00% | 100.00% | |
| LiConvFormer | 94.98% | 97.19% | 99.17% | 99.91% | 100.00% | 100.00% | 100.00% | |
| MIXCNN2 | 97.00% | 98.61% | 99.91% | 100.00% | 100.00% | 100.00% | 100.00% | |
| LMAFCNN | 97.37% | 98.93% | 99.91% | 100.00% | 100.00% | 100.00% | 100.00% | |
| Model | Number of Parameters | FLOPs |
|---|---|---|
| WDCNN | 4.79 × 104 | 3.9 × 105 |
| MA1DCNN | 3.24 × 105 | 7.48 × 107 |
| DRSN-CW | 6.64 × 106 | 7.09 × 108 |
| ResNet18 | 3.85 × 106 | 1.76 × 108 |
| MobileNetV2 | 2.19 × 106 | 9.69 × 107 |
| LiConvFormer | 3.23 × 105 | 1.44 × 107 |
| MIXCNN2 | 8.17 × 104 | 2.04 × 107 |
| LMAFCNN | 5.52 × 104 | 1.48 × 107 |
| Model | SNR (dB) | |||||
|---|---|---|---|---|---|---|
| −8 | −4 | 0 | 4 | 8 | None | |
| WDCNN | 57.98% | 61.55% | 66.28% | 71.18% | 75.93% | 85.05% |
| MA1DCNN | 55.10% | 59.08% | 62.98% | 68.58% | 71.93% | 83.17% |
| DRSN_CW | 53.15% | 54.48% | 56.03% | 57.98% | 58.67% | 87.90% |
| ResNet18 | 57.22% | 58.95% | 60.53% | 61.93% | 65.03% | 86.58% |
| MobileNetV2 | 57.67% | 60.73% | 63.05% | 64.48% | 66.68% | 88.80% |
| LiConvFormer | 57.70% | 60.83% | 64.25% | 68.45% | 72.00% | 94.13% |
| MIXCNN | 62.05% | 65.67% | 70.48% | 77.62% | 83.22% | 94.42% |
| LMAFCNN | 64.33% | 70.82% | 76.48% | 81.58% | 84.80% | 93.12% |
| Model | SNR | ||||
|---|---|---|---|---|---|
| −8 dB | −4 dB | 0 dB | 4 dB | 8 dB | |
| Baseline Model | 83.65% | 90.72% | 94.93% | 97.74% | 98.83% |
| ReLU Activation in Place of PReLU | 83.35% | 89.89% | 94.81% | 97.41% | 98.70% |
| Residual Connections without ECA Module | 83.13% | 90.06% | 94.65% | 97.56% | 98.57% |
| Channel-wise Expanded Convolution with Small Kernels | 78.00% | 85.70% | 90.43% | 94.17% | 96.28% |
| Fixed dilation rate set to 2 | 83.30% | 89.50% | 94.85% | 97.35% | 98.26% |
| Three-Layer LMAF Module | 82.74% | 89.37% | 94.46% | 97.06% | 98.37% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Wang, G.; Shi, N.; Li, Y.; Hao, W.; Pang, C. A Lightweight Multi-Angle Feature Fusion CNN for Bearing Fault Diagnosis. Electronics 2025, 14, 2774. https://doi.org/10.3390/electronics14142774
Li H, Wang G, Shi N, Li Y, Hao W, Pang C. A Lightweight Multi-Angle Feature Fusion CNN for Bearing Fault Diagnosis. Electronics. 2025; 14(14):2774. https://doi.org/10.3390/electronics14142774
Chicago/Turabian StyleLi, Huanli, Guoqiang Wang, Nianfeng Shi, Yingying Li, Wenlu Hao, and Chongwen Pang. 2025. "A Lightweight Multi-Angle Feature Fusion CNN for Bearing Fault Diagnosis" Electronics 14, no. 14: 2774. https://doi.org/10.3390/electronics14142774
APA StyleLi, H., Wang, G., Shi, N., Li, Y., Hao, W., & Pang, C. (2025). A Lightweight Multi-Angle Feature Fusion CNN for Bearing Fault Diagnosis. Electronics, 14(14), 2774. https://doi.org/10.3390/electronics14142774







