Abstract
Label Distribution Learning (LDL) has emerged as a powerful paradigm for addressing label ambiguity, offering a more nuanced quantification of the instance–label relationship compared to traditional single-label and multi-label learning approaches. This paper focuses on the challenge of noisy label distributions, which is ubiquitous in real-world applications due to the annotator subjectivity, algorithmic biases, and experimental errors. Existing related LDL algorithms often assume a linear combination of true and random label distributions when modeling the noisy label distributions, an oversimplification that fails to capture the practical generation processes of noisy label distributions. Therefore, this paper introduces an assumption that the noise in label distributions primarily arises from the semantic confusion between labels and proposes a novel generative label distribution learning algorithm to model the confusion-based generation process of both the feature data and the noisy label distribution data. The proposed model is inferred using variational methods and its effectiveness is demonstrated through extensive experiments across various real-world datasets, showcasing its superiority in handling noisy label distributions.
1. Introduction
Label Distribution Learning (LDL) [1] is emerging as a potent paradigm for mitigating label ambiguity. In the context of LDL, the training instance is annotated with a label distribution vector, where each component signifies the degree to which each label describes the instance. Distinct from conventional single-label learning and multi-label learning, in which only the presence or absence of label relevance is indicated, LDL offers a more detailed quantification of the instance–label relationship. This nuanced approach enhances the applicability of LDL across various domains, including age estimation [2,3,4,5,6], affective analysis [7,8,9,10,11], and rating prediction [12,13,14,15].
Current works in LDL predominantly emphasize enhancing generalization performance. For instance, some research efforts have been directed towards developing more robust LDL models that effectively represent the mapping from features to label distributions [4,13,16]. Additionally, there studies have focused on devising regularized loss functions that encapsulate prior knowledge about the mapping from features to label distributions [17,18,19]. While these algorithms have demonstrated commendable performance across various datasets, they predominantly rely on high-quality training label distributions. However, the quality of training label distributions in many real-world applications is not assured. Human-annotated label distributions are particularly vulnerable to factors such as annotator subjectivity and expertise levels. Moreover, label distributions produced by non-human systems such as label smoothing algorithms and experimental apparatuses are prone to the limitations of algorithmic assumptions, data distribution biases, and intrinsic errors on the part of the experimental apparatus. These combined factors pose significant challenges in guaranteeing the quality of training label distributions, potentially leading to the unreliability of existing LDL algorithms. Although numerous efforts have been made to tackle this problem, they typically rely on the straightforward assumption that a noisy label distribution is a linear combination of the true label distribution and a random label distribution [20]. However, this simplified assumption falls short of accurately capturing the complex and nuanced processes of generating noisy label distributions in practical scenarios.
Therefore, in this paper we investigate the mechanisms underlying the generation of noisy label distributions and propose a novel generative label distribution learning algorithm. Specifically, we first propose that the noise in label distributions primarily arises from the semantic confusion between labels. Taking the image recognition task as an example, it is evident that cats and dogs can be accurately distinguished, whereas horses and donkeys are prone to being confused. Unlike the linear noise assumption, label noise based on semantic confusion more precisely captures the underlying noise generation mechanism between labels and is better able to model the complex uncertainties present in human-annotated label distributions. To address this noise generation mechanism, we construct a probabilistic graphical model to fundamentally model this process. The generation and inference processes of the proposed model are illustrated in Figure 1. During the generation process, the latent true label distribution is obtained by normalizing a normal vector through the softmax function. Meanwhile, we assume that the probabilities of semantic confusion between labels adhere to a Dirichlet distribution, allowing the complex dependencies between labels to be captured. Subsequently, in order to utilize the mutual confusion among labels, we assume that the value of each label in the noisy label distribution is affected by the weighted combination of the values of other labels, where the weights are the probabilities of other labels being misclassified as that label. Furthermore, the feature vector for each instance is assumed to be generated from a normal distribution, the parameters of which are determined by the nonlinear transformation of the true label distribution, thereby establishing the association between features and label distributions. In the inference process, we derive the posterior distribution of the true label distribution by variational methods and derive a differentiable variational lower bound through the aforementioned generation process. Finally, we conduct extensive experiments on a wide range of real-world datasets to validate the effectiveness and superiority of the proposed algorithm.
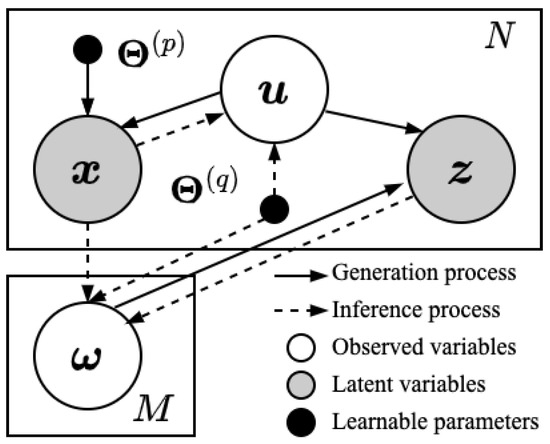
Figure 1.
Schematic diagram of our proposed model. The latent variables and correspond to the true label distribution and label confusion vector, respectively. The observed variables and correspond to the feature vector and noisy label distribution provided in the dataset, respectively.
2. Related Work
To predict the label distributions for unseen instances, the primary approach involves learning a mapping from feature vectors to label distributions based on the feature vectors of training instances and their corresponding label distributions (a process termed LDL, i.e., label distribution learning) and subsequently utilizing this mapping to output the label distribution for test instances. The crucial challenge of LDL lies in the design of LDL algorithms with robust generalization performance. Existing research on this issue predominantly focuses on two aspects, namely, model representation and loss functions.
Studies on model representation have primarily concentrated on the manner in which the mapping from feature vectors to label distributions is represented. To date, the findings about this issue can be categorized into three distinct classes. The first class comprises maximum entropy LDL models [1]. Maximum entropy LDL models are derived from the principle of maximum entropy [21]. Formally, these models typically perform exponential normalization on the linear or nonlinear mapping of feature vectors to produce the label distribution. The second class is prototype-based models, wherein the mapping from features to label distributions is constructed through existing examples in the training set. For example, the AAkNN algorithm [1] extends the traditional k-nearest neighbors algorithm to accommodate the task of LDL. The GMML-kLDL algorithm [22] introduces a distance metric that captures label correlation and classification information, which is then used to identify the nearest neighbors of a test instance and leverage their label distribution information to predict the label distribution of the test instance. Furthermore, the LDL-LCR algorithm [23] seeks several nearest neighbors of a test instance within the training set and reconstructs the feature vector of the test instance based on these neighbors, ultimately combining the reconstruction coefficients with the neighbors’ label distributions to derive the label distribution of the test instance. The LDSVR algorithm [13] utilizes kernel techniques to assess the correlation between test and training instances, then combines these correlations as weights to generate the label distribution for the test instance. The third class is ensemble models, which aim to directly extend existing ensemble learning models to meet the requirements of LDL. Specifically, the LDLogitBoost algorithm [16] extends the LogitBoost algorithm [24] to LDL by introducing weighted regressors, resulting in a boosting algorithm for LDL. The LDLFs algorithm [3,4] applies the differentiable decision tree model to LDL with the goal of enhancing the model’s ability to fit the distribution form. In addition, the ENN-LDL algorithm [25] integrates ensemble neural networks into LDL through an ensemble architecture designed to improve the model’s capacity to represent the highly correlated label distributions. Similarly, the StructRF algorithm [26] introduces the structured random forest model into label distribution learning tasks, which aims to enhance the representation of highly correlated label distributions.
Studies on loss functions can be roughly divided into three categories. The first class focuses on mining and utilizing the label correlation or sample correlation within label distributions. For example, the LDLLC algorithm [27] constructs a distance metric to calculate the label correlation based on the training label distributions, then uses the distance between any two labels to regulate the distance between the corresponding column vectors in the parameter matrix. This ensures that the learning process of the label distribution model maintains the label correlation based on the training label distributions. The LALOT algorithm [28] treats the process of mining label correlation as a metric learning problem, employing the optimal transport distance to capture the geometric information of the underlying label space. The LDL-SCL algorithm [29] introduces the local label correlation assumption, positing that label correlation within label distributions varies across different sample clusters; accordingly, it constructs a local correlation vector as an additional feature for each sample to capture this characteristic. The EDL-LRL algorithm [9], also based on the local label correlation, employs a low-rank structure on local samples to mine local label correlation. The LDL-LCLR algorithm [30] simultaneously learns global and local label correlations, then mines them through low-rank approximation and sample clustering, respectively. The LDLSF algorithm [31] proposes a new label correlation assumption in the field of LDL, i.e., that the correlated labels should have similar corresponding components in the output label distribution. The LDL-LDM algorithm [17] utilizes global and local label correlation in a data-driven manner which first learns the manifold structure of label distributions and promotes the model output to also distribute within this manifold. The LDL-LRR [18] and LDL-DPA [19] algorithms propose regularizing the learning process by using the label rankings within the label distributions. The second class explores how to improve the generalization ability of models through label embedding. For instance, the MSLP algorithm [32] achieves label embedding for label distribution learning via multi-scale location preservation. The BC-LDL algorithm [33] integrates the label distribution information into the binary coding process to produce high-quality binary codes. The DBC-LDL algorithm [34] considers an efficient discrete coding framework to learn the binary coding of instances. The third class designs loss functions for different variants of LDL task. For example, the IncomLDL algorithm [35] proposes that the label distribution matrix is of low rank and proposes an optimization objective based on trace norm minimization to address incomplete LDL scenarios where the training label distributions have missing values. The IncomLDL-LR algorithm [36] assumes that the label distribution of each example can be linearly reconstructed based on its neighbors; as such, it recovers the missing label distribution information through the label distributions of nearest neighbor examples based on feature vectors. The GRME [37] and IncomLDL-LCD [38] algorithms recover the missing label distribution values by mining the correlation between labels. GLDL [39] constructs a graph-structured LDL framework which explicitly models the instance relation and label relation. In addition, some LDL studies have focused on weakly supervised LDL; for example, certain LDL algorithms are specifically designed to address the noise in LDL [20,40,41]. It should be noted that although the GCIA algorithm [41] utilized confusion matrix to describe the noise generation process, which is similar to our work, these two approaches have two significant differences. First, GCIA implicitly captures the dependency between the ground-truth label distribution and the sample features using a latent clustering variable. In contrast, our method directly conditions the sample feature variable on the ground-truth label distribution. By modeling this dependency explicitly, our method aims to better exploit the relationship between features and labels. Second, GCIA treats the confusion matrix as a learnable parameter; however, this approach does not account for the inherent uncertainty of the confusion matrix in real-world scenarios. In contrast, our method models the confusion matrix as a set of Dirichlet random vectors to more effectively capture the uncertainty and variability of the semantic confusion. Finally, several LDL algorithms have proposed learning the label distributions by using more accessible label forms such as logical labels [42,43,44], ternary labels [45], or label rankings [46,47,48].
3. Methodology
The commonly used mathematical notation is shown in Table 1. We address training datasets that appear as data pairs . Our goal is to learn a label distribution predictor (i.e., a mapping from the feature space to the label distribution space) using the training dataset . The generation process of the observations can be formalized as follows.

Table 1.
Commonly used notation in this paper.
- Generate a sample of the latent logits from a standard normal prior:
- Generate a sample of the confusion vector of each label from a Dirichlet prior:where the t-th element of (i.e., ) denotes the probability of the t-th label being mis-annotated as the m-th label.
- Generate a sample of the noisy label distribution from a Dirichlet distribution conditioned on the latent logits and the confusion vector:
- Generate observations of the feature variables:where is the precision of the normal distribution for generating the feature vector.
The joint probability distribution of the complete data can be decomposed as follows:
4. Variational Inference
We aim to infer the posterior distribution of the latent variables for practical decision-making. However, due to the complicated dependencies among the variables, obtaining an exact solution for the posterior distribution of the latent variables is challenging. Consequently, we employ a parameterized variational distribution to approximate the true posterior distribution. Formally, we aim to minimize the Kullback–Leibler (KL) divergence between the variational posterior and the true posterior [49]:
where denotes the KL divergence and denotes the variational posterior family. Because is intractable, we rewrite Equation (6) as Equation (7):
Because is a constant that is independent of the inference process, the minimization process in Equation (6) is equivalent to the maximization process in Equation (8):
We denote the first and second terms in Equation (8) as and , respectively. Adhering to the mean-field principle, we assume the variational posterior as Equation (9):
It should be noted that due to the absence of noisy label information during the prediction phase we assume that is variationally conditioned on to facilitate the prediction process. Because adheres to a normal prior, we also employ a normal distribution to model the variational posterior of :
where is the softplus function, i.e., . To prevent the gradient information of the optimization objective from being removed by randomness, we can sample from by Equation (11):
Similarly, we employ a Dirichlet distribution to model the variational posterior of , as adheres to a Dirichlet prior:
As suggested by [50], the gradient-preserved sampling for can be approximately formalized as follows:
where . According to the decomposition in Equation (9), the first term in Equation (8), i.e., , can be estimated by Monte Carlo sampling:
where and . Intuitively, Equation (14) measures the quality of reconstructing the observations of features and labels from the variational posterior of latent variables, while maximizing Equation (14) encourages the latent variables to better explain the observations of features and noisy label distributions. The second term in Equation (8), i.e., , can be transformed as follows:
Intuitively, minimizing Equation (15) encourages the posteriors of the label distribution and confusion vectors to approach their priors. Computationally, Equation (15) entails the KL divergence between normal distributions as well as the KL divergence between Dirichlet distributions, both of which can be derived analytically. Therefore, by combining Equations (14) and (15), the final optimization objective can be summarized as follows:
5. Experiments
5.1. Datasets and Evaluation Metrics
The datasets used in this paper are shown in Table 2. The SJAFFE [51] dataset comprises 213 facial images, each annotated by 60 experts who rated six basic emotions (happiness, sadness, surprise, fear, anger, and disgust) on a five-point intensity scale. The emotional intensity for each image is represented by the average score across all raters, which is subsequently normalized to construct the emotion label distribution. Similarly, the SBU-3DFE [52] dataset contains 2500 facial expression images, with each image evaluated by 23 experts following the same rating protocol as SJAFFE to generate corresponding label distributions. The Yeast datasets [1] (i.e. the datasets with IDs ranging from 3 to 8) encompass empirical data gathered from ten distinct biological experiments conducted on budding yeast. Each dataset encompasses 2465 yeast genes, with each gene represented by a 24-dimensional vector. The labels within each dataset denote the discrete time points during the biological experiment. The label distribution represents the expression levels of yeast genes at each time point.

Table 2.
Dataset statistics.
We use six common LDL evaluation metrics: Cheb (Chebyshev distance), Clark (Clark distance), Canber (Canberra metric), KL (Kullback–Leibler divergence), Cosine (cosine coefficient), and Intersec (intersection similarity).
Lower values of distance-based measures (i.e., Cheb, Clark, Canber, KL) and higher value of similarity-based measures (i.e., Cosine and Intersec) represent better performance, which are denoted by ↓ and ↑, respectively.
5.2. Experimental Procedure
In this section, we illustrate the methodology employed to assess the efficacy of our approach. Overall, we introduce confusion-based noise into the label distribution of the noise-free training set, then utilize the noise-free test set to evaluate the performance of comparison algorithms trained on the training set with noisy label distributions. Specifically, given a noise-free LDL dataset, we randomly split the dataset into two chunks (70% for training and 30% for testing). We then obtain the noisy label distributions by adding noise to the label distributions of the training instances according to Equation (18):
where the parameter controls the extent of noiselessness of the dataset. We then train LDL models on the noisy training set and evaluate the prediction performance on the noise-free test set. We repeat the above process ten times and record the mean and standard deviation.
5.3. Comparison Algorithms
We compare our proposed algorithms with seven existing LDL algorithms: AAkNN [1], SABFGS [1], BD-LDL [53], Duo-LDL [54], LDL-LRR [18], LDL-LDM [17], and LDL-DPA [19]. The hyperparameter settings for each algorithm adhere to the recommendations provided in their respective papers. The hyperparameter k in AAkNN is set to 5. The hyperparameters and in BD-LDL are selected among . The hyperparameters and in LDL-LRR are selected among and , respectively. The hyperparameters , , and in LDL-LDM are selected among , while the hyperparameter g in LDL-LDM is selected among . The hyperparameters , , and in LDL-DPA are selected among , , and , respectively. Finally, the hyperparameters and of our proposed algorithm are set as 6 and , respectively.
5.4. Results and Discussions
The main experimental results are presented in Table 3, Table 4, Table 5 and Table 6, where Table 3 and Table 4 display the algorithm performance conducted under (low noise), and Table 5 and Table 6 display the algorithm performance conducted under (high noise). Each experimental result within these tables is formalized as “”, where “mean” represents the mean value of the algorithm’s performance, “std” denotes the standard deviation of the algorithm performance, “r” denotes the rank of the corresponding algorithm among all comparison algorithms, and “†” denotes the statistical significance under the pairwise two-tailed t-test at 0.05 significance level; in addition, “” denotes that the corresponding algorithm is significantly inferior to our algorithm, “” denotes that the corresponding algorithm is significantly superior to our algorithm, and “” denotes that there is no significant difference between the corresponding algorithm and our proposed algorithm. The best performance is highlighted by boldface. In these experiments, we systematically evaluate the performance of different weakly supervised learning methods when the data quality () varies. When the data are noisy (), our method demonstrates a significant advantage on the SJAFFE and SBU-3DFE datasets; in particular, it is about 10–15% ahead of the second-best algorithm in terms of the distance metrics (Cheb, Clark, and Canber), which suggests that our method is more robust to the noisy data. While the performance of all methods improves as the data quality is improved to , our method still maintains the leading position, especially in terms of the KL and Cosine metrics on the Yeast datasets, for which the standard deviation is significantly smaller than that of the other methods (e.g., the standard deviation of the KL metrics for Yeast-cold is only ). These results indicate that the proposed method has stable prediction ability under different data distributions. Notably, LDL-LDM slightly outperforms our method for the Cheb metric ( vs. ) on the SBU-3DFE dataset with high-quality data (), which may stem from this algorithm’s advantage in learning clean labels. On the other hand, Duo-LDL and BD-LDL perform relatively poorly in all types of settings. This is particularly the case in noisy data environments, where the performance fluctuates drastically (e.g., the standard deviation of the Clark metric for Duo-LDL on SJAFFE at reaches ), which reflects the sensitivity of these methods to data quality. Overall, the experimental results validate the superiority of our method in both robustness and accuracy.

Table 3.
Prediction performance on the first four datasets with .

Table 4.
Prediction performance on the last four datasets with .

Table 5.
Prediction performance on the first four datasets with .

Table 6.
Prediction performance on the last four datasets with .
5.5. Further Analysis
In this section, we provide an empirical demonstration and discussion on the characteristics of our algorithm, which is beneficial for its practical application.
5.5.1. Hyperparameter Analysis
Here, we investigate the impact of the hyperparameters and on the performance of our algorithm. Specifically, we define the value range of and as , where . As described in Section 5.2, we conduct the experimental procedure with for each pair of hyperparameter values within , obtaining the performance of the algorithm under each pair of hyperparameter values within . The experimental results are visualized in Figure 2. In the heatmap, the x-axis and y-axis represent the values of and , respectively, while the color indicates the performance quantified by the cosine coefficient or Kullback–Leibler divergence. The box plot shows the marginal impact of the hyperparameters or on the algorithm’s performance. It can be observed that the algorithm generally performs better when is small and that the impact of on performance is relatively minor. Therefore, in the actual implementation of the algorithm, can be typically set to a small value.
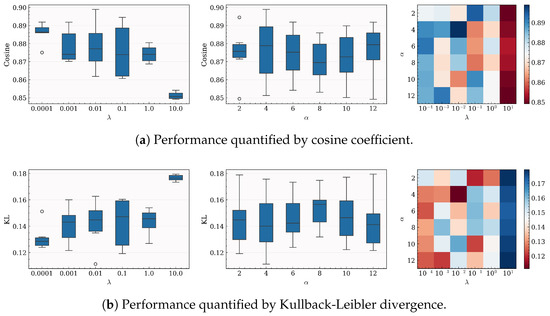
Figure 2.
Performance with different values of hyperparameters on the SJAFFE dataset with .
5.5.2. Convergence
Here, we demonstrate the convergence of the inference process of our proposed algorithm. As illustrated in Figure 3, the proposed algorithm demonstrates steady convergence behavior across multiple datasets. The curves are differentiated by color for each dataset and transparency for varying values. The results indicate that our algorithm rapidly approaches the optimal objective value within the first 100 iterations. This initial phase exhibits a steep descent, suggesting efficient gradient updates or search direction alignment. Subsequently, the optimization stabilizes, with marginal improvements in later iterations, indicating convergence to a near-optimal solution. The consistency of this trend across most datasets highlights the robustness of our algorithm to different data distributions.
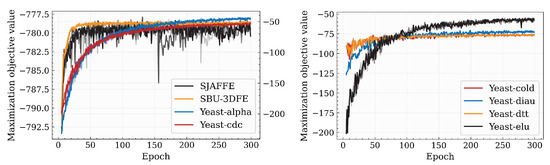
Figure 3.
Convergence process of our proposed algorithm. The color of the curve corresponds to the dataset, while the transparency of the curve corresponds to the value of .
6. Conclusions
This paper identifies a critical limitation of noise modeling in existing label distribution learning methods, i.e., the oversimplified assumption that noisy label distributions can be directly modeled as a mixture of the true label distribution and a random noise. To address this gap, we rigorously investigate the underlying generation mechanisms of noisy label distribution and propose an assumption that noisy label distributions primarily stem from semantic confusion among labels (i.e., inter-label semantic ambiguity). Grounded in this assumption, we develop a generative label distribution learning framework that explicitly accounts for label-wise semantic correlations and confusion patterns. To comprehensively validate our proposal, we conduct extensive experiments under varying noise levels across eight real-world benchmark datasets. The results demonstrate that our algorithm effectively models noisy label distributions originating from label semantic confusion, consistently achieving state-of-the-art performance in nearly all scenarios.
Author Contributions
Conceptualization, X.L., C.M., H.Z. and Y.L.; methodology, B.X., T.Y. and Y.L.; software, B.X. and T.Y.; validation, B.X. and T.Y.; formal analysis, B.X. and T.Y.; investigation, B.X. and T.Y.; resources, X.L., C.M. and H.Z.; data curation, B.X. and T.Y.; writing—original draft preparation, B.X. and T.Y.; writing—review and editing, X.L., C.M., H.Z. and Y.G.; visualization, B.X. and T.Y.; supervision, X.L.; project administration, X.L.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Project of China Southern Power Grid Company Limited, grant number 032000KC23120050/GDKJXM20231537.
Data Availability Statement
Restrictions apply to the availability of these data. Data were obtained from PALM lab and are available at https://palm.seu.edu.cn/xgeng/LDL/download.htm (accessed on 1 July 2025) with the permission of PALM lab.
Conflicts of Interest
Authors Xinhai Li, Chenxu Meng, and Heng Zhou were employed by the Zhongshan Power Supply Bureau, China Southern Power Grid Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The authors declare that this study received funding from the Science and Technology Project of China Southern Power Grid Company Limited. The funder was not involved in the study design, in the collection, analysis, and interpretation of data, in the writing of this article, or in the decision to submit it for publication.
References
- Geng, X. Label Distribution Learning. IEEE Trans. Knowl. Data Eng. 2016, 28, 1734–1748. [Google Scholar] [CrossRef]
- Geng, X.; Yin, C.; Zhou, Z.H. Facial Age Estimation by Learning from Label Distributions. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2401–2412. [Google Scholar] [CrossRef] [PubMed]
- Shen, W.; Guo, Y.; Wang, Y.; Zhao, K.; Wang, B.; Yuille, A. Deep Differentiable Random Forests for Age Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 404–419. [Google Scholar] [CrossRef]
- Shen, W.; Zhao, K.; Guo, Y.; Yuille, A. Label Distribution Learning Forests. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Hou, P.; Geng, X.; Huo, Z.W.; Lv, J. Semi-Supervised Adaptive Label Distribution Learning for Facial Age Estimation. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 2015–2021. [Google Scholar]
- Gao, B.B.; Zhou, H.Y.; Wu, J.; Geng, X. Age Estimation Using Expectation of Label Distribution Learning. In Proceedings of the International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 712–718. [Google Scholar]
- He, T.; Jin, X. Image Emotion Distribution Learning with Graph Convolutional Networks. In Proceedings of the International Conference on Multimedia Retrieval, Ottawa, ON, Canada, 10–13 June 2019; pp. 382–390. [Google Scholar]
- Yang, J.; Sun, M.; Sun, X. Learning Visual Sentiment Distributions via Augmented Conditional Probability Neural Network. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 224–230. [Google Scholar]
- Jia, X.; Zheng, X.; Li, W.; Zhang, C.; Li, Z. Facial Emotion Distribution Learning by Exploiting Low-Rank Label Correlations Locally. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 9841–9850. [Google Scholar]
- Peng, K.C.; Chen, T.; Sadovnik, A.; Gallagher, A. A Mixed Bag of Emotions: Model, Predict, and Transfer Emotion Distributions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 860–868. [Google Scholar]
- Machajdik, J.; Hanbury, A. Affective Image Classification Using Features Inspired by Psychology and Art Theory. In Proceedings of the ACM International Conference on Multimedia, Florence, Italy, 25–29 October 2010; pp. 83–92. [Google Scholar]
- Ren, Y.; Geng, X. Sense Beauty by Label Distribution Learning. In Proceedings of the International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 2648–2654. [Google Scholar]
- Geng, X.; Hou, P. Pre-Release Prediction of Crowd Opinion on Movies by Label Distribution Learning. In Proceedings of the International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015; pp. 3511–3517. [Google Scholar]
- Liu, S.; Huang, E.; Zhou, Z.; Xu, Y.; Kui, X.; Lei, T.; Meng, H. Lightweight Facial Attractiveness Prediction Using Dual Label Distribution. IEEE Trans. Cogn. Dev. Syst. 2025. early access. [Google Scholar] [CrossRef]
- Tang, Y.; Ni, Z.; Zhou, J.; Zhang, D.; Lu, J.; Wu, Y.; Zhou, J. Uncertainty-Aware Score Distribution Learning for Action Quality Assessment. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 9836–9845. [Google Scholar]
- Xing, C.; Geng, X.; Xue, H. Logistic Boosting Regression for Label Distribution Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4489–4497. [Google Scholar]
- Wang, J.; Geng, X. Label Distribution Learning by Exploiting Label Distribution Manifold. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 839–852. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.; Shen, X.; Li, W.; Lu, Y.; Zhu, J. Label Distribution Learning by Maintaining Label Ranking Relation. IEEE Trans. Knowl. Data Eng. 2023, 35, 1695–1707. [Google Scholar] [CrossRef]
- Jia, X.; Qin, T.; Lu, Y.; Li, W. Adaptive Weighted Ranking-Oriented Label Distribution Learning. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 11302–11316. [Google Scholar] [CrossRef]
- Kou, Z.; Wang, J.; Jia, Y.; Liu, B.; Geng, X. Instance-Dependent Inaccurate Label Distribution Learning. IEEE Trans. Neural Netw. Learn. Syst. 2023, 36, 1425–1437. [Google Scholar] [CrossRef]
- Guiasu, S.; Shenitzer, A. The Principle of Maximum Entropy. Math. Intell. 1985, 7, 42–48. [Google Scholar] [CrossRef]
- Zhai, Y.; Dai, J. Geometric Mean Metric Learning for Label Distribution Learning. In Proceedings of the International Conference on Neural Information Processing, Sydney, NSW, Australia, 12–15 December 2019; pp. 260–272. [Google Scholar]
- Xu, S.; Ju, H.; Shang, L.; Pedrycz, W.; Yang, X.; Li, C. Label Distribution Learning: A Local Collaborative Mechanism. Int. J. Approx. Reason. 2020, 121, 59–84. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive Logistic Regression: A Statistical View of Boosting. Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Zhai, Y.; Dai, J.; Shi, H. Label Distribution Learning Based on Ensemble Neural Networks. In Proceedings of the International Conference on Neural Information Processing, Siem Reap, Cambodia, 13–16 December 2018; pp. 593–602. [Google Scholar]
- Chen, M.; Wang, X.; Feng, B.; Liu, W. Structured Random Forest for Label Distribution Learning. Neurocomputing 2018, 320, 171–182. [Google Scholar] [CrossRef]
- Jia, X.; Li, W.; Liu, J.; Zhang, Y. Label Distribution Learning by Exploiting Label Correlations. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 3310–3317. [Google Scholar]
- Zhao, P.; Zhou, Z.H. Label Distribution Learning by Optimal Transport. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 4506–4513. [Google Scholar]
- Zheng, X.; Jia, X.; Li, W. Label Distribution Learning by Exploiting Sample Correlations Locally. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 4556–4563. [Google Scholar]
- Ren, T.; Jia, X.; Li, W.; Zhao, S. Label Distribution Learning with Label Correlations via Low-Rank Approximation. In Proceedings of the International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 3325–3331. [Google Scholar]
- Ren, T.; Jia, X.; Li, W.; Chen, L.; Li, Z. Label Distribution Learning with Label-Specific Features. In Proceedings of the International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 3318–3324. [Google Scholar]
- Peng, C.L.; Tao, A.; Geng, X. Label Embedding Based on Multi-Scale Locality Preservation. In Proceedings of the International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 2623–2629. [Google Scholar]
- Wang, K.; Geng, X. Binary Coding Based Label Distribution Learning. In Proceedings of the International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 2783–2789. [Google Scholar]
- Wang, K.; Geng, X. Discrete Binary Coding Based Label Distribution Learning. In Proceedings of the International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 3733–3739. [Google Scholar]
- Xu, M.; Zhou, Z.H. Incomplete Label Distribution Learning. In Proceedings of the International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 3175–3181. [Google Scholar]
- Zeng, X.Q.; Chen, S.F.; Xiang, R.; Wu, S.X.; Wan, Z.Y. Filling Missing Values by Local Reconstruction for Incomplete Label Distribution Learning. Int. J. Wirel. Mob. Comput. 2019, 16, 314–321. [Google Scholar] [CrossRef]
- Xu, C.; Gu, S.; Tao, H.; Hou, C. Fragmentary Label Distribution Learning via Graph Regularized Maximum Entropy Criteria. Pattern Recognit. Lett. 2021, 145, 147–156. [Google Scholar] [CrossRef]
- Xu, S.; Shang, L.; Shen, F.; Yang, X.; Pedrycz, W. Incomplete Label Distribution Learning via Label Correlation Decomposition. Inf. Fusion 2025, 113, 102600. [Google Scholar] [CrossRef]
- Jin, Y.; Gao, R.; He, Y.; Zhu, X. GLDL: Graph Label Distribution Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; pp. 12965–12974. [Google Scholar]
- Lu, Y.; Li, W.; Liu, D.; Li, H.; Jia, X. Adaptive-Grained Label Distribution Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; pp. 19161–19169. [Google Scholar]
- He, L.; Lu, Y.; Li, W.; Jia, X. Generative Calibration of Inaccurate Annotation for Label Distribution Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; pp. 12394–12401. [Google Scholar]
- Xu, N.; Tao, A.; Geng, X. Label Enhancement for Label Distribution Learning. In Proceedings of the International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 1632–1643. [Google Scholar]
- Xu, N.; Liu, Y.P.; Geng, X. Label Enhancement for Label Distribution Learning. IEEE Trans. Knowl. Data Eng. 2021, 33, 1632–1643. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, Y.; Geng, X. Label Enhancement for Label Distribution Learning via Prior Knowledge. In Proceedings of the International Joint Conference on Artificial Intelligence, Yokohama, Japan, 11–17 July 2020; pp. 3223–3229. [Google Scholar]
- Lu, Y.; Jia, X. Predicting Label Distribution from Ternary Labels. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 10–15 December 2024; pp. 70431–70452. [Google Scholar]
- Lu, Y.; Jia, X. Predicting Label Distribution from Multi-Label Ranking. In Proceedings of the Advances in Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022; pp. 36931–36943. [Google Scholar]
- Lu, Y.; Li, W.; Li, H.; Jia, X. Predicting Label Distribution from Tie-Allowed Multi-Label Ranking. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 15364–15379. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Li, W.; Li, H.; Jia, X. Ranking-Preserved Generative Label Enhancement. Mach. Learn. 2023, 112, 4693–4721. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. In Proceedings of the International Conference on Learning Representations, Scottsdale, AZ, USA, 2–4 May 2013. [Google Scholar]
- Joo, W.; Lee, W.; Park, S.; Moon, I.C. Dirichlet Variational Autoencoder. Pattern Recognit. 2020, 107, 107514. [Google Scholar] [CrossRef]
- Lyons, M.; Akamatsu, S.; Kamachi, M.; Gyoba, J. Coding Facial Expressions with Gabor Wavelets. In Proceedings of the IEEE International Conference on Automatic Face and Gesture Recognition, Nara, Japan, 14–16 April 1998; pp. 200–205. [Google Scholar]
- Yin, L.; Wei, X.; Sun, Y.; Wang, J.; Rosato, M.J. A 3D Facial Expression Database For Facial Behavior Research. In Proceedings of the International Conference on Automatic Face and Gesture Recognition, Southampton, UK, 10–12 April 2006; pp. 211–216. [Google Scholar]
- Liu, X.; Zhu, J.; Zheng, Q.; Li, Z.; Liu, R.; Wang, J. Bidirectional Loss Function for Label Enhancement and Distribution Learning. Knowl.-Based Syst. 2021, 213, 106690. [Google Scholar] [CrossRef]
- Zychowski, A.; Mandziuk, J. Duo-LDL Method for Label Distribution Learning Based on Pairwise Class Dependencies. Appl. Soft Comput. 2021, 110, 107585. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).