Peak Age of Information Optimization in Cell-Free Massive Random Access Networks

Abstract

With the vigorous development of Internet of Things technologies, Cell-Free Radio Access Network (CF-RAN), leveraging its distributed coverage and single/multi-antenna Access Point (AP) coordination advantages, has become a key technology for supporting massive Machine-Type Communication (mMTC). However, under the grant-free random access mechanism, this network architecture faces the problem of information freshness degradation due to channel congestion. To address this issue, a joint decoding model based on logical grouping architecture is introduced to analyze the correlation between the successful packet transmission probability and the Peak Age of Information (PAoI) in both single-AP and multi-AP scenarios. On this basis, a global Particle Swarm Optimization (PSO) algorithm is designed to dynamically adjust the channel access probability to minimize the average PAoI across the network. To reduce signaling overhead, a PSO algorithm based on local topology information is further proposed to achieve collaborative optimization among neighboring APs. Simulation results demonstrate that the global PSO algorithm can achieve performance closely approximating the optimum, while the local PSO algorithm maintains similar performance without the need for global information. It is especially suitable for large-scale access scenarios with wide area coverage, providing an efficient solution for optimizing information freshness in CF-RAN.

1. Introduction

With the rapid advancement of communication technologies, the Cell-Free Radio Access Network (CF-RAN) has emerged as a cutting-edge network architecture and a key technology for future 6G communications [1,2]. CF-RAN comprises numerous geographically distributed single/multi-antenna Access Points (APs), which are connected to a Central Processing Unit (CPU) via high-speed, low-latency fronthaul links (e.g., optical fibers) to enable joint operations such as encoding, decoding, resource allocation, and interference coordination [3]. The collaborative operation of distributed APs effectively reduces interference and extends network coverage, making CF-RAN particularly suitable for future Internet of Things (IoT) communication scenarios requiring wide-area coverage, such as ultra-high-voltage grid monitoring and vehicular networks.

Massive IoT applications predominantly adopt sporadic uplink transmission modes with small packets [4]. To address the signaling storm caused by grant-based access in traditional cellular networks, 3GPP introduced the grant-free random access protocol in the 5G NR standard [5]. This protocol allows users to directly transmit data during random access without establishing air interface bearer links with the core network. However, this distributed decision-making complicates the coordination of user access behaviors. In massive access scenarios, random access channels are prone to congestion, leading to significant increases in data transmission delays. In emerging applications such as industrial IoT, information freshness is a critical metric [6]. Delays in information sampling or transmission cause the value of information to deteriorate rapidly. Packets containing “stale” information not only fail to create value but also exacerbate congestion, severely degrading application service quality and user experience [7].

Information freshness is quantified using the Age of Information (AoI), which reflects data timeliness [8]. The Peak AoI (PAoI) further captures the worst-case timeliness performance under dynamic loads [9]. Optimizing grant-free random access mechanisms in cellular networks to enhance information freshness has become a key research focus. Studies [10,11] proposed dynamic transmission strategies based on AoI thresholds to mitigate channel contention by suppressing redundant transmissions. Studies [12,13] further utilized deep reinforcement learning to optimize AoI by adjusting transmission probabilities and access control mechanisms.

The aforementioned studies primarily focus on traditional single-cell cellular networks. Research on AoI optimization in CF-RAN scenarios is gradually gaining attention. For instance, Ref. [14] developed a two-disk model to derive closed-form approximations of average AoI under grant-free random access, exploring and optimizing the impact of different variables. Ref. [15] proposed a reinforcement learning framework to jointly optimize AoI and transmit power in uplink CF-RAN, designing state spaces, action spaces, and reward functions based on the soft actor–critic algorithm. Ref. [16] introduced priority-aware frame structures and device grouping strategies for cell-free massive MIMO industrial IoT networks to satisfy differentiated AoI requirements. However, existing studies on CF-RAN AoI suffer from limitations, such as reliance on Poisson assumptions for user spatial distribution [14] or centralized control algorithms with high signaling overhead [15], which hinder their applicability in large-scale, distributed massive access scenarios.

To address these challenges, this work extends the theoretical framework of [17] to grant-free CF-RAN massive random access networks. We construct a dynamic topology correlation model for multi-AP collaborative joint decoding scenarios. Based on this model, we derive expressions for average PAoI in single-AP and multi-AP networks. Subsequently, a global Particle Swarm Optimization (PSO) algorithm is proposed to dynamically adjust channel access probabilities for minimizing network-wide PAoI. However, since the global PSO algorithm requires full topology information and incurs high signaling overhead during iterative updates, we further design a local PSO algorithm that utilizes only neighboring AP topology information. Simulations demonstrate that the global PSO algorithm approaches theoretical optimality, while the local PSO algorithm maintains comparable performance without requiring global information, making it particularly suitable for large-scale access scenarios with wide-area coverage.

The remainder of this paper is organized as follows: Section 2 establishes the system model for cell-free massive random access networks, including the logical grouping architecture and grant-free transmission mechanism. Section 3 derives the closed-form expressions of successful transmission probability and PAoI for both single-AP and multi-AP scenarios. Building on these analytical models, Section 4 proposes two particle swarm optimization algorithms: a global PSO requiring full topology information and a local PSO utilizing neighbor AP information, both designed to minimize network-wide PAoI by dynamically adjusting channel access probabilities. Section 5 validates the theoretical analysis through comprehensive simulations and demonstrates the effectiveness of the proposed algorithms. Finally, Section 6 concludes the paper.

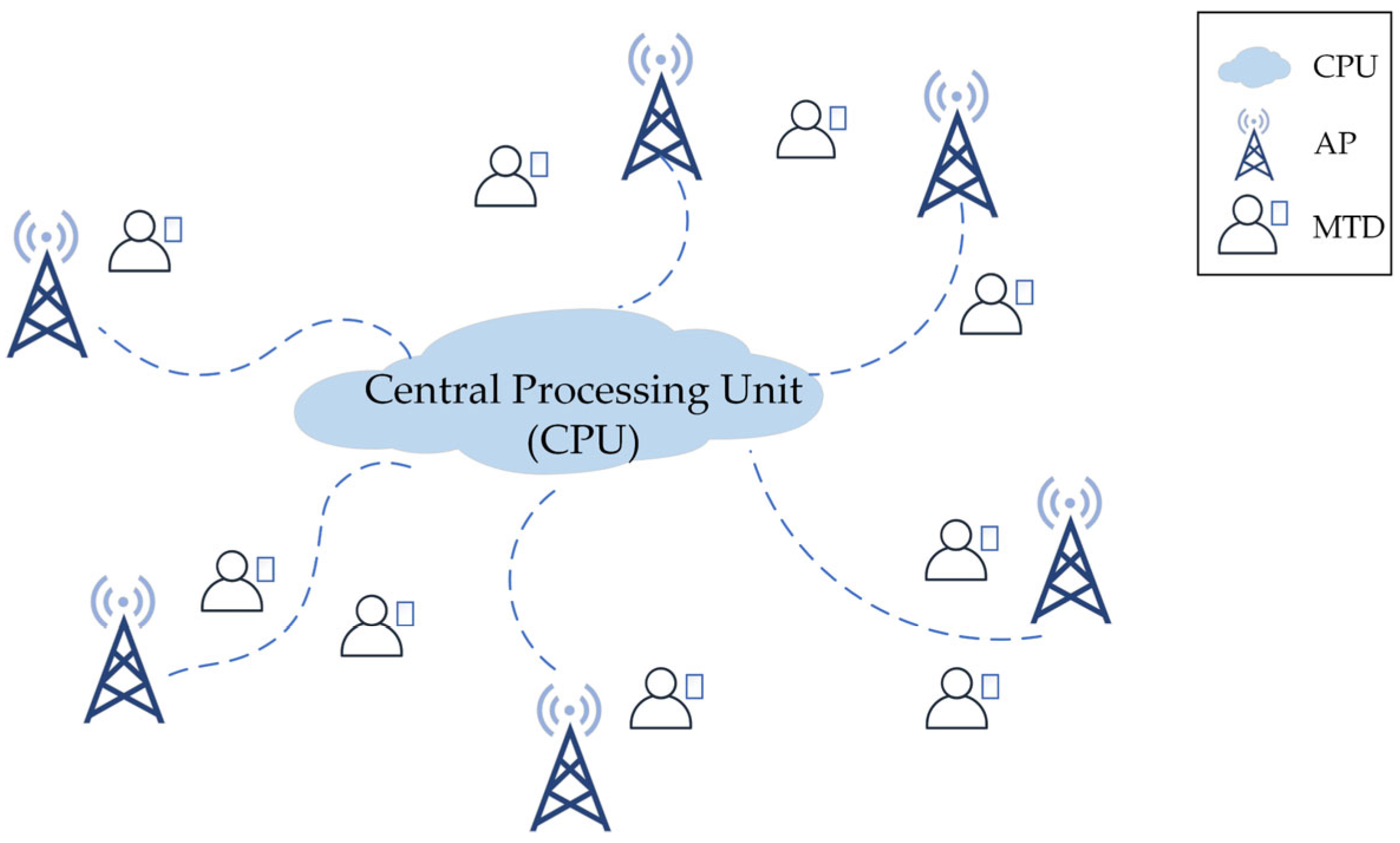
2. System Model

Consider a cell-free massive random access network serving massive Machine-Type Communication (mMTC) in IoT scenarios. Let $\mathcal{M}=\{1,2,\dots M\}$ denote the set of APs, each equipped with a single omnidirectional antenna. All APs collaboratively serve n Machine-Type Devices (MTDs), as illustrated in Figure 1. Unlike traditional cellular networks, MTDs in CF-RAN are not associated with a single AP but are dynamically served by neighboring AP clusters. Based on this architecture, MTDs are logically grouped according to the AP clusters that collaboratively serve them. Let ${\mathcal{G}}_A$ denote the group of MTDs that can communicate with all APs in set A, and the number of MTDs contained in this group is $\left|{\mathcal{G}}_A\right|=n^A$. For example, the green dots in Figure 2 represent group ${\mathcal{G}}_{\{1,2\}}$, which includes all MTDs served collaboratively by AP 1 and AP 2, and $n^{\left\{1,2\right\}}=4$. Similarly, in Figure 2, there also exist groups ${\mathcal{G}}_{\left\{1\right\}}$, ${\mathcal{G}}_{\left\{2\right\}}$, ${\mathcal{G}}_{\{2,3\}}$, and ${\mathcal{G}}_{\left\{3\right\}}$. Let G denote the total number of logical groups.

The CF-RAN employs the 3GPP grant-free random access mechanism, specifically the Small Data Transmission (SDT) protocol defined in the 5G NR standard [5], to serve all MTDs. The duration of a complete SDT signaling and data exchange process is defined as one time slot. All MTDs transmit synchronously with fixed packet lengths, occupying one time slot per transmission. A packet is assumed to traverse an ideal noiseless channel and is successfully received only if no other packets are transmitted to the same AP within the same time slot. APs are connected to a CPU via error-free fronthaul links. The CPU performs deduplication to retain the most reliable packet and discard duplicates. Thus, CF-RAN employs joint packet decoding: a packet is successfully decoded if received by at least one AP. After decoding, APs broadcast ACK/NACK signals.

Each MTD is equipped with a buffer queue of unit packet size. A new packet is generated at the beginning of each time slot with probability $\lambda \in \left(0.1\right]$, where packet generation time is negligible. For an MTD belonging to logical group ${\mathcal{G}}_A$, when its buffer is non-empty, it accesses the channel and transmits with probability $q^A$. This group-specific access probability $q^A$ corresponds to the “access class barring” factor in 3GPP standards and serves as the optimization variable for minimizing PAoI. A First-Come-First-Served (FCFS) queue discipline is adopted. If the buffer is full, newly arrived packets are discarded.

In CF-RAN dense deployments, AP coverage areas inevitably overlap, meaning data transmissions within a group are influenced not only by intra-group dynamics but also by inter-group interference. Based on this model, we analyze the successful transmission probability and the impact of inter-group interference on PAoI for any group ${\mathcal{G}}_A$, as well as design optimization algorithms to minimize the network-wide average PAoI.

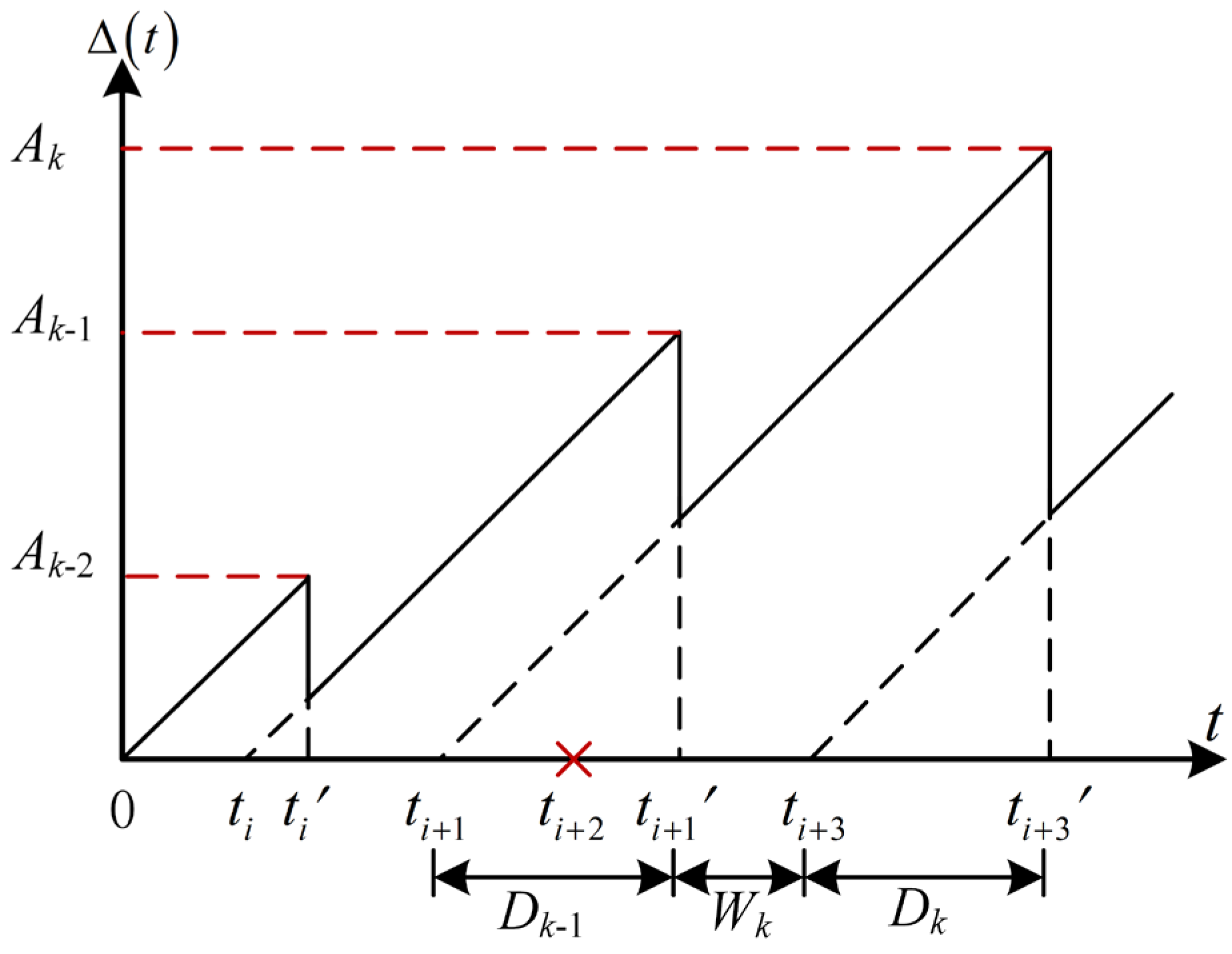
3. Peak Age of Information

This section derives expressions for the successful transmission probability and PAoI, starting from single-AP scenarios and extending to multi-AP networks. These derivations lay the theoretical foundation for subsequent optimization algorithms.

3.1. Successful Transmission Probability in Single-AP Scenarios

Consider the group ${\mathcal{G}}_{\left\{1\right\}}$ in the single-AP network scenario. The probability that the buffer queue of an MTD is empty is given by $1-{\rho }^{\left\{1\right\}}$, where ${\rho }^{\left\{1\right\}}={\displaystyle \frac{\lambda }{\lambda +p^{\left\{1\right\}}{q}^{\left\{1\right\}}}}$ is the offered load [18]. For $n^{\left\{1\right\}}$ MTDs in the group, the number of MTDs competing for channel access is $n^{\left\{1\right\}}{\rho }^{\left\{1\right\}}$. The successful transmission probability $p^{\left\{1\right\}}$ for a target MTD is the probability that all other $n^{\left\{1\right\}}-1$ MTDs either have empty buffers or do not access the channel. This is expressed as follows:

$$p^{\left\{1\right\}}={(1-{\rho }^{\left\{1\right\}}+{\rho }^{\left\{1\right\}}(1-q^{\left\{1\right\}}))}^{(n^{\left\{1\right\}}-1)},$$

(1)

where $q^{\left\{1\right\}}$ is the channel access probability. In the scenario of massive access, we have $n-1\approx n$ and ${(1-x)}^n\approx \exp (-nx)$. Based on this, the probability of successful packet transmission can be obtained as follows:

$$p^{\left\{1\right\}}=\exp (-{\displaystyle \frac{n^{\left\{1\right\}}\lambda q^{\left\{1\right\}}}{\lambda +p^{\left\{1\right\}}{q}^{\left\{1\right\}}}}).$$

(2)

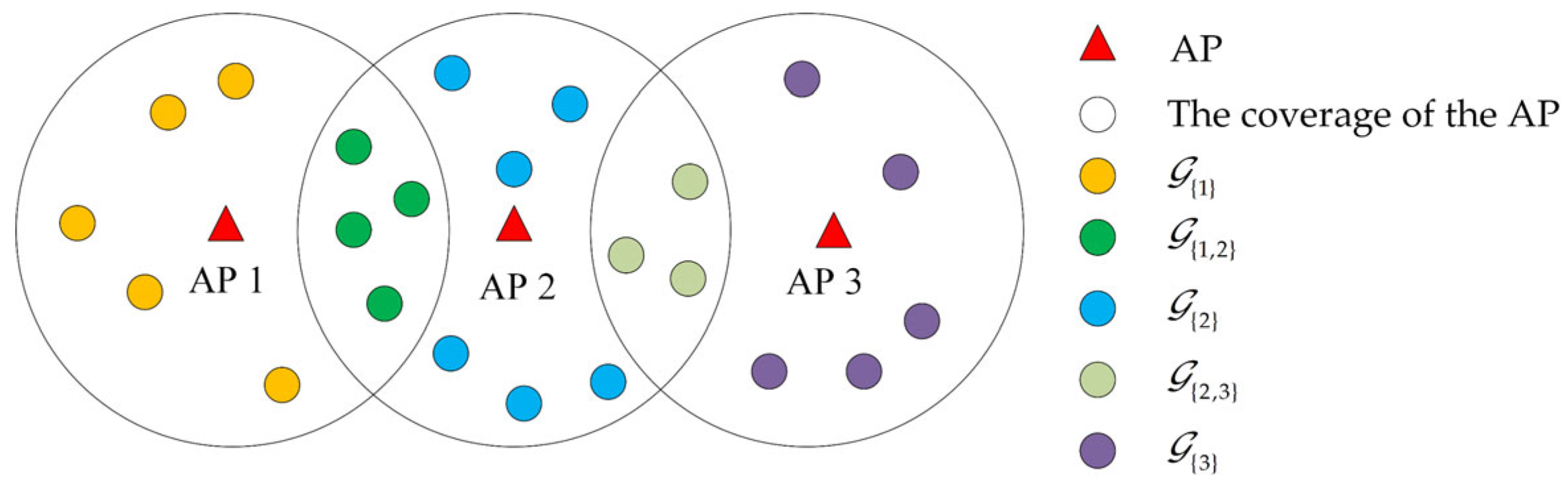
3.2. Successful Transmission Probability in Multi-AP Networks

In the scenario of multi-AP joint decoding, a packet can be successfully transmitted only if two conditions are met [17]: (1) Other MTDs in group ${\mathcal{G}}_A$ remain silent during the current time slot to prevent intra-group channel conflicts; (2) at least one of the APs in set A does not receive other packets during the same time slot, thus avoiding inter-group interference. Note that the above two conditions for successful packet decoding are applicable not only to the scenario where the MTD is covered by only one AP, i.e., $\left|A\right|=1$, but also to the scenario where the MTD is covered by multiple APs, i.e., $\left|A\right|\ge 2$.

We can then write the successful packet transmission probability $p^A$ as the combined effect of the probability that other MTDs within the group do not transmit and the probability of avoiding inter-group interference, that is as follows:

$$\begin{array}{c}{p}^A\approx \mathrm{Pr}\left\{\mathrm{MTD} \mathrm{in} \mathrm{group} {\mathcal{G}}_A \mathrm{makes} \mathrm{no} \mathrm{request}\right\}{n}^A\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times \left(1-{\displaystyle \prod _{j\in A}\left(1-{\displaystyle \prod _{\begin{array}{l}D=\stackrel{\sim }{D}\cup \left\{j\right\}\\ \stackrel{\sim }{D}\subset M\backslash \left\{j\right\}\\ D\ne A\end{array}}\mathrm{Pr}{\left\{\mathrm{MTD} \mathrm{in} \mathrm{group} {\mathcal{G}}_D \mathrm{makes} \mathrm{no} \mathrm{request}\right\}}^{n^D}}\right)}\right).\end{array}$$

(3)

As previously elaborated, the probability that MTDs within group ${\mathcal{G}}_A$ make no request in the current time slot is $\exp \left(-{\displaystyle \frac{n^A\lambda q^A}{\lambda +p^A{q}^A}}\right)$.

Regarding inter-group interference, define $R_j$ as the probability that other groups ${\mathcal{G}}_D$ within the coverage of AP j cause interference to the data transmission of the current group, corresponding to the nested term in Equation (3). Based on the derivation logic of (1) and (2), we can obtain the following:

$$R_j=1-\exp \left\{{\displaystyle \sum _{\begin{array}{l}D=\stackrel{\sim }{D}\cup \left\{j\right\}\\ \stackrel{\sim }{D}\subset M\backslash \left\{j\right\}\\ D\ne A\end{array}}-\frac{n^D\lambda q^D}{\lambda +p^D{q}^D}}\right\}.$$

(4)

Then, (3) can be rewritten as follows:

$$p^A=\exp (-{\displaystyle \frac{n^A\lambda q^A}{\lambda +p^A{q}^A}})(1-{\displaystyle \prod _{j\in A}{R}_j}).$$

(5)

3.3. Average PAoI

For any MTD, Figure 3 illustrates an example of the evolution traces of AoI, where $t_i$ denotes the arrival time of the $i^{th}$ packet and $t_i\prime$ denotes the successful transmission time of the $i^{th}$ packet. As can be seen from Figure 3, the AoI will continuously increase with time until the packet is successfully transmitted, and then the AoI decreases to the elapsed time since the packet was generated. Due to the limited buffer queue, when there is a packet in the buffer queue, a newly arriving packet will be discarded, such as $t_{i+2}$. Let k denote the $k^{th}$ successfully transmitted packet, and its PAoI $A_k$ can be written as follows:

$$A_k=D_{k-1}+W_k+D_k,$$

(6)

where $D_k$ represents the access delay, which is the duration between the successful transmission of the $k-1^{th}$ packet and the successful transmission of the $k^{th}$ packet. $W_k$ represents the idle period, which is the duration from the successful transmission of the $k-1^{th}$ packet to the arrival of the next packet. Since $W_k$ and $D_k$ are independent identical distribution random variables, for simplicity, the subscript k will be dropped in the following analysis.

Denoting the access delay of MTDs in group ${\mathcal{G}}_A$ as $D^A$, and the idle period as $W^A$, the average access delay of group ${\mathcal{G}}_A$ is given by [19] the following:

$$E[D^A]={\displaystyle \frac{1}{p^A{q}^A}}.$$

(7)

Since the departure of successfully transmitted packets and the arrival of new packets may occur concurrently, in accordance with the Bernoulli arrival process of packets and the mathematical expectation of the Bernoulli distribution, the average idle time of group ${\mathcal{G}}_A$ is as follows:

$$E[W^A]={\displaystyle \frac{1}{\lambda }}-1.$$

(8)

Finally, combining Formulas (6)–(8), the PAoI of MTDs in group ${\mathcal{G}}_A$ is derived as follows:

$$A_A={\displaystyle \frac{2}{p^A{q}^A}}+{\displaystyle \frac{1}{\lambda }}-1.$$

(9)

Considering the presence of G logical groups in the network, the network-wide average PAoI is as follows:

$$A={\displaystyle \frac{{\displaystyle {\sum }_{g=1}^G{n}^g{A}_g}}{{\displaystyle {\sum }_{g=1}^G{n}^g}}}.$$

(10)

According to Formula (10), the optimization problem of PAoI can be formulated as follows:

$$A^{*}=\underset{0<\mathit{q}\le 1}{\min A}.$$

(11)

However, solving this problem entails significant complexity. The successful transmission probability under multi-AP scenarios, (5), is an implicit equation that cannot be explicitly resolved. $p^A$ depends not only on the channel access probability of its own group’s MTDs but is also nested with the channel access probabilities of other groups through the inter-group interference term $R_j$, resulting in a highly nonlinear objective function that is intractable for direct optimization. To address these challenges, the subsequent sections employ a heuristic PSO algorithm to dynamically adjust the channel access probabilities across all groups within the solution space.

4. Optimization of Average Peak Age of Information

4.1. Global PSO Algorithm Based on Full Topology Information

The PSO algorithm is a stochastic optimization method inspired by swarm intelligence [20]. In PSO, each particle represents a potential solution to the optimization problem, and the particle continuously adjusts its position in the search space to find the optimal solution [21]. The global PSO algorithm optimizes the channel access probability through global search to minimize the global average PAoI. The detailed implementation of PSO algorithm is described in Algorithm 1.

Algorithm 1 PAoI Optimization Algorithm Based on Global PSO

$\mathbf{Input}: \mathrm{Network} \mathrm{parameters} n^g,g=\{1,2,\dots G\}$,   $\lambda$$; \mathrm{algorithm} \mathrm{setting} \mathrm{parameters} K, c_1$$, c_2$$,{\mathit{v}}_{min}$$, {\mathit{v}}_{max}$$, {\mathit{q}}_{min}$$, {\mathit{q}}_{max}$$, {\omega }_{min}$$, {\omega }_{max}$ , Imax. $\mathbf{Output}: \mathrm{Optimal} \mathrm{channel} \mathrm{access} \mathrm{probability} {\mathit{d}}^{(I_{max})}=\left[q^{(1)},q^{(2)},\dots ,q^{(G)}\right]$$\mathrm{and} \mathrm{minimum} \mathrm{global} \mathrm{PAoI} A_d^{(I_{max})}$

1: for each particle k = 1 to K do

2:   $\mathrm{Initialize} \mathrm{position} {\mathit{q}}_k^{(1)}$$\mathrm{and} \mathrm{velocity} {\mathit{v}}_k^{(1)}$

3:   ${\mathit{b}}_k^{(1)}={\mathit{q}}_k^{(1)}$

4:   $\mathrm{Calculate} \mathrm{the} \mathrm{PAoI} A_k^{(1)}$ according to (10)

5: end for

6: $\mathrm{Initialize} {\mathit{d}}^{(1)}$$\mathrm{and} A_d^{(1)}$ according to (13) and (10)

7: Set the initial iteration value i = 1

8: $\mathbf{for} \mathrm{each} \mathrm{iteration} \mathrm{round} i<I_{max}$ do

9:   for each particle k = 1 to K do

10:    $\mathrm{Update} \mathrm{velocity} {\mathit{v}}_k^{(i+1)}$ according to (12) and (14)

11:    $\mathrm{Constrain} \mathrm{the} \mathrm{velocity} {\mathit{v}}_k^{(i+1)}$$\mathrm{within} \mathrm{the} \mathrm{range} [{\mathit{v}}_{min},{\mathit{v}}_{max}]$

12:    $\mathrm{Update} \mathrm{position} {\mathit{q}}_k^{(i+1)}={\mathit{v}}_k^{(i+1)}+{\mathit{q}}_k^{(i)}$

13:    $\mathrm{Constrain} \mathrm{the} \mathrm{position} {\mathit{q}}_k^{(i+1)}$$\mathrm{within} \mathrm{the} \mathrm{range} [{\mathit{q}}_{min},{\mathit{q}}_{max}]$

14:      Calculate the PAoI according to (10)

15:     $\mathrm{Update} {\mathit{b}}_k^{(i+1)}$$\mathrm{and} A_k^{(i+1)}$ according to (13) and (10)

16:   end for

17:  $\mathrm{Update} {\mathit{d}}^{(i+1)}$$\mathrm{and} A_d^{(i+1)}$ according to (13) and (10)

18:   i = i + 1

19: end for

Given the number of MTDs, n^g, and packet arrival rates, $\lambda$, for each logical group, assuming there are K particles in the network, $k=\left\{1,2,\dots ,K\right\}$, and each particle k has a position vector ${\mathit{q}}_k$ and a velocity vector ${\mathit{v}}_k$. ${\mathit{q}}_k$ represents the channel access probability vector, whose elements correspond to the channel access probabilities of different groups, and ${\mathit{v}}_k$ controls its search direction and step size. During each iteration, ${\mathit{v}}_k$ will perform a small amplitude random update on the elements of ${\mathit{q}}_k$, and the updated position needs to be within the legal range. Particles compute PAoI based on ${\mathit{q}}_k$ to identify optimal positions. The update rules are as follows [22]:

$$\left\{\begin{array}{l}{\mathit{v}}_k^{(i+1)}={\omega }^{(i)}\cdot {\mathit{v}}_k^{(i)}+c_1{r}_{1,k}^{(i)}\cdot ({\mathit{b}}_k^{(i)}-{\mathit{q}}_k^{(i)})+c_2{r}_{2,k}^{(i)}\cdot ({\mathit{d}}^{(i)}-{\mathit{q}}_k^{(i)}),\hfill \\ {\mathit{q}}_k^{(i+1)}={\mathit{v}}_k^{(i+1)}+{\mathit{q}}_k^{(i)},\hfill \end{array}\right.$$

(12)

where $c_1$ and $c_2$ are the learning weight, $r_{1,k}^{(i)}$ and $r_{2,k}^{(i)}$ are the random value generated from the range $\left[0,1\right]$, ${\mathit{b}}_k^{(i)}$ represents the best-experience position of the particle itself, ${\mathit{d}}^{(i)}$ represents the best-experience position among all particles, and they are determined by the following formulas:

$$\left\{\begin{array}{l}{\mathit{b}}_k^{(i)}=\underset{{\mathit{q}}_k^{(1)},{\mathit{q}}_k^{(2)},\dots ,{\mathit{q}}_k^{(i)}}{\arg \min A},\hfill \\ {\mathit{d}}^{(i)}=\underset{{\mathit{b}}_1^{(i)},{\mathit{b}}_2^{(i)},\dots ,{\mathit{b}}_K^{(i)}}{\arg \min A,}\hfill \end{array}\right.$$

(13)

where A is the calculated PAoI, and ${\omega }^{(i)}$ is the inertia weight, whose calculation formula is as follows:

$${\omega }^{(i)}={\omega }_{min}+{\displaystyle \frac{({\omega }_{max}-{\omega }_{min})\cdot i}{I_{max}}},$$

(14)

where I_max is the upper limit of the number of iterations, ${\omega }_{min}$ and ${\omega }_{max}$ represent the minimum and maximum inertia weights, respectively, and the parameter settings are shown in

Table 1. PSO algorithm parameter setting.

Parameters	Values
Number of particles K	50
Self-control factor $c_1$	0.003
Group control factor $c_2$	0.8
Position range $(q_{min},q_{max})$	(0, 0.1)
Velocity range $(v_{min},v_{max})$	(−0.002, 0.002)
$\mathrm{Inertia} \mathrm{range} ({\omega }_{min},{\omega }_{max})$	(0.4, 2)
Maximum iterations Imax	100

.

However, solving this problem exhibits significant complexity. The successful transmission probability, Formula (4), under multiple APs is an implicit equation and cannot be explicitly analytically solved. $p^A$ depends not only on the channel access probability of MTDs in its own group but is also interwoven with the channel access probabilities of other groups through the inter-group interference term $R_j$, leading to the objective function being highly nonlinear and challenging to solve directly. To address these challenges, a heuristic algorithm of PSO will be adopted subsequently to dynamically adjust the channel access probabilities of each group within the solution space.

4.2. Local PSO Algorithm Based on Neighboring Topology Information

To address the signaling overhead issue caused by the global PSO’s dependency on global topology information, we propose an improved algorithm (i.e., Algorithm 2) based on local topology information. The core idea stems from the spatial decay characteristic of inter-group interference in cell-free networks: the PAoI of a group is predominantly affected by the transmission behaviors of its neighboring groups, while the impact of distant groups is negligible. By restricting optimization to the current group and its immediate neighbors, the algorithm captures the dynamics of key interference sources while significantly reducing complexity.

Each group considers only its associated APs, the MTDs served by these APs, and their AP coverage relationships. Specifically, two logical groups are considered neighboring if they share at least one common AP. Based on this definition, the entire network is partitioned into local neighborhoods, and each group communicates with its neighboring groups to exchange necessary information for distributed optimization. The exchanged information includes the number of MTDs, n, the channel access probability vector, q, and the packet arrival rate, $\lambda$, of each neighboring group. To further elaborate, taking a group ${\mathcal{G}}_A$ as an example, whose neighboring groups are ${\mathcal{G}}_B$ and ${\mathcal{G}}_C$, when calculating the successful transmission probability $p^A$ of group ${\mathcal{G}}_A$, using only the information from these three groups, according to Equation (5), $p^A$ is given by

$$p^A=\exp (-{\displaystyle \frac{n^A\lambda q^A}{\lambda +p^A{q}^A}})(1-(1-\exp (-{\displaystyle \frac{n^B\lambda q^B}{\lambda +p^B{q}^B}}))(1-\exp (-{\displaystyle \frac{n^C\lambda q^C}{\lambda +p^C{q}^C}}))).$$

(15)

The PAoI optimization is confined to these three groups:

$$A={\displaystyle \frac{n^A{A}_A+n^B{A}_B+n^C{A}_C}{n^A+n^B+n^C}}.$$

(16)

The algorithm initializes the particle swarm at the start. During each iteration, each group determines its local optimal position. For group ${\mathcal{G}}_A$, the information from groups ${\mathcal{G}}_B$ and ${\mathcal{G}}_C$ are combined. The PAoI is computed for all three groups, and the position minimizing PAoI is selected. This process is repeated for all groups to obtain the optimal channel access probability vector. When group ${\mathcal{G}}_A$ runs the PSO under local information, the update rule becomes

$${\mathit{v}}_{k,A}^{(i+1)}={\omega }^{(i)}\cdot {\mathit{v}}_{k,A}^{(i)}+c_1{r}_{1,g}^{(i)}\cdot ({\mathit{b}}_{k,A}^{(i)}-{\mathit{q}}_{k,A}^{(i)})+c_2{r}_{2,g}^{(i)}\cdot ({\mathit{d}}_A^{(i)}-{\mathit{q}}_{k,A}^{(i)}),$$

(17)

where ${\mathit{b}}_k^{(i)}$ represents the best-experience position of the particle itself, while ${\mathit{d}}_A^{(i)}$ denotes the local optimal position of the group, selected from historical optima that minimize local PAoI. The inertia weight calculation and parameter settings are identical to those in Table 1.

Compared to the global PSO framework, which depends on centralized information aggregation and coordination via a CPU, the local PSO algorithm functions in a fully distributed manner. Each group independently executes its optimization process by utilizing only topology and access information from its neighboring groups. No global network state is required, and no signaling is exchanged with a centralized controller. This decentralized structure reduces signaling overhead and enhances the scalability of the algorithm.

Algorithm 2 PAoI Optimization Algorithm Based on Local PSO

$\mathbf{Input}: \mathrm{Network} \mathrm{parameters} n^g,g=\{1,2,\dots G\}$,   $\lambda$$; \mathrm{algorithm} \mathrm{setting} \mathrm{parameters} K, c_1$$, c_2$$,{\mathit{v}}_{min}$$, {\mathit{v}}_{max}$$, {\mathit{q}}_{min}$$, {\mathit{q}}_{max}$$, {\omega }_{min}$$, {\omega }_{max}$ , Imax. $\mathbf{Output}: \mathrm{Optimal} \mathrm{channel} \mathrm{access} \mathrm{probability} {\mathit{d}}^{(I_{max})}=\left[q^{(1)},q^{(2)},\dots ,q^{(G)}\right]$

1: for each particle k = 1 to K do

2:   $\mathrm{Initialize} \mathrm{position} {\mathit{q}}_k^{(1)}$$\mathrm{and} \mathrm{velocity} {\mathit{v}}_k^{(1)}$

3:   ${\mathit{b}}_k^{(1)}={\mathit{q}}_k^{(1)}$

4: end for

5: $\mathrm{Initialize} {\mathit{d}}^{(1)}$ according to (13)

6: Set the initial iteration value i = 1

7: $\mathbf{for} \mathrm{each} \mathrm{iteration} \mathrm{round} i<I_{max}$ do

8:   for each particle k = 1 to K do

9:    for each element g = 1 to G do

10:     $\mathrm{Update} \mathrm{velocity} {\mathit{v}}_{k,g}^{(i+1)}$ according to (14) and (17)

11:     $\mathrm{Constrain} \mathrm{the} \mathrm{velocity} {\mathit{v}}_{k,g}^{(i+1)}$$\mathrm{within} \mathrm{the} \mathrm{range} [{\mathit{v}}_{min},{\mathit{v}}_{max}]$

12:     $\mathrm{Update} \mathrm{position} {\mathit{q}}_{k,g}^{(i+1)}={\mathit{v}}_{k,g}^{(i+1)}+{\mathit{q}}_{k,g}^{(i)}$

13:     $\mathrm{Constrain} \mathrm{the} \mathrm{position} {\mathit{q}}_{k,g}^{(i+1)}$$\mathrm{within} \mathrm{the} \mathrm{range} [{\mathit{q}}_{min},{\mathit{q}}_{max}]$

14:      Calculate the PAoI according to (16)

15:     $\mathrm{Update} {\mathit{b}}_k^{(i+1)}$$\mathrm{and} A_{k,g}^{(i+1)}$ according to (13) and (16)

16:   end for

17:  $\mathrm{Update} {\mathit{d}}^{(i+1)}$ according to (13)

18:   i = i + 1

19: end for

20: end for

5. Simulation Results and Analysis

This section presents simulation results to verify the correctness of the theoretical analysis and the effectiveness of the algorithm.

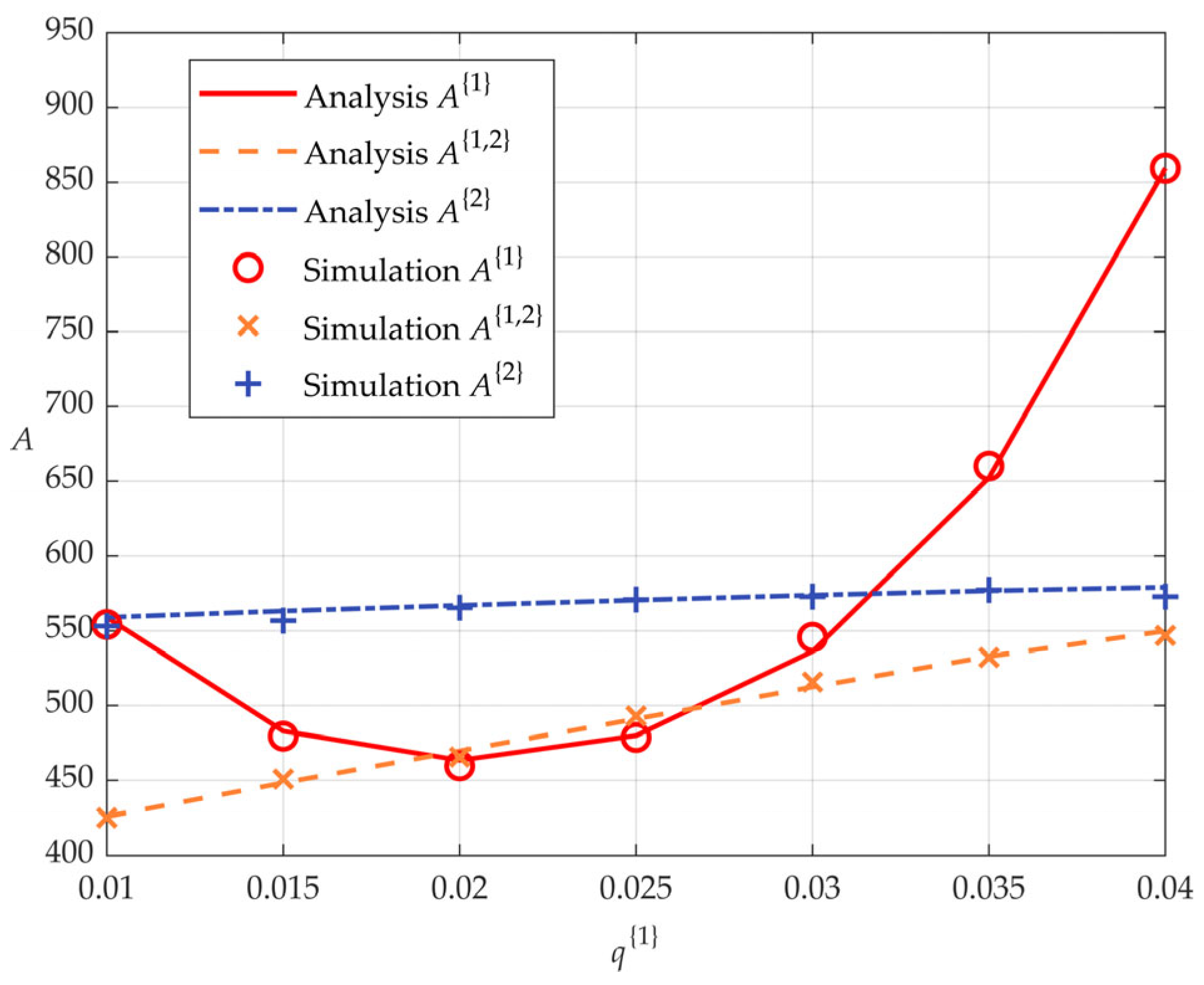
5.1. Validation of Theoretical Analysis

To optimize the network-wide average PAoI, we first verify the impact of channel access probability q on PAoI across groups. Consider a two-AP scenario: non-overlapping groups ${\mathcal{G}}_{\left\{1\right\}}$ and ${\mathcal{G}}_{\left\{2\right\}}$ each contain 75 MTDs, while the intermediate overlapping group ${\mathcal{G}}_{\{1,2\}}$ contains 50 MTDs. All groups have a packet arrival rate of 0.01. The initial value of $q^{\left\{1\right\}}$ is set to 0.01 and incremented by 0.005 in each step, while $q^{\{1,2\}}$ and $q^{\left\{2\right\}}$ remain fixed at 0.01. The simulation runs for 7 cycles.

As shown in Figure 4, as $q^{\left\{1\right\}}$ gradually increases, the PAoI for ${\mathcal{G}}_{\left\{1\right\}}$ initially decreases and then starts to rise. The optimal $q^{\left\{1\right\}}$ lies between 0.015 and 0.025, indicating potential optimization opportunities in the network. Furthermore, when $q^{\left\{1\right\}}$ varies, the adjacent group ${\mathcal{G}}_{\{1,2\}}$ is greatly affected by it, while the remote group ${\mathcal{G}}_{\left\{2\right\}}$ shows smaller variations. This observation validates the spatial attenuation characteristics of cross-group interference, where interference effects diminish with distance across groups.

5.2. Convergence Analysis

Figure 5 illustrates the convergence process of the global and local PSO algorithms in a network consisting of two APs. The total number of MTDs is set to 200, and the number of MTDs in the intermediate overlapping group is configured as 10, 40, and 80, respectively. The data packet arrival rate is uniformly set to 0.01. The figure records the optimal network-wide average PAoI obtained in each iteration of the PSO algorithms. Meanwhile, to verify the effectiveness of the algorithm, an exhaustive algorithm is used to traverse all possible channel access probability combinations, calculate the corresponding PAoI, and select the minimum value as the theoretical optimal solution. The optimal network-wide average PAoI obtained through the traversal search is also displayed in the same figure. It can be seen that the two algorithms can converge quickly within a limited number of iteration rounds and output an approximate optimal solution to the problem.

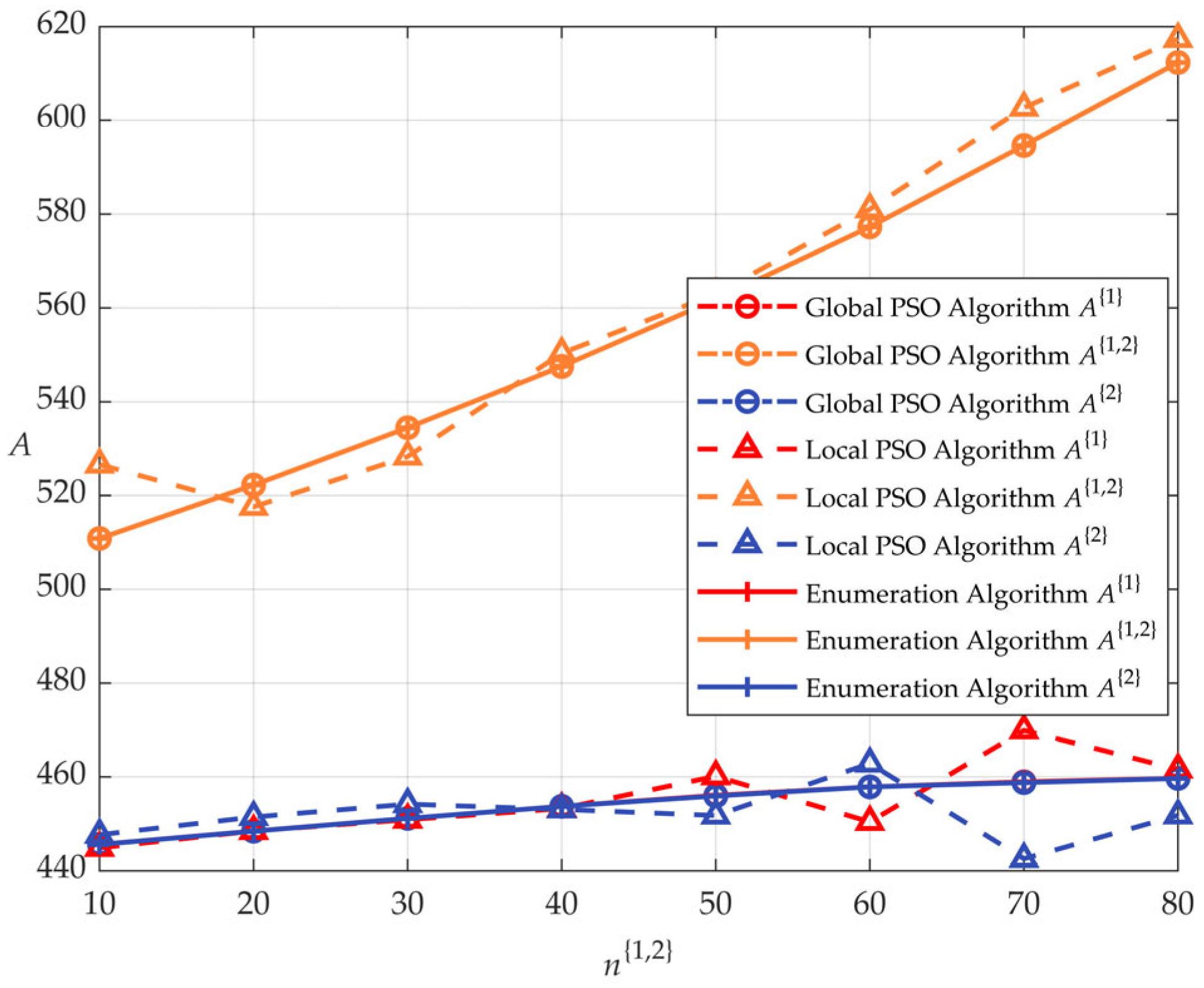
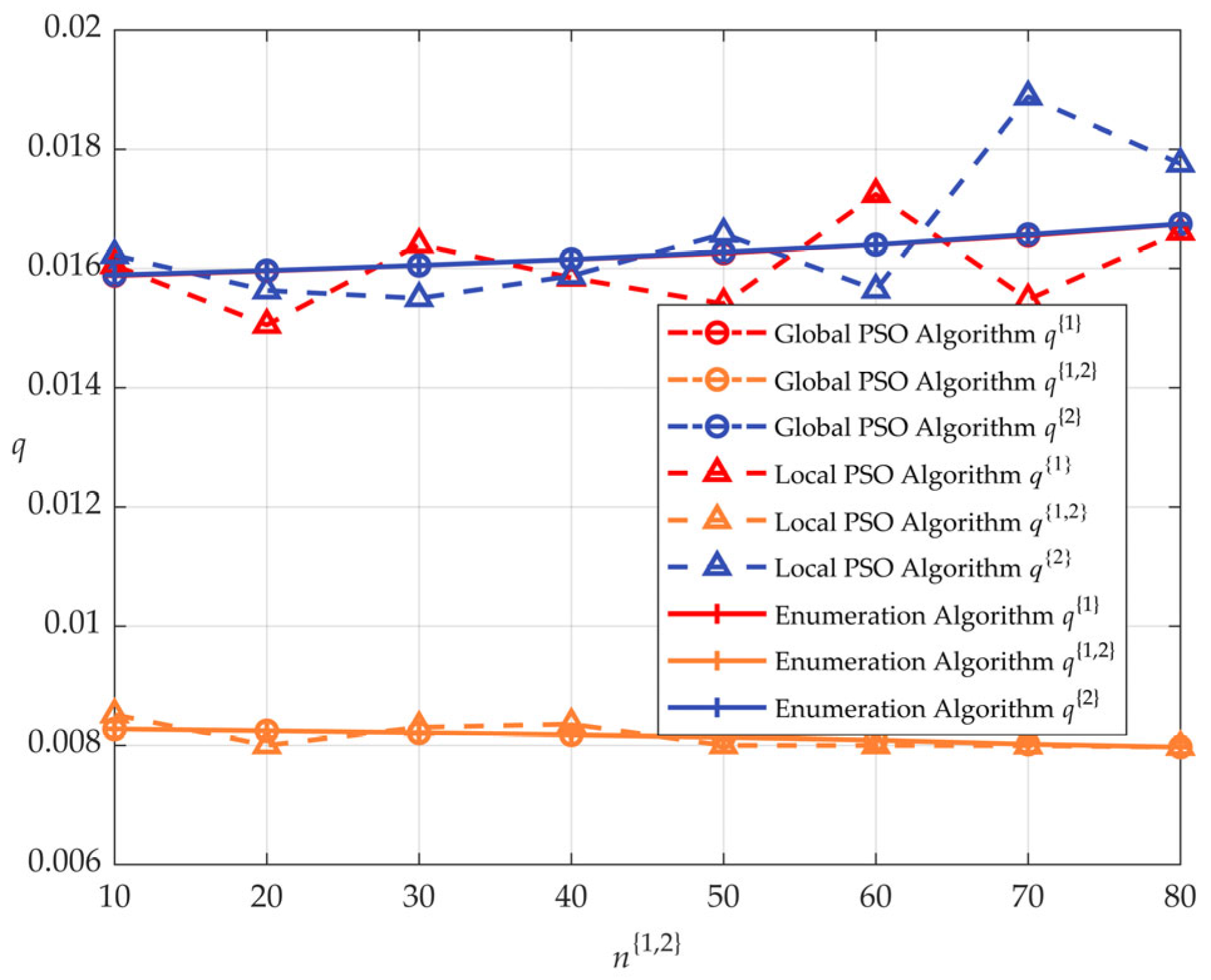
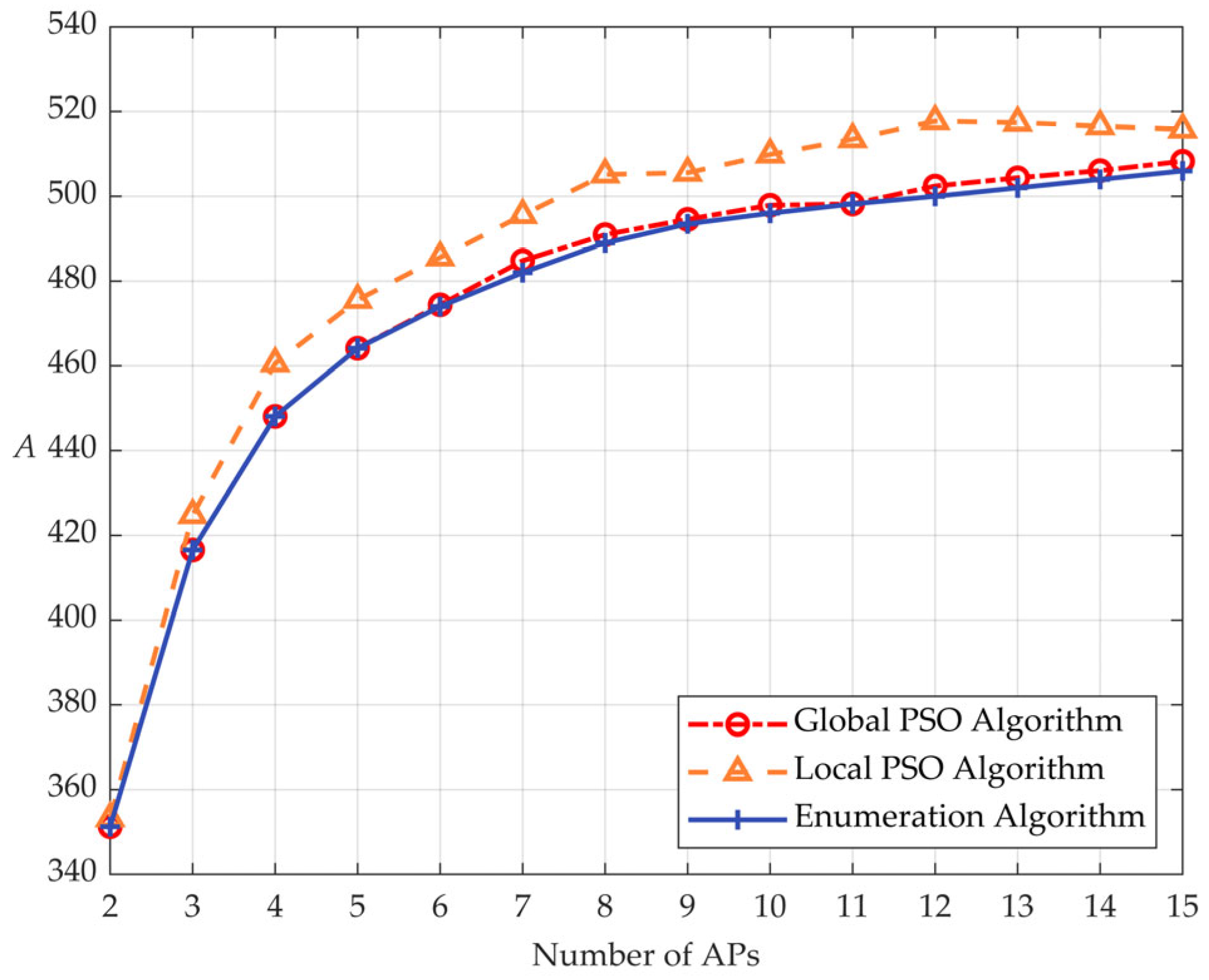
5.3. Algorithm Effectiveness and Performance Comparison

To further evaluate the effectiveness of the proposed algorithms, Figure 6, Figure 7 and Figure 8 present a detailed comparison of the network-wide average PAoI, the group-wise PAoI, and the channel access probabilities under varying MTD distributions. Specifically, the number of MTDs in the intermediate cross-coverage group ${\mathcal{G}}_{\{1,2\}}$ is varied from 10 to 80 in increments of 10, with all other parameters kept constant.

As can be seen from Figure 6, the PAoI optimization effect of the global PSO algorithm basically coincides with that of the enumeration algorithm and can effectively approach the theoretical optimal solution. However, the average PAoI under the local PSO algorithm is only slightly higher than that of the global PSO algorithm, and the error margin does not significantly increase with the increase in the number of MTDs in group ${\mathcal{G}}_{\{1,2\}}$, indicating that it can achieve performance similar to that of the global PSO and has good robustness against network topology changes. In addition to the three optimization algorithms, we present a baseline case where all groups adopt a fixed channel access probability of 0.01, regardless of network size or interference. The results clearly show that fixed access values lead to significantly higher PAoI, while all three optimization methods maintain consistently lower and more stable performance across different scenarios.

As can be seen from Figure 7, as $n^{\{1,2\}}$ gradually increases, the PAoI of ${\mathcal{G}}_{\{1,2\}}$ significantly rises, while the growth of PAoI in ${\mathcal{G}}_{\left\{1\right\}}$ and ${\mathcal{G}}_{\left\{2\right\}}$ is more gentle. Further combined with Figure 8, it can be seen that when the PAoI of ${\mathcal{G}}_{\{1,2\}}$ significantly rises, its channel access probability slowly decreases; on the contrary, the channel access probabilities of the other two groups gradually increase. This difference originates from the dynamic adjustment mechanism of the algorithm for channel access probability. As the load of ${\mathcal{G}}_{\{1,2\}}$ increases, the internal transmission conflicts intensify, and at the same time, the interference intensity on ${\mathcal{G}}_{\left\{1\right\}}$ and ${\mathcal{G}}_{\left\{2\right\}}$ increases. To alleviate the conflicts, the algorithm gradually reduces the channel access probability of this group. However, due to the nonlinear growth of the conflict rate caused by the increase in the number of MTDs, its PAoI ultimately rises significantly. While ${\mathcal{G}}_{\left\{1\right\}}$ and ${\mathcal{G}}_{\left\{2\right\}}$, by moderately increasing the access probability, under the combined effect of their own loads gradually decreasing and cross-group interference being locally alleviated, achieve relatively stable performance.

Because the local PSO algorithm can only obtain local topology information, although the influence of the distant group on this group is small, this influence still exists. This makes the local PSO algorithm unable to converge to the optimal solution, further causing the PAoI and channel access probability of each group to fluctuate with the change in the number of MTDs in the cross-coverage group. However, the fluctuation trends and amplitudes of the PAoI, as well as channel access probability of MTDs in the same group, are basically consistent with those of the global PSO algorithm. This indicates that the action law of the local PSO algorithm on each group of MTDs is consistent with that of the global PSO algorithm, and it will not locally change the performance of any group of MTDs or channel access behavior.

Figure 9 further considers the average PAoI of the entire network for the two algorithms when the number of APs changes. The simulation scenario includes multiple APs, with each logical group containing 50 MTDs, the number of APs taking 2, 3, …, 15, and the packet arrival rate being 0.01 each. As with the result in Figure 6, the global PSO algorithm can achieve an effect similar to the exhaustive algorithm and can converge to the optimal solution. Under the local PSO algorithm, the average PAoI of the entire network is only slightly higher than that of the global PSO algorithm, and the error margin does not significantly change with the change in network scale. In summary, the local PSO algorithm can achieve PAoI performance close to that of the global PSO algorithm without the need for global topology information.

6. Conclusions

This paper addresses the PAoI optimization problem in grant-free CF-RAN with mMTC services. We derive the PAoI expression by constructing a low-complexity and scalable topology model, and we propose channel access probability adjustment methods based on global/local PSO algorithms. Experimental results demonstrate that dynamically adjusting channel access probabilities significantly reduces network-wide PAoI. The global PSO algorithm achieves the optimal solution through global topology information exchange, but its signaling overhead grows substantially with network scale. Thus, it is more suitable for static or small-scale networks with fixed AP locations and controllable user density, where fine-grained channel access optimization enhances information freshness. In contrast, the local PSO algorithm, relying on information exchange among neighboring APs and performing independent optimization across different regions, confines signaling overhead within collaborative groups. While reducing signaling overhead, it effectively optimizes PAoI, making it applicable to large-scale access scenarios with wide coverage. Furthermore, this study is conducted under idealized conditions. Future work will explore more realistic system scenarios, including user mobility, non-ideal fronthaul links, and heterogeneous service demands. Additionally, promising directions such as online learning under dynamic topologies, joint optimization of PAoI and energy consumption, and experimental validation based on platforms like Open Radio Access Network are worth investigating in follow-up research.