Cluster Voltage Control of Active Distribution Networks Considering Power Deficit and Resource Allocation
Abstract
1. Introduction
2. Cluster Partitioning and Pilot Bus
2.1. Electrical Modularity
2.2. Design of Voltage Regulation Resource and Power Metrics
2.2.1. Voltage Regulation Resource Allocation
2.2.2. Active Power Coverage Metric
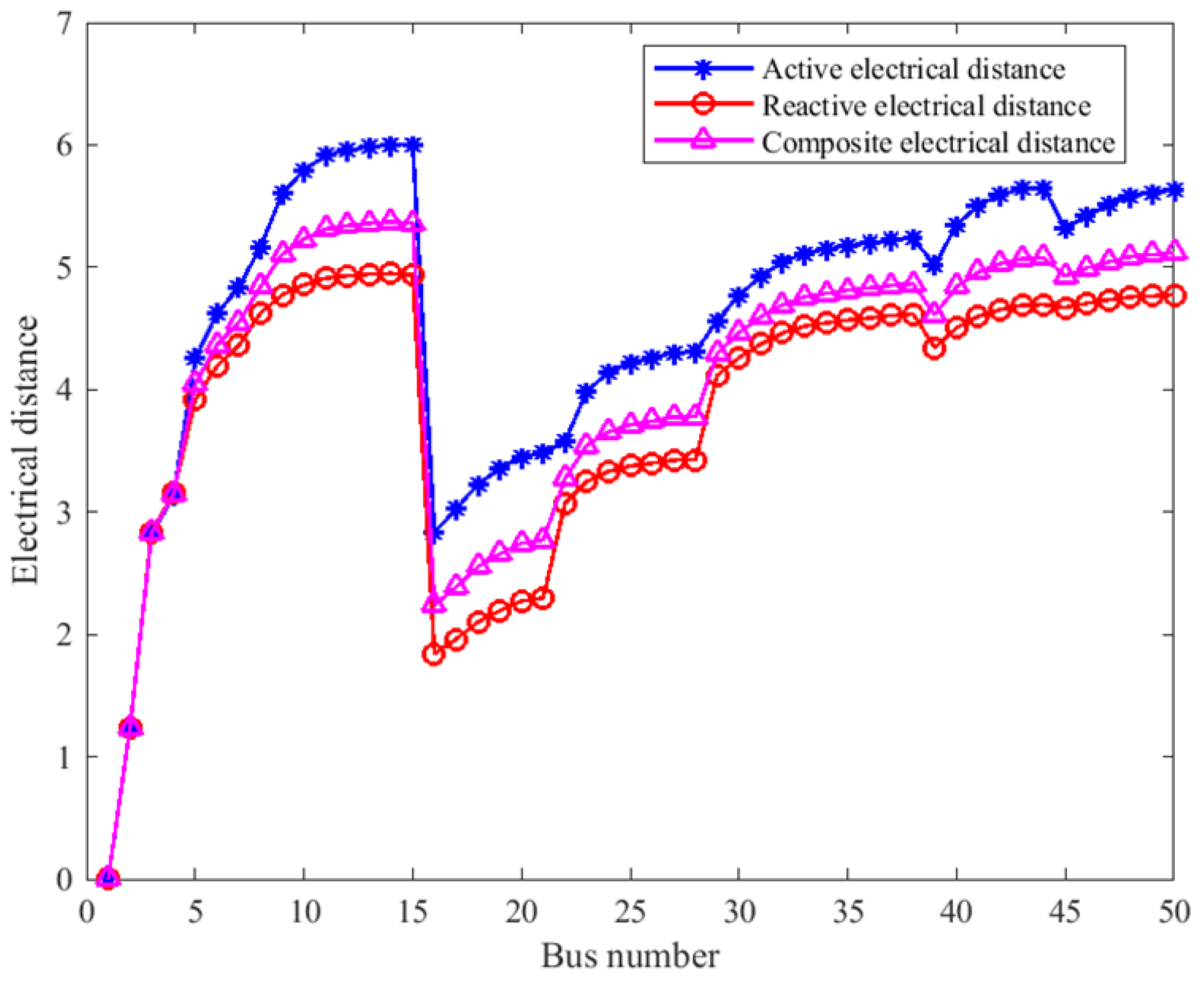
2.3. Communication Distance Metric
2.4. Comprehensive Evaluation Metric
2.5. Selection of Pilot Bus
3. Dynamic Cluster Control Strategy for Active Distribution Networks Based on NSGA-II
3.1. Active and Reactive Power Coordination Control
3.1.1. Objective Function
3.1.2. Constraints
3.2. Adaptive Correction Mechanisms Considering Uncertainty
3.2.1. Source Load Prediction Error Model
3.2.2. Uncertainty Model
3.3. NSGA-II Model Solution
4. Case Study
4.1. Case Overview and Parameter Settings
4.2. Cluster Partitioning Results
4.3. Multi-Objective Optimization Control Results
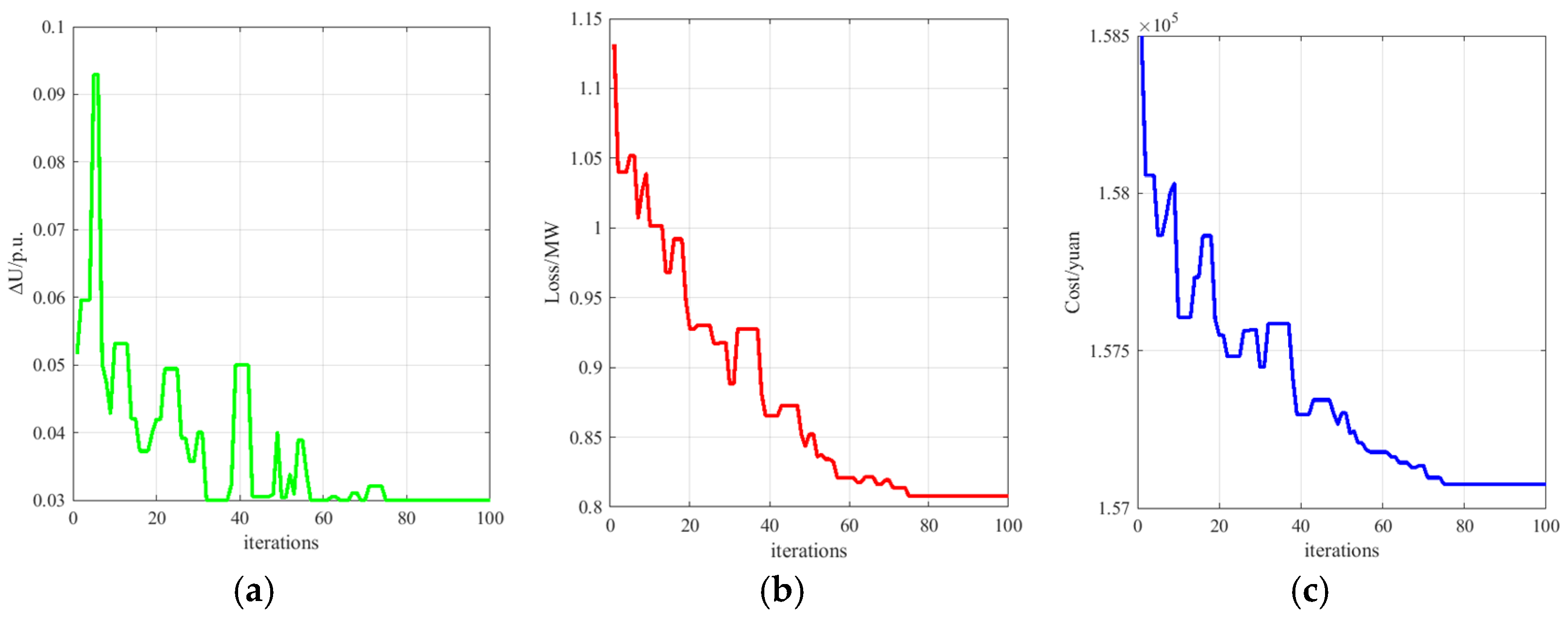
4.3.1. Analysis of NSGA-II Algorithm Results
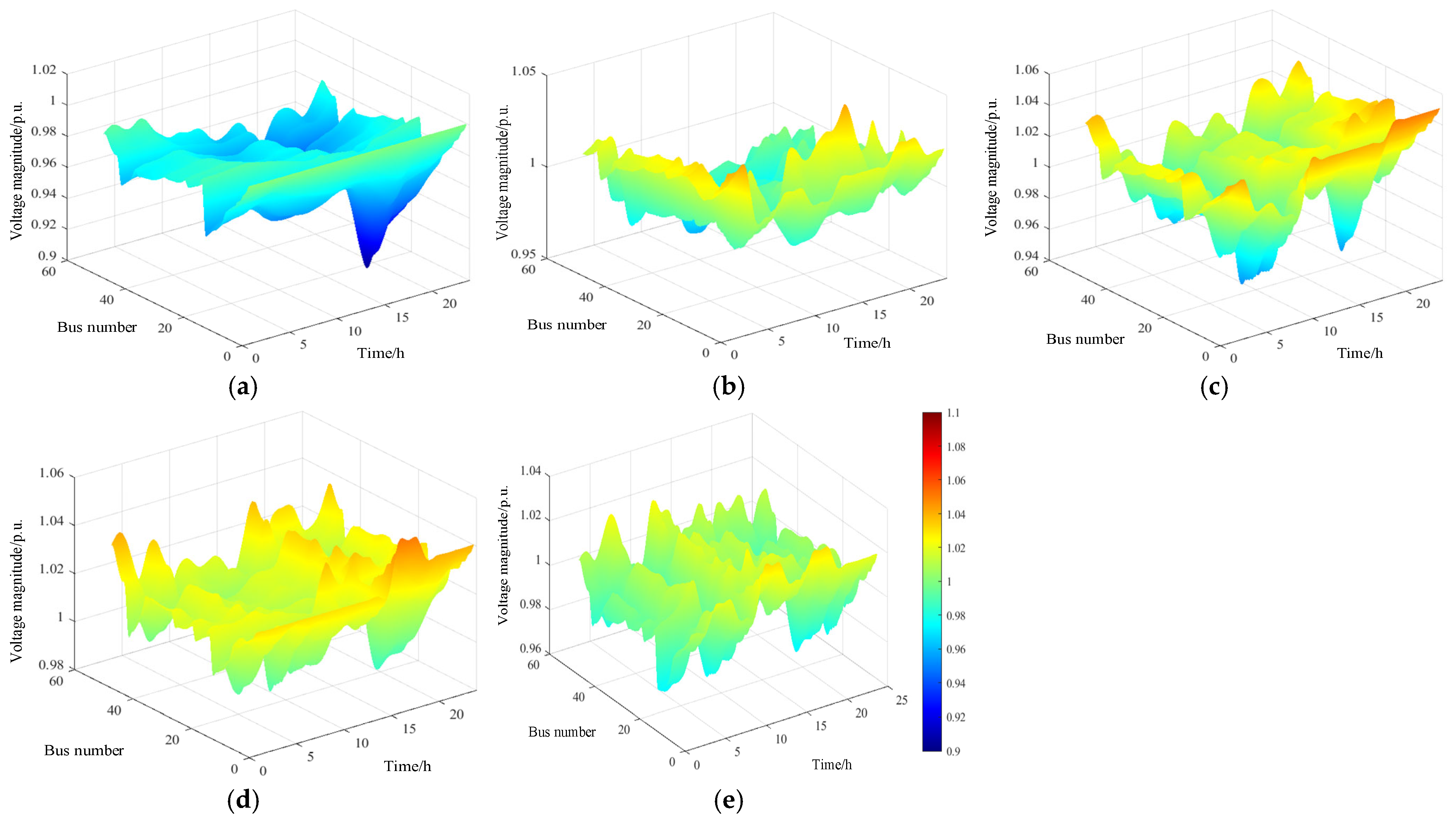
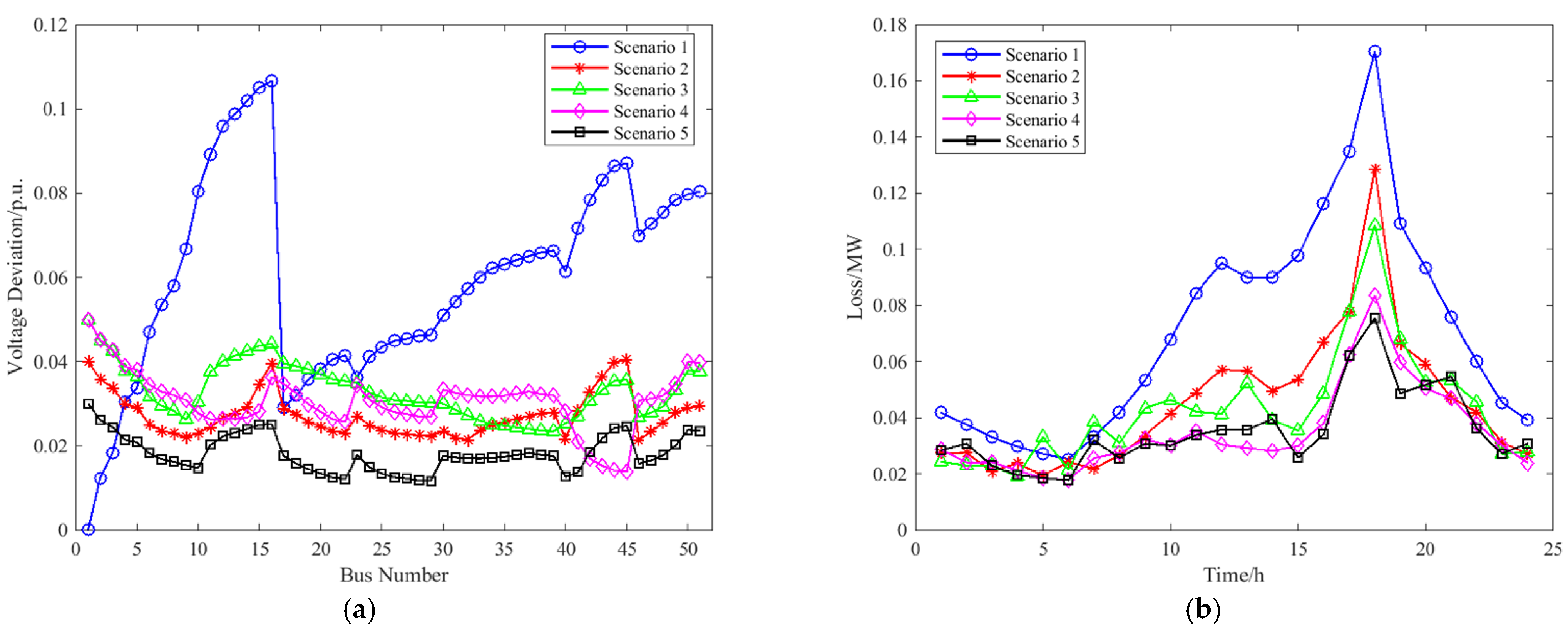
4.3.2. Multi-Scenario Safety Comparison
- (1)
- Scenario 1: Only DGs are employed for the network.
- (2)
- Scenario 2: Centralized control with DGs and resources (see Appendix A, Figure A5a).
- (3)
- Scenario 3: Active power regulation with DGs and ESS units (see Appendix A, Figure A5b).
- (4)
- Scenario 4: Reactive power regulation with DGs, SVCs, and CBs (see Appendix A, Figure A5c).
- (5)
- Scenario 5: Active and reactive power cluster voltage control (see Figure 1).
4.3.3. Multi-Scenario Economic Comparison
4.4. Uncertainty Impact Analysis
5. Conclusions
- (1)
- An improved clustering optimization method is proposed. Voltage regulation resources are introduced to address power deficit risk and uneven resource allocation in the distribution network. The results show that the proposed clustering partitioning metric makes a more uniform power distribution with lower margin requirements.
- (2)
- In the cluster voltage control model, the NSGA-II algorithm shows algorithmic superiority over the next best MOEA/D algorithm by reducing the network loss and power consumption cost by 8.7 kW and RMB 2550, respectively.
- (3)
- In multi-scenario comparative analyses, the full-day voltage deviation is reduced from 0.085 p.u. under centralized control to 0.062 p.u. Network losses and power consumption costs are reduced by 27.41% and 0.72%, respectively. This approach effectively suppresses voltage fluctuations and lowers both network losses and energy costs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A


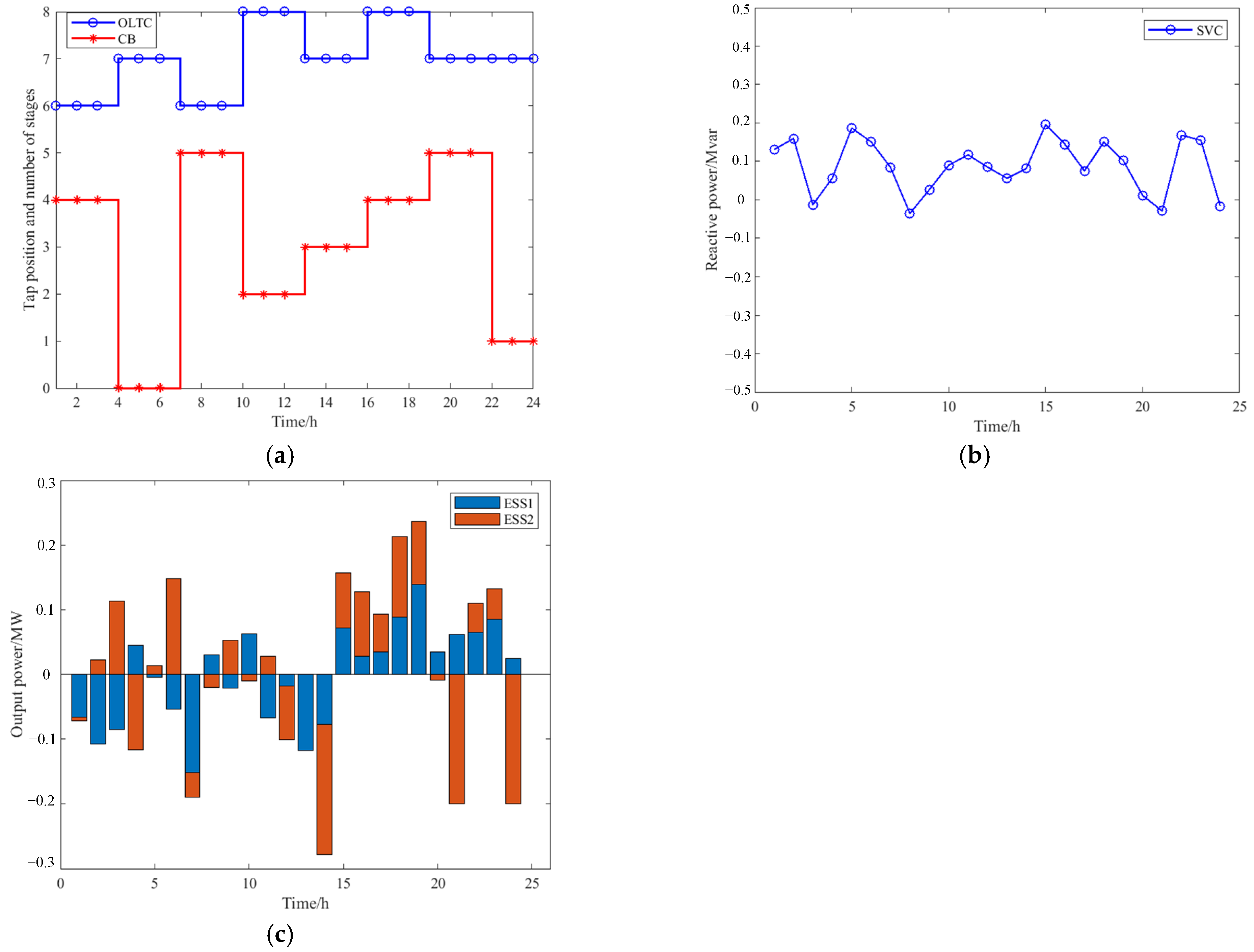

References
- Liang, Z.; Ye, C.; Liu, Z.; Li, M.; Wang, P.; Zhao, J. Grid-connected scheduling and control of distributed generations clusters: Architecture and key technologies. Power Syst. Technol. 2021, 45, 3791–3802. [Google Scholar]
- Chamana, M.; Chowdhury, B.H.; Jahanbakhsh, F. Distributed Control of Voltage Regulating Devices in the Presence of High PV Penetration to Mitigate Ramp-Rate Issues. IEEE Trans. Smart Grid 2018, 9, 1086–1095. [Google Scholar] [CrossRef]
- Xu, J.; Cao, Q. Research on the status and application of distributed photovoltaic grid-connected power generation in China. Energy Conserv. 2020, 6, 45–48. [Google Scholar]
- Liu, Z.; Zhao, S.; Luo, X.; Huang, Y.; Gu, R.; Li, J.; Li, L. Two-layer energy dispatching and collaborative optimization of regional integrated energy system considering stakeholders game and flexible load management. Appl. Energy. 2025, 379, 124918. [Google Scholar] [CrossRef]
- Su, Z.; Zheng, G.; Wang, G.; Mu, Y.; Fu, J.; Li, P. Multi-objective optimal planning study of integrated regional energy system considering source-load forecasting uncertainty. Energy 2025, 319, 134861. [Google Scholar] [CrossRef]
- Ding, T.; Li, C.; Yang, Y.; Jiang, J.; Bie, Z.; Frede, B. A two-stage robust optimization for centralized-optimal dispatch of photovoltaic inverters in active distribution networks. IEEE Trans. Sustain. Energy 2016, 8, 744–754. [Google Scholar] [CrossRef]
- Florez, H.; López, G.; Carreo-Franco, E.M.; Muñoz-Galeano, N.; López-Lezama, J.M. Application of intelligent systems in volt-var centralized control in modern distribution systems of electrical energy. Electronics 2022, 11, 446. [Google Scholar] [CrossRef]
- Samende, C.; Bhagavathy, S.; McCulloch, M. Power loss minimization of off-grid solar DC nano-grids-part I: Centralized control algorithm. IEEE Trans. Smart Grid 2021, 12, 4715–4725. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Wang, C.; Su, Y.; Wang, Y.; Dai, Y. Distributed Chance-Constrained Optimal Dispatch for Integrated Energy System With Electro-Thermal Couple and Wind-Storage Coordination. IEEE Trans. Ind. Appl. 2025, 61, 833–846. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, Y.; Wang, Q.; Liu, F.; Zhu, L. Fast Power Grid Partition for Voltage Control With Balanced-Depth-Based Community Detection Algorithm. IEEE Trans. Power Syst. 2022, 37, 1612–1622. [Google Scholar] [CrossRef]
- Hu, X.; Yin, R.; Shi, M.; Zhu, P.; Li, T. Distributed Photovoltaic Cluster Partition and Reactive Power Optimization Strategy Based on Improved Particle Swarm Optimization Algorithm. Power Capacitor React. Power Compens. 2021, 42, 14–21. [Google Scholar]
- Ge, J.; Liu, Y.; Pang, D.; Wang, C.; Wang, Z.; Liu, Z. Cluster Division Voltage Control Strategy of Photovoltaic Distribution Network with High Permeability. High Volt. Eng. 2024, 50, 74–82. [Google Scholar]
- Li, X.; Xie, J.; Zhang, S. A Two-Stage Robust Strategy for Voltage/Var Control in Distribution Networks Based on Cluster Partitioning. Proc. CSEE 2024, 1–14. Available online: https://link.cnki.net/urlid/11.2107.tm.20240930.1418.003 (accessed on 10 May 2025).
- Ding, M.; Liu, X.; Bi, R.; Hu, D.; Ye, L.; Zhang, J. Method for cluster partition of high-penetration distributed generators based on comprehensive performance index. Autom. Electr. Power Syst. 2018, 42, 47–52. [Google Scholar]
- Li, C.; Dong, Z.; Li, J.; Zhang, H.; Jin, Q.; Qian, K. Control strategy of voltage regulation for distributed energy storage cluster in distribution network. Autom. Electr. Power Syst. 2021, 45, 133–141. [Google Scholar]
- Kebebew, A.; Ababu, Y.; Mulugeta, L. Towards Developing Enhanced Cluster-Based QoS-Aware Routing in MANET. J. Comput. Netw. Commun. 2020, 2020, 5481916. [Google Scholar]
- Li, P.; Zhang, C.; Wu, Z.; Xu, Y.; Hu, M.; Dong, Z. Distributed adaptive robust voltage/var control with network partition in active distribution networks. IEEE Trans. Smart Grid 2020, 11, 2245–2256. [Google Scholar] [CrossRef]
- Qi, Y.; Shang, X.; Nie, J.; Huo, X.; Wu, B.; Su, W. Optimization of CCHP micro-grid operation based on improved multi-ob- jectivegrey wolf algorithm. Electr. Meas. Instrum. 2022, 59, 12–19. [Google Scholar]
- Hou, S.; Fu, A.; Duque, E.M.; Palensky, P.; Chen, Q.; Vergara, P.P. DistFlow Safe Reinforcement Learning Algorithm for Voltage Magnitude Regulation in Distribution Networks. J. Mod. Power Syst. Clean Energy 2025, 13, 300–311. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Z.; Wang, Z.; Pang, D.; Ge, J. Multi-time Scale Distributed Voltage Optimization for High Penetration Photovoltaic AC/DC Hybrid Distribution Networks. High Volt. Eng. 2024, 1–15. [Google Scholar] [CrossRef]
- He, Y.; Li, Y.; Liu, J.; Xiang, X. A Two-Stage Fault Reconfiguration Strategy for Distribution Networks with High Penetration of Distributed Generators. Electronics 2025, 14, 1872. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Gampa, S.; Das, D. Optimum placement and sizing of DGs considering average hourly variations of load. Int. J. Electr. Power Energy Syst. 2015, 66, 25–40. [Google Scholar] [CrossRef]
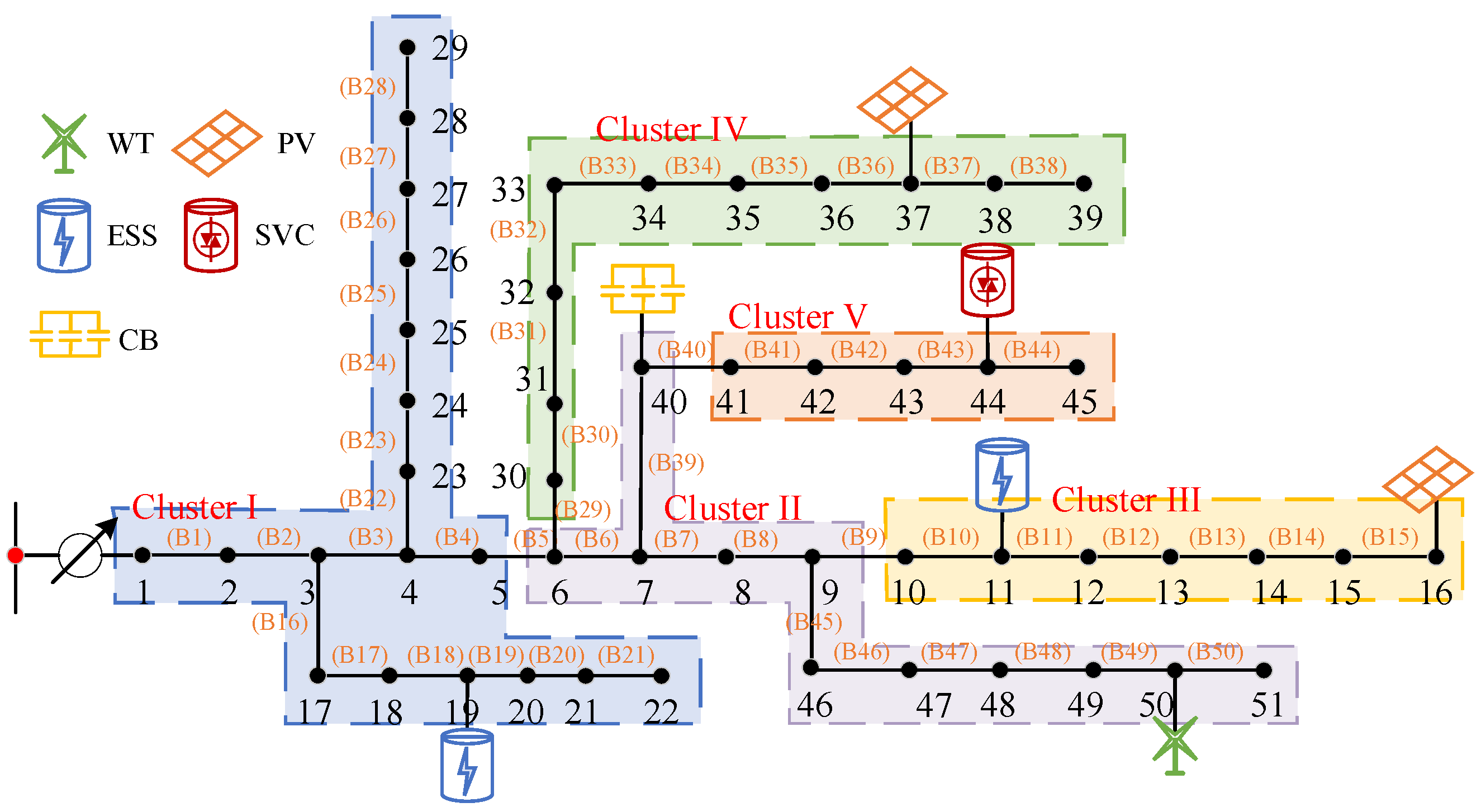

| Cluster ID | Bus Numbers | Reactive Power Margin/kvar | Active Power Margin/kW | Reactive Power Coverage | Active Power Coverage | Modularity Metric | Communication Distance Metric | |
|---|---|---|---|---|---|---|---|---|
| Comprehensive evaluation method | 1 | 1–5, 17–29 | −539 | −650 | 0.5052 | 0.3849 | 0.4464 | 0.2001 |
| 2 | 6–9, 40–51 | 217 | −148 | |||||
| 3 | 10–16 | 45 | 210 | |||||
| 4 | 30–39 | 57 | 23 | |||||
| 5 | 41–45 | 101 | −298 | |||||
| The literature [11] | 1 | 1–6, 17–30 | −287 | −928 | 0.4513 | 0.3410 | 0.4294 | 0.1719 |
| 2 | 7–16, 40–51 | −20 | −100 | |||||
| 3 | 31–39 | 337 | 263 | |||||
| 4 | 41–45 | −149 | −98 |
| Algorithm | Voltage Deviation (p.u.) | Network Losses (MW) | Power Consumption Cost (×104 CNY) |
|---|---|---|---|
| MOPSO | 0.05 | 0.8310 | 16.101 |
| MOEA/D | 0.03 | 0.8164 | 15.963 |
| NSGA-II | 0.03 | 0.8077 | 15.708 |
| Scenario 2 | Scenario 3 | Scenario 4 | Scenario 5 | |
|---|---|---|---|---|
| Power consumption cost (×104 CNY) | 15.821 | 15.753 | 15.723 | 15.708 |
| Operating cost (×104 CNY) | 1.857 | 1.826 | 1.815 | 1.807 |
| Network Losses (MWh) | Average Voltage Deviation (p.u.) | Power Consumption Cost (×104 CNY) | |
|---|---|---|---|
| Case1 | 0.1035 | 0.0204 | 2.0227 |
| Case2 | 0.0810 | 0.0167 | 1.8346 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, X.; Meng, P.; Zhou, D.; Tang, J.; Xiong, J.; Zou, Y. Cluster Voltage Control of Active Distribution Networks Considering Power Deficit and Resource Allocation. Electronics 2025, 14, 2639. https://doi.org/10.3390/electronics14132639
Wan X, Meng P, Zhou D, Tang J, Xiong J, Zou Y. Cluster Voltage Control of Active Distribution Networks Considering Power Deficit and Resource Allocation. Electronics. 2025; 14(13):2639. https://doi.org/10.3390/electronics14132639
Chicago/Turabian StyleWan, Xinglin, Peipei Meng, Dongguo Zhou, Jinrui Tang, Jianqiang Xiong, and Yongle Zou. 2025. "Cluster Voltage Control of Active Distribution Networks Considering Power Deficit and Resource Allocation" Electronics 14, no. 13: 2639. https://doi.org/10.3390/electronics14132639
APA StyleWan, X., Meng, P., Zhou, D., Tang, J., Xiong, J., & Zou, Y. (2025). Cluster Voltage Control of Active Distribution Networks Considering Power Deficit and Resource Allocation. Electronics, 14(13), 2639. https://doi.org/10.3390/electronics14132639







