Federated Learning-Based Location Similarity Model for Location Privacy Preserving Recommendation
Abstract
1. Introduction
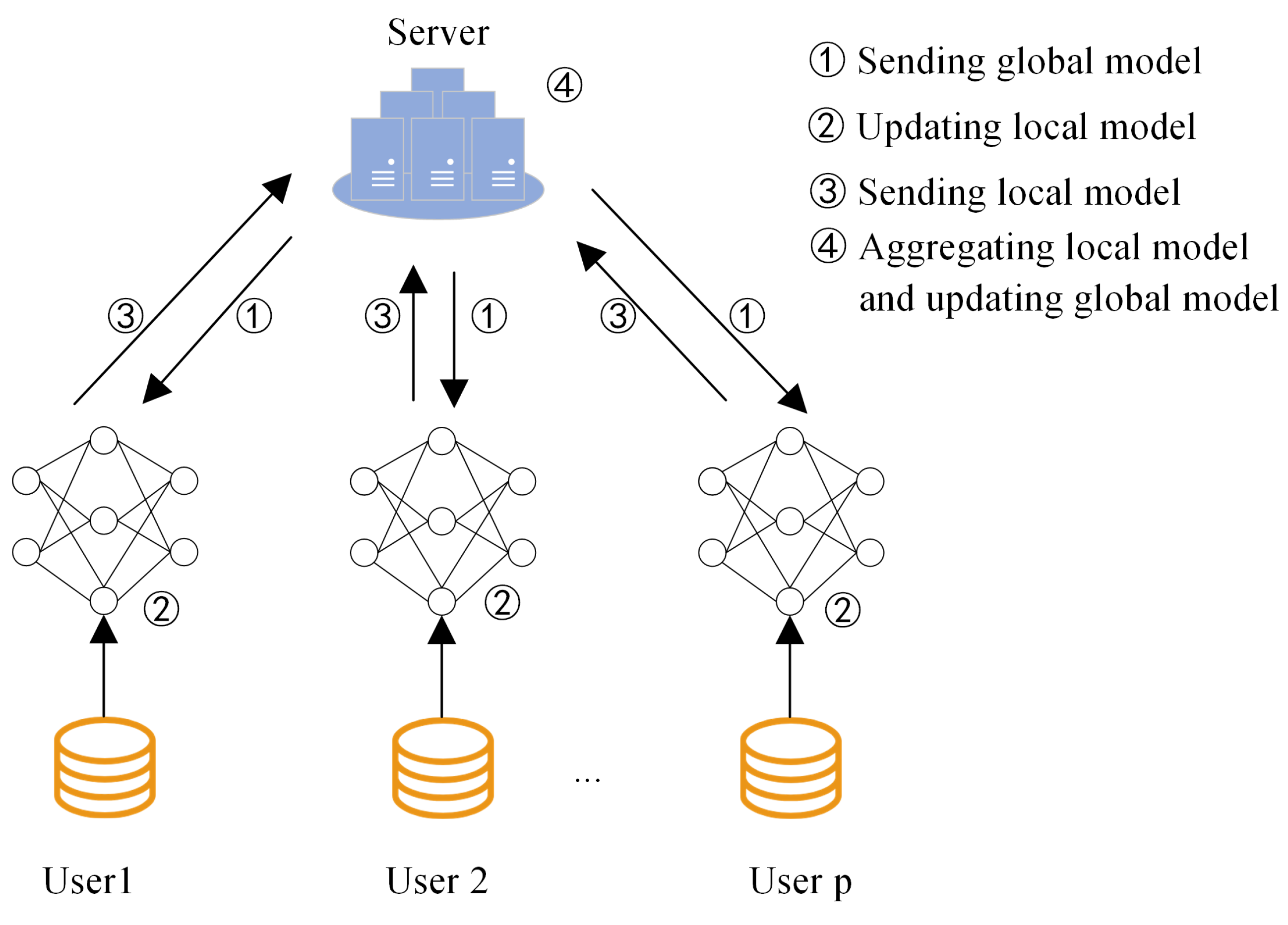
- The location similarity model based on federated learning is constructed to provide personalized location-related services for target users. The model will be employed on the client side in order to capture the subtle differences between locations and enhance the performance of location recommendations. Federated learning is utilized on the server side to ensure data privacy while aggregating the model.
- The clustering-based client selected algorithm is proposed to further mitigate the impact of non-IID data on the framework of location recommendation. The algorithm performs client clustering and combines client selection based on local loss and model similarity. Additionally, the penalty term is utilized in the client loss function to constrain the difference between the local model and the global model.
- Extensive experiments and analysis are conducted on two real datasets to validate the effectiveness of the proposed FedLSM-LPR scheme. The experimental results demonstrate that the performance is better than that of the other existing schemes.
2. Related Work
3. Preliminaries
3.1. Location-Based Similarity Model
3.2. Server Aggregation with REPAgg
3.3. Problem Definition
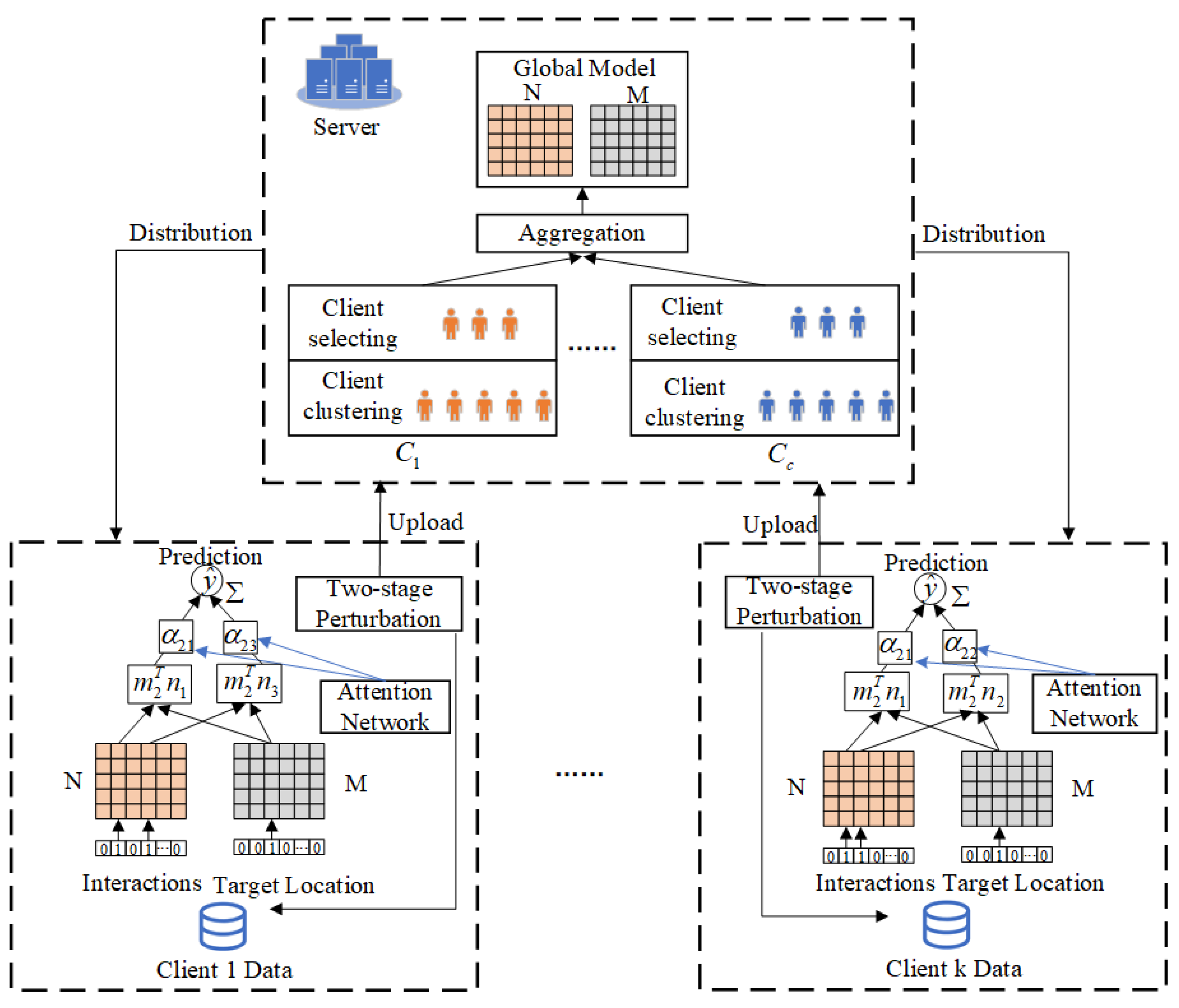
4. Proposed Framework
4.1. Model Overview
| Algorithm 1 FedLSM-LPR |
|
4.2. Client-Side Regularization
4.3. Clustering-Based Client-Selected REPAgg Aggregation Approach
- (i)
- Client Clustering
- (ii)
- Client Selection
| Algorithm 2 Client Selection |
|
- (iii)
- Model Aggregation
4.4. Two-Stage Perturbation
4.5. Privacy Analysis
5. Experiment
5.1. Experimental Settings
5.1.1. Dataset
5.1.2. Evaluation Metrics
5.1.3. Parameter Settings
5.1.4. Baseline Schemes
- MF-ALS [45]: This scheme builds on the traditional matrix factorization algorithm by considering the problem of modeling the user’s implicit feedback and using singular value decomposition inside the implicit feedback dataset.
- NAIS [39]: This scheme introduces an attention mechanism to compute the attention weights between locations, which improves the recommendation performance based on the location similarity model.
- FCF [28]: This scheme integrates CF and federated learning for the first time, and at the same time confirms the applicability of federated learning in the field of personalized recommendation, which lays the foundation for subsequent research.
- FedMF [29]: This scheme is a privacy-preserving recommendation system based on security matrix factorization, which protects the user’s privacy and security by using federated learning and homomorphic encryption.
- FedNCF [30]: This scheme uses neural CF to generate high-quality recommendations and employs SecAvg, a secure aggregation protocol, to protect the security of user privacy.
- FedBPR [46]: This scheme introduces a factorization model based on matrix factorization within the federated learning framework, allowing users to retain control over their data, thereby effectively enhancing data privacy protection.
- FedVAE [47]: This scheme combines a variational auto-encoder(VAE) with federated learning techniques to build a distributed CF recommendation system by learning deep feature representations of users and locations on individual clients.
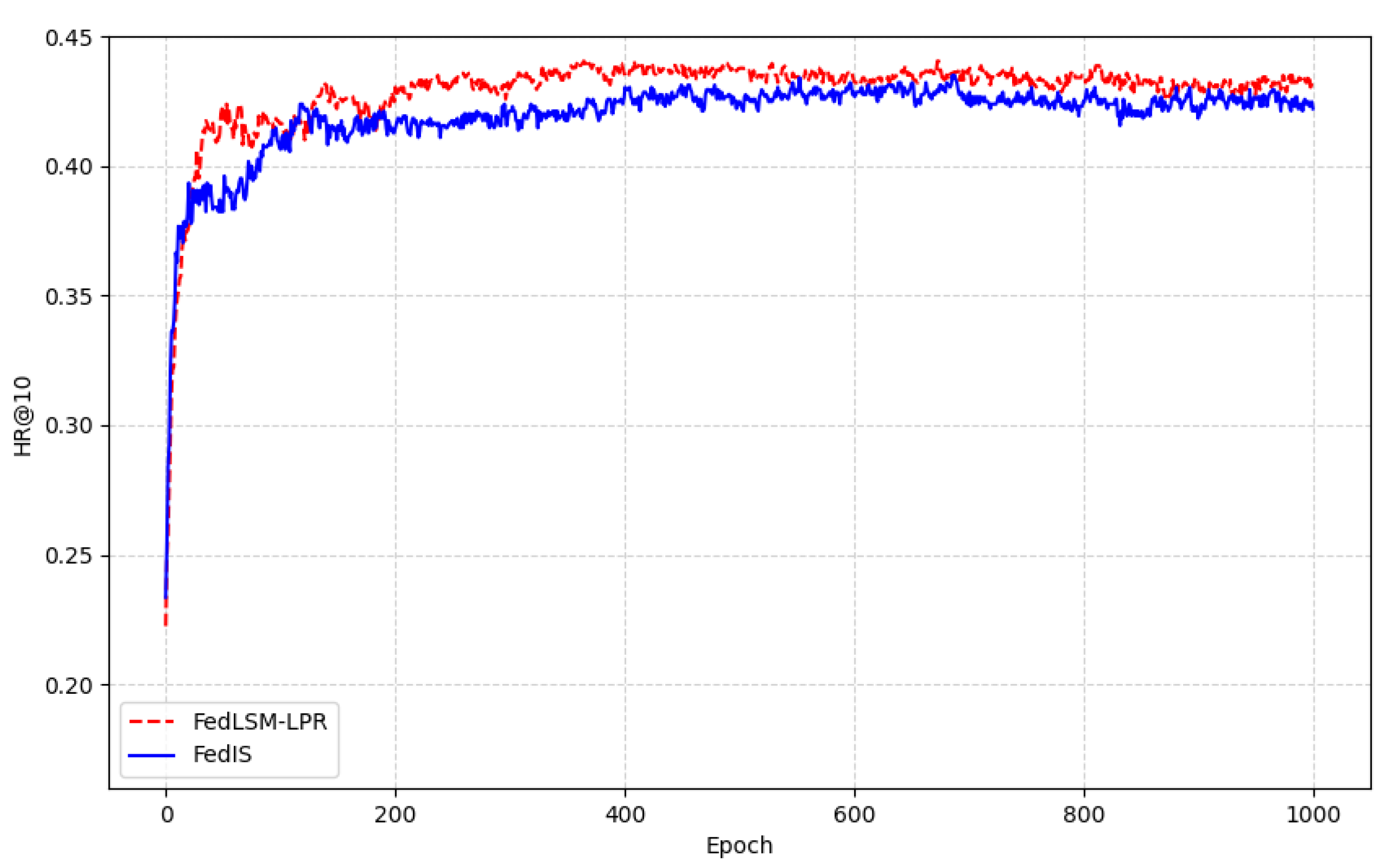
- FedIS [35]: This scheme proposes a novel federated learning aggregation method, REPAgg, to address the heterogeneity of data characteristics across different clients in federated learning.
5.2. Experimental Results and Comparative Analysis
5.3. Model Efficiency
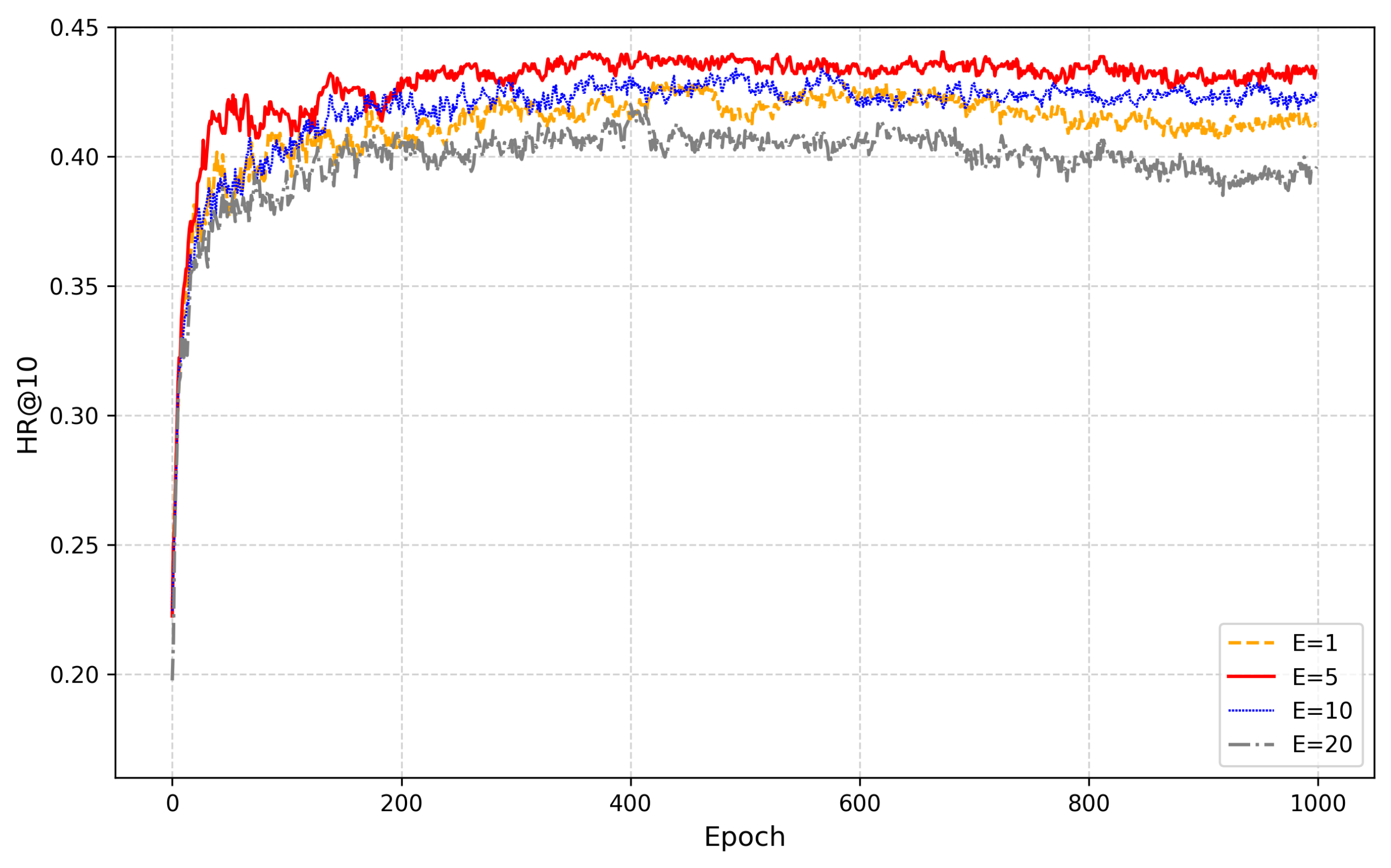
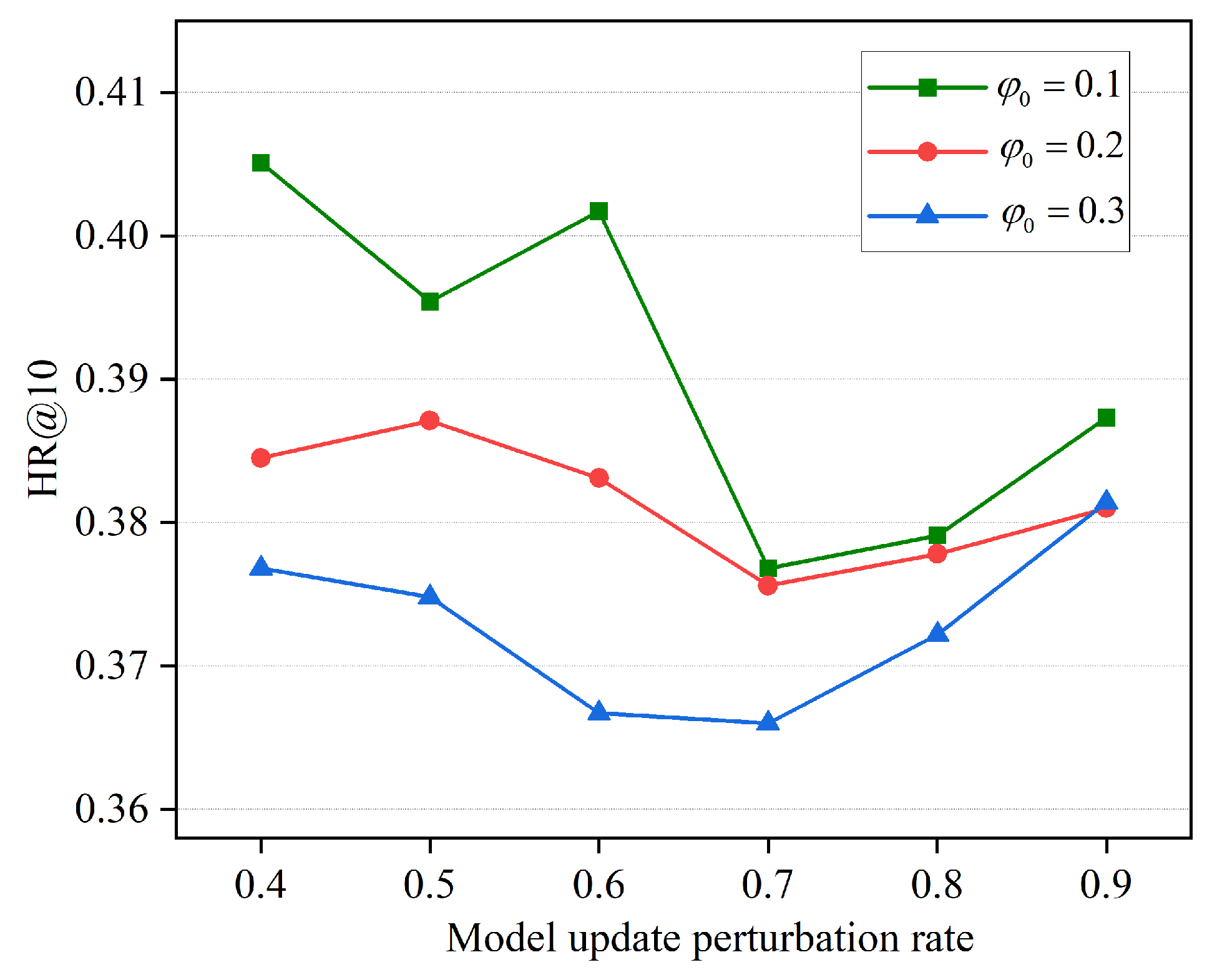
5.4. Analysis of Parameters
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bahgat, E.M.; Abo-alian, A.; Rady, S.; Gharib, T.F. Efficient Trajectory Prediction Using Check-In Patterns in Location-Based Social Network. Big Data Cogn. Comput. 2025, 9, 102. [Google Scholar] [CrossRef]
- Wang, H.; Xin, M. A Graph-Enhanced Dual-Granularity Self-Attention Model for Next POI Recommendation. Electronics 2025, 14, 1387. [Google Scholar] [CrossRef]
- Van Dat, N.; Van Toan, P.; Thanh, T.M. Solving distribution problems in content-based recommendation system with gaussian mixture model. Appl. Intell. 2022, 52, 1602–1614. [Google Scholar] [CrossRef]
- Fauzan, F.; Nurjanah, D.; Rismala, R. Apriori association rule for course recommender system. Indones. J. Comput. (Indo-JC) 2020, 5, 1–16. [Google Scholar]
- Lee, D.; Nam, K.; Han, I.; Cho, K. From free to fee: Monetizing digital content through expected utility-based recommender systems. Inf. Manag. 2022, 59, 103681. [Google Scholar] [CrossRef]
- Darraz, N.; Karabila, I.; El-Ansari, A.; Alami, N.; El Mallahi, M. Integrated sentiment analysis with BERT for enhanced hybrid recommendation systems. Expert Syst. Appl. 2025, 261, 125533. [Google Scholar] [CrossRef]
- Liu, Y.; Yin, M.; Zhou, X. A collaborative filtering algorithm with intragroup divergence for POI group recommendation. Appl. Sci. 2021, 11, 5416. [Google Scholar] [CrossRef]
- Zhang, Y.; Yin, C.; Wu, Q.; He, Q.; Zhu, H. Location-aware deep collaborative filtering for service recommendation. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 3796–3807. [Google Scholar] [CrossRef]
- Albrecht, J.P. How the GDPR will change the world. Eur. Data Prot. Law Rev. 2016, 2, 287. [Google Scholar] [CrossRef]
- Gui, R.; Gui, X.; Zhang, X. A trajectory privacy protection method based on the replacement of points of interest in hotspot regions. Comput. Secur. 2025, 150, 104279. [Google Scholar] [CrossRef]
- Li, L.; Lin, F.; Xiahou, J.; Lin, Y.; Wu, P.; Liu, Y. Federated low-rank tensor projections for sequential recommendation. Knowl.-Based Syst. 2022, 255, 109483. [Google Scholar] [CrossRef]
- Adnan, M.; Syed, M.H.; Anjum, A.; Rehman, S. A Framework for privacy-preserving in IoV using Federated Learning with Differential Privacy. IEEE Access 2025, 13, 13507–13521. [Google Scholar] [CrossRef]
- Banabilah, S.; Aloqaily, M.; Alsayed, E.; Malik, N.; Jararweh, Y. Federated learning review: Fundamentals, enabling technologies, and future applications. Inf. Process. Manag. 2022, 59, 103061. [Google Scholar] [CrossRef]
- Zhong, L.; Zeng, J.; Wang, Z.; Zhou, W.; Wen, J. SCFL: Spatio-temporal consistency federated learning for next POI recommendation. Inf. Process. Manag. 2024, 61, 103852. [Google Scholar] [CrossRef]
- Cong, Y.; Zeng, Y.; Qiu, J.; Fang, Z.; Zhang, L.; Cheng, D.; Liu, J.; Tian, Z. FedGA: A greedy approach to enhance federated learning with Non-IID data. Knowl.-Based Syst. 2024, 301, 112201. [Google Scholar] [CrossRef]
- Hu, H.; Kothari, A.N.; Banerjee, A. A Novel Algorithm for Personalized Federated Learning: Knowledge Distillation with Weighted Combination Loss. Algorithms 2025, 18, 274. [Google Scholar] [CrossRef]
- Pei, J.; Liu, W.; Li, J.; Wang, L.; Liu, C. A review of federated learning methods in heterogeneous scenarios. IEEE Trans. Consum. Electron. 2024, 70, 5983–5999. [Google Scholar] [CrossRef]
- Sun, L.; Zheng, Y.; Lu, R.; Zhu, H.; Zhang, Y. Towards privacy-preserving category-aware POI recommendation over encrypted LBSN data. Inf. Sci. 2024, 662, 120253. [Google Scholar] [CrossRef]
- Li, M.; Zheng, W.; Xiao, Y.; Zhu, K.; Huang, W. Exploring temporal and spatial features for next POI recommendation in LBSNs. IEEE Access 2021, 9, 35997–36007. [Google Scholar] [CrossRef]
- Zeng, J.; Tao, H.; Tang, H.; Wen, J.; Gao, M. Global and local hypergraph learning method with semantic enhancement for POI recommendation. Inf. Process. Manag. 2025, 62, 103868. [Google Scholar] [CrossRef]
- Do, P.M.T.; Nguyen, T.T.S. Semantic-enhanced neural collaborative filtering models in recommender systems. Knowl.-Based Syst. 2022, 257, 109934. [Google Scholar] [CrossRef]
- Ye, M.; Yin, P.; Lee, W.C.; Lee, D.L. Exploiting geographical influence for collaborative point-of-interest recommendation. In Proceedings of the 34th international ACM SIGIR Conference on Research and Development in Information Retrieval, Beijing, China, 24–28 July 2011; pp. 325–334. [Google Scholar]
- Zheng, Y.; Xie, X. Learning location correlation from gps trajectories. In Proceedings of the 2010 Eleventh International Conference on Mobile Data Management, Kansas City, MO, USA, 23–26 May 2010; pp. 27–32. [Google Scholar]
- Liu, B.; Lv, N.; Guo, Y.; Li, Y. Recent advances on federated learning: A systematic survey. Neurocomputing 2024, 597, 128019. [Google Scholar] [CrossRef]
- Xie, Q.; Jiang, S.; Jiang, L.; Huang, Y.; Zhao, Z.; Khan, S.; Dai, W.; Liu, Z.; Wu, K. Efficiency optimization techniques in privacy-preserving federated learning with homomorphic encryption: A brief survey. IEEE Internet Things J. 2024, 11, 24569–24580. [Google Scholar] [CrossRef]
- Gunasekaran, E.; Muthuraman, V. A new double layer multi-secret sharing scheme. China Commun. 2024, 21, 287–309. [Google Scholar] [CrossRef]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A.y. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Ammad-Ud-Din, M.; Ivannikova, E.; Khan, S.A.; Oyomno, W.; Fu, Q.; Tan, K.E.; Flanagan, A. Federated collaborative filtering for privacy-preserving personalized recommendation system. arXiv 2019, arXiv:1901.09888. [Google Scholar]
- Chai, D.; Wang, L.; Chen, K.; Yang, Q. Secure federated matrix factorization. IEEE Intell. Syst. 2020, 36, 11–20. [Google Scholar] [CrossRef]
- Perifanis, V.; Efraimidis, P.S. Federated neural collaborative filtering. Knowl.-Based Syst. 2022, 242, 108441. [Google Scholar] [CrossRef]
- Huang, J.; Tong, Z.; Feng, Z. Geographical POI recommendation for Internet of Things: A federated learning approach using matrix factorization. Int. J. Commun. Syst. 2022, 35, e5161. [Google Scholar] [CrossRef]
- Lin, G.; Liang, F.; Pan, W.; Ming, Z. FedRec: Federated Recommendation With Explicit Feedback. IEEE Intell. Syst. 2021, 36, 21–30. [Google Scholar] [CrossRef]
- Dong, Q.; Liu, B.; Zhang, X.; Qin, J.; Wang, B. Sequential POI Recommend Based on Personalized Federated Learning. Neural Process. Lett. 2023, 55, 7351–7368. [Google Scholar] [CrossRef]
- Li, Z.; Bilal, M.; Xu, X.; Jiang, J.; Cui, Y. Federated learning-based cross-enterprise recommendation with graph neural networks. IEEE Trans. Ind. Inform. 2022, 19, 673–682. [Google Scholar] [CrossRef]
- Ding, X.; Li, G.; Yuan, L.; Zhang, L.; Rong, Q. Efficient federated item similarity model for privacy-preserving recommendation. Inf. Process. Manag. 2023, 60, 103470. [Google Scholar] [CrossRef]
- Sarwar, B.; Karypis, G.; Konstan, J.; Riedl, J. Item-based collaborative filtering recommendation algorithms. In Proceedings of the 10th International Conference on World Wide Web, Hong Kong, China, 1–5 May 2001; pp. 285–295. [Google Scholar]
- Ning, X.; Karypis, G. Slim: Sparse linear methods for top-n recommender systems. In Proceedings of the 2011 IEEE 11th International Conference on Data Mining, Vancouver, BC, Canada, 11–14 December 2011; pp. 497–506. [Google Scholar]
- Kabbur, S.; Ning, X.; Karypis, G. Fism: Factored item similarity models for top-n recommender systems. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, London, UK, 19–23 August 2013; pp. 659–667. [Google Scholar]
- He, X.; He, Z.; Song, J.; Liu, Z.; Jiang, Y.G.; Chua, T.S. NAIS: Neural attentive item similarity model for recommendation. IEEE Trans. Knowl. Data Eng. 2018, 30, 2354–2366. [Google Scholar] [CrossRef]
- Nichol, A.; Achiam, J.; Schulman, J. On first-order meta-learning algorithms. arXiv 2018, arXiv:1803.02999. [Google Scholar]
- Dwork, C.; Roth, A. The algorithmic foundations of differential privacy. Found. Trends® Theor. Comput. Sci. 2014, 9, 211–407. [Google Scholar] [CrossRef]
- Jiang, J.Y.; Li, C.T.; Lin, S.D. Towards a more reliable privacy-preserving recommender system. Inf. Sci. 2019, 482, 248–265. [Google Scholar] [CrossRef]
- Jain, P.; Kulkarni, V.; Thakurta, A.; Williams, O. To drop or not to drop: Robustness, consistency and differential privacy properties of dropout. arXiv 2015, arXiv:1503.02031. [Google Scholar]
- Vadhan, S.; Wang, T. Concurrent composition of differential privacy. In Proceedings of the Theory of Cryptography: 19th International Conference, TCC 2021, Raleigh, NC, USA, 8–11 November 2021; Proceedings, Part II. Springer: Cham, Switzerland, 2021; pp. 582–604. [Google Scholar]
- Hu, Y.; Koren, Y.; Volinsky, C. Collaborative filtering for implicit feedback datasets. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 263–272. [Google Scholar]
- Anelli, V.W.; Deldjoo, Y.; Di Noia, T.; Ferrara, A.; Narducci, F. User-controlled federated matrix factorization for recommender systems. J. Intell. Inf. Syst. 2022, 58, 287–309. [Google Scholar] [CrossRef]
- Polato, M. Federated variational autoencoder for collaborative filtering. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 20 September 2021; pp. 1–8. [Google Scholar]


| Symbol | Definition |
|---|---|
| Number of users and locations | |
| User and the user set | |
| Location and the location set | |
| Historical interacted locations of user u | |
| Location feature matrix | |
| Location feature vector of location i | |
| E | Number of iterations for local training |
| T | Number of global training iterations |
| Prediction of user u for location i | |
| Updates of client k at tth epoch | |
| Global model parameters at tth epoch | |
| Local model parameters at tth epoch |
| Schemes | HR@10 | NDCG@10 |
|---|---|---|
| MF-ALS | 0.4294 | 0.2751 |
| NAIS | 0.4303 | 0.2773 |
| FCF | 0.4285 | 0.2748 |
| FedMF | 0.4275 | 0.2749 |
| FedNCF | 0.4109 | 0.2560 |
| FedBPR | 0.4257 | 0.2754 |
| FedVAE | 0.4284 | 0.2756 |
| FedIS | 0.4294 | 0.2758 |
| FedLSM-LPR | 0.4342 | 0.2776 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, L.; Mu, J.; Yu, L.; Liu, Y.; Zhu, F.; Gu, J. Federated Learning-Based Location Similarity Model for Location Privacy Preserving Recommendation. Electronics 2025, 14, 2578. https://doi.org/10.3390/electronics14132578
Zhu L, Mu J, Yu L, Liu Y, Zhu F, Gu J. Federated Learning-Based Location Similarity Model for Location Privacy Preserving Recommendation. Electronics. 2025; 14(13):2578. https://doi.org/10.3390/electronics14132578
Chicago/Turabian StyleZhu, Liang, Jingzhe Mu, Liping Yu, Yanpei Liu, Fubao Zhu, and Jingzhong Gu. 2025. "Federated Learning-Based Location Similarity Model for Location Privacy Preserving Recommendation" Electronics 14, no. 13: 2578. https://doi.org/10.3390/electronics14132578
APA StyleZhu, L., Mu, J., Yu, L., Liu, Y., Zhu, F., & Gu, J. (2025). Federated Learning-Based Location Similarity Model for Location Privacy Preserving Recommendation. Electronics, 14(13), 2578. https://doi.org/10.3390/electronics14132578







