GAML-YOLO: A Precise Detection Algorithm for Extracting Key Features from Complex Environments

Abstract

This study addresses three major challenges in non-motorized vehicle rider helmet detection: multi-spectral interference between the helmet and hair color (HSV spatial similarity > 0.82), target occlusion in high-density traffic flows (with peak density reaching 11.7 vehicles/frame), and perception degradation under complex weather conditions (such as overcast, foggy, and strong light interference). To tackle these issues, we developed the GMAL-YOLO detection algorithm. This algorithm enhances feature representation by constructing a Feature-Enhanced Neck Network (FENN) that integrates both global and local features. It employs the Global Mamba Architecture Enhancement (GMET) to reduce parameter size while strengthening global context capturing ability. It also incorporates Multi-Scale Spatial Pyramid Pooling (MSPP) combined with multi-scale feature extraction to improve the model’s robustness. The enhanced channel attention mechanism with self-attention (ECAM) is designed to enhance local feature extraction and stabilize deep feature learning through partial convolution and residual learning, resulting in a 13.04% improvement in detection precision under occlusion scenarios. Furthermore, the model’s convergence speed and localization precision are optimized using the modified Enhanced Precision-IoU loss function(EP-IoU). Experimental results demonstrate that GMAL-YOLO outperforms existing algorithms on the self-constructed HelmetVision dataset and public datasets. Specifically, in extreme scenarios, the false detection rate is reduced by 17.3%, and detection precision in occluded scenes is improved by 13.6%, providing an effective technical solution for intelligent traffic surveillance.

1. Introduction

Every year, a large number of cyclists worldwide suffer fatal head injuries due to not wearing helmets, highlighting the critical importance of helmet detection for road traffic safety. Traditional strategies, such as placing population monitoring at traffic intersections, are not only inefficient but also unable to operate around the clock. Therefore, automatic helmet detection has become a key research direction in the field of computer vision, playing a crucial role in enhancing traffic safety and enforcing traffic regulations. Although applying object detection strategies to helmet detection is not uncommon, there is still significant room for improvement. This is because the size of helmet targets in an image is relatively small, and the dense targets contain less effective feature information, making it a persistent challenge to improve detection performance in dense and complex scenes. In traffic scenarios, the weather conditions vary greatly. On sunny days with good lighting, cameras can capture more details, resulting in clearer images and better detection performance. However, in adverse weather conditions such as rainy, foggy, or snowy days, various factors lead to blurred and occluded images, causing missed detections (Figure 1). Particularly at night, the CMOS sensor of the camera fails to capture enough light, leading to excessive noise that severely impacts detection.

The YOLOv8 object detection framework has significant advantages in real-time performance. By adjusting the depth and width coefficients, the model size can be flexibly controlled, which provides certain advantages for the detection scenarios in this study. Due to the large-scale deployment of object detectors in the transportation field, economic considerations impose strict requirements on the model size. Thus, the selected adjustment factor in this study is N, which offers the smallest number of parameters, the least computational load, and the fastest speed. Although YOLOv8 performs excellently in general object detection tasks, it still exhibits notable limitations when dealing with dense targets, complex environmental backgrounds, image blurring, and occlusion in extreme scenarios. In dense target detection, YOLOv8’s anchor-based mechanism lacks the ability to distinguish highly overlapping targets, leading to failure in non-maximum suppression (NMS) for tightly packed targets, resulting in missed or false detections. For instance, in traffic monitoring scenarios where non-motorized vehicles and cyclists are densely distributed, the model may fail to accurately separate the feature responses of adjacent targets, causing missed detections (Figure 1a). In complex environmental backgrounds, YOLOv8’s global receptive field is limited by the local nature of convolution operations, making it difficult to suppress background noise interference effectively. For example, abrupt lighting changes or similar texture interference (such as confusion between leaves and helmet colors) can cause feature confusion, reducing detection confidence (Figure 1b). In occlusion scenarios, YOLOv8 lacks an explicit modeling mechanism for local feature reconstruction. When a target is partially occluded (e.g., pedestrians hidden by vehicles), the model’s reliance on global context perception is limited, leading to misaligned object localization or classification errors (Figure 1c). Experimental results show that on the self-constructed HelmetVision dataset, YOLOv8’s recall rate is 5.3% lower than the FENN-improved solution, validating its inherent limitations in such scenarios. These limitations stem from the lack of dense feature interaction, dynamic de-blurring, and occlusion robustness modules in YOLOv8, which urgently require optimization through cross-scale attention mechanisms and adaptive feature enhancement strategies. However, Wang et al. [1] designed the multi-scale geometric-aware Transformer (MGT) model, which improves point cloud classification and cutting-point detection performance by introducing multi-scale patch segmentation, geometric-aware patch representations (SLFE module), and a geodesic distance-based self-attention mechanism. At the same time, geometric prior fusion improves target detection and localization precision through multiplication with the soft point mask and foreground point loss term. However, this method has insufficient occlusion association modeling, and detection accuracy drops under target occlusion and variable weather conditions. Wu et al. [2] designed an enhanced CycleGAN framework with a novel generator structure, including ResNeXt blocks, optimized upsampling modules, and hyperparameter optimization strategies. Compared with the original CycleGAN, the FID score is reduced by 29.7%, effectively solving the issues of night-time detail restoration, color distortion, and artifacts. However, this solution overly relies on static channels and has limited robustness to weather conditions, making it difficult to adapt to complex meteorological conditions. Tang et al. [3] designed the Confluent Triple-Flow Network, which uses three-stream fusion networks and cross-modal feature interaction techniques. However, it still has shortcomings in spectral decoupling and occlusion association modeling, struggling to handle complex weather, high-density occlusion, and low-light scenarios, limiting detection accuracy and generalization performance. Therefore, this study designs a feature-enhanced detection algorithm aimed at dense targets, complex environmental backgrounds, and image blur, occlusion, and other challenges. It is a precise detection algorithm for extracting key features from complex GMAL-YOLO.

In this study’s model, we propose four key optimizations and innovations. Through the carefully designed position deployment, GMET, MSPP, and FENN form an organic whole, fully utilizing their respective advantages while achieving the synergistic effect of each module within the overall network. Finally, an ECAM attention mechanism is designed at the detection head, providing an efficient solution for helmet detection in complex scenarios.

In the non-motorized vehicle rider helmet detection task, due to the small scale of helmet targets and their susceptibility to background interference, features from a single scale are often insufficient to accurately describe the target’s feature information. Additionally, low-resolution images and occlusion phenomena in high-density traffic further exacerbate the difficulty in feature extraction. To address these challenges, the Feature Enhancement Neck Network (FENN) designed in this paper draws from the concepts of GD [4] and PAN, utilizing a cross-layer feature fusion mechanism. The SimF module collects and aligns features, and operations such as Inpool adjust the feature dimensions, enabling effective fusion and transmission of features from different layers, thereby enhancing feature expression. The innovative components of FENN include PyPoolAgg, APFusion, TopBasicLayer, and SSFF structures. These components further enhance feature expression while reducing computational demands. For example, PyPoolAgg adjusts feature maps of different spatial sizes to the same target size through adaptive average pooling, performs channel dimension concatenation to form high-dimensional feature maps, and then adjusts the channel number through convolutional operations. The SSFF structure normalizes the P3, P4, and P5 feature maps to the same size, upsamples them, stacks them together, and inputs them as three-dimensional convolutions into Add, which are then combined with GMET features from different layers and input to the detection head, effectively integrating multi-resolution image information and improving helmet target detection accuracy.

The Global Mamba Architecture Enhancement (GMET) algorithm is inspired by the VSS (Vision State Space) module in the VMamba [5] architecture and integrates with the C2f [6] module from YOLOv8. By combining state space modeling and a four-direction scanning strategy, GMET enhances global context capture while reducing parameter count. The GMET module is connected after the Inpool of the FENN neck network. This positioning choice is based on a comprehensive consideration of the spatial size and semantic information of the feature maps, allowing GMET to extract key information from features of different scales and pass it on to subsequent classification or regression tasks, providing the model with more discriminative feature inputs. In the backbone network, GMET focuses on the initial extraction and enhancement of base features, while in the neck network, it places greater emphasis on the further fusion and optimization of features from different stages to achieve better feature transmission and utilization.

The Multi-Scale Spatial Pyramid Pooling layer (MSPP) combines the advantages of SPPF [7] and LSKA [8], introducing multi-dilation rate convolutions and an adaptive kernel selection strategy, effectively capturing multi-scale features and enhancing the model’s cross-scale feature aggregation ability. As part of the P5 feature map layer in the backbone network, MSPP uses pyramid pooling to adjust and fuse feature maps of different spatial sizes to retain multi-scale information. During the feature fusion process, MSPP adjusts the P5 feature map to the appropriate target size using operations like adaptive average pooling, and concatenates it with other feature maps along the channel dimension, forming high-dimensional feature maps that preserve multi-scale information. These fused feature maps are then passed into the PyPoolAgg of the FENN neck network, where they are combined with features fused from different layers of SimF and used as input, further enhancing the neck network’s ability to handle multi-scale features.

Finally, inspired by the SEAM [9] attention mechanism, we propose the ECAM attention mechanism, which enhances detection accuracy by 13.6% in densely occluded scenes through residual channel reweighting and local context modeling. At the same time, the introduction of the PIoU [10] loss function, incorporating a target scale penalty factor, optimizes localization precision and reduces false detection rates by 17.3% in low-light scenarios. These innovations, through the collaborative optimization of feature fusion, lightweight architecture, and multi-scale perception capabilities, provide a systematic solution for helmet detection in complex weather, high-density occlusion, and low-light conditions. GAM-YOLO visualizes the helmet region under occlusion or low-light conditions, as shown in Figure 1d–f.

Main contributions:

• This study innovatively constructs a multi-dimensional feature enhancement system: We have developed a multi-dimensional feature enhancement system that includes the Feature Enhancement Neck Network (FENN), Global Mamba Enhancement Algorithm (GMET), Multi-Scale Spatial Pyramid Pooling (MSPP) layer, and ECAM attention mechanism. FENN alleviates the attenuation of deep feature information through cross-layer feature fusion. GMET enhances the model’s global spatial perception range. MSPP strengthens the ability to aggregate multi-scale features. The ECAM attention mechanism improves detection precision by 13.6% in complex scenarios, demonstrating the exceptional performance of GMAL-YOLO in detection robustness.
• We have constructed the first full-scene coverage helmet detection benchmark dataset, HelmetVision. This dataset adopts a multi-source heterogeneous data fusion framework, integrating three major data sources: professional equipment field collection, intelligent web crawler engines, and open APIs from social media. This ensures the diversity and representativeness of the data, providing high-quality benchmark data for object detection research in complex scenarios.
• GMAL-YOLO has made significant breakthroughs in detection performance, surpassing YOLOv8, Faster R-CNN, YOLOv9, and RT-DETR with an mAP@%50 of 83.7%, and improving inference speed by 23%. It performs particularly well in extreme scenarios such as low light and heavy occlusion. This provides a robust solution for rider helmet detection in intelligent transportation systems, supporting the development of smart city safety monitoring systems.

2. Related Work

2.1. Overview of Target Detection Algorithms

The importance of object detection in the field of computer vision is undeniable. Its goal is to accurately identify objects within images and precisely locate their positions and categories. The development of this technology has undergone several significant stages, starting from early methods such as template matching and traditional approaches based on handcrafted features, including Haar features, HOG features, and SVM-based classifiers, to the mainstream deep learning methods of today. Early object detection relied on carefully designed features and traditional machine learning algorithms. While effective, these methods began to show limitations as data complexity and demands increased. With the rise in deep learning, particularly Convolutional Neural Networks (CNNs), object detection has seen significant advancements. Modern object detection algorithms are mainly divided into two categories: two-stage detectors and single-stage detectors. Two-stage detectors introduced the concept of region proposals, such as R-CNN [11], Fast R-CNN [12], and Faster R-CNN [13]. These methods first generate potential object frames, then classify and refine the bounding boxes, improving accuracy and reliability, but sacrificing some real-time performance due to the multi-stage process. Subsequently, single-stage detectors like YOLO (You Only Look Once) and SSD [14] (Single Shot MultiBox Detector) directly predict the object’s category and position through a single neural network, significantly improving processing speed and simplifying the design process, making them suitable for scenarios requiring fast responses. To address challenges in multi-scale and small object detection, researchers introduced various feature pyramid networks and attention mechanisms. Recently, new methods based on Transformer [15] architecture, such as DETR [16], have introduced entirely new approaches. DETR completely discards traditional candidate box generation and non-maximum suppression (NMS) strategies, instead using attention mechanisms for global detection of the entire image, marking a shift toward more flexible and efficient object detection techniques. These developmental stages demonstrate the rapid evolution of object detection algorithms from traditional methods to deep learning-driven approaches, continuously improving detection accuracy and efficiency through the introduction of new architectures and techniques, thus driving progress and innovation in the field of computer vision.

2.2. YOLOv8 Benchmark Modeling

The YOLO series algorithm, especially the classic first-generation models, has gained significant attention due to its efficiency and accuracy. The latest version, YOLOv8, was released by Ultralytics in 2023. YOLOv8 is an integrated and improved version built upon the foundation of previous YOLO generations. It is the most recent detection algorithm in the YOLO series. YOLOv8 is capable of performing detection, classification, and segmentation tasks. The network structure is shown in Figure 2.

The network structure of YOLOv8 consists of three main parts: backbone, neck, and head. The backbone uses convolutional and deconvolutional layers to extract features, employing the C2f module as the basic unit. Compared to the C3 module used in YOLOv5, the C2f module offers superior feature extraction capabilities and fewer parameters. The neck section enhances feature representation through multi-scale feature fusion techniques, including SPPF, PAA [17], and two PAN [18] modules. The head is responsible for object detection and classification tasks and is divided into a detection head and a classification head. The detection head generates detection results using convolutional and deconvolutional layers, while the classification head performs feature map classification via global average pooling. YOLOv8 continues the design principles from YOLOv5, such as the compact and separable CSP backbone network and multi-scale model considerations. In terms of improvements, the backbone uses the lightweight C2 module to replace the C3 module and retains the application of the SPPF module. The PAN-FPN structure preserves the core idea of PAN but optimizes the upsampling stage by removing the convolutional structure and replacing the C3 module with the C2f module. The introduction of decoupled-head [19], new loss functions (such as VFL Loss [20], DFL Loss [21], and CIOU Loss [22]), and the Task-Aligned Assigner sample matching method further enhances YOLOv8’s performance and efficiency in object detection tasks while maintaining a lightweight nature.

Despite its excellent performance in object detection, YOLOv8 faces significant technical bottlenecks in complex traffic scenarios: the C2f module uses a fixed-size convolution kernel (3 × 3) for local feature extraction, and the static weight mechanism fails to decouple multi-spectral features. When the helmet and background (such as a black helmet and dark hair) have a similarity greater than 0.82 in the HSV color space, spectral confusion causes a dramatic increase in false detection rates by 9.3%. The PANet structure relies on repeated 3 × 3 convolution stacks with a local receptive field, which can only model short-range spatial relationships. In dense traffic flow, when the object bounding box overlap exceeds 60%, the loss of long-range occlusion correlations leads to an increase in missed detections. The SPPF layer, using a single dilation rate pooling, is ill-suited to handle weather degradation issues—such as atmospheric scattering on foggy days causing edge gradient attenuation and a drop in AP, or halo artifacts from strong light leading to positioning errors exceeding 15 pixels. Moreover, the CIoU loss function lacks dynamic adaptability due to its fixed geometric penalty term. In multi-scale targets (e.g., small helmets) and high-density occlusion scenarios, anchor box regression deviation is significant, and convergence speed decreases. These flaws collectively restrict the model’s detection robustness and generalization ability in complex environments. This study aims to address the three core challenges in non-motorized vehicle rider helmet detection. Regarding the multispectral interference between helmets and hair colors, Hamada et al. [23] pointed out that when the HSV similarity exceeds 0.8, two colors visually exhibit high similarity, making them prone to interference. In our study, we observed significant interference between helmets and hair color in multispectral images and therefore set this threshold as a baseline limit. Regarding the target occlusion issue in high-density traffic flow, Zhai Y et al. [24] indicated that vehicle occlusion significantly affects object detection and tracking performance in high-density traffic. Observations and data collection from real traffic scenarios revealed that when traffic density reaches a peak value of 11.7 vehicles/frame, the occlusion problem becomes particularly prominent, with the occlusion rate significantly increasing. Finally, concerning the perception degradation in complex weather conditions, Özdenizci O et al. [25] studied the impact of overcast or foggy weather on image contrast and color, pointing out that the contrast decreases and colors become dull in such weather conditions.

To address these challenges, many researchers have reconstructed object detection frameworks by incorporating additional perception modules to adapt to helmet datasets and corresponding scenarios. Although Qian et al. [26] reduced model complexity and extended feature map resolution and receptive fields by improving the IR structure [27], introducing subpixel convolution [28], and using layer-by-layer dilated convolutions [29], this approach overly relies on static channels. Its ability to decouple spectral features is weak, making it difficult to distinguish between helmets and hair color or other similar features, leading to feature confusion. Additionally, its adaptive feature fusion module can only focus on key information to a limited extent. In occlusion scenarios, the model inadequately models occlusion correlations, leading to difficulties in accurately distinguishing and locating occluded helmet targets. Lin et al. [30] proposed an improved YOLOv8 algorithm combined with mosaic data augmentation [31], coordinate attention mechanism [32], slim-neck structure [33], and small object detection layers, enhancing detection accuracy and performance. However, this algorithm still has limitations in handling occlusion scenarios. While the coordinate attention mechanism and slim-neck structure show some effectiveness, the model lacks a robust local feature reconstruction mechanism for severe occlusion, resulting in target localization shifts. Moreover, its loss function is rigid and does not fully consider target scale variations and localization accuracy optimization in occlusion situations. Wei et al. [34] improved the YOLOv5 model, which performed well on a self-built dataset. However, it mainly relies on a ternary attention mechanism [35] and uses soft-NMS [36] instead of the original NMS, which lacks deep modeling of occlusion correlations. Additionally, the model’s robustness under complex meteorological conditions is insufficient, as it does not effectively address the helmet-hair color feature confusion in low-light environments. Li et al. [37] optimized the YOLO-PL algorithm for small object detection and occlusion problems, but its expansion convolution-crossed phase (DCSPX) module with X-residual units and a lightweight VoVNet structure has a limited capability in multispectral feature extraction, making it challenging to handle helmet hair color multispectral interference. Furthermore, the feature pyramid network in this solution has room for improvement in multi-scale feature fusion and cannot fully adapt to the diverse target scales in complex traffic scenarios. Chen et al. [38] designed WHU-YOLO by introducing the lightweight Ghost module [39] and Bi-FPN [40] to reconstruct the neck network, achieving a certain balance between complexity and performance. However, the Ghost module may lose some critical information in feature representation, and Bi-FPN may not fully integrate multi-scale features when dealing with occlusion and multispectral interference, resulting in limited detection precision.

In general, the existing solutions have limitations in spectral decoupling, occlusion correlation modeling, meteorological robustness, and loss function flexibility, which restrict their detection accuracy and generalization performance in complex meteorological, high-density occlusion, and low-light scenarios. These approaches still have significant room for improvement in key feature extraction, occluded target localization, and adaptation to complex environments. These shortcomings indicate that current methods cannot fully address the challenges of multispectral interference, target occlusion, and variable meteorological conditions in helmet detection tasks in complex traffic scenarios.

Therefore, this paper proposes a systematic solution, the GMAL-YOLO algorithm, which overcomes the inherent flaws of YOLOv8 through multi-dimensional technological innovations. The algorithm enhances YOLOv8’s feature representation capabilities in complex environments by constructing a Feature-Enhanced Neck Network (FENN) that improves multi-scale target representation through cross-layer feature fusion, mitigating feature loss in dense scenarios and weather interference. It also designs the Global Mamba Architecture Enhancement (GMET) algorithm, which reduces the parameter count by 4.8% while enhancing global perception through state-space modeling. A Cross-Scale Spatial Pyramid Pooling (MSPP) layer, integrating LSKA attention mechanism and multi-dilation convolution, is used to resolve helmet hair feature confusion in low-light scenarios. Furthermore, the ECAM attention mechanism, combined with residual channel re-weighting and the scale penalty factor in the EPIoU loss function, improves occlusion scene detection accuracy by 13.6% and reduces false detection rates in low-light scenarios by 17.3%. This model optimizes feature fusion, lightweight architecture, and multi-scale perception, significantly improving helmet detection performance in complex environments. Experimental results show that the GMAL-YOLO algorithm achieves an mAP of 83.7% in complex traffic scenarios, significantly outperforming YOLOv8 (79.0%), and demonstrates strong generalization ability in cross-domain tests.

2.3. Overview of Feature Pyramid Development

Traditionally, features at different levels carry information about the positions of objects of various sizes. Larger feature maps contain low-dimensional texture details and positional information for smaller objects, while smaller feature maps contain high-dimensional information and positions for larger objects. The core idea of the Feature Pyramid Network (FPN) [41] is to construct pyramid-like feature maps to extract object features from multiple scales, thereby improving detection accuracy. FPN effectively fuses multi-scale features through cross-scale connections and information exchange, enabling more accurate detection of objects of various sizes.

FPN, proposed by Facebook AI Research (FAIR) in 2017, is a method for addressing the multi-scale problem. It is constructed by downsampling high-resolution feature maps and upsampling low-resolution feature maps to form a pyramid structure. During this process, the information from each layer’s feature map is fused with adjacent layers’ feature maps to preserve object information in high-level features, while background information is supplemented with low-level features. FPN improves the accuracy of multi-scale detection tasks without affecting detection speed. However, its disadvantages include high computational cost, long training and inference times, and the potential loss of some detailed information during the feature fusion process.

The Path Aggregation Network (PAN), based on FPN, introduces a bottom-up path to more fully fuse information across different layers. PAN is also a pyramid-like feature extraction network but uses a bottom-up feature propagation method. PAN upsamples from low-resolution feature maps and downsamples from high-resolution feature maps to form a path. The information from each layer’s feature map is fused with adjacent layers, but unlike FPN, PAN concatenates the fused results from different levels rather than simply adding them, which avoids information loss and retains more detailed information, thereby improving detection accuracy. However, PAN faces issues such as high computational complexity, large memory consumption, poor flexibility, and uneven information transfer.

Gold-YOLO introduces the concept of global information fusion and proposes a new information exchange mechanism called GD. The GD mechanism consists of shallow and deep collection and distribution branches that extract and fuse feature information through convolutional and attention-based blocks. Global fusion of multi-layer features and the injection of global information into higher levels can enhance the information fusion capability of the neck module, but it may also lead to the loss of some detailed information.

3. Methodology

To address the aforementioned issues, this study designs the reconstructed neck network FENN to enhance the feature fusion capability while avoiding information loss. Additionally, a Global Mamba Architecture Enhancement Algorithm (GMET) is proposed to improve the model’s global perception ability. The MSPP module is designed to enhance the network’s ability to aggregate features across multiple scales and improve model performance. To improve detection in occluded scenarios, an ECAM attention mechanism is introduced, and the loss function is modified to EPIoU to further enhance the detection accuracy of the model. The overall framework of GMAL-YOLO is shown in Figure 3, and the details are provided in Section 3.1, Section 3.2, Section 3.3, Section 3.4 and Section 3.5.

3.1. Feature-Enhanced Neck Network

In real-world applications, traffic cameras often suffer from varying resolutions, making multi-resolution feature fusion crucial. However, low-resolution images often lack detailed information due to blurring, which can negatively impact the model’s detection capability. Popular neck networks, such as Feature Pyramid Networks (FPNs), Path Aggregation Networks (PANets), and Globally Distributed (GD) mechanisms, attempt to address this challenge. FPN transmits semantic information through a top-down path, but the semantic confusion between hierarchical levels of low-resolution feature maps can weaken the ability to detect small objects. PANet introduces lateral paths to better integrate features from different levels, but it is structurally complex and computationally expensive. The GD mechanism effectively utilizes global information through global pooling and information distribution, but at the cost of local details. The FPN variant used in the classic YOLO series achieves feature fusion between adjacent levels, but the efficiency of cross-level information transmission is insufficient, and features obtained indirectly suffer from information degradation.

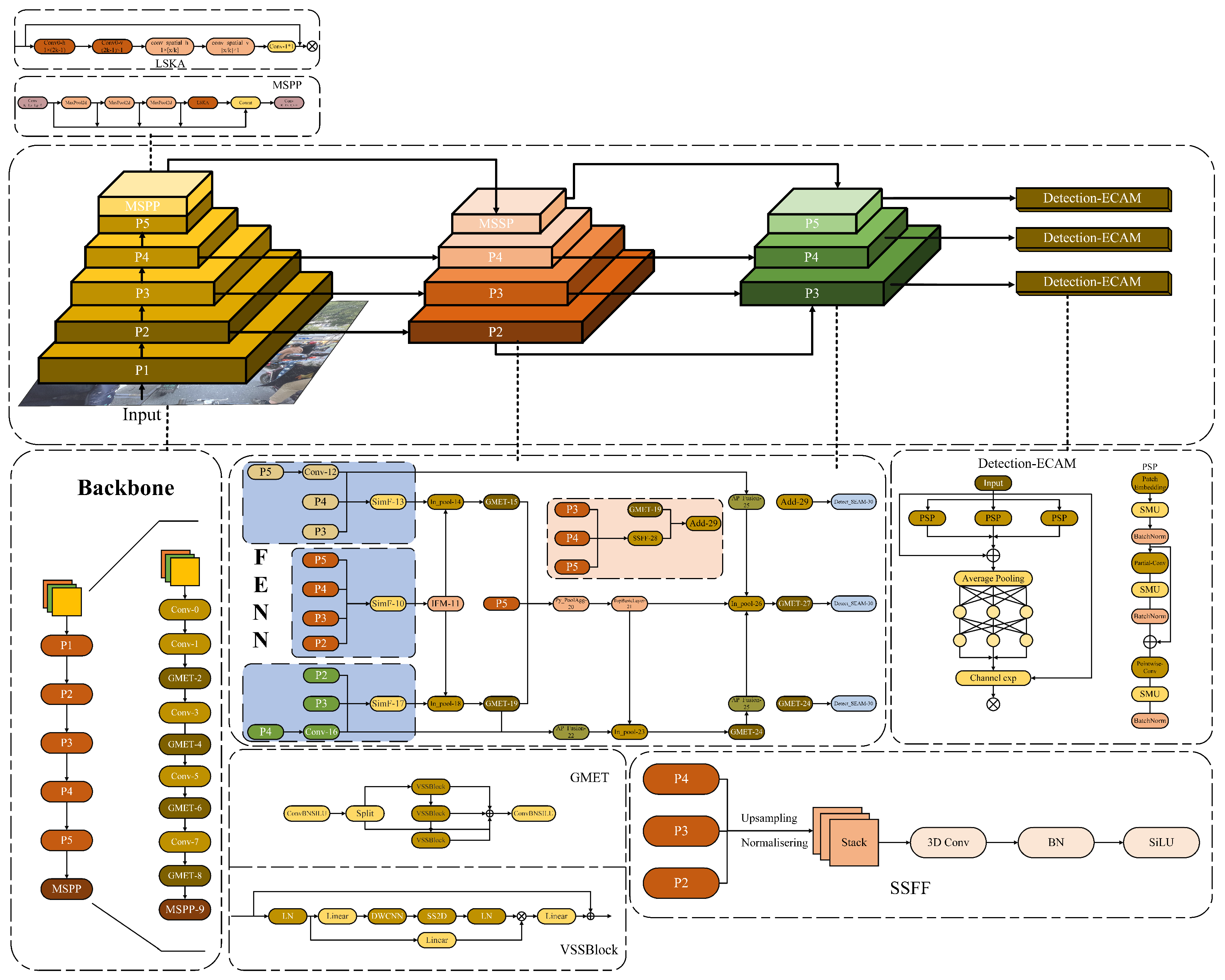
To address these bottlenecks, this study proposes a Feature-Enhanced Neck Network (FENN), which innovatively integrates the core ideas of the GD mechanism with the SSFF module [42]. FENN constructs a dual-path cross-level fusion architecture, utilizing convolutional operators and self-attention mechanisms to efficiently fuse multi-resolution features. As shown in Figure 4, FENN enhances multi-scale features through the cross-level feature interaction module.

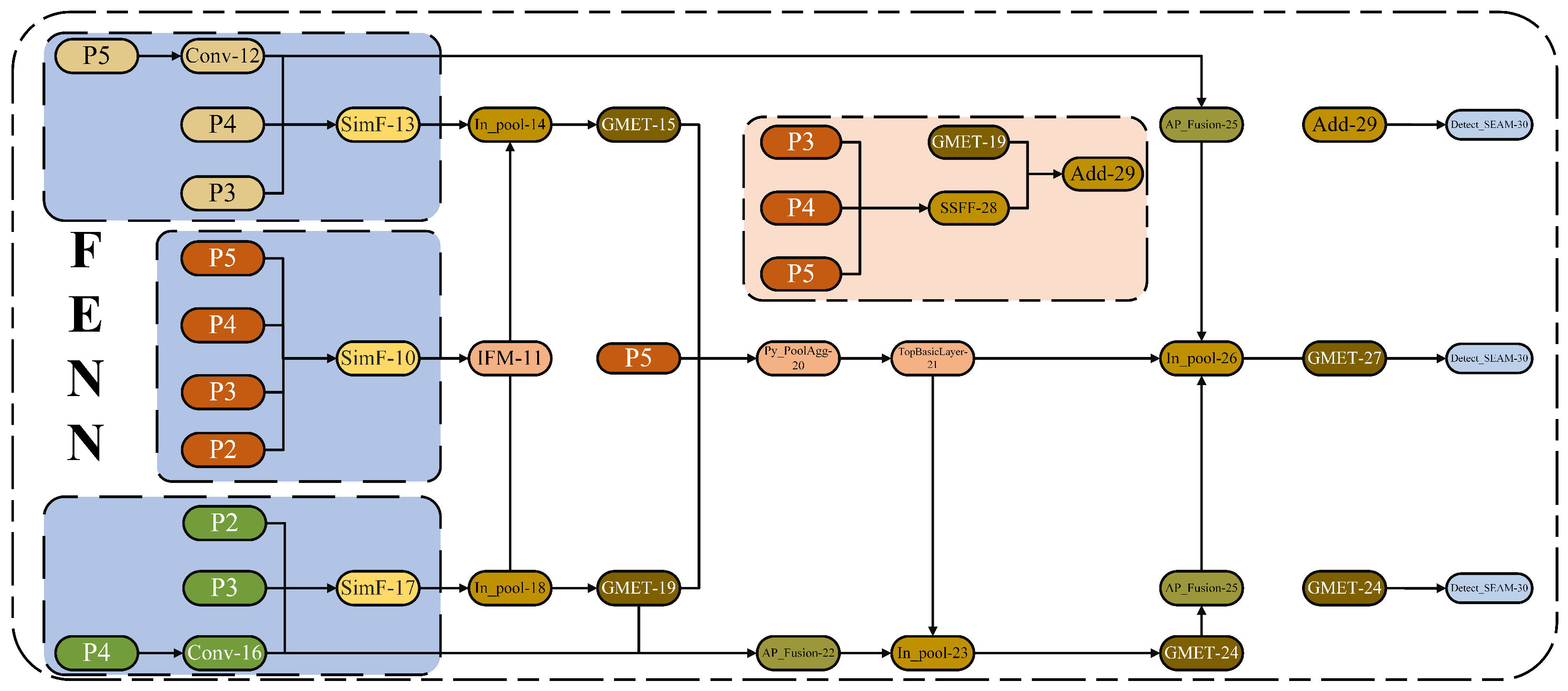
To prevent information loss during transmission, a novel network structure, the FENN mechanism, designed for non-motorized vehicle and helmet recognition, is used in the neck part of this study. It abandons the original recursive method and employs a unified module (SimF) to collect and fuse information from all layers, which is then distributed to different layers. This approach not only avoids the inherent information loss problem of traditional FPN structures but also enhances the information fusion capability of intermediate layers without significantly increasing latency. The FENN neck network first uses the CSPDarknet53 backbone network P2, P3, P4, and P5 to extract multidimensional feature information from the image for fusion, thereby obtaining high-resolution features that retain small target information. To address the challenges of multi-resolution target images and dense scenes, SimF collects and aligns features from different layers, fusing three input feature maps into one more informative output feature map. Then, IFM further extracts and fuses the aligned features via a series of convolutions and feature fusion to obtain global information, providing richer feature information for subsequent network layers. Specifically, Inpool is used to convert the convolution embeddings of local (SimF) and global (IFM) feature maps, reducing the dimension of input features to a unified size using specific global feature channel weighting during the feature fusion process. The fused features are activated and distributed across different layers, achieving more efficient information transmission and richer feature representation.

The two global Mamba-enhanced architectures GMET (detailed later) utilize state space modeling and four-direction scanning strategies to extract key information from multi-scale features and enhance global context capture, resulting in deep global feature information. To enhance the model’s ability to process features at different scales, the PyPoolAgg module adjusts the spatial dimensions of P5 and deep feature maps to the same target size using adaptive mean pooling for channel dimension concatenation, forming a high-dimensional feature map that retains multi-scale information. Convolution operations then adjust the channel number to the target number of channels, outputting the fused feature map, effectively enhancing feature expression while reducing the computational demand of subsequent steps.

APFusion adjusts the size of the two input tensors, Conv-16 and GMET, to match GMET through an adaptive mean pooling operation, and then performs concatenation along the channel dimension. This operation is used to fuse information from different sources when processing feature maps for further processing or feature extraction. To construct a large-scale neural network model with Transformer characteristics, this study builds the TopBasicLayer on the Transformer block. By gradually passing the input features through multiple Transformer blocks, followed by a convolutional layer for feature transformation, feature extraction, and conversion, the model is refined. Finally, at the end of the network, Inpool adjusts the channel number of the local features (APFusion) to the output channel number through convolution layers, extracts specific parts of the global features (TopBasicLayer) to generate global features and activation weights, and dynamically selects pooling or upsampling operations based on the spatial dimensions of the local features. This ensures that the spatial dimensions of both are consistent. The local and global features are then fused using a weighted sum (with weights generated by the activated global features), enhancing the expression capability of the local features. This design enables the effective fusion of local details and global context information, which is further captured by GMET for key feature information.

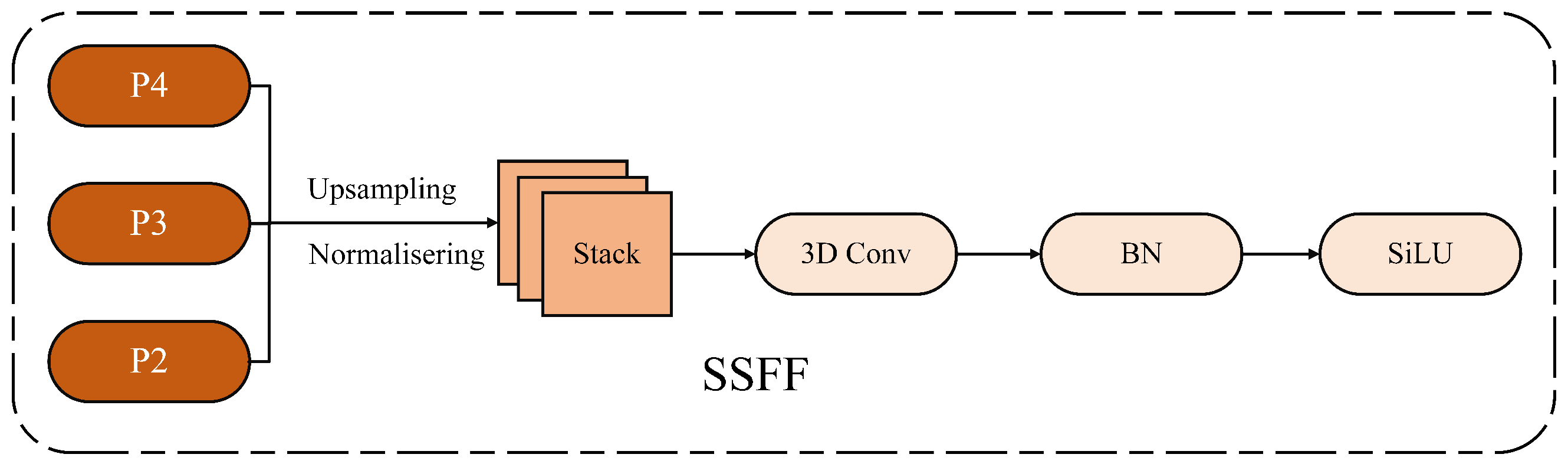
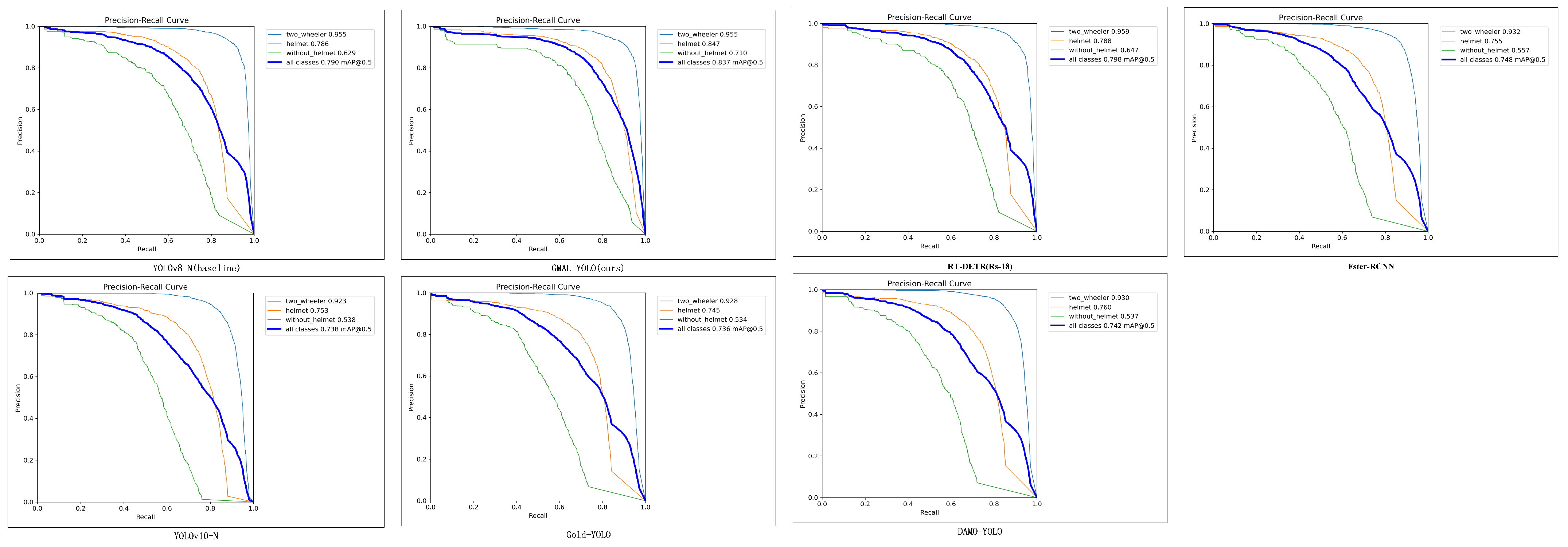
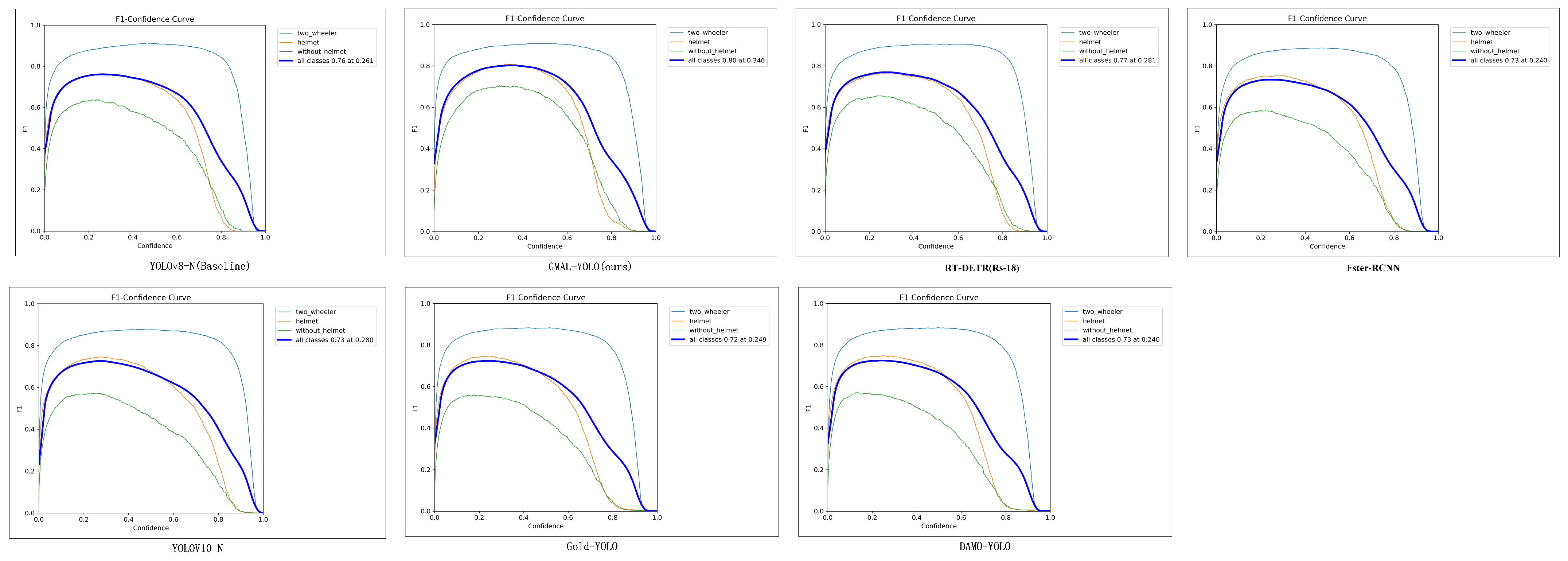
The neck network finally integrates the SSFF scale sequence feature fusion module, as shown in Figure 5. It aims to effectively fuse the feature maps of P3, P4, and P5 to capture non-motorized vehicles and riders wearing helmets at different spatial scales, sizes, and shapes. The P3, P4, and P5 feature maps are normalized to the same size, upsampled, and stacked together as 3D convolution inputs to Add. These are then combined with two GMET feature inputs from different layers and passed to the detection head, which integrates information from multi-resolution images. This allows for a better combination of high-dimensional information from deep feature maps with detailed information from shallow feature maps, further improving helmet target detection accuracy. According to the evaluation of this study’s helmet dataset, the neck network outperforms other state-of-the-art methods in terms of detection accuracy and speed.

3.2. Global Mamba Architecture Enhancement Algorithm

In traffic scenarios with dense and complex weather conditions (e.g., low light), the model must be capable of efficiently understanding and processing the distribution of non-motorized vehicles and helmets under challenging meteorological conditions, while capturing key features from a global perspective. Recent advancements in image analysis have established important benchmarks with Convolutional Neural Networks (CNNs) and Vision Transformers (ViTs) [43]. CNNs excel in capturing local features through convolution operations, while ViT significantly enhances global context understanding using self-attention mechanisms. However, both architectures have limitations in perceiving global information in images, which makes it difficult to maintain global perception while significantly reducing computational complexity—an essential aspect for the accuracy and speed of object detection.

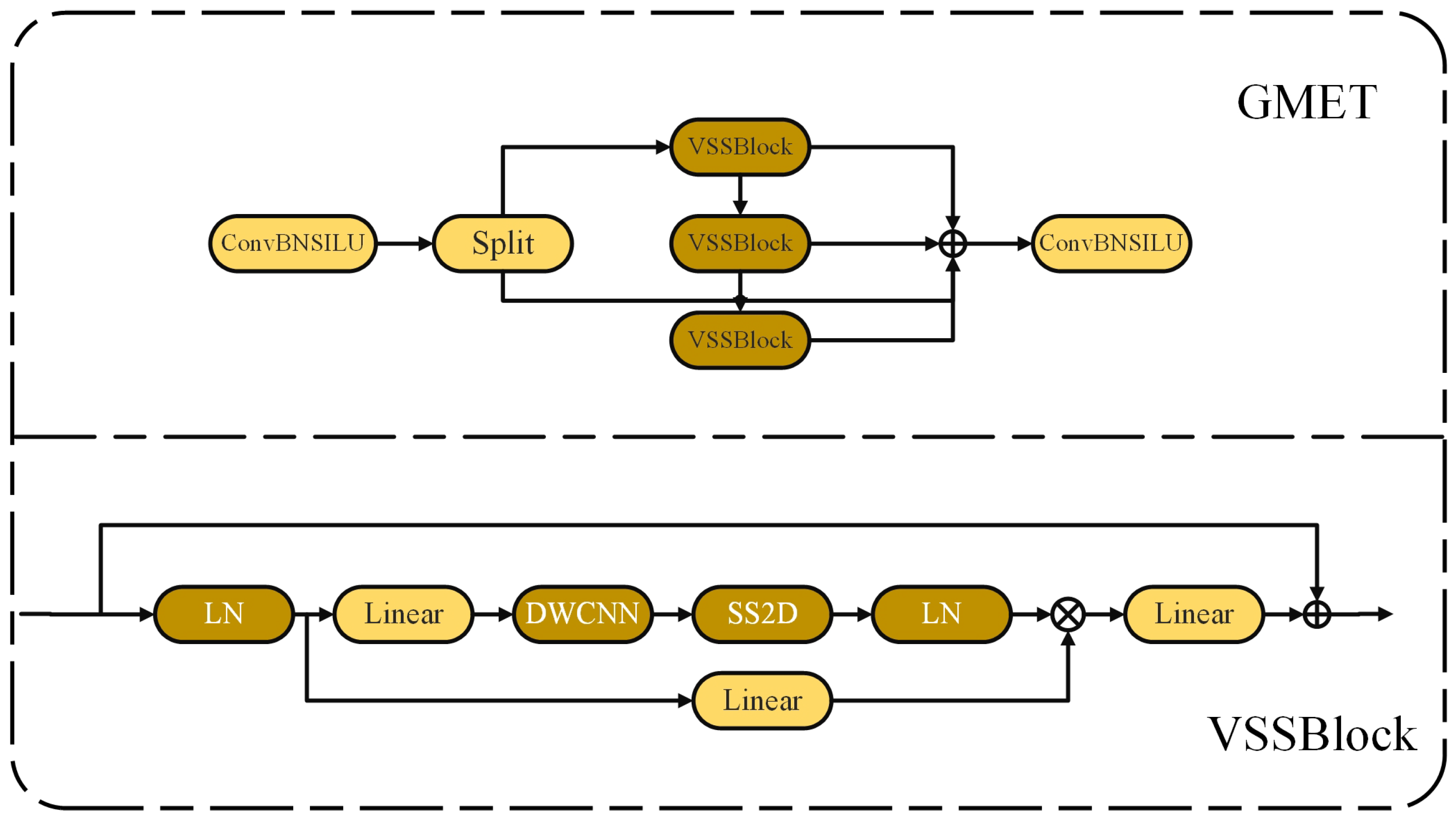
To address the aforementioned issues, this study draws inspiration from the Visual State Space (VSS) module in the VMamba architecture and constructs the Global Mamba Architecture Enhancement Algorithm (GMET). The GMET mechanism is illustrated in Figure 6. The GMET module is a custom neural network component inherited from the C2f class, where the Bottleneck in C2f is replaced by the VSS module. By utilizing a four-directional scanning strategy and the selective scanning spatial state sequence model S6, GMET enables a more comprehensive scan of information and captures diverse features. At the same time, it significantly reduces computational complexity while maintaining global perception capability. This approach enhances detection precision in complex environments. Based on the C2f module, the input data is processed through the first convolutional layer, followed by a Split operation, which divides the output into two parts. One part is directly passed to the output, while the other part is processed through multiple VSS modules. The VSS module normalizes the data through a linear layer and splits it into two branches. The first branch is processed by a linear layer and activation function, while the second branch undergoes linear layers, depthwise separable convolutions, and activation functions before entering the 2D Selective Scan (SS2D) [44]. The SS2D module unfolds the input image into sequences in four directions through a scanning operation, followed by the self-selective scanning spatial state sequence model S6 [45] to extract features. S6 is an extension of the state space model (SSM), allowing the model to dynamically adjust weights by introducing an input-dependent selection mechanism to ensure comprehensive scanning and capture of diverse features. A subsequent scan merging operation sums the sequences from the four directions and restores the output image to the input size, helping retain relevant information and filter out irrelevant details. The processed features are then normalized again and element-wise multiplied with the output from the first branch. After a linear layer that mixes the features, they are added with a residual connection to form the output of the VSS block. Finally, the results of the two parts are concatenated along the channel dimension and passed through a second convolutional layer to obtain the final output. GMET achieves a more enriched gradient flow while ensuring lightweight processing. Unlike the typical ViT, it adopts a simplified structure without the MLP stage, enabling denser block stacking within the same depth budget. GMET thus offers lower computational complexity while enhancing the ability to capture key features across a global range.

State space models (SSMs) originated from the Kalman filter and are mathematical models used to describe the dynamic behavior of systems. They map input signals to output responses through hidden states. $h\left(t\right)\in R^N$ is the hidden state. $u\left(t\right)\in R$ is the input signal, $y\left(t\right)\in R$ is the output response:

Continuous-Time State Space Model:

$$\begin{array}{c}\hfill h^{\prime }\left(t\right)=Ah\left(t\right)+Bu\left(t\right),y\left(t\right)=Ch\left(t\right)+Du\left(t\right)\end{array}$$

(1)

where $A\in {\mathbb{R}}^{N\times N}$, $B\in {\mathbb{R}}^{N\times 1}$, $C\in {\mathbb{R}}^{1\times N}$, and $D\in {\mathbb{R}}^1$ are the weighting parameters.

Discrete-Time State Space Model:

To integrate continuous-time state space models into deep learning models, they need to be discretized. Specifically, for the time interval $[t_a,t_b]$, the analytical solution of the hidden state $h\left(t\right)$ at $t=t_b$ can be expressed as:

$$h\left(t_b\right)=e^{A(t_{b}0-t_a)}h\left(t_a\right)+e^{A(t_b-t_a)}{\int }_{t_a}^{t_b}B\left(\tau \right)u\left(\tau \right)e^{-A(\tau -t_a)}{d}_{\tau }$$

(2)

By sampling with the time-scale parameter $\mathrm{\Delta }$ (i.e., ${d\tau |}_{t_{i+1}}^{t_i}={\mathrm{\Delta }}_i)$, the hidden state $h\left(t_b\right)$ can be discretized as:

$$h_b=e^{A({\mathrm{\Delta }}_a+\dots +{\mathrm{\Delta }}_{b-1})}{h}_a+\sum _{i=a}^{b-1}{B}_i{u}_i{e}^{-A({\mathrm{\Delta }}_a+\dots +{\mathrm{\Delta }}_i)}{\mathrm{\Delta }}_i$$

(3)

where $h_b$ and $h_a$ are the hidden states at time steps b and a. $B_i$ and $u_i$ are the input matrix and input signal at time step i. ${\mathrm{\Delta }}_i$ is the time step length at time step i. This discretization method is based on the Zero-Order Hold (ZOH) method, which is widely used for discretizing state space models. The discretized version achieves linear complexity through a parallel scanning algorithm, but it is only applicable to one-dimensional sequences. For two-dimensional image data, directly applying the one-dimensional scanning would result in the loss of spatial structure information.

S6 is an extension of the state-space model that enables the model to dynamically adjust the weights to better capture contextual information by introducing an input-dependent selection mechanism, which is formulated as follows:

$$S6=\sum _{i=a}^{b-1}{w}_i{h}_i+\sum _{i=a}^{b-1}{w}_i{B}_i{u}_i$$

(4)

where $w_i$ is the weight matrix, representing the weight at time step i. $w_i$ is calculated as:

$$w_i=\underset{j=1}{\prod ^i}{e}^{A{\mathrm{\Delta }}_j}$$

(5)

This means that the weights $w_i$ are computed from the exponential function of the state matrix A of the accumulated time steps j. The selective scanning mechanism (S6) improves the flexibility and efficiency of the model by dynamically adjusting the weights $w_i$ so that the model can selectively focus on different time steps according to the input signals $u_i$.

GMET (Generalized Matrix Expansion Technique) unfolds a 2D image into multiple 1D sequences through the SS2D four-way scanning path, which is represented mathematically as:

$$Y=M\mathrm{erge}(S6\left(U_{scan1}\right),S6\left(U_{scan2}\right),S6\left(U_{scan3}\right),S6\left(U_{scan4}\right))$$

(6)

Scan: The input image is unfolded into four independent 1D sequences along four directions (such as from top-left to bottom-right, bottom-right to top-left, etc.). Each sequence is processed by an independent S6 module, generating intermediate state sequences $\left\{h_i^{\left(k\right)}\right\}(k=1,2,3,4)$. Merge: The four processed sequences are then merged back into a 2D feature map. SS2D, through the four-way scanning path, covers all spatial positions, and each pixel’s hidden state $h_i^{\left(k\right)}$ integrates contextual information from different directions. In contrast to the traditional SSM’s 1D scanning, its response computation can be expanded as:

$$y_{i,j}=\sum _{k=1}^4(C^{\left(k\right)}{h}_{i,j}^k+D_{u_{i,j}}^{\left(k\right)})$$

(7)

Here, $C^{\left(k\right)},D^{\left(k\right)}$ represents the direction-dependent dynamic parameters, which are adjusted through an input-dependent selection mechanism, enhancing the dynamic perception of both local and global information. The complexity of GMET is $O(4\times HW)$, still maintaining linear growth (in contrast to the traditional ViT self-attention, which has a complexity of $O({(HW)}^2)$, further reducing the actual computational overhead. The corresponding computation formula is:

$$G=Softmax(Q{(K/w)}^T\odot M)V$$

(8)

Here, w represents the accumulated weights along the scanning path, and M is the mask matrix. GMET, through the superposition of multi-directional scanning paths, implicitly constructs global interactions similar to self-attention but avoids quadratic complexity.

In order to more effectively extract global features and reduce the number of parameters, the GMET module is not only deployed in the backbone network but is also incorporated after the In_pool in the neck network of FENN. The choice of this position is carefully designed, based on a comprehensive consideration of the spatial dimensions and semantic information of the feature maps. In the backbone network, the GMET module primarily extracts basic features layer by layer. In the neck network, feature maps from different layers contain various scales and semantic information. By integrating the GMET module after In_pool, the feature maps at this location can be fully utilized, allowing for effective fusion of multi-scale features. This design enables the GMET module to extract key information from features at different scales and pass it on to subsequent classification or regression tasks, providing the model with more discriminative feature inputs. Although the GMET module is applied in both the backbone and neck networks, its focus in the backbone network is mainly on the initial extraction and enhancement of basic features, while in the neck network, it emphasizes the further fusion and optimization of features from different stages to achieve better feature transfer and utilization. Therefore, this design allows the GMET module to exert its unique advantages at different stages of the model.

The parameter setting of the GMET module typically configures the output channel number (c2) to be the same as the input channel number (c1) to maintain consistency in feature dimensions. For instance, when the input channel number is 256, c2 is also set to 256. When channel fusion or dimensionality reduction is required, c2 can be set to other values (e.g., 128), which helps reduce the number of parameters while preserving the feature representation capability. The repetition count of the VSSBlock (n) is typically set to 3 to 5. For complex tasks or deep networks, the value of n can be increased to enhance the feature representation capability. For example, when the FENN network processes high-resolution images or performs fine-grained classification tasks, n can be set to 5.

Through the detailed integration and tuning strategies outlined above, the GMET module can effectively extract and enhance global features while maintaining a low parameter count, providing high-quality feature inputs for subsequent tasks.

3.3. Multi-Scale Spatial Pyramid Pooling

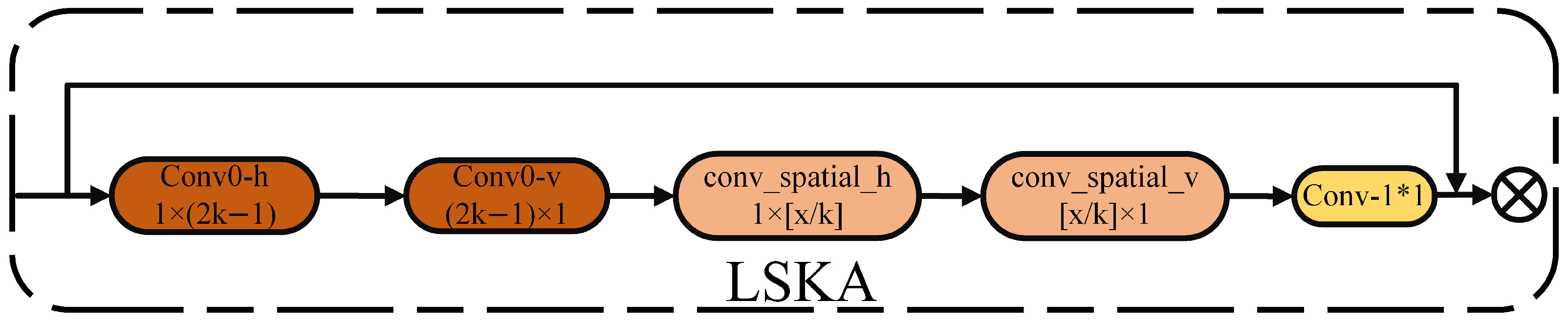
In real-world traffic scenarios, the scale of helmets constantly changes, and in low-light and dim environments, the model’s detection precision decreases. This requires the model to enhance its ability to fuse cross-scale features. In the feature extraction process, although SPPF can divide the receptive fields of different sizes into multiple levels and generate fixed-length feature representations for input images of any size through pooling operations, it tends to lose detailed information and incur high computational costs, especially when dealing with higher-level pooling during the pyramid pooling and feature fusion stages. To address this issue, this paper designs a Multi-Scale Spatial Pyramid Pooling (MSPP) module, which integrates SPPF with the LSKA attention mechanism and introduces multi-dilation convolution and adaptive kernel selection strategies, enabling more effective capture of multi-scale features. The LSKA mechanism achieves this by decomposing the two-dimensional convolution kernels of deep convolution layers into cascaded horizontal and vertical one-dimensional convolution kernels, allowing the direct use of large convolution kernels in the attention module without the need for additional modules. This design not only enhances the ability to extract cross-scale features but also effectively alleviates the secondary increase in computational and memory overhead caused by the larger convolution kernel sizes in the SPPF module.

The structure of LSKA mainly consists of an initialization convolution layer, spatial dilated convolution layers, and fusion with attention application. The shape of the input feature map X is (B, D, H, W), where B represents the batch size, D is the number of channels, and H and W are the spatial dimensions. conv0h and conv0v perform one-dimensional convolutions in the horizontal and vertical directions, respectively, to initially extract horizontal and vertical information. This step generates an initial attention map to help the model focus on the important parts of the image. Subsequently, spatial dilated convolutions conv-spatial-h and conv-spatial-v, with different dilation rates, perform large kernel convolutions in the horizontal and vertical directions to capture long-range spatial dependencies. These convolution operations use dilated convolutions to expand the receptive field, enabling the model to process image features with greater precision and enhance its understanding of spatial relationships within the image. They effectively increase the receptive field without significantly increasing computational cost, allowing for the capture of broader contextual information. Afterward, LSKA adjusts the number of channels() in the feature map to D through a convolution, merging horizontal and vertical feature information. The fused features are then used to generate the final attention map. The input feature map X is element-wise multiplied by the generated attention map to enhance the representational power of the input feature map. In this way, each element of the original feature map is weighted according to the values of the attention map, highlighting important features while suppressing irrelevant ones. The structure of LSKA is shown in Figure 7.

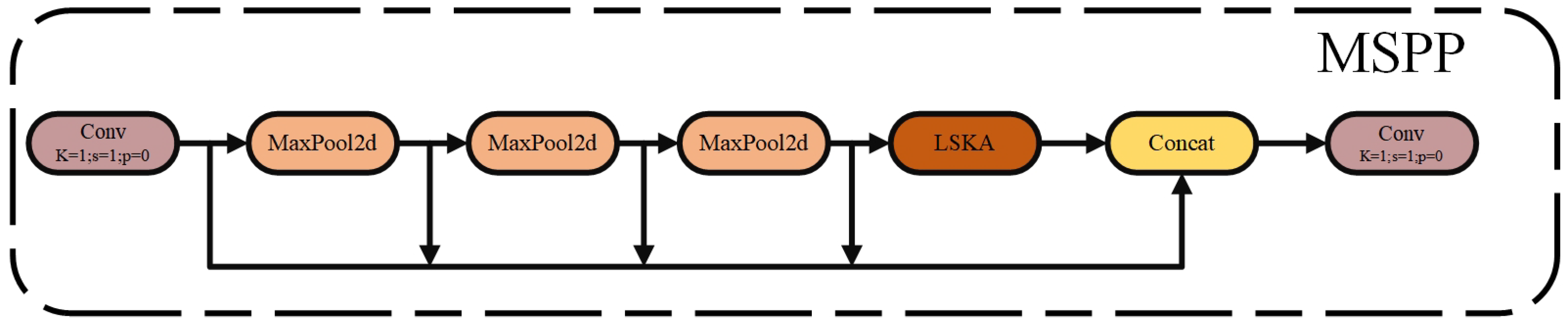
This study proposes a Multi-Scale Spatial Pyramid Pooling (MSPP) mechanism, which significantly enhances the multi-scale feature aggregation ability in complex traffic scenarios by reconstructing the traditional SPPF architecture and deeply integrating the large-kernel separable attention mechanism (LSKA). The MSPP structure first receives the input feature map and undergoes preliminary processing through a convolutional layer. Then, the feature map sequentially undergoes three consecutive maximum pooling operations with residual structures. In each pooling operation, the kernel size is 5 × 5, and padding is added to maintain the feature map dimensions. The pooled feature maps are concatenated with the original feature map to form a feature map that contains multi-scale information. The pooling formula is as follows:

$$L_{\mathrm{out}}={\displaystyle \frac{L_{in}+2\times padding-dilation\times \left(kernel\_size-1\right)-1}{stride}}+1$$

(9)

Here, $L_{in}$ refers to the input size, padding denotes the convolution padding pixels, and kernel size represents the size of the convolution kernel.

This study integrates the SPPF attention mechanism with the LSKA module, referred to as the Multi-Scale Spatial Pyramid Pooling (MSPP) attention mechanism. The goal is to enhance feature representation by leveraging multi-scale feature fusion and attention mechanisms. In the structure of MSPP, the LSKA module is added after all max-pooling operations and before the second convolutional layer. The input feature map X has the shape of ($B,C,H,W$), where B is the batch size, C is the number of channels, and H and W are the spatial dimensions. The channel number of the input feature map is halved, and the output feature map has the shape of ($B,{\displaystyle \frac{C}{2}},H,W$). The MaxPool layer is applied multiple times to perform max-pooling operations on the feature map, generating feature maps at different scales. Each pooling operation maintains the spatial dimensions while gradually reducing the detail of information, thus extracting features at different scales. This process can be expressed as:

$$y_1=MaxPool\left(x\right),y_2=MaxPool\left(y_1\right),y_3=MaxPool\left(y_2\right)$$

(10)

Next, the original feature map X, along with the pooled feature maps $y_1$, $y_2$, and $y_3$, are concatenated along the channel dimension to form a high-dimensional feature map with the shape of ($B,4\times {\displaystyle \frac{C}{2}},H,W$). This concatenated high-dimensional feature map is then input into the LSKA module, where the attention mechanism is applied to enhance the feature representation. Finally, a convolutional layer is used to adjust the number of channels to $C2$, producing the final output feature map.

However, as part of the $P5$ feature map layer in the backbone network, MSPP plays a role in the feature fusion process and is integrated into the FENN neck network, providing richer multi-scale feature inputs for the neck network. Specifically, MSPP adjusts the $P5$ feature map to the appropriate target size through operations such as adaptive average pooling, and concatenates it along the channel dimension with other feature maps, forming a high-dimensional feature map that retains multi-scale information. This feature map is then passed to the PyPoolAgg module in the FENN neck network, where it is fused with features from different levels of SimF as input, significantly enhancing the neck network’s ability to process multi-scale features. This design allows MSPP and FENN to complement each other’s strengths, forming an organic whole.

By embedding the LSKA module into the MSPP structure, the model is able to focus more precisely on the key information in the image, significantly enhancing the fusion ability of multi-scale features in complex traffic scenarios. This also effectively improves the understanding of spatial relationships, ultimately achieving more accurate feature extraction and classification. The MSPP structure is shown in Figure 8.

3.4. Detection-ECAM (Enhanced Channel Attention Mechanism with Self-Attention)

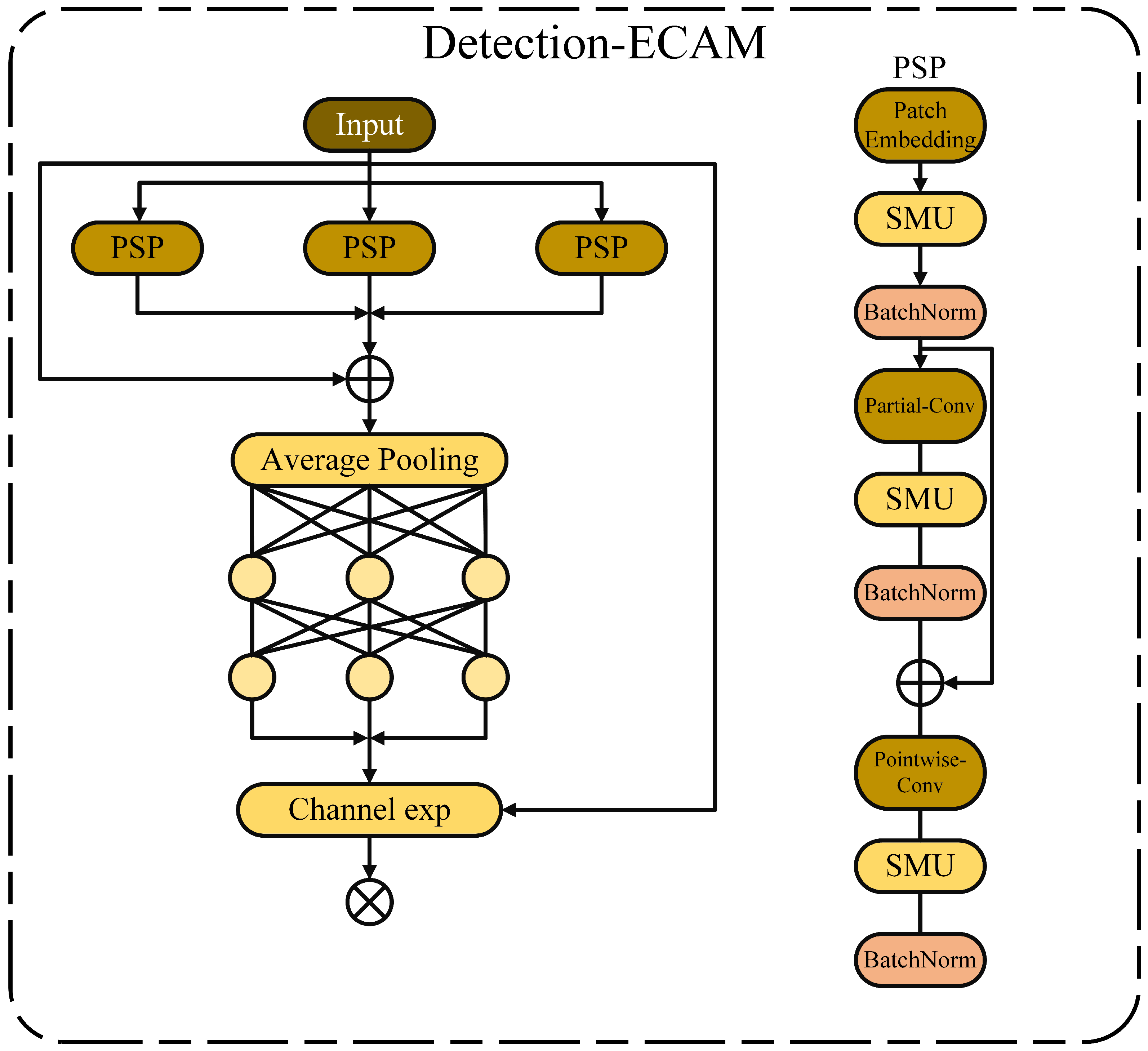
Helmet occlusion frequently occurs in traffic-dense environments, often leading to the detector’s inability to accurately detect helmets, thereby reducing the system’s precision and recall rate. Occlusion results in the loss of some data, making it difficult for the model to extract sufficient features for precise localization and detection. Helmet occlusion can be categorized into two types: occlusion between different helmets and occlusion caused by other objects. The former makes detection accuracy highly sensitive to the NMS threshold, leading to missed detections, while the latter causes feature disappearance and inaccurate localization. To address this challenge, this paper proposes the enhanced channel attention mechanism with self-attention (ECAM). ECAM enhances the detection capability of occluded targets, emphasizes the helmet regions in the image, and weakens the background areas accordingly, as shown in Figure 9.

This study observes that the feature maps of different channels are highly similar, leading to feature map redundancy in both standard convolution and depthwise separable convolution. However, when utilizing depthwise convolution (DWConv) or group convolution (GConv) to extract spatial features, while DWConv can effectively reduce FLOPs, it cannot simply replace regular convolution, as it causes a significant drop in precision. Chen J et al. [46] pointed out that partial convolution (PConv) can automatically mask invalid regions in the input feature map during the convolution process, demonstrating excellent performance when handling incomplete or unevenly distributed data. This characteristic allows PConv to focus better on valid information areas when processing images with complex backgrounds or occlusions, thereby improving the precision of feature extraction. We have experimentally verified that PConv achieves higher feature extraction precision than traditional convolutions when handling occluded images, as confirmed in the ablation experiment Section 4.4.5. The masking mechanism of PConv effectively reduces the interference from invalid regions during feature extraction, enhancing the model’s ability to capture valid information. In the first part of ECAM, the convolution with residual connections is PConv, which has lower FLOPs compared to regular convolution and higher computational speed (FLOPs) than DWConv/GConv. The working principle of PConv is shown in Figure 10. It applies regular convolution to a subset of the input channels for spatial feature extraction, without modifying the remaining channels. For continuous or regular memory access, this study considers the first or last contiguous channel as the representative of the entire feature map for computation. Without loss of generality, we assume that the input and output feature maps have the same number of channels. The computational cost (FLOPs) of PConv is defined as follows:

$$\mathrm{h}\times w\times k^2\times C_P^2$$

(11)

The memory access pattern of PConv is as follows:

$$h\times w\times 2c_p+k^2\times c_p^2$$

(12)

Here, h and w represent the width and height of the feature map, k is the size of the convolution kernel, and $C_p$ is the number of channels in a standard convolution. With a typical partial ratio $r={\displaystyle \frac{c_p}{c}}={\displaystyle \frac{1}{4}}$, the FLOPs of a PConv is only ${\displaystyle \frac{1}{16}}$ of a regular Conv. The memory access of PConv is only one-quarter of that of the standard convolution.

To fully and effectively utilize the information from all channels, this study further adds pointwise convolution (PWConv) after PConv, which can leverage the redundancy in intermediate convolutions and further reduce FLOPs, that is:

$$h\times w\times (k^2\times c_p^2+c^2)$$

(13)

The second part of ECAM utilizes a two-layer fully connected network to integrate information from each channel, enabling the network to strengthen the connections between all channels. By learning the relationship between occluded and non-occluded helmets in previous steps, the model aims to address the missing cases in occlusion scenarios. However, excessive use of these layers throughout the network could limit feature diversity, thereby degrading network performance and potentially reducing overall computation speed. The SMU (Sigmoid-Multiplied Unit) activation function is a self-gating activation function. Biswas K et al. [47] pointed out that it adapts features by multiplying the input features with the output of the sigmoid function. Compared to the GELU (Gaussian Error Linear Unit) activation function, the SMU activation function is more effective in preserving the detailed information of features while reducing the over-smoothing phenomenon. We conducted a detailed comparison experiment between the SMU and GELU activation functions, as confirmed in the ablation experiment Section 4.4.5. The experimental results show that the SMU activation function better preserves the detailed information of features when processing images with rich details, thereby demonstrating higher performance in image classification and object detection tasks. To avoid this, this study places BatchNorm and the activation function SMU after each intermediate layer of PWConv to maintain feature diversity and achieve lower latency. The ECAM structure is shown in Figure 9. This exponential normalization provides a monotonic mapping relationship, making the results more tolerant of positional errors. Finally, the output of the ECAM module is used to scale the attention of the original features, allowing the model to more effectively handle the occlusion of non-motorized vehicles, riders, and helmets, while also reducing computational load. This is confirmed in the visual experiments in Section 4.4.6.

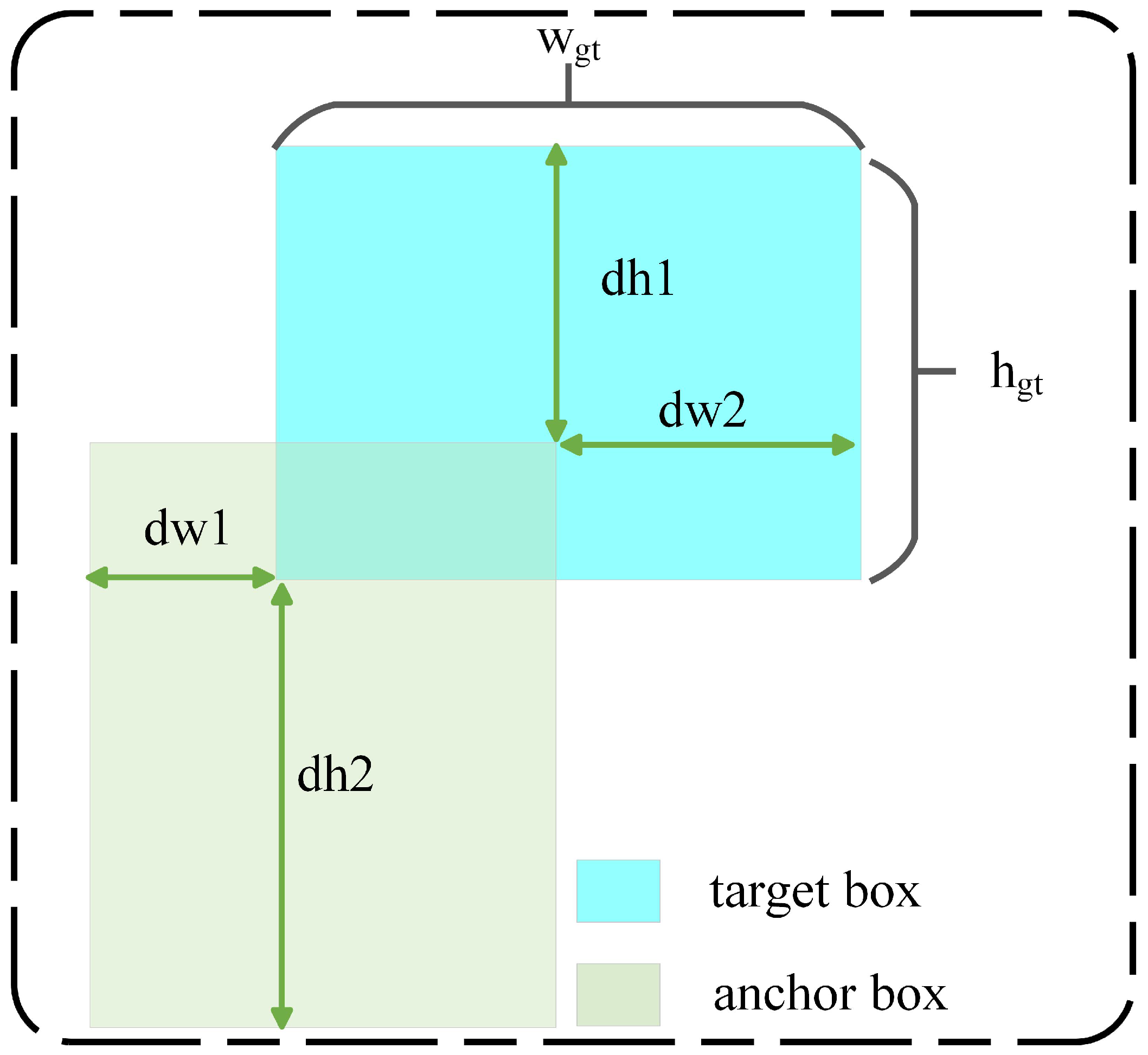
3.5. Enhanced Precision-IoU

There are currently many regression-based loss functions, such as GIoU [48], which introduces the minimum enclosing box of the predicted and ground truth boxes to obtain the relative weight of the predicted and ground truth boxes in the closure area. However, the minimum enclosing rectangle must be computed for each predicted and ground truth box, limiting the computation and convergence speed. DIoU builds upon IoU by directly regressing the Euclidean distance between the centers of the two boxes, improving convergence speed. CIoU extends DIoU by incorporating the consistency of aspect ratios between the predicted and ground truth boxes. EIoU [49] adds a penalty term that splits the aspect ratio influence factor into separate calculations for the target box and anchor box’s width and height, based on the penalty term of CIoU. This loss function consists of three components: overlap loss, center distance loss, and width–height loss. The first two components follow the approach in CIoU, while the width–height loss directly minimizes the width and height differences between the target and anchor boxes, leading to faster convergence. SIoU [50] redefines the distance loss, effectively reducing the degrees of freedom in regression, thus accelerating network convergence and further enhancing regression accuracy. However, existing IoU loss functions suffer from unreasonable penalty factors, causing anchor boxes to enlarge and slowing convergence in object detection. Although CIoU and EIoU acknowledge this issue, they do not address its root cause. Additionally, the current IoU loss functions have limitations, such as failing to accurately reflect the differences between the anchor box and the target box, neglecting object size, or degrading performance under certain conditions. The formula is as follows.

$$IoU={\displaystyle \frac{A\bigcap B}{A\bigcup B}}$$

(14)

However, this study thoroughly analyzes the underlying causes of anchor box enlargement in existing loss functions. It was observed that using a factor related to the size of the smallest enclosing box between the anchor box and the target box as the denominator in the penalty term is inappropriate, as it leads to the expansion of the anchor boxes during the regression process and significantly slows down the convergence speed. Therefore, IoU-based regression loss functions require more appropriate penalty terms. To address the issue of anchor box enlargement and the limitations of existing IoU-based loss functions, EPIoU introduces a penalty factor P, that adapts to the target size. Since the denominator of P solely depends on the size of the target box and is independent of the size of the smallest enclosing box between the anchor and target boxes, using P as the penalty factor in the loss function does not cause anchor box expansion. Unlike penalty factors used in other loss functions, the expansion of the anchor box does not alter P. The penalty factor P is defined as follows:

$$P={\displaystyle \frac{\left(\frac{d{w}_1}{w_{gt}}+\frac{d{w}_2}{w_{gt}}+\frac{d{h}_1}{h_{gt}}+\frac{d{h}_2}{h_{gt}}\right)}{4}}$$

(15)

where $d{w}_1$, $d{w}_2$, $d{w}_3$ and $d{w}_4$ represent the absolute distances between the edges of the predicted and target boxes, while $w_{gt}$ and $h_{gt}$ denote the width and height of the target box, respectively.

Using (P) as a penalty factor in the loss function does not cause the anchor boxes to expand because the denominator of (P) depends solely on the size of the target box and is independent of the size of the minimal enclosing box of the anchor box as well as the target box. Unlike the penalty factors used in other loss functions, the expansion of the anchor box does not affect (P). Furthermore, unless the anchor box fully overlaps with the target box, (P) will always degrade to zero. Additionally, (P) adapts to the size of the target. Through the effective design of the loss function, the regression process of the anchor box can be better aligned with the practical needs of object detection, thereby improving the overall model performance.

Therefore, this study designs a gradient adjustment function $f\left(x\right)$ based on the quality of the anchor boxes to meet these requirements. The improved EPIoU combines a target size adaptive penalty factor and a gradient adjustment function based on the quality of the anchor boxes. This includes a penalty term with the size of the target box as the denominator. The EPIoU loss thus guides the anchor boxes to regress along an effective path, leading to faster convergence compared to the existing IoU-based losses, preventing anchor box expansion, and better adapting to the target size. This results in faster convergence and higher detection precision. In the $L_{EPIoU}$, the EPIoU loss only uses the edges of the target box as the denominator in the loss factor. $L_{EPIoU}$ is illustrated in Figure 11. The computation formula is as follows:

$$f\left(x\right)=1-e^{-x^2}$$

(16)

$$EPIoU=IoU-f\left(p\right),-1\le EPIoU\le 1$$

(17)

$$L_{EPIoU}=1-EPIoU=L_{IoU}+f\left(P\right),0\le L_{EPIoU}\le 2$$

(18)

The study designs an EPIoU loss with a stronger penalty factor, addressing the issue of box expansion and a series of limitations in the existing IoU, thereby achieving faster convergence and higher precision. It can more accurately assess the quality of object detection results, as confirmed in Section 4.

4. Experimental Results and Analysis

4.1. Data Sets and Preprocessing

The HelmetVision dataset constructed in this study, through systematic multi-dimensional data collection and full-process quality control, has created a comprehensive, finely annotated, and highly robust benchmark dataset for two-wheeled vehicle helmet detection. During the data collection phase, a three-source fusion strategy was employed to ensure scene diversity: Firstly, high-precision 4K cameras (resolution 3840 × 2160@30 fps) were deployed in six major domestic city transportation hubs (covering core areas of both first- and second-tier cities). Over the course of 3 months, 1200 h of continuous video data were collected, covering five typical weather conditions: clear, cloudy, rainy, foggy, and snowy. Through a 5 s interval frame extraction strategy, 82,000 raw images were extracted, with environmental light intensity (Lux values across 4 orders of magnitude, from 10,000 in bright glare conditions) recorded synchronously. Secondly, a distributed web crawler was built based on the Scrapy framework to capture 34,000 publicly available surveillance images, focusing on augmenting data from special conditions such as backlighting, haze, and nighttime. The data samples cover seven types of mainstream helmets (full-face, half-face, open-face helmets, etc.), with strict control of the weather distribution (clear 40%/cloudy 25%/rain 20%/fog 10%/snow 5%) and occlusion levels (no occlusion 50%/partial occlusion 35%/heavy occlusion 15%).

In the data cleaning phase, a two-level filtering mechanism was constructed to enhance data quality: Firstly, the dHash perceptual hash algorithm was used to calculate image similarity, removing redundant samples with a similarity of >95% (a total of 30.3% removal rate). Then, Laplacian variance detection (with a threshold set to 500) was used to identify and remove 3200 blurry images. Notably, 15% of difficult samples were retained (defined by standards including visible area 40%) to enhance the model’s adaptability to real complex scenarios. The annotation process followed industrial-grade standards: a team of three professionally trained annotators (with an average annotation experience of >500 h) used the LabelImg++ (V2.4.0) tool for multi-dimensional annotation. The Kappa consistency coefficient during the annotation process was >0.85, ensuring the reliability of the annotation results. The generated XML format files were then converted to txt format. The bounding boxes were strictly aligned with the target’s outer contour (with a maximum localization error controlled within ±2 pixels), and three semantic labels were defined: helmet (helmet correctly worn), without-helmet (no helmet worn), and two-wheel (overall bounding box of the electric vehicle). The dataset division followed rigorous scientific principles: A total of 9200 images were split into a training set (8280 images) and a test set (920 images) at a 9:1 ratio. Among them, small targets (96 × 96) account for 15%. The dataset covers typical scenes such as urban roads (50%), intersections (30%), commercial areas (15%), and tunnels (5%). The resolution distribution simulates the configuration of real surveillance systems: 4K (30%), 1080p (50%), and 720p (20%) form a multi-tiered image quality system. As shown in Figure 12, typical annotated sample cases include partially occluded targets on foggy days, samples from strong light environments, and high-density scenes (up to 14 vehicles detected in a single frame).

The dataset construction process forms a three-stage closed-loop system of “source diversity control—annotation specification constraint—enhancement strategy adaptation.” Through the cross-control of geographic distribution, environmental variables, and device parameters, scene generalization is achieved. Strict quality cleaning and difficult sample retention mechanisms reinforce the data’s representativeness. The use of physical simulation and generative adversarial technologies helps to overcome data bottlenecks. All technical details are fully recorded, and related parameter configurations are open-sourced to ensure experimental reproducibility, providing high-precision and robust benchmark data support for the development of two-wheeled vehicle safety monitoring algorithms.

4.2. Evaluation Indicators

Model performance evaluation is particularly important in model validation. For helmet detection tasks, the following metrics are primarily used: Precision (P) measures how many of the detected helmet targets are actually true helmet targets. Recall (R) refers to the proportion of correctly detected positive samples out of all actual positive samples. Mean Average Precision (mAP) provides a comprehensive evaluation of the model’s performance across multiple categories by calculating the Average Precision (AP) for each category and taking the average, reflecting the detection results for different categories. IoU (Intersection over Union) measures the overlap between the predicted bounding box and the ground truth bounding box. mAP can be calculated at different IoU thresholds, such as mAP@0.5, which represents the average precision when the IoU threshold is 0.5. Parameters (Params) refer to the total number of trainable parameters in the model, which is important for model selection and optimization. FLOPs (Floating Point Operations) measure the total number of floating-point operations required during inference or training, reflecting the computational complexity of the model. FPS (frames per second) represents the model’s inference speed, calculated by dividing the total number of images by the total time taken. The F1 score is the harmonic mean of precision and recall.

$$\mathrm{Precision}={\displaystyle \frac{TP}{TP+FP}}$$

(19)

$$Recall={\displaystyle \frac{TP}{TP+FN}}$$

(20)

$$\mathrm{AP}={\int }_0^1\mathrm{Precision}\left(R\right)dR$$

(21)

$$\mathrm{mAP}={\displaystyle \frac{{\sum }_{n=1}^{N}A{P}_n}{N}}$$

(22)

$$\mathrm{FLOPS}=(2\times c_{in}\times K^2)\times H\times W\times C_{out}$$

(23)

$$\mathrm{FPS}={\displaystyle \frac{f_n}{T}}$$

(24)

$$\mathrm{F}1\mathrm{Score}=2\times {\displaystyle \frac{\mathrm{Precision}\times Recall}{\mathrm{Precision}+Recall}}$$

(25)

In this context, P represents precision, and R represents recall. $C_{in}$ denotes the number of input channels, K refers to the size of the convolution kernel, and $C_{out}$ indicates the number of output channels. The dimensions of the output feature map are $H\times W$. N represents the number of classes, and $P_n$ refers to the average precision of the n-th class. $f_n$ represents the total number of images, and T indicates the total time.

In object detection systems, the performance parameters are prioritized in the following order: mAP, precision, and recall. This is because mAP takes both precision and recall into account, thereby eliminating the bias introduced by a single evaluation metric. Additionally, FPS (frames per second) is used to assess the detection speed of the system. Params represents the number of model parameters, with a smaller number of parameters implying a more lightweight model.

4.3. Experimental Environment

The experiment is conducted on a high-performance computing system equipped with a single RTX 4090 GPU (24 GB) (NVIDIA, Santa Clara, CA, USA ), an AMD EPYC 7T83 64-core processor(AMD, Austin, USA), and 90 GB of memory, running Ubuntu 20.04 LTS as the operating system. The experiment is executed under the PyTorch 1.11.0 framework, with development carried out using Python 3.8, ensuring ample computational resources and up-to-date software support for efficient training and inference tasks in deep learning models. Additionally, the system provides 30 GB of disk space to store large-scale datasets and model files. To achieve a well-trained model, the number of training epochs is set to 300, with the mosaic data augmentation disabled in the last 10 epochs. The learning rate is set to 0.01, and the SGD (Stochastic Gradient Descent) optimization method is used. This experimental setup is employed for subsequent experiments.

4.4. Comparison and Ablation Experiments

4.4.1. Backbone Feature Enhancement Experiments

With the rapid development of object detection, numerous innovations in neck networks have emerged. To demonstrate the high performance of the FENN neck network, this study compares the FENN neck network with other state-of-the-art neck networks, including Bi-FPN, HS-FPN [51], AFPN [52], GFPN [53], and GD, based on the original model incorporating the GMET module, MSPP module, SEAM attention mechanism, and EPIoU loss function. The experimental results are shown in

Table 1. Neck Network Comparison Experiment.

Reconstruction Mechanism	P%	R%	mAP@0.5%	Parameters/M	FLOPs/G	Weight/MB	Time/ms	F1%
Baseline (YOLOv8)	79.1	74.2	79.0	3.01	8.1	6.3	3.1	76.6
BiFPN (CVPR)	77.4	70.9	76.6 (−2.4)	1.71	7.1	3.9	2.2	74.0
HSFPN (CBM)	78.3	69.3	75.8 (−3.2)	1.86	6.7	4.0	1.7	73.6
AFPN (SMC)	78.6	66.8	75.3 (−2.7)	2.37	8.0	5.2	2.0	72.5
GFN (ICCv)	75.7	66.5	76.1 (−2.9)	3.0	7.9	6.4	2.5	73.0
GD (NeurIPS)	78.6	71.3	76.4 (−2.6)	5.69	9.9	6.4	3.1	74.8
FENN (ours)	84.4	76.4	83.7 (+4.7)	5.95	8.7	12.5	2.4	80.2

.

This study validates the superiority of the FENN neck network in complex visual tasks by comparing it with mainstream feature pyramid network improvements. Although Bi-FPN enhances multi-scale representation capabilities through a bidirectional feature transfer mechanism, its precision (77.4%), recall (70.9%), and mAP@0.5 (76.6%) decrease by 1.7%, 8.2%, and 2.4%, respectively, compared to the baseline model (YOLOv8n). HS-FPN, which employs a hierarchical feature pyramid structure, experiences a more significant decline in recall (69.3%) and mAP@0.5 (75.8%). AFPN, while achieving a precision (78.6%) close to the baseline, suffers a sharp drop in recall (66.8%), which decreases by 12.3%, exposing deficiencies in semantic information integration. GFPN introduces global features, leading to a significant increase in computational cost (6.4 G) and inference time (73.0 ms), but its mAP@0.5 (76.1%) decreases by 2.9%. The GD mechanism, with a parameter count (5.69 M) close to FENN (5.95 M), still exhibits a 6.4% gap in mAP@0.5 (76.4%).

The FENN network, through its innovative feature architecture, surpasses the comparison models comprehensively with a precision of 84.4%, recall of 76.4%, and mAP@0.5 of 83.7%, while maintaining a reasonable parameter count (5.95 M) and computational cost (8.7 G). This results in improvements of 5.3%, 2.2%, and 4.7% over the baseline, respectively. Notably, in small object detection tasks, the FENN network reduces the missed detection rate by 9.6% compared to the best performing comparison model, effectively solving the challenge of co-detecting non-motorized vehicles and rider helmets in low-resolution images. This provides reliable technical support for intelligent transportation scenarios.

4.4.2. Comparison of Multiple Attention Mechanisms Experiments

The uniqueness of Mamba lies in the core module VSS mechanism, which is detached from the traditional attention and MLP modules. By integrating selective SSM and removing the attention and MLP modules, Mamba provides a simpler and more unified architecture, which leads to better scalability and performance. The architecture effectively improves the model’s ability to perceive the global information of the image through the four-way scanning strategy, which allows the model to understand the scene more comprehensively and enhances the ability to capture the helmet distribution features in complex scenes, thus exceeding the performance of the Transformer model. The GMET attention mechanism well solves the problems of information loss or blurring and gradient vanishing. In order to verify the advantages of this study’s model after integrating the GMET module, based on the original model integrating the FENN neck network, the MSPP module, and the SEAM attention mechanism, this study is conducted by comparing six mainstream attention mechanism modules, CBAM [54], EMA [55], CA [32], GMA [56], SE [57], and SA [58], with the GMET module Comparisons were made, mainly in terms of P, R, Map@0.5, mAP@0.5-0.95, number of parameters, and computation of multiple evaluation criteria.

The experimental results, as shown in

Table 2. Attention mechanism module comparison experiment.

Reconstruction Mechanism	P/%	R/%	mAP@0.5/%	Parameter/MB	FLOPs/G	F1/%
CBAM (ECCV)	81.9	76.1	81.3	5.04	13.0	79.2
EMA (CASSP)	82.1	76.5	80.2	5.32	12.9	79.9
CA (CVPR)	83.2	76.7	80.9	5.11	12.0	79.8
GAM (TIP)	83.7	76.3	81.4	7.21	17.1	79.8
SE (CVPR)	82.6	77.9	81.6	5.18	13.1	80.2
SA (ICASSP)	82.9	76.0	81.2	5.04	12.9	79.4
GMET (ours)	84.4	76.4	83.7	5.93	8.7	80.2

, demonstrate the groundbreaking advancements of the GMET mechanism in terms of global feature perception and computational efficiency. With an increase in parameters to only 5.93 MB, the GMET module achieves leading performance in both precision (84.4%) and recall (76.4%), outperforming the second-best GAM and SE modules by 0.7 and 1.8 percentage points, respectively. Its mAP@0.5 of 83.7% not only significantly surpasses the SE module’s 81.6%, but also improves the average precision benchmark by 2.1 percentage points. The computational load of GMET has been compressed to 8.7 GB, representing a 49.1% reduction compared to the traditional GAM module (17.1 GB) and a 33.1% reduction compared to the CA module (13.0 GB), while maintaining an F1 score of 80.2%, which is on par with the SE module. The experimental data indicates that this mechanism can better capture key features across the entire global scope, successfully overcoming the technical bottleneck of balancing global perception and computational efficiency in complex scenarios, all while keeping the model lightweight (with a 17.8% reduction in parameters compared to GAM).

4.4.3. Loss Function Comparison Experiment

To verify the effectiveness of the EPIoU loss function in the GMAL-YOLO model, this study compares the EPIoU with CIoU, DIoU, Alpha-IoU [59], EIoU, SIoU, and WIoUv3 [60], respectively, based on the model fusion of the FENN neck network, the GMET module, the MSPP module, and the SEAM attention mechanism. Based on the experimental results of the loss function comparison shown in

Table 3. Loss function comparison experiment. An upward arrow indicates the improvement over the baseline model, while a downward arrow indicates the decline from the baseline model.

Loss Function	P%	R%	mAP@0.5%	mAP@0.5–0.95%
CIoU (baseline)	79.1	74.2	79.0	49.2
DIoU (AAAI)	83.3	68.9	81.9 (↓2.9)	52.2
Alpha-IoU (NeurIPS)	83.1	77.6	80.2 (↓1.2)	51.9
EIoU (Neurocomputing)	80.8	77.5	82.1 (↓3.1)	52.4
WIoUv3	84.0	79.1	81.2 (↓2.2)	52.7
Shape-IoU	82.3	79.5	81.8 (↓1.8)	52.3
EPIoU (ours)	84.4	76.4	83.7 (↑4.7)	53.2

, the proposed PloU loss function demonstrates significant performance advantages. In the tasks of non-motorized vehicle and rider helmet detection, PloU leads comprehensively with a precision of 84.4%, recall of 76.4%, and mAP@50% of 83.7%, outperforming the traditional CloU baseline by 5.3%, 2.2%, and 4.7%, respectively. Its mAP@50–95% metric of 53.2% also surpasses the current state-of-the-art methods. The comparison experiments reveal that although DloU performs well in terms of precision (83.3%) and mAP@50–95% (52.2%), its recall drops sharply by 5.3% to 68.9%. Alpha-IoU, while achieving a recall of 77.6% close to PloU, shows a notable gap in mAP@50% (80.2%). Shape-IoU, though exhibiting good balance, lags behind PloU by 1.9 percentage points across all metrics. These data thoroughly validate the unique advantage of PloU in balancing bounding box regression accuracy and convergence speed in complex scenarios, providing an innovative solution for intelligent monitoring of safety protective equipment.

4.4.4. Comparative Experiments with Classical Algorithms

To comprehensively validate the superiority of the GMAL-YOLO algorithm, we conducted comparative experiments with state-of-the-art object detection algorithms under identical experimental conditions for non-motorized vehicle and rider helmet detection tasks, including YOLOv8-N, Gold-YOLO, DAMO-YOLO [61], Faster R-CNN, YOLOv10, and RT-DETR(R18) [62]. As demonstrated in

Table 4. Classical algorithm model comparison experiment.

Classical Algorithm	P/%	R/%	mAP@0.5%	mAP@0.5-0.95%	Params (M)	FLOPs (G)	Time (ms)	F1/%
YOLOv8-N	79.1	74.3	79.0	49.2	3.01	8.1	3.1	76.6
Gold-YOLO (NeurIPS)	79.4	76.2	73.6	45.2	5.97	12.1	2.0	72.2
DAMO-YOLO (arXiv)	78.5	67.0	74.2	44.3	8.55	18.1	9.8	73.4
Faster-RCNN (NIPS)	79.3	68.0	74.8	48.5	6.23	13.5	10.9	73.5
YOLOv10-N (arXiv)	75.4	71.2	73.8	44.5	2.70	8.2	11.9	73.2
RT-DETR (Res-18)(CVPR)	81.5	71.5	79.8	52.9	19.88	56.9	12.8	77.3
YOLOv9-N	78.9	65.0	76.9	43.6	2.10	8.0	2.4	71.3
Grounding DINO (ECCV)	82.2	75.1	80.1	52.8	13.76	37.6	14.2	78.5
GMAL-YOL (ours)	84.4	76.4	83.7	53.2	5.93	8.7	2.4	80.2

, the proposed GMAL-YOL algorithm exhibits breakthrough performance in this specialized detection task. Based on the cross-model comparison experiment results in Table 4, along with the corresponding precision–recall curves and F1 scores (Figure 13 and Figure 14), the proposed GMAL-YOL algorithm demonstrates groundbreaking performance in the tasks of the non-motorized vehicle and rider helmet detection. Compared to the baseline model YOLOv8-N, GMAL-YOL achieves a triple improvement in precision with a parameter size of 5.93 MB: precision (84.4%, ↑5.3%), recall (76.4%, ↑2.1%), and mAP@0.5 (83.7%, ↑4.7%), while also enhancing detection speed (2.4 ms) by 23.0% compared to YOLOv8-N (3.1 ms). In comparison with models of similar parameter size, Gold-YOLO shows a performance gap of 10.1% in mAP@0.5 (73.6%), while DAMO-YOLO, with a significantly larger parameter size of 8.55 MB, still lags behind by 9.5 percentage points, achieving mAP@0.5 of 74.2%. It is noteworthy that GMAL-YOL maintains a computational load (8.7 G) similar to that of YOLOv10-N (8.2 G), while improving mAP@50–95% to 53.2%, surpassing the two-stage benchmark Faster R-CNN (48.5%) by 4.7 percentage points. Even when compared to the large-scale model RT-DETR-R18 (19.88MB/56.9G), GMAL-YOL achieves a 3.9% advantage in mAP@0.5 while maintaining parameter compression. The mAP@50 for YOLOv9-N is 76.9%, and the mAP@50–95 is 43.6%; the mAP@50 for Grounding DINO is 80.1%, and the mAP@50–95 is 52.8%. Although these advanced models achieve promising results, there is still a certain gap when compared to GMAL-YOLO. These results confirm that the algorithm, through its global multi-granularity attention mechanism, optimizes detection accuracy and inference efficiency in complex scenarios.

To rigorously validate the model’s generalization capability and robustness, cross-dataset evaluations were conducted on the VisDrone2019 and Tiny-person benchmarks, with experimental results detailed in

Table 5. Comparison experiments of classical algorithmic models on VisDrone2019 and Tiny-person datasets.

Datasets	Algorithms	P/%	R/%	mAP@0.5%
VisDrone2019	YOLOv8-N	44.4	32.7	32.9
	Gold-YOLO	46.0	34.1	34.4
	YOLOv10-N	44.4	33.0	33.2
	RT-DETR(Rs-18)	59.1	45.7	47.3
	GMAL-YOL (ours)	58.3	42.5	41.1
Tiny-person	YOLOv8-N	44.6	29.1	28.4
	Gold-YOLO	46.2	29.4	28.6
	YOLOv10-N	46.2	28.0	26.9
	RT-DETR(Rs-18)	56.0	39.3	28.9
	GMAL-YOL (ours)	55.7	40.3	29.6

. The proposed GMAL-YOL demonstrates exceptional cross-domain adaptability, achieving 55.7% precision and 40.3% recall on VisDrone2019, while maintaining a competitive 40.3% mAP@50% on the Tiny-person dataset. Notably, though RT-DETR(R18) shows superior single-dataset performance in VisDrone2019 (59.1% P, 47.3% mAP@50%), its Tiny-person performance plummets to 28.9% mAP@50%, revealing significant domain sensitivity. Comparatively, GMAL-YOL exhibits more balanced cross-domain capabilities, outperforming YOLOv8-N by 11.3% in VisDrone2019 precision (55.7% vs. 44.4%) and surpassing Gold-YOLO’s Tiny-person mAP@50% by 5.9 percentage points. Particularly noteworthy is the model’s 7.4% precision advantage over YOLOv10-N in VisDrone2019 while maintaining equivalent computational efficiency (8.7 G vs. 8.2 G FLOPs). The mAP@50 for YOLOv9-N is 76.9%, and the mAP@50–95 is 43.6%; the mAP@50 for Grounding DINO is 80.1%, and the mAP@50–95 is 52.8%. Although these advanced models achieve satisfactory results, there is still a certain gap when compared to GMAL-YOLO. These results substantiate that GMAL-YOL achieves optimal equilibrium between domain-specific accuracy and cross-domain stability, effectively addressing the performance degradation challenges typically observed in conventional detectors when transitioning between crowded urban scenes and small-object detection scenarios.

4.4.5. Ablation Experiments

According to the ablation experiment results in

Table 6. Ablation experiment. X indicates that the module was not included based on the baseline; ✓ indicates that the module was included based on the baseline.

Improved Name	FENN	ECAM	MSPP	GMET	EPIoU	mAP@0.5%	Parameter (MB)	FLOPs (G)	Time (ms)	Weight (MB)
baseline model	X	X	X	X	X	79.0	3.01	8.1	3.1	6.2
Improvement 1	✓	X	X	X	X	81.2 (↑2.2)	6.01	10.5	1.4	12.5
Improvement 2	✓	✓	X	X	X	81.8 (↑2.8)	5.93	9.6	2.2	12.2
Improvement 3	✓	✓	✓	X	X	82.6 (↑3.6)	6.12	9.8	2.3	12.7
Improvement 4	✓	✓	✓	✓	X	83.4 (↑4.4)	5.85	8.7	2.3	12.4
Improvement 5	✓	✓	✓	✓	✓	83.7 (↑4.7)	5.95	8.8	2.4	12.5

, this study achieves a balance between performance optimization and technological breakthroughs through a modular improvement strategy. First, the introduction of the FENN module increased the mAP@0.5 of the baseline model from 79.0% to 81.2% (↑2.2%), with the parameter size increasing from 3.01 MB to 6.01 MB and the computational load (FLOPs) rising from 8.1 G to 10.5 G, laying the foundation for subsequent optimizations. After incorporating the ECAM module, the parameter size decreased to 5.93 MB (a reduction of 1.3% compared to the FENN stage), the computational load was optimized to 9.6 G (an 8.6% reduction), and the mAP@0.5 improved to 81.8%. With the addition of the MSPP module, the parameter size slightly increased to 6.12 MB, and the computational load rose to 9.8G, but the average precision increased by 0.8%. Following this, the GMAL module was added, which, through lightweight design, reduced the parameter size to 5.85 MB, optimized the computational load to 8.7 G, and improved the mAP@0.5 to 83.4% (↑4.4%), also enhancing the detection performance of small objects. Finally, the EPIoU loss function completed the technological loop, bringing the mAP@0.5 to 83.7% (↑4.7%), with the parameter size at 5.95 MB and the computational load at 8.8 G under the lightweight architecture. Moreover, the inference time was optimized to 2.4 ms (a 23.0% reduction from the baseline of 3.1 ms). This step-by-step optimization path validates the synergistic effect of the modules in improving accuracy, controlling computational load, and enhancing small object detection performance.

To verify the effectiveness of the PConv and SMU activation functions in the ECAM attention mechanism, we conducted an ablation experiment using SEAM as the baseline model. We gradually added the PConv and SMU modules and observed the changes in the model’s performance metrics, including AP, mAP@0.5, and mAP@0.5–0.95, while also recording the number of parameters, FLOPs, and inference time. The experimental results presented in

Table 7. Ablation study of ECAM on PConv and SMU.

Module	AP%	mAP@0.5 /%	mAP@0.5–0.95%	Parameter/MB	FLOPs/G	Time/ms
SEAM	80.0	79.8	49.3	7.12	16.1	5.0
SEAM + Pconv	81.0	80.8 (↑ 1.0)	51.5	6.10	8.9	2.3
SEAM + SMU	80.5	80.2 (↑ 0.4)	49.8	6.82	13.2	3.4
SEAM + Pcon + SMU	81.3	81.0 (↑1.2)	52.2	6.12	9.1	2.2

indicate that adding either PConv or SMU alone improves performance, and their combined addition leads to further performance enhancement, with an AP of 81.3%, mAP@0.5 of 81.0%, and mAP@0.5–0.95 of 52.2%. The two components work together to improve detection performance. Moreover, after adding these modules, the model’s number of parameters and FLOPs are reduced, making it more efficient and lightweight, which is highly practical for resource-constrained devices. The inference time is also shortened, making it particularly attractive for real-time applications.

This paper independently evaluates the FENN, GMET, MSPP, ECAM, and EPIoU modules of GAML, as shown in

Table 8. Independent evaluation of each module in GAML (FENN, GMET, MSPP, ECAM, and EPloU).

Model	mAP@0.5 /%	mAP@0.5–0.95%	Parameter/MB	FLOPs/G	Time/ms
Baseline	79.0	49.0	3.01	8.1	3.1
+FENN	81.2 (↑2.2)	52.5	6.01	10.5	1.4
+ECAM	81.0 (↑2.0)	51.2	6.12	9.1	2.2
+MSPP	82.1 (↑3.1)	53.0	7.23	9.8	2.3
+GMET	83.2 (↑4.2)	52.4	5.68	8.5	2.3
+EPIoU	80.2 (↑1.2)	50.3	3.0	8.8	2.4

. Starting with the baseline model, each module was added individually. The results show that the FENN, ECAM, MSPP, GMET, and EPIoU modules improved mAP@0.5 to 81.2%, 81.0%, 82.1%, 83.2%, and 80.2%, respectively, and mAP@0.5–0.95 to 52.5%, 51.2%, 53.0%, 52.4%, and 50.3%, respectively. Each module plays a role in improving detection accuracy, enhancing object feature capture, multi-scale feature extraction, optimizing geometric metrics, and improving the robustness of detection results. Furthermore, the model’s number of parameters, computational complexity, and inference time remain reasonable after adding the modules, demonstrating the effectiveness and importance of each module, as well as the model’s efficiency and practicality.

4.4.6. Analysis of Qualitative Results

This study conducted a comprehensive comparison experiment across multiple scenarios, including sunny, cloudy, nighttime, occlusion, and dense traffic conditions, to verify the robustness advantage of GMAL-YOLO in complex environments. As shown in Figure 15, in a normal traffic scenario (Figure 15a), the baseline model YOLOv8 misidentified a traffic signal as an electric bike under sufficient sunlight (with a misdetection rate of 50%), while GMAL-YOLO achieved a dual breakthrough in electric bike detection precision of 0.96 and helmet recognition rate of 0.84, improving by 7.2% and 15.1%, respectively, compared to the baseline model. In a dense traffic scenario (Figure 15b), GMAL-YOLO, leveraging mechanisms such as multi-scale feature fusion (MSPP), reduced the missed detection rate from 46.1% to 15.3%. In extreme weather scenarios, such as rainy conditions (Figure 15c), its global Mamba architecture enhancement algorithm maintained electric bike and helmet detection precision at 90% and 83%, respectively, with a 28.5% reduction in missed detection rate compared to the baseline model, significantly overcoming target confusion caused by reduced visibility. In low-light environments with small targets (Figure 15d), GMAL-YOLO achieved a helmet detection precision of 0.81, reducing the missed detection rate for small electric bikes from 33.2% to 6.7% (with a precision of 0.81, an improvement of 8.6% over YOLOv8), enabling precise target recognition even under foggy and rainy conditions, fully meeting industrial-grade detection standards. These technological innovations form a synergistic effect, allowing the model’s overall performance metrics (F1 score) to reach 0.80, providing a theoretically sound and practically applicable solution for rider safety monitoring in intelligent transportation scenarios. Under the same test conditions, GMAL-YOLO’s comprehensive performance significantly outperformed the current mainstream models Gold-YOLO and YOLOv10, validating the advancement of its technical solution and its practicality in intelligent transportation safety detection.

Based on the results of the multi-dimensional ablation experiment in Figure 16, this study quantitatively validates the effectiveness of the model improvement components from three aspects: In low-resolution occlusion scenarios (Figure 16a), the FENN neck network, through the cross-layer feature fusion mechanism, improves non-motorized vehicle detection precision from 0.77 in the baseline model to 0.83 (+14.2% mAP), significantly overcoming the feature confusion issue in low-resolution settings. In heavily occluded scenarios (Figure 16a,b), the ECAM attention mechanism, through spatial-channel dual-path collaborative feature residual compensation, improves detection precision by 13% when 70% of the rider and electric bike are occluded, while reducing the helmet missed detection rate, effectively solving the problem of missing local features of the target. For multi-scale scenarios (Figure 16c), the GMET module’s global receptive field expansion strategy and MSPP mechanism capture broad contextual information of the image, generating an attention map. This attention map then weights the original features, reducing the misdetection rate of small electric bikes by 50%. The three sets of experimental results reveal the FENN network builds basic feature representations, the GMET module enhances the model’s ability to capture crowd distribution features in complex scenarios and increases the global receptive field, MSPP improves the model’s ability to aggregate multiple scales in complex scenes, and the ECAM mechanism enhances the detection accuracy of occluded targets. Meanwhile, P-IOU achieves faster convergence speed, forming a synergistic effect in the technological chain. As a result, the model’s overall missed detection rate is reduced by 31.3% compared to the baseline, while the model’s precision increases to 84.4%. The three sets of control experiments systematically validate the synergistic effect of the GMAL-YOLO technological innovation chain in terms of resolution robustness, occlusion adaptability, and scale sensitivity.

Based on the cross-domain generalization experiment results in Figure 17, this study verifies the multi-scene adaptability of GMAL-YOLO through dual benchmark tests on the VisDrone2019 (drone perspective) and Tiny-person (dense small target scene) datasets. In the VisDrone2019 dataset, GMAL-YOLO significantly outperforms the comparison models in detecting most target objects, with an average improvement of 3.8% over Gold-YOLO and 5.2% over YOLOv10-N. In the Tiny-person dataset, although it did not achieve the highest precision (1.3% lower than RT-DETR), it improved detection precision for coastline pedestrians (mAP 68.1%) and miniature boats (mAP 62.4%) by 6.8% compared to the baseline model YOLOv8-N. Additionally, it maintains a 9.3% advantage in missed detection rate in dense crowd scenes (>50 people/frame). The experimental results indicate that GMAL-YOLO demonstrates strong robustness in cross-domain feature transfer and multi-scale target detection, particularly showcasing exceptional cross-domain generalization capabilities in urban traffic and coastline monitoring scenarios.

5. Conclusions

This study aims to develop a detection algorithm for non-motorized vehicles and rider helmet compliance, proposing an enhanced GMAL-YOLO framework based on the YOLOv8 architecture. Key innovations include a restructured Feature Enhancement Neck Network (FENN) to strengthen multi-scale feature fusion capabilities, along with the integration of Global Multi-scale Enhancement Transformer (GMET) and Multi-Scale Pyramid Pooling (MSPP) modules in the backbone network. These architectural advancements enhance global feature perception and multi-scale aggregation while reducing computational complexity. The redesigned detection head incorporates a robust self-supervised equivariant attention mechanism (ECAM) to optimize critical feature extraction efficiency. Furthermore, the optimized Position-aware Intersection over Union (EPIoU) loss function precisely quantifies bounding box overlap, effectively resolving helmet occlusion challenges and boosting performance across complex scenarios. The GMAL-YOLO algorithm performs excellently in the helmet detection task but has certain limitations. Despite the introduction of GMET and MSPP modules to reduce computational complexity, its demand for computational resources remains high, limiting its real-time application on embedded systems and mobile devices. In complex scenarios such as extreme weather and insufficient lighting, the algorithm’s detection performance may be affected, and its ability to detect rare or abnormal helmet-wearing patterns still needs further optimization. Additionally, its generalization ability is limited, and directly applying it to other object detection tasks may require adjustments to the network structure and parameters. However, the GMAL-YOLO algorithm has broad application potential and can be extended to various fields, such as intelligent transportation systems, security monitoring, industrial production, and smart logistics. Future research will focus on improving the algorithm’s speed and accuracy, exploring more efficient receptive field expansion methods and attention mechanisms, enhancing the model’s adaptability and generalization ability, integrating multi-modal data, achieving model compression and hardware acceleration, and promoting collaborative applications with other technologies to further improve the algorithm’s performance and expand its application scope. Overall, the GMAL-YOLO algorithm proposed in this study provides an innovative and effective solution to the challenge of helmet-wearing detection in real-world scenarios. Future research will be dedicated to further optimizing the algorithm’s speed and accuracy and exploring its application in broader areas, such as traffic safety.