Robust H_∞ Time-Varying Formation Tracking for Heterogeneous Multi-Agent Systems with Unknown Control Input

Abstract

This paper studies the robust $H_{\infty }$ time-varying formation tracking (TVFT) problem for heterogeneous nonlinear multi-agent systems (MASs) with parameter uncertainties, external disturbances, and unknown leader inputs. The objective is to ensure that follower agents track the leader’s trajectory while achieving a desired time-varying formation, even under unmodeled dynamics and disturbances. Unlike existing methods that rely on global topology information or homogeneous system assumptions, an adaptive control protocol is proposed in full distribution, requiring no global topology information, and integrates nonlinear compensation terms to handle unknown leader inputs and parameter uncertainties. Based on the Lyapunov theory and laplacian matrix, a robust $H_{\infty }$ TVFT criterion is developed. Finally, a numerical example is given to verify the theory.

1. Introduction

In the last few years, multi-agent system (MAS) strategy has received considerable attention [1,2]. The main goal of the strategy is to develop efficient control protocols that allow the agents with the ability to interact with each other to realize and keep the preset formation in accordance with the particular mission needs. Conventional robotic approaches, such as the ones described in [3], the virtual architecture [4] and the leading follower strategies, have been widely investigated. But, there are intrinsic limits to approaches that influence MAS performance [5]. For instance, the virtual structure approach faces challenges in controlling autonomous agents with purely distributed information. Additionally, behavior-based methods often face difficulties in constructing accurate mathematical models to analyze system stability. In leader–follower strategies, the failure of a leader may destabilize the entire system.

Along with the progress of the consensus control theory, there is increased research on MAS formation control because of its robust performance, low computation cost, and stable performance [6,7,8,9,10,11,12,13,14,15]. In [16], a control protocol is proposed to guarantee high-order linear MAS to obtain the expected formation.

What should be noticed is that MAS must not only set up the desired pattern of the formation, but also make sure it follows the path of the leader precisely. This is especially important in the case of a target siege or combined assault. Expanding on consensus theory, a formation tracking (FT) protocol was suggested in [17] for linear MAS. Taking into account that every agent’s behavior is affected not only by the interaction with other agents, but also by their nonlinear dynamics, an FT criterion for MAS with nonlinear dynamics is proposed in [18].

Existing studies [16,17,18] have primarily focussed on consensus tracking and fixed-form FT problems of MASs. But, in the real world, MASs usually need to adapt dynamically. An unmanned surface ship, for instance, might have to quickly alter its formation in order to navigate a narrow channel. Thus, it is essential to develop a time-varying Formation Tracing (TVFT) control protocol adapted to MASs. Previous studies [19,20,21,22] focused on TVFT for first-order non-holonomic, second-order, and generic MASs. A novel TVFT scheme is presented in [23] for the management of a plurality of lower-triangle nonlinear MASs. In addition, the TVFT criterion has been developed in [2] for second-order linear MASs. However, because of the intrinsic nonlinearity of the agent, which satisfies Lipschitz conditions, it is very difficult to develop a distributed control protocol. The TVFT problem of Lipschitz MASs has not been solved yet.

In practice, MASs are usually composed of a variety of robots, which results in a variety of nonlinearities and variable parameters. Thus, addressing the FT problem in heterogeneous systems is of great importance. In this study, the FT problem for linear heterogeneous MASs is investigated by means of an output adjustment policy [24,25,26]. Hua et al. in [27] proposed a completely distributed TVFT model in order to deal with different parameters and different sizes of MASs. But, it is difficult to realize FT for heterogeneous nonlinear MASs because of the complexity of their dynamical behavior. Although numerous control strategies have been explored in relation to the TVFT problem [28,29,30], due to the complexity of the layer information derivatives in the analytical and design process, they are not suitable for TVFT. The TVFT problem of inhomogeneous nonlinear MASs is not resolved due to the presence of extraneous interference, parameter uncertainty, and unknown inputs [31].

To address this challenge, we present a kind of TVFT with a high robustness, $H_{\infty }$ TVFT, which can be used to deal with the outside interference and the uncertain parameters in spite of the master’s unknown input. The key contributions of this study are:

• To enhance the robust performance of MASs, which are not consistent with each other, such as dynamical instability, extraneous interference, and parameter uncertainty, an adaptive controller scheme is presented. This is different from the current FT control scheme, which is not dependent on the global topological information as described in [32]. In addition, several adaptive control methods are proposed in [27], these methods cannot deal with the extraneous interference and parameter uncertainty in the system.
• In this thesis, we build a robust $H_{\infty }$ TVFT criterion of heterogenous MASs. While prior studies [28,29,30] have examined consensus tracing for MASs, they have not been applied to the TVFT issue.

2. Problem Description

This paper examines a specific category of heterogeneous MASs, where the dynamics of the i-th follower are formulated by:

$$\begin{array}{c}\hfill {\dot{x}}_i\left(t\right)=\left(A+\Delta A_i\right)x_i\left(t\right)+{\mu }_i\left(t\right)+B\left(u_i\left(t\right)+f_i\left(x_i\left(t\right)\right)\right).\end{array}$$

(1)

Here, $x_i\left(t\right)\in {\mathbb{R}}^n$ and $u_i\left(t\right)\in {\mathbb{R}}^m$ denote the state and control input vectors of the i-th follower, respectively. B is a constant matrix with a rank of m, while $A\in {\mathbb{R}}^{n\times n}$ and $\Delta A_i$ denotes the time-varying unknown parameter uncertainty. The inherent nonlinear dynamical behavior of the system is characterized by the function $f_i\left(x_i\left(t\right)\right)\in {\mathbb{R}}^m$, while ${\mu }_i\left(t\right)\in {\mathbb{R}}^n$ represents the unmodeled external disturbance affecting the i-th follower. This disturbance is constrained to be a square integrable, satisfying the condition:

$$\begin{array}{c}\hfill {\int }_0^t\ell \left({\mu }_i\left(\tau \right)\right)d\tau <+\infty ,\end{array}$$

for $t\ge 0$, and $\ell \left(y\right)=y^{T}y$

Additionally, the dynamical model of the leader is expressed as:

$$\begin{array}{c}\hfill {\dot{x}}_0\left(t\right)=A{x}_0\left(t\right)+B\left(u_0\left(t\right)+f_0\left(x_0\left(t\right)\right)\right),\end{array}$$

(2)

Here, $x_0\left(t\right)\in {\mathbb{R}}^n$ and $u_0\left(t\right)\in {\mathbb{R}}^m$ denote the state vectors and external control input of the leader, respectively, satisfying that $f_0\left(x_0\left(t\right)\right)\in {\mathbb{R}}^n$ and $u_0\left(t\right)$ are continuous and bounded, i.e.,

$$\begin{array}{c}\hfill \parallel u_0{\left(t\right)\parallel }_{\infty }<\chi ,\end{array}$$

where $\chi$ is totally unknown for any follower, satisfying $\chi >0$.

Assumption 1.

For any $y_1\in {\mathbb{R}}^n$ and $y_2\in {\mathbb{R}}^n,$ we can find $0<{\varsigma }_i\in \mathbb{R}$, which satisfies

$$\begin{array}{c}\hfill \parallel f_i\left(y_1\right)-f_0\left(y_2\right)\parallel ⩽{\varsigma }_i\parallel y_1-y_2\parallel .\end{array}$$

(3)

Remark 1.

Assumption 1 represents the Lipschitz condition, which is commonly applicable in many real-world systems. For instance, the function $f_i(·)$ has been extensively used to study the cooperative control issues of heterogeneous nonlinear MASs, as shown in [7,8,13,14,33,34,35,36,37,38,39,40,41,42,43,44,45]. Thus, this technical assumption is considered to be relatively mild.

Assumption 2.

There exists a time-varying matrix $N_i$, such that $\Delta A_i=B{N}_i$, with $\parallel N_i\parallel ⩽{\zeta }_i$, where ${\zeta }_i(i=1,2,\dots ,M)$ are unknown positive constants.

To define the target formation at time t, let $h={(h_1^T,h_2^T,\dots ,h_M^T)}^T\in {\mathbb{R}}^{Mn}$ be a piecewise continuously differentiable function that meets the following inequality:

$$\begin{array}{c}\hfill {\int }_0^{t^{*}}\ell \left(h\left(\tau \right)\right)d\tau ⩽{\sigma }_1<\infty ,\end{array}$$

for any $0⩽t^{*}\in \mathbb{R}$, in which $0<{\sigma }_1$.

The communication topology among agents is modeled by a graph $\mathfrak{G}$, which adheres to the following condition.

Assumption 3.

The graph $\mathfrak{G}$ contains a spanning tree with the leader as the root node, and the communication topology among the followers is undirected.

Utilizing Assumption 2, the corresponding Laplacian matrix L for the graph $\mathfrak{G}$ can be formulated as follows:

$$\begin{array}{ccc}\hfill L& =& \left[\begin{array}{cc}0& \mathbf{0}\\ L_1& L_2\end{array}\right].\hfill \end{array}$$

Here, $L_1={(-{\vartheta }_{10},-{\vartheta }_{20},\dots ,-{\vartheta }_{M0})}^T\in {\mathbb{R}}^M,L_2={\left(l_{ij}\right)}_{M\times M}\in {\mathbb{R}}^{M\times M}.$  

Moreover, the definition of robust $H_{\infty }$ TVFT is introduced as follows.

Definition 1.

The robust $H_{\infty }$ TVFT for heterogeneous nonlinear MASs with external disturbance given by (1) and (2) is achieved if the FT error ${\epsilon }_i\left(t\right)(i=1,2,\dots ,M)$ satisfying

$$\begin{array}{ccc}& & \sum _{i=1}^M{\int }_0^t\ell \left({\epsilon }_i\left(\tau \right)\right)d\tau ⩽a+r^2\sum _{i=1}^M{\int }_0^t\ell \left({\mu }_i\left(\tau \right)\right)d\tau \hfill \end{array}$$

for any $t\ge 0$, where $0<r$, ${\epsilon }_i\left(t\right)={({\epsilon }_{i1}\left(t\right),{\epsilon }_{i2}\left(t\right),\dots ,{\epsilon }_{in}\left(t\right))}^T=x_i\left(t\right)-x_0\left(t\right)-h_i\left(t\right)\in {\mathbb{R}}^n,r$ represents the disturbance attenuation level, and a is a small positive constant.

For simplicity, the variable t is omitted later, except for those within the integral expression.

3. Main Results

This section presents the main results of the proposed adaptive robust $H_{\infty }$ TVFT control protocol, developed for heterogeneous nonlinear MASs with an unknown leader input. The proposed control strategy leverages relative information from neighboring agents to achieve a robust FT performance. A novel three-step algorithm is introduced for calculating the control parameters within the distributed control protocol, ensuring system stability and adaptability under uncertain conditions.

The adaptive robust $H_{\infty }$ TVFT control protocol is designed to handle inherent challenges of heterogeneous nonlinear MASs, particularly when the leader’s input is unknown. The protocol employs Lyapunov theory to guarantee system stability and robustness, demonstrating that the designed control method effectively mitigates the influence of external disturbances and parameter uncertainties. The application of Lyapunov theory not only ensures the convergence of the tracking errors, but also establishes the stability of the entire closed-loop system under the proposed control scheme. For the i-th follower agent, the FT neighborhood error, denoted by ${\xi }_i$, is a critical metric for evaluating the tracking performance. The error ${\xi }_i$ is defined based on the relative information obtained from the agent’s neighboring nodes, which forms the foundation for constructing the distributed control protocol. The neighborhood error is mathematically expressed as follows:

$$\begin{array}{c}\hfill {\xi }_i={\vartheta }_{i0}(x_i-h_i-x_0)+\sum _{j=1}^M{\vartheta }_{ij}\left[x_i-h_i-(x_j-h_j)\right].\end{array}$$

(4)

where ${\vartheta }_{ij}$ represents the adjacency matrix of the communication graph, $x_i$ and $x_j$ are the states of the follower agents, and $h_i$ is the FT offest vector.

The distributed control protocol for achieving adaptive robust $H_{\infty }$ TVFT is designed as:

$$\begin{array}{c}\hfill u_i=v_i-b_{1i}{g}_{1i}-c_{1i}{g}_{2i}-d_{1i}{B}^{T}P{\xi }_i.\end{array}$$

(5)

Here, $u_i$ is the control input for the i-th follower, and $v_i\in {\mathbb{R}}^m$ denotes the FT compensation determined by the desired dynamic formation information. The parameters $b_{1i},c_{1i}$, and $d_{1i}$ are time-varying adaptive parameters that will be updated dynamically using specific adaptive updating laws, which will be elaborated in subsequent sections. P is a positive definite matrix, integral to the stability proof and will also be designed at a later stage.

To address the uncertainties in the system parameters and the leader’s unknown input, the proposed control protocol incorporates nonlinear functions $g_{1i}$ and $g_{2i}$. These functions are crucial for enhancing the robustness of the control system against unpredictable disturbances and parameter variations. The functions are formulated as follows:

$$\begin{array}{cc}\hfill g_{1i}& =\left\{\begin{array}{c}{\displaystyle \frac{B^{T}P{\xi }_i}{\parallel B^{T}P{\xi }_i\parallel }},\mathrm{if}\parallel B^{T}P{\xi }_i\parallel \ne 0,\\ 0,\mathrm{otherwise},\end{array}\right.\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill g_{2i}& =\left\{\begin{array}{c}{\displaystyle \frac{\parallel x_i\parallel B^{T}P{\xi }_i}{\parallel B^{T}P{\xi }_i\parallel }},\mathrm{if}\parallel B^{T}P{\xi }_i\parallel \ne 0,\\ 0,\mathrm{otherwise},\end{array}\right.\hfill \end{array}$$

(7)

Let $Z={[{\tilde{B}}^T,{\overline{B}}^T]}^T$ consisting of $\tilde{B}\in {\mathbb{R}}^{m\times n}$ and $\overline{B}\in {\mathbb{R}}^{(n-m)\times n}$ denote a nonsingular matrix, which $\tilde{B}B=I_m$, and $\overline{B}B=0$.

In what follows, we propose Algorithm 1 to determine the control parameters in the control protocol (5).

Algorithm 1: The control parameters with the protocol (5) can be systematically determined through the following steps:

Verify the following $H_{\infty }$ TVFT feasibility condition (8): $$\begin{array}{c}\hfill \parallel -\overline{B}A{h}_i+\overline{B}{\dot{h}}_i\parallel =0.\end{array}$$ (8) If the feasible condition holds, then continue; otherwise, the desired $h_i$ is not feasible for MASs (1) under the control protocol (5) and stop. The FT compensation $v_i$ is designed as follows: $$\begin{array}{c}\hfill v_i=-\tilde{B}A{h}_i+\tilde{B}{\dot{h}}_i,\end{array}$$ (9) where $v_i$ has been defined in the control protocol (5). For the i-th follower, the time-varying adaptive parameters $b_{1i},c_{1i}$, and $d_{1i}$ are governed by the following adaptive laws: $$\begin{array}{cc}\hfill {\dot{b}}_{1i}& =∥B^{T}P{\xi }_i∥,\hfill \\ \hfill {\dot{c}}_{1i}& =\parallel x_i\parallel ∥B^{T}P{\xi }_i∥,\hfill \\ \hfill {\dot{d}}_{1i}& ={\xi }_i^T{\xi }_i,\hfill \end{array}$$ (10) where $i=1,2,\dots ,M,b_{1i}\left(0\right),c_{1i}\left(0\right)$ and $d_{1i}\left(0\right)$ are, respectively, positive constants.

According to Assumption 2, Algorithm 1, substituting (5) into the system (1), it follows:

$$\begin{array}{cc}\hfill {\dot{x}}_i=& \left(A+B{N}_i\right)x_i+B{f}_i\left(x_i\right)+{\mu }_i+B{v}_i-b_{1i}B{g}_{1i}-c_{1i}B{g}_{2i}-d_{1i}B{B}^{T}P{\xi }_i,\hfill \end{array}$$

(11)

where $i=1,2,\dots ,M.$

In light of (1)–(2), (11), and the definition of ${\epsilon }_i$, we have

$$\begin{array}{cc}\hfill {\dot{\epsilon }}_i=& A{\epsilon }_i+B{N}_i{x}_i+B{f}_i\left(x_i\right)+{\mu }_i-B{f}_0\left(x_0\right)-b_{1i}B{g}_{1i}-c_{1i}B{g}_{2i}-d_{1i}B{B}^{T}P{\xi }_i+B{v}_i\hfill \\ \hfill & -B{u}_0-{\dot{h}}_i+A{h}_i.\hfill \end{array}$$

(12)

Here, $i=1,2,\dots ,M.$

Let $\epsilon ={({\epsilon }_1^T,{\epsilon }_2^T,\dots ,{\epsilon }_M^T)}^T\in {\mathbb{R}}^{Mn},$ then system (12) is described in the compact form:

$$\begin{array}{cc}\hfill \dot{\epsilon }=& (I_M\otimes A)\epsilon +(I_M\otimes B)\Gamma x+\mu +(I_M\otimes B)\overline{f}\left(x\right)-({\mathbf{1}}_M\otimes B)f\left(x_0\right)-\left({\widehat{B}}_1\otimes B\right)g_1\hfill \\ \hfill & -\left({\widehat{C}}_1\otimes B\right)g_2-\left({\widehat{D}}_1\otimes B{B}^{T}P\right)\xi +(I_M\otimes B)v-({\mathbf{1}}_M\otimes B)u_0-\dot{h}-(I_M\otimes A)h,\hfill \end{array}$$

(13)

where $x={(x_1^T,x_2^T,\dots ,x_M^T)}^T,\Gamma =\mathrm{diag}\{N_i,N_2,\dots ,N_M\},\mu ={({\mu }_1^T,\dots ,{\mu }_M^T)}^T,\overline{f}\left(x\right)=(f_1^T\left(x_1\right),\dots ,f_M^T{\left(x_M\right)}^T),{\widehat{B}}_1=\mathrm{diag}\{b_{11},b_{12},\dots ,b_{1M}\},{\widehat{C}}_1=\mathrm{diag}\{c_{11},c_{12},\dots ,c_{1M}\},{\widehat{D}}_1=\mathrm{diag}\{d_{11},d_{12},\dots ,d_{1M}\},g_1={(g_{11}^T,g_{12}^T,\dots ,g_{1M}^T)}^T,g_2={(g_{21}^T,\dots ,g_{2M}^T)}^T,\xi ={({\xi }_1^T,{\xi }_2^T,\dots ,{\xi }_M^T)}^T,\dot{h}={({\dot{h}}_1^T,{\dot{h}}_2^T,\dots ,{\dot{h}}_M^T)}^T,v={(v_1^T,v_2^T,\dots ,v_M^T)}^T.$

The following theorem ensures that the proposed control protocol (5) enables the system to achieve robust $H_{\infty }$ TVFT.

Theorem 1.

Given Assumptions 1 and 2, the heterogeneous nonlinear MASs with external disturbances and unknown control inputs can achieve robust $H_{\infty }$ TVFT through the implementation of the $H_{\infty }$ TVFT control protocol (5), as defined by Algorithm 1.

Proof. 

Consider the Lyapunov function selected for (13):

$$\begin{array}{c}\hfill V_1={\epsilon }^T\Lambda \epsilon +\sum _{i=1}^M{\left(b_{1i}-b_1\right)}^2+\sum _{i=1}^M{\left(c_{1i}-c_1\right)}^2+\sum _{i=1}^M{(d_{1i}-d_1)}^2,\end{array}$$

(14)

where $b_1,c_1$, and $d_1$ denote, respectively, positive constants with $b_1⩾b,c_1⩾a_i$. Here, $\Lambda =L_2\otimes P$, with P being a positive definite matrix that satisfies the algebraic Riccati equation:

$$\begin{array}{c}\hfill \Theta -\Psi +I_n=0,\end{array}$$

(15)

where $\Theta =A^{T}P+PA$ and $\Psi =PB{B}^{T}P$.

The Lyapunov function in (14), which incorporates both the tracking error term ${\epsilon }^T\Lambda \epsilon$ and the deviations of adaptive parameters ${\sum }_{i=1}^M{\left(b_{1i}-b_1\right)}^2+{\sum }_{i=1}^M{\left(c_{1i}-c_1\right)}^2+{\sum }_{i=1}^M{(d_{1i}-d_1)}^2$, is selected to holistically address stability and robustness under parameter uncertainties and external disturbances. This design ensures simultaneous convergence of state tracking errors and adaptive parameter estimates (toward $b_1$, $c_1$, and $d_1$), aligning with standard adaptive control methodologies. The inclusion of parameter deviations enables the Lyapunov derivative to satisfy negative definiteness while achieving the $H_{\infty }$ performance criterion.

According to (13) and (14), it follows

$$\begin{array}{cc}\hfill {\dot{V}}_1=& 2{\epsilon }^T\Lambda [(I_M\otimes A)\epsilon +(I_M\otimes B)\Gamma x+\mu +(I_M\otimes B)\overline{f}\left(x\right)\hfill \\ \hfill & -({\mathbf{1}}_M\otimes B)f\left(x_0\right)+(I_M\otimes B)v-({\mathbf{1}}_M\otimes B)u_0-\dot{h}-(I_M\otimes A)h]\hfill \\ \hfill & +2{\epsilon }^T(L_2{\widehat{B}}_1\otimes PB)g_1-2{\epsilon }^T\left(L_2{\widehat{C}}_1\otimes PB\right)g_2\hfill \\ \hfill & -2{\epsilon }^T\left(L_2{\widehat{D}}_1\otimes \Psi \right)\xi +2\sum _{i=1}^M\left(b_{1i}-b_1\right)∥B^{T}P{\xi }_i∥\hfill \\ \hfill & +2\sum _{i=1}^M\left(c_{1i}-c_1\right)\parallel x_i\parallel ∥B^{T}P{\xi }_i∥+2\sum _{i=1}^M\left(d_{1i}-d_1\right){\xi }_i^T\Psi {\xi }_i.\hfill \end{array}$$

(16)

From the definition of $\epsilon$ and $\xi$, it follows that $\xi =\left(L_2\otimes I_n\right)\epsilon .$ Then, in light of the property of $f_m(·)(m=0,1,\dots ,M)$ and Lemma 2.1, we have:

$$\begin{array}{c}\hfill 2{\xi }_i^{T}PB\left[f_i\left(x_i\right)-f_0\left(x_0\right)\right]⩽{\xi }_i^T\Psi {\xi }_i+{\varsigma }_i\left[{\epsilon }_i^T-h_i^T\right]\left[{\epsilon }_i-h_i\right]\\ \hfill ⩽{\xi }_i^T{\xi }_i+2\varsigma {\epsilon }_i^T{\epsilon }_i^T+2\varsigma h_i^T{h}_i,\end{array}$$

(17)

where $i=1,2,\dots ,M,\varsigma =\max \{{\varsigma }_1,{\varsigma }_2,\dots ,{\varsigma }_M\}$, and ${\varsigma }_i$ is defined in (3).

Moreover, from the definition of $g_{1i}$ and $g_{2i}$, one derives

$$\begin{array}{cc}\hfill & 2{\epsilon }^T(L_2{\widehat{B}}_1\otimes PB)g_1+2\sum _{i=1}^M\left(b_{1i}-b_1\right)∥B^{T}P{\xi }_i∥\hfill \\ \hfill =& -2\sum _{i=1}^M{b}_{1i}{\xi }_i^{T}PB{g}_{1i}+2\sum _{i=1}^M\left(b_{1i}-b_1\right)∥B^{T}P{\xi }_i∥\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill =& -2b_1\sum _{i=1}^M\parallel B^{T}P{\xi }_i\parallel ,\hfill \\ \hfill & -2e^T\left(L_2{\widehat{C}}_1\otimes PB\right)g_2+2\sum _{i=1}^M\left(c_{1i}-c_1\right)\parallel x_i\parallel ∥B^{T}P{\xi }_i∥\hfill \\ \hfill =& -2\sum _{i=1}^M{c}_{1i}{\xi }_i^{T}PB{g}_{2i}+2\sum _{i=1}^M\left(c_{1i}-c_1\right)\parallel x_i\parallel ∥B^{T}P{\xi }_i∥\hfill \\ \hfill =& -2c_1\sum _{i=1}^M\parallel x_i\parallel ∥B^{T}P{\xi }_i∥,\hfill \end{array}$$

(19)

and

$$\begin{array}{cc}\hfill & -2{\epsilon }^T\left(L_2{\widehat{D}}_1\otimes \right)\xi +2\sum _{i=1}^M\left(d_{1i}-d_1\right){\xi }_i^T{\xi }_i\hfill \\ \hfill =& -2\sum _{i=1}^M{d}_{1i}{\xi }_i^T\xi +2\sum _{i=1}^M\left(d_{1i}-d_1\right){\xi }_i^T{\xi }_i\hfill \\ \hfill =& -2d_1\sum _{i=1}^M{\xi }_i^T{\xi }_i.\hfill \end{array}$$

(20)

Since $\parallel u_0{\parallel }_{\infty }<\chi$, one derives

$$\begin{array}{cc}\hfill -2{\epsilon }^T\left(L_2{\mathbf{1}}_M\otimes PB\right)u_0& =-2{\displaystyle \sum _{i=1}^M}{\xi }_{i}PB{u}_0\hfill \\ \hfill & ⩽2{\displaystyle \sum _{i=1}^M}\parallel B^{T}P{\xi }_i\parallel \parallel u_0\parallel \hfill \\ \hfill & ⩽2\chi \sum _{i=1}^M\parallel B^{T}P{\xi }_i\parallel .\hfill \end{array}$$

(21)

In light of Assumption 2, one obtains

$$\begin{array}{c}2{\epsilon }^T(L_2\otimes PB)\Gamma x=2{\displaystyle \sum _{i=1}^M}{\xi }_i^{T}PB{N}_i{x}_i\\ 2{\displaystyle \sum _{i=1}^M}{\zeta }_i{B}^{T}P{\xi }_i{x}_i.\end{array}$$

(22)

Noting that $b_1⩾\chi ,c_1⩾{\zeta }^{*}$ with ${\zeta }^{*}=\max \{{\zeta }_1,{\zeta }_2,\dots ,{\zeta }_M\}$, and substituting the results of (17)–(22) to (16), we have

$$\begin{array}{cc}\hfill {\dot{V}}_1⩽& {\epsilon }^T\left[L_2\otimes \left(A^{T}P+PA\right)+L_2^2\otimes -2d_1(L_2^2\otimes )+2\varsigma I_{Mn}\right]\epsilon \hfill \\ \hfill & +2\varsigma h^{T}h+2{\epsilon }^T\Lambda \mu +2{\epsilon }^T(I_M\otimes P)\tilde{h},\hfill \end{array}$$

(23)

where $\tilde{h}=(I_M\otimes PA)h+(I_M\otimes PB)v-(I_M\otimes P)\dot{h}$.

Since (8) holds, one obtains

$$\begin{array}{c}\hfill \left[\overline{B}A{h}_i+\overline{B}B{v}_i-\overline{B}{\dot{h}}_i\right]=0.\end{array}$$

(24)

According to (9), one yields

$$\begin{array}{c}\hfill \tilde{B}A{h}_i+\tilde{B}B{v}_i-\tilde{B}{\dot{h}}_i=0.\end{array}$$

(25)

Following the definition of Z, one derives

$$\begin{array}{c}\hfill \left[A{h}_i+B{v}_i-{\dot{h}}_i\right]=0,\end{array}$$

(26)

which implies that $\parallel \tilde{h}\parallel =0$.

Together with (26), it can be obtained from (23) that

$$\begin{array}{cc}\hfill {\dot{V}}_1⩽& {\epsilon }^T\left[L_2\otimes \Theta +2\varsigma I_{Mn}-(2d_1-1)(L_2^2\otimes )\right]\epsilon +2\varsigma h^{T}h\hfill \\ \hfill & +2{\epsilon }^T\Lambda \mu .\hfill \end{array}$$

(27)

From (27), it holds

$$\begin{array}{cc}\hfill & {\int }_0^t\left(\ell \left(\epsilon \left(\tau \right)\right)-r^2\ell \left(\mu \left(\tau \right)\right)\right)d\tau \hfill \\ \hfill =& {\int }_0^t\left(\ell \left(\epsilon \left(\tau \right)\right)-r^2\ell \left(\mu \left(\tau \right)\right)\right)d\tau +{\int }_0^t{\dot{V}}_1\left(\tau \right)d\tau -V_1\left(t\right)+V_1\left(0\right)\hfill \\ \hfill ⩽& {\int }_0^t\left(\ell \left(\epsilon \left(\tau \right)\right)-r^2\ell \left(\mu \left(\tau \right)\right)\right)d\tau +2\varsigma {\int }_0^t\ell \left(h\left(\tau \right)\right)d\tau +V_1\left(0\right)\hfill \\ \hfill & +{\int }_0^t{\epsilon }^T\left(\tau \right)\left[L_2\otimes \Theta +2\varsigma I_{Mn}+{\displaystyle \frac{1}{r^2}}(L_2^2\otimes PP)-(2d_1-1)(L_2^2\otimes )\right]\epsilon \left(\tau \right)d\tau \hfill \\ \hfill =& V_1\left(0\right)+2\varsigma {\int }_0^t\ell \left(h\left(\tau \right)\right)d\tau -{\int }_0^t{\left[{\displaystyle \frac{\Lambda \epsilon \left(\tau \right)}{r}}-r\mu \left(\tau \right)\right]}^T\left[{\displaystyle \frac{\Lambda \epsilon \left(\tau \right)}{r}}-r\mu \left(0\right)\right]d\tau \hfill \\ \hfill & +{\int }_0^t{\epsilon }^T\left(\tau \right)\left[L_2\otimes \Theta +\left(2\varsigma +1\right)I_{Mn}-(2d_1-1)(L_2^2\otimes )+{\displaystyle \frac{1}{r^2}}(L_2^2\otimes PP)\right]\epsilon \left(\tau \right)d\tau \hfill \\ \hfill ⩽& a+{\int }_0^t{\epsilon }^T\left(\tau \right)\left[L_2\otimes \Theta +(2\varsigma +1)I_{Mn}+{\displaystyle \frac{1}{r^2}}(L_2^2\otimes PP)-(2d_1-1)(L_2^2\otimes )\right]\epsilon \left(\tau \right)d\tau ,\hfill \end{array}$$

(28)

where $t\ge 0$ and $a=V_1\left(0\right)+2\varsigma {\sigma }_1$.

According to the definition of $L_2$, and Assumption 2, it holds that $L_2>0,$ and there exists a unitary matrix $U\in {\mathbb{R}}^{M\times M}$ satisfying $U^T{L}_{2}U=J_L=\mathrm{diag}\{{\eta }_1,{\eta }_2,\dots ,{\eta }_M\}\in {\mathbb{R}}^{M\times M}$ where $0<{\eta }_1⩽{\eta }_2⩽\dots ⩽{\eta }_M$. Let $\zeta ={({\zeta }_1^T,{\zeta }_2^T,\dots ,{\zeta }_M^T)}^T=(U^T\otimes I_n)\epsilon .$ Consequently, one derives

$$\begin{array}{cc}\hfill & {\int }_0^t{\epsilon }^T\left(\tau \right)\left[L_2\otimes \Theta +\left(2\varsigma +1\right)I_{Mn}-(2d_1-1)(L_2^2\otimes )+{\displaystyle \frac{1}{r^2}}(L_2^2\otimes PP)\right]\epsilon \left(\tau \right)d\tau \hfill \\ \hfill =& {\int }_0^t{\zeta }^T\left(\tau \right)\left[J_L\otimes \Theta +\left(2\varsigma +1\right)I_{Mn}-(2d_1-1)(J_L^2\otimes )+{\displaystyle \frac{1}{r^2}}(J_L^2\otimes PP)\right]\zeta \left(\tau \right)d\tau \hfill \\ \hfill =& -\sum _{i=1}^M{\int }_0^t{\eta }_i{\zeta }_i^T\left(\tau \right)Q_i{\zeta }_i\left(\tau \right)d\tau ,\hfill \end{array}$$

(29)

where $Q_i=\Theta +{\displaystyle \frac{(2\varsigma +1)}{{\eta }_i}}{I}_n-(2d_1-1){\eta }_i+{\displaystyle \frac{{\eta }_i}{r^2}}PP,i=1,2,\dots ,M.$

Choose a sufficiently large parameter $d_1$ satisfying $d_1>{\displaystyle \frac{1}{2{\eta }_1}}+{\displaystyle \frac{1}{2}}$, and select a sufficiently small parameter $\sigma$, such that $\sigma <{\displaystyle \frac{{\eta }_1{r}^2-{\eta }_M{r}^2{\eta }_{\max }\left(PP\right)-2\varsigma -1}{{\eta }_{\max }\left(P\right)}},$ where ${\eta }_{\max }(·)$ denotes the maximum eigenvalues of ${\eta }_{\max }\left(P\right).$ From (15), it follows that $-Q_i<\Theta +\Psi +I_n=0$, thereby guaranteeing that $Q_i$ is a positive definite matrix. Therefore, one derives

$$\begin{array}{c}\hfill {\int }_0^t\ell \left(\epsilon \left(\tau \right)\right)d\tau ⩽r^2{\int }_0^t\ell \left(\mu \left(\tau \right)\right)d\tau +a.\end{array}$$

(30)

Therefore, for heterogenous nonlinear MASs, a robust $H_{\infty }$ TVFT can be achieved (1) and (2) under external disturbances and unknown control inputs, utilizing the designed distributed adaptive control protocol (5). This concludes the proof. □

Remark 2.

“Fully distribution” means each follower agent utilizes only locally available information from its immediate neighbors (via the communication topology) and requires no global knowledge of the network (e.g., eigenvalues of the Laplacian matrix). This contrasts with conventional distributed control methods that may rely on centralized graph parameters. The adaptive control protocol is executed locally by each follower, relying solely on information from adjacent agents. This is achieved through real-time estimation of neighboring states via local communication, autonomous adjustment of control inputs based on this local information, and the use of decoupled adaptation laws to handle system uncertainties without requiring global coordination.

Remark 3.

The proposed adaptive robust $H_{\infty }$ TVFT protocol features low-complexity distributed computation, and the following analysis is provided:

• Neighbor error ${\xi }_i$ calculation: Each follower agent computes ${\xi }_i$ using local neighbor information. For a follower with k neighbors, the calculation involves vector additions and multiplications proportional to the state dimension n. The complexity is $O\left(kn\right)$, which scales linearly with the number of neighbors and state dimensions.
• Adaptive parameter updates: $b_{1i}$ and $c_{1i}$ depend on $∥B^{T}P{\xi }_i∥$, requiring vector norm computations ($O\left(n\right)$) and scalar updates. Update $d_{1i}$ via ${\xi }^T\xi$, involving an inner product ($O\left(n\right)$). Overall, each parameter update has $O\left(n\right)$ complexity, independent of the total number of agents.
• Nonlinear functions ($g_{1i}$, $g_{2i}$): Both functions involve conditional checks and normalization operations. The normalization requires $O\left(n\right)$ computations for vector norms and divisions. No iterative loops are needed, ensuring a low overhead.
• Matrix P and offline computations: The positive definite matrix P is derived from an ARE, which is solved offline. This step does not contribute to the online computational burden.
• Distributed nature: The protocol is fully distributed, meaning each agent’s computations rely only on local and neighbor data. The complexity for each agent is independent of the total number of agents and scales only with local variables (n, k).

The proposed protocol exhibits linear computational complexity in the state dimension n and neighbor count k, with no dependence on the total number of agents. This ensures scalability and practicality for heterogeneous MASs with time-varying formations.

Remark 4.

The initial gains $b_{1i}\left(0\right)$, $c_{1i}\left(0\right)$, and $d_{1i}\left(0\right)$ in the adaptive law (10) should be selected according to the following considerations. Firstly, to ensure positive definiteness, all initial values must be strictly positive (e.g., $b_{1i}\left(0\right)>0$) so that the adaptive law starts with a reasonable update direction. Secondly, the values can be empirically chosen based on the system’s dynamic range. For instance, if the upper bound of external disturbances χ or the Lipschitz constant ${\zeta }_i$ of the nonlinear term is known, one may set $b_{1i}\left(0\right)>\chi$ and $c_{1i}\left(0\right)>{\zeta }_i$. In the absence of prior knowledge, a uniform small positive constant (e.g., $b_{1i}\left(0\right)=c_{1i}\left(0\right)=d_{1i}\left(0\right)=1$) is recommended. Finally, while the initial values influence the transient adaptation speed, they do not affect the system’s asymptotic convergence or stability, as the adaptive law dynamically tunes the parameters to their steady-state values.

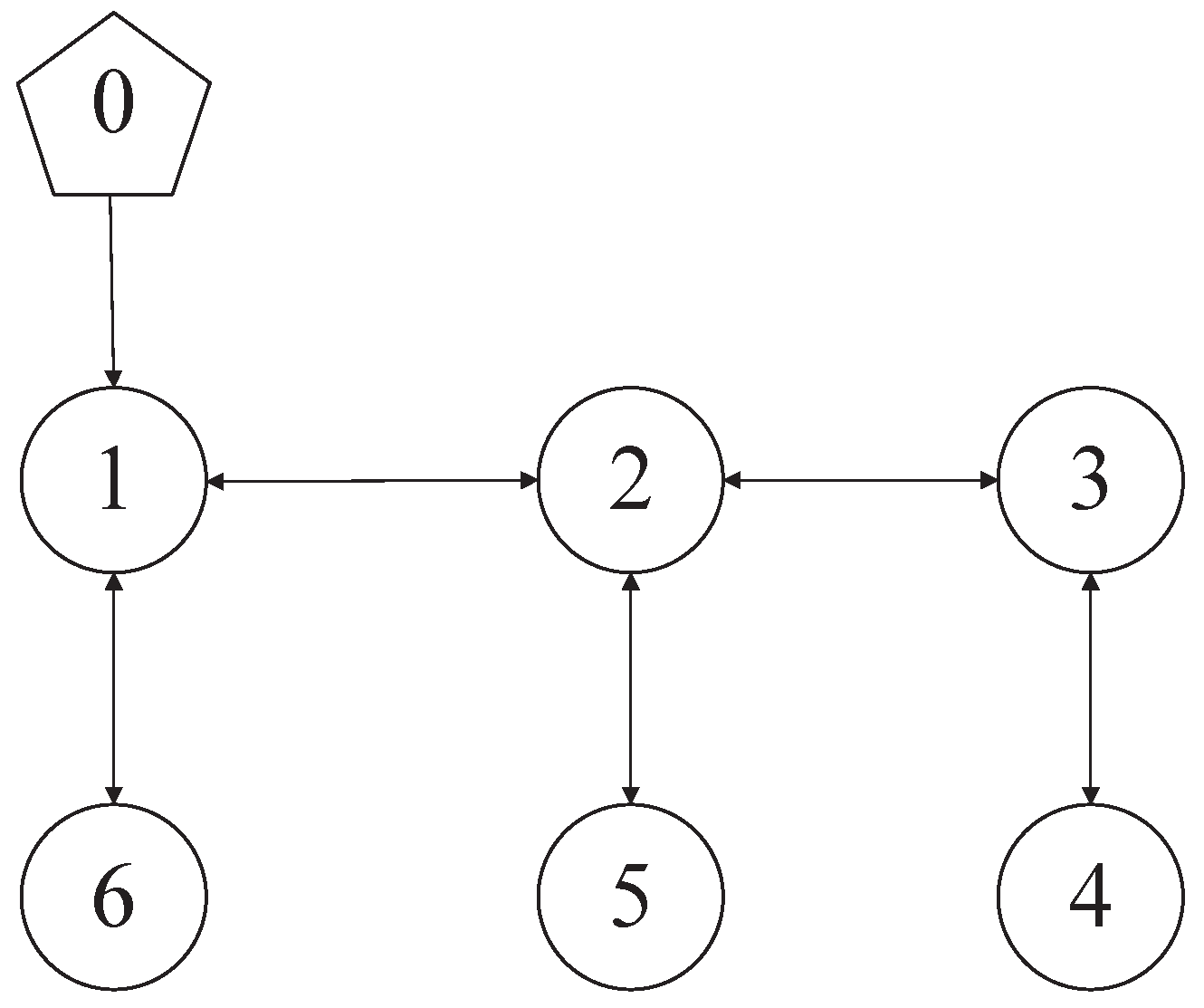
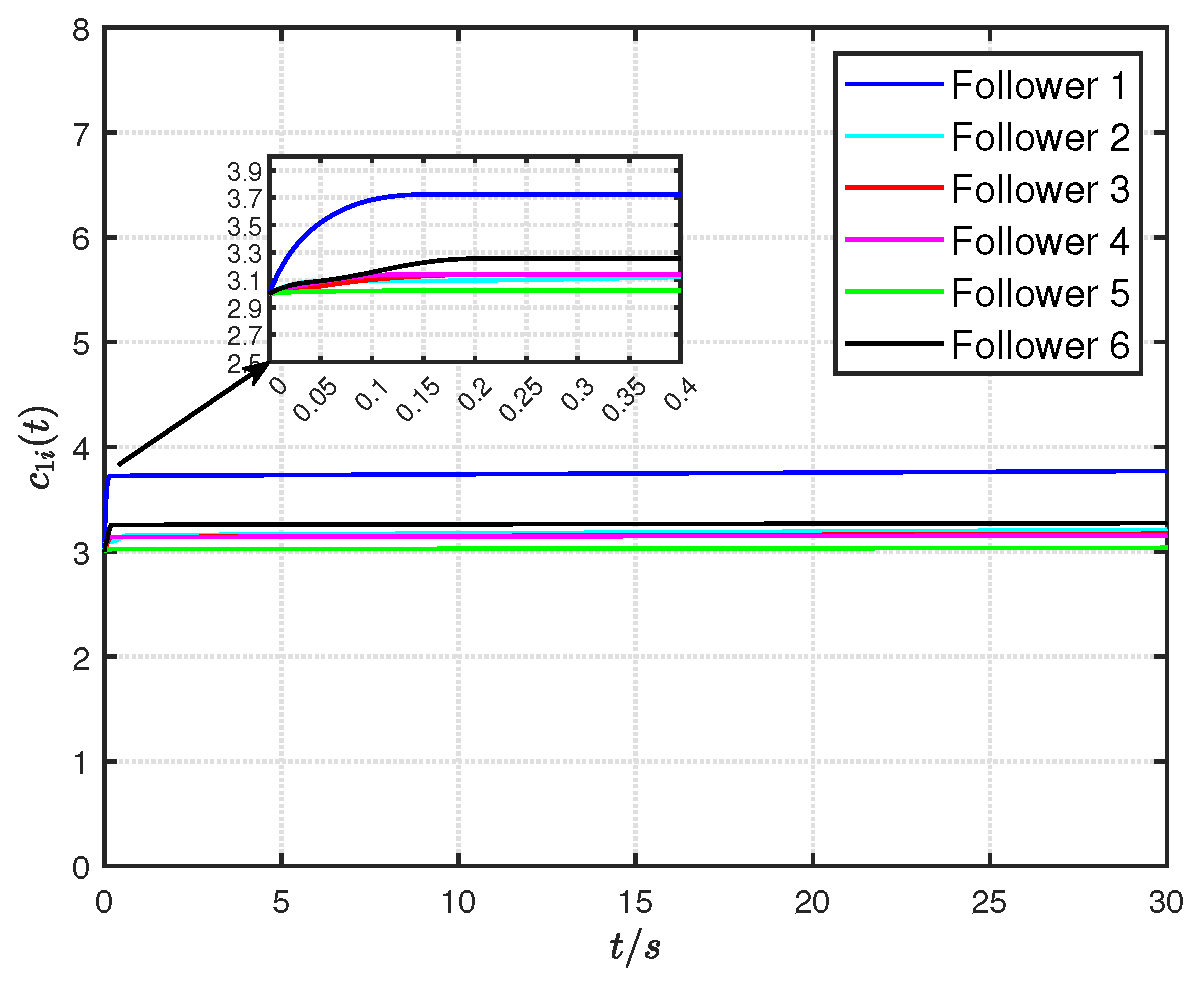
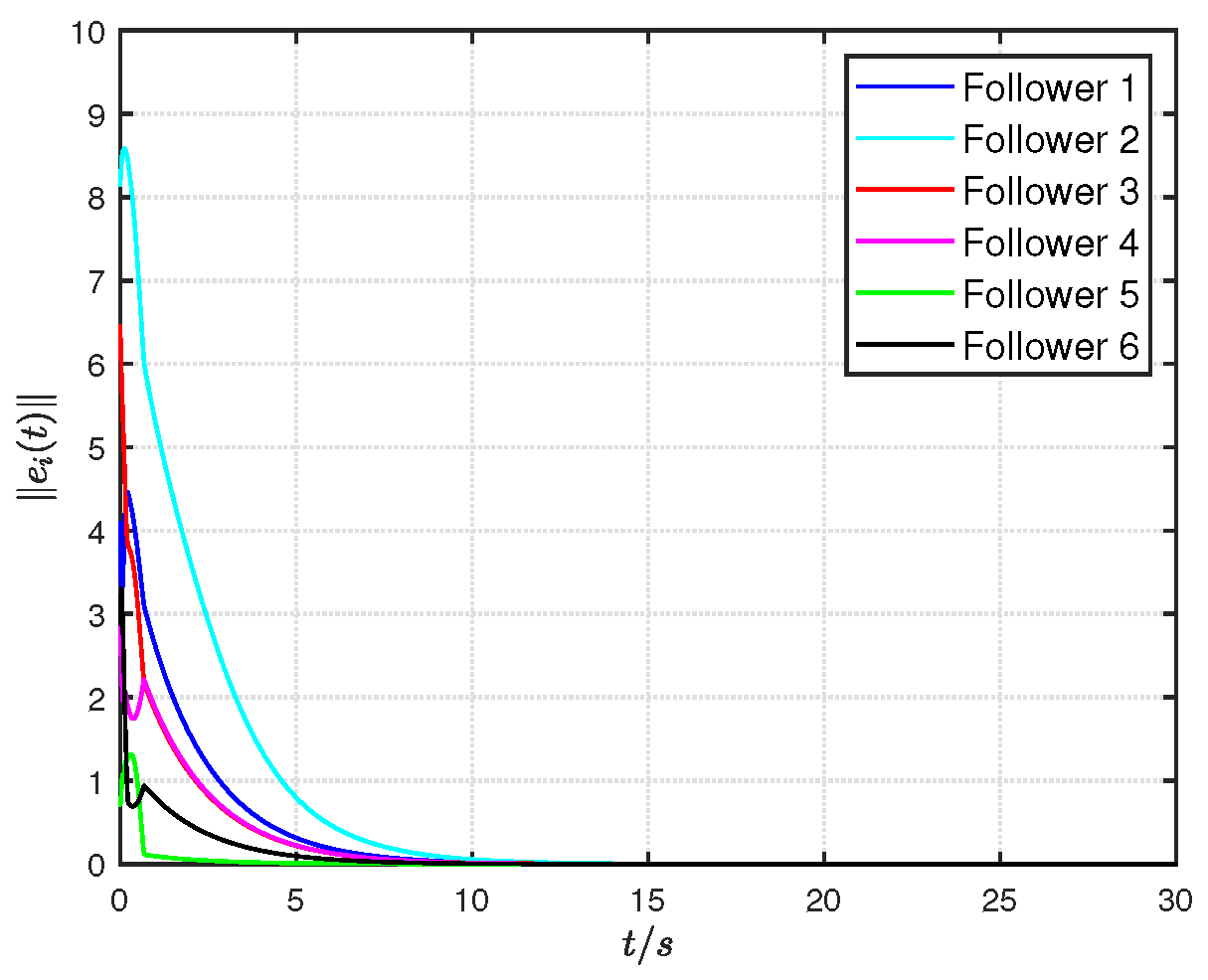
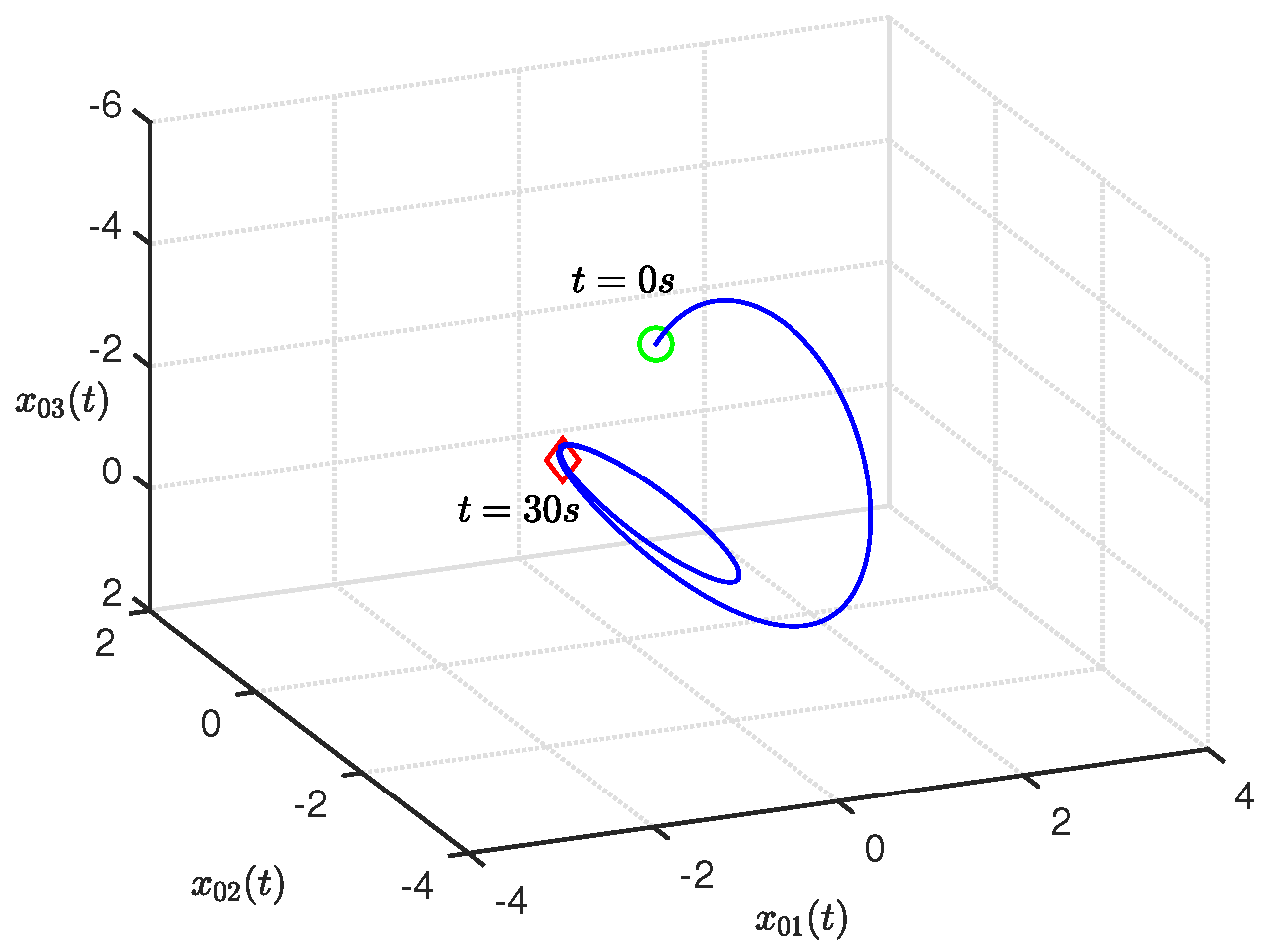
4. Numerical Examples

In the chapter, the proposed distributed adaptive robust $H_{\infty }$ TVFT control strategies are applied to the following numerical example.

$$\begin{array}{l}\Delta A_1=\left[\begin{array}{ccc}0& 0.5\cos \left(2t\right)& 0\\ 0& -0.5\cos \left(2t\right)& 0\\ \sin \left(2t\right)& 0& 0\end{array}\right],\Delta A_2=\left[\begin{array}{ccc}0& 0.5e^{-t}& 0\\ 0& 0& 0\\ 0& 0& 0.5e^{-t}\end{array}\right],\Delta A_3\\ =\left[\begin{array}{ccc}0.5\sin \left(t\right)& 0& -\cos \left(t\right)\\ -0.5\sin \left(t\right)& 0& \cos \left(t\right)\\ 0& 0& 0\end{array}\right],\Delta A_4=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right],\Delta A_5=\left[\begin{array}{ccc}-0.5e^{-t}& 0& 0\\ 0.5e^{-t}& 0& 0\\ 0& 0& -\sin \left(0.5t\right)\end{array}\right],\\ \Delta A_6=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right],\end{array}$$

$f_1\left(x_1\right)={(0.1\sin \left(x_{11}\right),0.1\sin \left(x_{12}\right))}^T,f_2\left(x_2\right)={(0.2\sin \left(x_{21}\right),0.2\sin \left(x_{22}\right))}^T,f_3\left(x_3\right)={(0.3\sin \left(x_{31}\right),f_4\left(x_4\right)={(0.4\sin \left(x_{41}\right),0.4\sin \left(x_{42}\right))}^T,f_5\left(x_5\right)={(0.5\sin \left(x_{51}\right),0.5\sin \left(x_{52}\right))}^T,f_6\left(x_6\right)={(0.6\sin \left(x_{61}\right),0.6\sin \left(x_{62}\right))}^T,{\mu }_1={(0.5,-0.5,\sin \left(0.5t\right))}^T,{\mu }_2={(\cos \left(5t\right),-\sin \left(0.5t\right),\cos \left(5t\right))}^T,0.3\sin \left(x_{32}\right))}^T,{\mu }_3={(e^{-0.1t},-e^{-0.1t},1)}^T,{\mu }_4={(\cos \left(t\right),-\cos \left(t\right),2e^{-0.2t})}^T,{\mu }_5={(\sin \left(2t\right),-2\sin \left(2t\right),1)}^T,{\mu }_6={(0.5,-0.5,\sin \left(0.5t\right))}^T.$

A heterogeneous nonlinear MAS comprising seven agents is considered, with the communication topology illustrated in Figure 1. The dynamic models of the followers and the leader are given by the MASs in (1) and (2) with $x_i\in {\mathbb{R}}^3,x_0\in {\mathbb{R}}^3$, and

$$\begin{array}{ccc}\hfill A& =& \left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ -4& -6& -4\end{array}\right],B=\left[\begin{array}{cc}0& 1\\ 0& -1\\ 1& 0\end{array}\right],\hfill \end{array}$$

where $i=1,2,\dots ,6$.

Obviously, there exists the following positive definite matrix satisfying (15):

$$\begin{array}{ccc}\hfill P& =& \left[\begin{array}{ccc}1.4060& 1.1559& 0.1155\\ 1.1559& 1.9389& 0.2208\\ 0.1155& 0.2208& 0.1750\end{array}\right],\hfill \end{array}$$

Let $f_0\left(x_0\right)=(2\sin \left(x_{01}\right),2\sin \left(x_{02}\right)){{)}^T,{\mu }_0=(0.3\sin \left(x_{01}\right),0.18\sin \left(x_{02}\right)))}^T,f_i(·)$ satisfies Assumption 1 with ${\varsigma }_i=0.1i(i=1,2,\dots ,6)$ and $\parallel u_0{\parallel }_{\infty }<2=\chi .$

In addition, the expected formation can be selected as:

$$\begin{array}{ccc}\hfill h_i& =& \left[\begin{array}{c}3\sin \left(t+\phi \right)\\ -3\cos \left(t+\phi \right)\\ 3\cos \left(t+\phi \right)\end{array}\right],\hfill \end{array}$$

where $\phi ={\displaystyle \frac{\left(i-1\right)\pi }{3}}$, $i=1,2,\dots ,6$. Select $b_{1i}\left(0\right)=3,c_{1i}\left(0\right)=3$, and $d_{1i}\left(0\right)=3$ in the distributed adaptive control protocol (5) to demonstrate Theorem 1.

Figure 2, Figure 3 and Figure 4 depict the evolution of the adaptive parameters $b_{1i},c_{1i}$, and $d_{1i}$, respectively. Figure 5 illustrates the progression of the FT errors $\parallel {\epsilon }_i\parallel$ for the MAS under the adaptive control protocol (5). Due to the presence of external disturbances ${\mu }_i,i=1,\dots ,6$, the FT errors converge to a finite positive value. Consequently, the heterogeneous nonlinear MASs represented by Equations (1) and (2) achieve robust $H_{\infty }$ TVFT according to Definition 1. The leader’s trajectory is shown in Figure 6, and the simulation results effectively support the theoretical conclusions drawn in Theorem 1.

Although the numerical simulation results validate the effectiveness of the proposed method, certain limitations remain in the experimental outcomes. Firstly, the simulations rely on idealized assumptions and do not account for practical factors such as sensor noise, actuator saturation, or communication delays, which may lead to deviations between the actual performance of the control protocol and simulation results. For instance, the communication topology is assumed to be fixed and interference-free, whereas dynamic topology changes or packet losses in real-world scenarios could compromise the robustness of the distributed control. Secondly, external disturbances are required to satisfy the square-integrable condition (${\int }_0^t\ell \left({\mu }_i\left(\tau \right)\right)d\tau <+\infty$), yet practical disturbances may exhibit non-stationary characteristics (e.g., abrupt spikes or persistent drifts), potentially undermining the applicability of the $H_{\infty }$ performance criterion. Furthermore, parameter uncertainties $\Delta A_i$ are explicitly modeled as time-varying functions in simulations (e.g., terms involving $cos\left(2t\right)$). However, real-world uncertainties could be more complex and challenging to model accurately, thereby reducing the efficacy of adaptive parameter compensation.

5. Conclusions

This study explored the robust $H_{\infty }$ TVFT problem for a class of heterogeneous nonlinear MASs with parameter uncertainties, external disturbances, and an unknown input from the leader. An adaptive robust $H_{\infty }$ TVFT control protocol was proposed using neighboring information, adopting a fully distributed approach. Nonlinear functions were introduced to address parameter uncertainties and mitigate the influence of the leader’s unknown input. Additionally, a three-step algorithm was developed to establish the control parameters in the TVFT control protocol. The stability and effectiveness of the proposed method were rigorously demonstrated through Lyapunov theory.