A Convex Constraint Approach for High-Type Control Loop Design
Abstract
1. Introduction
- (i)
- This paper proposes a high-type control loop design method for LQR-LMI based on Lyapunov and polyhedral model theory. The high-type control loop design problem is simplified into a convex constraint problem, which achieves higher tracking accuracy and stronger disturbance suppression ability.
- (ii)
- In this paper, the input amplitude of the control signal, disturbance suppression and other practical requirements are considered in the design of high-type control loops, which are expressed as LQR cost, performance, regional pole constraint and so on. Then the LMI method is used to effectively solve the problem.
- (iii)
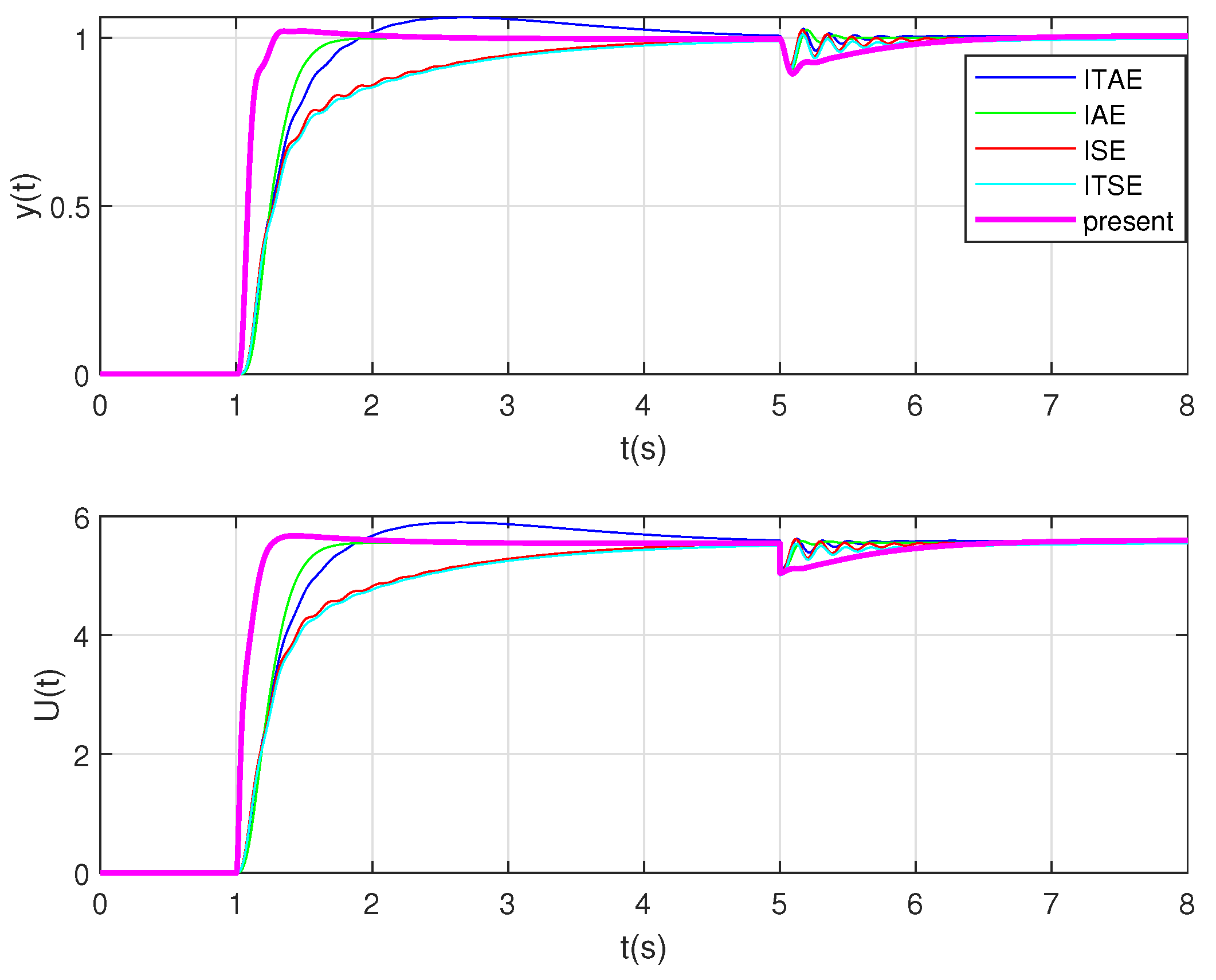
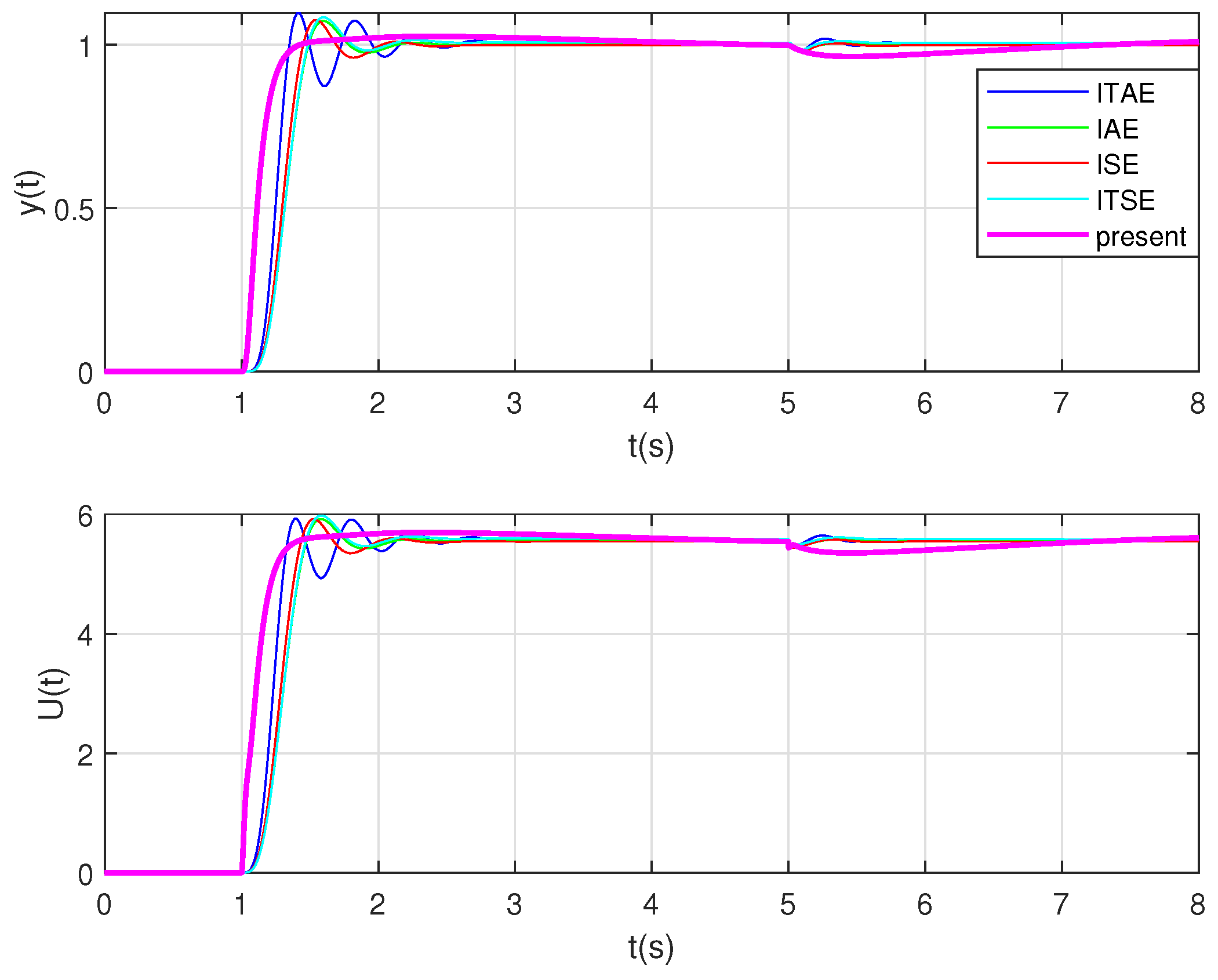
- Compared with the simulation results of other optimization algorithms (ITAE, ITSE, ISE, IAE), the effectiveness and superiority of the controller parameter tuning rules in the proposed high-type control loop are verified.
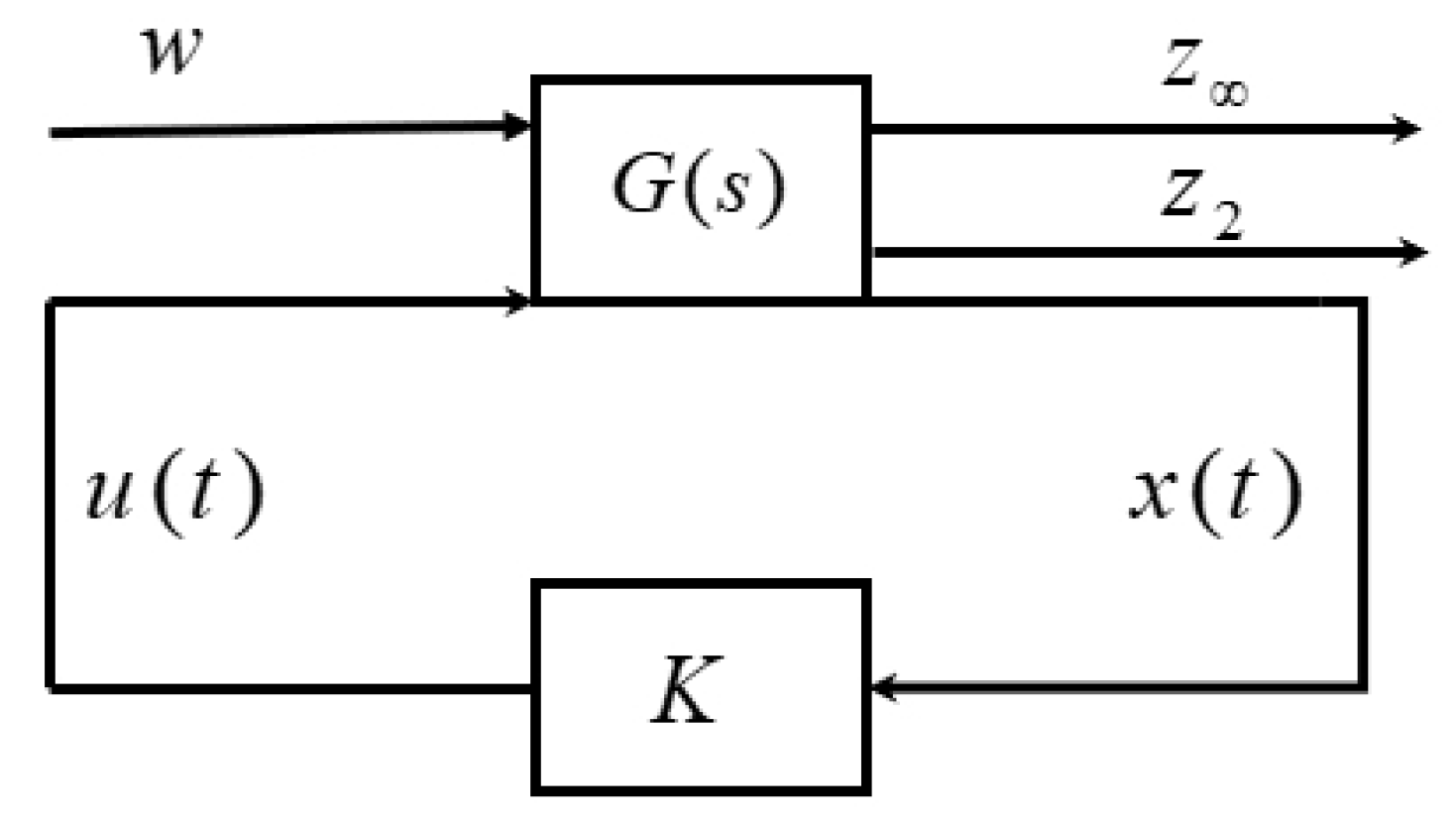
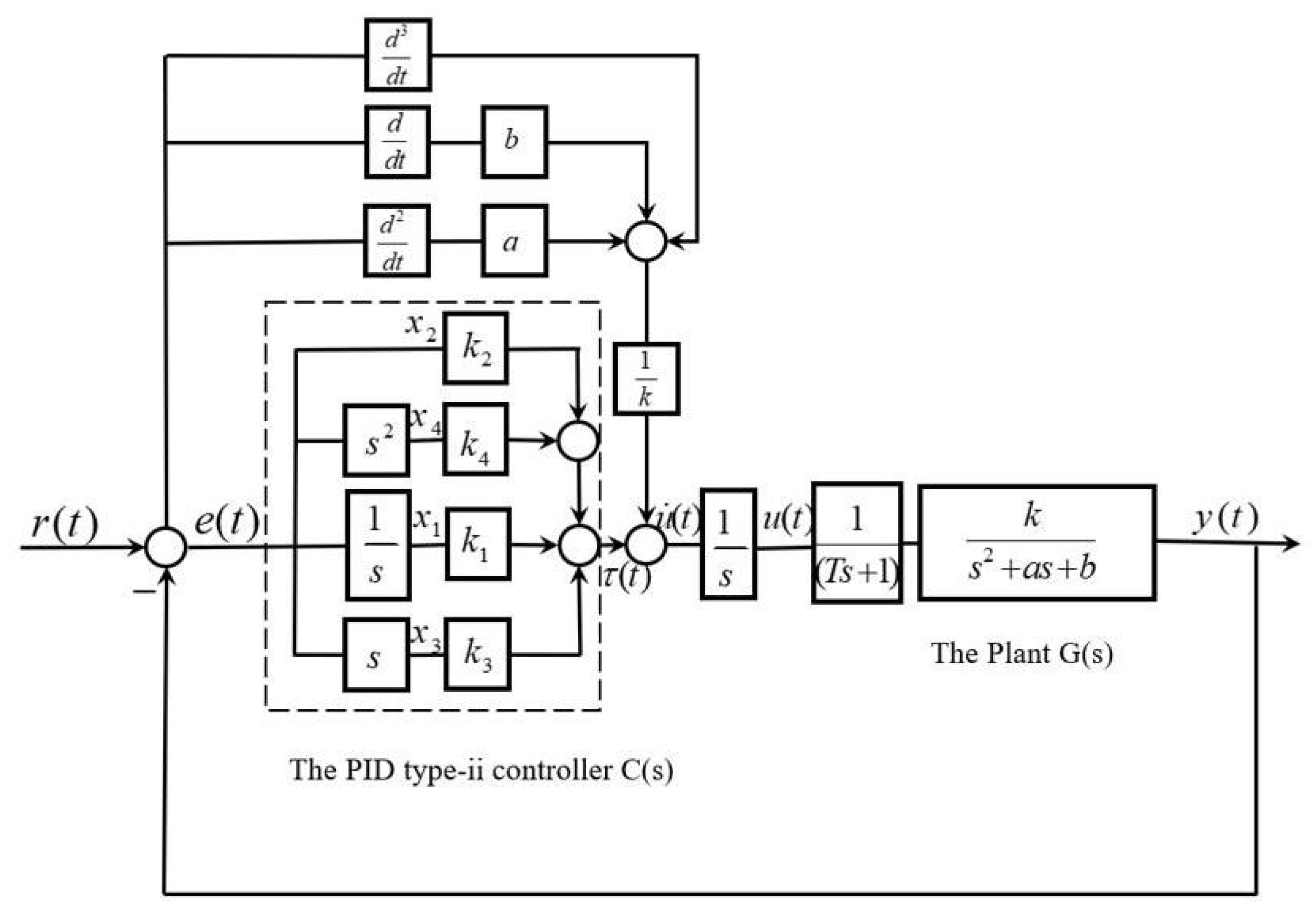
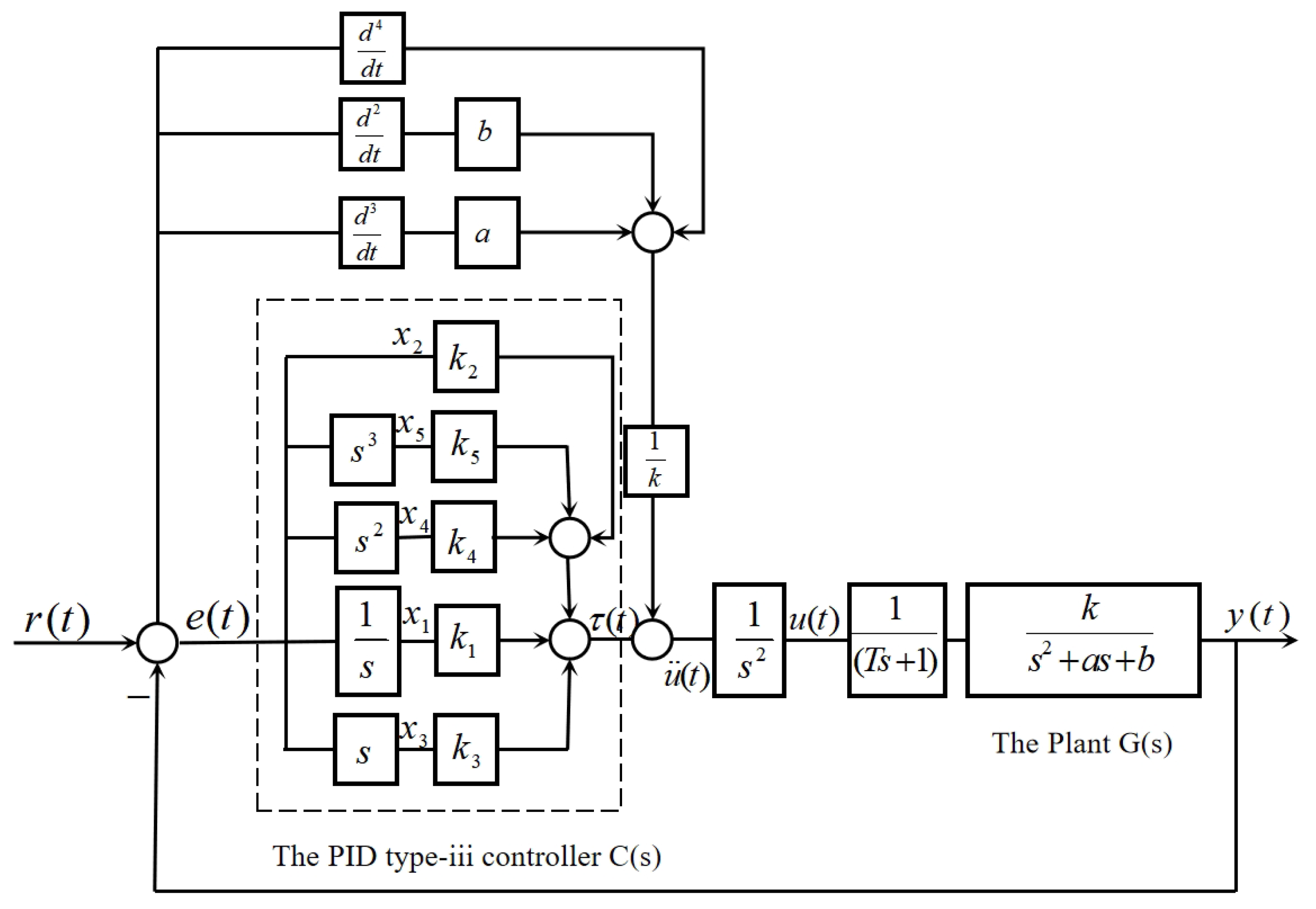
2. The Theory of Controller Parameter Tuning in the High-Type Control Loop
The LQR-LMI Framework
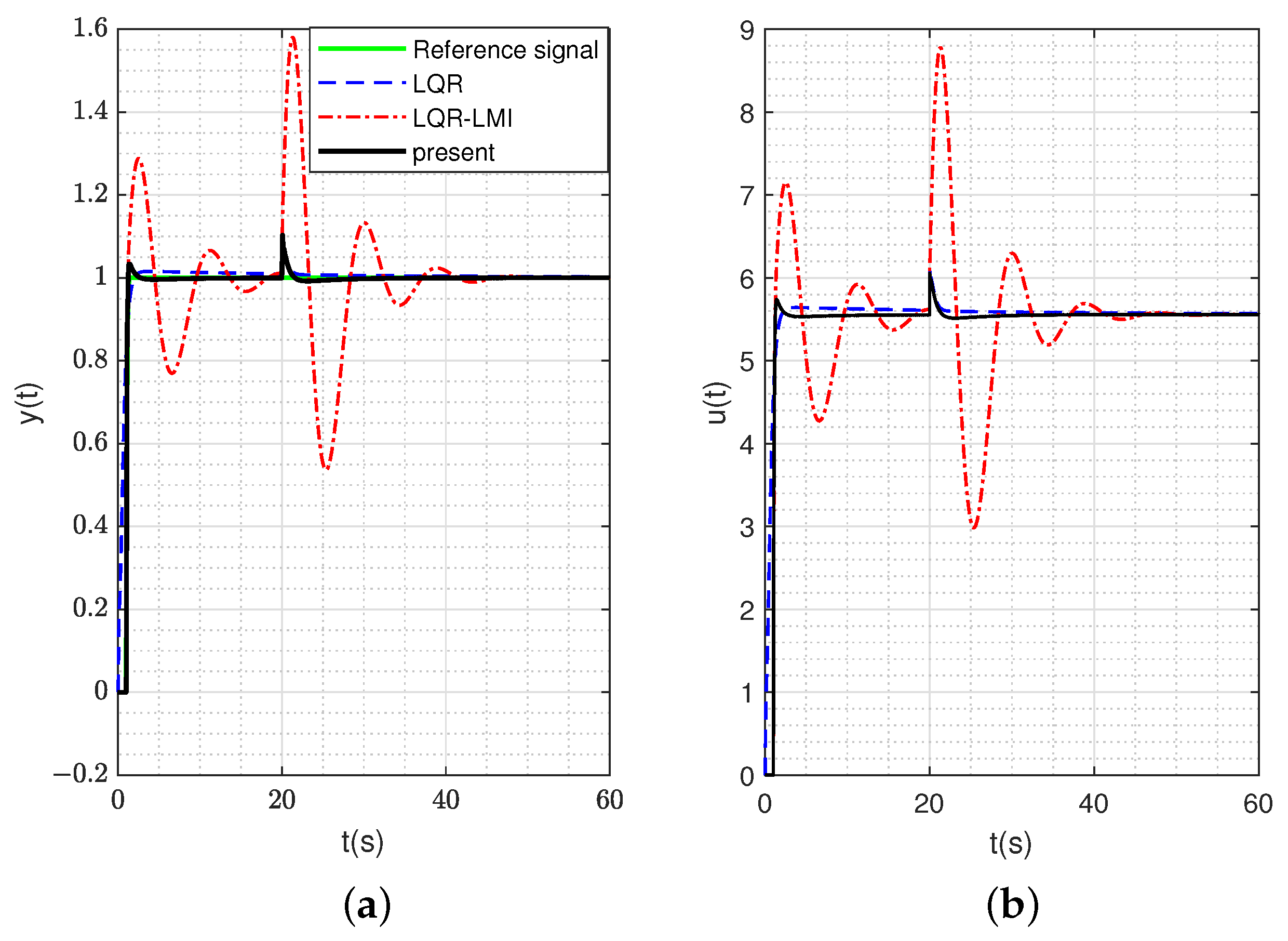
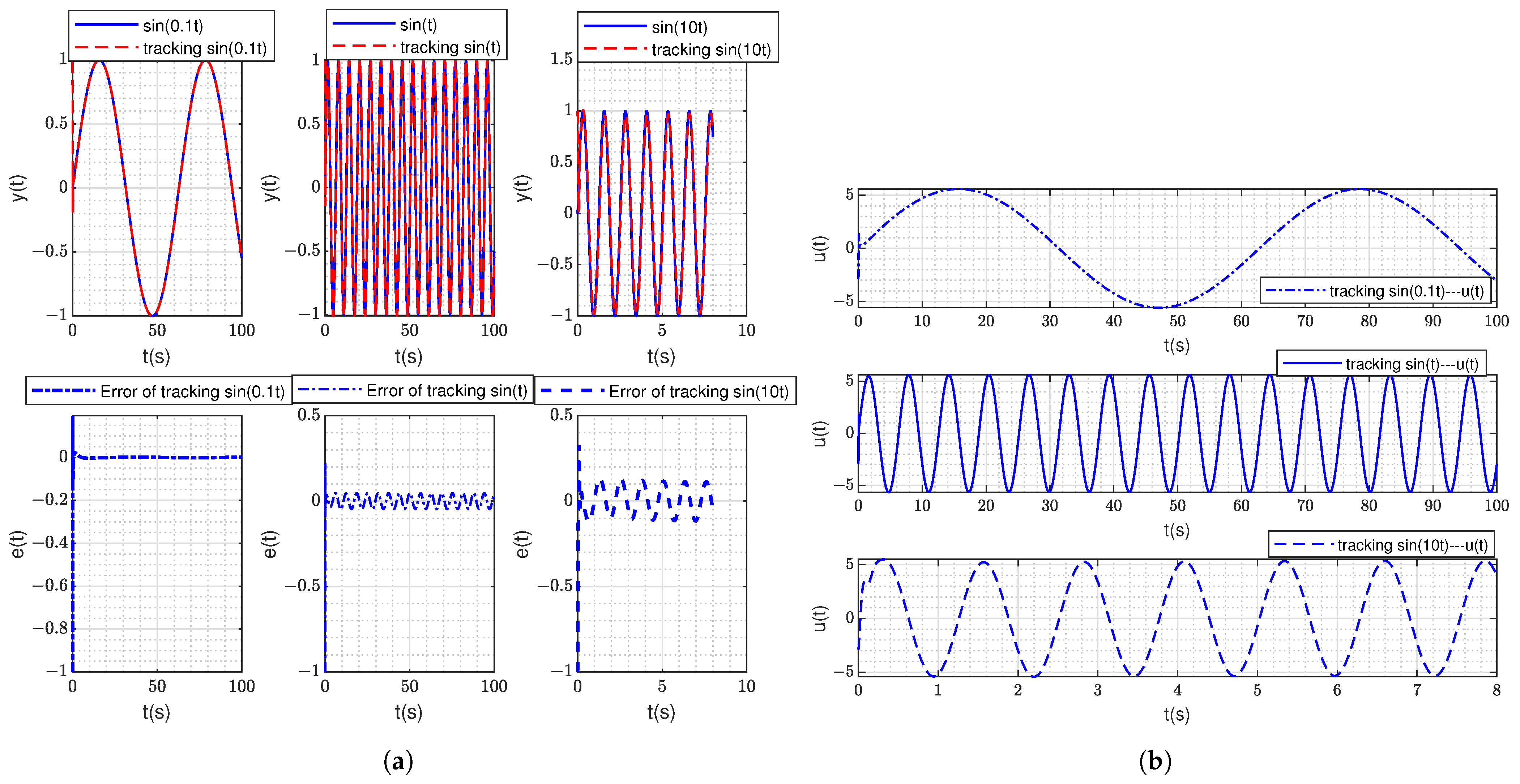
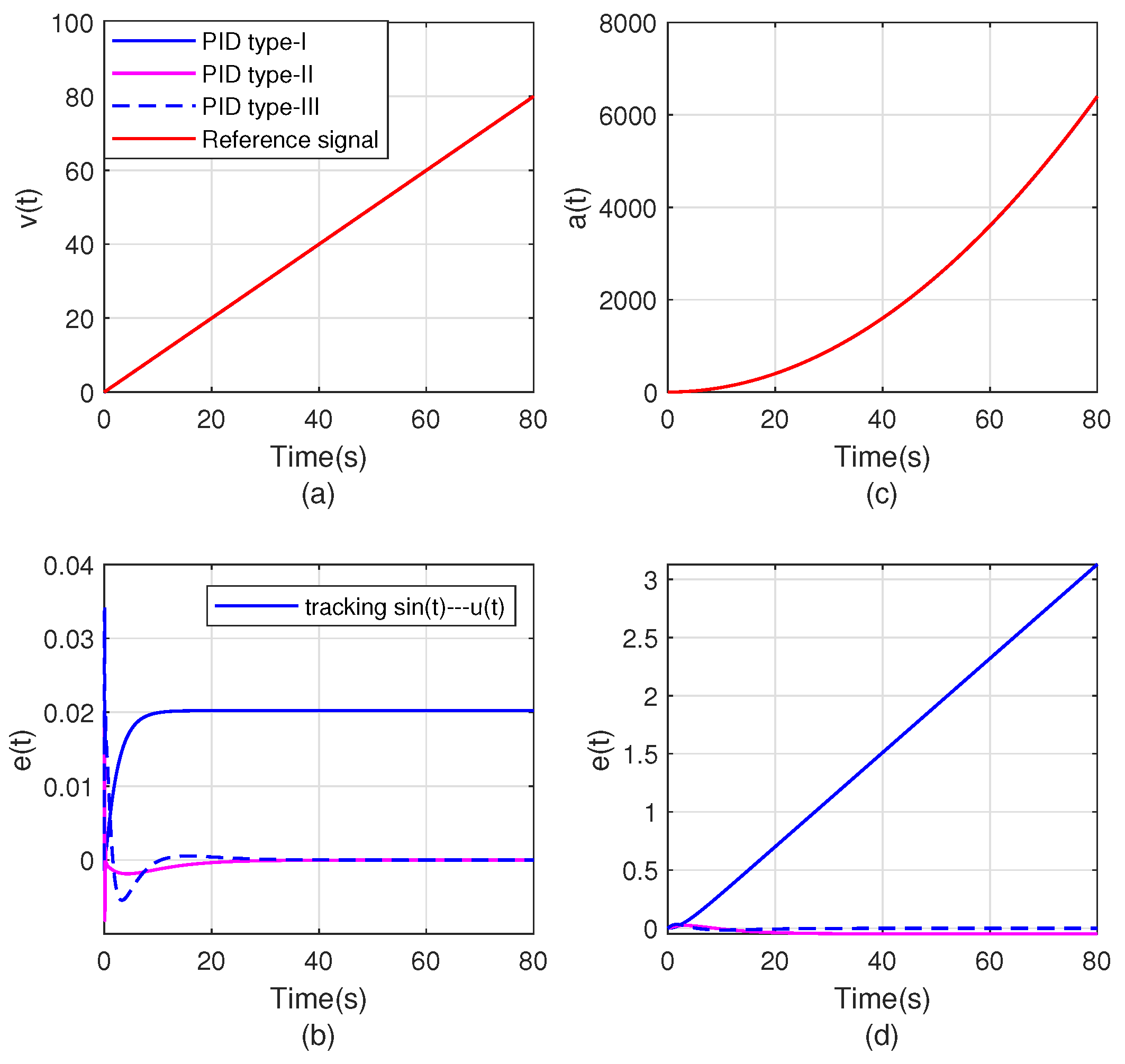
3. Simulation Analysis and Experimental Verification
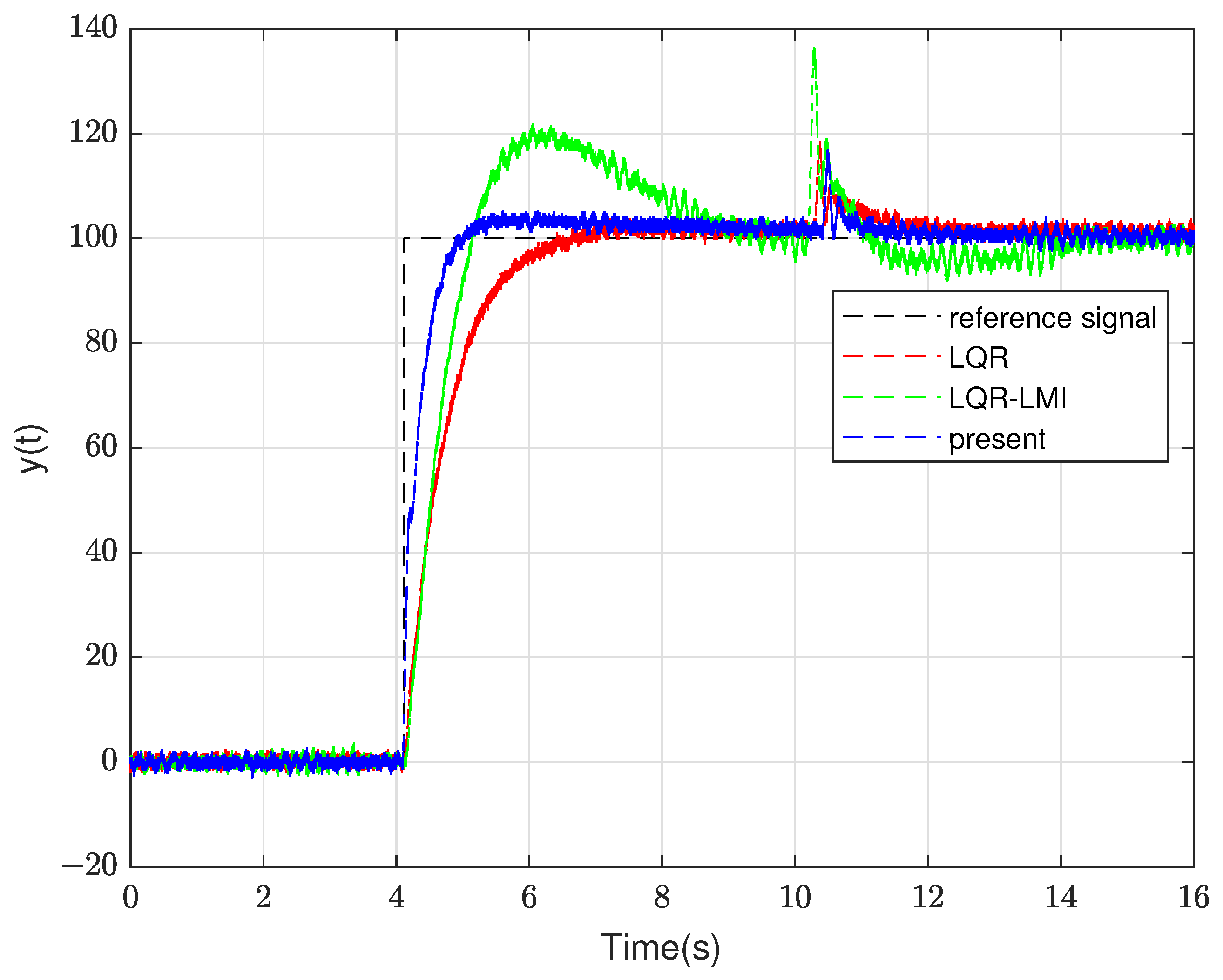
3.1. The Simulation Part of the High-Type Control Loop
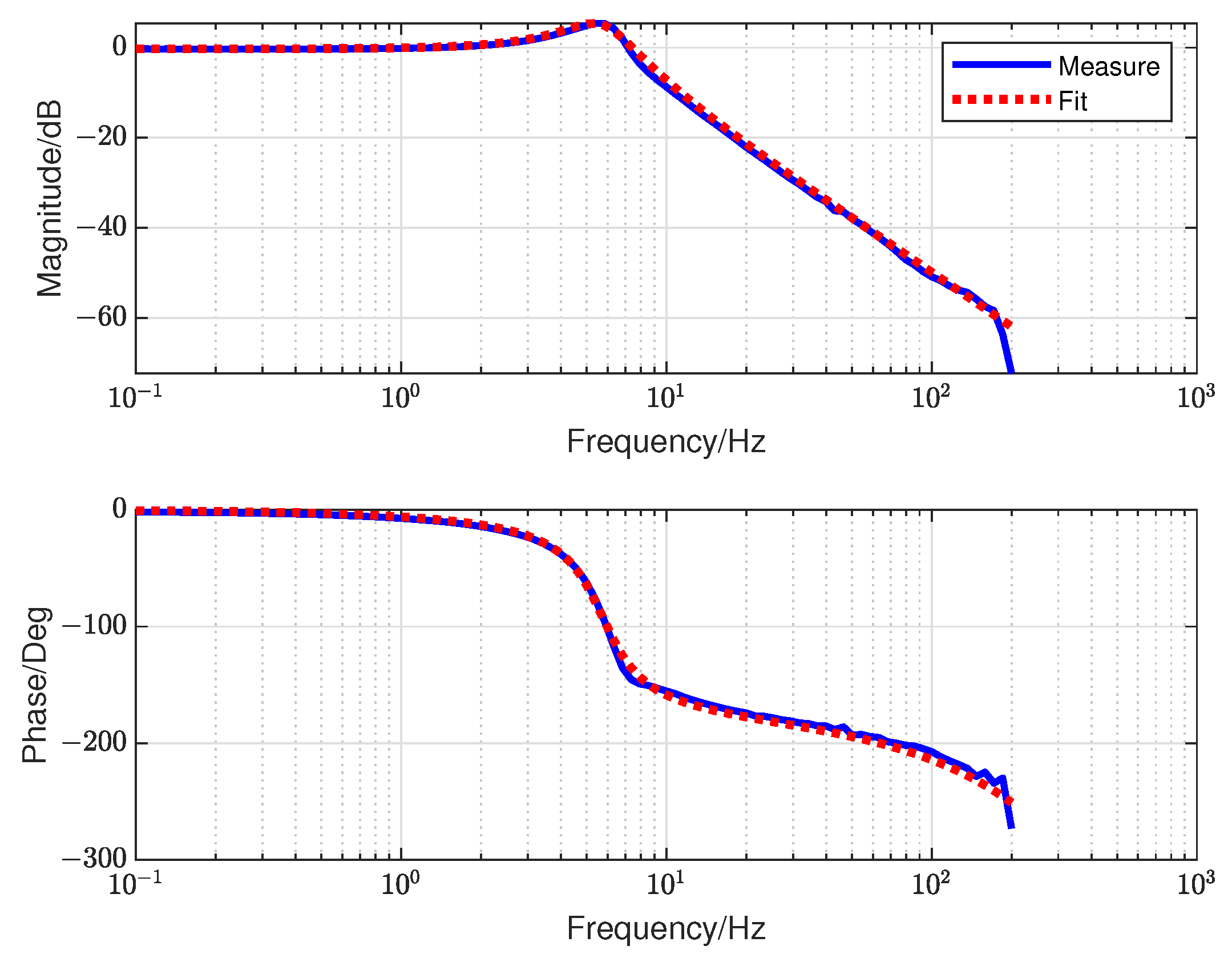
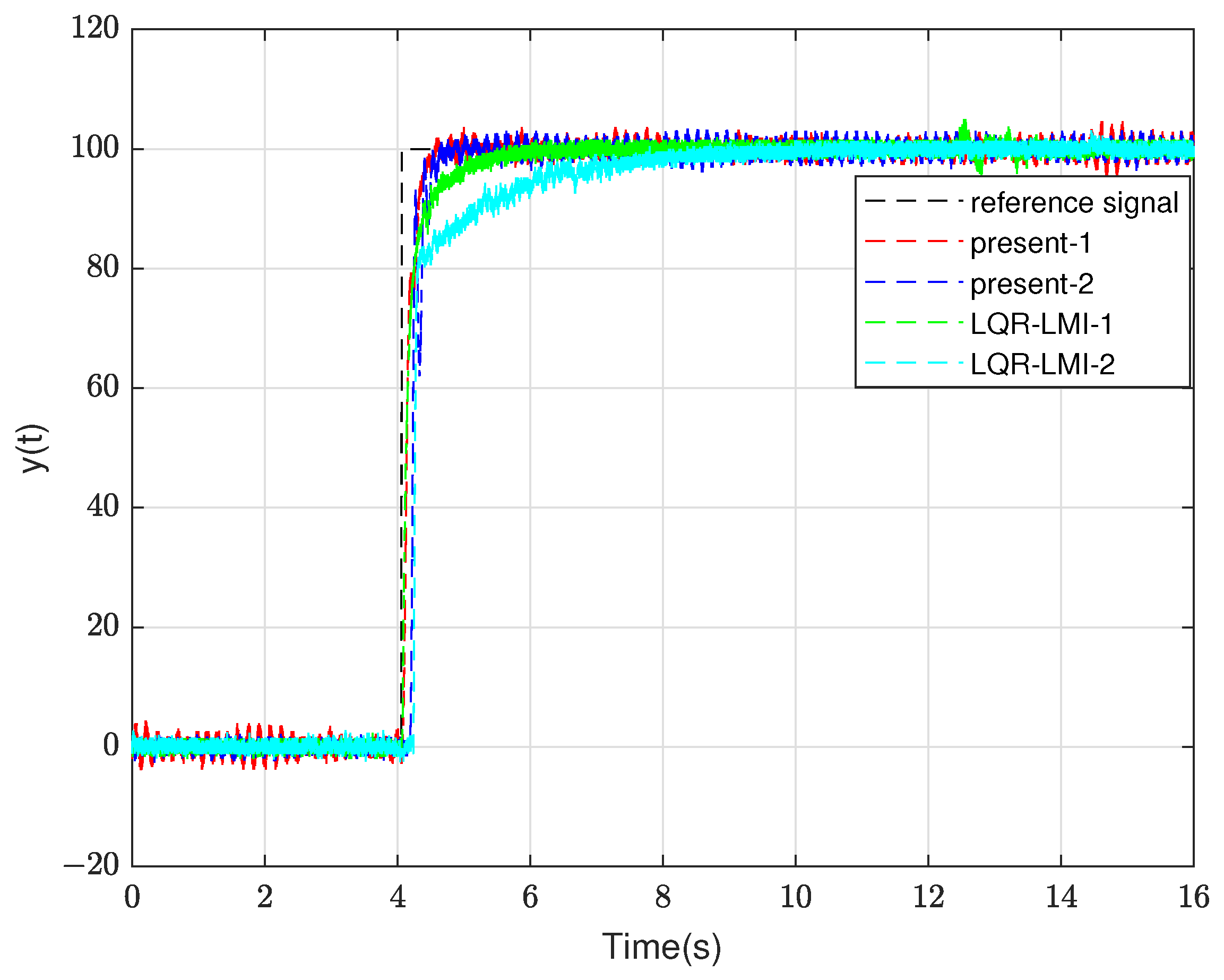
3.2. The Experiment Part of the High-Type Control Loop
4. Conclusions and Future Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deng, J.; Xue, W.; Zhou, X.; Mao, Y. On dual compensation to disturbances and uncertainties for inertially stabilized platforms. Int. J. Control Autom. Syst. 2022, 20, 1521–1534. [Google Scholar] [CrossRef]
- Zhou, X.; Mao, Y.; Duan, Q.; Zhang, H. Multi-order cascade lag control for high precision tracking systems. ISA Trans. 2022, 120, 318–329. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Mao, Y.; Qiu, X. Disturbance-observer-based LQR tracking control for electro-optical system. Photonics 2023, 10, 900. [Google Scholar] [CrossRef]
- Duan, Q.; Zhou, X.; He, Q.; Chen, X.; Liu, W.; Mao, Y. Pointing control design based on the PID type-III control loop for two-axis gimbal systems. Sens. Actuators A Phys. 2021, 331, 112923. [Google Scholar] [CrossRef]
- Chen, P.; Zhang, Y.; Wang, J.; Azar, A.T.; Hameed, I.A.; Ibraheem, I.K.; Kamal, N.A.; Abdulmajeed, F.A. Adaptive internal model control based on parameter adaptation. Electronics 2022, 11, 3842. [Google Scholar] [CrossRef]
- Chen, C.-W.; Wu, H.-M.; Nian, C.-Y. A Class of Anti-Windup Controllers for Precise Positioning of an X-Y Platform with Input Saturations. Electronics 2025, 14, 539. [Google Scholar] [CrossRef]
- Behnamgol, V.; Asadi, M.; Aphale, S.S.; Sohani, B. Recursive PID-NT Estimation-Based Second-Order SMC Strategy for Knee Exoskeleton Robots: A Focus on Uncertainty Mitigation. Electronics 2025, 14, 1455. [Google Scholar] [CrossRef]
- Tran, G.Q.B.; Pham, T.-P.; Sename, O.; Costa, E.; Gaspar, P. Integrated comfort-adaptive cruise and semi-active suspension control for an autonomous vehicle: An LPV approach. Electronics 2021, 10, 813. [Google Scholar] [CrossRef]
- Wang, T.; Wang, X. Polytopic Model Weighted Hoo Output Feedback Control of Switched Lpv System Based on Mdadt. J. Phys. Conf. Ser. 2019, 1267, 012089. [Google Scholar] [CrossRef]
- Tang, W.; Li, B.; Hou, S.; Shao, X.; Yu, H. Transient Stability Analysis for Grid-Connected Renewable Power Generation Systems Based on LMI Optimization Modelling. Electronics 2024, 13, 5052. [Google Scholar] [CrossRef]
- Song, R.; Huang, S.; Xiong, L.; Zhou, Y.; Li, T.; Tan, P.; Sun, Z. Takagi–Sugeno Fuzzy Parallel Distributed Compensation Control for Low-Frequency Oscillation Suppression in Wind Energy-Penetrated Power Systems. Electronics 2024, 13, 3795. [Google Scholar] [CrossRef]
- İnci, M.; Altun, Y. Disturbance compensator design based on dilated lmi for linear parameter-varying systems. Electronics 2024, 13, 3055. [Google Scholar] [CrossRef]
- Gao, J.; Li, H. Tuning Parameters of the Fractional Order PID-LQR Controller for Semi-Active Suspension. Electronics 2023, 12, 4115. [Google Scholar] [CrossRef]
- Rauniyar, S.; Bhalla, S.; Choi, D.; Kim, D. EKF-SLAM for quadcopter using differential flatness-based LQR control. Electronics 2023, 12, 1113. [Google Scholar] [CrossRef]
- Mosavi, A.; Qasem, S.N.; Shokri, M.; Band, S.S.; Mohammadzadeh, A. Fractional-order fuzzy control approach for photovoltaic/battery systems under unknown dynamics, variable irradiation and temperature. Electronics 2020, 9, 1455. [Google Scholar] [CrossRef]
- Wang, S.; Yu, F.; Qi, J. Model Predictive Voltage Control Strategy for Dual Active Bridge Converters Based on Super-Twisting Integral Sliding Mode Observer. Electronics 2025, 14, 1496. [Google Scholar] [CrossRef]
- Liu, C.; Qiu, X.; Xu, T.; Wei, W.; Sun, H.; Hou, Y. A Linear Quadratic Regulation Controller Based on Radial Basis Function Network Approximation. Electronics 2024, 13, 4279. [Google Scholar] [CrossRef]
- da Ponte Caun, R.; Assunção, E.; Minhoto Teixeira, M.C. H2/H∞ formulation of LQR controls based on LMI for continuous-time uncertain systems. Int. J. Syst. Sci. 2021, 52, 612–634. [Google Scholar] [CrossRef]
- Liu, C.; Qiu, X.X.; Mao, Y. The PID high-type controller based on LQR and model-assisted LESO. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2025, 239, 74–89. [Google Scholar] [CrossRef]
- Papadopoulos, K.G.; Papastefanaki, E.N.; Margaris, N.I. Optimal tuning of PID controllers for type-III control loops. In Proceedings of the 2011 19th Mediterranean Conference on Control & Automation (MED), Corfu, Greece, 20–23 June 2011; pp. 1295–1300. [Google Scholar]
- Deng, J.; Meng, X.; Jiang, B. Observer-Based Robust Hoo Control for Stochastic Markov Jump Delay Systems Through Dual Adaptive Sliding Mode Approach. Electronics 2024, 14, 132. [Google Scholar] [CrossRef]
- Kim, C. Robust Hoo Static Output Feedback Control for TCP/AQM Routers Based on LMI Optimization. Electronics 2024, 13, 2165. [Google Scholar] [CrossRef]
- Duan, G.R.; Yu, H.H. LMIs in Control Systems: Analysis, Design and Applications; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Belov, A.A. State-feedback anisotropy-based robust control of linear systems with polytopic uncertainties. J. Phys. Conf. Ser. 2020, 1536, 012008. [Google Scholar] [CrossRef]
- Ding, W.; Li, W.; Qiao, J. Anti-Disturbance Multi-Objective H2/H∞ Fusion Scheme for End-Effector Position Estimation of Space Manipulator. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; pp. 7265–7271. [Google Scholar]
- Sereni, B. Two-Stage Static Output Feedback Controller Design for Linear Systems Under LMI Pole Placement and H2/H∞ Guaranteed Cost Constraints. Ph.D. Thesis, São Paulo State University, São Paulo, Brazil, 2023. [Google Scholar]
- Wu, H.N.; Zhu, H.Y.; Wang, J.W. Hoo Fuzzy Control for a Class of Nonlinear Coupled ODE-PDE Systems with Input Constraint. IEEE Trans. Fuzzy Syst. 2014, 23, 593–604. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Qiu, X.; Mao, Y. A Convex Constraint Approach for High-Type Control Loop Design. Electronics 2025, 14, 2491. https://doi.org/10.3390/electronics14122491
Liu C, Qiu X, Mao Y. A Convex Constraint Approach for High-Type Control Loop Design. Electronics. 2025; 14(12):2491. https://doi.org/10.3390/electronics14122491
Chicago/Turabian StyleLiu, Chao, Xiaoxia Qiu, and Yao Mao. 2025. "A Convex Constraint Approach for High-Type Control Loop Design" Electronics 14, no. 12: 2491. https://doi.org/10.3390/electronics14122491
APA StyleLiu, C., Qiu, X., & Mao, Y. (2025). A Convex Constraint Approach for High-Type Control Loop Design. Electronics, 14(12), 2491. https://doi.org/10.3390/electronics14122491





