Theory of Diffraction by Holes of Arbitrary Sizes

Abstract

High-gradient accelerating radio frequency (RF) ] cavities are currently being developed in several national laboratories for applications in high-energy physics. Ultra-high accelerating gradients, reaching up to the GV/m range, can be achieved using ultra-compact accelerating structures operating in the sub-terahertz (sub-THz) regime. However, accurately measuring the key RF parameters of such compact structures presents significant experimental challenges, and even minor inaccuracies can lead to substantial errors. Additionally, RF simulations for these cavities often require extensive computational resources. Among the most critical parameters to determine is the reflection coefficient. To provide a fast and accurate analytical estimation, we have developed an electromagnetic theory describing the coupling between a resonant cavity and an RF waveguide. This approach is based on Bethe’s small-aperture polarization method, further developed by Collin. An exact analytical expression for the reflection coefficient is presented, formulated as a function of the physical parameters of the cavity waveguide system and applicable to arbitrary geometries, materials, and frequencies.

1. Introduction

The reflection coefficient plays a fundamental role in high-gradient accelerating periodic structures. Electromagnetic energy can be coupled from one waveguide to another, or into a cavity resonator, via a small aperture strategically placed in the common wall between the two. The electromagnetic theory used to calculate this coupling is based on the assumption that the aperture can be modeled as equivalent electric and/or magnetic dipole moments [1]. These moments are proportional to the normal electric field and the tangential magnetic field of the incident wave, respectively. Originally developed by Bethe [1], this theory was extended by Collin [2], and later refined by De Santis et al. for apertures small compared to the wavelength [3,4]. The solution method relies on Schelkunoff’s field equivalence principle [2], where the aperture is replaced by a perfect magnetic wall. The incident field defined as the field in the absence of the aperture induces a magnetic current $J_m$ and a magnetic charge ${\rho }_m$ on the wall surface. These act as sources of a scattered field, which can be expressed in terms of radiation from the resulting dipole moments. The total electromagnetic field, comprising the incident and scattered components, represents a unique solution to the coupling problem. In our case, a dielectric iris, supported by a thin, perfectly conducting screen, is placed between the waveguide and the cavity.

By invoking Babinet’s principle [2,5], the diffraction fields produced by a conducting screen, such as a circular wall between a waveguide and a cavity, are related to those of the complementary screen with an aperture. This configuration gives rise to transmitted and reflected fields, collectively referred to as the scattered field. A generalized diffraction theory is developed for apertures of arbitrary size and applied to the coupling of the transverse magnetic $T{M}_{01}$ mode of a pillbox cavity with a waveguide through a sub-wavelength aperture of comparable size to the wavelength. By “comparable,” we specifically refer to aperture radii that are on the same order of magnitude as the wavelength: neither significantly smaller nor substantially larger. This intermediate regime is particularly challenging for standard approximations and is often encountered in practical applications, making a general analytical treatment essential. Our approach bridges the gap between the small-hole (Bethe-type) and large-hole (geometrical optics) limits, offering a unified formalism. The resulting scattered field amplitudes are determined based on the polarizability of the aperture.

Bethe’s diffraction theory states that the hole is equivalent to an electric and a magnetic dipole whose moments are given by

$${\mathbf{P}}_{\mathbf{e}}=ϵ{\alpha }_e\widehat{z}\left({\mathbf{E}}_{\mathbf{0}}+{\mathbf{E}}_{\mathbf{sF}}-{\mathbf{E}}_{\mathbf{sB}}\right),$$

(1)

$${\mathbf{P}}_{\mathbf{m}}={\alpha }_m\widehat{t}\left({\mathbf{H}}_{\mathbf{0}}+{\mathbf{H}}_{\mathbf{sF}}-{\mathbf{H}}_{\mathbf{sB}}\right),$$

(2)

where ${\alpha }_e$ and ${\alpha }_m$ are the polarizabilites of the hole, ${\mathbf{E}}_{\mathbf{0}}$ and ${\mathbf{H}}_{\mathbf{0}}$ are the primary fields in the waveguide, ${\mathbf{E}}_{\mathbf{sF}}$ and ${\mathbf{H}}_{\mathbf{sF}}$ are the scattered fields (radiation fields) due to the polarizability of the iris, and ${\mathbf{E}}_{\mathbf{sB}}$, ${\mathbf{H}}_{\mathbf{sB}}$ are the scattered fields (radiation fields) due to the polarizability of the iris from the field entered into the cavity, reflected with a phase reversal and propagated back to the iris where they become an incoming wave with a certain amplitude which can polarize the iris and, due to this polarization, generate another radiation field, as shown in Figure 1.

The Electro-Magnetic (EM) analytical method proposed in this paper can be applied for the estimation of the scattering parameters in any power-coupling network through small holes compared/comparable to the wavelength. Scattering parameters, or S-parameters, describe how electromagnetic waves are reflected and transmitted through a network or structure. In the context of RF cavities and waveguides, the most relevant S-parameters are the reflection coefficient ($S_{11}$) and transmission coefficient ($S_{21}$), which quantify the portion of an incident wave reflected back and transmitted forward, respectively. In particular, through this approach we propose a viable tool for determining the main RF scattering parameters in particle accelerators made out of any material (metallic [6,7,8] or dielectric [9,10]), at any frequency and any temperature. For example, as the geometric dimensions of components such as the coupling slot between a metallic waveguide and a resonant cavity shrink to the order of a few millimeters, the determination of the reflection coefficient becomes increasingly sensitive to small geometrical variations. This sensitivity can lead to reduced accuracy in both experimental measurements and numerical simulations due to fabrication tolerances, alignment errors, and the discretization limits of full-wave solvers. For example, it is not always trivial at high frequencies, especially at mm-wave range and below, to determine the scattering parameters due to the difficulty of obtaining a reliable robust measurement setup. Although these parameters can be calculated through numerical softwares, the meshing tolerances required for good accuracy can easily result in long time consuming simulations. As a specific example, we will perform the comparison between our derived analytical formulation of the reflection coefficient with the formula derived for a resonant cavity through circuit analysis [2]. Our approach generalizes Bethe’s small-hole diffraction theory, which is originally valid for holes much smaller than the wavelength, by incorporating higher-order terms and using a polarizability-based formalism. As a result, our theory remains accurate for holes that are small or comparable in size to the wavelength.

While it offers analytical convenience and improved accuracy beyond the deep sub-wavelength regime, it does not extend to apertures that are significantly larger than the wavelength, where full-wave numerical methods become necessary. We have clarified this limitation in the manuscript to avoid ambiguity.

This paper is structured as follows. Section 2 presents a detailed analysis of the electromagnetic fields inside the structure, laying the foundation for subsequent calculations. In Section 3, we examine the power flow associated with the nth mode, which is essential for understanding energy transfer within the system. Section 4 focuses on the calculation of the electric polarizability, providing key parameters for characterizing the structure’s response. Section 5 then derives the reflection coefficient based on the previous results, connecting theory to measurable quantities. Finally, Section 6 summarizes the main findings and outlines possible directions for future research.

2. The Fields into the Structure

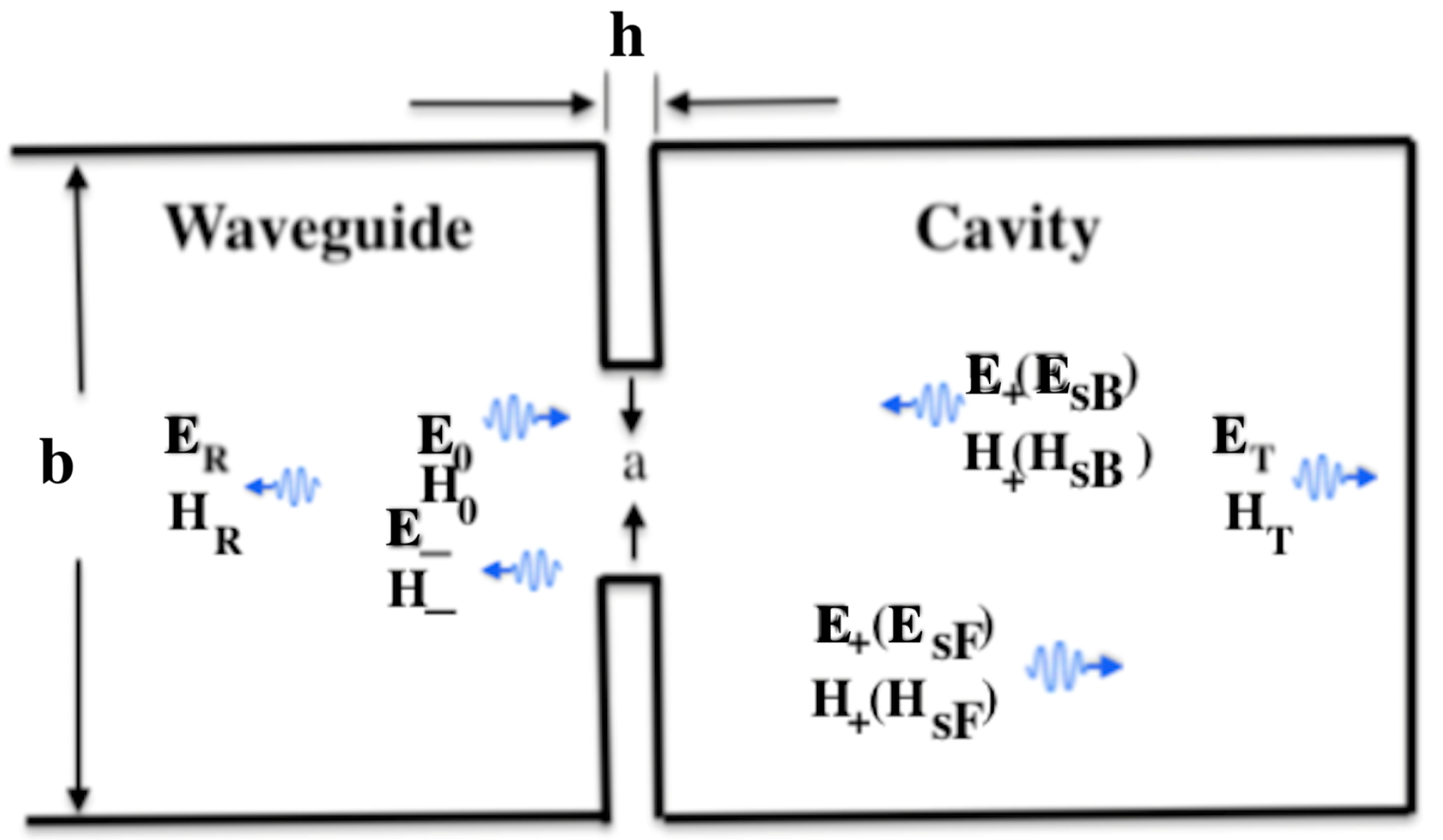
The structure we are going to consider is a pillbox cavity coupled by the iris to a waveguide and the cavity will be excited in a $T{M}_{01}$ standing-wave mode. The starting point in the process is the incident field on the iris a of Figure 1 which polarizes the iris. The consequence of the polarization is the electric and magnetic current induction. These currents radiate scattered electric and magnetic fields into the structure (waveguide and cavity) which we have called $E_{BF}$, $H_{BF}$ and $E_{SF}$, $H_{SF}$ respectively. With the assumption that the only propagating mode inside the structure is the $T{M}_{01}$, the total electric and magnetic fields in the waveguide, including both incident and scattered components can be written as,

$$\mathbf{E}={\mathbf{E}}_{\mathbf{0}}+{\mathbf{E}}_{\mathbf{sF}}-{\mathbf{E}}_{\mathbf{sB}}=\xi J_0\left(k_{c}r\right)e^{-j\beta z}+{\xi }_{01}^{-}(\widehat{t}{e}_{t01}-\widehat{z}{e}_{z01})e^{j\beta z}-j{\xi }_{01}^{+}(\widehat{t}{e}_{t01}+\widehat{z}{e}_{z01})e^{-(2\alpha \ell +j\beta z)}$$

(3)

$$\mathbf{H}={\mathbf{H}}_{\mathbf{0}}+{\mathbf{H}}_{\mathbf{sF}}-{\mathbf{H}}_{\mathbf{sB}}=-{\displaystyle \frac{\xi }{{\eta }_{01}}}{J}_0^{\prime }\left(k_{c}r\right)e^{-j\beta z}+{\xi }_{01}^{-}(-\widehat{t}{h}_{t01}+\widehat{z}{h}_{z01})e^{j\beta z}-j{\xi }_{01}^{+}(\widehat{t}{h}_{t01}+\widehat{z}{h}_{z01})e^{-(2\alpha \ell +j\beta z)}$$

(4)

where,

$\beta$: Propagation constant ($\sqrt{k^2-k_c^2}$);

${\eta }_{01}$: Wave impedance of the $T{M}_{01}$;

k: wavenumber;

$\alpha$: Attenuation constant per unit length;

ℓ: The length of the cavity;

j is the imaginary unit that satisfies $j^2=-1$;

$k_c$ is cutoff wavenumber;

$e_{t01},h_{t01}$: Transverse modal fields for $T{M}_{01}$ mode;

$e_{z01},h_{z01}$: Longitudinal modal fields for $T{M}_{01}$ mode;

$J_0\left(k_{c}r\right)$ is the zeroth-order Bessel function of the first kind;

$\xi$: Amplitude of the incident wave;

${\xi }_{01}^{-}$ is the $T{M}_{01}$ mode amplitude of scattered field propagating into the waveguide;

${\xi }_{01}^{+}$ is the $T{M}_{01}$ mode amplitude of scattered field propagating into the cavity.

The aperture undergoes a secondary polarization due to the combined effect of the incident waves and the forward and backward scattered fields. This results in induced electric and magnetic currents on the iris aperture. Specifically, the summation of the incident field with both scattered components continuously polarizes the aperture, generating new currents that act as sources of subsequent scattered fields. The infinitesimal electric and magnetic polarization currents in cylindrical coordinates can thus be expressed as [2]:

$${\mathbf{P}}_{\mathbf{e}}={\displaystyle \frac{1}{r}}{ϵ}_0{\alpha }_e\widehat{z}{E}_z\delta (r-r_0)\delta (\theta -{\theta }_0)\delta (z-z_0)$$

(5)

$${\mathbf{P}}_{\mathbf{m}}=-{\displaystyle \frac{1}{r}}{\alpha }_m\widehat{t}{H}_t\delta (r-r_0)\delta (\theta -{\theta }_0)\delta (z-z_0)$$

(6)

where,

${\mathbf{P}}_{\mathbf{e}}$: infinitesimal electric polarization currents

${\mathbf{P}}_{\mathbf{m}}$: infinitesimal magnetic polarization currents

${ϵ}_0$: Electric permitivity

${\alpha }_e$: electric polarizability of the aperture

${\alpha }_m$: magnetic polarizability of the aperture.

In Equations (5) and (6), we use cylindrical coordinates $(r,\theta ,z)$, where r denotes the radial distance from the axis, $\theta$ the azimuthal angle measured from a reference direction, and z the axial coordinate along the beam direction. Subscripted quantities such as $r_0$, ${\theta }_0$, and $z_0$ refer to fixed reference positions on the iris aperture surface. The vector components $J_r$, $J_{\theta }$, and $J_z$ correspond to the electric or magnetic current densities along these respective coordinate directions.

The electric and magnetic polarizabilities are constants that depend on the size and shape of the aperture through the fields. Substituting Equations (3) and (4) into the Equations (5) and (6) we obtain:

$${\mathbf{P}}_{\mathbf{e}}={ϵ}_0{\alpha }_e[\xi J_0\left(k_{c}r\right)e^{-j\beta z}-{\xi }_{01}^{-}{J}_0\left(k_{c}r\right)e^{j\beta z}-j{\xi }_{01}^{+}{J}_0\left(k_{c}r\right)e^{-(2\alpha \ell +j\beta z)}]\delta (r-r_0)\delta (\theta -{\theta }_0)\delta (z-z_0),$$

(7)

$${\mathbf{P}}_{\mathbf{m}}={\alpha }_m[-{\displaystyle \frac{\xi }{{\eta }_{01}}}{e}^{-j\beta z}+{\xi }_{01}^{-}{\displaystyle \frac{j\beta }{{\eta }_{01}{k}_c}}{e}^{j\beta z}-j{\xi }_{01}^{+}{\displaystyle \frac{j\beta }{{\eta }_{01}{k}_c}}{e}^{-(2\alpha \ell +j\beta z)}{J}_0^{\prime }\left(k_{c}r\right)]\delta (r-r_0)\delta (\theta -{\theta }_0)\delta (z-z_0).$$

(8)

The electric and magnetic moments are related to electric and magnetic current sources, $\mathbf{J}$ and $\mathbf{M}$, as follows [1]:

$$\mathbf{J}=j\omega {\mathbf{P}}_{\mathbf{e}}$$

(9)

$$\mathbf{M}=j\omega {\mu }_0{\mathbf{P}}_{\mathbf{m}}$$

(10)

where $\omega$ is the angular frequency and ${\mu }_0$ denotes the permeability of free space. The fields radiated from the sources propagate into the waveguide (${\overline{E}}_{-}$ and ${\overline{H}}_{-}$) and into the cavity (${\overline{E}}_{+}$ and ${\overline{H}}_{+}$). They can be written as the superpositions of the modes [11]:

$${\displaystyle {\mathbf{E}}_{+}=\sum _n{\xi }_n^{+}{\mathbf{E}}_{\mathbf{n}}^{+}=\sum _n{\xi }_n^{+}\left(\widehat{t}{e}_{tn}+\widehat{z}{e}_{zn}\right)e^{-j{\beta }_{n}z},}$$

(11)

$${\displaystyle {\mathbf{H}}_{+}=\sum _n{\xi }_n^{+}{\mathbf{H}}_{\mathbf{n}}^{+}=\sum _n{\xi }_n^{+}\left(\widehat{t}{h}_{tn}+\widehat{z}{h}_{zn}\right)e^{-j{\beta }_{n}z},}$$

(12)

$${\displaystyle {\mathbf{E}}_{-}=\sum _n{\xi }_n^{-}{\mathbf{E}}_{\mathbf{n}}^{-}=\sum _n{\xi }_n^{-}\left(\widehat{t}{e}_{tn}-\widehat{z}{e}_{zn}\right)e^{j{\beta }_{n}z},}$$

(13)

$${\displaystyle {\mathbf{H}}_{-}=\sum _n{\xi }_n^{-}{\mathbf{H}}_{\mathbf{n}}^{-}=\sum _n{\xi }_n^{-}\left(-\widehat{t}{h}_{tn}+\widehat{z}{h}_{zn}\right)e^{j{\beta }_{n}z},}$$

(14)

where the single index n is used to represent any possible transverse electric TE or TM mode. We denote the forward and backward traveling wave components of the fields using subscripts “+” and “−”, respectively. This replaces the earlier notation (e.g., $E_1$, $H_1$), to more explicitly indicate the direction of propagation along the z-axis. The subscript “n” continues to index the transverse modal profiles, while the z-dependence is reflected in the exponential terms $e^{\pm j{\beta }_{n}z}$. These notational conventions are adopted to maintain consistency with standard waveguide mode expansion formulations. 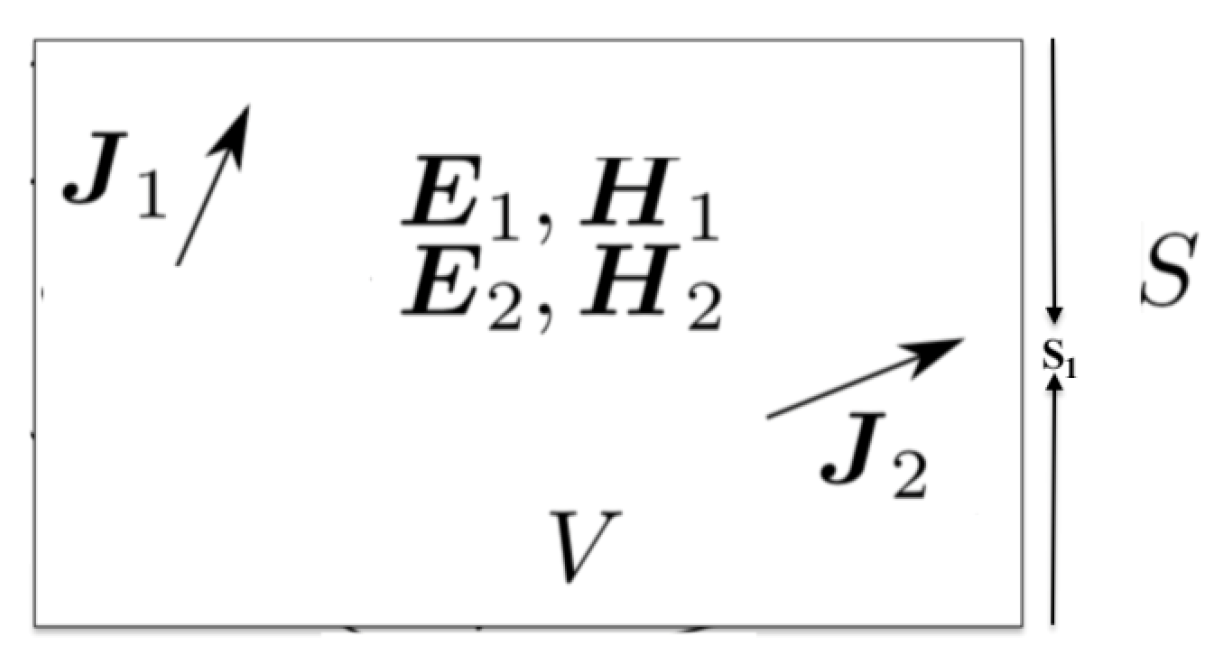For a given current we can determine the amplitude ${\xi }_n^{+}$ and ${\xi }_n^{-}$ by using Lorentz reciprocity theorem, which, in our case, can be written as:

$${\oint }_S({\mathbf{E}}_{\mathbf{1}}\times {\mathbf{H}}_{\mathbf{2}}-{\mathbf{E}}_{\mathbf{2}}\times {\mathbf{H}}_{\mathbf{1}}).nds={\int }_V(\mathbf{J}.{\mathbf{E}}_{\mathbf{2}}-\mathbf{M}.{\mathbf{H}}_{\mathbf{2}})dv$$

(15)

where S is a closed surface of the waveguide enclosing the volume V. $E_1,H_1$ are the scattered fields of $T{M}_{01}$ mode given by Equations (13) and (14) propagating into the waveguide, $E_2,H_2$ are the the unperturbed fields inside the waveguide, $\overline{J}$, $\overline{M}$ are the electric and magnetic current sources related to strength of electric and magnetic moments (see Figure 2).

Equation (15) represents a specific formulation of the Lorentz reciprocity theorem adapted for the modal expansion and scattering problem considered in this work. Unlike the classical integral form, this expression relates the modal amplitudes and field components at the aperture by enforcing electromagnetic field continuity and power flow conservation. The equation is derived by applying the Lorentz reciprocity theorem to the waveguide modes interacting at the iris aperture, taking into account the forward and backward scattered fields. This tailored formulation enables a concise and computationally effective treatment of the coupling between incident and scattered modes. By applying Lorentz Reciprocity Theorem to our problem, we obtain:

$${\oint }_S({\mathbf{E}}^{-}\times {\mathbf{H}}_{\mathbf{01}}^{+}-{\mathbf{E}}_{\mathbf{01}}^{+}\times {\mathbf{H}}^{-}).\widehat{z}ds={\int }_V(\mathbf{J}.{\mathbf{E}}_{\mathbf{01}}^{+}-\mathbf{M}.{\mathbf{H}}_{\mathbf{01}}^{+})dv$$

(16)

where ${\mathbf{E}}_{\mathbf{01}}^{+}$, ${\mathbf{H}}_{\mathbf{01}}^{+}$ are the fields of the $T{M}_{01}$ mode traveling in the positive z direction,

$${\mathbf{E}}_{\mathbf{2}}={\mathbf{E}}_{\mathbf{01}}^{+}=(\widehat{t}{e}_{t01}+\widehat{z}{e}_{z01})e^{-j\beta z},$$

(17)

$${\mathbf{H}}_{\mathbf{2}}={\mathbf{H}}_{\mathbf{01}}^{+}=(\widehat{t}{h}_{t01}+\widehat{z}{h}_{z01})e^{-j\beta z},$$

(18)

where $\beta$ is the propagation constant of the $T{M}_{01}$ mode. With some simplifications and considering that the tangential electric field and normal magnetic field vanishes on the waveguide walls so that surface integral of the Equation (15) reduces to just integration over the cross section in which the aperture is located ($S_1$):

$${\oint }_{S_1}({\mathbf{E}}^{-}\times {\mathbf{H}}_{\mathbf{01}}^{+}-{\mathbf{E}}_{\mathbf{01}}^{+}\times {\mathbf{H}}^{-}).\widehat{z}ds={\int }_V(\mathbf{J}.{\mathbf{E}}_{\mathbf{01}}^{+}-\mathbf{M}.{\mathbf{H}}_{\mathbf{01}}^{+})dv.$$

(19)

This equation can be written explicitly as:

$$\begin{array}{c}{\xi }_{01}^{-}{\int }_{S_1}[(\widehat{t}{e}_{t_{01}}-\widehat{z}{e}_{z_{01}})\times (\widehat{t}{h}_{t_{01}}+\widehat{z}{h}_{z01})-(\widehat{t}{e}_{t_{01}}+\widehat{z}{e}_{z_{01}})\times (-\widehat{t}{h}_{t_{01}}+\widehat{z}{h}_{z_{01}})].\widehat{z}ds\hfill \\ \hfill \hspace{1em}={\int }_V(\mathbf{J}.{\mathbf{E}}_{\mathbf{01}}^{+}-\mathbf{M}.{\mathbf{H}}_{\mathbf{01}}^{+})dv\end{array}$$

(20)

Finally, we obtain:

$${\xi }_{01}^{-}={\displaystyle \frac{-1}{P_{01}}}{\int }_V(\mathbf{J}.{\mathbf{E}}_{\mathbf{01}}^{+}-\mathbf{M}.{\mathbf{H}}_{\mathbf{01}}^{+})dv={\displaystyle \frac{-1}{P_{01}}}{\int }_V[(\widehat{t}{e}_{t01}+\widehat{z}{e}_{z01}).\mathbf{J}-(\widehat{t}{h}_{t01}+\widehat{z}{h}_{z01}).\mathbf{M}]e^{-j\beta z}dv$$

(21)

where $P_{01}=2{\int }_{S_1}{e}_{t01}\times h_{t01}.\widehat{z}ds$ is a normalization constant proportional to the power flow of the $T{M}_{01}$ mode. Substituting Equations (9) and (10) into the equation above yields:

$$\begin{array}{c}\hfill {\xi }_{01}^{-}={\displaystyle \frac{-1}{P_{01}}}{\int }_V[(\widehat{t}{e}_{t_{01}}+\widehat{z}{e}_{z_{01}}).\left(j\omega {\mathbf{P}}_{\mathbf{e}}\right)-(\widehat{t}{h}_{t_{01}}+\widehat{z}{h}_{z_{01}}).\left(j\omega {\mu }_0{\mathbf{P}}_{\mathbf{m}}\right)]e^{-j\beta z}dv\end{array}$$

(22)

where the longitudinal modal electric and magnetic field components for the $T{M}_{01n}$ mode are expressed as [5]:

$$e_z(r,\varphi )=(\Xi sinn\varphi +\xi cosn\varphi )J_n\left(k_{c}r\right),$$

(23)

$$h_t(r,\varphi )={\displaystyle \frac{-j\omega ϵ}{k_c}}(\Xi sinn\varphi +\xi cosn\varphi )J_n^{\prime }\left(k_{c}r\right)$$

(24)

where $k_c$ is the cutoff wavenumber, n is the azimuthal mode number (number of zeros in $E_z$ along the radial direction), $J_n^{\prime }\left(k_{c}r\right)$ is the derivative of the Bessel function of the first kind. Here, $\Xi$ and $\xi$ represent the amplitude coefficients of the $sin\left(n\varphi \right)$ and $cos\left(n\varphi \right)$ angular dependencies, respectively, which arise from the general solution of the Helmholtz equation in cylindrical coordinates using separation of variables. This formulation ensures a complete representation of the azimuthal variation of the field in cylindrical waveguides. Replacing Equations (7) and (8) into the above equation, we obtain:

$$\begin{array}{c}{\xi }_{01}^{-}={\displaystyle \frac{-1}{P_{01}}}\int \left[(\widehat{t}{e}_{t_{01}}+\widehat{z}{e}_{z_{01}})e^{-j\beta z}\right](\widehat{z}{\displaystyle \frac{j\omega }{r}}{ϵ}_0{\alpha }_e[\xi J_0\left(k_{c}r\right)e^{-j\beta z}\hfill \\ -{\xi }_{01}^{-}{J}_0\left(k_{c}r\right)e^{j\beta z}-j{\xi }_{01}^{+}{J}_0\left(k_{c}r\right)e^{-(2\alpha \ell +j\beta z)}\left]\right)-\left[(\widehat{t}{h}_{t_{01}}+\widehat{z}{h}_{z_{01}})e^{-j\beta z}\right].(\widehat{t}{\displaystyle \frac{j\omega }{r}}{\alpha }_m[(-{\displaystyle \frac{\xi }{{\eta }_{01}}}{e}^{-j\beta z}\hfill \\ +{\xi }_{01}^{-}{\displaystyle \frac{j\beta }{{\eta }_{01}{k}_c}}{e}^{j\beta z}-j{\xi }_{01}^{+}{\displaystyle \frac{j\beta }{{\eta }_{01}{k}_c}}{e}^{-(2\alpha \ell +j\beta z)})J_0^{\prime }\left(k_{c}r\right)\left]\right)\delta (r-r_0)\delta (\theta -{\theta }_0)\delta (z-z_0))rdrd\theta dz.\hfill \end{array}$$

(25)

The above equation can be simplified by placing the aperture at the center of the wall between the waveguide and the cavity. In the next section, we obtain the normalization constant proportional to the power flow of the $T{M}_{01}$ mode ($P_{01}$).

3. The Power Flow of the nth Mode

In this section, we aim to compute $P_{01}$, the normalization constant proportional to the power flow of the $T{M}_{01}$ mode, as defined in the previous section. The transverse components of the TM modal fields are given as [12]:

$$e_t(r,\varphi )={\displaystyle \frac{-j\beta }{k_c}}(\Xi sinn\varphi +\xi cosn\varphi )J_n^{\prime }\left(k_{c}r\right)$$

(26)

$$h_t(r,\varphi )={\displaystyle \frac{-j\beta }{{\eta }_{01}{k}_c}}(\Xi sinn\varphi +\xi cosn\varphi )J_n^{\prime }\left(k_{c}r\right)$$

(27)

Equation (27) above is essentially equivalent to Equation (24). Specifically, the term ${\displaystyle \frac{-j\omega ϵ}{k_c}}$ has been rewritten as ${\displaystyle \frac{-j\beta }{{\eta }_{01}{k}_c}}$, using the identity ${\eta }_{01}=\sqrt{{\displaystyle \frac{\mu }{ϵ}}}$ and $\beta =\omega \sqrt{\mu ϵ}$, which implies that $\omega ϵ={\displaystyle \frac{\beta }{{\eta }_{01}}}$. This substitution expresses the modal fields in terms of the propagation constant $\beta$ and ${\eta }_{01}$, which is the intrinsic impedance of free space, with SI units of ohms ($\Omega$), both of which are standard in waveguide theory. For the specific case of the $T{M}_{01}$ mode, the azimuthal number is $n=0$, the azimuthal variation disappears since $sin\left(0\varphi \right)=0$ and $cos\left(0\varphi \right)=1$, and $\xi =1$ is typically set for normalization; thus, the expressions simplify to:

$$e_{t_{01}}={\displaystyle \frac{-j\beta }{k_c}}{J}_0^{\prime }\left(k_{c}r\right)$$

(28)

$$h_{h_{01}}={\displaystyle \frac{-j\beta }{{\eta }_{01}{k}_c}}{J}_0^{\prime }\left(k_{c}r\right).$$

(29)

Substituting the above expressions into the definition of $P_{01}$:

$$\begin{array}{c}\hfill P_{01}=2{\int }_{S_1}{e}_{t_{01}}\times h_{h_{01}}.\widehat{z}ds=-{\displaystyle \frac{2{\beta }^2}{{\eta }_{01}{k}_c^2}}{\int }_0^{2\pi }{\int }_0^b{J}_0^{\prime 2}\left(k_{c}r\right)rdrd\theta .=-{\displaystyle \frac{4\pi {\beta }^2}{{\eta }_{01}{k}_c^2}}{\int }_0^{b}r{J}_0^{\prime 2}\left(k_{c}r\right)dr\end{array}$$

(30)

Here, b denotes the radius of the cavity cross section, over which the integration is performed. Since $J_0^{\prime }\left(k_{c}r\right)=-J_1\left(k_{c}r\right)$, replacing $k_{c}r={\chi }_{01}$, we obtain:

$$P_{01}={\displaystyle \frac{2\pi b^2{\beta }^2}{{\eta }_{01}{k}_c^2}}{J}_1^2\left({\chi }_{01}\right)={\displaystyle \frac{2\pi b^2}{{\eta }_{01}}}[1-{({\displaystyle \frac{k}{k_c}})}^2]J_1^2\left({\chi }_{01}\right)$$

(31)

4. Calculation of Electric Polarizability

According to Bethe’s theory, the electric polarization coefficient for a small circular hole is given by ${\alpha }_e=-2/3a^3$ as explicitly stated in Equation (3.8) of [1]. The assumption for using this coefficient is that the holes should be small compared with the wavelength. In Bethe’s theory of diffraction through small holes, the electromagnetic field near the aperture is often expressed using the Green’s function of the wave equation, which describes the response at a point due to a point source. The Green’s function includes a factor of the form

$$G(\mathbf{r},{\mathbf{r}}^{\prime })\propto {\displaystyle \frac{e^{ik|\mathbf{r}-{\mathbf{r}}^{\prime }|}}{|\mathbf{r}-{\mathbf{r}}^{\prime }|}},$$

where $k={\displaystyle \frac{2\pi }{\lambda }}$ is the wavenumber. For very small holes ($a\ll \lambda$), the spatial variation in the phase term $e^{ik|\mathbf{r}-{\mathbf{r}}^{\prime }|}$ across the hole can be neglected, simplifying the analysis. However, as the hole size a approaches the order of the wavelength, this phase factor varies significantly over the aperture, and the assumption of a constant field becomes invalid. Specifically, the phase term $e^{ika}$ introduces corrections to the field distribution that are proportional to powers of $ka$. Expanding the exponential:

$$e^{ika}=1+ika-{\displaystyle \frac{{\left(ka\right)}^2}{2}}+\dots ,$$

which shows that the first-order term $ika$ and higher-order terms like ${\left(ka\right)}^2$ contribute to the effective field at the hole. In particular, the second-order term ${\left(ka\right)}^2$ becomes significant for larger holes and must be included for accurate determination of the polarization coefficients and scattering parameters. Neglecting these terms leads to underestimation of the interaction effects and inaccuracies in predicting waveguide coupling and attenuation. Eggimann [11] addressed the diffraction of an arbitrary electromagnetic field by a circular, perfectly conducting disk using a series expansion in powers of the wavenumber k. Employing the generalized Babinet’s principle [2], which establishes the equivalence between the diffraction problems of a disk and its complementary aperture, the induced electric polarization $P_z$ at the aperture can be expressed as:

$$P_z={\displaystyle \frac{4}{3}}{a}^3{ϵ}_0\left(1-{\displaystyle \frac{3}{10}}{\left(ka\right)}^2+j{\displaystyle \frac{4}{9\pi }}{\left(ka\right)}^3\right)E_z^0+{\displaystyle \frac{2a^5{ϵ}_0}{15}}{\displaystyle \frac{{\partial }^2{E}_z^0}{\partial z^2}}$$

(32)

$$={\displaystyle \frac{4}{3}}{a}^3{ϵ}_0{E}_z^0-{\displaystyle \frac{2}{5}}{a}^3{ϵ}_0{\left(ka\right)}^2{E}_z^0+{\displaystyle \frac{2a^5{ϵ}_0}{15}}{\displaystyle \frac{{\partial }^2{E}_z^0}{\partial z^2}}+j{\displaystyle \frac{16}{27\pi }}{a}^3{ϵ}_0{\left(ka\right)}^3{E}_z^0.$$

(33)

Here, $E_z^0$ is the incident electric field component normal to the aperture plane (along the z-direction), evaluated at the aperture position. The series expansion accounts for higher-order corrections in powers of $ka$, where a is the aperture radius, including spatial variations in the incident field via the second derivative term. For the small holes compared to the wavelength, the second, third, and fourth terms vanish as the radius of the holes is in the order of 6, 5, and 6, respectively. One can derive the electric polarizability of Bethe’s theory by small holes. For the bigger holes, all terms have a contribution on electric polarizability. It should be noted that the imaginary part of the equation means that electric moment is out of phase with the electric field and there is a phase delay between the application of the electric field and the induced dipole moment. The imaginary term is responsible for the $\pi /2$ phase shift of the iris located between cavity resonators. For more information about the $\pi /2$ phase shift, one can refer to [13]. The third term contribution where we have the second derivative of the electric field is field oscillations, and converting this term in the time domain, we obtain a term with a ${\displaystyle \frac{1}{c^2}}$ coefficient which destroys the effect of the second derivatives, and the equation becomes:

$$P_z={\displaystyle \frac{4}{3}}{a}^3{ϵ}_0(1-{\displaystyle \frac{3}{10}}{\left(ka\right)}^2+j{\displaystyle \frac{4}{9\pi }}{\left(ka\right)}^3)E_z^0.$$

(34)

where the electric polarization coefficient can be obtained as

$${\alpha }_e={\displaystyle \frac{4}{3}}{a}^3{ϵ}_0(1-{\displaystyle \frac{3}{10}}{\left(ka\right)}^2+j{\displaystyle \frac{4}{9\pi }}{\left(ka\right)}^3).$$

(35)

To recover the classical result from Bethe’s theory [1], we take the limit $ka\ll 1$, where only the leading-order term is significant. In this limit, the correction terms vanish, and the expression reduces to ${\alpha }_e\approx {\displaystyle \frac{4}{3}}{a}^3{ϵ}_0$. However, in Bethe’s original formulation, the electric polarizability of a small circular aperture in a thin screen is ${\alpha }_e=-{\displaystyle \frac{2}{3}}{a}^3$, where the negative sign reflects the boundary conditions and choice of field definitions specific to Bethe’s setup. The difference in sign and prefactor arises from different conventions and approximations used (such as normalization and screen thickness). Our result follows the modern convention used in [11], which includes the dielectric constant ${ϵ}_0$ and is consistent with a complementary problem approach via Babinet’s principle. We observe a term involving ${\left(ka\right)}^2$ for the hole size comparable to the wavelength. This is exactly the correction mentioned in Bethe’s theory for the diffraction by bigger holes.

For the small irises compared to wavelength, all the modes of waveguide are below cut-off and their attenuation is exponential with respect to the length of the iris. McDonald [14] has derived an electric polarizability in which the attenuation term can be considered and it is as follows,

$${\alpha }_e=C_E{\alpha }_e^{\ast }{e}^{-2.405h/a},\mathrm{with}{C}_E=0.83\mathrm{and}{\alpha }_e^{\ast }=-{\displaystyle \frac{2}{3}}{a}^3.$$

(36)

where h is the iris thickness, $C_E$ is the numerical value calculated by McDonald.

Gluckstern [15] has derived integral equations for the potential and field distribution within a circular hole in a plane conducting wall of finite thickness induced by uniform field. Then, he obtained variational expressions for the polarizability and susceptibility of the hole, from which one can obtain the electric and magnetic dipole moments induced on the inside (far field) and outside (no far field) boundaries of the hole [15]. His results were in good agreement with McDonald’s results.

One can use the Equation (35) when the holes are comparable to the wavelength. In the next section, first, we will calculate the amplitudes of scattered fields; then, we will obtain equations for reflection and transmission coefficients.

5. Reflection Coefficient

The reflection coefficient, commonly denoted as $\Gamma$, quantifies the ratio of the amplitude of the reflected wave to that of the incident wave at a boundary or discontinuity in a transmission line or waveguide. It plays a fundamental role in waveguide and cavity theory, as it provides direct insight into how much of the incident power is reflected back due to impedance mismatches or structural discontinuities. In the context of coupling between a waveguide and a cavity, the reflection coefficient becomes an essential parameter for analyzing energy transfer, resonance conditions, and field enhancement within the system. Accurate modeling of $\Gamma$ enables prediction and control of resonant behavior, energy losses, and bandwidth, thereby forming a cornerstone of electromagnetic and microwave circuit analysis.

The amplitude of the backward-propagating wave due to the induced electric dipole moment can be obtained by evaluating Equation (25) under the condition that only the ${\mathrm{TM}}_{01}$ mode propagates in the waveguide. Using the mode expressions from Equations (23), (24), and (26), and noting that the longitudinal magnetic field $h_z$ vanishes for TM modes, we arrive at the following expression:

$$\begin{array}{c}{\xi }_{01}^{-}={\displaystyle \frac{-1}{P_{01}}}j\omega {ϵ}_0{\alpha }_e\xi +{\displaystyle \frac{-1}{P_{01}}}{\int }_0^a{\int }_0^{2\pi }{\int }_0^{h}j\omega {ϵ}_0{\alpha }_e{\xi }_{01}^{-}(-J_0^2\left(k_{c}r\right))e^{j\beta z}\delta r\delta \theta \delta zdrd\theta dz\hfill \\ \hfill +{\displaystyle \frac{-1}{P_{01}}}{\int }_0^a{\int }_0^{2\pi }{\int }_0^{h}j\omega {ϵ}_0{\alpha }_e[-j{\xi }_{01}^{+}{J}_0^2\left(k_{c}r\right)e^{-2\alpha \ell -j\beta z}]\delta r\delta \theta \delta zdrd\theta dz,\end{array}$$

(37)

Here, $P_{01}={\displaystyle \frac{2\pi b^2}{{\eta }_{01}}}\left[1-{\left({\displaystyle \frac{k}{k_c}}\right)}^2\right]J_1^2\left({\chi }_{01}\right)$ is the normalization constant proportional to the power flow of the ${\mathrm{TM}}_{01}$ mode, and ${\alpha }_e$ is the electric polarizability, previously defined in Equation (35). This equation expresses ${\xi }_{01}^{-}$, the amplitude of the backward wave, as the sum of three contributions: from the incident field, the backscattered field, and the forward-scattered field, each integrated over the volume of the subwavelength aperture. The imaginary part of ${\alpha }_e$ indicates that the induced electric dipole is out of phase with the applied electric field. This phase lag accounts for the $\pi /2$ phase shift introduced by an iris placed between two resonant cavities. Finally, the amplitudes ${\xi }_{01}^{-}$ and ${\xi }_{01}^{+}$ represent the backward and forward propagating radiation fields generated by the iris, modeled as an electric dipole. These amplitudes can be conveniently described using reflection and transmission coefficients as follows:

$${\xi }_{01}^{-}=\Gamma \xi ,$$

(38)

$${\xi }_{01}^{+}=(1-\Gamma )\xi ,$$

(39)

where $\Gamma$ is the reflection coefficient at the iris, indicating the fraction of the incident wave $\xi$ that is reflected backward due to the dipole response of the aperture. Substituting Equations (38) and (39) into Equation (37), we obtain:

$$\begin{array}{cc}\hfill \Gamma =& {\displaystyle \frac{-1}{P_{01}}}j\omega {ϵ}_0{\alpha }_e(1-j{e}^{-2\alpha \ell })\hfill \\ & +{\displaystyle \frac{-1}{P_{01}}}{\int }_0^a{\int }_0^{2\pi }{\int }_0^{h}j\omega {ϵ}_0{\alpha }_e\Gamma (-J_0^2\left(k_{c}r\right))e^{j\beta z}(1+j{e}^{-2\alpha \ell -2j\beta z})\delta r\delta \theta \delta zdrd\theta dz.\hfill \end{array}$$

(40)

Equation (40) provides an intermediate formulation where the spatial distribution of the interaction is formalized through Bessel functions and exponential phase terms, reflecting the cylindrical symmetry and wave propagation characteristics of the $T{M}_{010}$ mode. The equation above can be expressed in a more compact form as:

$$\Gamma ={\Gamma }_0+D{\int }_V\Gamma f\left(r\right)g\left(z\right)h\left(\theta \right)\delta r\delta \theta \delta zdV,$$

(41)

where

${\Gamma }_0={\displaystyle \frac{-1}{P_{01}}}j\omega {ϵ}_0{\alpha }_e(1-j{e}^{-2\alpha \ell })$,

$D={\displaystyle \frac{-1}{P_{01}}}j\omega {ϵ}_0{\alpha }_e$,

$f\left(r\right)=J_0^2\left(k_{c}r\right)$,

$g\left(z\right)=e^{j\beta z}(1+j{e}^{-2\alpha \ell -2j\beta z})$,

and

$h\left(\theta \right)$: Heaviside step function.

The inclusion of the Heaviside step function $h\left(\theta \right)$ in Equation (41) serves an important role both mathematically and physically. Mathematically, the Heaviside function acts as an angular domain selector within the volume integral. Since the integration is performed over the cylindrical coordinates $(r,\theta ,z)$, $h\left(\theta \right)$ effectively restricts the angular range over which the integrand contributes. This is equivalent to setting the integrand to zero outside the angular interval where the physical aperture or perturbation exists. The step function thus allows us to model a piecewise domain in $\theta$, ensuring that only the portion of the iris or scatterer within the specified angular limits contributes to the scattering integral. Physically, the iris or aperture often does not occupy a full $2\pi$ angular extent around the waveguide axis but rather covers a sector or partial angular region. The Heaviside step function models this angular asymmetry by “turning on” the scattering contributions only within the angular sector where the aperture exists, while “turning off” contributions elsewhere. This angular truncation corresponds to real physical situations such as a slit-like or sector-shaped iris, which affects the electromagnetic field distribution and scattering behavior accordingly. Therefore, the use of $h\left(\theta \right)$ in Equation (41) is essential to accurately represent the spatial domain of the aperture and to ensure that the integral properly accounts for the physical geometry and angular constraints of the structure. This inclusion leads to a more precise and realistic calculation of the reflection coefficient $\Gamma$.

To derive the equation above, the iris is assumed to be located at the center of the cavity’s cross section. This assumption simplifies the expressions for the infinitesimal electric and magnetic dipole moments given in Equations (5) and (6), reducing them to the following forms:

$${\mathbf{P}}_{\mathbf{e}}={\displaystyle \frac{1}{r}}{ϵ}_0{\alpha }_e\widehat{z}{E}_z\delta \left(r\right)\delta \left(\theta \right)\delta \left(z\right)$$

(42)

$${\mathbf{P}}_{\mathbf{m}}=-{\displaystyle \frac{1}{r}}{\alpha }_m\widehat{t}{H}_t\delta \left(r\right)\delta \left(\theta \right)\delta \left(z\right).$$

(43)

These expressions for the infinitesimal electric and magnetic dipole moments represent the localized polarization of the aperture positioned at the center of the waveguide-cavity interface. The delta functions allow us to perform convolution integrals effectively, enabling the analytical simplification of the electromagnetic field interactions. By considering the aperture at the origin of the coordinate system and modeling it as an electric dipole, the problem becomes mathematically tractable using a self-consistent solution method. This approach is necessary because the backward-propagating field amplitude ${\xi }_{01}^{-}$ appears both explicitly and implicitly within the resulting field expressions. Specifically, the scattered field produced by the dipole depends on the total field, which in turn includes the field scattered by the dipole itself. Physically, this reflects a mutual interaction or feedback loop between the dipole and the electromagnetic field. Mathematically, this leads to a recursive formulation that cannot be solved in closed form but instead requires an iterative or self-consistent procedure to find a convergent solution.

Using this framework, we obtain the reflection coefficient as:

$$\Gamma ={\displaystyle \frac{\frac{-1}{P_{01}}j\omega {ϵ}_0{\alpha }_e(1-j{e}^{-2\alpha \ell })}{1+j\frac{-1}{P_{01}}\omega {ϵ}_0{\alpha }_e(1+j{e}^{-2\alpha \ell })}}.$$

(44)

The equation above represents the reflection coefficient $\Gamma$, derived using the self-consistent solution method. This approach is required because of the mutual dependence between the induced dipole moment at the aperture and the scattered field it generates. In this framework, the incident field induces an electric polarization at the iris, which subsequently radiates and contributes back to the total field. To maintain consistency, the scattered field must be included in the total field used to induce the original polarization, leading to a feedback loop that is resolved through a self-consistent formulation.

The numerator in Equation (44) accounts for the direct contribution of the electric dipole moment, characterized by the electric polarizability ${\alpha }_e$, and includes the exponential term $e^{-2\alpha \ell }$, which models the phase delay due to propagation and reflection within the structure. The imaginary part of ${\alpha }_e$ indicates that the induced dipole moment is out of phase with the applied electric field. This is typical of resonant behavior, where a phase shift occurs between driving and response.

The denominator ensures that the recursive interaction between the induced moment and the total field is included, rendering the solution self-consistent. As such, Equation (44) captures the essential physics of the interaction between the aperture and the propagating mode in the waveguide, including both resonant enhancement and energy dissipation.

Additionally, the presence of the Heaviside step function $H\left(t\right)$ in the derivation reflects the causality and time-domain behavior of the system. In the frequency domain, the Fourier transform of the Heaviside function is given by the distribution:

$$\widehat{H}\left(s\right)={\displaystyle \frac{1}{2}}\left(\delta \left(s\right)-{\displaystyle \frac{i}{\pi }}\mathrm{p}.\mathrm{v}.{\displaystyle \frac{1}{s}}\right),$$

(45)

where $\delta \left(s\right)$ is the Dirac delta function and $\mathrm{p}.\mathrm{v}.{\displaystyle \frac{1}{s}}$ represents the Cauchy principal value. The right-hand side of this equation consists of two terms: the Dirac delta function $\delta \left(s\right)$, which accounts for the DC component due to the non zero average of the Heaviside function, and the distributional term $\mathrm{p}.\mathrm{v}.{\displaystyle \frac{1}{s}}$, which is the Cauchy principal value. The principal value is a generalized function (distribution) used to make sense of the otherwise divergent integral of $1/s$, and is defined through its action on test functions.

The imaginary coefficient ${\displaystyle \frac{i}{\pi }}$ in front of the principal value introduces a phase shift, reflecting the asymmetry and non-analyticity of the Heaviside function. This decomposition is essential in the theory of distributions and complex analysis, especially when modeling causal systems where signals or responses begin at $t=0$. In the context of our analysis, this expression helps in transforming step-like behavior or abrupt changes into the frequency domain, making it easier to calculate the reflection coefficient around the resonance by convolving the system response with appropriate distributions. This approach also provides a clearer understanding of the singular behavior near resonances. This transformation plays an important role in describing the system’s frequency response near resonance and allows for the identification of singularities and phase shifts in the reflection spectrum [16]. Through this representation, the analytic structure of the reflection coefficient becomes evident, particularly in how energy is stored and dissipated by the resonant aperture.

For comparison, we report below the expression of the reflection coefficient derived by Collin for the $T{E}_{10}$ mode using an equivalent circuit model [2]:

$$\Gamma =1-{\displaystyle \frac{4j{\alpha }_m{\beta }_{10}/ab}{1+jX+W}},$$

(46)

where $X=2{\alpha }_m{\beta }_{10}/ab$ and

$$W=-{\displaystyle \frac{4{\alpha }_m{k}_0^2{\pi }^2}{k_{101}^{2}ab{d}^3\left[k_{101}^2-k_0^2\left(1+\frac{1-j}{Q}\right)\right]}}.$$

(47)

This expression models the reflection at the junction between a waveguide and a cavity through a small aperture, where ${\alpha }_m$ is the magnetic polarizability, ${\beta }_{10}$ is the propagation constant of the $T{E}_{10}$ mode, a and b are the waveguide dimensions, d is the cavity length, $k_{101}$ is the resonant wavenumber of the $(1,0,1)$ cavity mode, $k_0$ is the free-space wavenumber, and Q is the quality factor. The denominator accounts for detuning from resonance, and the Q-dependent term introduces cavity losses. Our result in Equation (44) generalizes this approach to the $TM$ mode and uses a self-consistent field-theoretical method incorporating electric polarizability, providing a more fundamental description compared to the equivalent circuit model. This classical result is presented here not to suggest a direct equivalence between the $T{E}_{10}$ and $T{M}_{010}$ modes, but rather to provide a conceptual and structural analogy. Both expressions describe the reflection coefficient of a wave interacting with an aperture-coupled cavity, and their forms exhibit similar dependence on the polarizability of the coupling element. Including Collin’s result serves to place our field-theoretical formulation within a broader theoretical context and supports its physical consistency through comparison with well-established models.

A comparison between Equation (44) and the analogous expression derived by Collin for the $T{E}_{10}$ mode reveals several similarities: both equations contain real and imaginary components; the real parts exhibit a first-order dependence on the electric or magnetic polarizability (${\alpha }_e$ or ${\alpha }_m$, respectively); and each includes a normalization constant related to the power flow—$P_{01}$ for the $T{M}_{010}$ mode and ${\beta }_{10}$ for the $T{E}_{10}$ mode. Additionally, both expressions feature second-order dependencies, such as ${\left({\displaystyle \frac{k}{k_c}}\right)}^2$ and its counterpart ${\left({\displaystyle \frac{k_0}{k_{101}}}\right)}^2$, indicating similar scaling behavior. Finally, both equations reflect geometrical dependencies—cylindrical symmetry for the $T{M}_{01}$ mode and rectangular symmetry for the $T{E}_{10}$ mode—demonstrating how the structure influences the form of the reflection coefficient.

Equation (25) can be simplified by noting that the magnetic moment does not contribute to the $T{M}_{01}$ mode, allowing the second term to be completely eliminated. The subsequent analysis demonstrates that the magnetic moment associated with the $T{M}_{01}$ mode does not contribute to the reflection coefficient. Accordingly, Equation (25) for the magnetic moment component is expressed as:

$${\xi }_n^{-}={\displaystyle \frac{1}{P_{01}}}{\int }_V({\overline{h}}_{t01}+\widehat{z}{h}_{z01}).\left(j\omega {\mu }_0{\overline{P}}_m\right)e^{-j{\beta }_{n}z}dv$$

(48)

substituting Equation (8) into the above equation we obtain

$$\begin{array}{c}{\xi }_{01}^{-}={\displaystyle \frac{1}{P_{01}}}\int \left[(\overline{h_{t01}}+\widehat{z}{h}_{z01})e^{-j{\beta }_{n}z}\right](\widehat{t}{\displaystyle \frac{j\omega }{r}}{\alpha }_m(-{\displaystyle \frac{\xi }{{\eta }_{01}}}{e}^{-j\beta z}+{\xi }_{01}^{-}{\displaystyle \frac{j\beta }{{\eta }_{01}{k}_c}}{e}^{j\beta z}\hfill \\ \hfill -j{\xi }_{01}^{+}{\displaystyle \frac{j\beta }{{\eta }_{01}{k}_c}}{e}^{-(2\alpha \ell +j\beta z)}\left)J_0^{\prime }\left(k_{c}r\right)\right)\delta r\delta \theta \delta zrdrd\theta dz.\end{array}$$

(49)

In the equation above, the unit vector $\widehat{t}$ appears because it defines the direction of the magnetic dipole moment, which is transverse to the direction of wave propagation. This aligns with the orientation of the induced magnetic moment ${\mathbf{P}}_m$, which, by definition, lies in the plane perpendicular to the waveguide axis. The factor ${\displaystyle \frac{1}{r}}$ in the integrand arises from the expression for the magnetic dipole moment density in cylindrical coordinates. Specifically, this term appears due to the coordinate transformation from Cartesian to cylindrical form, as reflected in the delta function normalization and the integration measure. Including this factor ensures the correct dimensionality and proper normalization when integrating over a cylindrical volume with the measure $r,dr,d\theta ,dz$. Due to the properties of the Dirac delta function, the derivative of the Bessel function of the zero kind and first kind at the center of the holes is zero and leads to ${\xi }_{01}^{-}$ = 0, as a consequence, for the $T{M}_{01}$ mode, the iris aperture between the pill-box cavity coupled with a cylindrical waveguide, acts as an electric moment.

6. Conclusions

A theoretical framework has been developed for analyzing diffraction through apertures of arbitrary size. This approach has been specifically applied to a $T{M}_{01}$ mode cavity coupled to a cylindrical waveguide via a small hole with dimensions comparable to the wavelength. The amplitudes of the scattered fields, arising from the polarizability of the aperture situated between the waveguide and the cavity, have been determined, leading to explicit expressions for the reflection and transmission coefficients. The electromagnetic (EM) analytical method presented here is broadly applicable for estimating the scattering parameters in power-coupling networks involving small apertures.