Generalized Maximum Delay Estimation for Enhanced Channel Estimation in IEEE 802.11p/OFDM Systems
Abstract
1. Introduction
- 1.
- A novel log-likelihood ratio (LLR) expression is derived by exploiting the inherent correlation characteristics introduced by the cyclic prefix (CP) in the received OFDM symbols. This formulation enables the robust detection of the channel delay profile.
- 2.
- An approximated maximum likelihood (ML) estimator for the maximum access delay is proposed. The proposed estimator adopts a generalized form incorporating a weighting function applied to the observation random variables, thus enhancing detection accuracy under various channel conditions.
- 3.
- The unification and generalization of existing methods are achieved by explicitly formulating the bias term associated with the geometric mean. It is analytically demonstrated that the estimator proposed in [6] represents a special case within the proposed framework, thereby extending and generalizing the prior approach.
- 4.
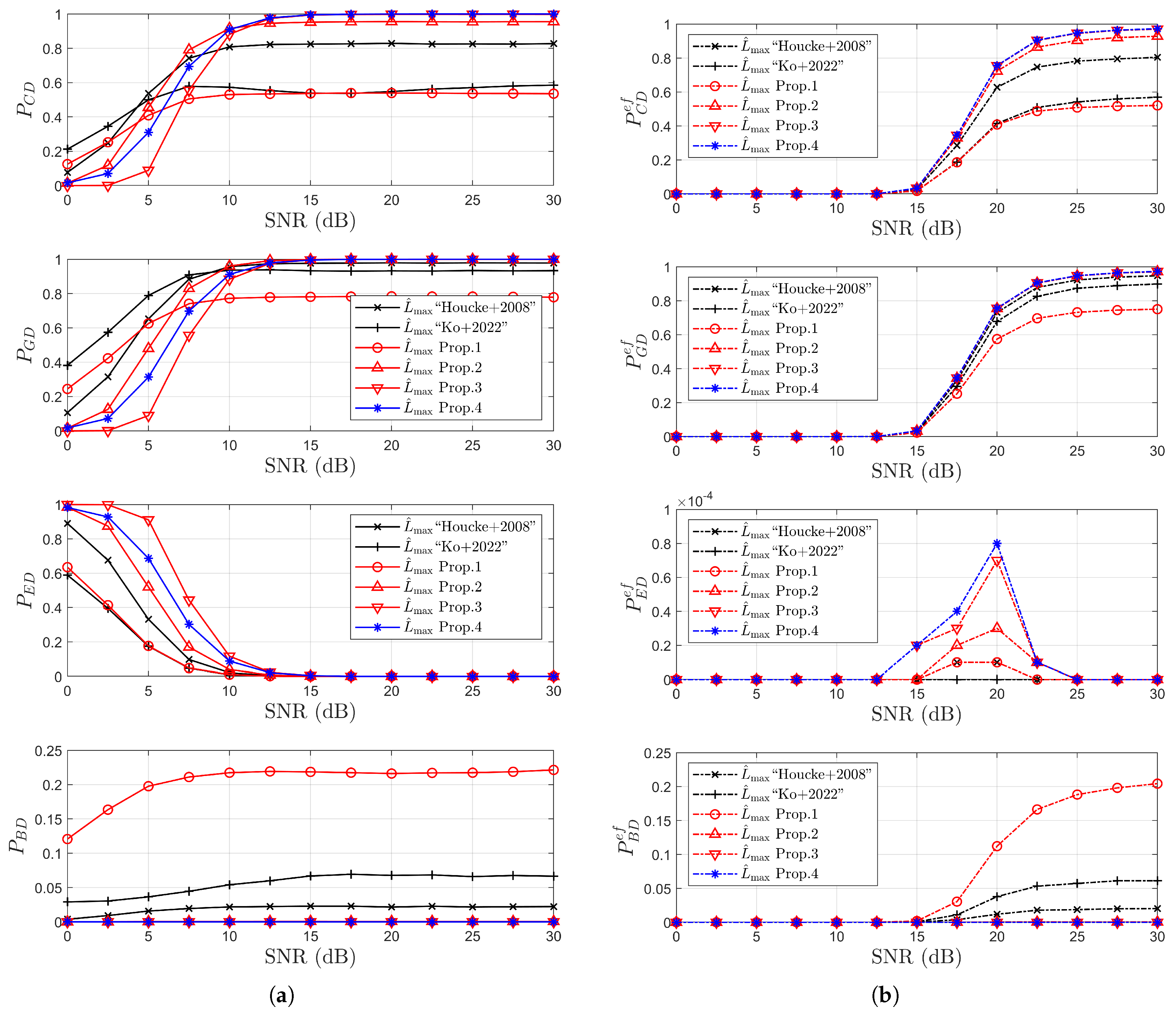
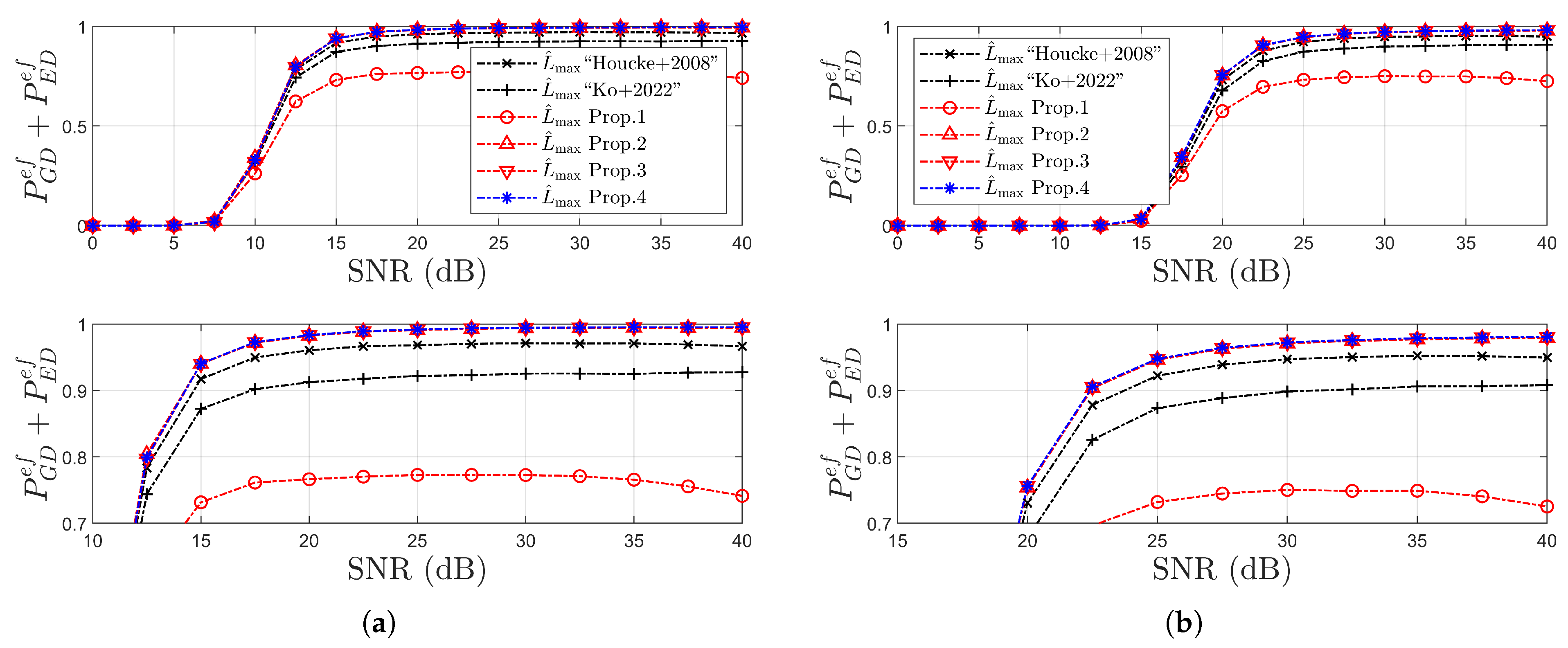
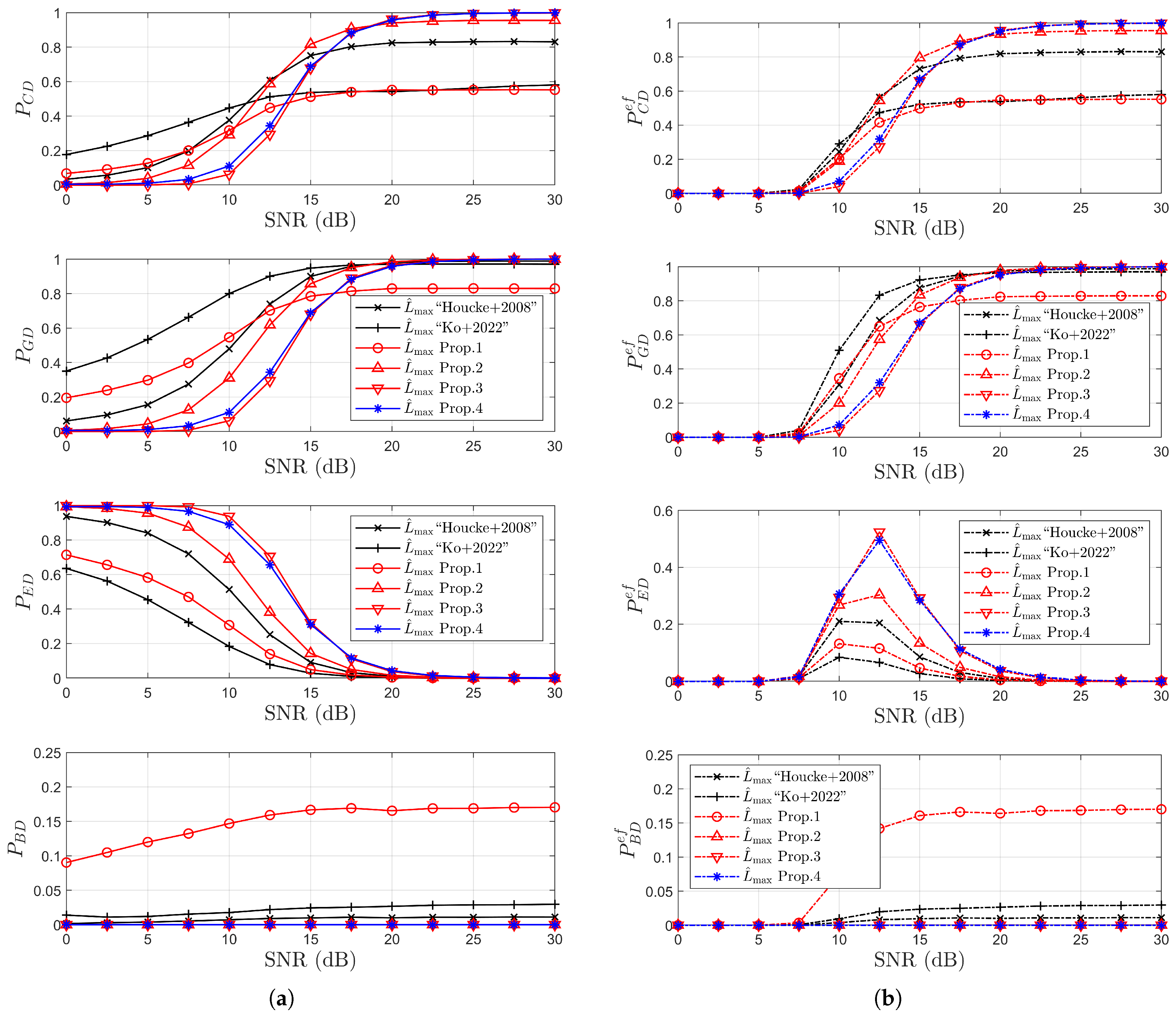
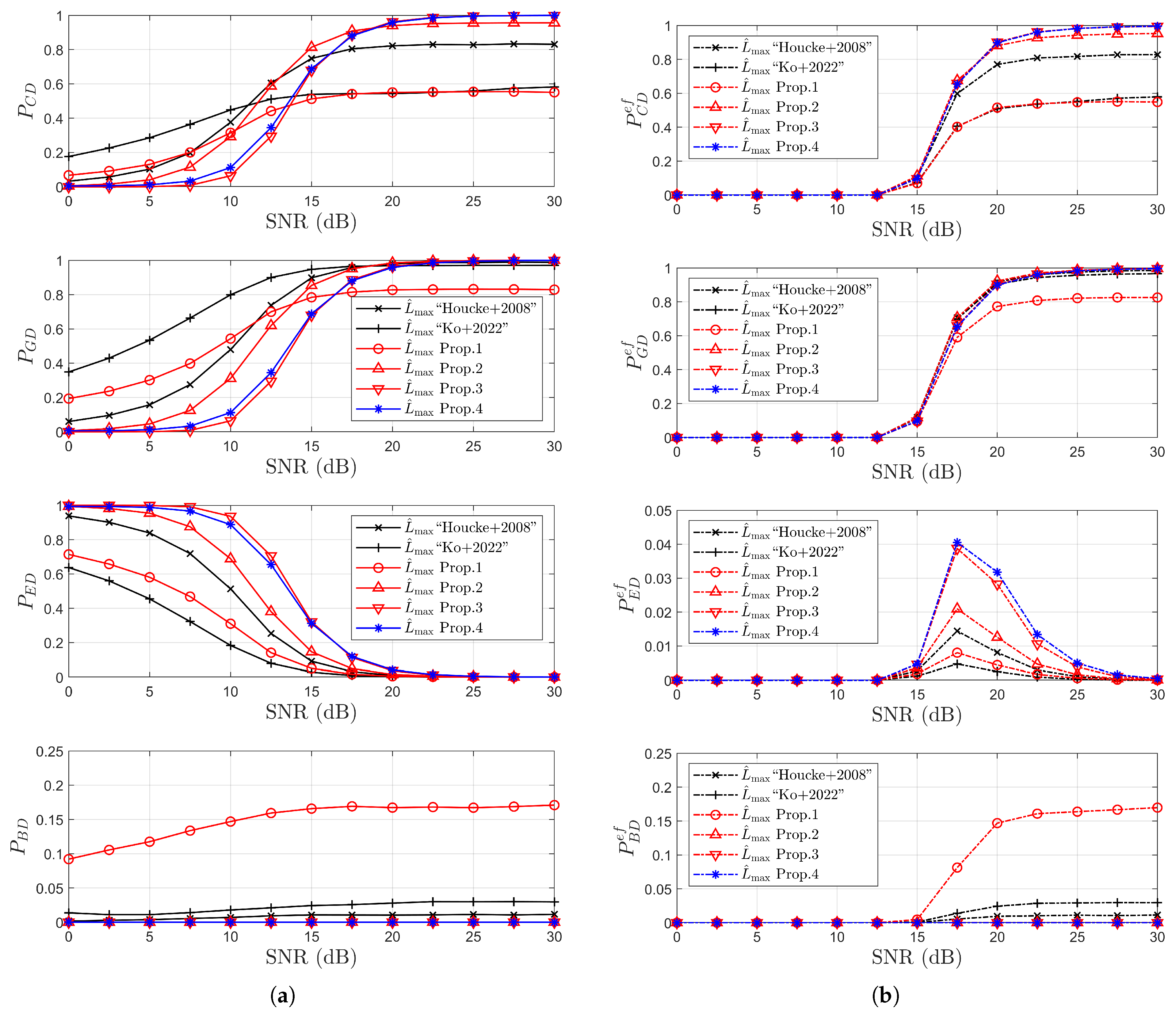
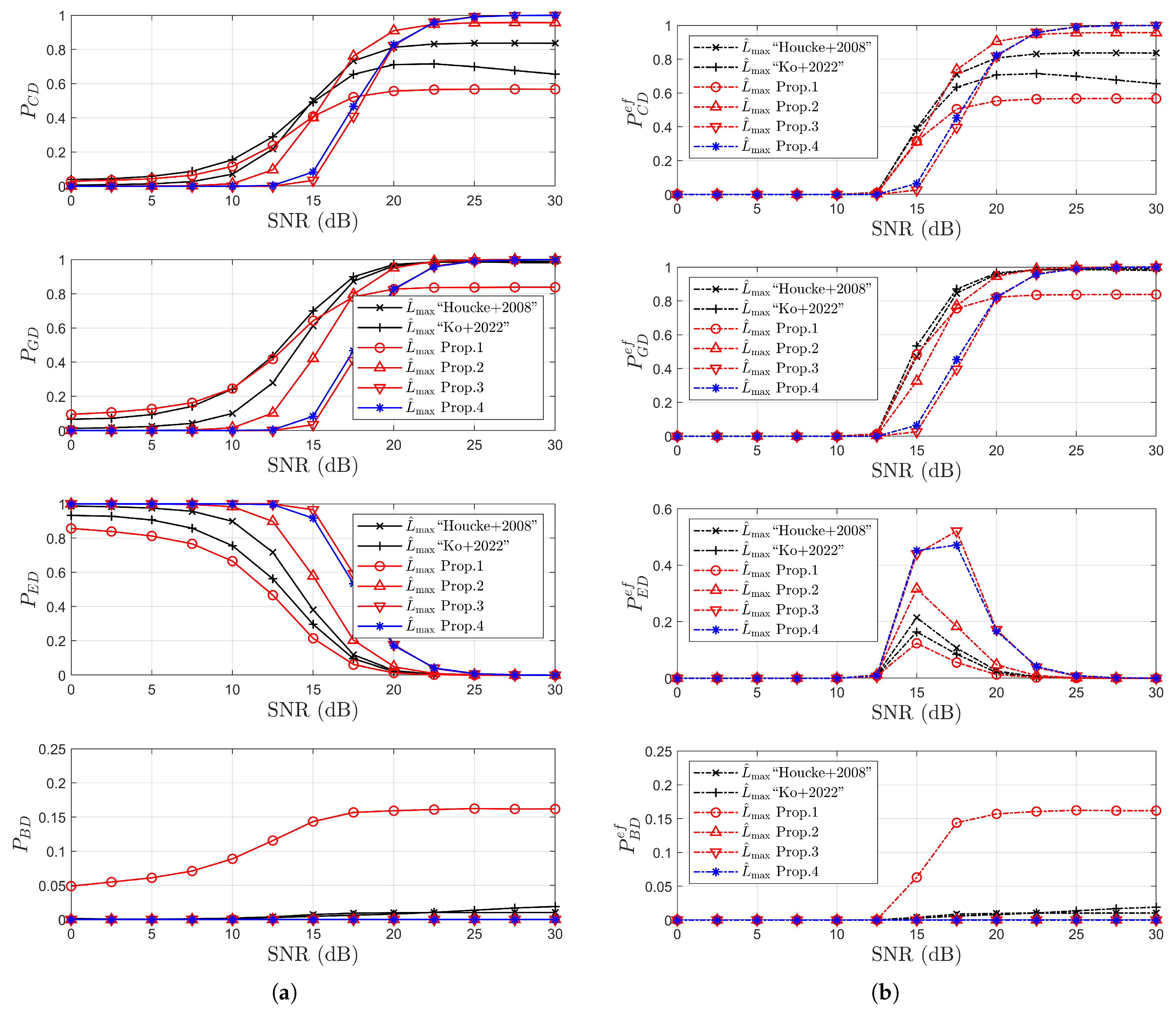
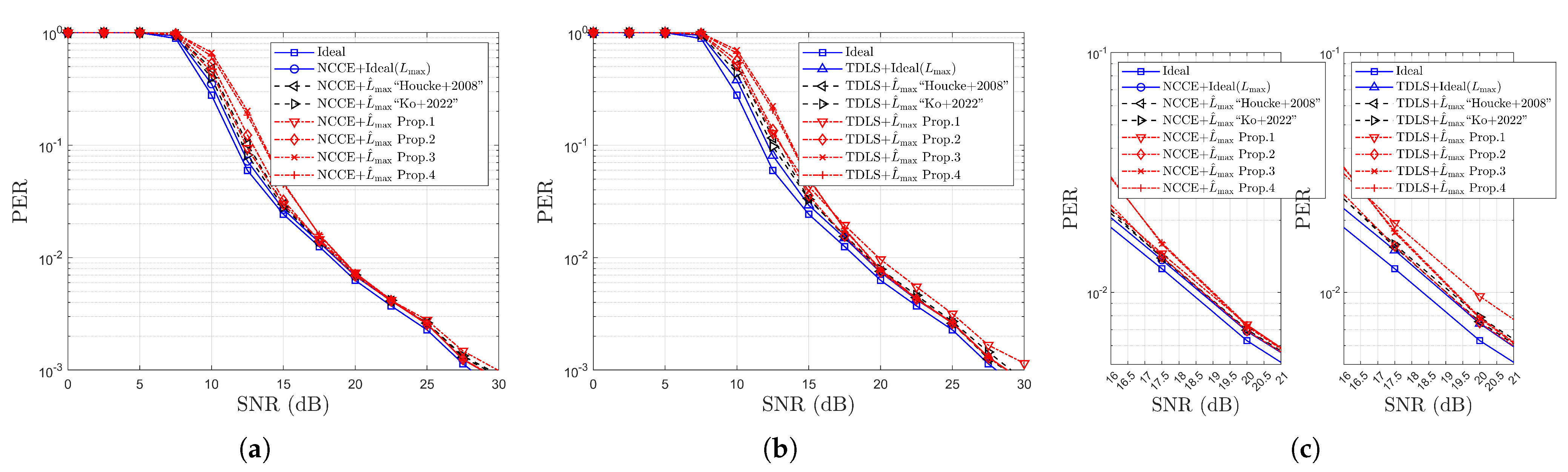
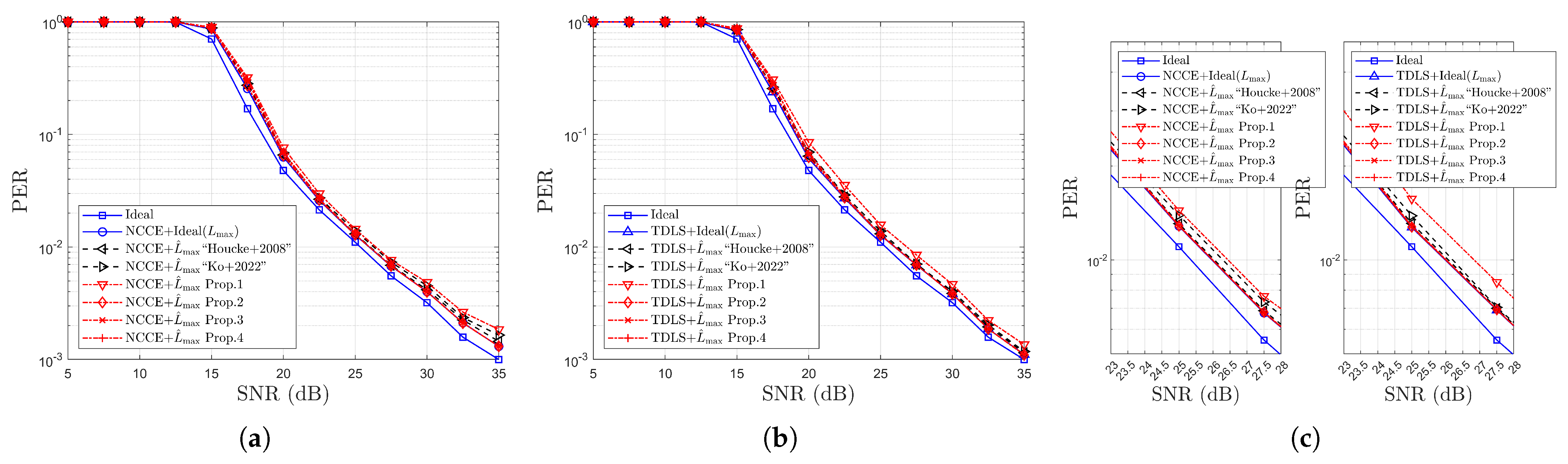
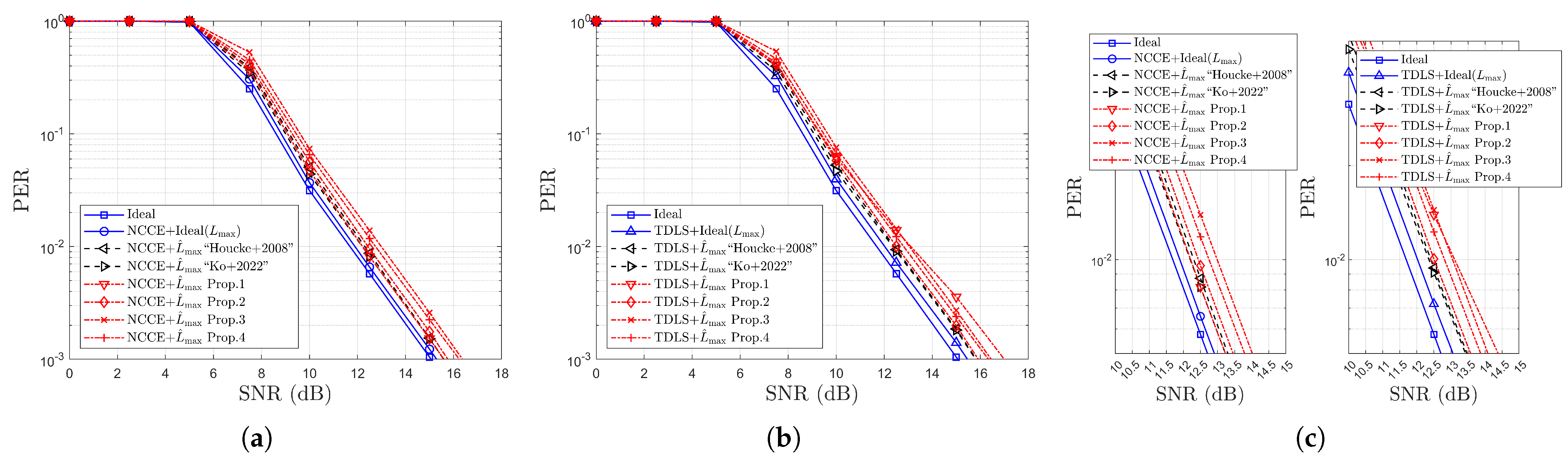
- Performance advantages are demonstrated through extensive simulations, where the proposed scheme is applied to both the NCCE and the time-domain least square (TDLS) channel estimation methods. Simulation results under IEEE 802.11p/OFDM system conditions confirm the superiority of the proposed estimator in terms of correct and good detection probabilities. Notably, with respect to error rates, the proposed method closely approaches the performance bound of the ideal MADT estimation across all three considered channel environments.
2. OFDM System and Discrete Signal Model
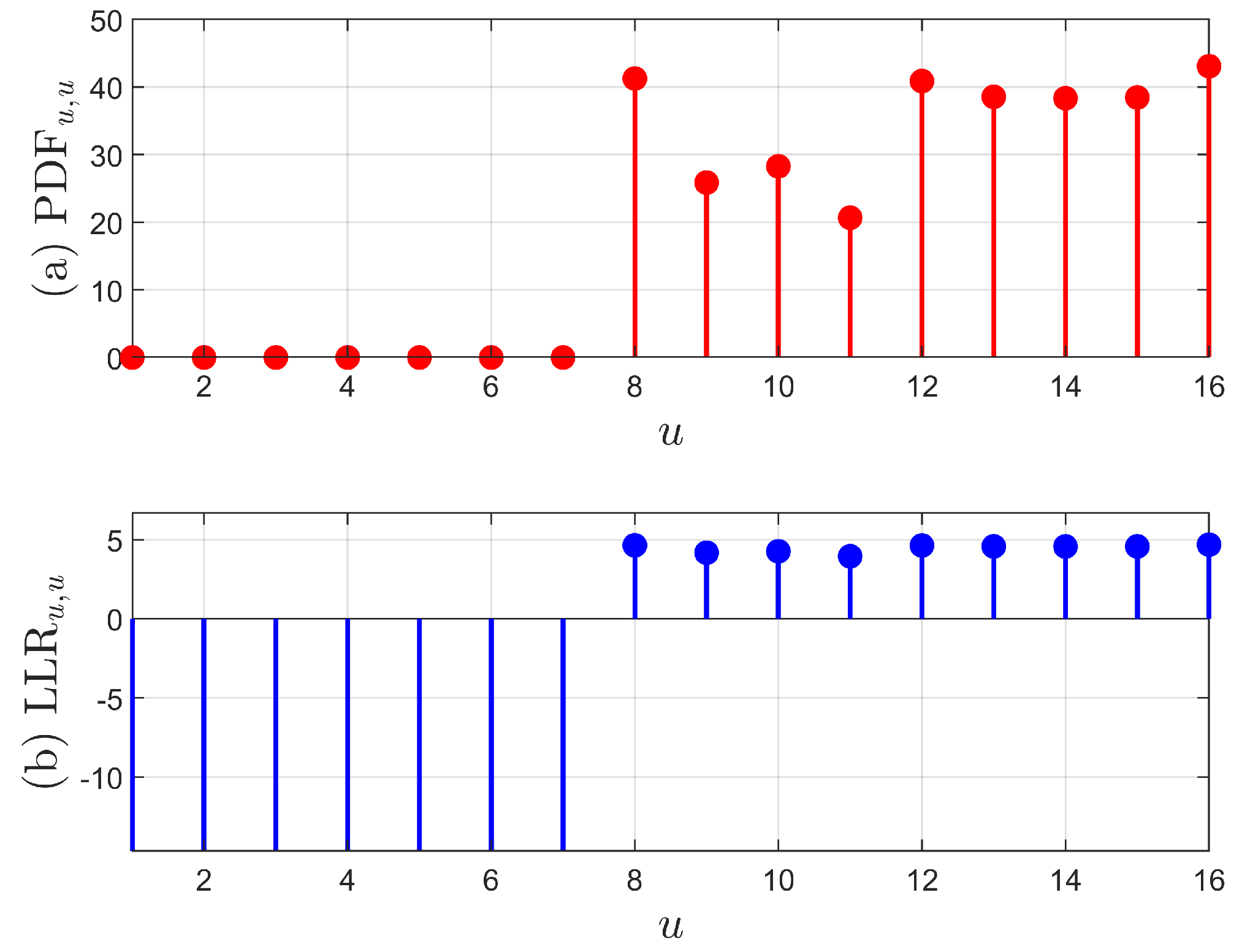
2.1. Joint PDFs
2.2. Ng Noise Power Estimators
3. Proposed Lmax Estimation Method in a Generalized Framework
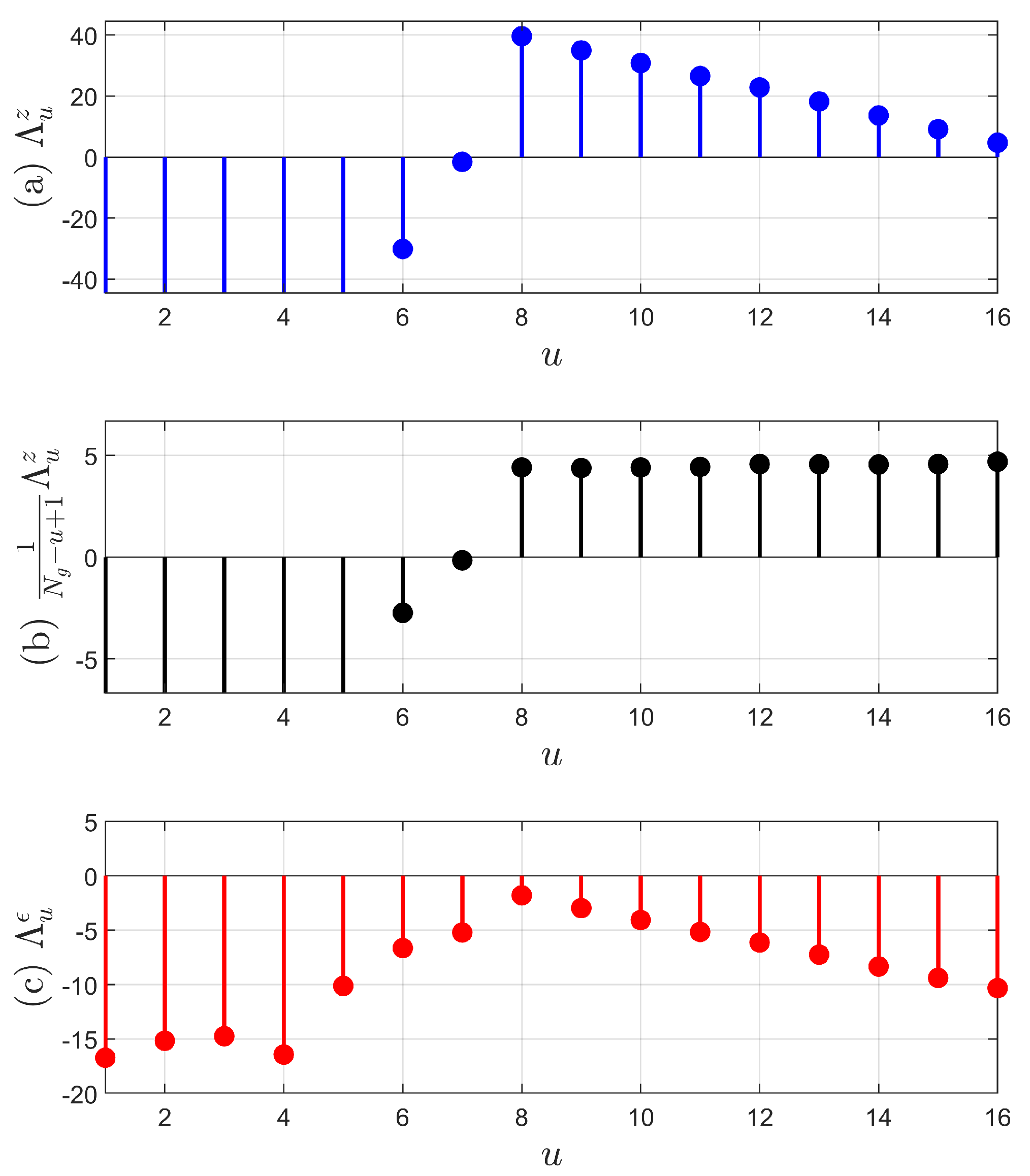
3.1. PDF Multiplication and Geometric Mean
3.2. LLR Summation and Average
3.3. Special Cases for
3.3.1. Method in [6] with
3.3.2. Proposed
- (Prop.1) →.
- (Prop.2) →.
- (Prop.3) →.
- (Prop.4) →.
3.4. Computational Complexity
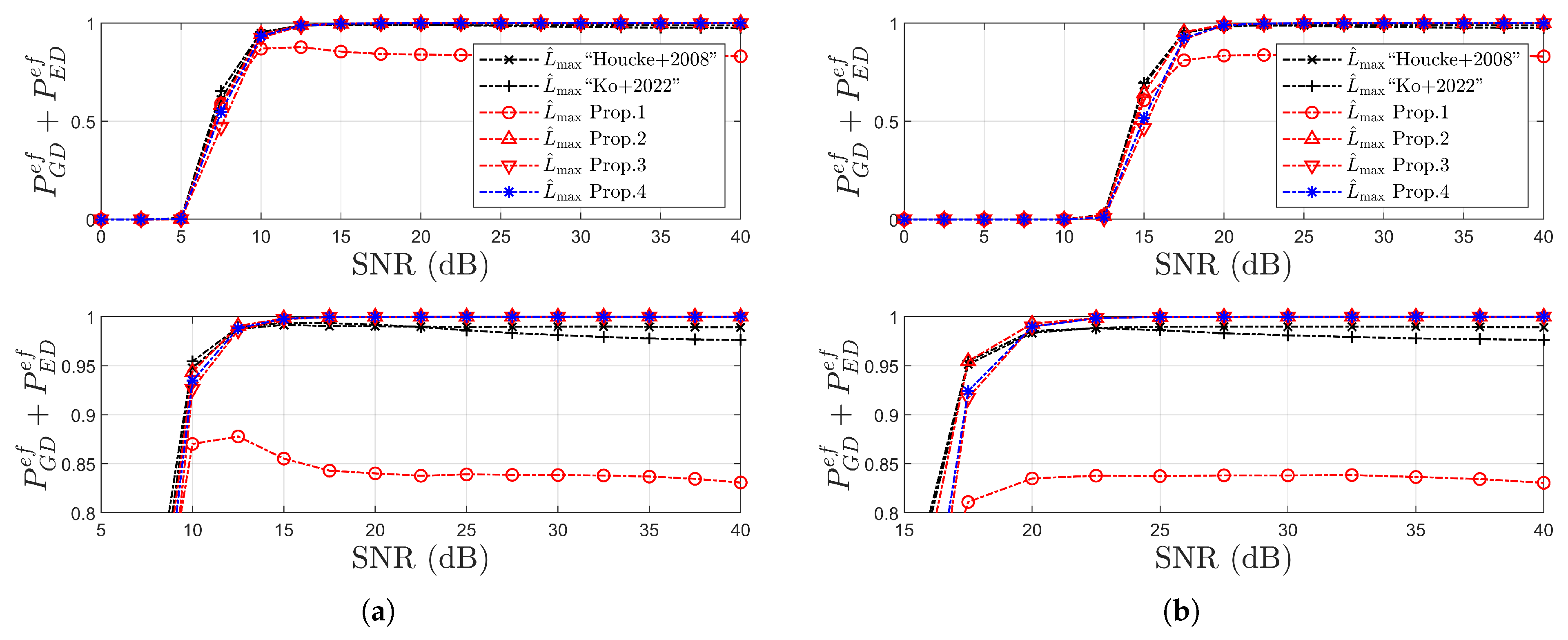
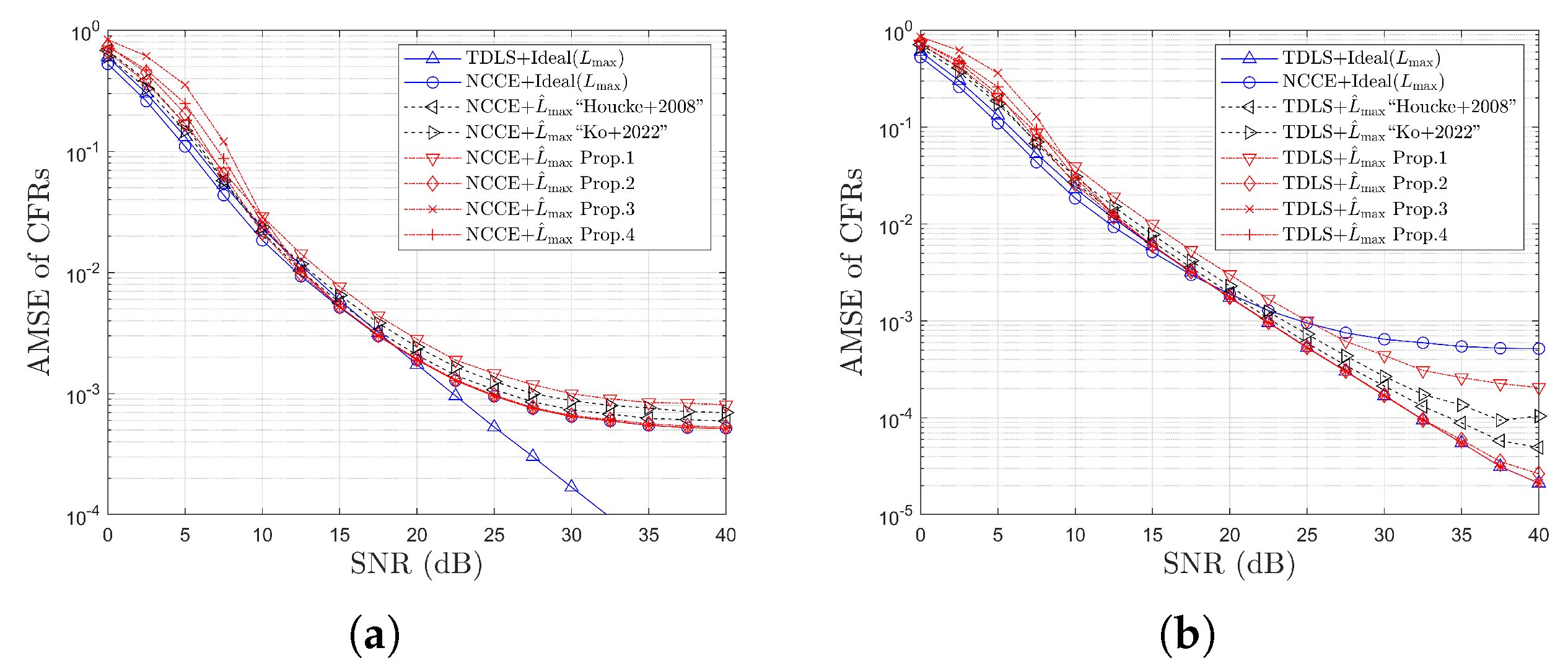
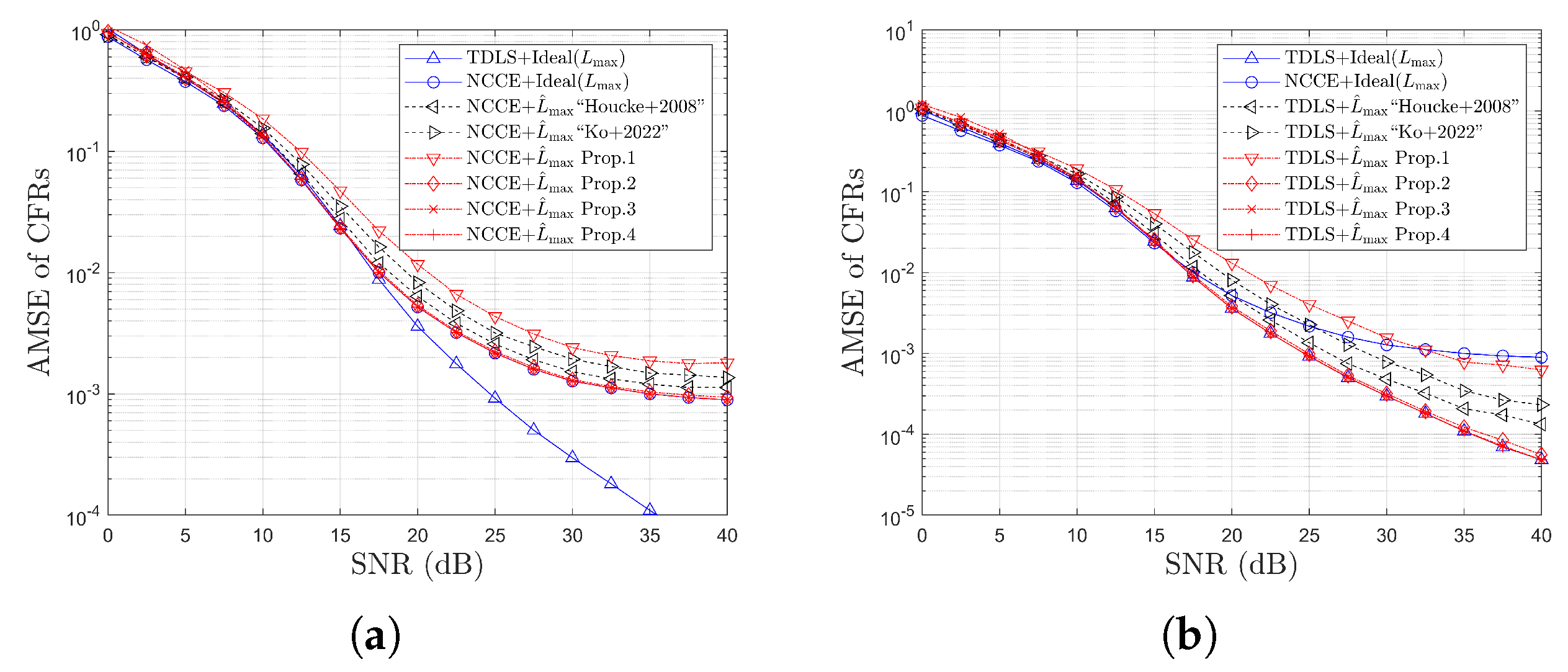
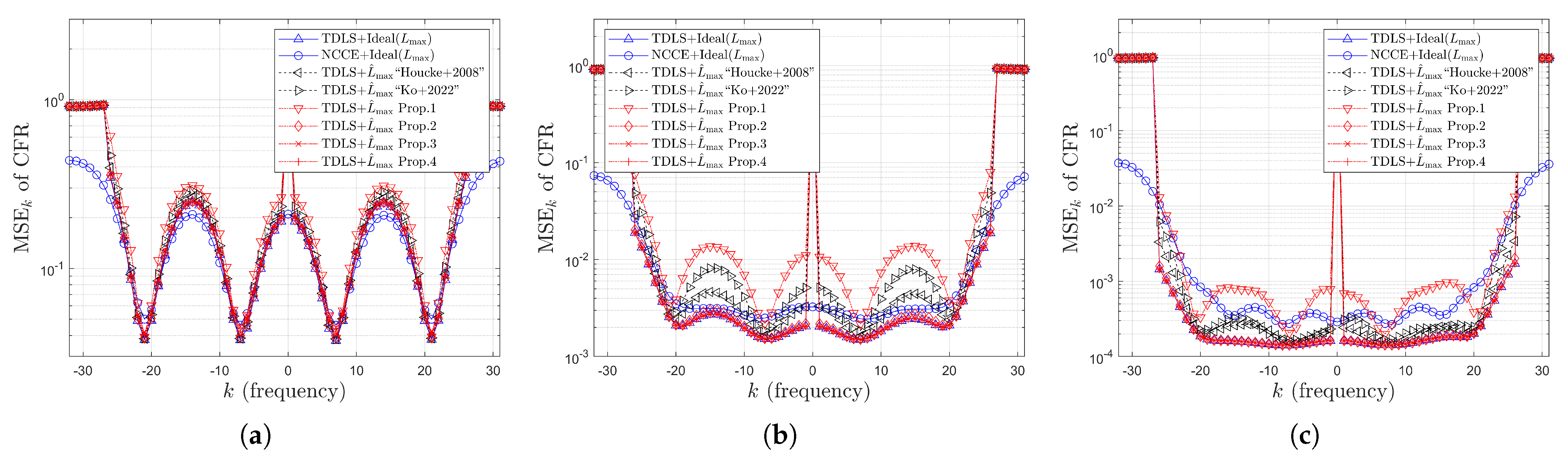
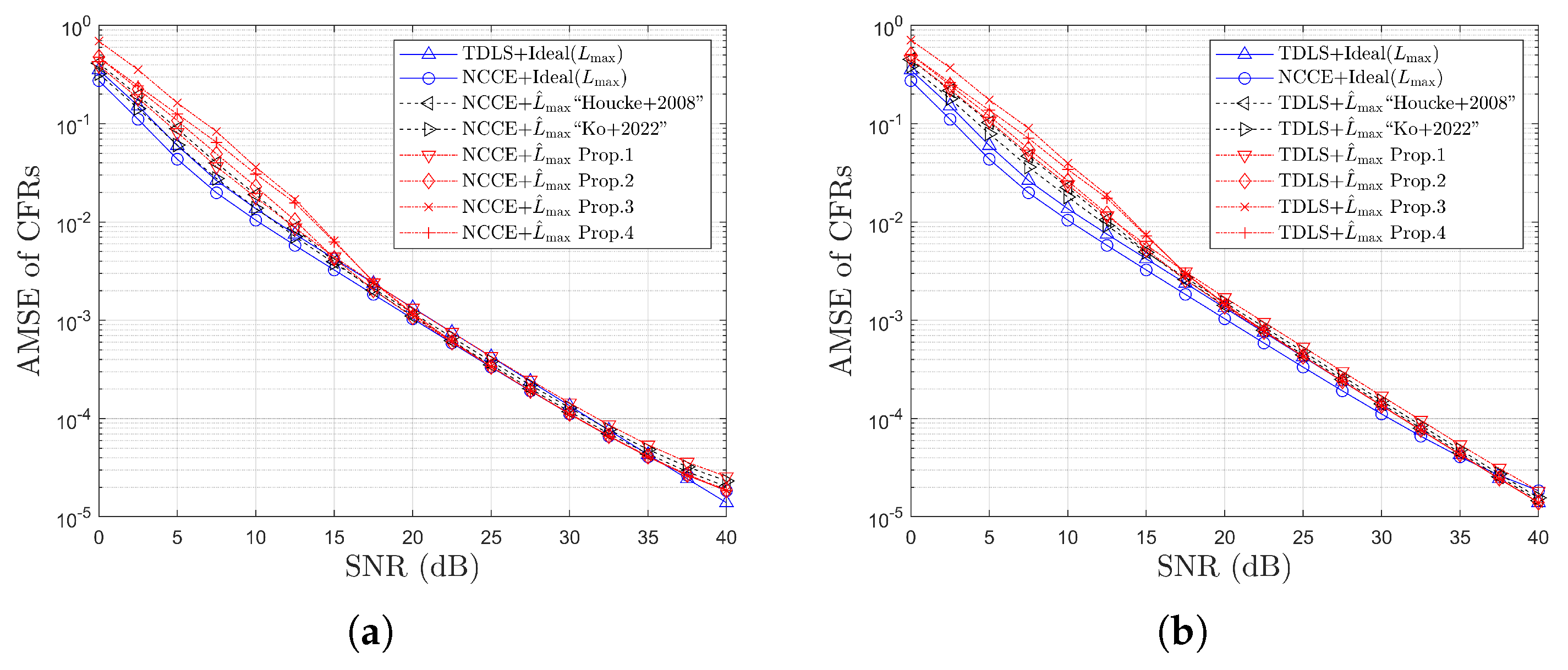
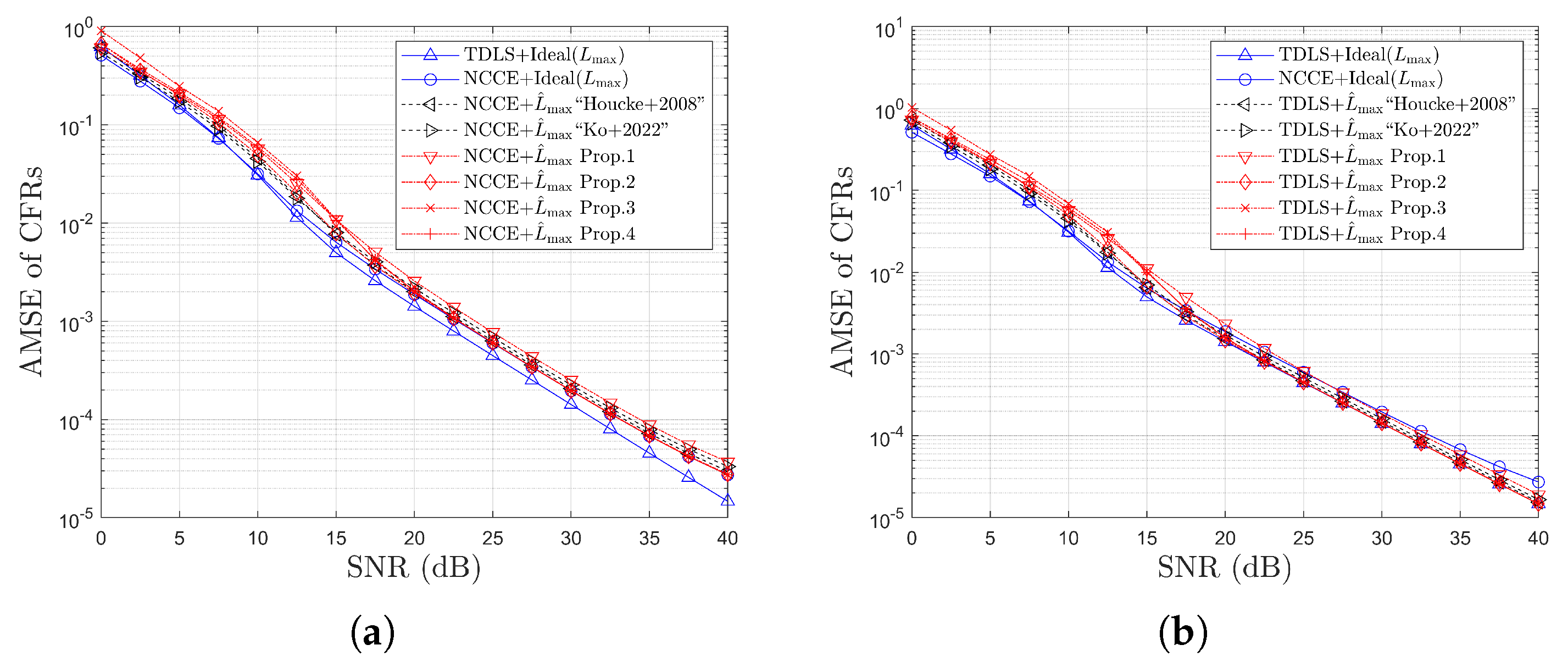
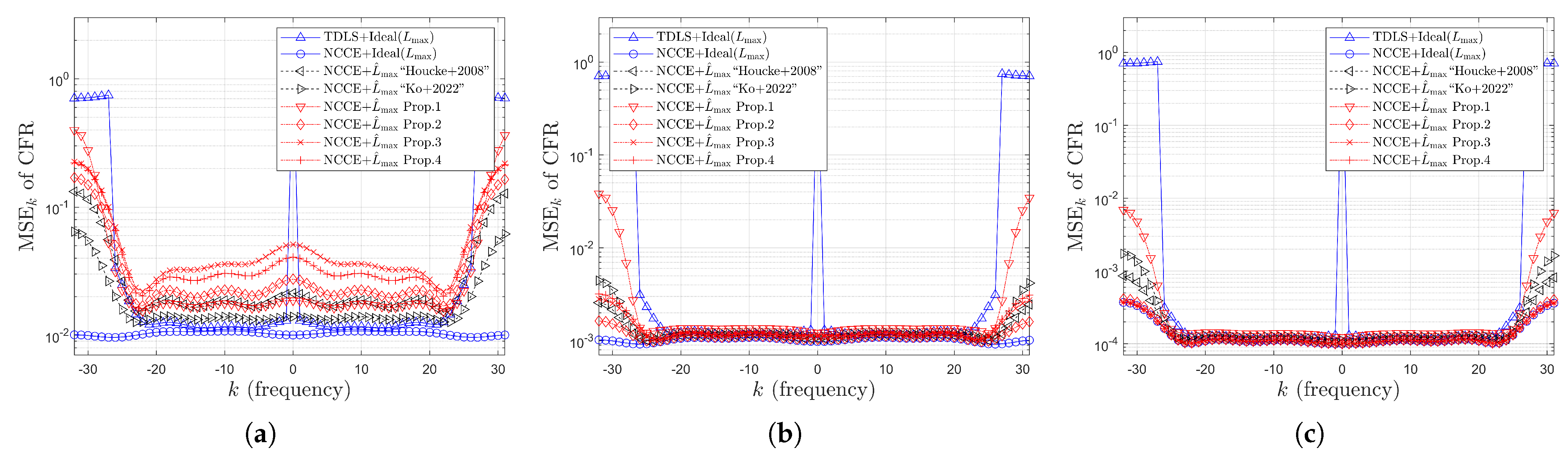
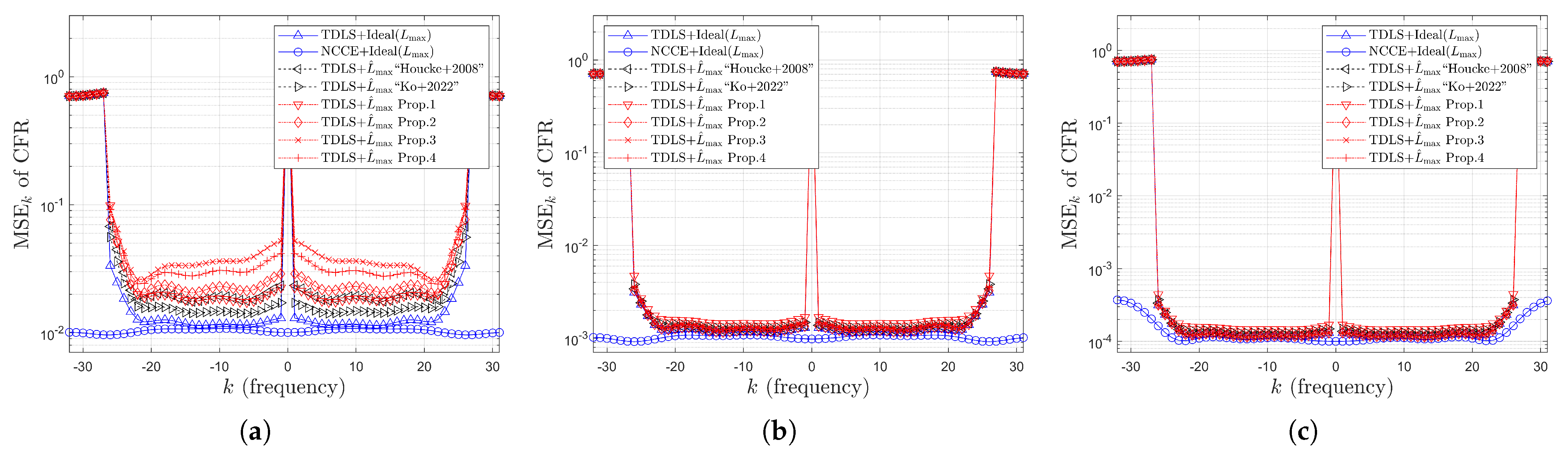
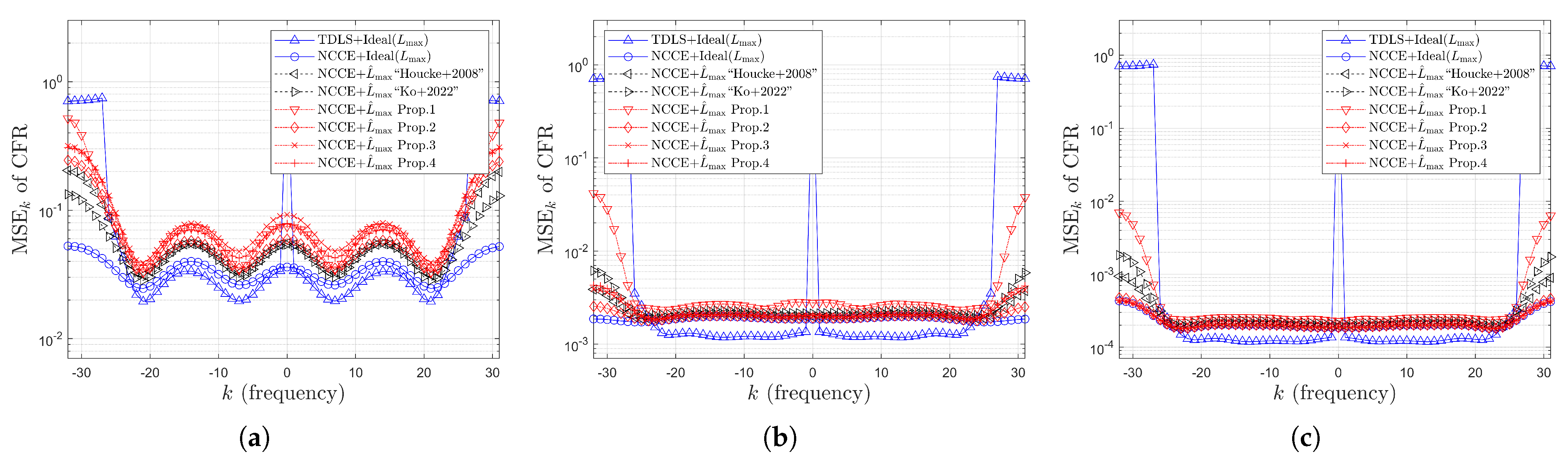
4. Simulation Results
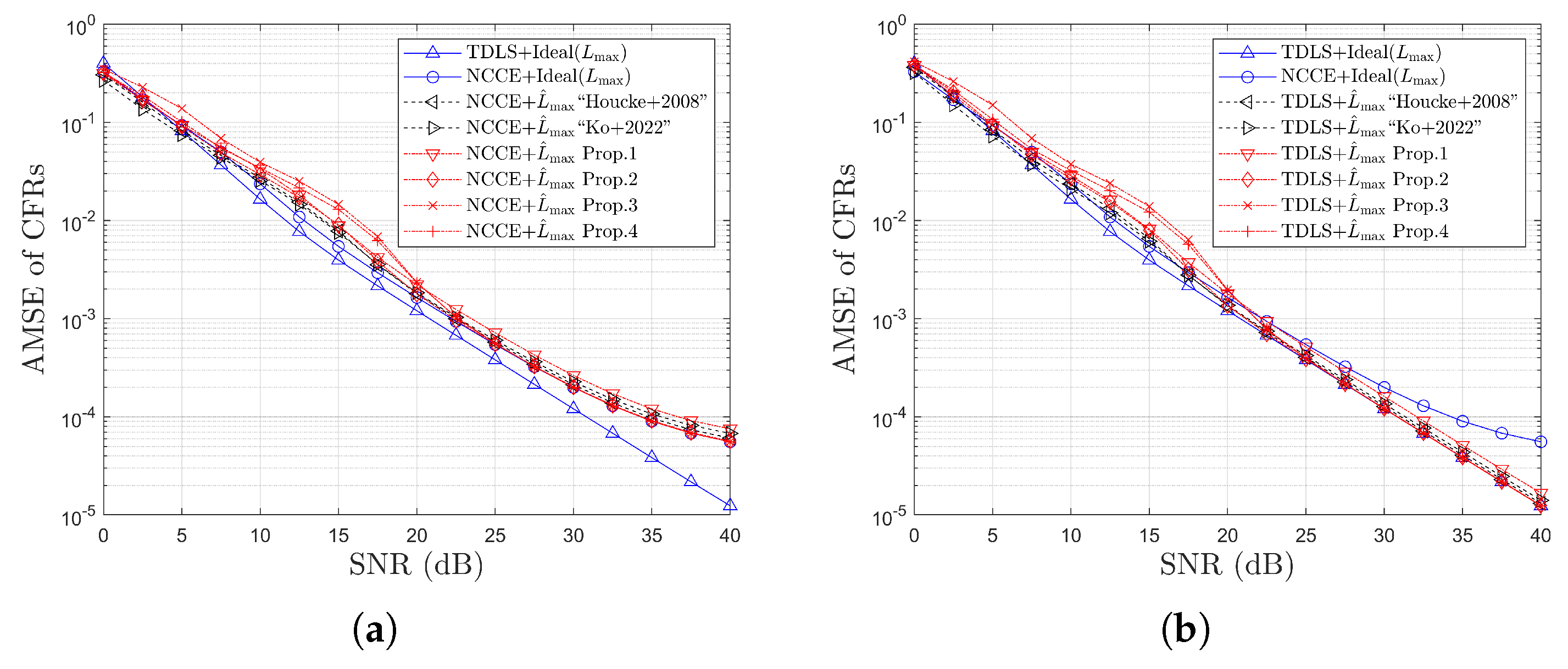
4.1. Simulation Results for Detection Probabilities
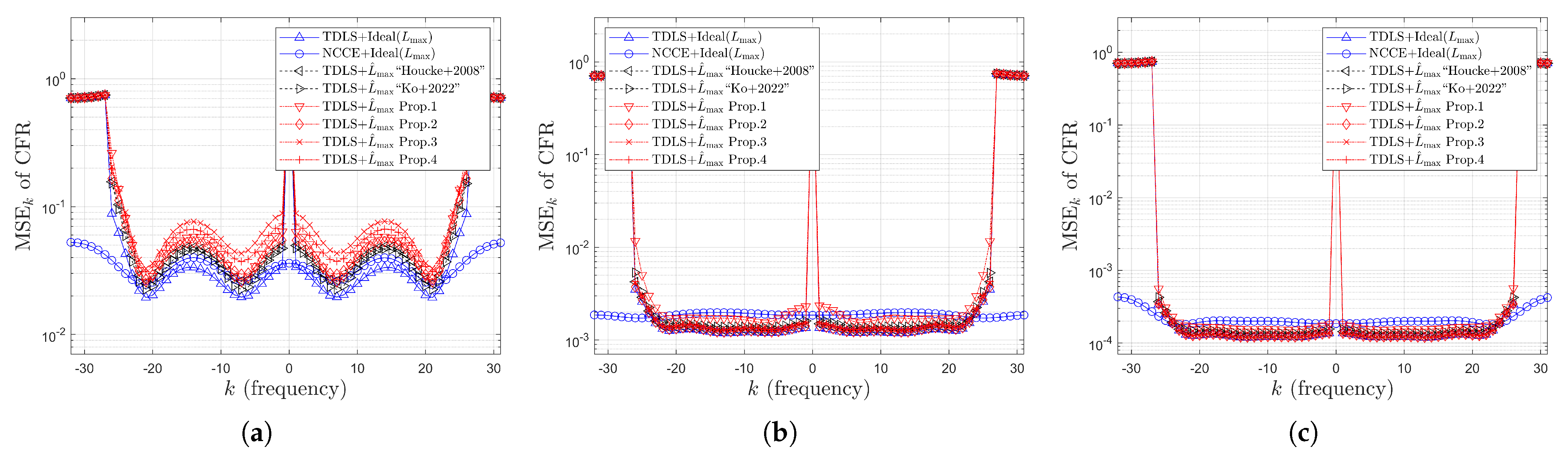
4.2. Simulation Results for MSE
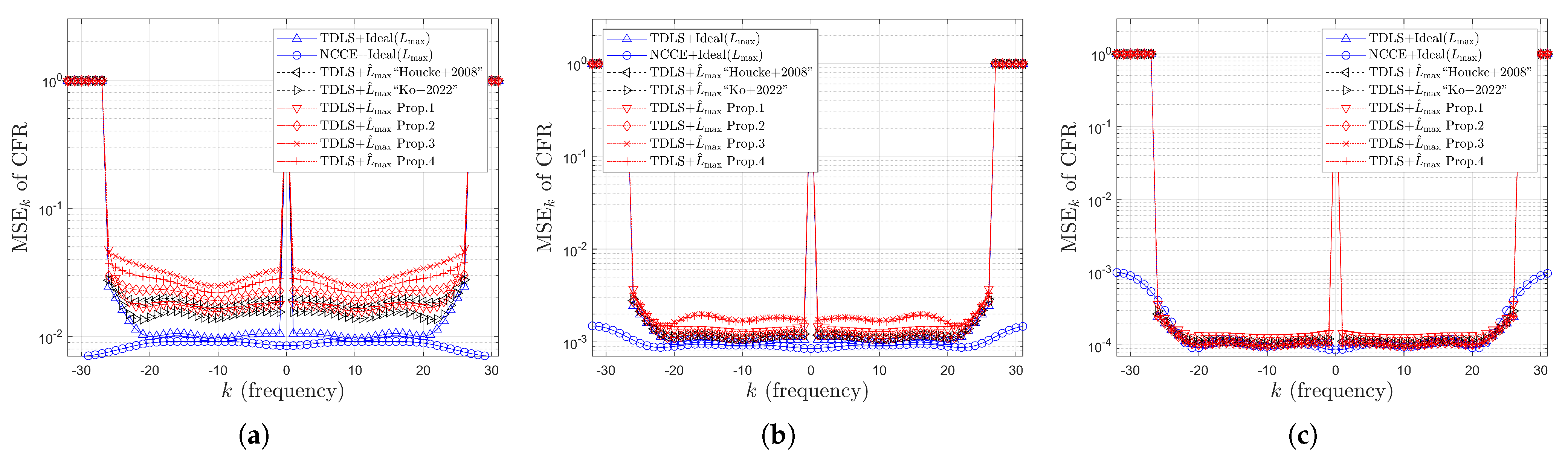
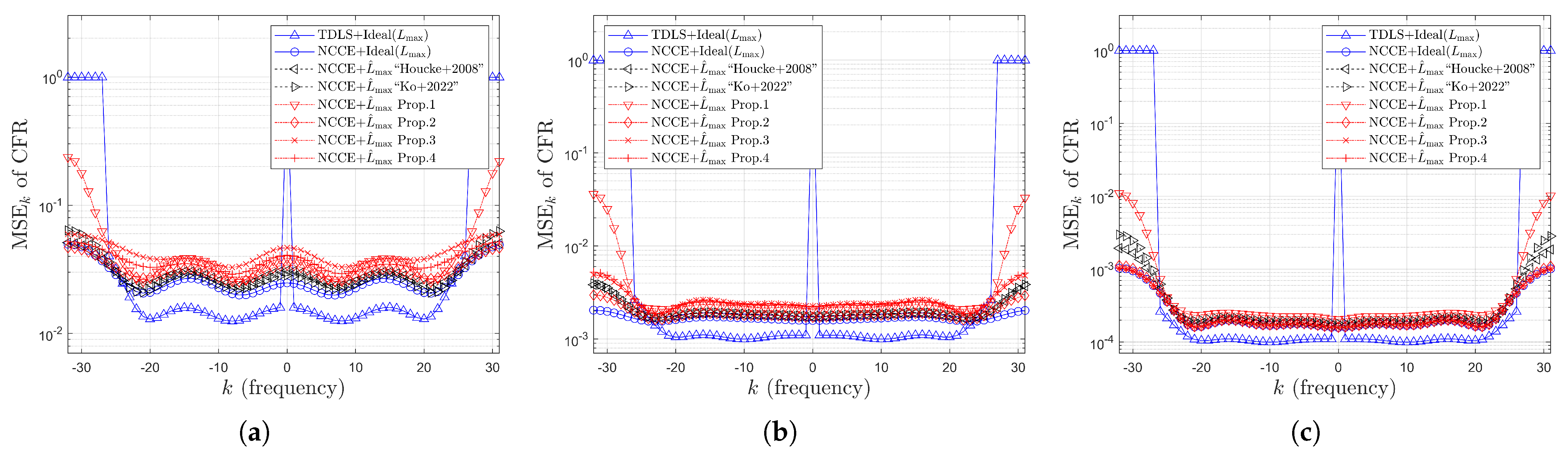
4.3. Simulation Results for Error Rates
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AMSE | average mean square error |
| AWGN | additive white Gaussian noise |
| BD | bad detection |
| CD | correct detection |
| CDP | constructed data pilots |
| CE | channel estimation |
| CFR | channel frequency response |
| C-ITS | cooperative intelligent transportation systems |
| CIR | channel impulse response |
| CLT | central limit theorem |
| CP | cyclic prefix |
| CSI | channel state information |
| GD | good detection |
| GI | guard interval |
| ED | erroneous detection |
| ISI | inter-symbol interference |
| LLR | log-likelihood ratio |
| LS | least square |
| LSTM | long short-term memory |
| MAC | medium access control |
| MADT | maximum access delay time |
| ML | maximum likelihood |
| MSE | mean square error |
| NCCE | noise-canceling channel estimation |
| FFT | fast Fourier transform |
| IDFT | inverse discrete Fourier transform |
| IFFT | inverse fast Fourier transform |
| OFDM | orthogonal frequency division multiplexing |
| probability density function | |
| QAM | quadrature amplitude modulation |
| QPSK | quadrature phase shift keying |
| SNR | signal-to-noise ratio |
| TRFI | time-domain reliability test and frequency-domain interpolation |
| TDLS | time-domain least square |
| V2X | vehicle-to-everything |
| WAVE | wireless access in vehicular environments |
| WSSUS | wide-sense stationary uncorrelated scattering |
References
- Zhao, Z.; Cheng, X.; Wen, M.; Jiao, B.; Wang, C.X. Channel Estimation Schemes for IEEE 802.11p Standard. IEEE Intell. Transp. Syst. Mag. 2013, 5, 38–49. [Google Scholar] [CrossRef]
- IEEE Std. 1609.0-2013; IEEE Guide for Wireless Access in Vehicular Environments (WAVE)-Architecture. IEEE: Piscataway, NJ, USA, 2014.
- Bourdoux, A.; Cappelle, H.; Dejonghe, A. Channel Tracking for Fast Time-Varying Channels in IEEE802.11p Systems. In Proceedings of the 2011 IEEE Global Telecommunications Conference—GLOBECOM 2011, Houston, TX, USA, 5–9 December 2011; pp. 1–6. [Google Scholar]
- Lim, S. A New Channel Estimation Scheme Using Virtual Subcarriers based on Successive Interpolation in IEEE 802.11p WAVE Systems. In Proceedings of the 2021 International Conference on Convergence Content (ICCC 2021), Jeju, Republic of Korea, 19–20 December 2021; pp. 441–442. [Google Scholar]
- Han, S.; Park, J.; Song, C. Virtual Subcarrier Aided Channel Estimation Schemes for Tracking Rapid Time Variant Channels in IEEE 802.11p Systems. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–5. [Google Scholar]
- Socheleau, F.; Aissa-El-Bey, A.; Houcke, S. Non data-aided SNR estimation of OFDM signals. IEEE Commun. Lett. 2008, 12, 813–815. [Google Scholar] [CrossRef]
- Wang, H.; Lim, S.; Ko, K. Improved Maximum Access Delay Time, Noise Variance, and Power Delay Profile Estimations for OFDM Systems. KSII Trans. Internet Inf. Syst. 2022, 16, 4099–4113. [Google Scholar]
- Lim, S.; Wang, H.; Ko, K. Power-Delay-Profile-Based MMSE Channel Estimations for OFDM Systems. Electronics 2023, 12, 510. [Google Scholar] [CrossRef]
- Kim, Y.; Oh, J.; Shin, Y.; Mun, C. Time and frequency domain channel estimation scheme for IEEE 802.11p. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 1085–1090. [Google Scholar]
- Kwak, K.; Lee, S.; Kim, J.; Hong, D. A New DFT-Based Channel Estimation Approach for OFDM with Virtual Subcarriers by Leakage Estimation. IEEE Trans. Wirel. Commun. 2008, 7, 2004–2008. [Google Scholar] [CrossRef]
- Kim, K.; Hwang, H.; Choi, K.; Kim, K. Low-Complexity DFT-Based Channel Estimation with Leakage Nulling for OFDM Systems. IEEE Commun. Lett. 2014, 18, 415–418. [Google Scholar] [CrossRef]
- Cho, Y.; Son, H. Enhanced DFT-Based Channel Estimator for Leakage Effect Mitigation in OFDM Systems. IEEE Commun. Lett. 2019, 23, 875–879. [Google Scholar] [CrossRef]
- Ko, K.; Wang, H. Noise-Canceling Channel Estimation Schemes Based on the CIR Length Estimation for IEEE 802.11p/OFDM Systems. Electronics 2024, 13, 1110. [Google Scholar] [CrossRef]
- Ko, K.; Park, M.; Hong, D. Performance Analysis of Asynchronous MC-CDMA systems with a Guard Period in the form of a Cyclic Prefix. IEEE Trans. Commun. 2006, 2, 216–220. [Google Scholar]
- Park, M.; Ko, K.; Park, B.; Hong, D. Effects of asynchronous MAI on average SEP performance of OFDMA uplink systems over frequency-selective Rayleigh fading channels. IEEE Trans. Commun. 2010, 2, 586–599. [Google Scholar]
- Kwak, K.; Lee, S.; Min, H.; Choi, S.; Hong, D. New OFDM Channel Estimation with Dual-ICI Cancellation in Highly Mobile Channel. IEEE Trans. Wirel. Commun. 2010, 10, 3155–3165. [Google Scholar]
- Cui, T.; Tellambura, C. Power delay profile and noise variance estimation for OFDM. IEEE Commun. Lett. 2006, 1, 25–27. [Google Scholar]
- van de Beek, J.; Sandell, M.; Borjesson, P. ML estimation of time and frequency offset in OFDM systems. IEEE Trans. Signal Process 1997, 7, 1800–1805. [Google Scholar]
- Popoulis, A.; Pillai, S. Probability, Random Variables, and Stochastic Processes, 4th ed.; McGraw Hill: Boston, MA, USA, 2002. [Google Scholar]
- Kahn, M. IEEE 802.11 Regulatory SC DSRC Coexistence Tiger Team V2V Radio Channel Models. Doc.: IEEE 802.11-14, February 2014. Available online: https://mentor.ieee.org/802.11/dcn/14/11-14-0259-00-0reg-v2v-radio-channel-models.ppt (accessed on 22 October 2022).












| Term | 1 Operation | Number |
|---|---|---|
| Prop.1 and 2, [6] | ||
| log | ||
| 2 Prop.3 and 4 | ||
| log | ||
| 3 [7] | ||
| log |
| Comments | Legend | IFFT/Nulling/FFT | |
|---|---|---|---|
| Ideal | |||
| Bounds | Not applicable | ||
| 2 O | |||
| [3] + [6] | “Houcke+2008” | By (5) in [6] | Not applicable |
| [3] + [7] | “Ko+2022” | By (16) in [7] | Not applicable |
| [3] + | By (18) and (25) | Not applicable | |
| [13] + [6] | “Houcke+2008” | By (5) in [6] | 2 O |
| [13] + [7] | “Ko+2022” | By (16) in [7] | 2 O |
| [13] + | By (18) and (25) | 2 O |
| Ch. Type | Item | Tap 0 | Tap 1 | Tap 2 | Tap 3 | Unit |
|---|---|---|---|---|---|---|
| Highway | Power | 0 | dB | |||
| NLOS | Delay | 0 | 200 | 433 | 700 | ns |
| , | ||||||
| Doppler | 0 | 689 | 886 | Hz | ||
| Street Crossing | Power | 0 | dB | |||
| NLOS | Delay | 0 | 267 | 400 | 533 | ns |
| , | , | |||||
| Doppler | 0 | 295 | 591 | Hz | ||
| Highway | Power | 0 | dB | |||
| LOS | Delay | 0 | 100 | 167 | 500 | ns |
| , | ||||||
| Doppler | 0 | 689 | 886 | Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ko, K.; Lim, S. Generalized Maximum Delay Estimation for Enhanced Channel Estimation in IEEE 802.11p/OFDM Systems. Electronics 2025, 14, 2404. https://doi.org/10.3390/electronics14122404
Ko K, Lim S. Generalized Maximum Delay Estimation for Enhanced Channel Estimation in IEEE 802.11p/OFDM Systems. Electronics. 2025; 14(12):2404. https://doi.org/10.3390/electronics14122404
Chicago/Turabian StyleKo, Kyunbyoung, and Sungmook Lim. 2025. "Generalized Maximum Delay Estimation for Enhanced Channel Estimation in IEEE 802.11p/OFDM Systems" Electronics 14, no. 12: 2404. https://doi.org/10.3390/electronics14122404
APA StyleKo, K., & Lim, S. (2025). Generalized Maximum Delay Estimation for Enhanced Channel Estimation in IEEE 802.11p/OFDM Systems. Electronics, 14(12), 2404. https://doi.org/10.3390/electronics14122404