Optimal Design of a Fractional Order PIDD² Controller for an AVR System Using Hybrid Black-Winged Kite Algorithm

Abstract

This study addresses the optimization of control performance for automatic voltage regulator systems by proposing a fractional-order PIDD² (FOPIDD²) controller design method based on the hybrid Black-winged Kite Algorithm (BWOA). To overcome the challenges of complex parameter tuning and adaptability to high-dimensional nonlinear optimization in PID controllers, the BWOA integrates the precise search mechanism of the Black-winged Kite Algorithm (BKA) with the spiral encircling strategy of the Whale Optimization Algorithm (WOA). By dividing high-fitness individuals into subgroups for parallel optimization, combined with an elitism preservation mechanism and Levy flight perturbation, the BWOA effectively balances global exploration and local exploitation capabilities, preventing premature convergence. Furthermore, a multi-factor objective function is adopted to optimize the six parameters of the FOPIDD² controller. Numerical simulations in MATLAB evaluate the controller’s performance across multiple dimensions, including transient response, frequency-domain stability, trajectory tracking, parameter uncertainty, and disturbance rejection, with comparisons to other recent controllers. Simulation results demonstrate that the BWOA-FOPIDD² controller achieves superior performance in most metrics. Therefore, the proposed method provides an efficient hybrid optimization framework for AVR system controller design.

1. Introduction

In recent years, the rapid advancement of technology has led to increasingly complex research problems, many of which are mathematically abstracted as high-dimensional search space optimization tasks. Traditional optimization algorithms encounter significant difficulties in solving such issues, such as failing to obtain optimal solutions or requiring excessively complex computational procedures that lead to intolerable time consumption. Consequently, conventional methods often fail to meet the demands of addressing these intricate optimization problems. In contrast, metaheuristic algorithms have emerged as powerful tools for tackling such challenges, owing to their exceptional ability to fulfill optimization requirements. As a class of high-level strategies for complex optimization problems, metaheuristic algorithms are domain-independent, exhibiting remarkable versatility and flexibility [1]. They apply to issues with nonconvex, nondifferentiable, or multi-extremal search spaces, delivering satisfactory solutions within reasonable timeframes.

Furthermore, these algorithms require only a properly defined objective function, eliminate the need for gradient calculations, and can address optimization problems that lack analytical solutions. Their strengths extend to robust global search capabilities and the inherent ability to escape local optima. The design of metaheuristic algorithms is inspired by natural or physical phenomena, such as biological evolution, thermodynamic processes, collective behaviors of biological swarms, or social phenomena in human societies [2]. The procedure for searching for optimal solutions follows these steps: first, randomly generating a population, then evaluating their fitness, and subsequently iteratively updating each individual according to specific strategies. Through this iterative refinement, the fitness of candidate solutions is progressively enhanced, ultimately converging toward near-optimal or optimal solutions.

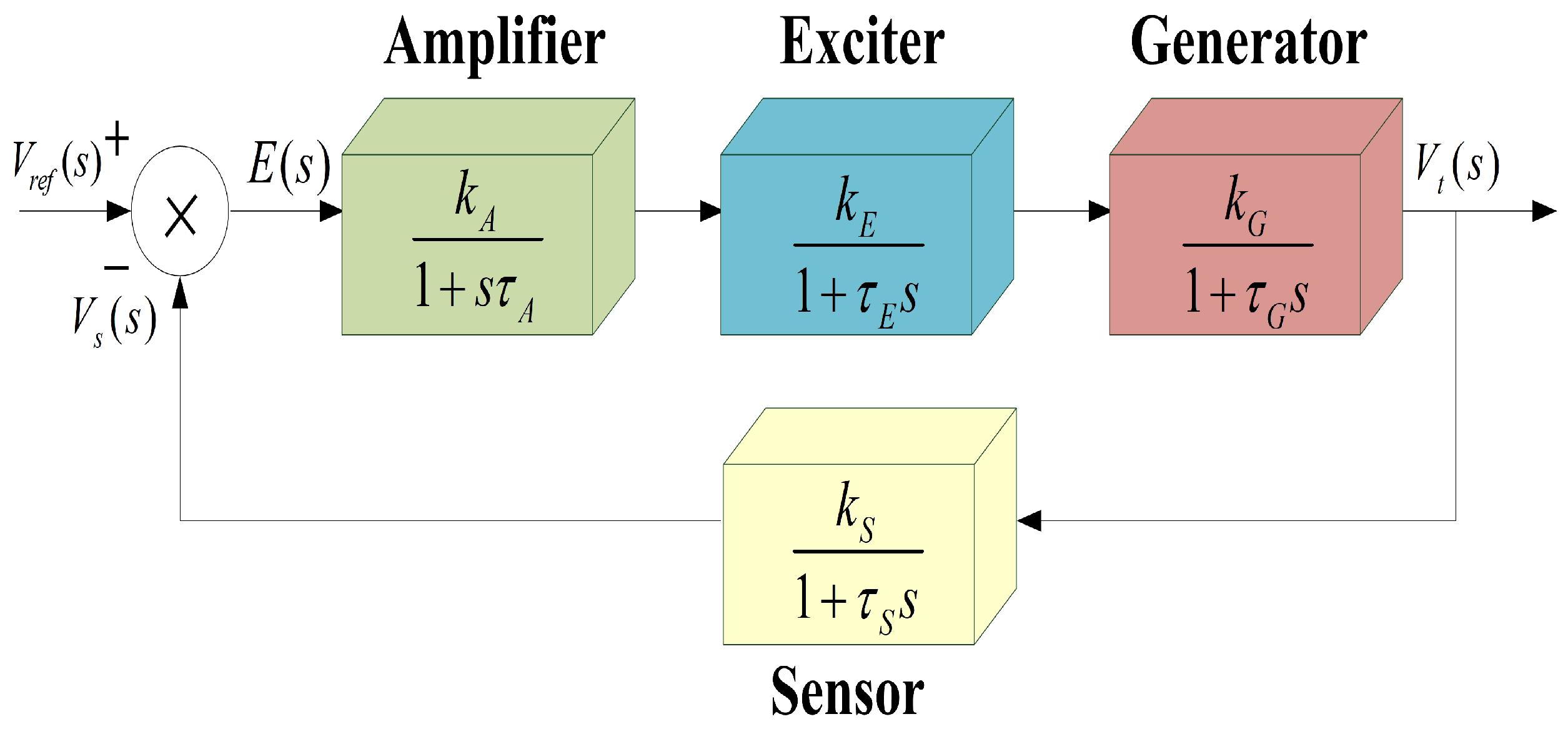
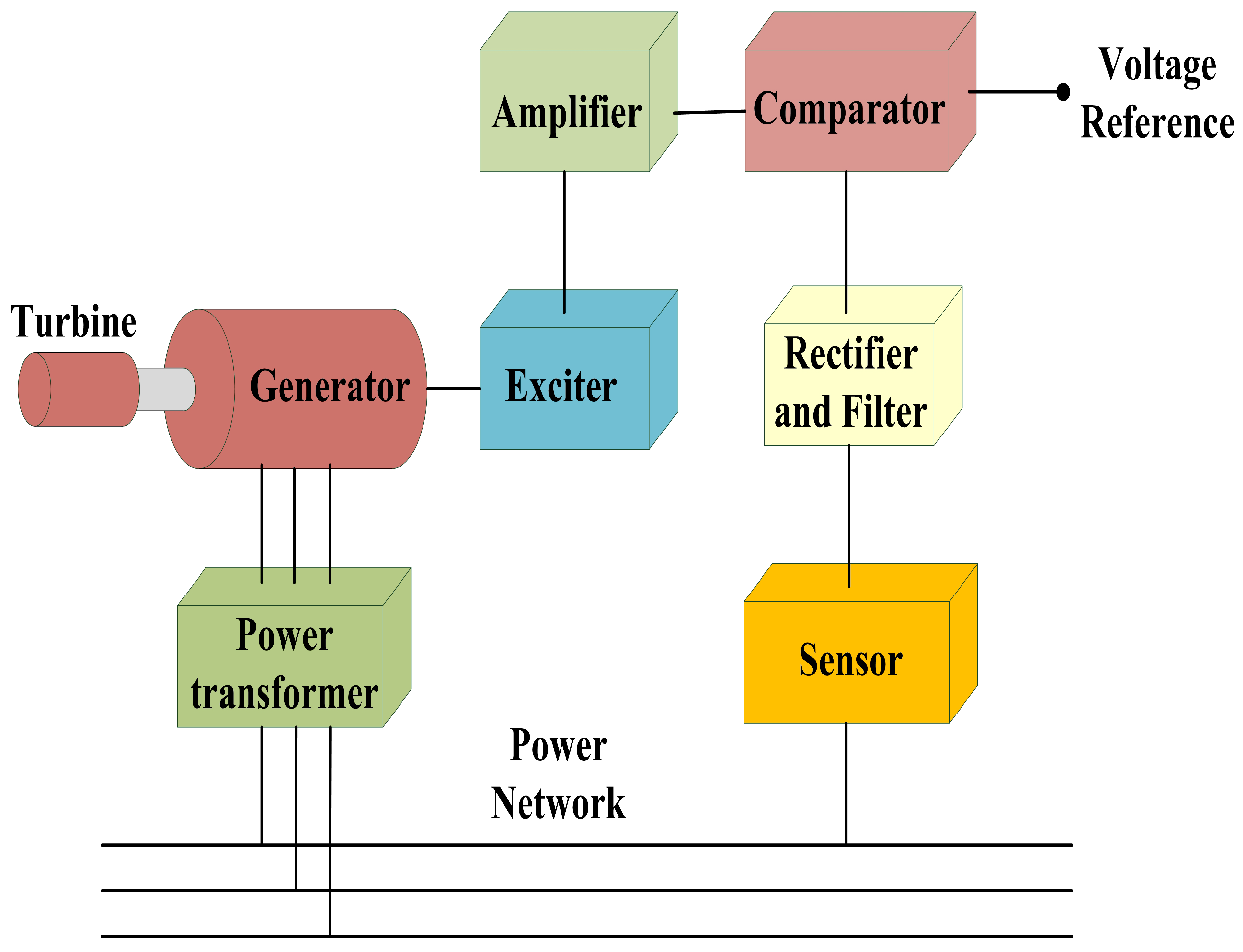
Electricity, like water, is a vital resource for humanity. Stability issues in power system operations have been continuously studied to date [3,4]. The automatic voltage regulator (AVR) is the most critical control device in power systems, utilized to maintain the terminal voltage of synchronous generators around a fixed value [5]. For equipment in power systems, stabilizing voltage and frequency within specific preset ranges is particularly essential, as deviations from preset values can lead to shortened equipment lifespans and significant performance degradation. However, numerous factors influence power system operations, including generator characteristics, control device responses, and load configurations. Synchronous AC generators, the primary devices for bulk power generation in power systems, are highly susceptible to oscillations caused by load variations. The AVR ensures the generator’s terminal voltage remains stable even during drastic load changes, highlighting the critical importance of the AVR in maintaining system integrity. According to prior studies, integrating control devices into the AVR control loop has been extensively explored, with various control devices proposed to substantially enhance AVR system performance. Among these, the PID controller is acknowledged as the most widely adopted and effective control solution.

The PID controller has become a widely used control solution due to its simple structure and excellent control performance. It requires the tuning of three parameters, i.e., proportional, integral, and derivative gains, while several extensions of PID controllers have been developed. In 1999, Podlubny [6] proposed the fractional-order PID (FOPID) controller, which introduced two additional tuning parameters, $\lambda$, and $\mu$, compared to the standard PID prototype. Furthermore, the PIDD² controller was developed by adding a second-order derivative term into the conventional PID structure; this modification introduces an additional tuning parameter $K_{d_2}$ to specifically govern the weighting of the second-order derivative component. In recent years, researchers have explored combining the FOPID and PIDD² controllers, resulting in a hybrid FOPIDD² controller, to achieve superior control performance. This advanced controller involves six tuning parameters, making it the most computationally demanding variant among all PID-based control architectures during the parameter tuning process.

Tuning the parameters of PID controllers remains a challenging task in industrial automation, particularly for systems with time-varying dynamics or significant nonlinearities, necessitating advanced optimization frameworks. To enhance the performance of AVR systems, numerous metaheuristic algorithms, including improved spotted hyena optimizer (ISHO) [7], artificial ecosystem-based optimization (AEO) [8], tree-seed algorithm (TSA) [9], sine-cosine algorithm (SCA for PID) [10], cuckoo search algorithm (CSA) [11], slime mould algorithm (SMA) [12], improved kidney-inspired algorithm (IKA) [13], simulated annealing-manta ray foraging optimization algorithm (SA-MRFA) [14], genetic algorithm (GA) [15], particle swarm optimization (PSO) [16], Archimedes optimization algorithm (AOA) [17], Whale Optimization Algorithm (WOA) [18], simulated annealing-gorilla troops optimization (SA-GTO) [19], salp swarm optimization (SSO) [20], gradient-based optimization (GBO) [21], modified smoothed function algorithm (MSFA) [22], sine-cosine algorithm (SCA for FOPID) [23], chaotic yellow saddle goatfish algorithm (C-YSGA) [24], ant lion optimizer (ALO) [25], chaotic black widow optimization (ChBWO) [26], multi-verse optimizer (MVO) [27], reptile search algorithm (RSA) [28], Henry gas solubility optimization (HGSO) [29], equilibrium optimizer (EO) [30], equilibrium optimizer-evaporation rate water cycle algorithm (EO-ERWCA) [31], nonlinear sine cosine algorithm (NSCA) [32], grey wolf optimization (GWO) [33], symbiotic organisms search (SOS) [34], coyote optimization algorithm (COA) [35], Cat Swarm Optimization (SCSO) [36], and improved coati optimization algorithm (ICOA) [37] have been employed to optimize PID controller parameters.

Another key to improving controller performance lies in selecting an objective function compatible with the optimization algorithm during the parameter optimization process. In previous studies, several objective functions have been designed and utilized. Conventional objective functions include: Integral of Time-weighted Absolute Error (ITAE), Integral of Time-weighted Squared Error (ITSE), Integral of Absolute Error (IAE), and Integral of Squared Error (ISE). Some objective functions incorporate time-domain performance metrics of controllers, such as overshoot, rise time, settling time, and steady-state error, with Zwee Lee Gaing’s (ZLG) being the most widely adopted. Others combine traditional objective functions with those embedding time-domain metrics to achieve enhanced control performance. The choice of the objective function is typically determined through extensive numerical simulation experiments and is heavily dependent on the chosen optimization algorithm. Further details on the application of the majority of algorithms to optimize PID-controlled AVR systems are summarized in

Table 1. Controller parameters from existing methods in the literature.

Method Number	Ref.	Method	${\mathit{k}}_{\mathit{p}}$	${\mathit{k}}_{\mathit{i}}$	${\mathit{k}}_{\mathit{d}}$	$\lambda$	$\mu$	${\mathit{k}}_{{\mathit{d}}_2}$	Population Size	Maximum Number of Iterations
1	[7]	PID/ISHO/ITAE	1.0263	0.7115	0.3154	-	-	-	50	20
2	[8]	PID/AEO/ITSE	1.4104	1.2062	0.7446	-	-	-	NM *	NM *
3	[9]	PID/TSA/ITSE	1.1281	0.9567	0.5671	-	-	-	50	100
4	[10]	PID/SCA/ZLG	0.9826	0.8337	0.4982	-	-	-	40	100
5	[11]	PID/CSA/ZLG	0.5995	0.4126	0.2007	-	-	-	25	50
6	[12]	PID/SMA/ZLG	0.6173	0.4166	0.2035	-	-	-	40	50
7	[13]	PID/IKA/ITSE+ZLG	1.0426	1.0093	0.5999	-	-	-	30	40
8	[14]	PID/SA–MRFO/ModefiedZLG	0.6778	0.3802	0.2663	-	-	-	30	50
9	[15]	PID/GA/ModefiedITAE	1.9427	1.3782	0.5708	-	-	-	30	100
10	[16]	PIDD2/PSO/ITAE	2.7784	1.8521	0.9997	-	-	0.073	30	50
11	[17]	PIDD2/AOA/ModefiedITAE	2.9999	2.9875	1.5887	-	-	0.1036	30	50
12	[18]	PIDD2/WOA/ISE	777.401	397.741	500.652	-	-	103.02	100	100
13	[19]	PIDD2/SA–GTO/Other	4.8252	5.0000	1.8100	-	-	0.2140	50	100
14	[20]	FOPID/SSO/ITAE	1.9982	1.1706	0.5749	1.1656	1.1395	-	50	50
15	[21]	FOPID/GBO/ITAE	0.9961	1.4861	0.6124	1.1131	0.4932	-	30	30
16	[22]	FOPID/MSFA/ZLG	1.4745	0.7510	0.3700	-	-	-	NM *	250
17	[23]	FOPID/SCA/ZLG	1.4509	0.6567	0.3076	1.1442	1.2145	–	50	100
18	[24]	FOPID/C-YSGA/Other	1.7775	0.9463	0.3525	1.2606	1.1273	-	40	50
19	[25]	FOPID/ALO/Not Mentioned	3.407	1.0468	0.5568	1.2244	1.3918	-	NM *	NM *
20	[26]	FOPID/ChBWO/ModefiedITAE	2.8204	0.7387	0.428	1.1294	1.3558	-	50	50
21	[27]	FOPIDD2/MVO/ZLG	3	3	2.3086	0.8726	0.8979	0.1361	30	300
22	[28]	FOPIDD2/RSA/ZLG	2.6436	2.6883	2.0635	0.8797	0.9143	0.12394	30	50

[*] Not mentioned in the cited references.

.

As shown in Table 1, these studies focus on combining different algorithms, types of PID controllers, and objective functions to optimize the performance of AVR systems. Among them, PID variants constitute more than half of the cases, with a predominant emphasis on fractional-order PID and PIDD² controllers. The ZLG method is the most frequently adopted objective function, followed by ITAE. Additionally, hybrid metaheuristic algorithms have begun to emerge in recent research, such as SA–MRFO, EO-ERWCA, and SA–GTO. 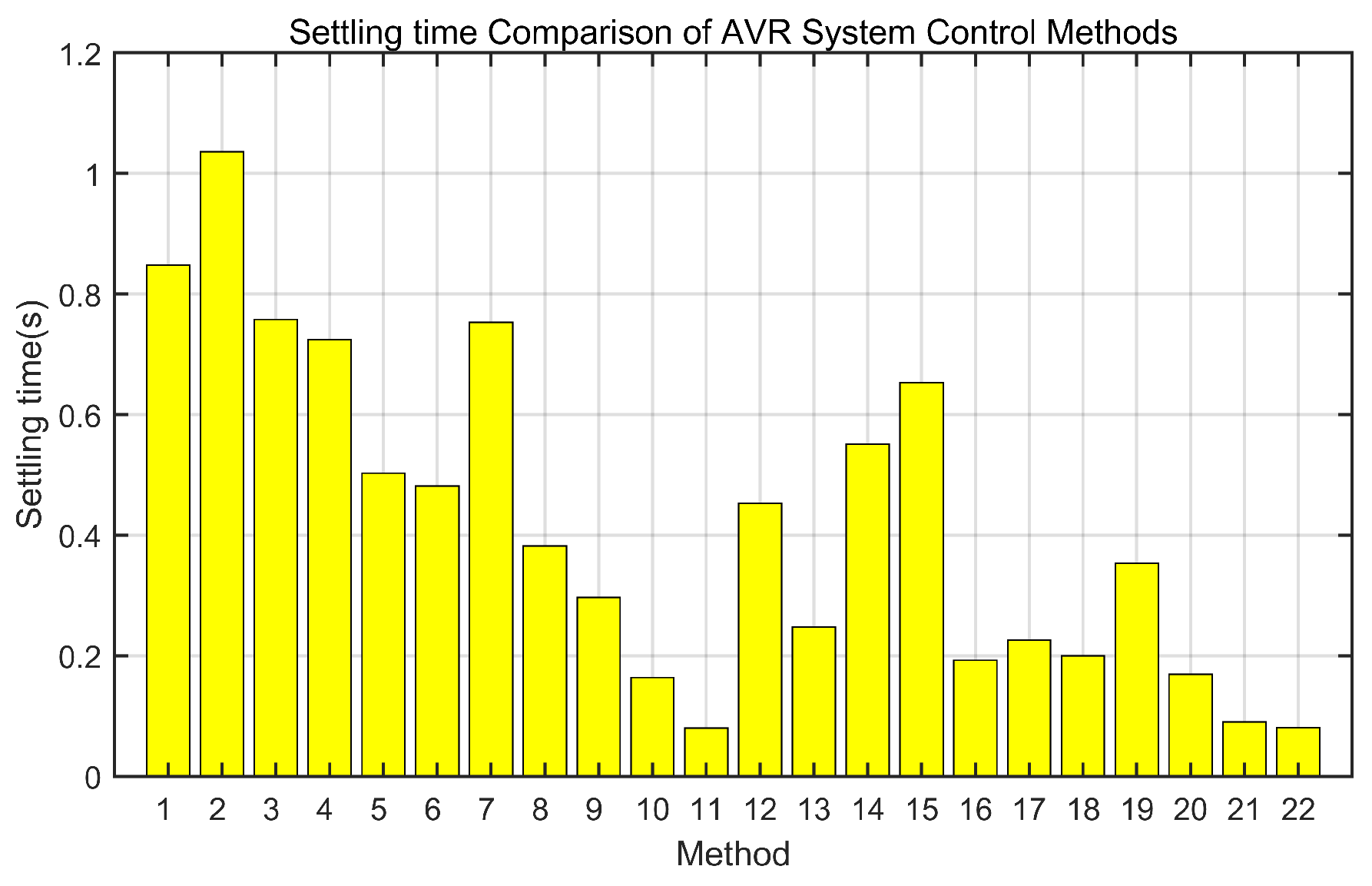Figure 1, Figure 2 and Figure 3 present comparative evaluations of the overshoot, rise time, and settling time characteristics produced by the AVR system control methods enumerated in Table 1, respectively.

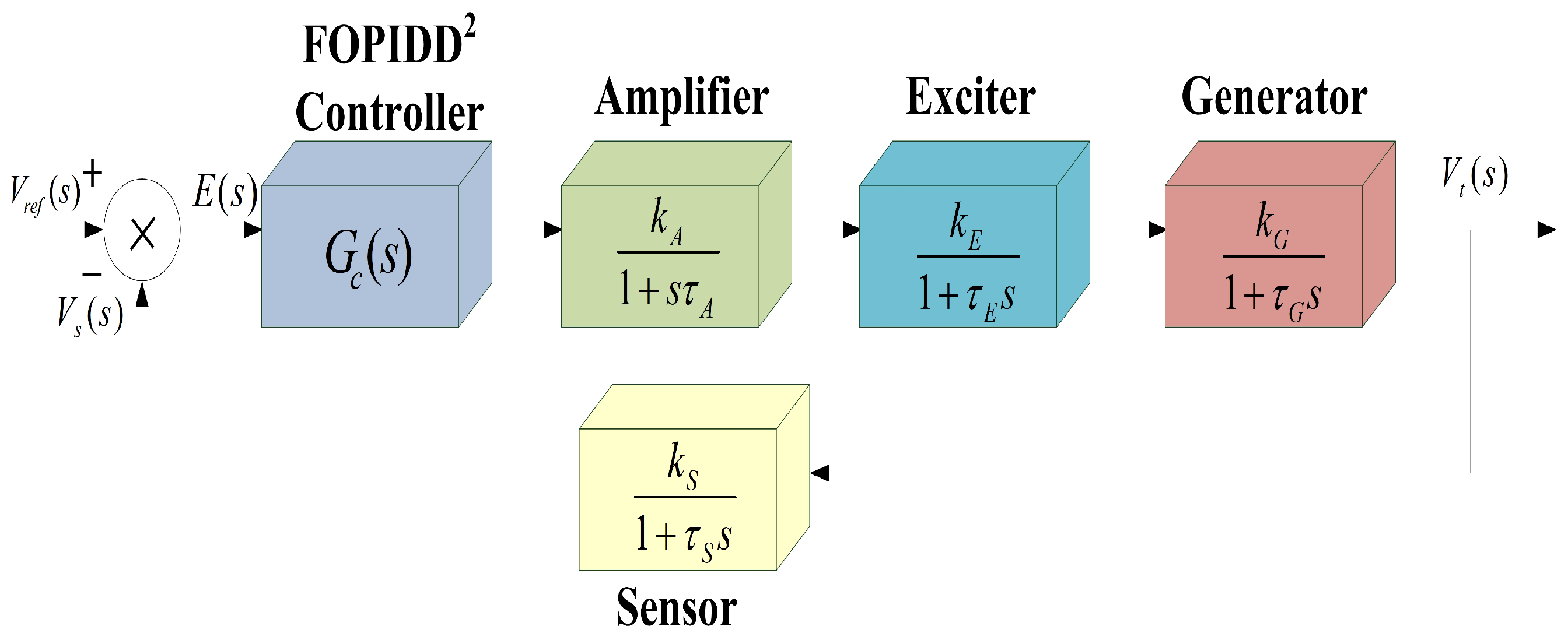
A review of the literature reveals that using novel metaheuristic algorithms, advanced controllers, and more complex objective functions can significantly enhance the performance and robustness of PID-controlled AVR systems. However, this entails an increase in both the number of tuning parameters and computational complexity. Furthermore, few studies have provided a comprehensive analysis of the controller’s effectiveness across multiple performance dimensions. To explore superior control efficacy, this study first integrates the Black-winged kite algorithm and Whale Optimization Algorithm into a hybrid Black-winged kite Optimization Algorithm. The Whale Optimization Algorithm is renowned for its strong local exploitation capabilities, bubble-net attacking mechanism, and rapid convergence speed. However, it is prone to falling into local optima. In contrast, the Black-winged Kite Algorithm excels in global exploration, enabling it to effectively avoid local optima traps. This hybrid algorithm thoroughly explores the potential search space by partitioning the population in each generation and iteratively applying both optimization strategies, thereby preventing premature convergence to local optima. Subsequently, the proposed BWOA is applied to tune the parameters of a fractional-order FOPIDD² controller, where a novel objective function is adopted during the optimization process. Finally, to comprehensively demonstrate the control capabilities of the proposed BWOA-FOPIDD² controller, the AVR system governed by this controller is rigorously evaluated in terms of transient response, frequency-domain response, trajectory tracking, parameter uncertainty, and disturbance rejection. Comparative analyses are conducted against controllers optimized by other algorithms, including PSO [16], SCA [23], C-YSGA [24], MVO [27], and SA-GTO [19], to validate its superior performance.

Therefore, the main contributions of this study are as follows:

1. Proposing a hybrid Black-winged Kite Optimization Algorithm (BWOA) by integrating the Black-winged Kite algorithm and Whale Optimization Algorithm.

2. Applying the BWOA to the parameter tuning of a FOPIDD² controller.

3. Conducting a comprehensive analysis of the performance and robustness of the BWOA-FOPIDD² controller, with comparisons to results from the existing literature.

The remaining sections of this paper are organized as follows. Section 2 briefly introduces the AVR system, conventional PID controllers, and their various modifications. Section 3 elaborates on the design of BWOA. Section 4 describes the process of optimizing the proposed controller using BWOA proposed in this study. Section 5 provides a detailed analysis of all numerical simulation results and comparisons with other controllers. Finally, the conclusion is presented in Section 6.

2. Mathematical Preliminaries

2.1. Description of the AVR System

This section briefly introduces the structure of the AVR system. In power systems, the AVR system regulates the excitation system of synchronous generators to maintain the terminal voltage magnitude at a specified level, thereby ensuring the stable operation of the equipment. The AVR system comprises four main components: amplifier, exciter, generator, and sensor. To facilitate the analysis of the system’s dynamic characteristics, linearized models of each component are employed, while the nonlinearities of the components are neglected. Figure 4 illustrates the block diagram of the AVR system, and a typical arrangement of an AVR system is given in Figure 5.

The amplifier provides the exciter with a properly powered signal by amplifying the error voltage, enabling the generator to output the desired terminal voltage. This error voltage originates from the difference between the sensor-measured terminal voltage and the reference voltage. The transfer functions of the AVR components (amplifier, exciter, generator, and sensor) share the same first-order structure, which can be modeled as follows [38]:

$$G_j\left(s\right)={\displaystyle \frac{K_j}{s{\tau }_j+1}},j\in \{A,E,G,S\},$$

(1)

where $K_j$ and ${\tau }_j$ denote the gain and time constant of each component, respectively, with the subscript j indicating the specific component: A for amplifier, E for exciter, G for generator, and S for sensor. The ranges and typical values of the parameters are listed in

Table 2. Components of the AVR system.

Component	Range of the Parameters	Typical Values
Amplifier	$10\le K_A\le 400$, 0.02 s $\le {\tau }_A\le 0.1$ s	$K_A=10,{\tau }_A=0.1$ s
Exciter	$1\le K_E\le 400$, 0.4 s $\le {\tau }_E\le 1$ s	$K_E=1,{\tau }_E=0.4$ s
Generator	$0.7\le K_G\le 1$, 1 s $\le {\tau }_G\le 2$ s	$K_G=1$,${\tau }_G=1$ s
Sensor	$K_S=1$, 0.001 s $\le {\tau }_S\le 0.06$ s	$K_S=1,{\tau }_S=0.01$ s

, which have been adopted in all prior studies on system controller tuning, including those listed in Table 1 [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37].

The closed-loop transfer function of the AVR system is, therefore, modeled as follows:

$$G_{AVR}={\displaystyle \frac{G_A{G}_E{G}_G}{1+G_A{G}_E{G}_G{G}_S}}.$$

(2)

2.2. Mathematical Generalizations of PID Controllers

Due to its simple structure and effective control performance, the PID controller is one of the most widely used controllers in practical applications. It processes the error signal through proportional, integral, and derivative operations, then sums these results to generate the control signal. The mathematical model of a standard PID controller is expressed as:

$$G_{PID}\left(s\right)=K_p+{\displaystyle \frac{K_i}{s}}+K_{d}s.$$

(3)

where $K_p$, $K_i$, and $K_d$ represent the proportional, integral, and derivative gains, respectively. These gains are the parameters to be optimized during PID controller tuning.

The fractional-order PID (FOPID) controller is more complex than the standard PID controller, incorporating two additional real-numbered parameters: $\lambda$ (fractional integration order) and $\mu$ (fractional differentiation order). Its transfer function is defined as:

$$G_{FOPID}\left(s\right)=K_p+{\displaystyle \frac{K_i}{s^{\lambda }}}+K_d{s}^{\mu }.$$

(4)

The PIDD² controller extends the standard PID by adding a second-order derivative term, introducing an additional optimization parameter $K_{d_2}$ (second-order derivative gain). Its mathematical formulation is as follows:

$$G_{PID{D}^2}\left(s\right)=K_p+{\displaystyle \frac{K_i}{s}}+K_{d}s+K_{d_2}{s}^2.$$

(5)

Finally, the fractional-order PIDD² (FOPIDD²) controller combines the FOPID structure with a second-order derivative term, requiring six tunable parameters. Its transfer function is as follows:

$$G_{FOPID{D}^2}\left(s\right)=K_p+{\displaystyle \frac{K_i}{s^{\lambda }}}+K_d{s}^{\mu }+K_{d_2}{s}^2.$$

(6)

The closed-loop transfer function of the FOPIDD²-controlled AVR system is given by Equation (7). Figure 6 illustrates the block diagram of an AVR system integrated with a PID controller.

$$G_{FOPID{D}^2-AVR}={\displaystyle \frac{G_{FOPID{D}^2}\left(s\right)G_A{G}_E{G}_G}{1+G_{FOPID{D}^2}\left(s\right)G_A{G}_E{G}_G{G}_S}}.$$

(7)

3. Black-Winged Kite and Whale Optimization Algorithm

3.1. Black-Winged Kite Algorithm

In recent years, an increasing number of metaheuristic algorithms have been developed and used to solve various practical problems. The design inspiration for metaheuristic algorithms comes from several aspects, including the behavioral characteristics of biological populations, human behavior or social phenomena, biological evolution, or the physical properties or chemical reactions of certain objects. Based on the behavior of black-winged kites during hunting and migration, Wang et al. developed an algorithm model for black-winged kites [1].

The black-winged kite is a small raptor, scientific name Elanus caeruleus, belonging to the genus Elanus in the Accipitridae family. The black-winged kite has a relatively small body size, typically ranging from 30 to 35 cm in length, with a wingspan of about 70 to 85 cm, and a weight of about 200 to 300 g. It has black and white feathers and red eyes. Known for its elegant flying posture and distinct black and white feathers, it is widely distributed in regions such as Africa, southern Europe, southern Asia, and Australia. Their hunting ability is extremely strong, and they prey on small insects, reptiles, birds, and mammals. When hunting, they will first adjust their posture in the air to hover, and then dive towards their prey. Affected by environmental factors such as climate and food, the black-winged kite also migrates like other birds.

3.1.1. Initialization

The location of each search agent denotes a feasible solution in the search space, and each search agent represents a black-winged kite. In the first step of the algorithm, n locations are randomly selected in the search space as the initial locations for each black-winged kite, and the following matrix is generally used to represent the locations of all black-winged kites.

$$X=\left(\begin{array}{ccccc}{X}_{1,1}& X_{1,2}& X_{1,3}& \dots & X_{1,dim}\\ X_{2,1}& X_{2,2}& X_{2,3}& \dots & X_{2,dim}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ X_{N,1}& X_{N,2}& X_{N,3}& \dots & X_{N,dim}\end{array}\right),$$

(8)

where N is the group size of the black-winged kite and $dim$ represents the size of the dimension of the problem to be solved. Thus, each row vector $X_i$ in the matrix represents the location of a black-winged kite. Then, calculate the fitness of each black-winged kite in the group and select the one with the best fitness as the leader $X_L$ in the initial group, which is considered to have the best location.

3.1.2. Attacking Process

As mentioned above, the hunting process of black-winged kites relies more on close-range observation, with hovering flight and precise capture as the core. This unique hunting strategy enables them to efficiently hunt small prey in open areas, hovering almost still in the air and maintaining balance by quickly flapping their wings and adjusting their tail feathers. This ability enables them to scan the ground with their keen vision and search for prey. Once the prey is locked, the black-winged kite will quickly dive down with extremely high precision. This strategy includes different attack behaviors for global exploration and search. In order to mathematically model the attack process, the following equations are proposed:

$$X_{t+1}=\left\{\begin{array}{cc}{X}_t+n(1+sinr)X_t\hfill & q<r\hfill \\ X_t+n(2r-1)X_t\hfill & otherwise\hfill \end{array}\right.,$$

(9)

where t is the current iteration, r is a random number in $[0,1]$, q is a constant, usually taking a value of 0.9 [1], and n is described in Reference [1]. With the equation above, black-winged kites can update their location inside the search space around their prey.

3.1.3. Migration Process

Migration refers to the periodic and directional long-distance movement of birds between their breeding grounds and wintering grounds. The main driving forces for migration include food supply, climate conditions, reproductive needs, and changes in sunlight. This is a highly adaptive behavior that reflects the precise response of organisms to their environment. The migration of black-winged kites mostly occurs in spring and autumn, generally belonging to short-distance migration, and sometimes migrating in small groups. They have flexible behavior and strong adaptability during the migration process and can adjust their migration strategies according to environmental and food changes. The mathematical modeling of the migration process of black-winged kites is as follows:

$$x_{t+1}^{ij}=\left\{\begin{array}{cc}{x}_t^{ij}+C_1\times (x_t^{ij}-L_t^j)\hfill & F_i<F_{ir}\hfill \\ x_t^{ij}+C_1\times (L_t^j-m\times x_t^{ij})\hfill & otherwise\hfill \end{array}\right.,$$

(10)

where $L_t^j$ denotes the best fitness of the black-winged kites in the $j_{th}$ dimension in the current iteration t, $x_t^{ij}$ and $x_{t+1}^{ij}$ are the location of the $i_{th}$ black-winged kites in the $j_{th}$ dimension in the current and next iteration, respectively, $F_i$ denotes the fitness value of any individual in the current group in the current iteration t, $F_{ir}$ denotes the fitness value of a random location of any black-winged kites in the current iteration t, $C_1$ is determined by the standard form of Cauchy mutation, and the description of m is provided in Reference [1].

Figure 7 shows the flowchart of BKA. T is the maximum number of iterations.

3.2. Whale Optimization Algorithm

Mirjalili et al. proposed the Whale Optimization Algorithm (WOA) inspired by the hunting behavior of humpback whales, which are among the most intelligent and emotionally complex marine mammals [39]. These creatures employ a unique bubble-net feeding strategy to capture schools of small near-surface organisms. Based on this predation mechanism, the WOA framework consists of three phases: search for prey, encircling prey, and bubble-net attack.

3.2.1. Search for Prey

To locate food sources, humpback whales adjust their locations based on randomly selected companions within the pod. This biological behavior is mathematically modeled as the exploration phase in the WOA, where each search agent updates its location according to a stochastically chosen individual. The governing equation for this mechanism is as follows:

$$X(t+1)=X_r\left(t\right)-A·|C·X_r\left(t\right)-X\left(t\right)|,$$

(11)

where $X_r\left(t\right)$ denotes the location of the randomly selected individual and A and C are key parameters designed to regulate the behavioral patterns of search agents. Their detailed mathematical formulations are provided in Reference [39]. When $\left|A\right|>1$, all whales stochastically select another individual within the group and adjust their locations in a direction diverging from the chosen one, thereby enhancing the algorithm’s global search capability.

3.2.2. Encircling Prey

After detecting prey, whales begin circling around the prey. After identifying the whale in the optimal hunting location, all individuals adjust their movement based on this best location. This behavior is modeled as follows:

$$X(t+1)=X^{*}\left(t\right)-A·D,$$

(12)

where $X^{*}\left(t\right)$ denotes the best location within the population during the t-th iteration and D represents the distance vector between the current location and the optimal solution, which is defined by:

$$D=|C·X^{*}\left(t\right)-X\left(t\right)|,$$

(13)

3.2.3. Bubble-Net Attack

After encircling prey, humpback whales first dive to a certain depth, then gradually ascend to the sea surface along a circular path with a continuously decreasing radius while continuously releasing bubbles around their prey. This constitutes the whales’ unique approach strategy toward their food source—they update their locations using spiral trajectories. The following equation describes this process:

$$X(t+1)=D·e^{bl}·cos\left(2\pi l\right)+X^{*}\left(t\right),$$

(14)

where b is a constant determining the size of the spiral trajectory and l is a random number between −1 and 1.

All whales are considered to have a 50% probability of being either in prey search mode or bubble-net attack mode. To determine how whales update their locations, a parameter p, a value between [0, 1], is designed. When $p<0.5$, individuals remain in prey search mode; otherwise, they update their locations using the spiral trajectory. The complete location update mechanism can be expressed as:

$$X(t+1)=\left\{\begin{array}{cc}{X}^{*}\left(t\right)-A·D,\hfill & ifp<0.5,\hfill \\ D·e^{bl}·cos\left(2\pi l\right)+X^{*}\left(t\right),\hfill & ifp>0.5,\hfill \end{array}\right.$$

(15)

Figure 8 shows the flowchart of WOA.

3.3. Black-Winged Kite and Whale Optimization Algorithm

This paper proposes a novel hybrid metaheuristic algorithm, the Black-winged kite Whale Optimization Algorithm, by integrating the Black-winged Kite Algorithm and the Whale Optimization Algorithm for tuning the FOPIDD² controller in an AVR system. Many hybrid algorithm construction strategies rely on partitioning or hybridizing populations, subpopulations, or individuals.

In this study, the proposed BWOA implements a population management strategy to intensively search the space around elite individuals. The workflow is structured as follows:

1.

Fitness-Based Population Ranking

Step 1: Calculate the fitness value $f\left(X_i\right)$ for each individual $X_i$ in the current population $P\left(t\right)=N$, where t denotes the current iteration and the population size N is set as an even number to ensure balanced partitioning during the elite selection phase of the algorithm.

Step 2: Rank all individuals in ascending order of fitness:

$$P_{sorted}\left(t\right)=Sort(f\left(X_1\right),f\left(X_2\right),\dots ,f\left(X_N\right)),$$

(16)

Step 3: Select the top 50% of individuals to form an elite subpopulation:

$$P_{elite}\left(t\right)=P_{sorted}\left(t\right)[1:\lfloor {\displaystyle \frac{N}{2}}\rfloor ],$$

(17)

2.

Parallel Subpopulation Optimization

Step 4: Simultaneously apply two distinct optimization algorithms to the same subpopulation $P_{elite}\left(t\right)$.

$$P_{BKA}\left(t\right)=BK{A}_{update}\left(P_{elite}\left(t\right)\right),$$

(18)

$$P_{WOA}\left(t\right)=WO{A}_{update}\left(P_{elite}\left(t\right)\right),$$

(19)

3.

Population Merging and Iteration

Step 5: Combine the optimized subpopulations while strictly maintaining the original population size.

$$P(t+1)=P_{BKA}\left(t\right)\cup P_{WOA}\left(t\right),$$

(20)

where $N=P(t+1)$.

Step 6: Repeat Steps 1–5 until $t=T$, where T is the maximum number of iterations.

The purpose of this approach is to incorporate the excellent bubble-net attacking strategy from WOA, a spiral-based iterative mechanism proven to be an effective search strategy. By applying multiple iterative strategies to high-fitness individuals, the algorithm enhances the exploration of potential solutions around these individuals, thereby accelerating convergence.

To address population segmentation and merging processes while safeguarding historical optima, preventing solution quality deterioration, and enhancing algorithmic robustness, the elitism preservation mechanism has been integrated into the BWOA framework. Post-population regeneration, the protocol executes a bidirectional elite evaluation between the current optimum and archival elite specimen. When the historical elite demonstrates superior fitness, the algorithm performs targeted displacement by replacing the worst-performing individual with the preserved elite solution, thereby maintaining evolutionary advantages while controlling population diversity. Additionally, Lévy flight is incorporated into the attacking behavior of BKA to improve the algorithm’s search capability. Therefore, Equation (13) is modified:

$$X_{t+1}=\left\{\begin{array}{cc}{X}_t+n(1+sinr)X_t\hfill & q<r\hfill \\ X_t+n(2r-1)X_t\hfill & \frac{2}{q}<r\le q\hfill \\ X_t^{*}+|X_t^{*}-X_t|·\mathrm{Lévy};\hfill & otherwise\hfill \end{array}\right.,$$

(21)

Figure 9 shows the flowchart of BWOA.

4. Problem Formulation

This paper aims to utilize the Black-winged Kite Algorithm to determine the parameters of the FOPIDD² controller for an AVR system. It is crucial to explore the combination of the research algorithm, objective function, type of PID controller, and the controlled object to achieve superior results. Therefore, this section begins by delineating the objective function used in this study. Commonly utilized metrics for assessing controller performance encompass IAE, ISE, ITAE, ITSE, and ZLG, each with its applicable scenarios, merits, and demerits.

To determine the optimal parameters of the controller using the algorithm proposed in this paper, a novel objective function is used, which is a combination of ITAE and ZLG. The expression for this objective function is as follows:

$$OF\left(X\right)={\int }_0^{t_{sim}}t\left|e\left(t\right)\right|dt+(1-e^{-\beta })(OV+E_{ss})+e^{-\beta }(T_s-T_r),$$

(22)

where X is a vector composed of all the parameters of the controller, which means $X=(K_P,K_i,K_d,\lambda ,\mu ,K_{d_2})$, $t_{sim}$ represents the termination time of the simulation experiment. OV is the overshoot, $E_{ss}$ is the steady-state error, $T_s$ is the settling time, $T_r$ is the rise time, and $\beta$ is a weighting factor, typically ranging between 0.5 and 1.5. When the value of $\beta$ exceeds 0.7, the overshoot and steady-state error are reduced; conversely, the rise time and settling time decrease [40]. Based on extensive numerical simulations, $\beta$ is set to 0.98 in this study.

Thus, the tuning of the proposed controller is formulated as a constrained optimization problem, which is mathematically expressed as follows:

$$\left\{\begin{array}{c}Minimize:OF\left(X\right),\hfill \\ subjectto:X_{lb}\le X\le X_{ub}\hfill \end{array}\right.$$

(23)

where the $X_{lb}$ and $X_{ub}$ are the lower and upper bounds of the decision variables in the constrained optimization problem.

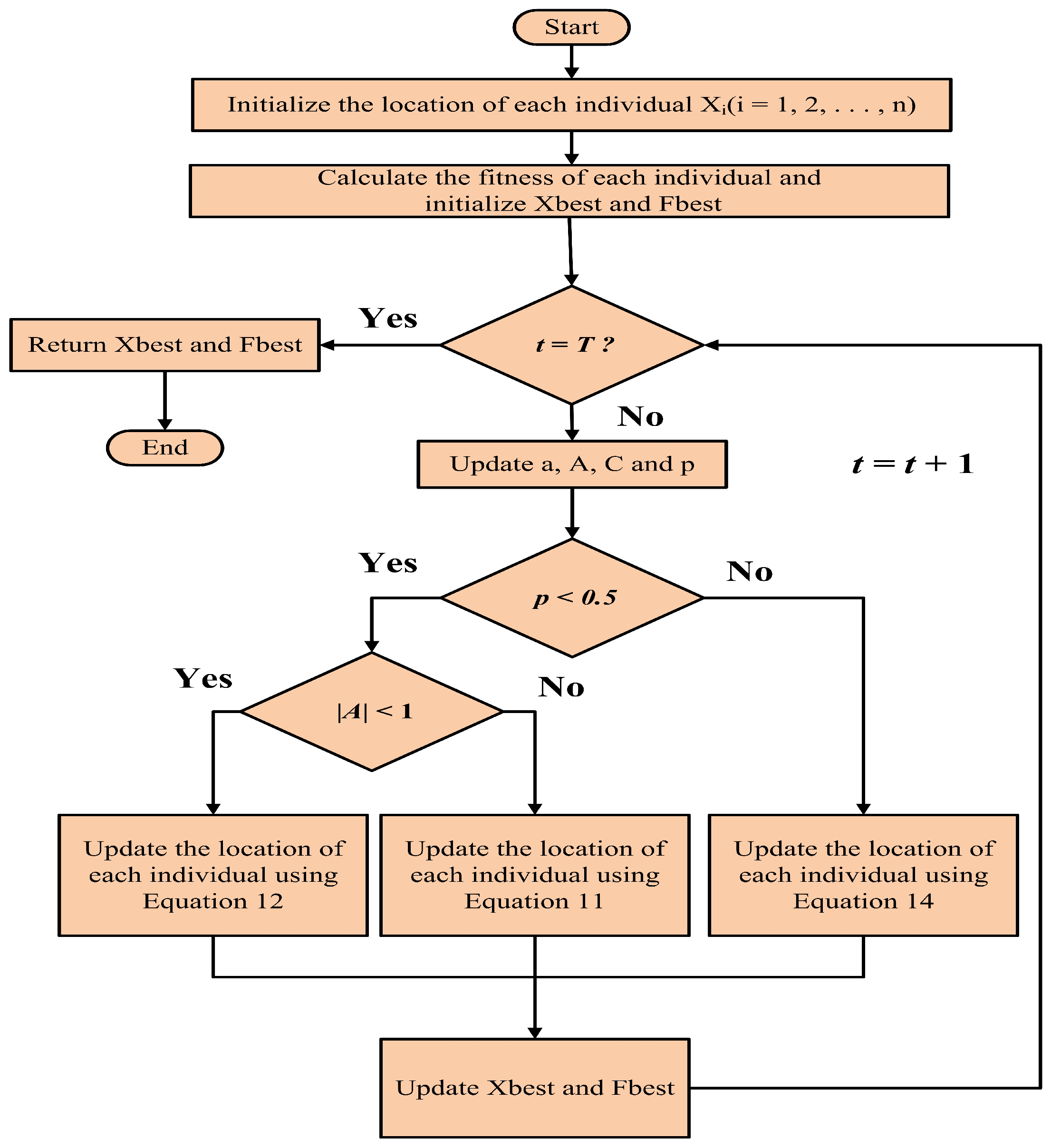
A detailed flowchart illustrating the application of the BWOA to optimize the performance of the AVR system is presented in Figure 10.

5. Simulation Results

This section presents the numerical simulation results of the FOPIDD² controller optimized by the BWOA for controlling the AVR system, which employs the linear AVR system detailed in Section 2.1, featuring an AC synchronous generator. The results include the system’s transient response, trajectory tracking analysis, and parameter uncertainty in the time domain to demonstrate the performance of the recommended controller. Additionally, the section provides stability analysis and disturbance rejection capability to show the robustness imparted by the recommended controller. Each simulation result of the BWOA controller is compared with some recently reported controllers to evaluate its efficiency. All numerical simulations in this study were implemented using MATLAB 2022a, running on a PC equipped with an Intel i5-8400 CPU (Intel Corporation, Santa Clara, CA, USA) and 16 GB of RAM (Kingston Technology Corporation, Fountain Valley, CA, USA). The parameter settings of the BWOA are as follows: the number of iterations is set to 100 and the population size is 30.

5.1. Step Response

This subsection provides a detailed description of the quality of the unit step response of the AVR system controlled by the proposed controller.

Table 3. Searching range of parameters.

Parameter	Lower Bound	Upper Bound
$K_p$	0.0001	3
$K_i$	0.0001	3
$K_d$	0.0001	3
$K_{d_2}$	0.0001	3
$\lambda$	0.5	1.5
$\mu$	0.5	1.5

specifies all parameters to be optimized for tuning the FOPIDD2 controller: $K_p$ (proportional gain), $K_i$ (integral gain), $K_d$ (derivative gain), $K_{d_2}$ (second-order derivative gain), $\lambda$ (integral order), and $\mu$ (derivative order). The range of parameters are directly adopted from Reference [27] to eliminate bias in performance comparisons. The parameters of components in the AVR system adopt typical values listed in Table 2 to maintain consistency with configurations in other literature. To determine the parameters of the controller, the program incorporating BWOA is executed 30 times, and a result with the overall optimal response parameters is selected.

The optimal parameters of the BWOA-FOPIDD² controller are listed in

Table 4. The optimal values of the parameters of the proposed controllers.

Controller	${\mathit{K}}_{\mathit{p}}$	${\mathit{K}}_{\mathit{i}}$	${\mathit{K}}_{\mathit{d}}$	${\mathit{K}}_{{\mathit{d}}_2}$	$\lambda$	$\mu$
FOPIDD2	3	$2.4412$	$2.9601$	$0.1733$	$0.9105$	$0.8525$

. Figure 11 presents the unit step response of the AVR system under the proposed controller, along with the recently reported response results of AVR systems controlled by other controllers, including the MVO-FOPIDD² controller, PSO-PIDD² controller, C-YSGA-FOPID controller, and SCA-FOPID controller.

Table 5. Comparison of the transient response metrics of different controllers.

Controllers	$\mathbf{OV}$ (%)	${\mathit{T}}_{\mathit{r}}$ (s)	${\mathit{T}}_{\mathit{s}}$ (s)
BWOA-FOPIDD2	$0.0049$	$0.0442$	$0.0791$
MVO-FOPIDD2 [27]	$0.1695$	$0.0547$	$0.0901$
PSO-PIDD2 [16]	0	$0.0929$	$0.1635$
SA-GTO-PIDD2 [19]	$0.1126$	$0.0237$	$0.2475$
C-YSGA-FOPID [24]	$1.89$	$0.1347$	$0.2$
SCA-FOPID [23]	$2.4223$	$0.1660$	$0.2260$

provides a detailed comparison of step response metrics between the proposed controller and controllers from other literature.

Table 5 contains step response metrics including overshoot, rise time, and settling time, abbreviated as OV, Tr, and Ts, respectively. It can be observed that the overshoot of the proposed controller is slightly higher than that of the PSO-PIDD² controller but outperforms all other controllers. Specifically, it achieves reductions of approximately 96.6% and 94.8% in overshoot compared to the MVO-FOPIDD² and SA-GTO-PIDD² controllers, respectively, and is significantly lower than the results from the C-YSGA-FOPID and SCA-FOPID controllers. In terms of rise time, the proposed controller delivers the second-best performance, reducing rise time by at least 45.3% compared to other controllers, with only the SA-GTO-PIDD² controller performing marginally better. For settling time, the AVR system controlled by the BWOA-FOPIDD² controller achieves the shortest settling time, outperforming other controllers by at least 50.3%.

Since the controller parameters are determined through 30 independent runs of the BWOA algorithm, with the optimal result subsequently selected, the statistical characteristics of the controller’s performance are described as follows: Figure 12 presents box plots of the overshoot, rise time, and settling time, while

Table 6. Statistical Analysis of Transient Response Metrics.

Metrics	Median	Mean	Standard Deviation	95% CI
overshoot (%)	$0.0022$	$0.0040$	$0.0048$	$[0.0022,0.0057]$
rise time (s)	$0.0702$	$0.1203$	$0.1402$	$[0.0680,0.1727]$
settling time (s)	$0.1449$	$0.2064$	$0.2085$	$[0.1286,0.2843]$

summarizes the median, mean, standard deviation, and $95\%$ confidence intervals of these metrics.

Overall, the AVR system controlled by the BWOA controller demonstrates competitive overshoot and rise time, along with the shortest settling time. These results highlight its notable performance in transient step response comparisons among various controllers.

5.2. Stability Analysis

This subsection discusses the stability of the AVR system controlled by the proposed controller using a Bode diagram in the frequency domain. Figure 13 illustrates the magnitude and phase curves of the AVR system controlled by the proposed controller, with corresponding curves from controllers in existing literature included for comparative purposes.

Table 7. Comparison of the frequency response metrics of different controllers.

Controllers	Peak Gain (dB)	Phase Margin (deg)	Delay Margin (s)	Bandwidth (rad/s)
BWOA-FOPIDD2	0	171.97	0.34	68.93
MVO-FOPIDD2 [27]	0.000798	170	0.33	49.8
PSO-PIDD2 [16]	0	180	Inf	23.5
SA-GTO-PIDD2 [19]	1.5482	180	Inf	94.2
C-YSGA-FOPID [24]	0.131	163	0.99	16.3
SCA-FOPID [23]	0.0379	165	1.24	13.406

provides a detailed comparison of frequency domain response metrics across these controllers, including peak gain, phase margin, delay margin, and bandwidth as evaluation criteria.

From Table 7, it can be observed that the AVR systems controlled by the BWOA-FOPIDD² and PSO-PIDD² controllers both provide a peak gain of 0 dB, while the peak gains of the remaining controllers exceed 0 dB. In terms of phase margin, both the PSO-PIDD² and SA-GTO-PIDD² controllers achieve a phase margin of 180 deg, whereas the BWOA-FOPIDD² controller exhibits a slightly lower phase margin of 171.97 deg, which is marginally higher than that of the MVO-FOPIDD² controller using the same type of control strategy. Regarding bandwidth, the proposed controller demonstrates a bandwidth of 68.93 rad/s, which is only less than that of the SA-GTO-PIDD² controller, resulting in better tracking capability for input signal variations.

In summary, the proposed controller achieves the minimum peak gain, the second-best phase margin and bandwidth, and demonstrates superior performance across frequency-domain metrics compared to the C-YSGA-FOPID and SCA-FOPID controllers. The proposed controller demonstrates a mixed performance profile compared to other controllers; excelling in certain metrics while lagging in others, it exhibits notable stability advantages overall.

5.3. Trajectory Tracking Quality

When the input signal varies, the generator voltage of the system also adjusts dynamically. Evaluating the system’s ability to track the input voltage trajectory under set-point variations of the reference voltage is integral to assessing its robustness. In this subsection, predefined set-point variations in the reference voltage are configured. Several conventional metrics are then utilized to assess the tracking performance of the proposed controller for input signals, with comparisons made against controllers documented in other studies.

The trajectory tracking curves of the proposed controller under set-point variations are illustrated in Figure 14, alongside the curves of controllers from other literature for the same set-point variations. The black line represents the reference voltage, while the response curves of different controllers are marked with distinct colors. The reference signal is initially set to 1 pu, adjusted to 0.95 pu at 3 s, then to 1.05 pu at 5 s, and finally restored to 1 pu at 7 s. To compare the trajectory tracking performance of different controllers in detail, the ITAE, IAE, ITSE, and ISE metrics are employed as evaluation criteria. The detailed numerical values of these metrics are listed in

Table 8. Comparison of the trajectory tracking efficacy of different controllers.

Controllers	ITAE	IAE	ITSE	ISE
BWOA-FOPIDD2	0.8541	0.5251	0.1301	0.1240
MVO-FOPIDD2 [27]	0.7673	0.4840	0.1582	0.1522
PSO-PIDD2 [16]	0.7340	0.6455	0.2816	0.2694
SA-GTO-PIDD2 [19]	1.9974	1.3781	0.6963	0.6504
C-YSGA-FOPID [24]	2.3912	1.4737	0.7362	0.6852
SCA-FOPID [23]	5.3862	2.1486	0.9227	0.8165

. When using ITSE and ISE as benchmarks, the proposed controller achieves the minimum values, indicating that the terminal voltage generated by the BWOA controller aligns most closely with the reference voltage. Meanwhile, when evaluated by IAE and ITAE, the proposed controller ranks second and third, respectively. Therefore, comprehensively, the proposed controller demonstrates significantly superior trajectory tracking capability.

5.4. Parameter Uncertainty Capability

The robustness evaluation of the proposed controller is further conducted through systematic parameter uncertainty analysis. This investigation introduces variations to the time constants of components of the AVR system, including the amplifier, exciter, generator, and sensor. Transient response characteristics under these perturbations are quantitatively assessed using unit step response metrics, including overshoot, rise time, and settling time. This approach evaluates the system’s capability to maintain stable performance under variations of these parameters.

Figure 15 presents the transient response profiles under amplifier time constant (${\tau }_A$) variations, covering 50%, 75%, 100% (nominal), 125%, and 150% of the baseline value. The reference response (black dashed curve) corresponds to the nominal Ta, while colored traces (red: +50%, purple: +25%, blue: −25%, navy: −50%) illustrate the system behavior under parameter deviations. Analogous analyses for ${\tau }_E$, ${\tau }_G$, and ${\tau }_S$ perturbations are shown in Figure 16, Figure 17 and Figure 18, respectively.

A comprehensive comparison of transient metrics across all scenarios is provided in

Table 9. Transient response metrics with different values of time constants.

Parameter	Variation (%)	OV (%)	${\mathit{T}}_{\mathit{r}}$ (s)	${\mathit{T}}_{\mathit{s}}$ (s)
${\tau }_A$	+50%	3.5689	0.0596	0.2367
	+25%	1.5755	0.0525	0.0807
	−25%	0.0044	0.0348	0.1682
	−50%	0.0039	0.0244	0.2582
${\tau }_E$	+50%	1.5070	0.0696	0.1138
	+25%	0.6220	0.0568	0.0990
	−25%	0.0021	0.0316	0.0493
	−50%	3.0921	0.0198	0.6558
${\tau }_G$	+50%	0.2957	0.0733	0.1301
	+25%	0.0345	0.0586	0.1088
	−25%	0.0391	0.0309	0.0470
	−50%	4.9275	0.0188	0.0578
${\tau }_S$	+50%	2.6921	0.0357	0.0929
	+25%	0.2789	0.0391	0.0591
	−25%	0.0048	0.0509	0.1048
	−50%	0.0047	0.0583	0.1193

, which aggregates 16 experimental conditions. The maximum overshoot (4.93%) occurs when the generator time constant (${\tau }_G$) is reduced to 50% of its nominal value, exceeding deviations caused by ${\tau }_E$, ${\tau }_G$, and ${\tau }_S$ perturbations. Rise time exhibits limited sensitivity to parameter variations, with fluctuations confined within 0.0545 s. Settling time demonstrates comparable behavior, with its variations constrained to a minimal range.

These results empirically demonstrate that the proposed controller maintains stable transient performance across $\pm 50\%$ variations in component time constants, confirming its robustness against modeled parameter uncertainties.

5.5. Rejection of Disturbance

To evaluate the disturbance rejection capability of the proposed controller, a load disturbance signal was introduced to the generator voltage. Figure 19 illustrates the block diagram of the AVR system incorporating load disturbances. The load disturbance was modeled as a step signal superimposed on the generator voltage profile, with an initial value of 0 p.u., stepping down to −0.1 p.u. during 8–12 s before returning to 0 p.u. beyond 12 s. The corresponding step responses under load disturbance conditions are demonstrated in Figure 20.

The results in Figure 20 are presented in two subplots: the upper subplot compares the undisturbed reference signal (black dashed line) with transient responses under disturbance conditions from various controllers, where the proposed controller’s response is highlighted in dark blue; the temporal variation of the load disturbance is explicitly shown in the lower subplot.

A comprehensive quantitative analysis was conducted through multiple evaluation metrics, as summarized in

Table 10. The ITAE obtained using different PIDD² controllers with load disturbance.

Controllers	ITAE	IAE	ITSE	ISE
BWOA-FOPIDD2	1.0520	1.0009	0.2526	0.5090
MVO-FOPIDD2 [27]	1.0847	1.0037	0.2512	0.5094
PSO-PIDD2 [16]	1.1367	1.0096	0.2526	0.5185
SA-GTO-PIDD2 [19]	1.3371	1.0349	0.2648	0.5424
C-YSGA-FOPID [24]	1.3170	1.0285	0.2619	0.5431
SCA-FOPID [23]	1.3040	1.0239	0.2678	0.5593

. Notably, while the proposed controller achieved the second-best ITSE value of 0.2526, which is slightly greater than the MVO-FOPIDD² controller, it yielded optimal values across the remaining three metrics (IAE, ISE, and ITAE), highlighting its superior disturbance rejection capability compared to other controllers. These findings confirm that the proposed controller enables rapid voltage recovery to steady-state conditions following load disturbances, demonstrating robust reference tracking and effective disturbance suppression in the AVR systems.

5.6. Algorithm Analysis

To investigate the convergence characteristics of the algorithm, BWOA and other comparison algorithms used in this study underwent 10 independent runs each under identical simulation conditions. The mean values of their convergence characteristics were statistically analyzed to plot Figure 21. For all algorithms, the population size was set to 30 and the number of iterations to 50. As shown in Figure 21, the proposed algorithm converges at the 14th iteration, which is the result of multiple independent runs. This indicates that the BWOA algorithm possesses excellent convergence characteristics.

Table 11. Comparison of transient response metrics under different objective functions.

Objective Function	OV (%)	${\mathit{T}}_{\mathit{r}}$ (s)	${\mathit{T}}_{\mathit{s}}$ (s)
ITAE+ZLG	0.0039	0.0549	0.0912
ITAE	0.7008	0.0670	0.2608
ITSE	5.8823	0.0144	0.3324
ZLG	3.4073	0.4793	1.7171

lists the step response performance metrics obtained by combining the proposed BWOA with different objective functions, including ITAE, ITSE, ZLG, and the proposed ITAE+ZLG approach. The results demonstrate that ITAE+ZLG achieves the lowest overshoot and the fastest settling time. Although ITSE provides a faster rise time compared to ITAE+ZLG, it exhibits excessive overshoot, which is undesirable for practical AVR systems. These findings highlight the strong compatibility of the BWOA algorithm with the ITAE+ZLG objective function in addressing automatic voltage regulation challenges.

The computational-cost-related data are presented in

Table 12. Comparison of computational costs for controller optimization algorithms.

Controllers	Dim	Population Size	Iterations
BWOA-FOPIDD2	6	30	100
MVO-FOPIDD2 [27]	6	30	300
PSO-PIDD2 [16]	4	30	50
SA-GTO-PIDD2 [19]	5	50	100
C-YSGA-FOPID [24]	5	40	50
SCA-FOPID [23]	5	50	100

. The MVO-FOPIDD² controller and the proposed controller share the same controller structure. When using identical population sizes, the proposed controller requires only one-third the number of iterations of the MVO-FOPIDD² controller. Regarding maximum iterations, only the PSO-PIDD² and C-YSGA-FOPID controllers use fewer iterations than the MVO-FOPIDD² controller. However, these controllers also require tuning fewer parameters than the proposed controller.

6. Conclusions

This study systematically investigates the optimization of fractional-order PIDD² controllers for automatic voltage regulators using the novel Black-winged kite and Whale Optimization Algorithm (BWOA). The proposed BWOA implements an innovative hybrid optimization framework that strategically integrates two metaheuristic algorithms through a hierarchical population management approach. The algorithm first ranks all individuals in ascending order based on their objective function values. The top 50% of high-performance candidates are then divided into two subpopulations undergoing parallel optimization processes: one subpopulation is updated using Black-winged Kite Optimization principles, while the other evolves through Whale Optimization Algorithm mechanisms. The updated subpopulations are subsequently merged to form a new population, enabling extensive exploration of high-quality solution spaces while maintaining population diversity and preventing premature convergence to local optima. For controller optimization, a composite objective function integrating Integral Time Absolute Error (ITAE) and ZLG criteria was implemented. Extensive numerical simulations were conducted to evaluate the proposed controller’s performance across multiple metrics: transient response characteristics, stability robustness, parameter uncertainty tolerance, trajectory tracking capability, and disturbance rejection effectiveness. Comparative analyses with existing controllers from the literature demonstrate the superiority of the BWOA-optimized controller in most evaluation aspects.

However, the proposed controller has not demonstrated comprehensive optimality across all evaluation metrics. Based on current findings and existing research, several potential research directions are identified for future investigation: (1) Incorporating recently developed metaheuristic algorithms to improve optimization efficiency; (2) Exploring novel objective function formulations that better capture complex system requirements; (3) Considering using other control strategies, such as adaptive PID controllers, to control AVR systems to seek better control performance; (4) Conducting numerical experiments under more realistic operational conditions to enhance practical applicability. For example, first, the AVR model used in this study is a first-order simplified model, whereas real-world nonlinear AVR models would degrade control performance; second, practical AVR systems must also account for factors such as exciter saturation and amplifier dead zones during operation; finally, the implementation of the proposed fractional-order controller requires high-order digital filters for approximation, which would likewise compromise control performance. These extensions could further advance the development of intelligent optimization techniques for the AVR system.