An Efficient and Low-Cost Design of Modular Reduction for CRYSTALS-Kyber

Abstract

After being selected as a standard for Post-Quantum Cryptography Key Encapsulation Mechanisms by NIST, CRYSTALS-Kyber has driven the transformation of the information security field toward new standards. In CRYSTALS-Kyber, modular reduction is crucial for performance optimization. This paper proposes a bitwise modular reduction design based on Dadda tree compression arrays, achieving higher parallelism through a strategy that combines bitwise modular reduction with hybrid compression arrays. As our experiments show, it only costs 91 LUTs when implemented on Xilinx Artix-7 FPGA. Compared with the leading hardware implementations, the Area–Time Product (ATP) is reduced by 16.43%~87.69%.

1. Introduction

With the rapid development of quantum computing technology, traditional public key cryptography systems (such as RSA and ECC) face growing threats from quantum algorithms like Shor’s algorithm [1]. To address this challenge, the National Institute of Standards and Technology (NIST) launched the Post-Quantum Cryptography Standardization Project in 2016, to evaluate and standardize cryptographic algorithms resistant to quantum attacks [2]. After multiple rounds of selection, the lattice-based Key Encapsulation Mechanism (KEM) CRYSTALS-Kyber was officially standardized for its superior efficiency and robust security [3].

The core operation of CRYSTALS-Kyber is polynomial modular multiplication, where modular reduction is a critical step for efficient modulo operation. The efficiency of modular reduction directly impacts the overall performance of the algorithm. Recent research has increasingly focused on hardware optimizations for CRYSTALS-Kyber, including implementations of Montgomery’s reduction [4,5], Plantard’s reduction [6], K-RED/K2-RED [7], Barrett’s reduction [8], and bitwise modular reduction [9]. Ding et al. [10] implemented modular reduction using the Montgomery algorithm, while Huang et al. [11] proposed a variant of the Plantard reduction that supports signed number operations. Further refinements in [12] optimized input/output ranges to improve the efficiency of modular reduction. This algorithm can be considered a special case of the Montgomery reduction. However, it requires a larger multiplication bit width, resulting in higher hardware resource consumption. Both the K-RED and the K2-RED algorithms exploit the property that q = 3329 can be decomposed into $3329=13\cdot 2^8+1$, with additional optimizations proposed in the References Section [13,14,15,16,17]. However, these methods introduce constant coefficients during polynomial multiplication, which require additional cycles for elimination, complicating efficient point-wise multiplication (PWM) operations.

Since the Barrett reduction produces the expected result without additional conversion, it is widely adopted in CRYSTALS-Kyber implementations. Current research primarily targets the Barrett reduction and its variants: the literature [18,19] has directly employed the Barrett reduction for modular operations, while Xing et al. [20] enhanced Barrett’s reduction via combined multiple shift operations. Additionally, Li et al. [21] optimized the Barrett reduction by leveraging the characteristics of $q=\delta \cdot 2^e+1$ to decompose the modulus into smaller components. However, due to data dependencies between operations in the Barrett reduction, its parallelism is inherently limited, resulting in long delays for individual reductions. Although the frequency can be increased by using two-stage pipelining, this approach incurs a significant resource overhead as the registers must be inserted into the butterfly unit (the basic operation unit of NTT). Guo et al. [22] and Yaman et al. [23] proposed a recursive decomposition method, termed bitwise modular reduction, by using $2^{12}\equiv (2^9+2^8-1)\mathrm{mod}3329$ to recursively decompose $r=c\mathrm{mod}3329$. Similar to the Barrett reduction, this method avoids extra coefficients and relies solely on additions, subtractions, and comparisons, enabling better parallelism. Nevertheless, the bit tree structures proposed in [22,23] exhibit substantial redundancy, and their excessive height poses challenges for frequency improvement. Therefore, there is considerable scope for further optimization.

Based on the above analysis, we deeply optimize the bitwise modular algorithm and propose an efficient and low-cost modular reduction design. The contributions of this article are as follows:

• A highly efficient modular reduction algorithm for CRYSTALS-Kyber is proposed. By rederiving the bit tree of the bitwise modular algorithm and proposing three universal methods for eliminating redundant bits, we achieve a more streamlined approach that can be flexibly transferred to other modular parameters. For the parameter $q=3329$, compared with the original algorithm, the computational effort is reduced by 21.5%.
• A reduction unit based on the Dadda tree compression array is designed. A customized compression path design is adopted to effectively reduce resource consumption and latency. Compared with related implementations, the ATP is reduced by 16.5%.
• We evaluate the reduction unit at the polynomial operation level. The experimental results show that the design reduces the ATP of the polynomial operation unit by 16.04% and increases the operating frequency by 9.56%.

The remainder of this paper is organized as follows: Section 2 introduces the bitwise modular reduction algorithm; Section 3 details the optimized hardware architecture; Section 4 presents experimental results and compares them with previous work; and finally, Section 5 summarizes the entire paper.

2. Bitwise Modular Reduction Algorithm

2.1. Bitwise Modular Reduction

In CRYSTALS-Kyber, the module q is fixed at 3329, and the polynomial coefficients are defined over the integer ring Z_q. Let $a$ and $b$ represent points corresponding to the NTT (Number Theoretic Transform) values of two polynomials. Then, their product $c$ is 24 bits and the maximum value is ${(q-1)}^2={24}^{\prime }hA90000$. The mathematical principle behind bitwise modular reduction involves recursively decomposing $r=c\mathrm{mod}3329$ by using the congruence properties of modular addition. Given that $3329=2^{12}-2^9-2^8+1$, one can derive $2^{12}\equiv (2^9+2^8-1)\mathrm{mod}3329$ through congruence transformation. For simplicity, let $x[msb:lsb]$ denote the bits from the least significant bit (LSB) to the most significant bit (MSB) of the decimal number $x$. Decompose $c$ into $2^{12}c[23:12]+c[11:0]$ and iteratively replace $2^{12}$. The decomposition process is as follows:

$$\begin{array}{ll}r& =(2^{12}c[23:12]+c[11:0])\mathrm{mod}3329\\ & \equiv (2^9+2^8-1)\cdot c[23:12]+c[11:0]\\ & \equiv 2^{9}c[23:12]+2^{8}c[23:12]-c[23:12]+c[11:0]\\ & \equiv 2^{12}c[23:15]+2^{12}c[23:16]+c[11:0]+2^{9}c[14:12]+2^{8}c[15:12]-c[23:12]\\ & \equiv (2^9+2^8-1)\cdot (c[23:15]+c[23:16])+c[11:0]+2^{9}c[14:12]+2^{8}c[15:12]-c[23:12]\\ & \equiv 2^{9}c[23:15]+2^{8}c[23:15]+2^{9}c[23:16]+2^{8}c[23:16]+c[11:0]+2^{9}c[14:12]\\ & +2^{8}c[15:12]-c[23:12]-c[23:15]-c[23:16]\\ & \cdots \\ & \equiv c[11:0]+2^{11}C[16]+2^{10}c[21:20]+2^9(c[14:12]+c[15]+c[19:17]+c[23:21]\\ & +c[22:20]+c[23:22]+c[23])+2^8(c[15:12]+c[15]+c[19:16]+c[20:17]+c[23:21]\\ & +c[23:22]+c[23])-c[23:12]-c[23:15]-c[23:16]-c[23:17]-2\cdot c[23:20]\\ & -c[23:21]-c[23:22]-c[23]\end{array}$$

(1)

Organize Equation (1) into a bit tree as shown in Figure 1 according to the weight. For instance, the orange dashed box in Figure 1 expands according to $c[11:0]=2^{11}{c}_{11}+\cdots +2^0{c}_0$. Among them, the default bits in the black dashed box are all 0. The bit tree can be seen as a binary addition and subtraction in the vertical direction and the elements on its column can be flexibly moved up or down.

For example, the section highlighted by the purple dashed box can be resolved through summation. For bits exceeding a weight $2^{12}$ after summation, the recursive decomposition method described previously can be reapplied to eliminate them (corresponding method 1). Meanwhile, the selected segment enclosed by the green dashed box can be directly eliminated through subtraction (corresponding method 2). Other redundant bits can be removed by splitting or merging according to the property $2^m{c}_m=2\cdot 2^{m-1}{c}_m$ (corresponding method 3). In the process of elimination, the following principles should be followed: (1) identical elements appearing in consecutive columns, as indicated by the blue dashed box, can be eliminated through splitting or merging; (2) elements with negative signs should be eliminated whenever possible to minimize conversions involving complement arithmetic and reduce the overall height of the bit tree.

The bit tree after eliminating redundant bits is depicted in Figure 2a. To complement the bit tree in Figure 2a and convert the subtraction operation to the addition operation, that is, negate the three lines with negative signs and add 1. In Figure 2a, the highest bit weight in the first row of the bit tree is $2^{11}$, for rows 2 through 6 it is $2^{10}$, and for row 7 it is $2^0$. Consequently, the sum result can be up to 14 bits. Due to the complement operation, the sign needs to be extended to 15 bits. The bit tree after complement adjustment is shown in Figure 2b, where the bar ${\overline{c}}_n$ represents negation. The “1” bits in high positions are the expansion of the sign bit, and the remaining bit 1 is added due to the operation of negation or addition of 1.

By resolving and adjusting element 1 in Figure 2b, the final bit tree is obtained, which is illustrated in Figure 3. For ease of subsequent descriptions, these elements are coded from t0_0 to t0_11 in ascending order of weight, where ti_j represents the j-th column of the bit tree after the i-th compression.

2.2. Algorithm Discussion

Table 1 presents a comparison of the results with those reported in [22,23]. For the rederived optimized bit tree, the total number of bits (representing all elements in the bit tree) is 62, marking a reduction of 27.9% and 21.5% compared with [22,23], respectively. The height of the tree (defined as the length of the longest column in the bit tree) is 8, corresponding to a one-level reduction compared with conventional implementations. The output range of the results matches that reported in [23].

Table 1. Comparison of bit trees with bitwise modular reduction.

Ref	No. of bit	Height of Tree	Result Range
Guo [22]	86	9	(−q, 8q)
Yaman [23]	79	9	(−q, 3q)
Ours	62	8	(−q, 3q)

Table 1. Comparison of bit trees with bitwise modular reduction.

Ref	No. of bit	Height of Tree	Result Range
Guo [22]	86	9	(−q, 8q)
Yaman [23]	79	9	(−q, 3q)
Ours	62	8	(−q, 3q)

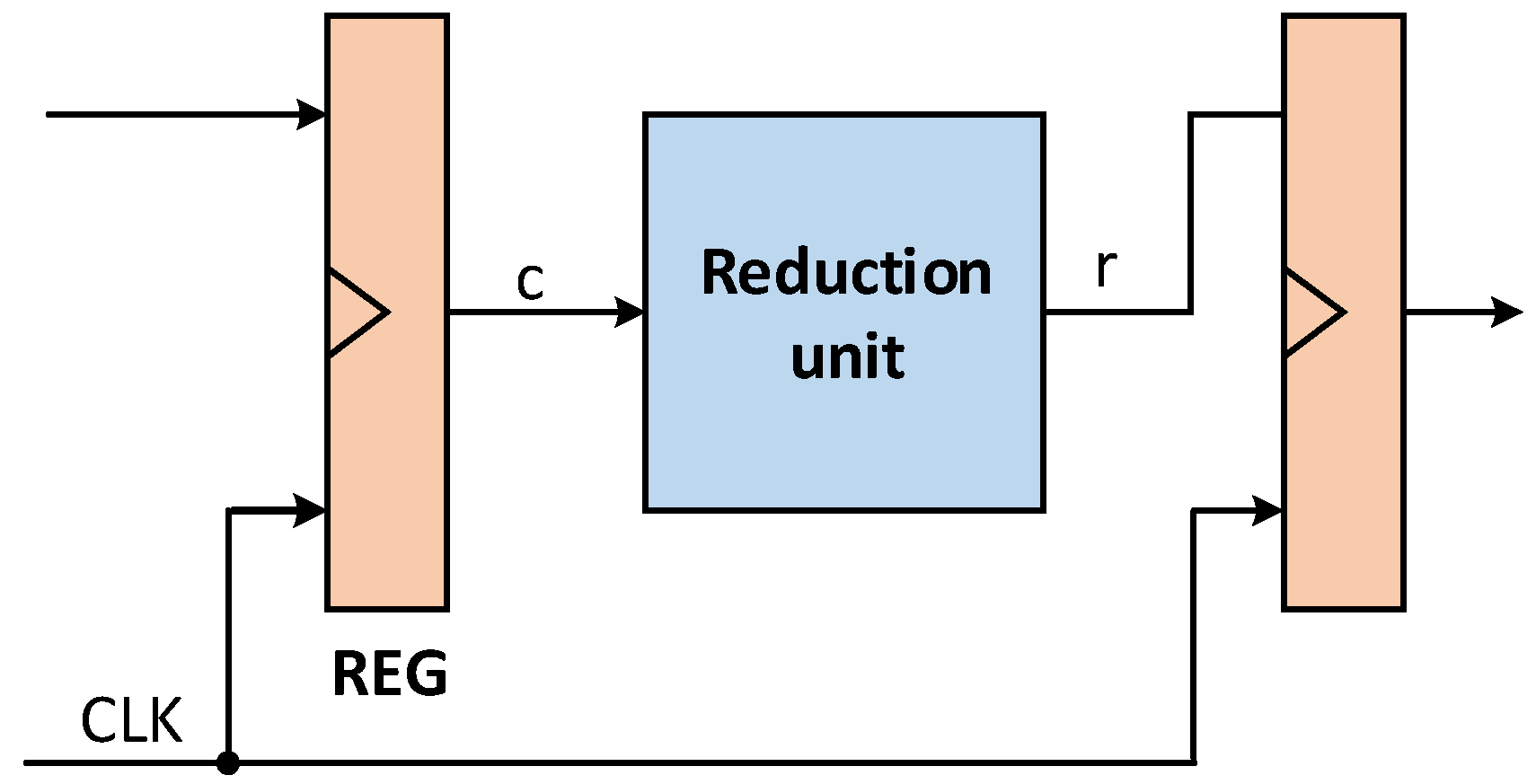
3. Overall Architecture

3.1. Design of Bitwise Modular Reduction

Figure 4a illustrates the hardware architecture of the bitwise modular reduction unit proposed in this paper. The design is composed of a Dadda Tree Hybrid Compression Array (DTHCA), four 15-bit full adders (FAs), and a 4-to-1 multiplexer (MUX). To mitigate the delays caused by multi-stage full adders, this paper employs the Dadda tree [24] for the bit tree compression. The Dadda tree is an optimized variant of the Wallace tree, capable of rapidly compressing tree height while preserving area efficiency and speed advantages. Also, it is more suitable for cases with irregular structures. As depicted in Figure 4a, the DTHCA features a three-stage structure, including 33 3-to-2 compressors (CSA2), 7 2-to-2 compressors (CSA1), and 29 CSA0. The functions of CSA2, CSA1, and CSA0 are detailed in Figure 4b. Specifically, CSA2 and CSA1 function as a 1-bit full adder and a 1-bit half adder, respectively, whereas CSA0 is just a virtual concept used for visualization purposes, directly connected via wire networks in actual implementations.

The operational principle of the modular reduction unit proceeds as follows: First, the encoded signal illustrated in Figure 3 is fed into the DTHCA to generate a 15-bit carry-reserved value d0[14:0] and a partial sum S0[14:0], respectively, which are then summed through FA0. Since the summation result range is (−q, 3q), we utilize three parallel full adders to correct the results. Finally, the output is selected through a 4-to-1 MUX, where the selection signal is generated by priority encoding the MSBs of the four FA outputs.

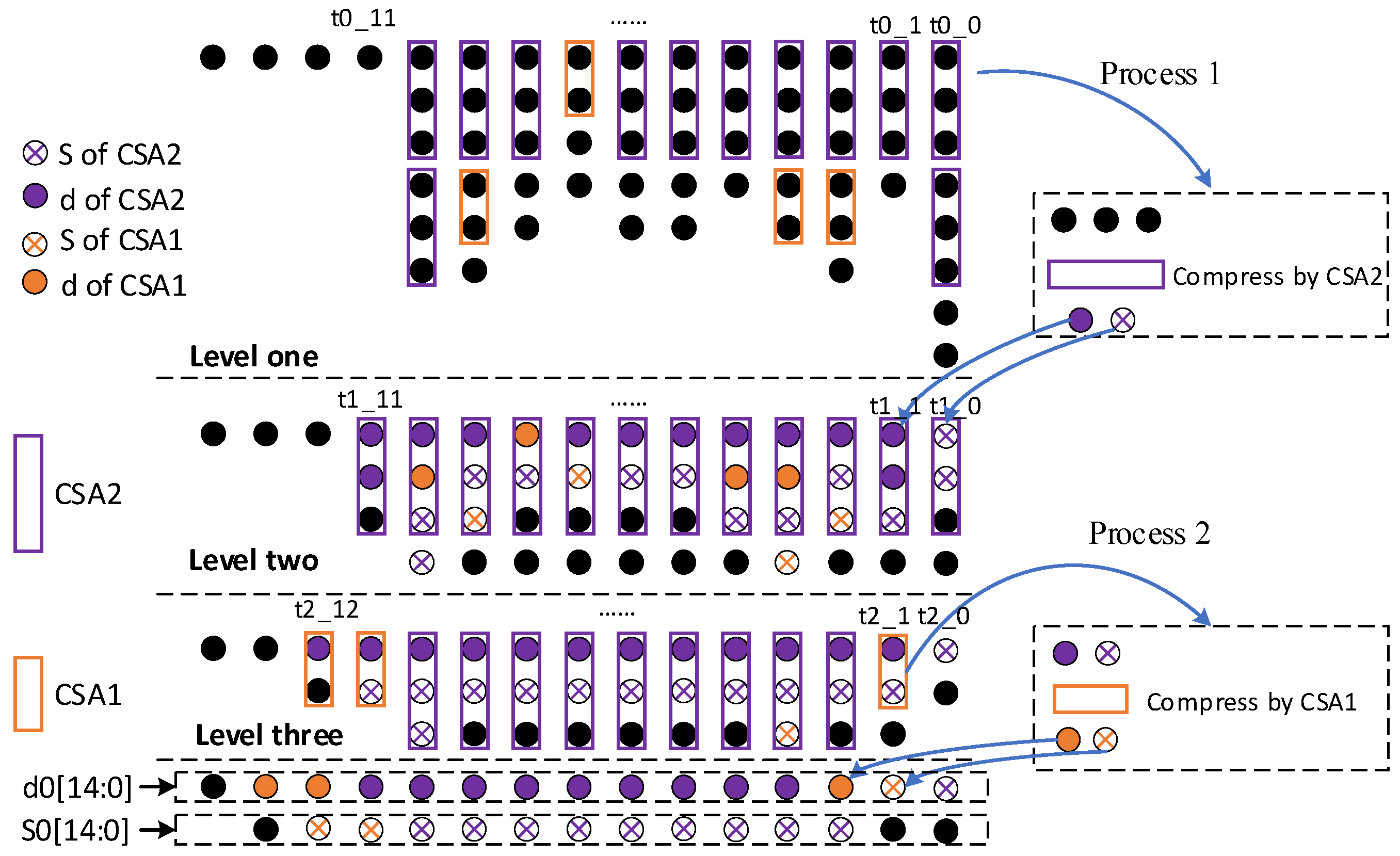
3.2. DTHCA Compression Process

The complete process of DTHCA compressing the bit tree is illustrated in Figure 5. The purple and orange boxes represent CSA2 and CSA1 units, respectively, while the black dots denote corresponding bits within the bit tree. Taking CSA2 as an example, starting from column 0 at level one, CSA2 processes three enclosed input bits to generate sum s and carry d. Here, s directly propagates to column 0 at level two, whereas carry d is passed to column 1 at level two, as indicated by process 1 in the figure. It is evident that after the first level of compression, the irregular height of the bit tree is normalized to four or fewer, and then it can be output to the full adder after two levels of compression. When addressing irregular bit trees, some studies propose using a 5-to-3 compressor, which offers a greater compression capacity, to design hybrid compression arrays [23], such as the CSA3 shown in Figure 4b. Although a carefully optimized 5-to-3 compressor consumes fewer gate circuits than two 3-to-2 compressors, its integration into FPGA designs via LUTs(lookup tables) does not reduce resource usage. Moreover, compared with two parallel CSA2, it increases the delay path in the first-level LUT. Consequently, this design exclusively utilizes 3-to-2 and 2-to-2 compression techniques.

4. Experimental Results and Comparison

4.1. Experimental Results

The bitwise modular reduction unit proposed in this paper is implemented on the Xilinx Artix-7 FPGA (xc7a200tffg1156-3) using the default synthesis strategy in Vivado 2024.1. As the modular reduction unit is a pure combinatorial logic circuit, its input and output can only be constrained via two register groups for timing evaluation to obtain the clock frequency, as shown in Figure 6. The implementation results demonstrate that the proposed modular reduction unit consumes 91 LUTs, and the maximum clock frequency can reach 215.38 MHz.

4.2. Comparison with Related Works

Since the Montgomery, K-RED/K2-RED, and the Plantard algorithms all require the conversion of calculation results, to ensure a fair comparison, this paper exclusively compares these with Barrett’s reduction and bitwise modular reduction. Xing et al. [20] and Yaman et al. [23] have provided their open-source implementations. However, to guarantee a fair comparison, the registers inserted in the code from [20] were removed to facilitate single-cycle operation completion, whereas for [23], only the synthesis tool needed adjustment. Since [18,19,21,22] do not provide reference data or open-source code, this study uniformly reimplements these works, and also completes the operation in a single cycle. All the above work undergo identical evaluation methods, and the results are shown in Table 2.

Table 2. Comparison of related work on the FPGA platform.

Ref	Technique	LUT	DSP	Freq (MHz)	Power (w)	Latency (ns)	ATP * ($\mathit{L}\mathit{a}\mathit{t}\mathit{e}\mathit{n}\mathit{c}\mathit{y} \mathbf{\times } \mathit{A}\mathit{r}\mathit{e}\mathit{a}$)
DETE’21 [23]	bitwise	156	0	202.27	0.162	4.94	771.25
TCAS’22 [22]	bitwise	279	0	167.48	0.172	5.97	1665.87
CISCE’21 [19]	Barrett	37	2	102.88	0.150	7.70	3431.18
Integration’21 [18]	Barrett	126	0	129.87	0.147	9.72	970.2
TCHES’21 [20]	Barrett	94	0	138.89	0.151	7.20	676.79
TCAD’23 [21]	Barrett	79	0	156.25	0.153	6.40	505.6
ours	bitwise	91	0	215.38	0.162	4.64	422.51

*: ATP = 1 × 10⁹ × Area/Freq.

Table 2. Comparison of related work on the FPGA platform.

Ref	Technique	LUT	DSP	Freq (MHz)	Power (w)	Latency (ns)	ATP * ($\mathit{L}\mathit{a}\mathit{t}\mathit{e}\mathit{n}\mathit{c}\mathit{y} \mathbf{\times } \mathit{A}\mathit{r}\mathit{e}\mathit{a}$)
DETE’21 [23]	bitwise	156	0	202.27	0.162	4.94	771.25
TCAS’22 [22]	bitwise	279	0	167.48	0.172	5.97	1665.87
CISCE’21 [19]	Barrett	37	2	102.88	0.150	7.70	3431.18
Integration’21 [18]	Barrett	126	0	129.87	0.147	9.72	970.2
TCHES’21 [20]	Barrett	94	0	138.89	0.151	7.20	676.79
TCAD’23 [21]	Barrett	79	0	156.25	0.153	6.40	505.6
ours	bitwise	91	0	215.38	0.162	4.64	422.51

*: ATP = 1 × 10⁹ × Area/Freq.

We use the Area–Time Product (ATP) as the metric for area efficiency, where a smaller ATP value indicates better efficiency. To avoid discrepancies in the comparison due to DSP, we employ the conversion method proposed in [25] (Area = LUT + DSP*158) to calculate the equivalent area. As shown in Table 2, our design achieves higher frequency and better area efficiency than the prior work. Also, our design achieves a medium level of power consumption.

Specifically, when modifying the d0[14:0] and S0[14:0] generated by the hybrid compression array, Yaman et al. first performed a 3-to-2 compression operation on three expressions: (d0 + S0−2q), (d0 + S0-q), and (d0 + S0 + q). Subsequently, carry-reserved values and partial sums from four groups (including d0 and S0) were added in parallel. Due to redundant calculations, it consumes three more one-level compression arrays than this paper. Furthermore, the bit tree deduced by Yaman et al. is higher than ours, necessitating four levels of compression arrays instead of three. Consequently, our design reduces LUT usage by 41.67%, increases the frequency by 6.48%, and decreases the ATP by 45.22%. Similarly, Guo et al.’s [21] bit tree involves more levels and points, and has a larger range, so it consumes more resources. Also, the multiplexer delay associated with a larger range is also higher. Our design demonstrates 67.38% fewer LUTs requirements, 28.6% higher maximum frequency, and 74.64% ATP reduction compared with [21].

Ma et al.’s [19] work is a naive Barrett’s implementation where two multiplications consume two DSPs. Chen et al. [18] used shift addition to avoid multiplication in Barrett reduction algorithm, but the multiple shift operations have dependency chains, leading to longer delays. Xing et al. further optimized this approach by integrating shift operations and finalizing the result through an MUX, thereby reducing resource consumption and increasing frequency. Li et al. [21] leveraged the property of the modulus 3329 being a Proth prime to replace a large number modulus with a smaller one, thus simplifying the Barrett algorithm complexity. They provided four parameter sets, yet the first and fourth sets are too aggressive for correct computation. Therefore, we only implement their third parameter set with a moderate area overhead. Although the design in Li et al. requires 15.19% fewer LUTs than our design, our design achieves a 37.84% increase in frequency and a 16.43% reduction in ATP than [21] through enhanced parallelism.

4.3. System-Level Evaluation and Comparison

To quantify the area improvements achieved by our design, we adopted the polynomial multiplication processing element (PE) unit from Yaman et al.’s [23] work as the evaluation framework. We replaced the modular reduction unit in Yaman et al.’s open-source code with the proposed design and implemented it on Xilinx Artix-7 FPGA (xc7a200tffg1156-3). The synthesis results from Vivado 2024.1 are presented in Figure 7.

As shown in Figure 7a, our design exhibits a moderate LUT resource consumption. Regarding DSP resource utilization, Figure 7b indicates that except for the naive Barrett reduction algorithm employed by Ma et al. [18], which requires two additional DSP blocks, the remaining work only consumes one DSP. Furthermore, Figure 7c demonstrates that our design achieves a 9.56% improvement in the polynomial multiplication unit’s operating frequency compared with Yaman et al.’s implementation. Additionally, as illustrated in Figure 7d, our design achieves a 16.04% improvement in ATP compared with Yaman et al.’s design, demonstrating enhanced area efficiency.

5. Conclusions

In this work, we propose a hardware architecture for bitwise modular reduction based on the Dadda Tree Hybrid Compression Array. We rederive the process of bitwise modular reduction, and obtain a bit tree with a minimized height by simplifying and merging redundant bits. Based on this optimized bit tree structure, we designed the hardware architecture of our algorithm using the Dadda tree principle. Finally, we evaluated our design under a unified benchmark alongside similar designs. Compared with related work of the same type, the proposed modular reduction unit achieves improvements of 6.48% in frequency and 16.43% in the ATP. Furthermore, our proposed design achieves significant improvements in both the maximum operating frequency and the area efficiency for polynomial multiplication.