Performance Analysis of FSO-UWOC Mixed Dual-Hop Relay System with Decode-and-Forward Protocol
Abstract
1. Introduction
- A new composite fading channel model was proposed to comprehensively represent the fading statistics of FSO and/or UWOC transmission links. For the FSO link, in the light of the findings in [15], the channel is modeled as a hybrid-fading channel that integrates the GG atmospheric turbulence, zero-boresight pointing errors, and Beer–Lambert single-exponential path loss. For the UWOC link, leveraging the laboratory measurement data from [16,17], along with the MC simulations and data-fitting results from [19], the channel is modeled as a hybrid-fading one, incorporating the GGD oceanic turbulence, zero-boresight pointing errors, and Elamassie underwater path loss.
- Based on the proposed composite fading channel model described above, the PDF and cumulative distribution function (CDF) closed-form expressions of the instantaneous SNR for both the FSO and UWOC links are derived using the advanced transcendental Meijer-G functions, in the case of HD and IM/DD receiver detection methods, respectively.
- Employing the derived expressions for the PDF and CDF of the instantaneous SNR of the hybrid-fading FSO and UWOC links, the theoretical closed-form expressions for the average OP, average BER, and average channel capacity of the mixed dual-hop FSO-UWOC system are obtained by using the Meijer-G functions and the bivariate Fox-H functions. Moreover, asymptotic analyses for the average OP and average BER under high-SNR conditions are also presented.
- MC numerical simulations are conducted to verify the accuracy of the theoretical expressions for the average OP, average BER, and average channel capacity of the mixed dual-hop FSO-UWOC system, along with their corresponding asymptotic expressions. Furthermore, the influence of different core system parameters on the whole system performance is also explored.
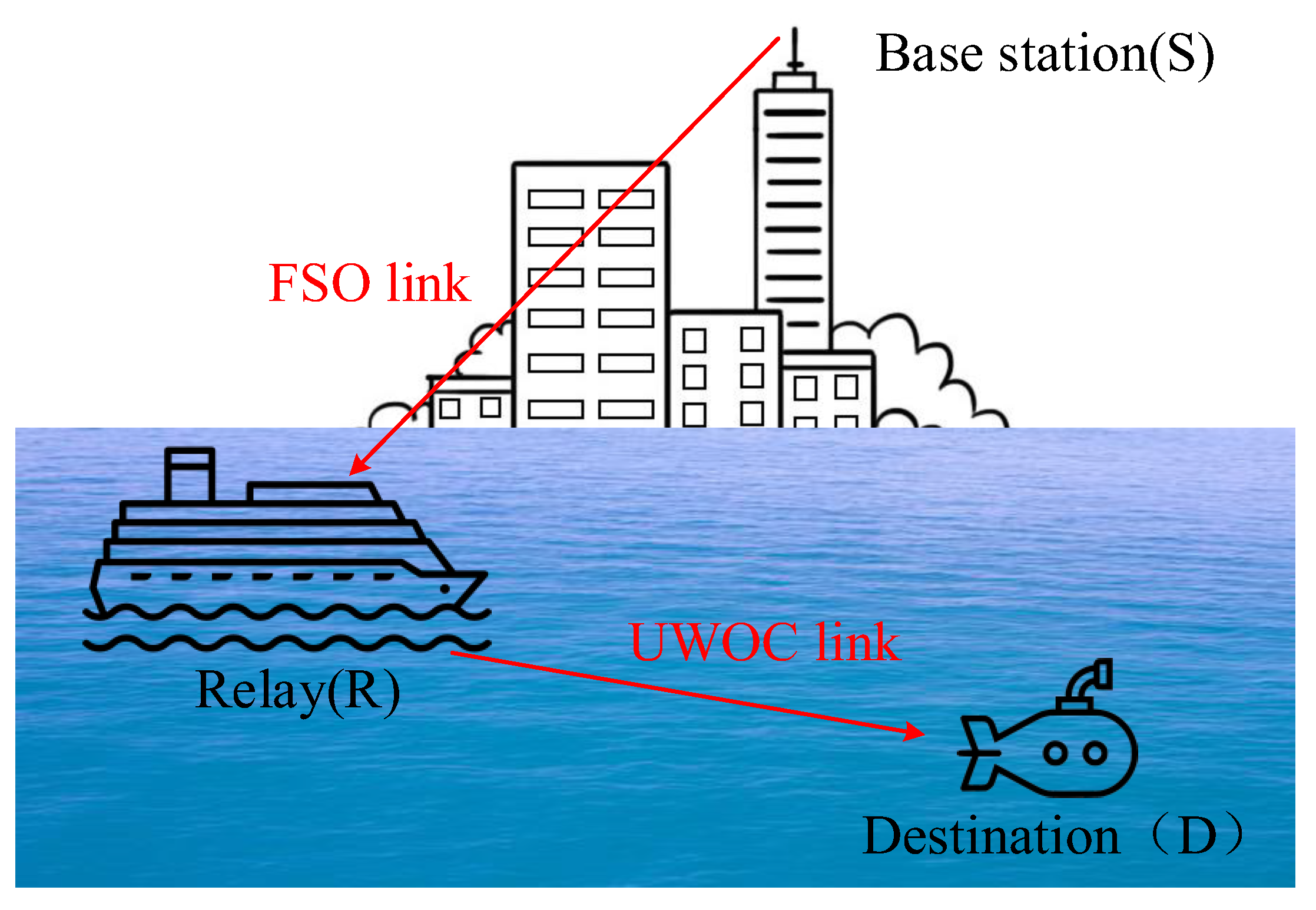
2. System and Channel Modeling
2.1. Derivation of the PDF and CDF of Instantaneous SNR PDF and CDF for S-R Ink
- (1)
- The HD [31], i.e., coherent detection, combines a weak optical signal with a strong local oscillator signal at a photodetector. Based on the formulae in [31], in the case of the HD scheme, the instantaneous received SNR for the S-R link is denoted as , the average electronic received SNR is . Let , then , and the PDF of the instantaneous SNR is given by:
- (2)
- In the case of the IM/DD scheme [31], the instantaneous received SNR for the S-R link is denoted as , and the average electronic received SNR is . Let , then , and the PDF of the instantaneous SNR is given by:
2.2. Derivation of the PDF and CDF of Instantaneous SNR PDF and CDF for the R-D Link
- (1)
- Similarly, in HD, the instantaneous received SNR of the UWOC link is , and the average electronic SNR is . Clearly, , so the PDF of the instantaneous received SNR is given by:
- (2)
- In IM/DD, the instantaneous received SNR of the UWOC link is , and the average electronic SNR is . Therefore, , and based on this, the PDF of the instantaneous received SNR can be derived as:
3. Statistical Characteristics for End-to-End Instantaneous SNR
3.1. Derivation of the CDF for End-to-End Instantaneous SNR
3.2. Derivation of the PDF for End-to-End Instantaneous SNR
4. System Performance Analysis
4.1. Outage Probability and Its Asymptotic Behavior
4.2. Average Bit Error Rate and Its Asymptotic Value
4.3. Average Channel Capacity
5. Simulation Results and Analysis
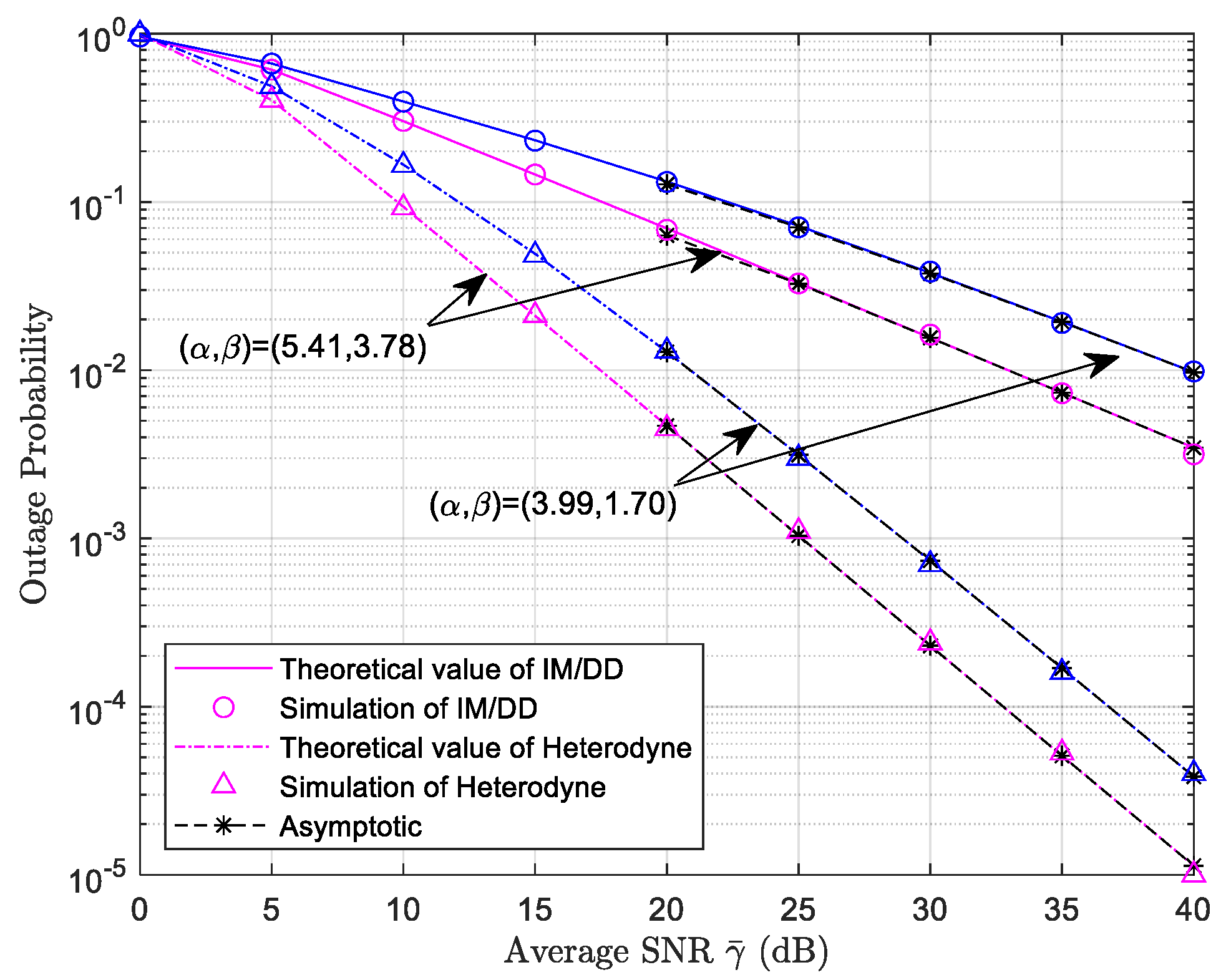
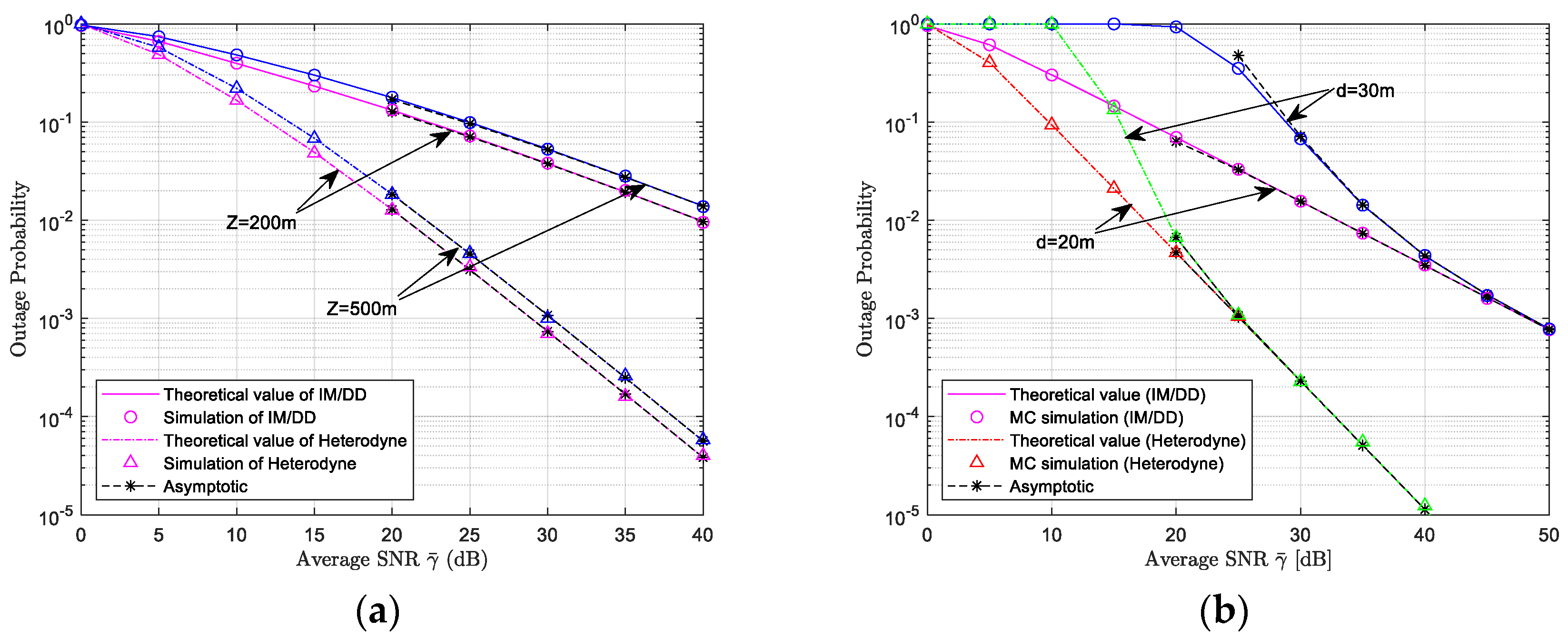
5.1. Outage Probability Simulation Results and Analysis
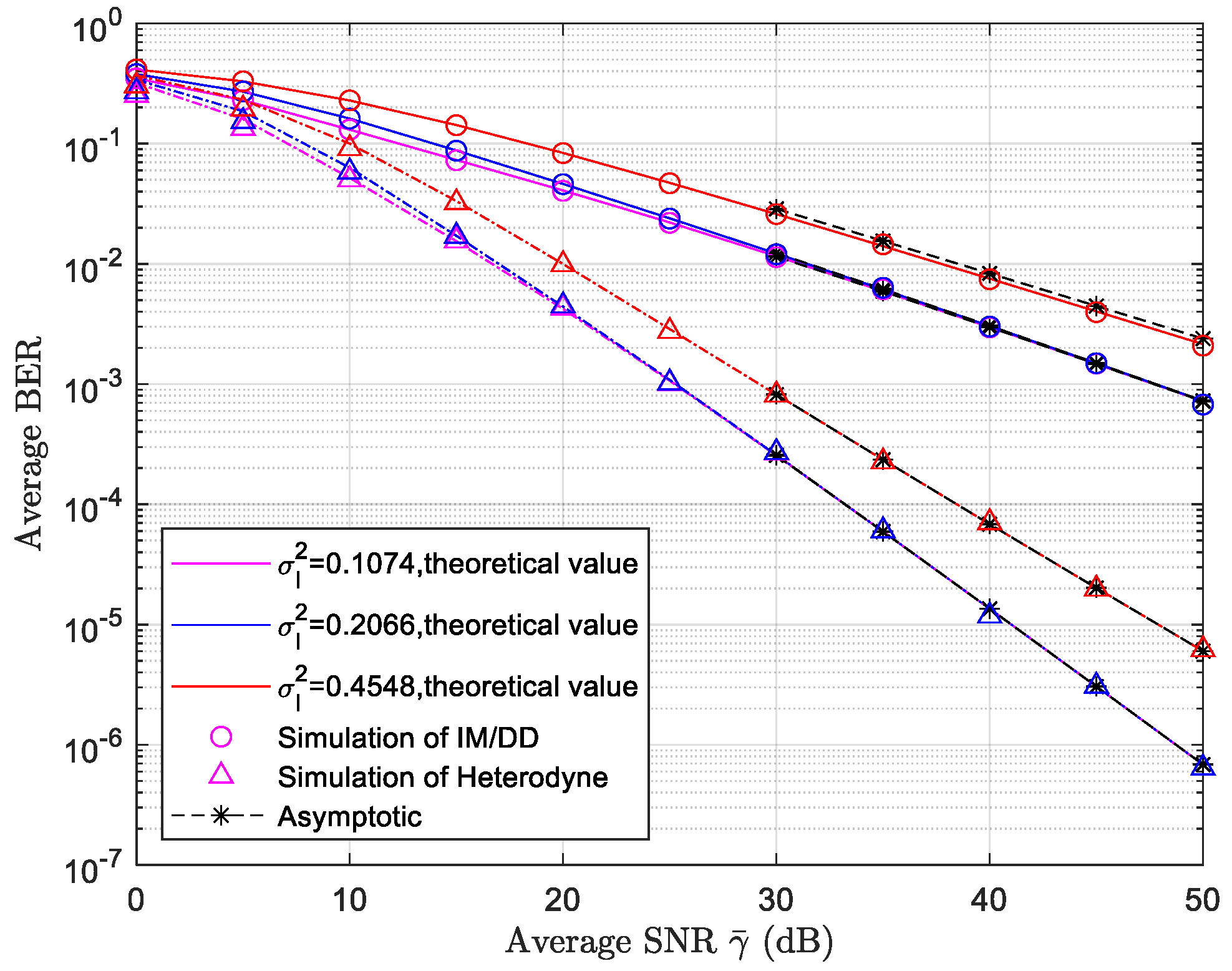
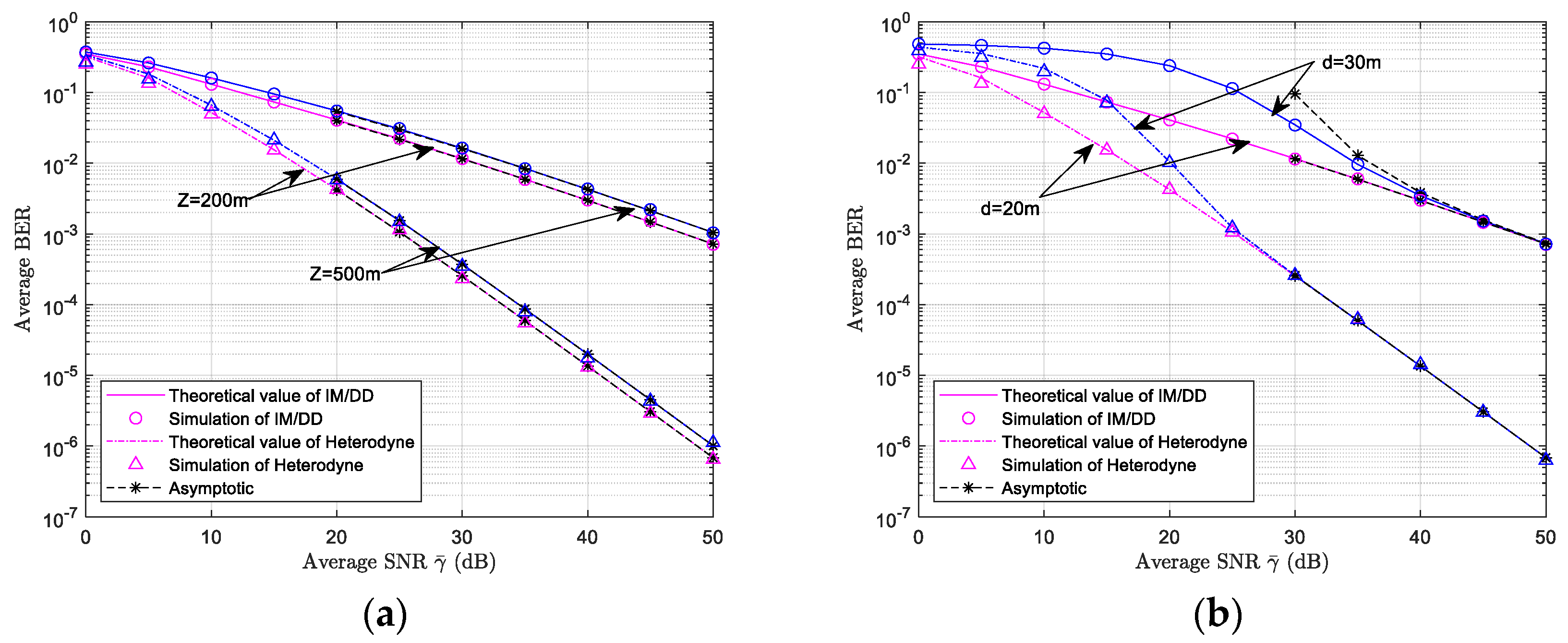
5.2. Average BER Simulation Results and Analysis
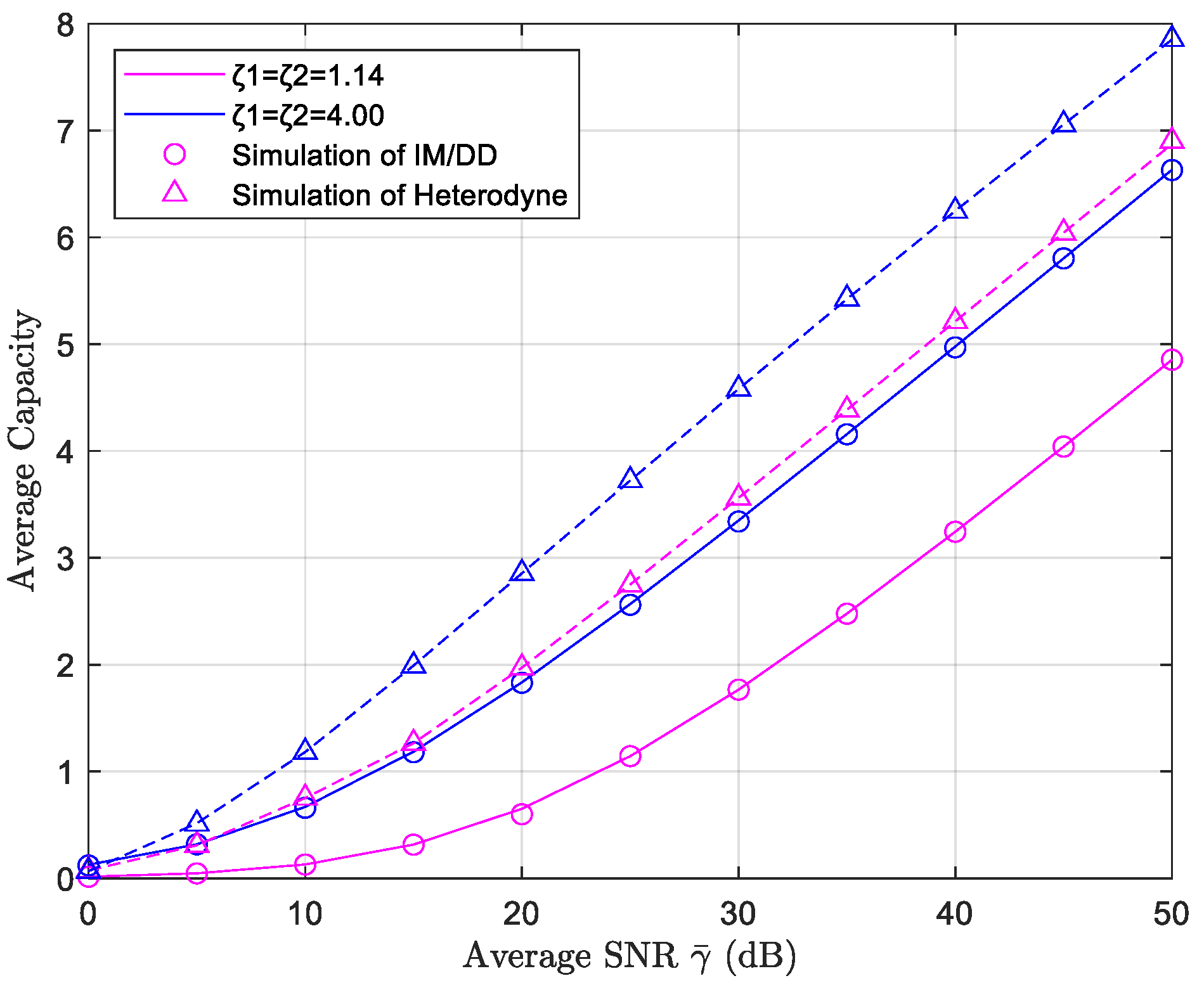
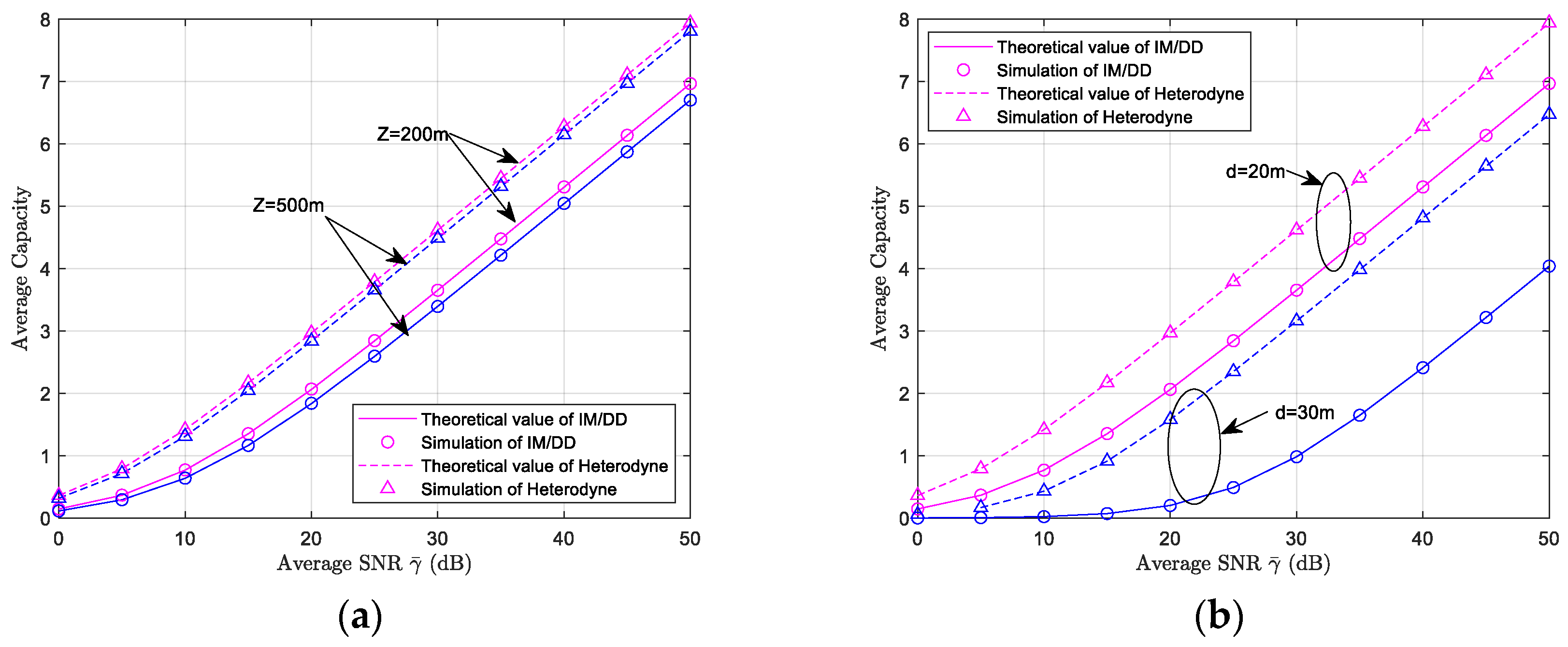
5.3. Average Channel Capacity Simulation Results and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- You, X.H.; Wang, C.-X.; Huang, J.; Gao, X.; Zhang, Z.; Wang, M.; Huang, Y.; Zhang, C.; Jiang, Y.; Wang, J.; et al. Towards 6G wireless communication networks: Vision, enabling technologies, and new paradigm shifts. Sci. China Inf. Sci. 2021, 64, 110301. [Google Scholar] [CrossRef]
- Ali, M.F.; Jayakody, D.N.; Li, Y. Recent trends in underwater visible light communication (UVLC) systems. IEEE Access 2022, 10, 22169–22225. [Google Scholar] [CrossRef]
- Mondal, A.; Hossain, A. Channel characterization and performance analysis of unmanned aerial Vehicle-Operated communication system with multihop radio Frequency–Free-Space optical link in dynamic environment. Int. J. Commun. Syst. 2020, 33, e4568. [Google Scholar] [CrossRef]
- Li, S.; Yang, Y.; Yang, L.; Bian, Y. On the Study of Multiuser Mixed Dual-Hop RF/THz Systems. IEEE Trans. Veh. Technol. 2023, 72, 9175–9188. [Google Scholar] [CrossRef]
- Wang, S.; Yang, L.; Li, X.; Guo, K.; Liu, H.; Song, H.; Jhaveri, R.H.; Quo, K. Performance Analysis of Satellite-Vehicle Networks with a Non-Terrestrial Vehicle. IEEE Trans. Intell. Veh. 2024, 9, 1691–1700. [Google Scholar] [CrossRef]
- Li, S.; Yang, L.; Costa, D.B.; Di Renzo, M.; Alouini, M.-S. On the Performance of RIS-assisted dual-hop mixed RF-UWOC systems. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 340–353. [Google Scholar] [CrossRef]
- Yadav, S.; Vats, A.; Aggarwal, M.; Ahuja, S. Performance Analysis and Altitude Optimization of UAV-Enabled Dual-Hop Mixed RF-UWOC System. IEEE Trans. Veh. Technol. 2021, 70, 12651–12660. [Google Scholar] [CrossRef]
- Samir, A.; Elsayed, M.; El-Banna, A.A.A.; Ansari, I.S.; Rabie, K.; ElHalawany, B.M. Performance analysis of dual-hop hybrid RF-UOWC NOMA systems. Sensors 2022, 22, 4521. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Wang, P.; Cao, T.; Li, G.; Li, S.; Yang, P. Performance analysis of AUV-Carried RISs-Aided multihop UWOC convergent with RF MRC systems over WGG oceanic turbulence. Veh. Commun. 2024, 45, 100722. [Google Scholar] [CrossRef]
- Agarwal, A.; Singh, K. Energy-Efficient UOWC-RF systems with SLIPT. Trans. Emerg. Telecommun. Technol. 2024, 35, e4889. [Google Scholar] [CrossRef]
- Yang, L.; Zhu, Q.; Li, S.; Ansari, I.S.; Yu, S. On the performance of mixed FSO-UWOC dual-hop transmission systems. IEEE Wirel. Commun. Lett. 2021, 10, 2041–2045. [Google Scholar] [CrossRef]
- Naik, R.P.; Chung, W.Y. Performance evaluation of re-Configurable intelligent Surface-Assisted underwater and Free-Space wireless optical communication in the Skip-Zones. ICT Express 2024, 10, 320–329. [Google Scholar]
- Sharma, D.; Agrawal, R.; Joshi, D.; Rani, R.; Shariff, A.S.M.; Singh, H. Performance analysis of mixed FSO-UWOC dual-hop transmission system. In Proceedings of the 2024 IEEE International Conference on Computing, Power and Communication Technologies (IC2PCT), Greater Noida, India, 9–10 February 2024; pp. 658–662. [Google Scholar]
- Kumar, L.B.; Ramavath, P.N.; Krishnan, P. Performance analysis of Multi-Hop FSO convergent with UWOC system for security and tracking in navy applications. Opt. Quant. Electron. 2022, 54, 327. [Google Scholar] [CrossRef]
- Farid, A.A.; Hranilovic, S. Outage capacity optimization for Free-Space optical links with pointing errors. J. Light. Technol. 2007, 25, 1702–1710. [Google Scholar] [CrossRef]
- Oubei, H.M.; Zedini, E.; Elafandy, R.T.; Kammoun, A.; Abdallah, M.; Ng, T.K.; Hamdi, M.; Alouini, M.-S.; Ooi, B.S. Simple statistical channel model for weak Temperature-Induced turbulence in underwater wireless optical communication systems. Opt. Lett. 2017, 42, 2455–2458. [Google Scholar] [CrossRef]
- Jamali, M.V.; Mirani, A.; Parsay, A.; Abolhassani, B.; Nabavi, P.; Chizari, A.; Khorramshahi, P.; Abdollahramezani, S.; Salehi, J.A. Statistical studies of fading in underwater wireless optical channels in the presence of air bubble, temperature, and salinity random variations. IEEE Trans. Commun. 2018, 66, 4706–4723. [Google Scholar] [CrossRef]
- Zedini, E.; Oubei, H.M.; Kammoun, A.; Hamdi, M.; Ooi, B.S.; Alouini, M.-S. Unified statistical channel model for Turbulence-Induced fading in underwater wireless optical communication systems. IEEE Trans. Commun. 2019, 67, 2893–2907. [Google Scholar] [CrossRef]
- Elamassie, M.; Miramirkhani, F.; Uysal, M. Performance characterization of underwater visible light communication. IEEE Trans. Commun. 2019, 67, 543–552. [Google Scholar] [CrossRef]
- Deka, R.; Anees, S. On the performance of DF based triple hop RF–FSO–UWOC cooperative system. Opt. Quantum Electron. 2024, 56, 1155. [Google Scholar] [CrossRef]
- Le-Tran, M.; Kim, S. Performance analysis of Multi-Hop underwater wireless optical communication systems over Exponential-Generalized gamma turbulence channels. IEEE Trans. Veh. Technol. 2022, 71, 6214–6227. [Google Scholar] [CrossRef]
- Jamali, M.V.; Nabavi, P.; Saleihi, J.A. MIMO underwater visible light communications: Comprehensive channel study, performance analysis, and Multiple-Symbol detection. IEEE Trans. Veh. Technol. 2018, 67, 8223–8237. [Google Scholar] [CrossRef]
- Ye, N.; Miao, S.; Pan, J.; Xiang, Y.; Mumtaz, S. Dancing with Chains: Spaceborne Distributed Multi-User Detection Under Inter-Satellite Link Constraints. IEEE J. Sel. Top. Signal Process. 2025, 19, 430–446. [Google Scholar] [CrossRef]
- Zhuo, X.; Liu, M.; Wei, Y.; Yu, G.; Qu, F.; Sun, R. AUV-Aided Energy-Efficient Data Collection in Underwater Acoustic Sensor Networks. IEEE Internet Things J. 2020, 7, 10010–10022. [Google Scholar] [CrossRef]
- Jayakody, D.N.K.; Flanagan, M.F. A Soft Decode-Compress-Forward Relaying Scheme for Cooperative Wireless Networks. In Proceedings of the 2013 IEEE 24th International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC Workshops), London, UK, 8–11 September 2013; pp. 205–209. [Google Scholar]
- Wang, J.Y.; Ma, Y.; Lu, R.R.; Wang, J.-B.; Lin, M.; Cheng, J. Hovering UAV-Based FSO communications: Channel modelling, performance analysis, and parameter optimization. IEEE J. Sel. Areas Commun. 2021, 39, 2946–2959. [Google Scholar] [CrossRef]
- Lin, Z.; Xu, G.; Zhang, Q.; Song, Z. Average symbol error probability and channel capacity of the underwater wireless optical communication systems over oceanic turbulence with pointing error impairments. Opt. Express 2022, 30, 15327–15343. [Google Scholar] [CrossRef] [PubMed]
- Proakis, J.G. Digital Communications, 5th ed.; McGraw-Hill Companies: New York, NY, USA, 2007. [Google Scholar]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series: Volume 3: More Special Functions; Revista De Ciencias Farmaceuticas: Moscow, Russia, 1989. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products, 7th ed.; Academic Press: Boston, MA, USA, 2007. [Google Scholar]
- Ansari, I.S.; Alouini, M.-S.; Yilmaz, F. A Unified Performance Analysis of Free-Space Optical Links Over Gamma-Gamma Turbulence Channels with Pointing Errors. 2013. Available online: http://hdl.handle.net/10754/305353 (accessed on 20 May 2024).
- Li, S.; Yang, L.; Costa, D.B.D.; Zhang, J.; Alouini, M.-S. Performance analysis of mixed RF-UWOC Dual-Hop transmission systems. IEEE Trans. Veh. Technol. 2020, 69, 14043–14048. [Google Scholar] [CrossRef]
- Simon, M.K.; Alouini, M.S. Digital Communications Over Fading Channels: A Unified Approach to Performance Analysis; Wiley-IEEE Press: New York, NY, USA, 2005. [Google Scholar]
- Wolfram. The Wolfram Functions Site. Available online: https://functions.wolfram.com (accessed on 10 April 2025).
- Ashrafzadeh, B.; Nasab, E.S.; Kamandar, M.; Uysal, M. A framework on the performance analysis of dual-hop mixed fso-rf cooperative systems. IEEE Trans. Commun. 2019, 67, 4939–4954. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover Publications: Garden City, NK, USA, 1966. [Google Scholar]
- Zedini, E.; Soury, H.; Alouini, M.S. Dual-Hop FSO transmission systems over Gamma–Gamma turbulence with pointing errors. IEEE Trans. Wirel. Commun. 2017, 16, 784–796. [Google Scholar] [CrossRef]
- Lapidoth, A.; Moser, S.M.; Wigger, M.A. On the capacity of Free-Space optical intensity channels. IEEE Trans. Inf. Theory 2009, 55, 4449–4461. [Google Scholar] [CrossRef]
- Farhadi, G.; Beaulieu, N.C. On the ergodic capacity of Multi-Hop wireless relaying systems. IEEE Trans. Wirel. Commun. 2009, 8, 2286–2291. [Google Scholar] [CrossRef]
- Kilbas, A.A. H-Transforms; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Mittal, P.K.; Gupta, K.C. An Integral Involving Generalized Function of Two Variables. Proc. Indian. Acad. Sci.-Sect. A 1972, 75, 117–123. [Google Scholar] [CrossRef]

| Refs | Year | Air Link Statistics | UWOC Link Statistics | Pointing Error | Path Loss | Relay Type | Detec. Method | Derived Metrics | Asym. Analysis |
|---|---|---|---|---|---|---|---|---|---|
| [6] | 2021 | RF/ Generalized K | EGG | No | No | AF/ DF | HD, IM/DD | OP, BER, capacity | Yes |
| [7] | 2021 | RF/Nakagami | EGG | No | RF/ Exponent | DF | IM/DD | OP, BER | No |
| [8] | 2022 | RF/Rayleigh | EGG | No | No | DF | HD, IM/DD | OP, capacity | Yes |
| [9] | 2024 | RF/Fisher-Snedecor F | Weibull-GGD | UWOC | UWOC/ BL | DF | IM/DD | OP, BER | No |
| [10] | 2023 | RF/Rayleigh | Lognormal/GG | No | UWOC/ Elamassie | DF | IM/DD | capacity | No |
| [11] | 2021 | FSO/GG | EGG | Dual link | No | AF | HD, IM/DD | OP, BER, capacity | Yes |
| [12] | 2024 | FSO/GG | Lognormal | FSO | No | DF | HD, IM/DD | OP, BER | Yes |
| [13] | 2024 | FSO/Fisher-Snedecor F | EGG | Dual link | No | AF | IM/DD | OP | No |
| [14] | 2022 | FSO/GG | Lognormal | Dual link | Dual/BL | DF | IM/DD | OP, BER | No |
| Coefficient | Symbol | Value |
|---|---|---|
| Rytov variance | ||
| Atmospheric attenuation coefficients | ||
| Atmospheric transmission distance | ||
| Full-width beam divergence | ||
| correction factor | ||
| Underwater transmission distance | ||
| jitter deviation | ||
| Receiver radius | ||
| Beam width | ||
| Oceanic turbulence scintillation index | ||
| underwater extinction coefficients | ||
| GGD shape parameters |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Li, Y.; Ju, M.; Lv, Y. Performance Analysis of FSO-UWOC Mixed Dual-Hop Relay System with Decode-and-Forward Protocol. Electronics 2025, 14, 2227. https://doi.org/10.3390/electronics14112227
Zhou Y, Li Y, Ju M, Lv Y. Performance Analysis of FSO-UWOC Mixed Dual-Hop Relay System with Decode-and-Forward Protocol. Electronics. 2025; 14(11):2227. https://doi.org/10.3390/electronics14112227
Chicago/Turabian StyleZhou, Yu, Yueheng Li, Meiyan Ju, and Yong Lv. 2025. "Performance Analysis of FSO-UWOC Mixed Dual-Hop Relay System with Decode-and-Forward Protocol" Electronics 14, no. 11: 2227. https://doi.org/10.3390/electronics14112227
APA StyleZhou, Y., Li, Y., Ju, M., & Lv, Y. (2025). Performance Analysis of FSO-UWOC Mixed Dual-Hop Relay System with Decode-and-Forward Protocol. Electronics, 14(11), 2227. https://doi.org/10.3390/electronics14112227







