Research on a Prediction Model Based on a Newton–Raphson-Optimization–XGBoost Algorithm Predicting Environmental Electromagnetic Effects for an Airborne Synthetic Aperture Radar
Abstract
1. Introduction
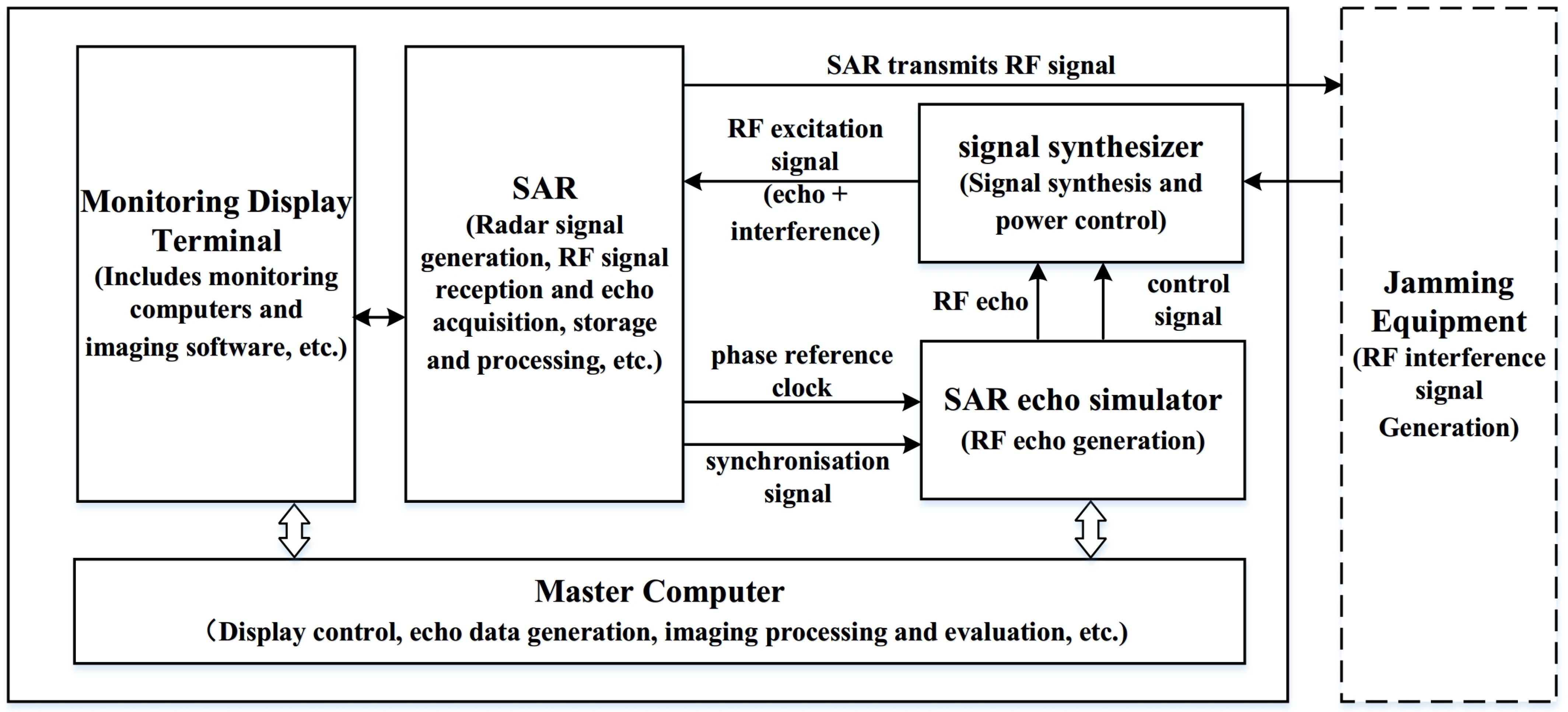
2. Airborne SAR EMI Test System
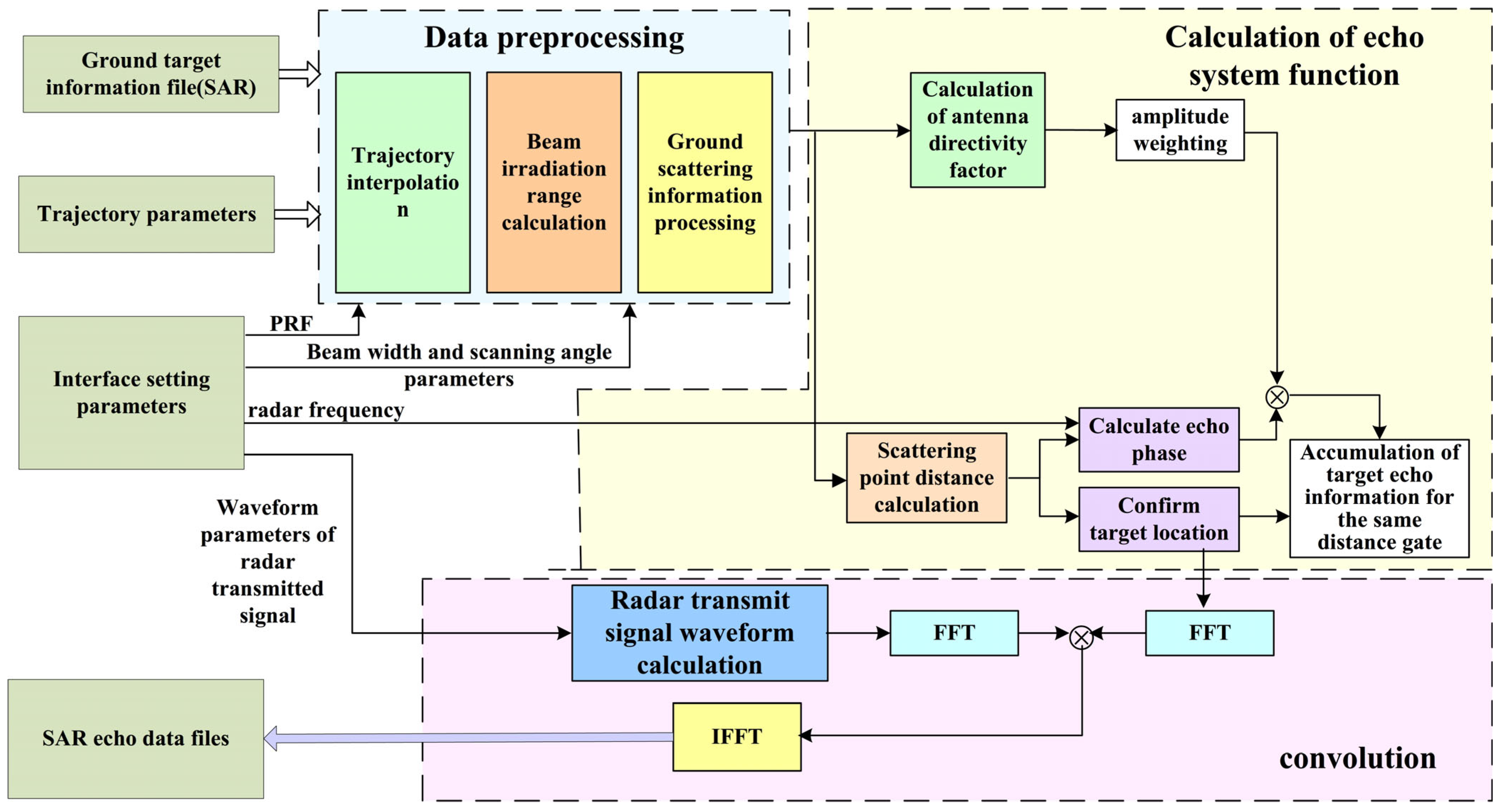
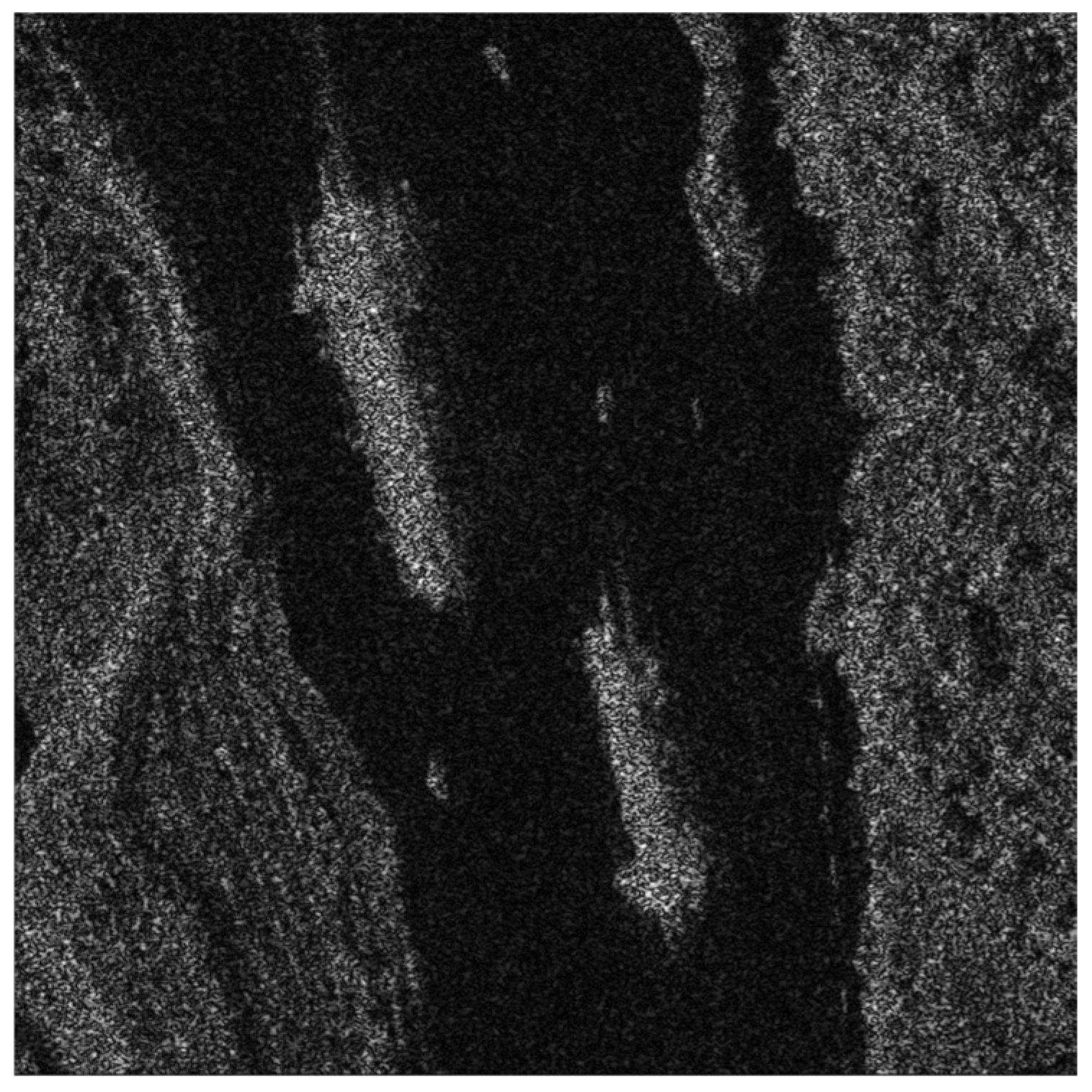
3. Evaluation Method for EMI-Based Effects in SAR Images
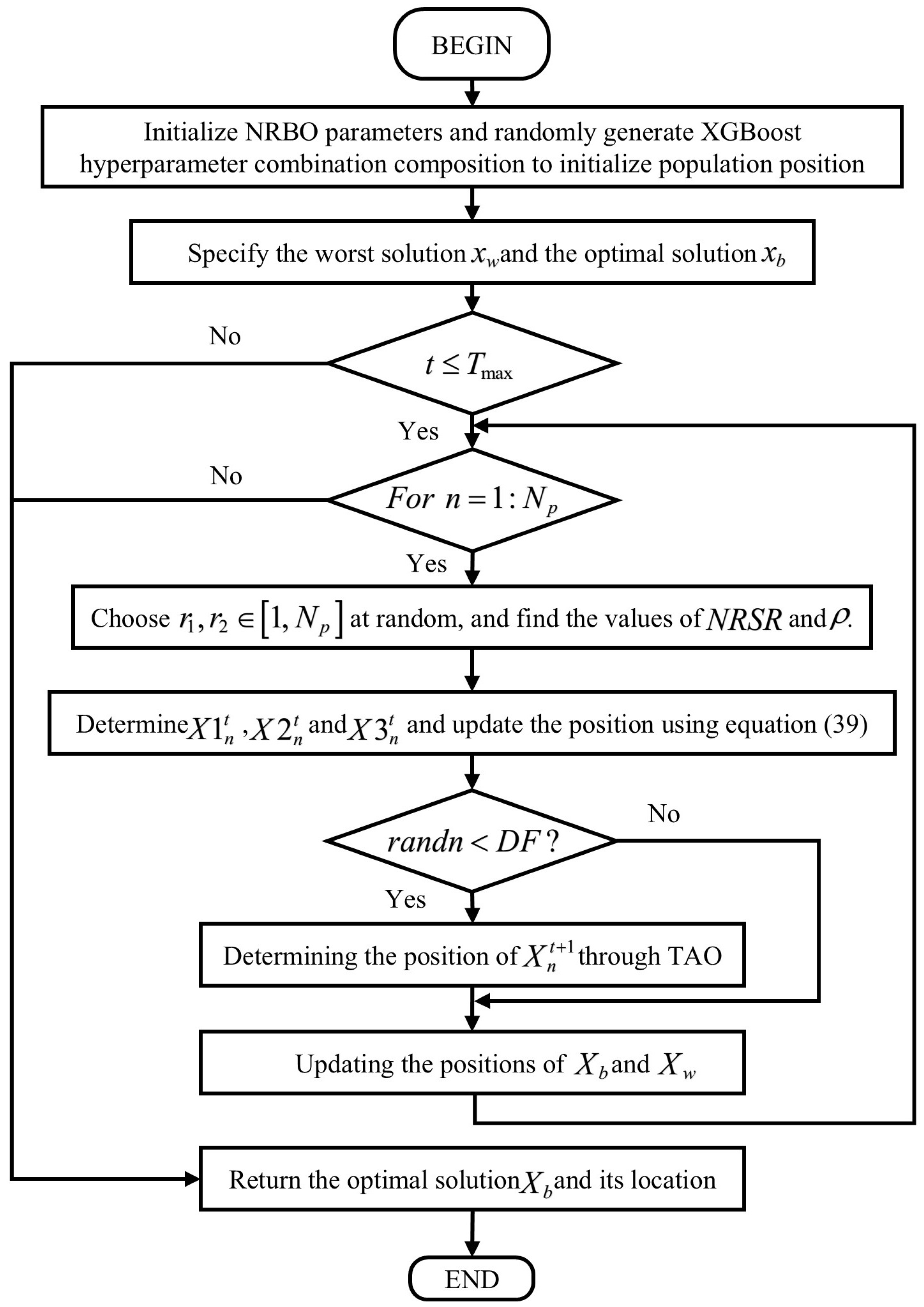
4. NRBO–XGBoost Prediction Algorithm
4.1. Optimization of Hyperparameters by NRBO Algorithm
4.1.1. Population Initialization
4.1.2. Newton–Raphson Search Rule (NRSR)
4.1.3. Trap Avoidance Operation (TAO)
4.1.4. Mathematical Intuition of the NRBO Algorithm
4.2. Indicators for Model Evaluation
5. Model Training Results and Analysis
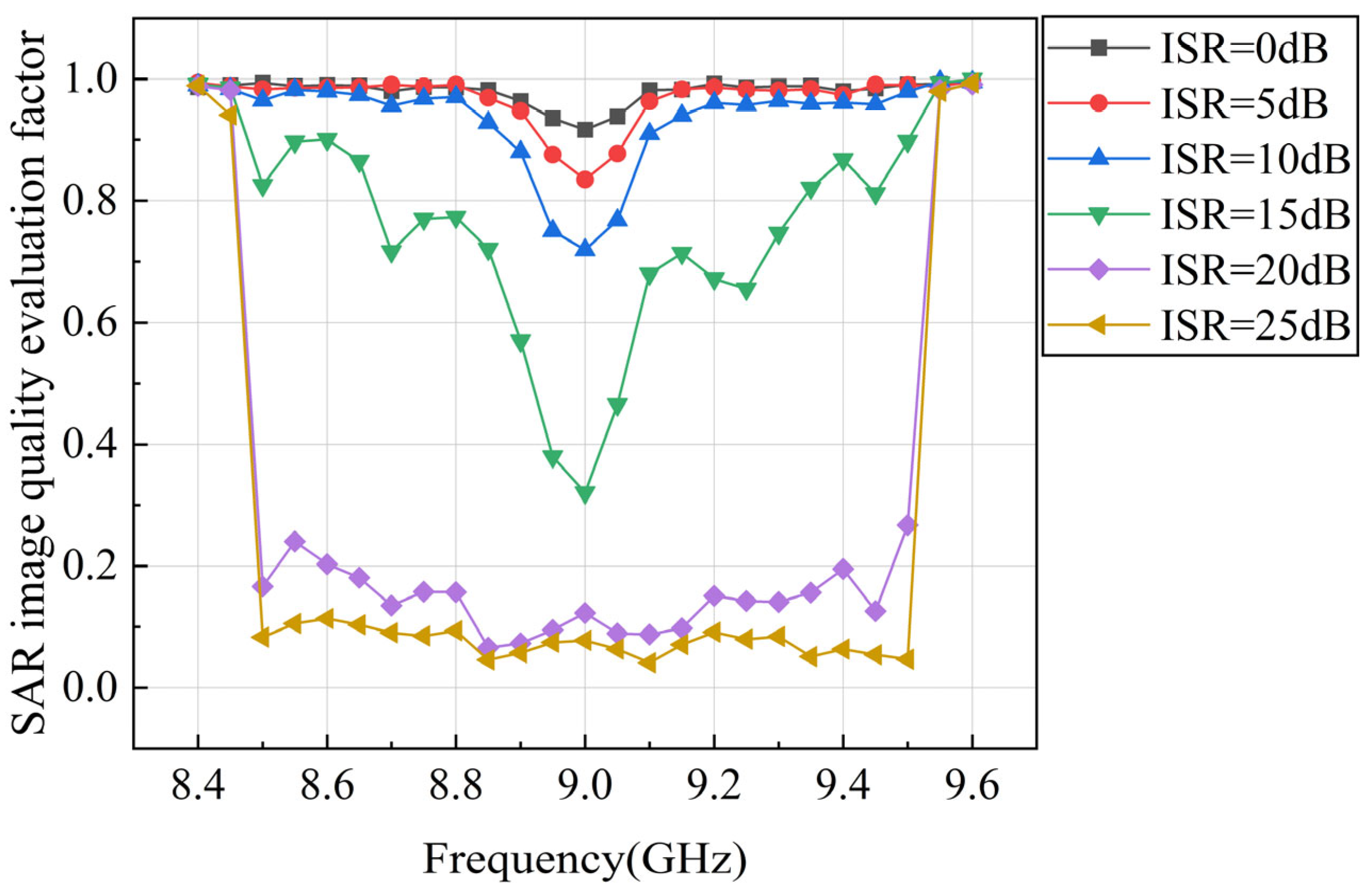
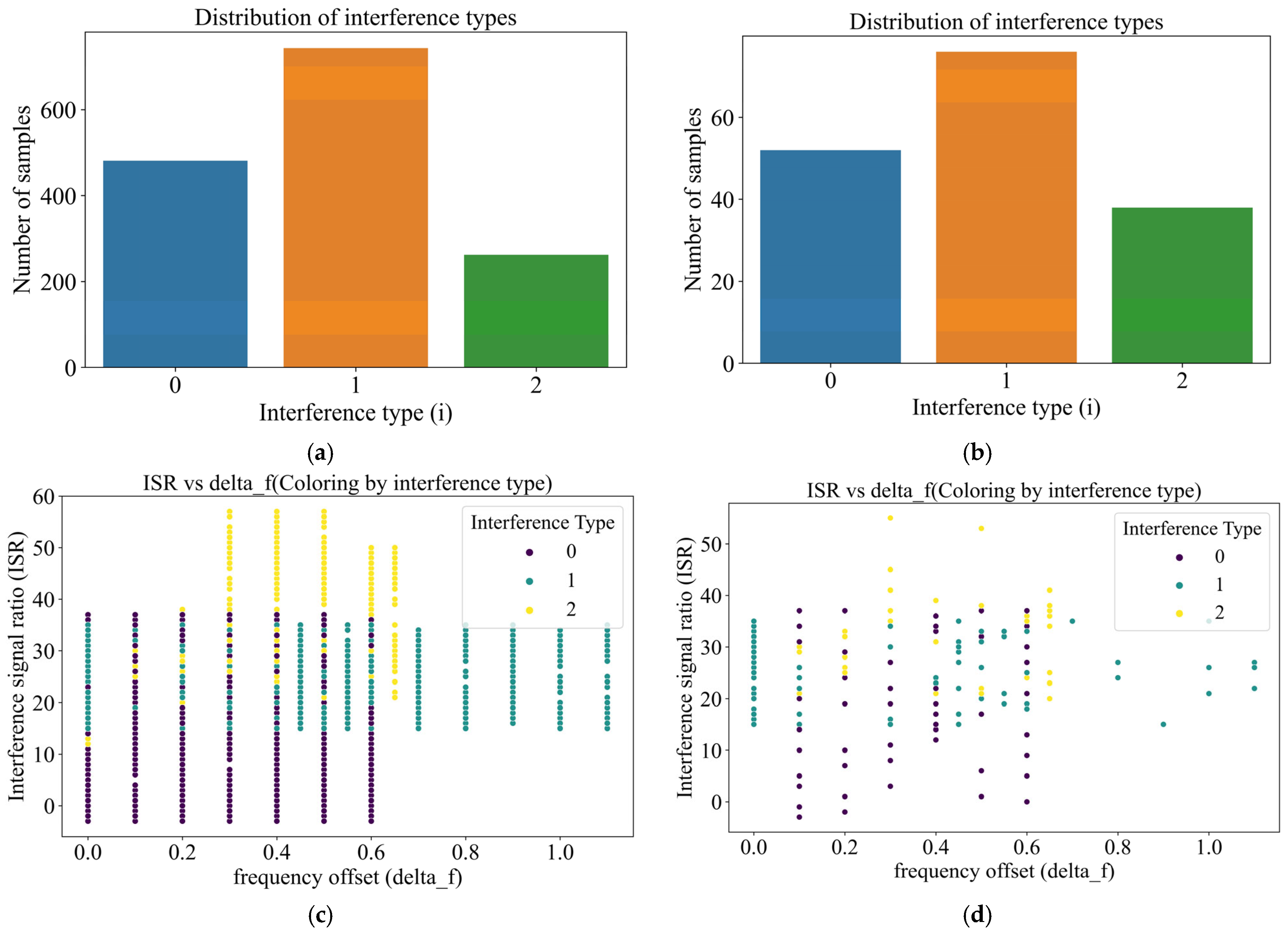
5.1. Feature Selection and Data Sets
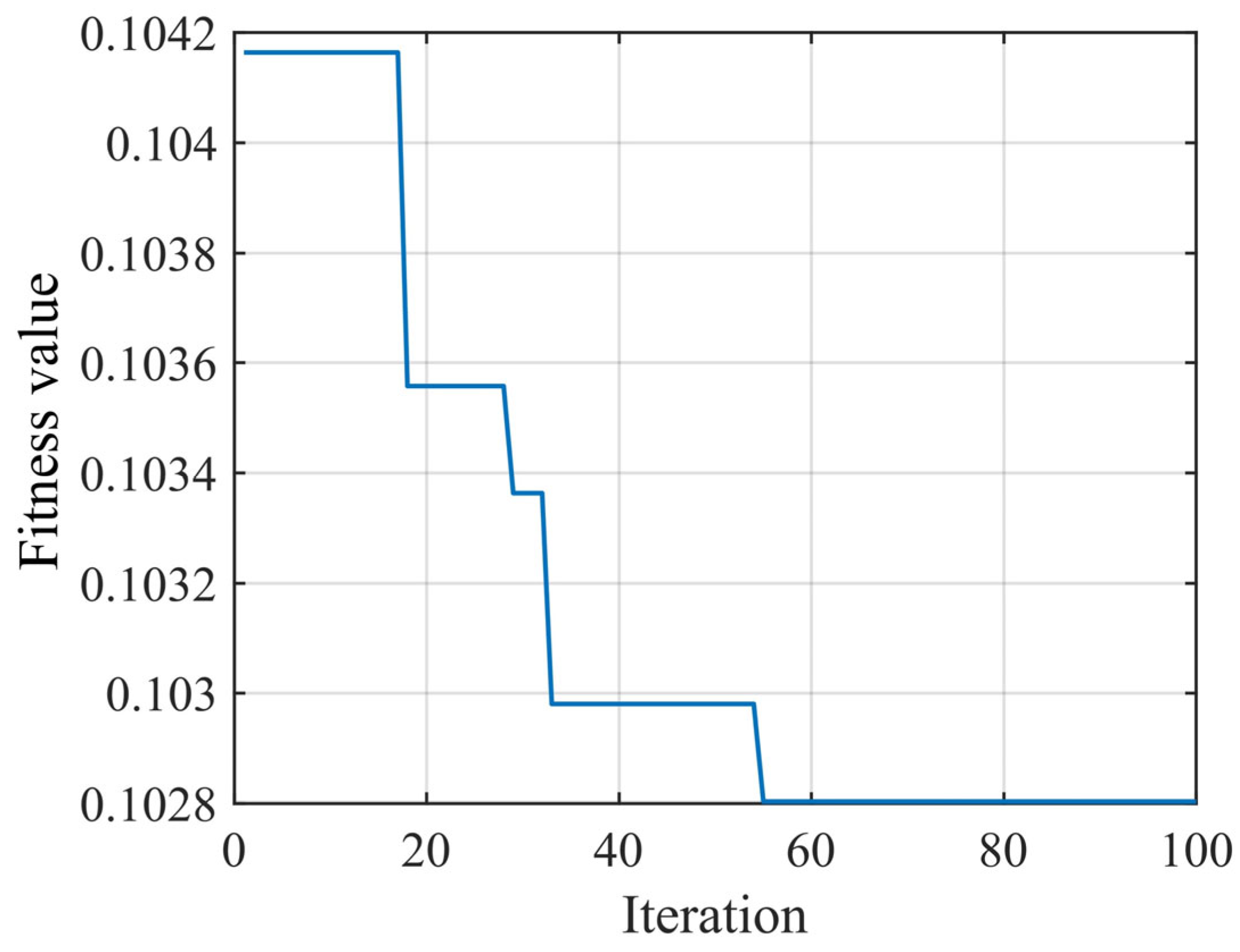
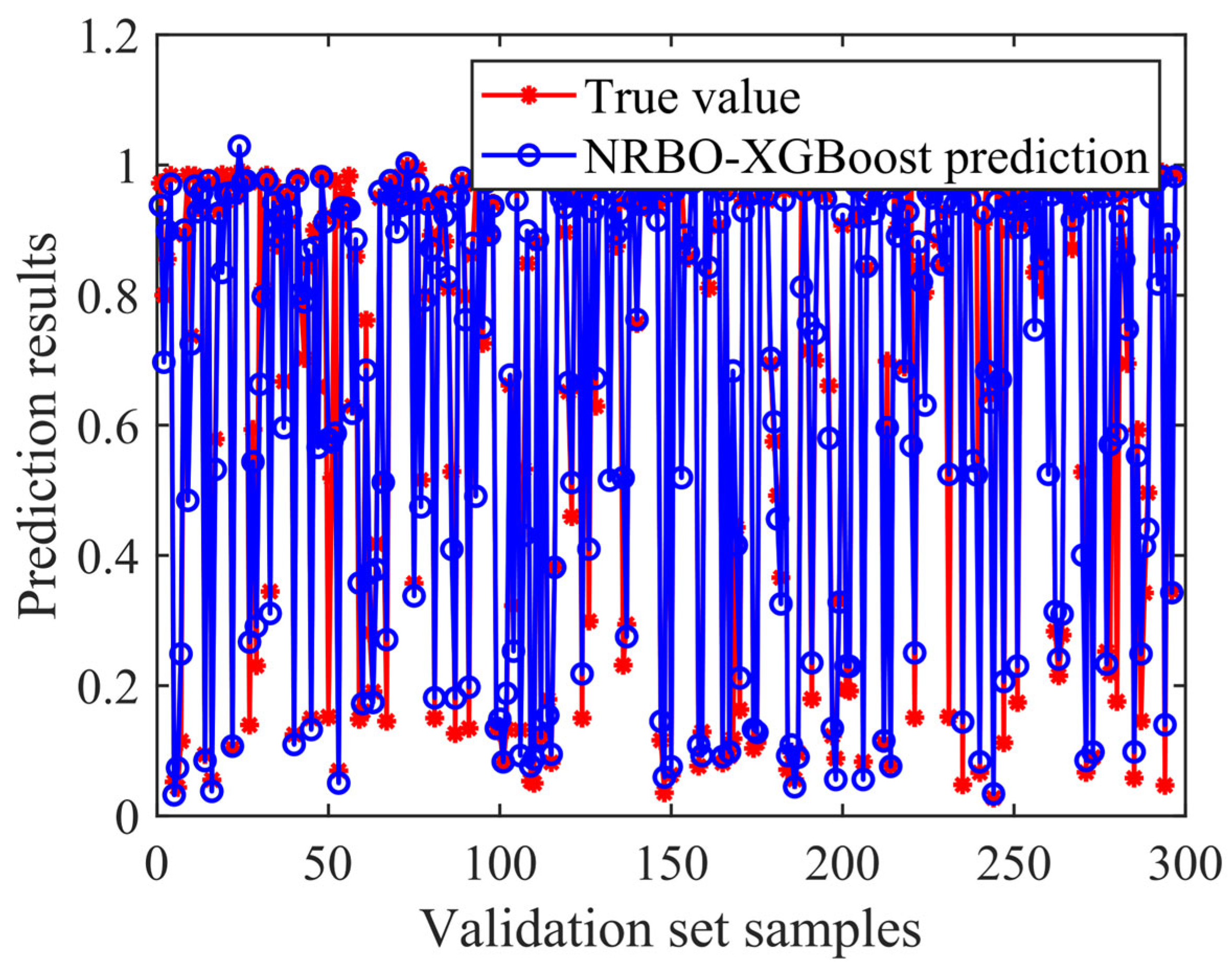
5.2. Model Training Results
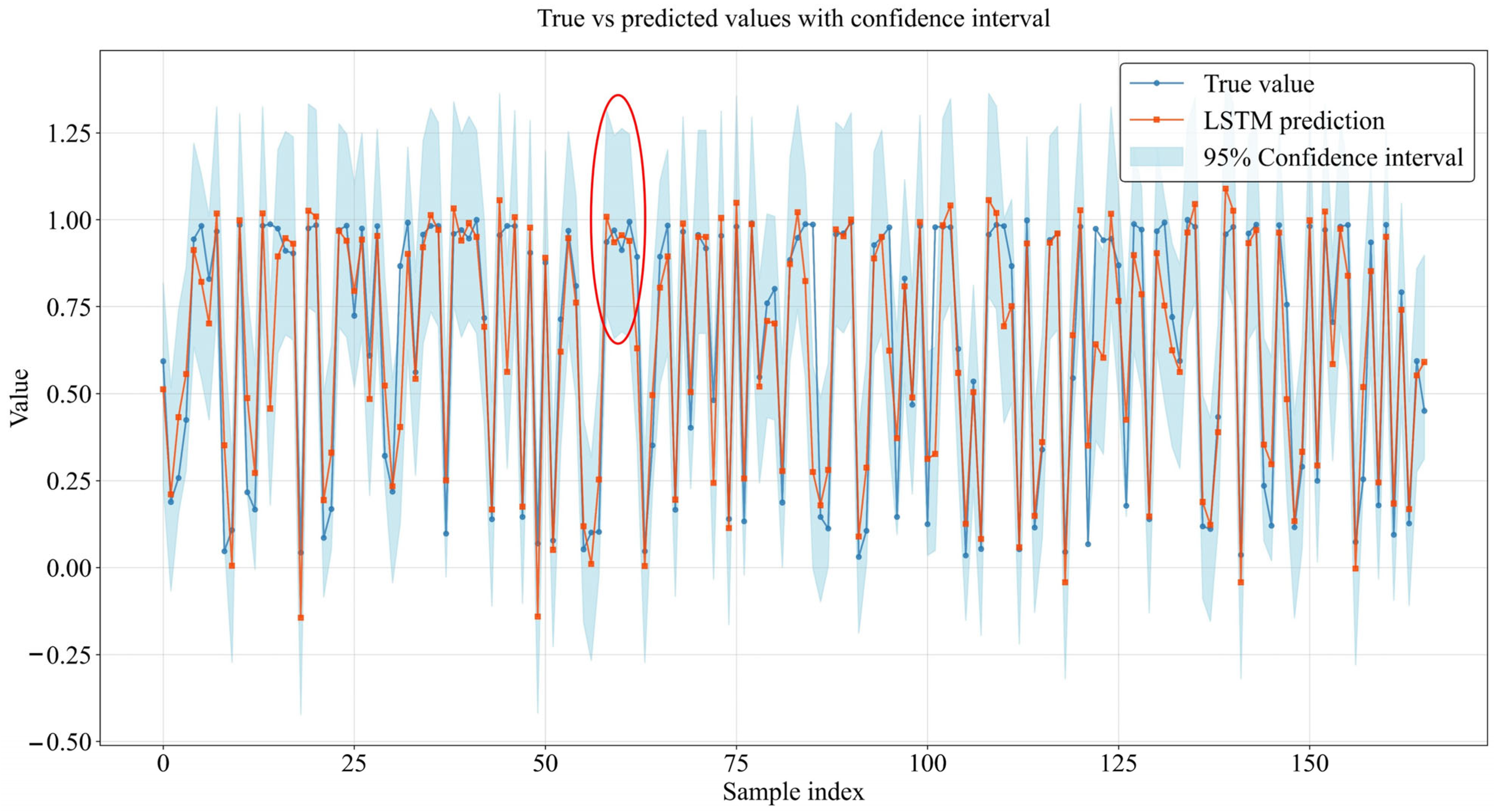
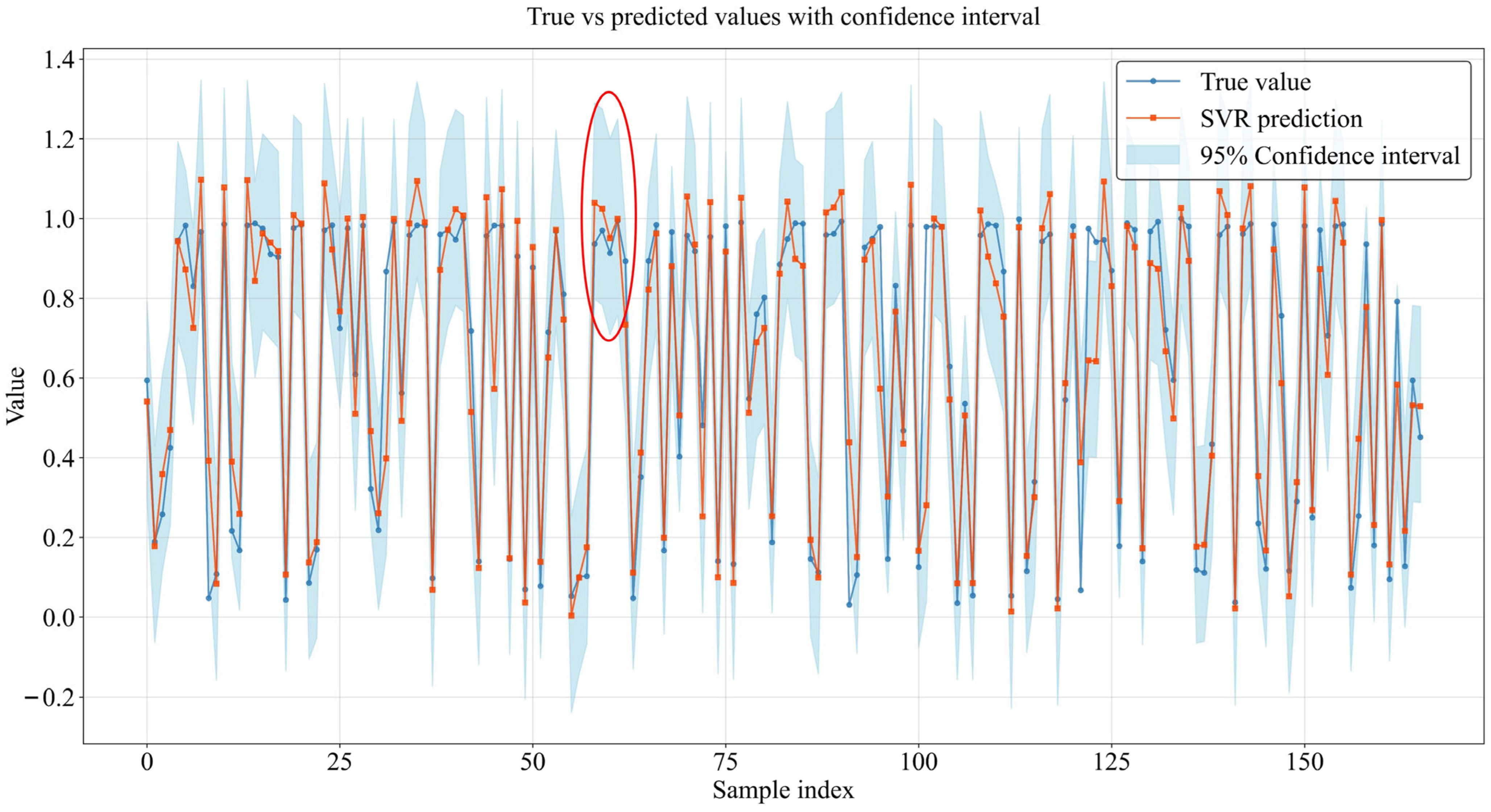
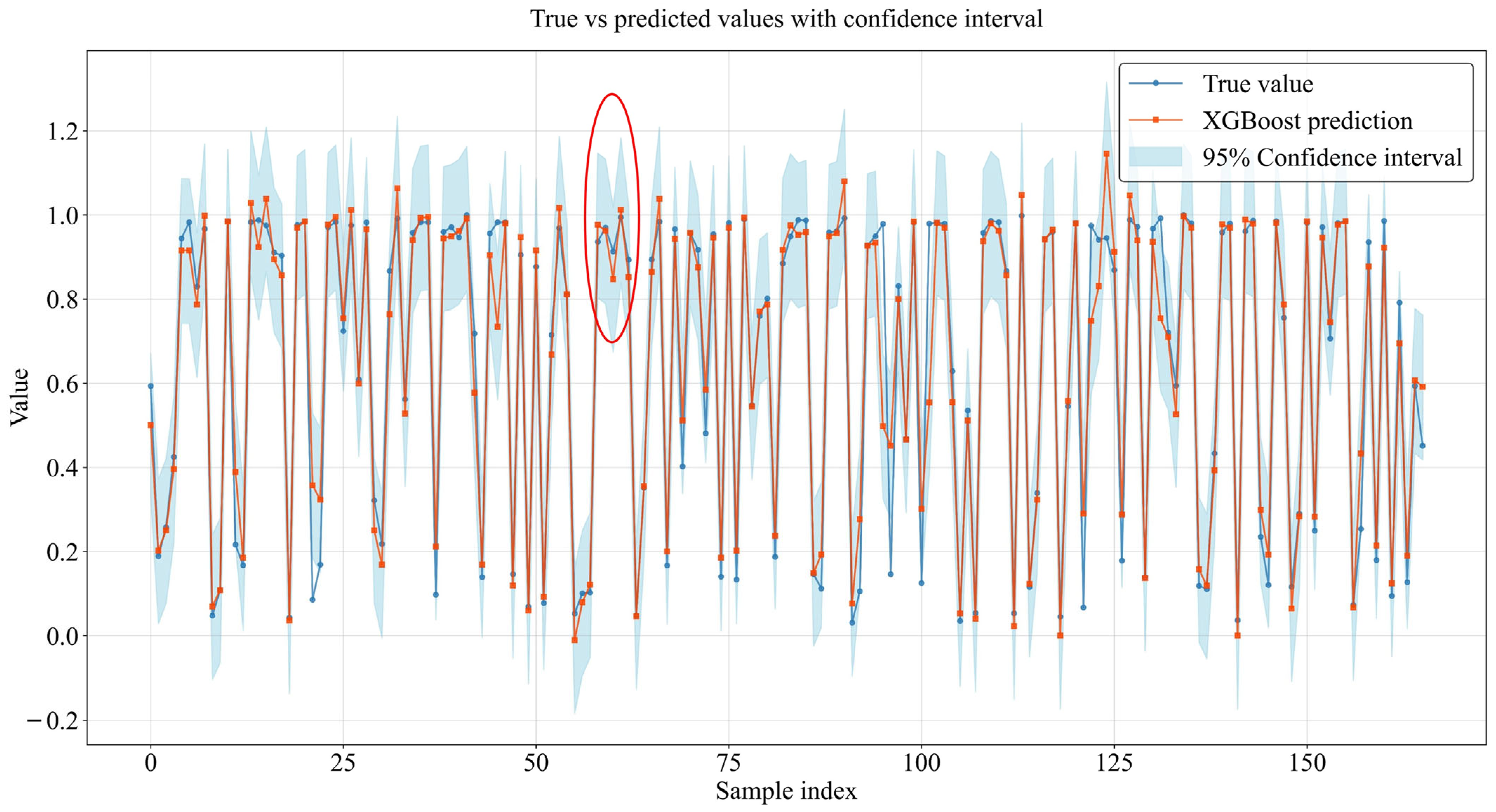
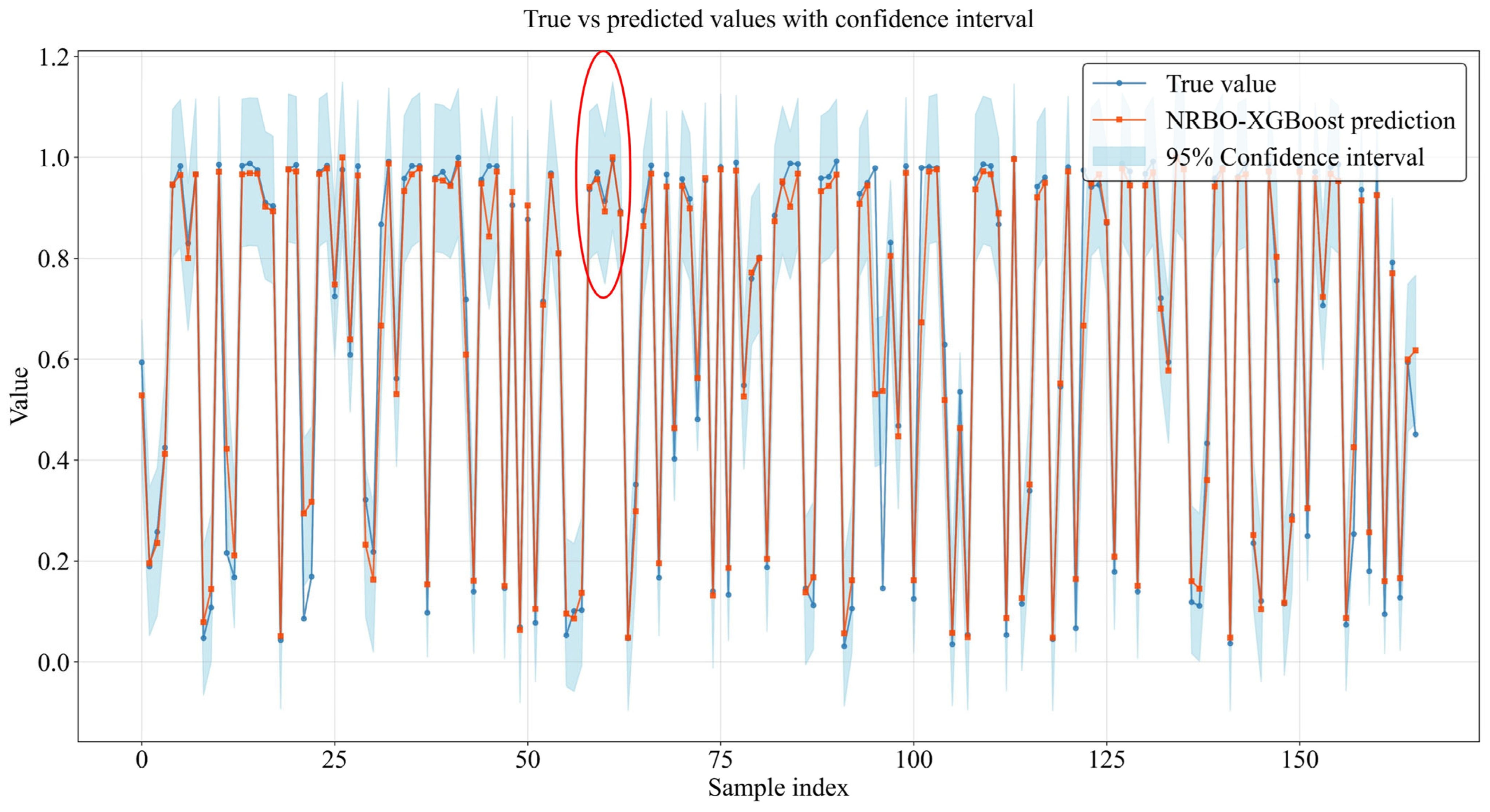
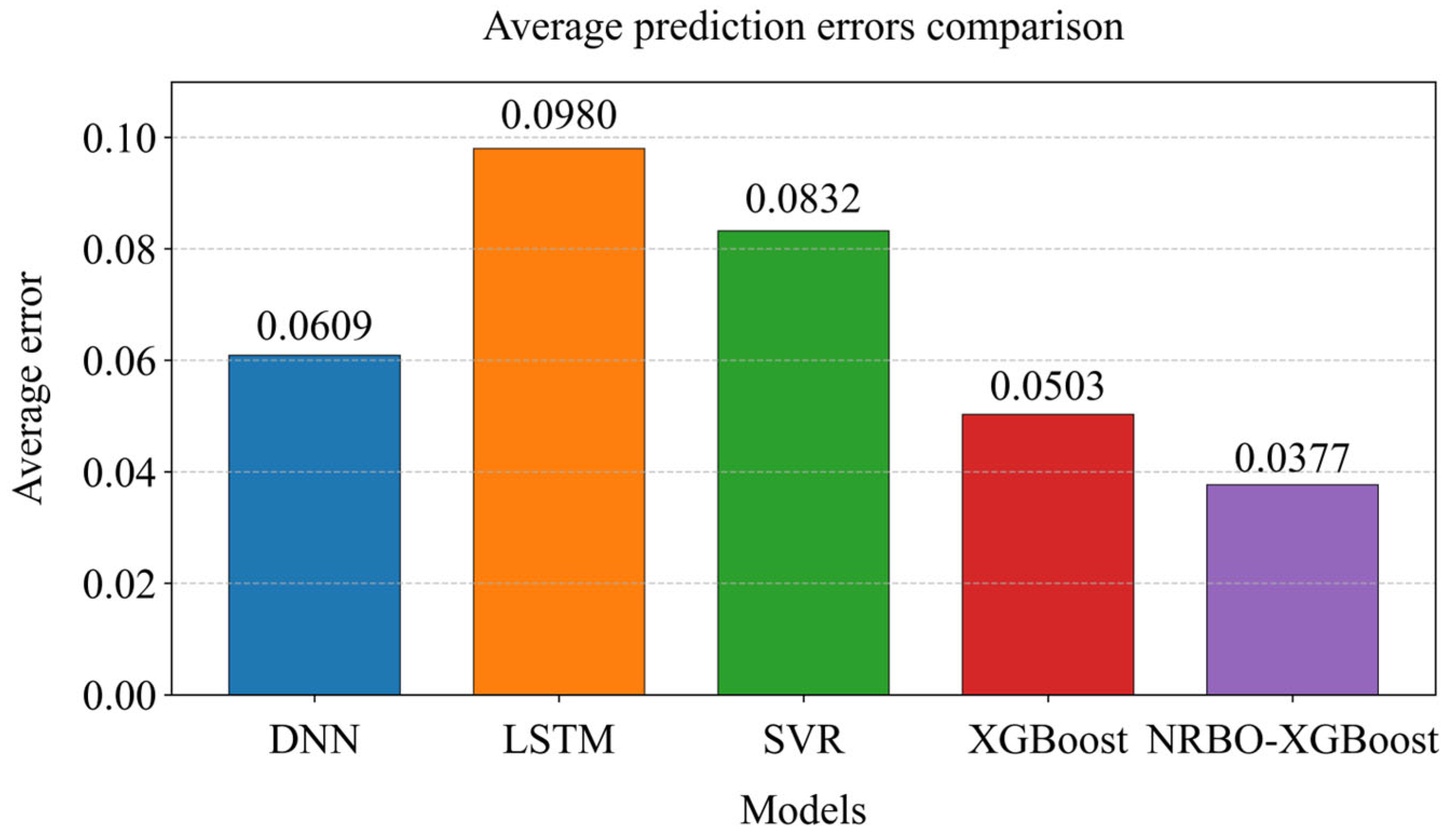
5.3. Results of Model Comparison Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gallucci, S.; Fiocchi, S.; Bonato, M.; Chiaramello, E.; Tognola, G.; Parazzini, M. Exposure Assessment to Radiofrequency Electromagnetic Fields in Occupational Military Scenarios: A Review. Int. J. Environ. Res. Public Health 2022, 19, 920. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.-F.; Zheng, S.-Q.; Zuo, Y.; Zhang, H.-Q.; Liu, J.-W. Electromagnetic Environment Effects and Protection of Complex Electronic Information Systems. In Proceedings of the IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO), Beijing, China, 7–9 December 2020. [Google Scholar] [CrossRef]
- Chen, S.; Yuan, Y.; Wang, S.-X.; Yang, H.; Zhu, L.; Zhang, S.; Zhao, H. Multi-Electromagnetic Jamming Countermeasure for Airborne SAR Based on Maximum SNR Blind Source Separation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5240211. [Google Scholar] [CrossRef]
- Tao, M.-L.; Li, J.-S.; Fan, Y.-F.; Su, J.; Wang, L. Effects of Interference on Synthetic Aperture Radar Measurements: An Illustrative Example. In Proceedings of the 2020 XXXIIIrd General Assembly and Scientific Symposium of the International Union of Radio Science (URSI GASS), Rome, Italy, 29 August–5 September 2020. [Google Scholar] [CrossRef]
- Hu, X.; Shi, J.; Wei, T.; Li, N. An Enhanced Extraction and Mitigation Scheme of Mutual RFI Between Spaceborne SARs Based on Pulse Compression. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5208720. [Google Scholar] [CrossRef]
- Natsuaki, R.; Jäger, M.; Prats-Iraola, P. Similarity Approach for Radio Frequency Interference Detection and Correction in Multi-Receiver SAR. In Proceedings of the IGARSS 2020—IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020. [Google Scholar] [CrossRef]
- Fang, L.; Zhang, J.; Ran, Y.; Chen, K.; Maidan, A.; Huan, L.; Liao, H. Blind Signal Separation with Deep Residual Networks for Robust Synthetic Aperture Radar Signal Processing in Interference Electromagnetic Environments. Electronics 2025, 14, 1950. [Google Scholar] [CrossRef]
- Feng, Y.; Han, B.; Wang, X.; Shen, J.; Guan, X.; Ding, H. Self-Supervised Transformers for Unsupervised SAR Complex Interference Detection Using Canny Edge Detector. Remote Sens. 2024, 16, 306. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, Y.-M.; Ma, L.-Y.; Chen, Y.-Z. Research on Simulation Method for Nonlinear Effects of Airborne SAR EMI. AIP Adv. 2023, 13, 105002. [Google Scholar] [CrossRef]
- Chen, S.; Lin, Y.; Yuan, Y.; Li, X.; Hou, L. Suppressive Interference Suppression for Airborne SAR Using BSS for Singular Value and Eigenvalue Decomposition Based on Information Entropy. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5205611. [Google Scholar] [CrossRef]
- Fang, F.-P.; Li, H.-L.; Meng, W.-Z.; Dai, D.; Xing, S. Synthetic-Aperture Radar Radio-Frequency Interference Suppression Based on Regularized Optimization Feature Decomposition Network. Remote Sens. 2024, 16, 2540. [Google Scholar] [CrossRef]
- Kim, S.; Lee, D.; Park, Y.; Joo, J.; Kim, J.; Kim, J.; Bang, J.-H. Deceptive Jamming for Spaceborne SAR Using Estimated Signal Parameters and Intercepted Signal Phase. IEEE Access 2024, 12, 169388–169403. [Google Scholar] [CrossRef]
- Guo, X.; Tian, T.; Tan, H.; Fan, W.; Zhou, F. A Deceptive Jamming Technology Against SAR Based on Optical-to-SAR Template Translation. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 5715–5729. [Google Scholar] [CrossRef]
- Liu, Z.; Cheng, D.; Li, N.; Min, L.; Guo, Z. Two-Dimensional Precise Controllable Smart Jamming Against SAR via Phase Errors Modulation of Transmitted Signal. IEEE Geosci. Remote Sens. Lett. 2024, 21, 4000705. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, Q.; Huang, Z.; Chen, T.; Mu, B.; Guo, H. SAR Imaging of Dense False Target Jamming Based on Phase Modulation. IEEE Geosci. Remote Sens. Lett. 2025, 22, 4000105. [Google Scholar] [CrossRef]
- Hu, H.; Ao, Y.; Bai, Y.; Cheng, R.; Xu, T. An Improved Harris’s Hawks Optimization for SAR Target Recognition and Stock Market Index Prediction. IEEE Access 2020, 8, 65891–65910. [Google Scholar] [CrossRef]
- Xu, W.; Xing, W.; Fang, C.; Huang, P.; Tan, W. RFI Suppression Based on Linear Prediction in Synthetic Aperture Radar Data. IEEE Geosci. Remote Sens. Lett. 2021, 18, 2127–2131. [Google Scholar] [CrossRef]
- Huang, M.; Zhao, H.; Chen, Y.-Z. Research on SAR Image Quality Evaluation Method Based on Improved Harris Hawk Optimization Algorithm and XGBoost. Sci. Rep. 2024, 14, 28364. [Google Scholar] [CrossRef]
- Macchiarulo, V.; Giardina, G.; Milillo, P.; Aktas, Y.D.; Whitworth, M.R.Z. Integrating Post-Event Very High Resolution SAR Imagery and Machine Learning for Building-Level Earthquake Damage Assessment. Bull. Earthq. Eng. 2024, 22, 1–27. [Google Scholar] [CrossRef]
- Ponmani, E.; Saravanan, P. Image Denoising and Despeckling Methods for SAR Images to Improve Image Enhancement Performance: A Survey. Multimed. Tools Appl. 2021, 80, 26547–26569. [Google Scholar] [CrossRef]
- Wei, S.-J.; Zhang, H.; Zeng, X.-F.; Zhou, Z.; Shi, J.; Zhang, X. CARNet: An Effective Method for SAR Image Interference Suppression. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103019. [Google Scholar] [CrossRef]
- Liu, S.; Tian, S.; Zhao, Y.; Hu, Q.; Li, B.; Zhang, Y.-D. LG-DBNet: Local and Global Dual-Branch Network for SAR Image Denoising. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5205515. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Y.; Shi, C.; Yuan, Y.; Zhang, X. ANED-Net: Adaptive Noise Estimation and Despeckling Network for SAR Image. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 4036–4051. [Google Scholar] [CrossRef]
- Yang, C.; Li, C.; Zhu, Y. Denoising and Feature Enhancement Network for Target Detection Based on SAR Images. Remote Sens. 2025, 17, 1739. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Y.; Cheng, E.; Ma, L.; Chen, Y. Investigation on the Effect of the B1I Navigation Receiver Under Multifrequency Interference. IEEE Trans. Electromagn. Compat. 2022, 64, 1097–1104. [Google Scholar] [CrossRef]
- Chen, F.; Huang, L.; Zhou, Q.; Ren, C. GNSS Cognitive Interference Mitigation Method Based on Deep Learning. In Proceedings of the 2024 5th International Conference on Electronic Communication and Artificial Intelligence (ICECAI), Shenzhen, China, 24–26 May 2024. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, Q.; Yu, H.; Guo, X.; Gong, C. GNSS Interference Suppression for Spacecraft Using Integrated Navigation Based on Support Vector Regression. In Proceedings of the 2024 43rd Chinese Control Conference (CCC), Kunming, China, 25–27 July 2024. [Google Scholar] [CrossRef]
- Lu, F.; Fan, Z.; Hu, C.; Ma, C.; Chen, Y.; Jiang, H. Deep Reinforcement Learning-Driven Analog Self-Interference Cancellation for LEO Navigation Augmentation Systems. In Proceedings of the 2024 IEEE 24th International Conference on Communication Technology (ICCT), Chengdu, China, 18–20 October 2024. [Google Scholar] [CrossRef]
- Zhang, D.-X.; Cheng, E.-W.; Wan, H.-J.; Zhou, X.; Chen, Y. Prediction of Electromagnetic Compatibility for Dynamic Datalink of UAV. IEEE Trans. Electromagn. Compat. 2018, 61, 1474–1482. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y.; Zhao, M.; Li, Y. Assessment of EMI Effects on UAV Data Links. IEEE Trans. Electromagn. Compat. 2025, 67, 1–14. [Google Scholar] [CrossRef]
- Xu, T.; Chen, Y.; Zhao, M.; Wang, Y.; Zhang, X. Adaptive EMS Test Design Method on UAV Data Link Based on Bayesian Optimization. IEEE Trans. Electromagn. Compat. 2023, 65, 716–724. [Google Scholar] [CrossRef]
- Sowmya, R.; Premkumar, M.; Jangir, P. Newton-Raphson-Based Optimizer: A New Population-Based Metaheuristic Algorithm for Continuous Optimization Problems. Eng. Appl. Artif. Intell. 2024, 128, 107532. [Google Scholar] [CrossRef]
- Chen, T.-Q.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Yang, L.; Xu, C. SAR Jamming Effect Evaluation Method Combining Texture Structure Similarity and Image Contour Similarity. Mod. Electron. Tech. 2023, 46, 34–38. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle Swarm Optimization: A Comprehensive Survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Lambora, A.; Gupta, K.; Chopra, K. Genetic Algorithm—A Literature Review. In Proceedings of the 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 14–16 February 2019; pp. 380–384. [Google Scholar] [CrossRef]
- Bilal; Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A. Differential Evolution: A Review of More than Two Decades of Research. Eng. Appl. Artif. Intell. 2020, 90, 103479. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris Hawks Optimization: Algorithm and Applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Bozorg-Haddad, O.; Chu, X. Gradient-Based Optimizer: A New Metaheuristic Optimization Algorithm. Inf. Sci. 2020, 540, 131–159. [Google Scholar] [CrossRef]
- Chaves, A.A.; Resende, M.G.C.; Schuetz, M.J.A.; Brubaker, J.K.; Katzgraber, H.G.; de Ar-ruda, E.F.; Silva, R.M.A. A Random-Key Optimizer for Combinatorial Optimization. arXiv 2024, arXiv:2411.04293. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalini, S. Equilibrium Optimizer: A Novel Optimization Algorithm. Knowl. Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]

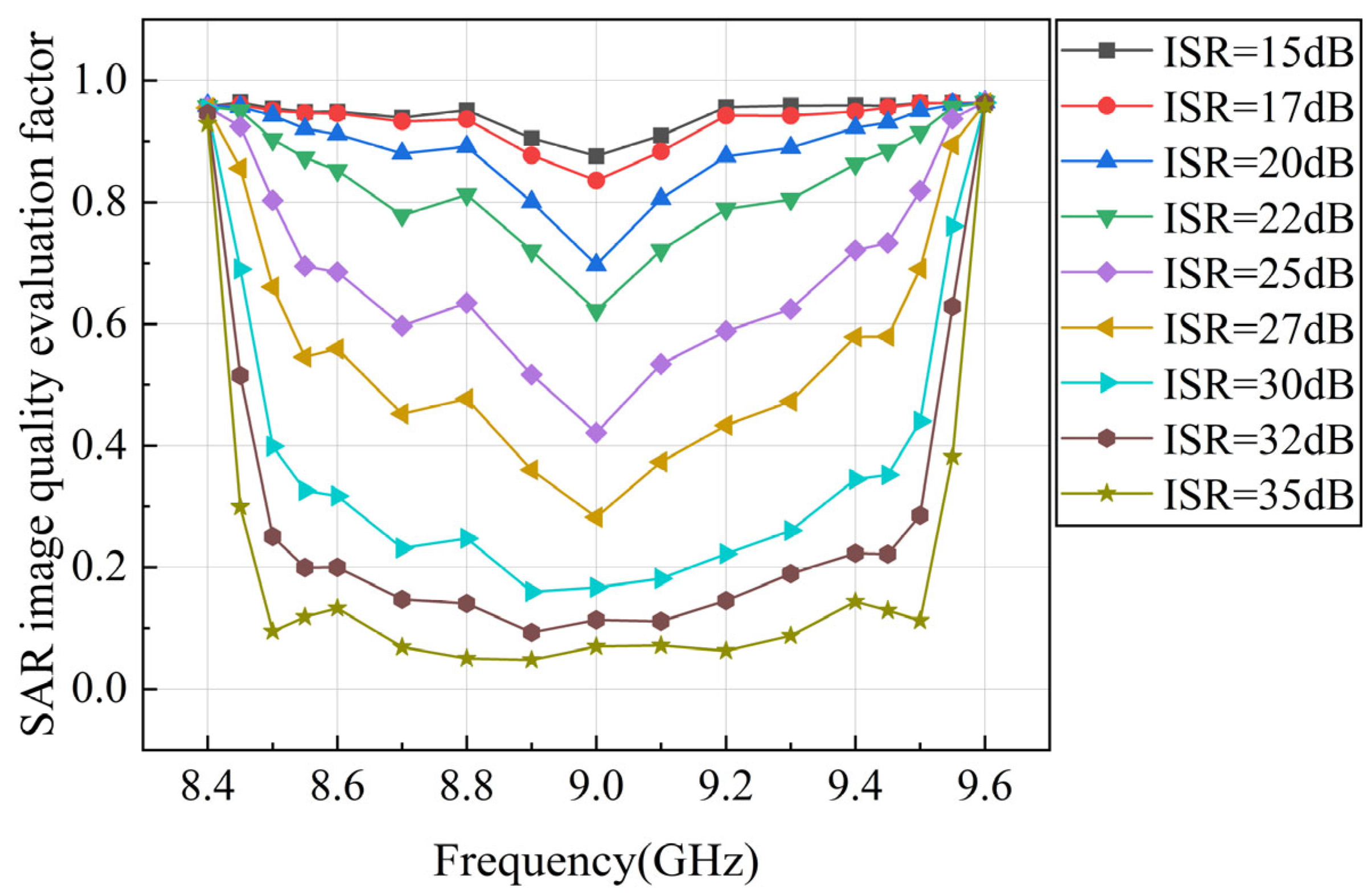
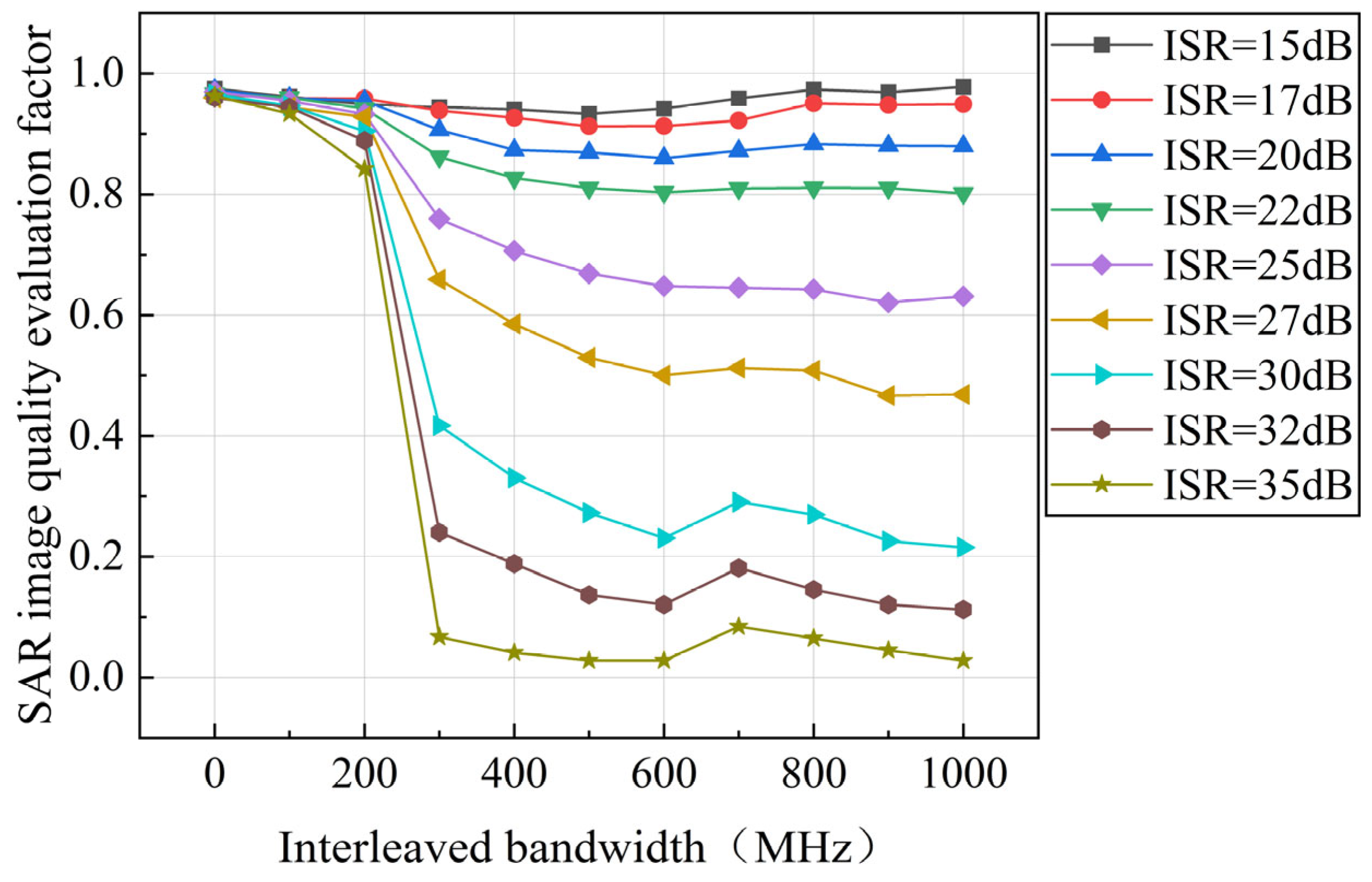
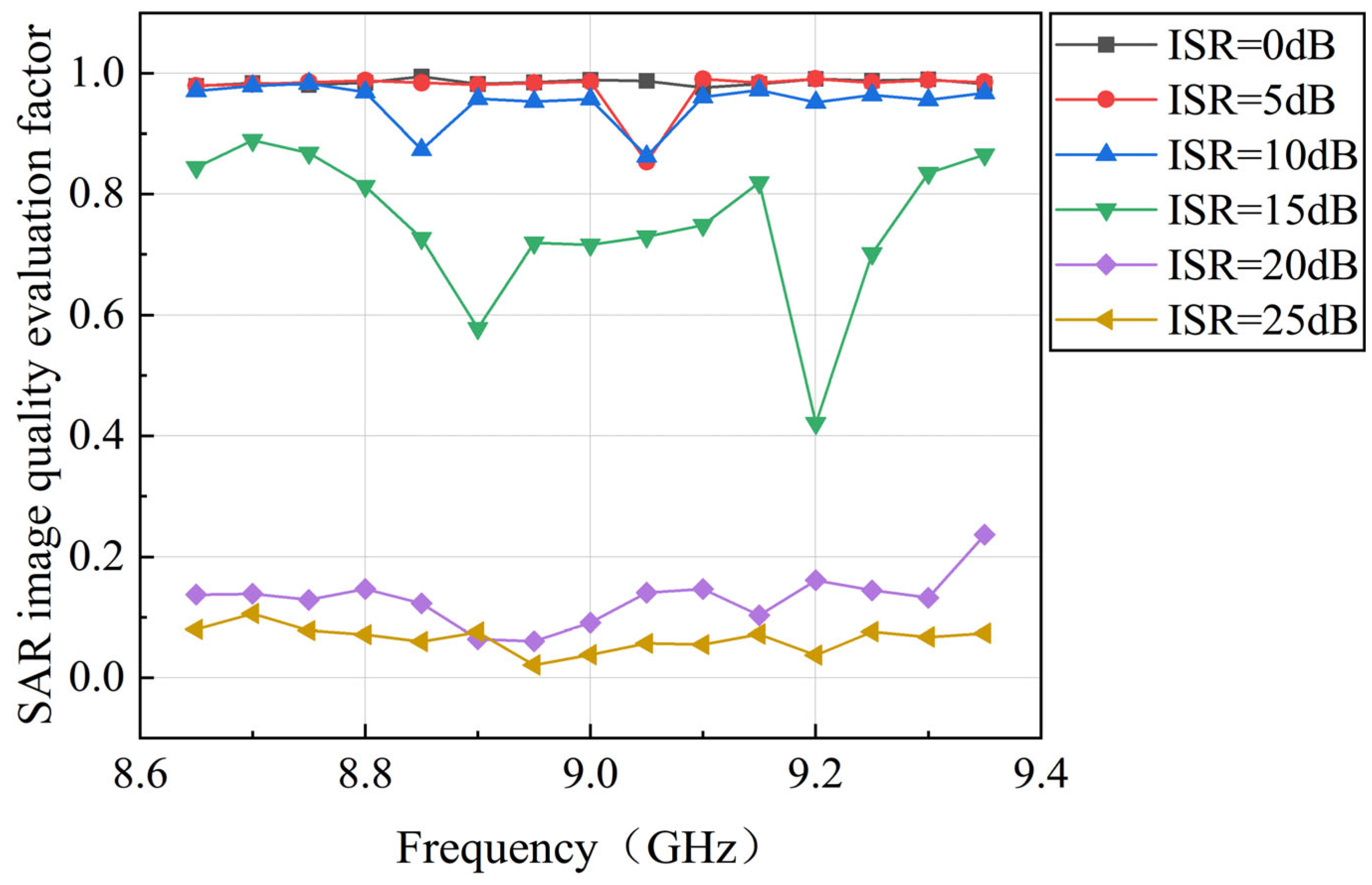
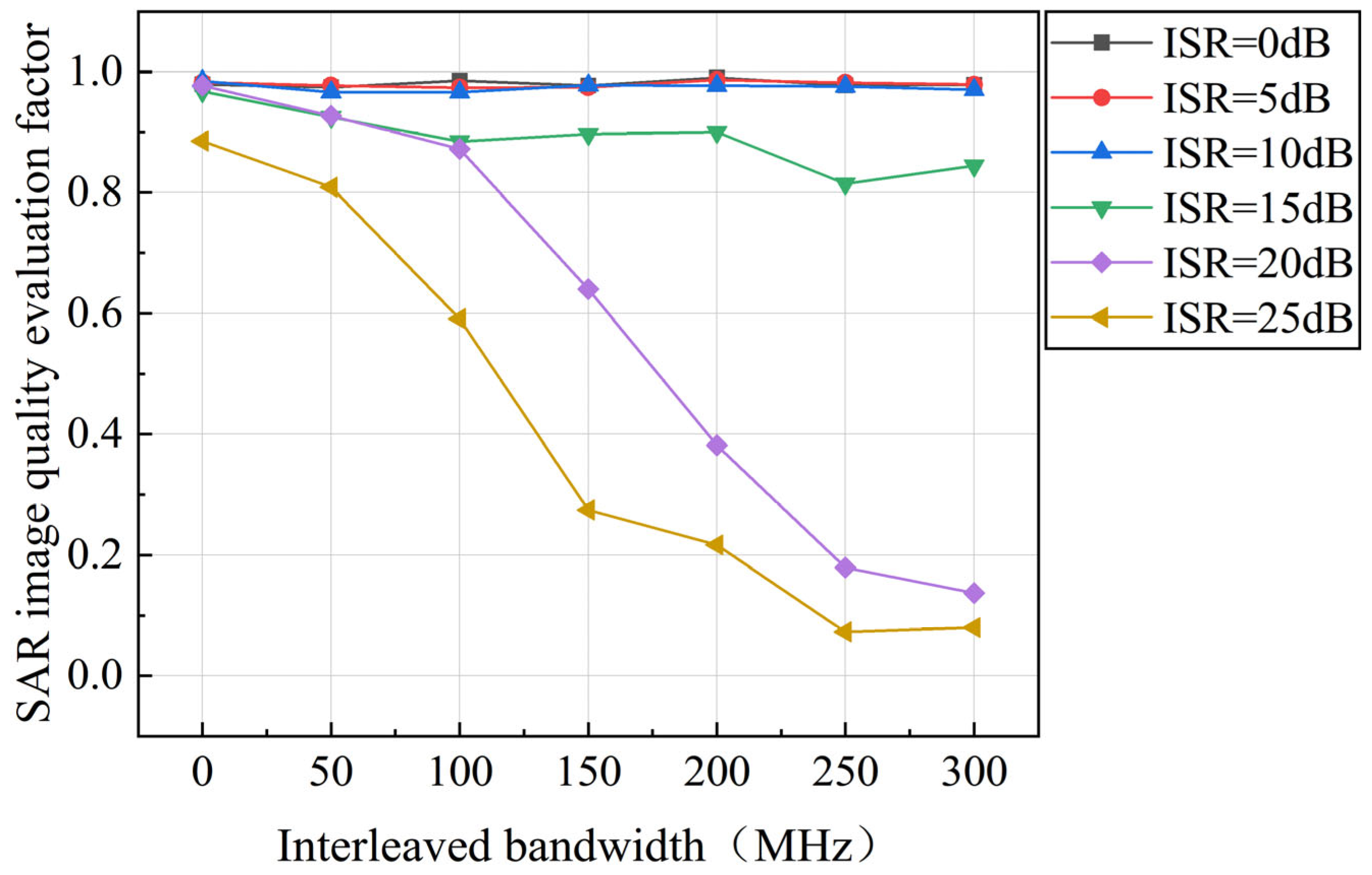
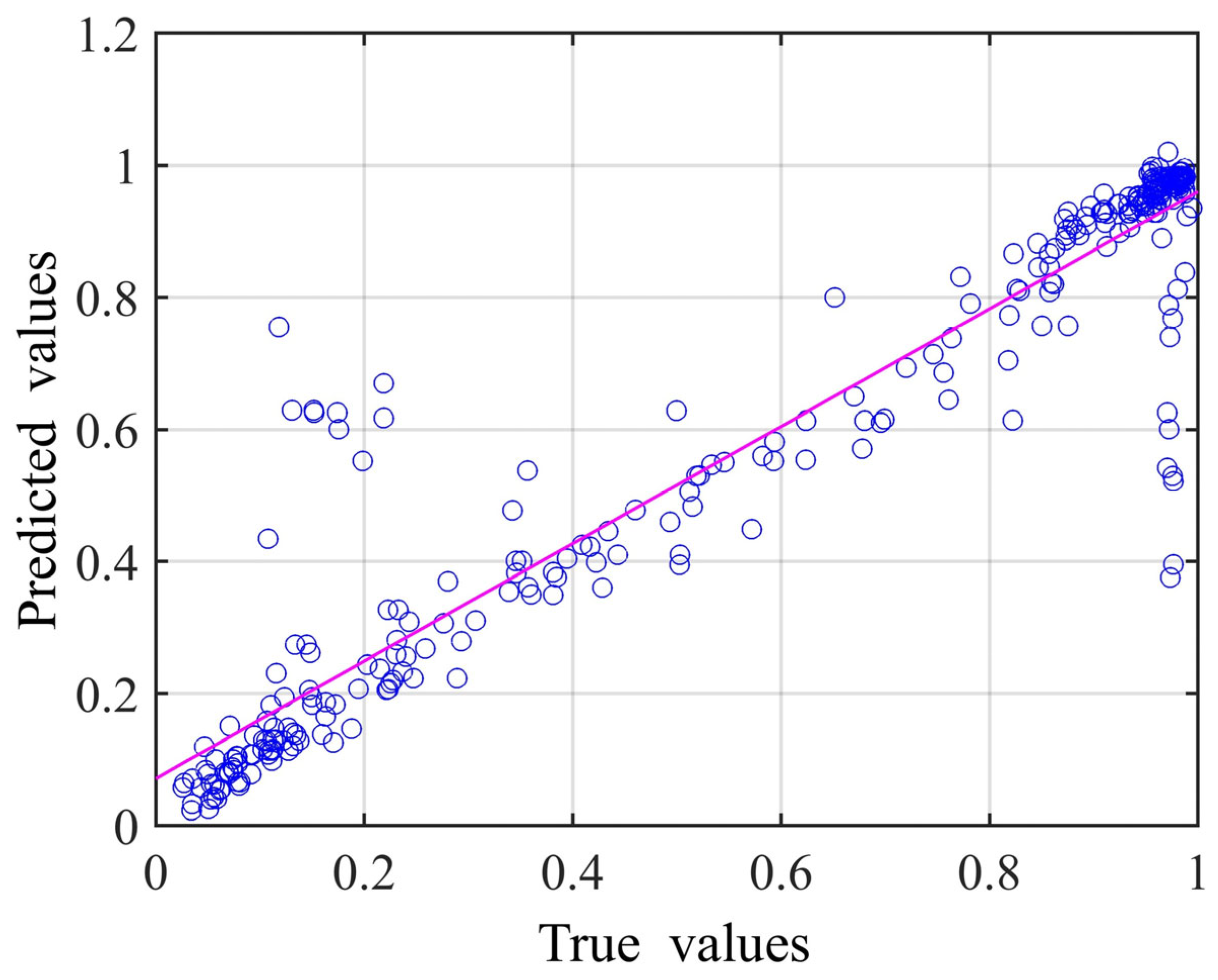
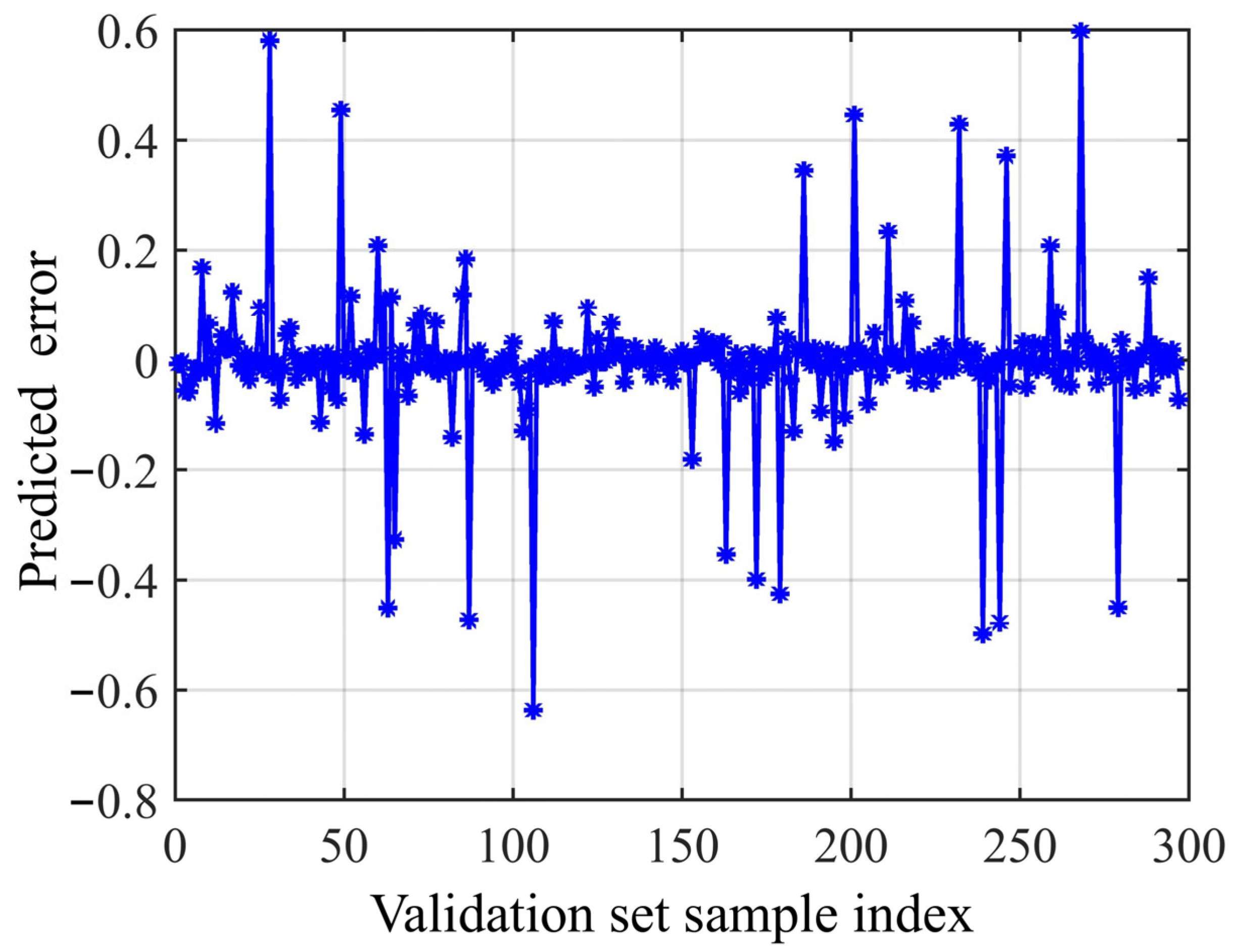
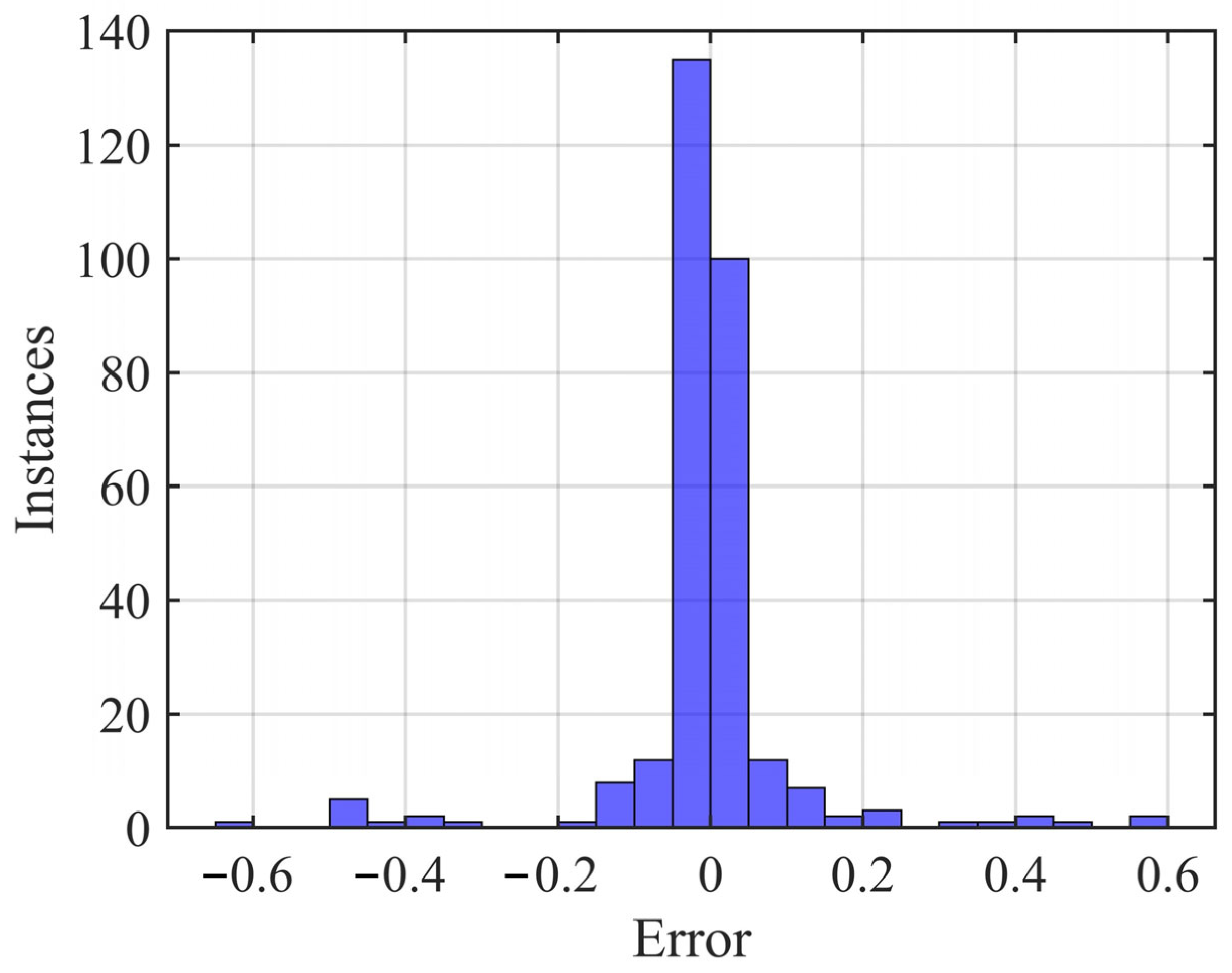
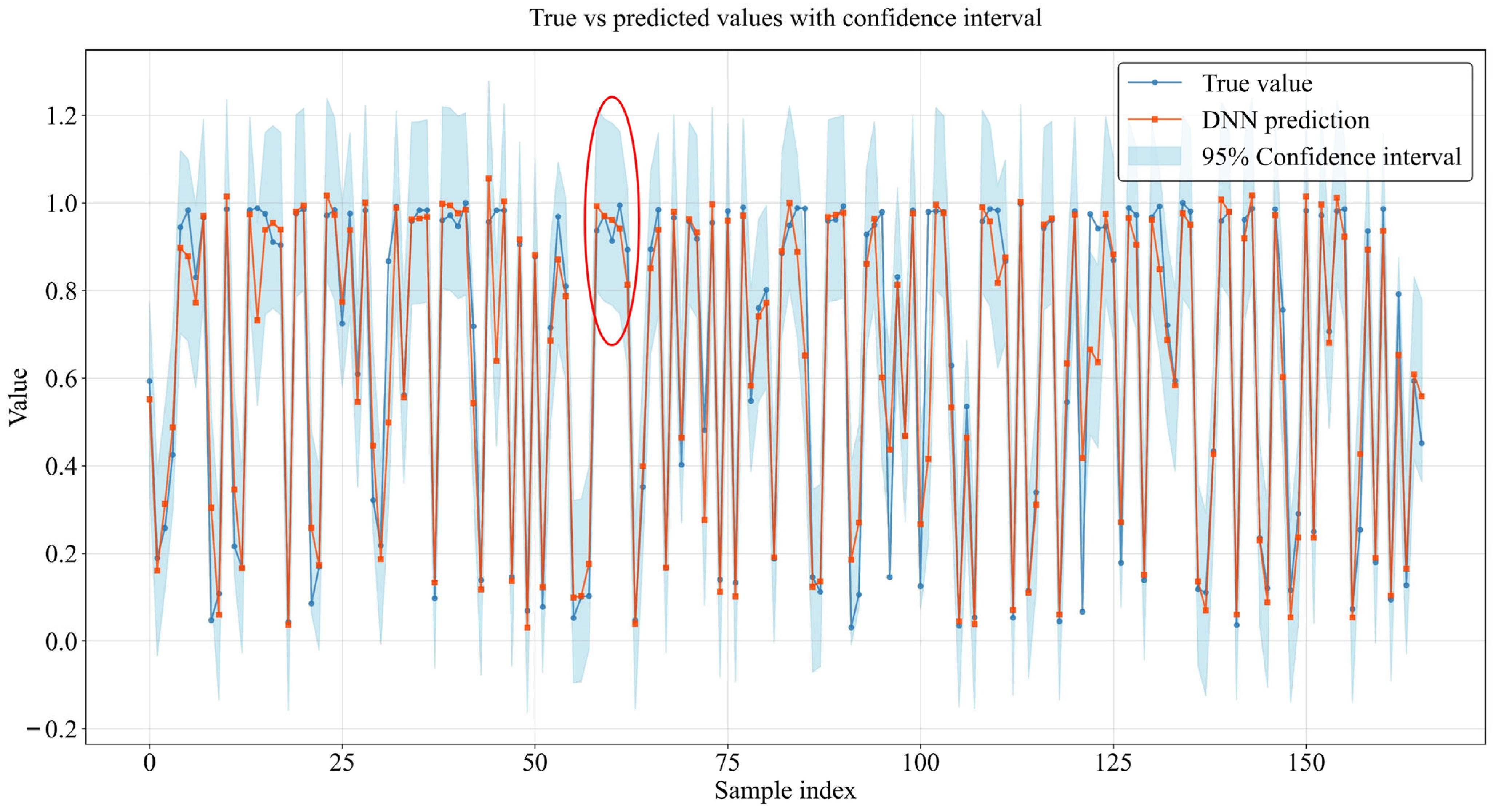
| Name | Value |
|---|---|
| SAR imaging mode | strip imaging |
| Carrier frequency | 9 GHz |
| Signal bandwidth | 300 MHz |
| Pulse width | 20 µs |
| Pulse repetition frequency | 1000 Hz |
| Signal sampling rate | 600 MHz |
| Aircraft platform speed | 250 m/s |
| Range resolution | 0.5 m |
| Azimuth resolution | 0.5 m |
| Evaluation Criterion | NRBO | Gradient-Free Algorithms (e.g., PSO [35], GA [36], and DE [37]) | Other Swarm Intelligence Algorithms (e.g., GWO [38], HHO [39]) |
|---|---|---|---|
| Convergence Speed | Leverages gradient directions for accelerated convergence; Reduced iteration counts by 30–50% in CEC2017 benchmarks. | Rely on stochastic search mechanisms, resulting in slower convergence rates. | Moderate convergence speed with susceptibility to local oscillations. |
| Global Exploration | TAO mechanism enhances population diversity; Balance index > 90% across 23 benchmark functions. | Prone to premature convergence, diversity degradation in high-dimensional spaces. | Limited exploration capabilities, parameter-sensitive performance. |
| Local Exploitation | NRSR strategy enables precise extremum approximation; Standard deviation < 1 × 10−10 in CEC2022 composite functions. | Lacks gradient guidance, inefficient local development. | Neighborhood-based search with precision constraints. |
| High-Dimensional Adaptability | Maintains stability in 1000D problems, outperforms GBO [40]/RKO [41]. | Suffers from “curse of dimensionality”, performance collapse. | Certain algorithms (e.g., EO [42]) exhibit suboptimal scalability. |
| Engineering Applicability | Achieved optimal solutions in 12/12 CEC2020 engineering optimization problems. | Feasibility constraint violations in complex scenarios. | Requires extensive parameter tuning; limited robustness. |
| Name | Mean |
|---|---|
| Learning rate | Control the scaling of each tree’s weights |
| Max depth | Limit the maximum depth of the tree to prevent overfitting |
| Subsample | Proportion of samples used to train each tree |
| Column sample by tree | Proportion of feature columns used to train each tree |
| Min child weight | Sum of weights controlling further division of leaf nodes |
| Gamma | Minimum gain threshold to control further cutting of leaf nodes |
| Reg lambda | L2 regularization factor for controlling model complexity |
| Reg alpha | L1 regularization factor for controlling model complexity |
| Scale pos weight | Weighting adjustment factors for dealing with category imbalances |
| Algorithm | Hyperparameter | Configuration |
|---|---|---|
| DNN | Activation function | Relu |
| Optimizer | Adam | |
| Learning rate | 0.001 | |
| Batchsize | 24 | |
| Dropout ratio | 0.1 | |
| LSTM | Activation function | data |
| Optimizer | Adam | |
| Learning rate | 0.001 | |
| Batchsize | 24 | |
| Time step | 3 | |
| SVR | Kernel function | rbf |
| C parameter | 1.0 | |
| Gamma parameter | Auto | |
| Tol parameter | 0.001 | |
| Original XGBoost | Learning rate | 0.1 |
| Maximum tree depth | 4 | |
| Subsampling ratio | 0.8 | |
| Column Sampling Ratio | 0.8 | |
| Gamma parameter | 0.1 | |
| Min child weight | 5 | |
| Scale pos weight | 1 |
| Algorithm | RMSE | MAE | ED | R2 |
|---|---|---|---|---|
| DNN | 0.1231 | 0.0677 | 2.1253 | 0.8828 |
| LSTM | 0.1556 | 0.0948 | 2.6859 | 0.8127 |
| SVR | 0.1419 | 0.0908 | 2.4498 | 0.8442 |
| XGBoost | 0.1069 | 0.0593 | 1.8458 | 0.9116 |
| NRBO–XGBoost | 0.0971 | 0.04619 | 1.6739 | 0.9273 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Chen, Y.; Wang, Y.; Ma, L.; Zhang, X. Research on a Prediction Model Based on a Newton–Raphson-Optimization–XGBoost Algorithm Predicting Environmental Electromagnetic Effects for an Airborne Synthetic Aperture Radar. Electronics 2025, 14, 2202. https://doi.org/10.3390/electronics14112202
Shen Y, Chen Y, Wang Y, Ma L, Zhang X. Research on a Prediction Model Based on a Newton–Raphson-Optimization–XGBoost Algorithm Predicting Environmental Electromagnetic Effects for an Airborne Synthetic Aperture Radar. Electronics. 2025; 14(11):2202. https://doi.org/10.3390/electronics14112202
Chicago/Turabian StyleShen, Yan, Yazhou Chen, Yuming Wang, Liyun Ma, and Xiaolu Zhang. 2025. "Research on a Prediction Model Based on a Newton–Raphson-Optimization–XGBoost Algorithm Predicting Environmental Electromagnetic Effects for an Airborne Synthetic Aperture Radar" Electronics 14, no. 11: 2202. https://doi.org/10.3390/electronics14112202
APA StyleShen, Y., Chen, Y., Wang, Y., Ma, L., & Zhang, X. (2025). Research on a Prediction Model Based on a Newton–Raphson-Optimization–XGBoost Algorithm Predicting Environmental Electromagnetic Effects for an Airborne Synthetic Aperture Radar. Electronics, 14(11), 2202. https://doi.org/10.3390/electronics14112202





