Efficient Delay-Sensitive Task Offloading to Fog Computing with Multi-Agent Twin Delayed Deep Deterministic Policy Gradient
Abstract
1. Introduction
- Formulate the task offloading and resource allocation problem as a Markov decision process (MDP) with a stochastic continuous action space to address computational and transmission delays in a multi-task, multi-node environment.
- Develop a Multi-Agent Fully Cooperative Partial Task Offloading and Resource Allocation (MAFCPTORA) algorithm that enables parallel task execution across adjacent fog nodes in an F2F architecture, leading to faster execution, reduced latency and energy consumption, and balanced workload distribution.
- Evaluate the performance of our algorithm, demonstrating its effectiveness in improving the deadline fulfillment rate for IoT tasks while minimizing the total energy consumption and makespan of the system, thereby benefiting fog service providers.
2. Related Work
2.1. Machine Learning-Based Approaches
| Domain | Problem | RL Method | QoS Objectives | Agent Type | Network | Papers |
|---|---|---|---|---|---|---|
| VFC | V2V Partial Computation Offloading | SAC | Minimize task execution delay and energy consumption | Multi-Agent (UAV) | Dynamic | [16] |
| IoT-edge-UAV | Task offloading and Resource allocation | MADDPG | Minimize computation cost | Multi-Agent (UAV) | Dynamic | [20] |
| Vehicular Fog | Optimize Ratio-Based Offloading | DQN | Minimize average system latency, and lower decision and convergence time | Single-Agent | Dynamic | [21] |
| VFC | Minimize waiting time and end-to-end delay of tasks | PPO | Minimize waiting time, end-to-end delay, packet loss; Maximize percentage of in-time completed tasks | Single-Agent | Dynamic | [22] |
| Multi-Fog Networks | Joint Task Offloading and Resource Allocation | DRQN | Maximize processing tasks and minimize task drops from buffer overflows | Multi-Agent | Dynamic | [23] |
| Edge-UAV | Task offloading | MADDPG | Minimize energy consumption and delay | Multi-Agent UAV | Unstable | [11] |
| IoMT | Computation offloading and resource allocation | MADDPG | Latency Reduction | Multi-Agent | unstable | [13] |
| Multi-cloud (Fog) | Dynamic Computation Offloading | CMATD3 | Minimize long-term average total system cost | Multi-Agent (Cooperative) | Dynamic | [24] |
| MEC | Multi-channel access and task offloading | DPPG | Minimize task computation delay | MTA | Stable | [25] |
| Vehicular Fog | Load Balancing problem | TPDMAAC | Minimize system cost | MV | hybrid | [14] |
| Vehicular Fog | Task offloading and computation load | AC | Maximize resource trading | MA-GAC | hybrid | [9] |
| Fog-RAN | Computation Offloading and Resource Allocation | DDPG | Minimize task computation delay and energy consumption | Multi-agent (Federated) | Dynamic | [26] |
| MEC and Vehicular Fog | Trafic congestion and MEC overload | TD3 | Minimize latency and energy consumption | Multi-agent | hybrid | [18] |
2.2. Reinforcement Learning
2.3. Deep Reinforcement Learning (DRL)
2.4. Multi-Agent Deep Reinforcement Learning
3. System Model
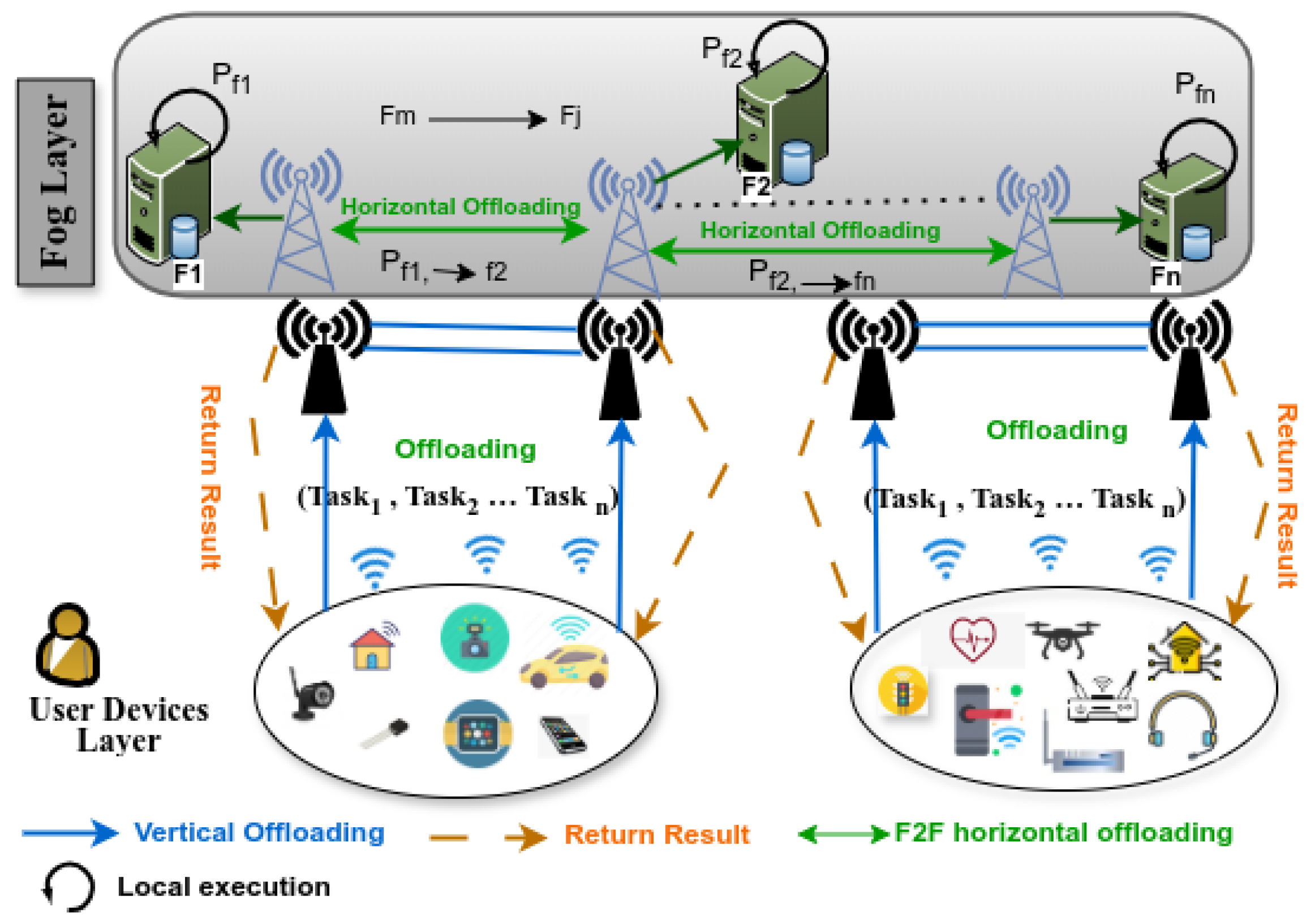
3.1. Network Model
3.2. Task Model
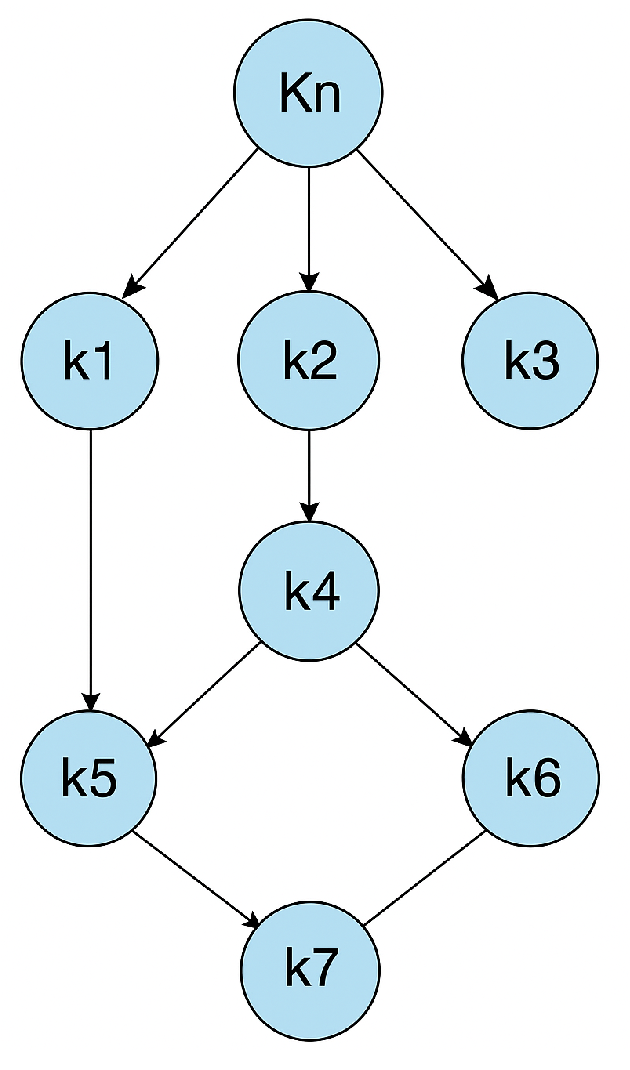
3.3. Dynamic Task Partitioning
3.4. Communication Model
3.4.1. U2F Communication
3.4.2. F2F Communication
3.4.3. Local Computations
3.4.4. Offloading Computation Delay
3.5. Energy Consumption
3.6. Problem Formulation
- (24b) defines the total task execution ratio between and multiple s should not exceed the maximum (i.e., ≤1).
- (24c) defines the probability of offloading ratio ranges from up to 1
- (24d) ensures that the size of the offloaded task to a fog node should not exceed the node’s maximum capacity.
- (24e) shows the latency constraints concerning the maximum tolerable delay threshold of offloaded tasks in terms of transmission and execution deadlines,
- (24f) verifies that the available energy in the fog node remains above a specified threshold.
- (24g) the sum of the offloaded tasks should not exceed the maximum task.
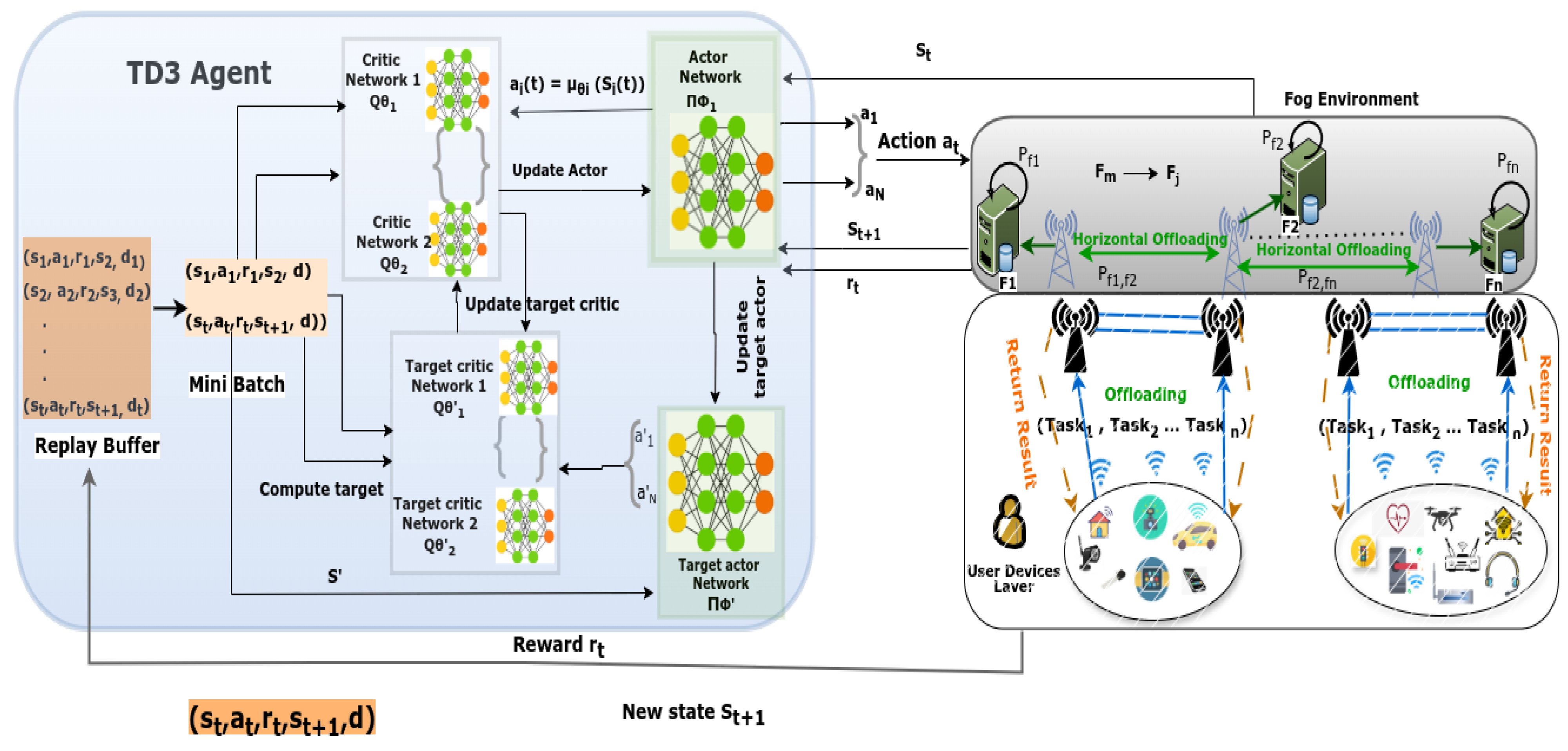
3.7. TD3 Algorithm Overview
4. A Decentralized Mult-Agent TD3 Based Task Offloading Architecture
- State Space : In this task offloading problem, referring to the state of the fog at time step observed by the agent from the environment. It includes the task node , resource status, and channel condition, modeled as a set of , , where represents a set of fog nodes and a set of resources at time step t.
- Action Space : the MATD3 agents observe the state and make a decision of action based on partial offloading. The agent’s decisions are based on partial observability of the system state. We consider a continuous action space where some tasks are executed at , and the remaining are offloaded to an adjacent fog node , as a set of actions is the action in time step t. The set of actions at each time step t is defined as , where represents the ratio of the task n allocated to available resource R.
- Reward : is the reward when action a is taken in state s, and the next state is . Where the reward is determined with the state transition function with the probability that state happens after action is taken in state .
- Done (d): Whether the TD3 agent in the fog environment reaches the terminal state or not is communicated by this element. In this environment, the agent knows that the termination occurs after a hundred offloading decisions or if an offloading action causes resources to enter a busy state.
5. Algorithm Design
Proposed MAFCPTORA-Algorithm
| Algorithm 1 Multi-agent cooperative Partial Task Offloading |
|
| Algorithm 2 Multi-agent Fully Cooperative Resource Allocation |
|
- : The action chosen by agent at time t.
- : The output of the actor network parameterized by , given the state .
- : illustrates the Gaussian noise in terms of mean and standard deviation Equation (41).
- x: A random variable sampled from the distribution.
- : The standard deviation controls the magnitude of the exploration.
6. Performance Evaluation
6.1. Simulation Setting
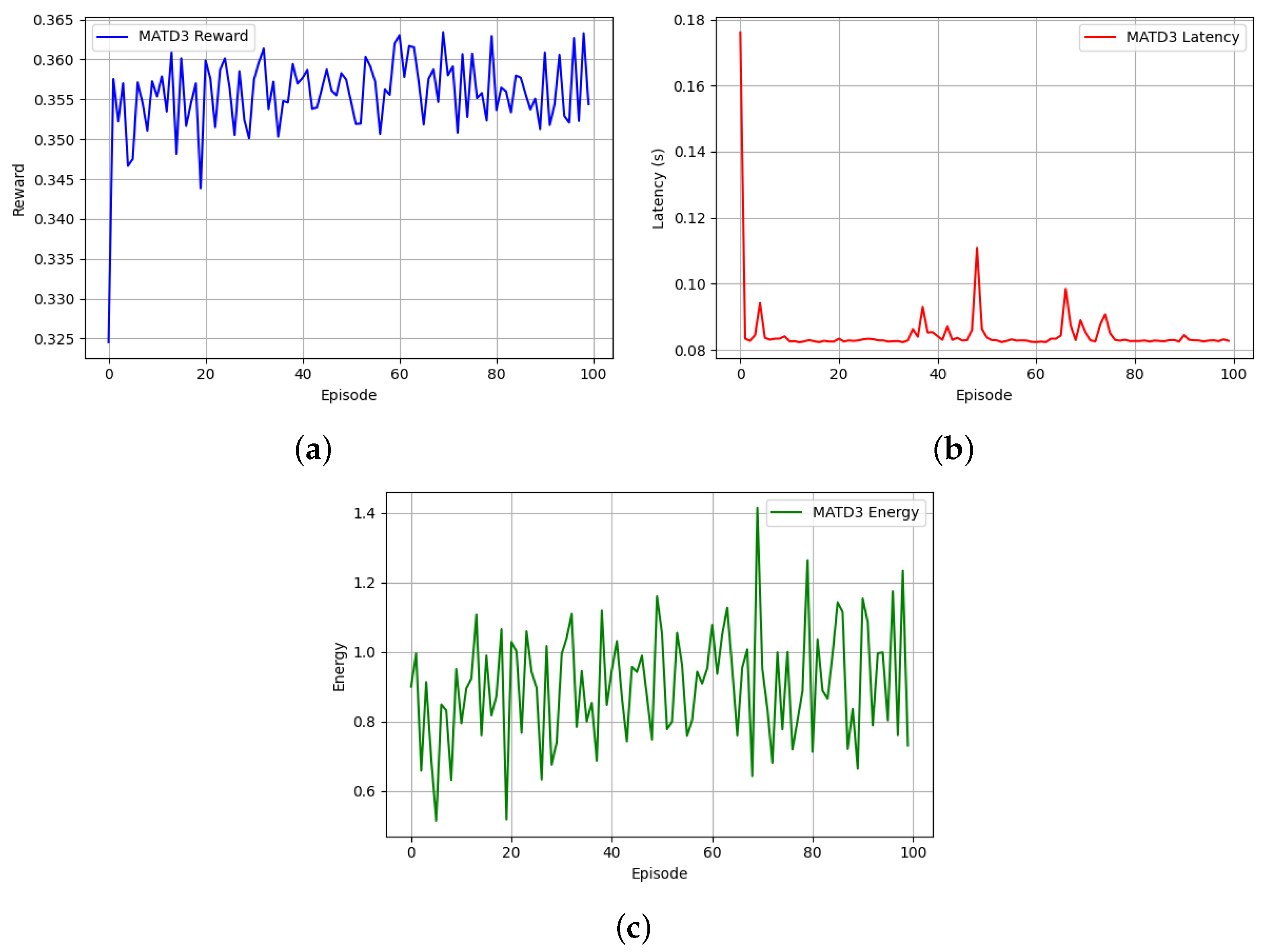
6.2. Result and Performance Analysis
7. Conclusions and Future Direction
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Statista. Consumer Electronics—Statista Market Forecast. 2023. Available online: https://www.statista.com/outlook/cmo/consumer-electronics/worldwide (accessed on 10 February 2025).
- Shahidinejad, A.; Abawajy, J. Efficient Provably Secure Authentication Protocol for Multidomain IIoT Using a Combined Off-Chain and On-Chain Approach. IEEE Internet Things J. 2024, 11, 15241–15251. [Google Scholar] [CrossRef]
- Li, X.; Xu, Z.; Fang, F.; Fan, Q.; Wang, X.; Leung, V.C.M. Task Offloading for Deep Learning Empowered Automatic Speech Analysis in Mobile Edge-Cloud Computing Networks. IEEE Trans. Cloud Comput. 2023, 11, 1985–1998. [Google Scholar] [CrossRef]
- Abawajy, J.H.; Hassan, M.M. Federated Internet of Things and Cloud Computing Pervasive Patient Health Monitoring System. IEEE Commun. Mag. 2017, 55, 48–53. [Google Scholar] [CrossRef]
- Okafor, K.C.; Achumba, I.E.; Chukwudebe, G.A.; Ononiwu, G.C. Leveraging fog computing for scalable IoT datacenter using spine-leaf network topology. J. Electr. Comput. Eng. 2017, 2017, 2363240. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, K.; Huang, H.; Miyazaki, T.; Guo, S. Traffic and Computation Co-Offloading with Reinforcement Learning in Fog Computing for Industrial Applications. IEEE Trans. Ind. Inform. 2019, 15, 976–986. [Google Scholar] [CrossRef]
- Hussein, M.K.; Mousa, M.H. Efficient task offloading for IoT-Based applications in fog computing using ant colony optimization. IEEE Access 2020, 8, 37191–37201. [Google Scholar] [CrossRef]
- Ghanavati, S.; Abawajy, J.; Izadi, D. An Energy Aware Task Scheduling Model Using Ant-Mating Optimization in Fog Computing Environment. IEEE Trans. Serv. Comput. 2020, 15, 2007–2017. [Google Scholar] [CrossRef]
- Wei, Z.; Li, B.; Zhang, R.; Cheng, X.; Yang, L. Many-to-Many Task Offloading in Vehicular Fog Computing: A Multi-Agent Deep Reinforcement Learning Approach. IEEE Trans. Mob. Comput. 2023, 23, 2107–2122. [Google Scholar] [CrossRef]
- Ren, Y.; Sun, Y.; Peng, M. Deep Reinforcement Learning Based Computation Offloading in Fog Enabled Industrial Internet of Things. IEEE Trans. Ind. Inform. 2021, 17, 4978–4987. [Google Scholar] [CrossRef]
- Li, Y.; Liang, L.; Fu, J.; Wang, J. Multiagent Reinforcement Learning for Task Offloading of Space/Aerial-Assisted Edge Computing. Secur. Commun. Networks 2022, 2022, 193365. [Google Scholar] [CrossRef]
- Shi, W.; Chen, L.; Zhu, X. Task offloading decision-making algorithm for vehicular edge computing: A deep-reinforcement-learning-based approach. Sensors 2023, 23, 7595. [Google Scholar] [CrossRef] [PubMed]
- Seid, A.M.; Erbad, A.; Abishu, H.N.; Albaseer, A.; Abdallah, M.; Guizani, M. Multi-agent Federated Reinforcement Learning for Resource Allocation in UAV-enabled Internet of Medical Things Networks. IEEE Internet Things J. 2023, 10, 19695–19711. [Google Scholar] [CrossRef]
- Gao, Z.; Yang, L.; Dai, Y. Fast Adaptive Task Offloading and Resource Allocation via Multi-agent Reinforcement Learning in Heterogeneous Vehicular Fog Computing. IEEE Internet Things J. 2022, 10, 6818–6835. [Google Scholar] [CrossRef]
- Azizi, S.; Shojafar, M.; Abawajy, J.; Buyya, R. Deadline-aware and energy-efficient IoT task scheduling in fog computing systems: A semi-greedy approach. J. Netw. Comput. Appl. 2022, 201, 103333. [Google Scholar] [CrossRef]
- Shi, J.; Du, J.; Wang, J.; Yuan, J. Deep reinforcement learning-based V2V partial computation offloading in vehicular fog computing. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 29 March–1 April 2021; pp. 1–6. [Google Scholar]
- Wu, G.; Xu, Z.; Zhang, H.; Shen, S.; Yu, S. Multi-agent DRL for joint completion delay and energy consumption with queuing theory in MEC-based IIoT. J. Parallel Distrib. Comput. 2023, 176, 80–94. [Google Scholar] [CrossRef]
- Wakgra, F.G.; Kar, B.; Tadele, S.B.; Shen, S.H.; Khan, A.U. Multi-objective offloading optimization in mec and vehicular-fog systems: A distributed-td3 approach. IEEE Trans. Intell. Transp. Syst. 2024, 25, 16897–16909. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, S.; Chen, S.; Yang, G. Energy and Delay Co-aware Computation Offloading with Deep Learning in Fog Computing Networks. In Proceedings of the 2019 IEEE 38th International Performance Computing and Communications Conference (IPCCC), London, UK, 29–31 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Seid, A.M.; Boateng, G.O.; Mareri, B.; Sun, G.; Jiang, W. Multi-Agent DRL for Task Offloading and Resource Allocation in Multi-UAV Enabled IoT Edge Network. IEEE Trans. Netw. Serv. Manag. 2021, 18, 4531–4547. [Google Scholar] [CrossRef]
- Wang, N.; Varghese, B. Context-aware distribution of fog applications using deep reinforcement learning. J. Netw. Comput. Appl. 2022, 203, 103354. [Google Scholar] [CrossRef]
- Jamil, B.; Ijaz, H.; Shojafar, M.; Munir, K. IRATS: A DRL-based intelligent priority and deadline-aware online resource allocation and task scheduling algorithm in a vehicular fog network. Ad Hoc Networks 2023, 141, 103090. [Google Scholar] [CrossRef]
- Baek, J.; Kaddoum, G. Heterogeneous Task Offloading and Resource Allocations via Deep Recurrent Reinforcement Learning in Partial Observable Multifog Networks. IEEE Internet Things J. 2021, 8, 1041–1056. [Google Scholar] [CrossRef]
- Bai, Y.; Li, X.; Wu, X.; Zhou, Z. Dynamic Computation Offloading with Deep Reinforcement Learning in Edge Network. Appl. Sci. 2023, 13, 2010. [Google Scholar] [CrossRef]
- Cao, Z.; Zhou, P.; Li, R.; Huang, S.; Wu, D. Multiagent Deep Reinforcement Learning for Joint Multichannel Access and Task Offloading of Mobile-Edge Computing in Industry 4.0. IEEE Internet Things J. 2020, 7, 6201–6213. [Google Scholar] [CrossRef]
- Tong, Z.; Li, Z.; Gendia, A.; Muta, O. Deep Reinforcement Learning Based Computing Resource Allocation in Fog Radio Access Networks. In Proceedings of the 2024 IEEE 100th Vehicular Technology Conference (VTC2024-Fall), Washington DC, USA, 7–10 October 2024; pp. 1–5. [Google Scholar]
- Ren, J.; Zhang, D.; He, S.; Zhang, Y.; Li, T. A Survey on End-Edge-Cloud Orchestrated Network Computing Paradigms. ACM Comput. Surv. 2020, 52, 1–36. [Google Scholar] [CrossRef]
- Tran-Dang, H.; Kim, D.-S. DISCO: Distributed computation offloading framework for fog computing networks. J. Commun. Networks 2023, 25, 121–131. [Google Scholar] [CrossRef]
- Tran-Dang, H.; Kim, D.S. FRATO: Fog resource based adaptive task offloading for delay-minimizing IoT service provisioning. IEEE Trans. Parallel Distrib. Syst. 2021, 32, 2491–2508. [Google Scholar] [CrossRef]
- Tran-Dang, H.; Bhardwaj, S.; Rahim, T.; Musaddiq, A.; Kim, D.S. Reinforcement learning based resource management for fog computing environment: Literature review, challenges, and open issues. J. Commun. Networks 2022, 24, 83–98. [Google Scholar] [CrossRef]
- Ke, H.; Wang, J.; Wang, H.; Ge, Y. Joint Optimization of Data Offloading and Resource Allocation with Renewable Energy Aware for IoT Devices: A Deep Reinforcement Learning Approach. IEEE Access 2019, 7, 179349–179363. [Google Scholar] [CrossRef]
- Zhang, J.; Du, J.; Shen, Y.; Wang, J. Dynamic Computation Offloading with Energy Harvesting Devices: A Hybrid-Decision-Based Deep Reinforcement Learning Approach. IEEE Internet Things J. 2020, 7, 9303–9317. [Google Scholar] [CrossRef]
- Qiu, X.; Zhang, W.; Chen, W.; Zheng, Z. Distributed and Collective Deep Reinforcement Learning for Computation Offloading: A Practical Perspective. IEEE Trans. Parallel Distrib. Syst. 2021, 32, 1085–1101. [Google Scholar] [CrossRef]
- Ghanavati, S.; Abawajy, J.; Izadi, D. Automata-based Dynamic Fault Tolerant Task Scheduling Approach in Fog Computing. IEEE Trans. Emerg. Top. Comput. 2022, 10, 488–499. [Google Scholar] [CrossRef]
- Chen, J.; Chen, P.; Niu, X.; Wu, Z.; Xiong, L.; Shi, C. Task offloading in hybrid-decision-based multi-cloud computing network: A cooperative multi-agent deep reinforcement learning. J. Cloud Comput. 2022, 11, 90. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, Z.; Başar, T. Multi-Agent Reinforcement Learning: A Selective Overview of Theories and Algorithms. Stud. Syst. Decis. Control 2021, 325, 321–384. [Google Scholar] [CrossRef]
- Suzuki, A.; Kobayashi, M.; Oki, E. Multi-Agent Deep Reinforcement Learning for Cooperative Computing Offloading and Route Optimization in Multi Cloud-Edge Networks. IEEE Trans. Netw. Serv. Manag. 2023, 20, 4416–4434. [Google Scholar] [CrossRef]
- Zhu, X.; Luo, Y.; Liu, A.; Bhuiyan, Z.A.; Member, S.; Zhang, S. Multiagent Deep Reinforcement Learning for Vehicular Computation Offloading in IoT. IEE Internet Things 2021, 8, 9763–9773. [Google Scholar] [CrossRef]
- Tadele, S.B.; Yahya, W.; Kar, B.; Lin, Y.D.; Lai, Y.C.; Wakgra, F.G. Optimizing the Ratio-Based Offloading in Federated Cloud-Edge Systems: A MADRL Approach. IEEE Trans. Netw. Sci. Eng. 2024, 12, 463–475. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Zhang, L.; Zhang, Y.; Li, Q.; Chen, K.C. Reliable Transmission for NOMA Systems With Randomly Deployed Receivers. IEEE Trans. Commun. 2023, 71, 1179–1192. [Google Scholar] [CrossRef]
- Hao, H.; Xu, C.; Zhang, W.; Yang, S.; Muntean, G.M. Joint task offloading, resource allocation, and trajectory design for multi-uav cooperative edge computing with task priority. IEEE Trans. Mob. Comput. 2024, 23, 8649–8663. [Google Scholar] [CrossRef]
- Sellami, B.; Hakiri, A.; Yahia, S.B.; Berthou, P. Energy-aware task scheduling and offloading using deep reinforcement learning in SDN-enabled IoT network. Comput. Networks 2022, 210, 108957. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Al-Khafajiy, M.; Baker, T.; Al-Libawy, H.; Maamar, Z.; Aloqaily, M.; Jararweh, Y. Improving fog computing performance via fog-2-fog collaboration. Future Gener. Comput. Syst. 2019, 100, 266–280. [Google Scholar] [CrossRef]
- Raju, M.R.; Mothku, S.K.; Somesula, M.K. DMITS: Dependency and Mobility-Aware Intelligent Task Scheduling in Socially-Enabled VFC Based on Federated DRL Approach. IEEE Trans. Intell. Transp. Syst. 2024, 25, 17007–17022. [Google Scholar] [CrossRef]
- Fu, X.; Tang, B.; Guo, F.; Kang, L. Priority and dependency-based DAG tasks offloading in fog/edge collaborative environment. In Proceedings of the 2021 IEEE 24th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Dalian, China, 5–7 May 2021; pp. 440–445. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. Openai gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]


| Symbol | Description |
|---|---|
| MAFCPTORA | Multi-Agent Fully Cooperative Task Offloading and Resource Allocation |
| MADRL | Multi-Agent Deep Reinforcement Learning |
| MADDPG | Multi-agent deep deterministic policy gradient |
| MAPPO | Multi-agent proximal policy optimization |
| TD3 | Twin Delayed Deep Deterministic |
| MATD3 | Multi-agent twin delayed DDPG |
| DRL | Deep Reinforcement Learning |
| MDP | Markov Decision Process |
| Notation | Description |
|---|---|
| Number of Fog nodes | |
| Number of User devices | |
| Available Memory at each Fog node | |
| Available CPU at each Fog node | |
| Task processing delay | |
| Task offloading delay | |
| Transmission Bandwidth | |
| Energy consumption of task k | |
| Battery life time | |
| Channel condition | |
| Number of channel available | |
| Task to be executed | |
| Total size of the task | |
| Channel transmission power | |
| Maximum tolerable delay | |
| Q | Waiting tasks in each Fog node |
| State of each agent | |
| Observation of environment at time t | |
| Individual agent action | |
| Offloading decision | |
| Resource allocation decision at time t | |
| and | Optimal and target policy |
| and | Individual and collective average reward |
| Fog ID | Status | CPU Core | CPU Usage (%) | Memory Usage (%) | Bandwidth | Queue | Idle Time (%) | Task Processed | Next Hope |
|---|---|---|---|---|---|---|---|---|---|
| Busy | 8 | 70% | 50% | 100 Mbps | 30% | 10 |
| Parameters | Quantity |
|---|---|
| Number of User devices | 100 |
| Number of Fog nodes | 6 |
| Distance between fog nodes | 1 km to 5 km |
| Task arrival rate at | 3 × 102 packet per second |
| Available CPU core | [2–4] |
| Bandwidth between fog nodes | 50 MHz |
| Channel condition H | |
| Computational capacity | [100–1000] MIPS |
| Computational capacity | 50 MIPS |
| CPU frequency range | – Hz |
| Path loss exponent | 2.7 |
| Channel transmission power | 10 dBm |
| Channel transmission power | 30 dBm |
| Number of episode | 10,000 |
| Observation step per episode | 100 |
| Learning rate | 0.001 |
| Discount Factor | 0.99 |
| Weight coefficient and | 0.7 and 0.3 |
| Model | Ave Reward | Ave Latency | Ave Energy Consumption |
|---|---|---|---|
| MAPPO | 0.34 ± 0.01 | 0.17 ± 0.02 | 0.96 ± 0.15 |
| MASAC | 0.35 ± 0.01 | 0.20 ± 0.03 | 0.92 ± 0.14 |
| MAIDDPG | 0.32 ± 0.01 | 0.14 ± 0.0143 | 0.9998 ± 0.1873 |
| MATD3 | 0.36 ± 0.01 | 0.08 ± 0.01 | 0.76 ± 0.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, E.M.; Lemma, F.; Srinivasagan, R.; Abawajy, J. Efficient Delay-Sensitive Task Offloading to Fog Computing with Multi-Agent Twin Delayed Deep Deterministic Policy Gradient. Electronics 2025, 14, 2169. https://doi.org/10.3390/electronics14112169
Ali EM, Lemma F, Srinivasagan R, Abawajy J. Efficient Delay-Sensitive Task Offloading to Fog Computing with Multi-Agent Twin Delayed Deep Deterministic Policy Gradient. Electronics. 2025; 14(11):2169. https://doi.org/10.3390/electronics14112169
Chicago/Turabian StyleAli, Endris Mohammed, Frezewd Lemma, Ramasamy Srinivasagan, and Jemal Abawajy. 2025. "Efficient Delay-Sensitive Task Offloading to Fog Computing with Multi-Agent Twin Delayed Deep Deterministic Policy Gradient" Electronics 14, no. 11: 2169. https://doi.org/10.3390/electronics14112169
APA StyleAli, E. M., Lemma, F., Srinivasagan, R., & Abawajy, J. (2025). Efficient Delay-Sensitive Task Offloading to Fog Computing with Multi-Agent Twin Delayed Deep Deterministic Policy Gradient. Electronics, 14(11), 2169. https://doi.org/10.3390/electronics14112169








