An Improved ADRC Parameters Self-Tuning Controller for Multi-Color Register System in Unit-Type Flexographic Printing Machines
Abstract
1. Introduction
2. Mathematical Modeling of the Register System
2.1. Mathematical Model Establishment
2.2. Mathematical Model Decoupling
3. Design of Decoupling Control Strategy
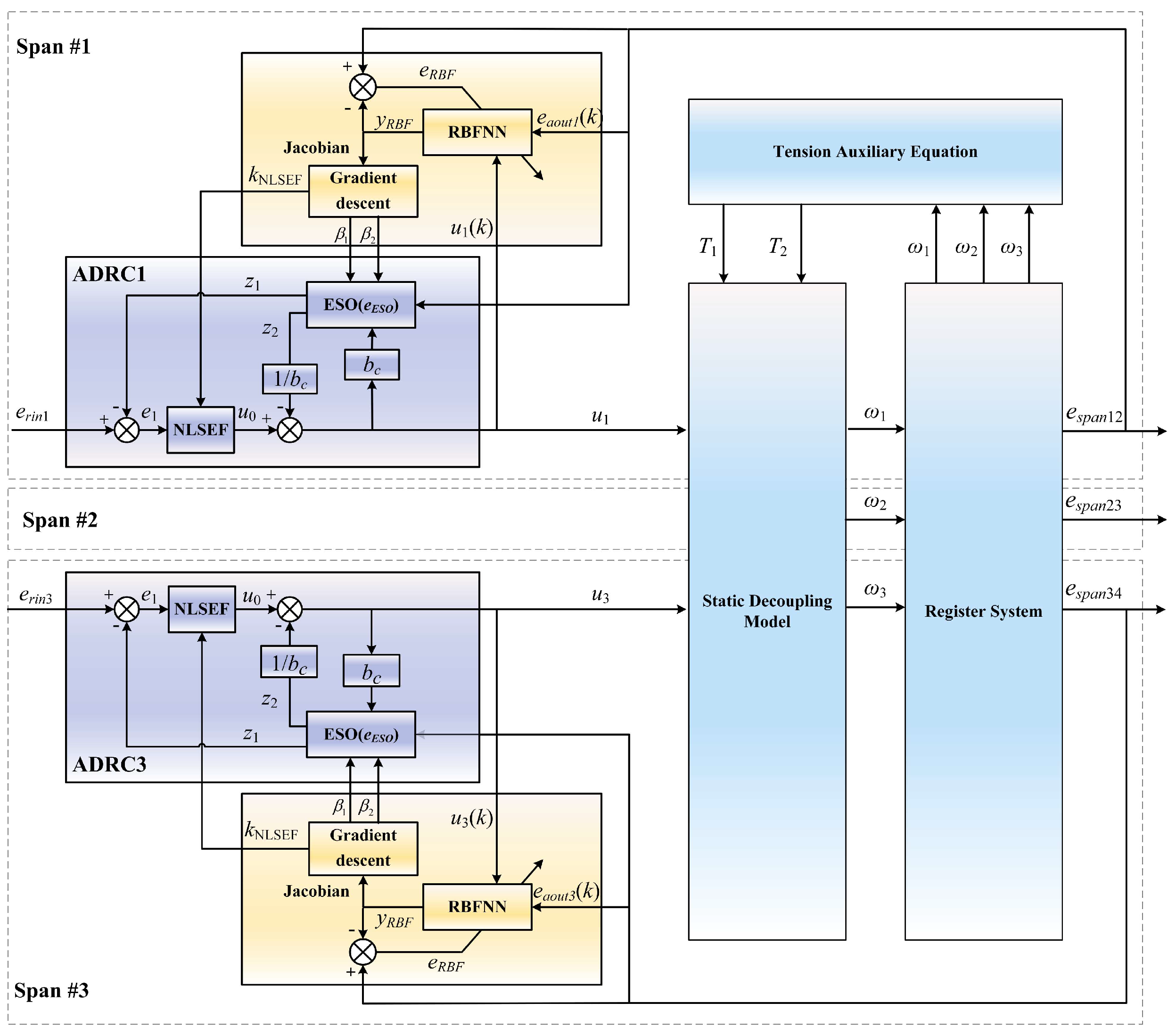
3.1. Analysis of ADRC Controller
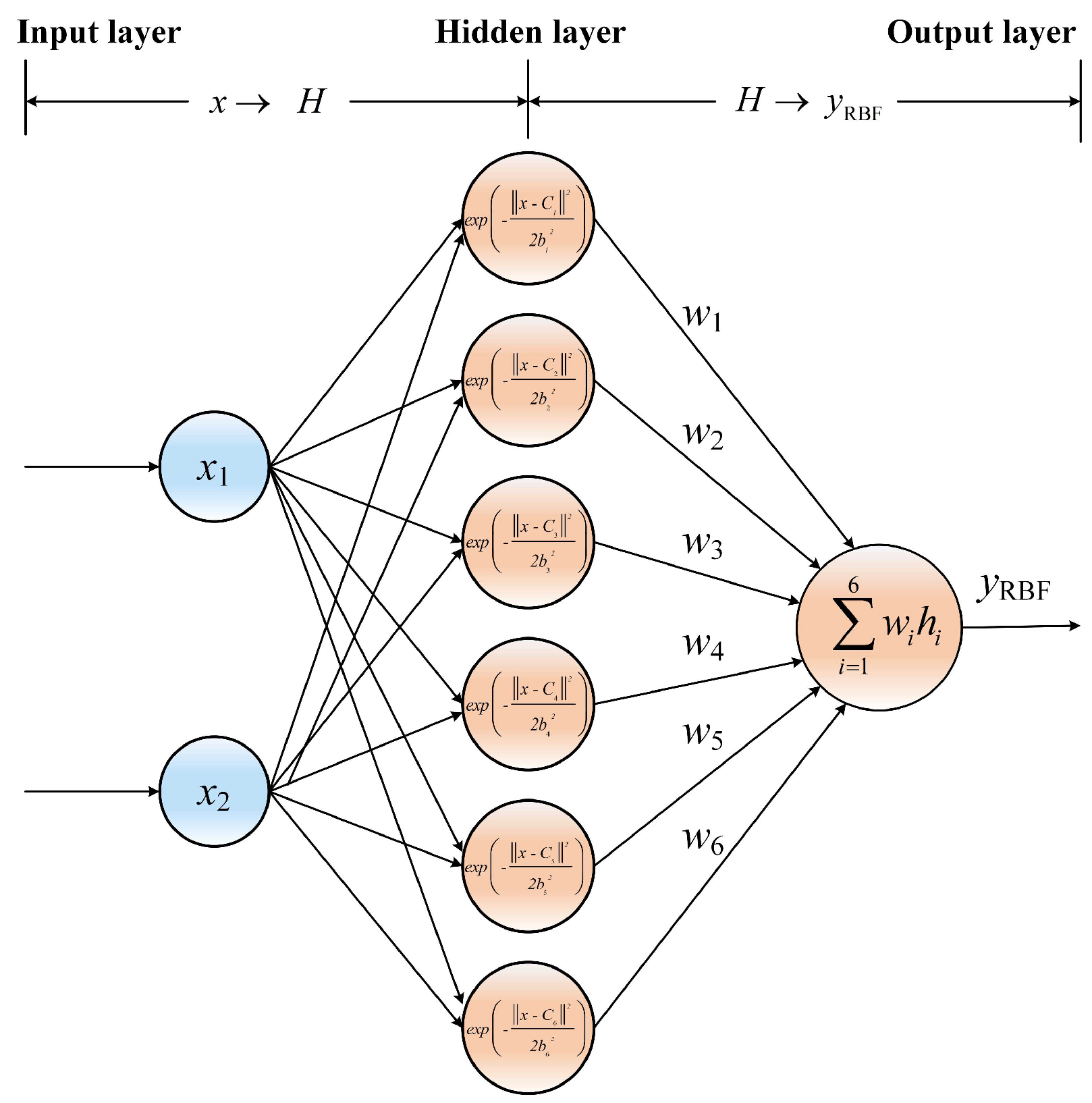
3.2. Adjustment of Controller Parameters
- Set the initial values of the RBF neural network parameters and the initial values of the ADRC controller parameters;
- The RBF neural network receives the output control signal u(k) from the ADRC controller and adjusts to the actual output error espan(k) of the system;
- Calculate the identification model error metric eRBF to update the RBF neural network parameters, including the center vector, basis width vector, and network weights; Then, calculate the system error metric Econtrol and, combined with the Jacobian information, update the ADRC controller parameters to correct β1, β2, kNLSEF, and bc;
- Judge whether the actual error espan of the tuning system is within the acceptable range, and decide whether to proceed to the next cycle or to terminate.
4. Simulation and Analysis
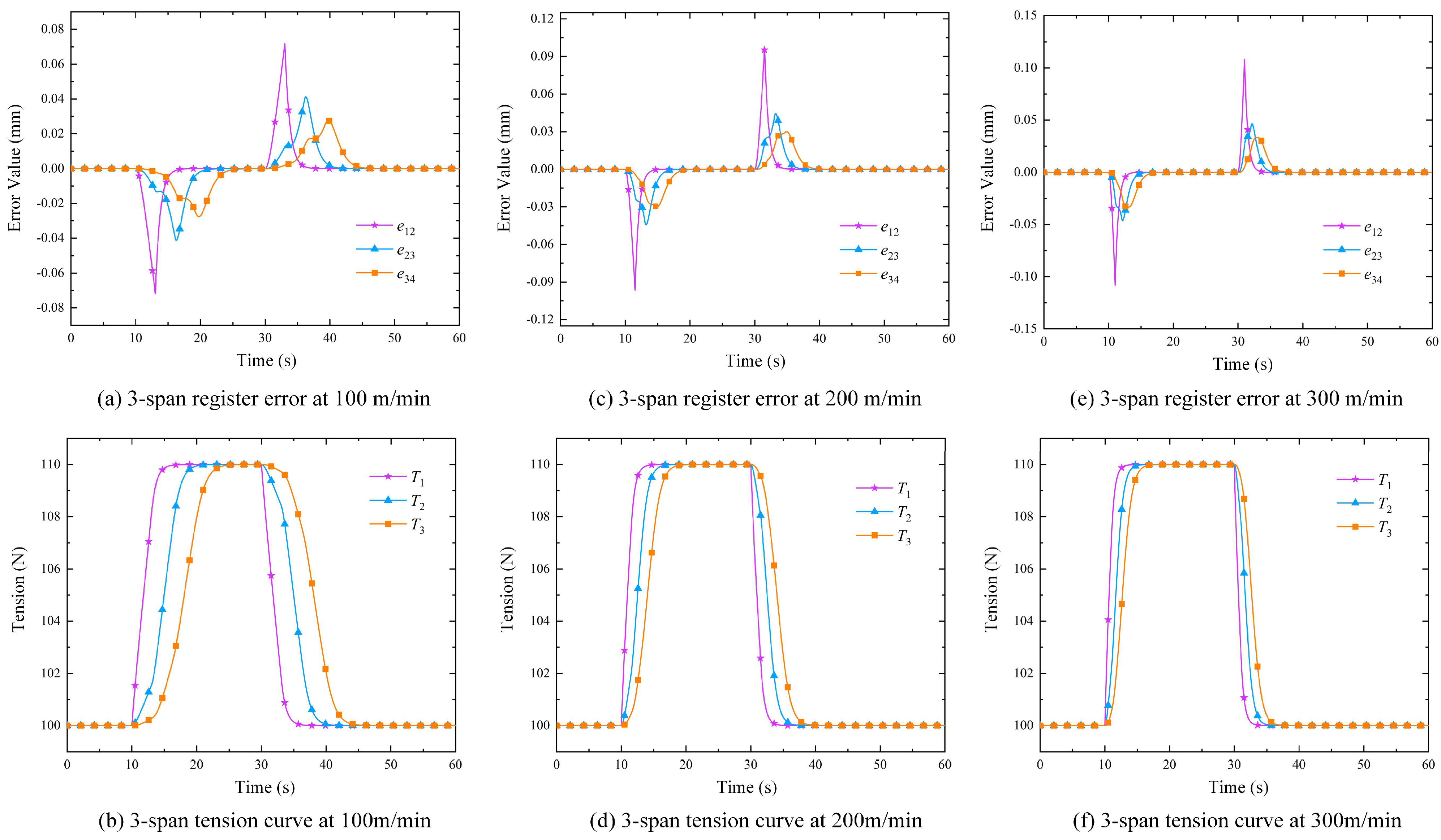
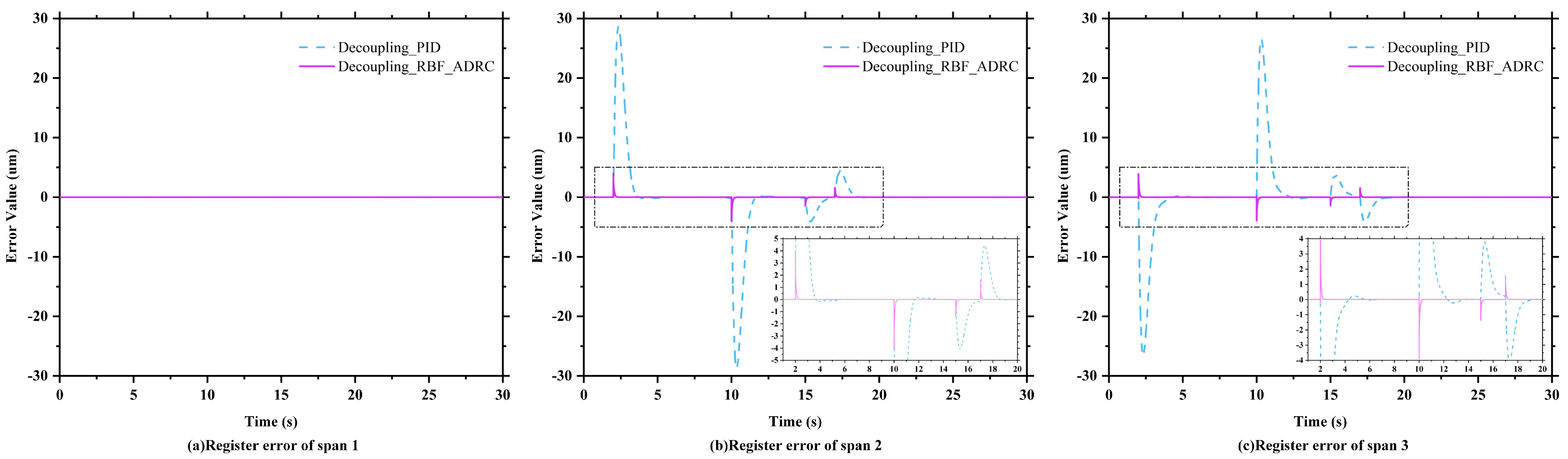
4.1. Verification of Decoupling Performance
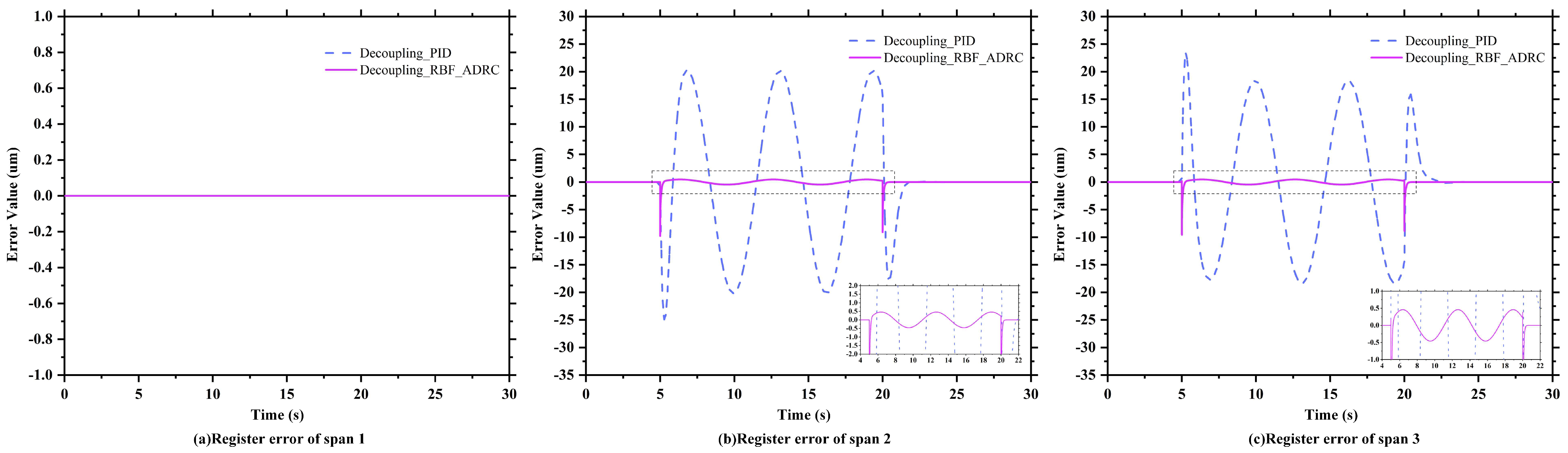
4.2. Verification of Robustness
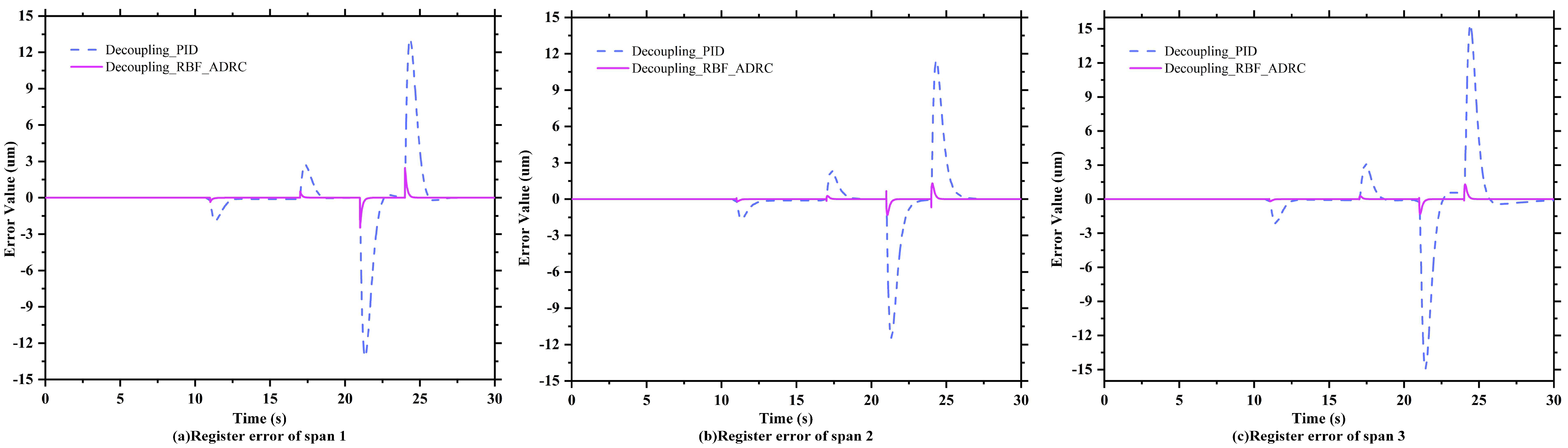
4.3. Verification of Anti-Interference Performance
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, H.; Xu, J.; Sun, K. Design and Analysis of Tension Control System for Transformer Insulation Layer Winding. IEEE Access. 2020, 8, 95068–95081. [Google Scholar] [CrossRef]
- Jabbar, K.A.; Pagilla, P.R. Modeling and Analysis of Web Span Tension Dynamics Considering Thermal and Viscoelastic Effects in Roll-to-Roll Manufacturing. J. Manuf. Sci. Eng. 2018, 140, 051005. [Google Scholar] [CrossRef]
- Lee, J.; Jo, M.; Lee, C. Advanced Tension Model for Highly Integrated Flexible Electronics in Roll-To-Roll Manufacturing. IEEE/ASME Trans. Mechatron. 2021, 27, 2908–2917. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, S.; Feng, L. Coupling Modeling and Analysis of the Tension System for Roll-to-Roll Gravure Printing Machines. J. Imaging Sci. Technol. 2021, 66, 020401–02040110. [Google Scholar] [CrossRef]
- Chen, Z.; Zheng, Y.; Zhang, T. Modeling and Register Control of the Speed-up Phase in Roll-to-Roll Printing Systems. IEEE Trans. Autom. Sci. Eng. 2018, 16, 1438–1449. [Google Scholar] [CrossRef]
- Chen, Z.; Ying, Z.; Zhou, M. Model-Based Feedforward Register Control of Roll-to-Roll Web Printing Systems. Control. Eng. Pract. 2016, 51, 58–68. [Google Scholar] [CrossRef]
- Chen, Z.; He, J.; Ying, Z. An Optimized Feedforward Decoupling PD Register Control Method of Roll-to-Roll Web Printing Systems. IEEE Trans. Autom. Sci. Eng. 2016, 13, 274–283. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, T.; Zheng, Y. Fully Decoupled Control of the Machine Directional Register in Roll-to-Roll Printing System. IEEE Trans. Ind. Electron. 2020, 68, 10007–10018. [Google Scholar] [CrossRef]
- Lee, J.; Shin, K.; Lee, C. Analysis of Dynamic Thermal Characteristic of Register of Roll-to-Roll Multi-Layer Printing Systems. Robot. Comput.-Integr. Manuf. 2015, 35, 77–83. [Google Scholar] [CrossRef]
- Lee, J.; Seong, J.; Park, J. Register Control Algorithm for High Resolution Multilayer Printing in the Roll-to-Roll Process. Mech. Syst. Signal Process. 2015, 60, 706–714. [Google Scholar] [CrossRef]
- Lee, J.; Shin, K.H.; Kang, H. Design of A Register Controller Considering Inherent Characteristics of a Roll-to-Roll Continuous Manufacturing System. Int. J. Adv. Manuf. Technol. 2019, 102, 3725–3737. [Google Scholar] [CrossRef]
- Lee, J.; Shin, K.; Jung, H. Control Scheme for Rapidly Responding Register Controller Using Response Acceleration Input in Industrial Roll-To-Roll Manufacturing Systems. IEEE Trans. Ind. Electron. 2021, 69, 5215–5224. [Google Scholar] [CrossRef]
- Kang, H.; Lee, C.; Shin, K. Modeling and Compensation of The Machine Directional Register in Roll-to-Roll Printing. Control Eng. Pract. 2013, 21, 645–654. [Google Scholar] [CrossRef]
- Kim, C.; Jeon, S.W.; Kim, C.H. Reduction of Linearly Varying Term of Register Errors Using a Dancer System in Roll-to-Roll Printing Equipment for Printed Electronics. Int. J. Precis. Eng. Manuf. 2019, 20, 1485–1493. [Google Scholar] [CrossRef]
- Jung, H.; Nguyen, A.D.; Choi, J. High-Precision Register Error Control Using Active-Motion-Based Roller in Roll-to-Roll Gravure Printing. Jpn. J. Appl. Phys. 2018, 57, 05GB04. [Google Scholar] [CrossRef]
- Liu, S.; Mei, X.; Li, J. Design Feedforward Active Disturbance Rejection Control Controller for Multi-Color Register System. J. Mech. Eng. 2015, 51, 143–150. [Google Scholar] [CrossRef]
- Li, M.; Feng, H.; Zhang, Y. RBF Neural Network Tuning PID Control Based on UMAC. J. Beijing Univ. Aeronaut. Astronaut. 2018, 44, 2063. [Google Scholar]
- Kumar, R.; Agrawal, H.P.; Shah, A. Maximum Power Point Tracking in Wind Energy Conversion System Using Radial Basis Function Based Neural Network Control Strategy. Sustain. Energy Technol. Assess. 2019, 36, 100533. [Google Scholar] [CrossRef]
- Guo, X.; Tan, A.; Wang, Q. Active disturbance rejection control with adaptive RBF neural network for a permanent magnet spherical motor. ISA Trans. 2025, 156, 678–688. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Mei, X.S.; Tao, T. Research on the Register System Modeling and Control of Gravure Printing Press. J. Mech. Eng. Sci. 2012, 226, 626–635. [Google Scholar] [CrossRef]
- Marrero, D.; Kern, J.; Urrea, C. A Novel Robotic Controller Using Neural Engineering Framework-Based Spiking Neural Networks. Sensors 2024, 24, 491. [Google Scholar] [CrossRef] [PubMed]
- Halaly, R.; Elishai, E.T. Autonomous Driving Controllers with Neuromorphic Spiking Neural Networks. Front. Neurorobotics 2023, 17, 1234962. [Google Scholar] [CrossRef] [PubMed]
- Merces, L. Advanced Neuromorphic Applications Enabled by Synaptic Ion-Gating Vertical Transistors. Adv. Sci. 2024, 11, 2305611. [Google Scholar] [CrossRef]
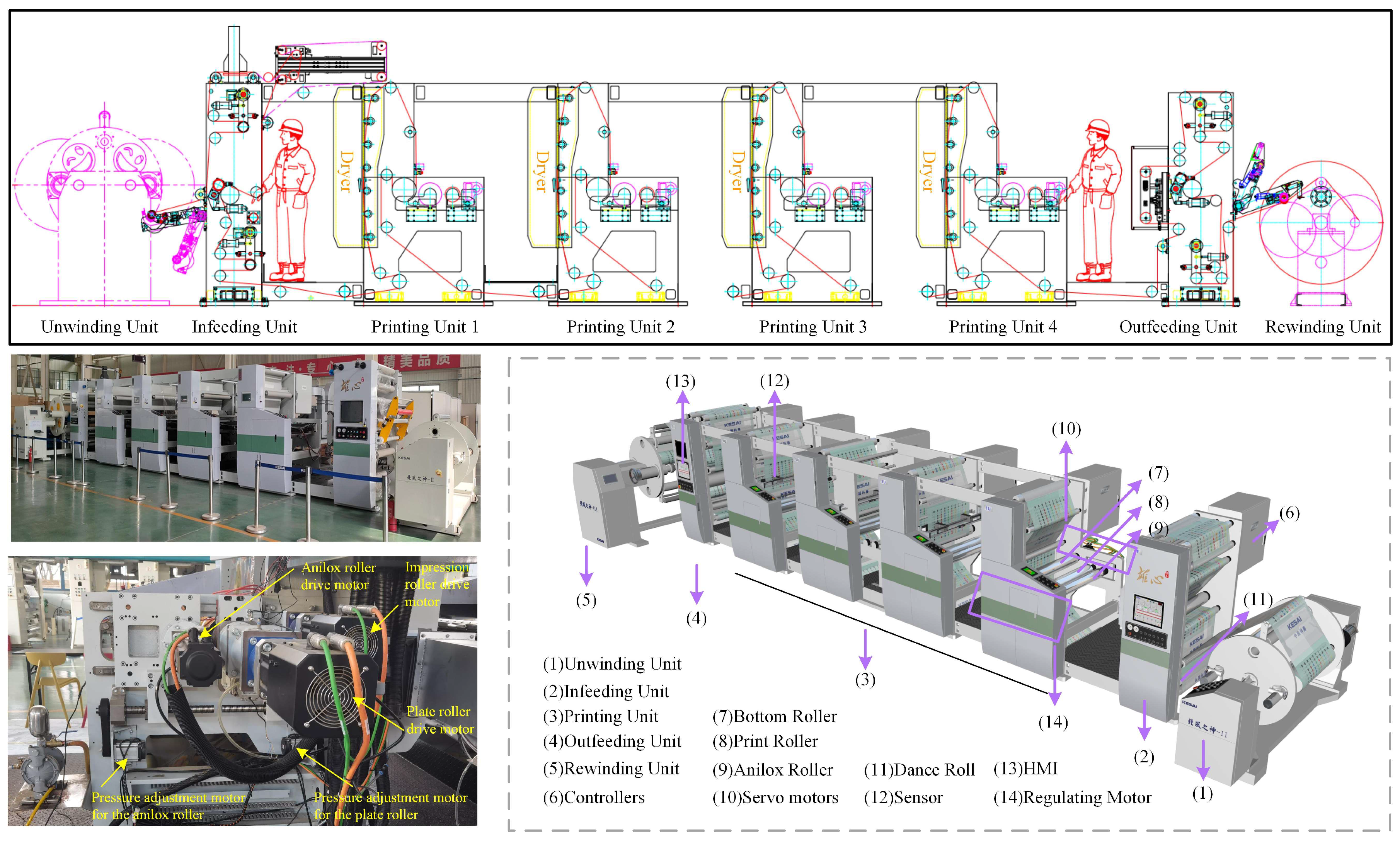






| Machine Parameters | Value | Simulink Parameters | Value |
|---|---|---|---|
| Size | 14 × 4 × 3 | A | 2.7 × 10−5 m2 |
| Substrate | BOPP\PET | R1, R2, R3, R4 | 0.5 m |
| EBOPP (10 °C) | 2.6 × 109 Pa | L1, L2, L3 | 5.05 m |
| EBOPP (20 °C) | 2.24 × 109 Pa | T * | 100 N |
| EBOPP (30 °C) | 2.02 × 109 Pa | Ω * | 1.66–3.32 m/s |
| EPET (20 °C) | 4.89 × 109 Pa | E * | 0 mm |
| LD | 1.8 m |
| Parameters | RBF_ADRC1 | RBF_ADRC2 | RBF_ADRC3 |
|---|---|---|---|
| β1 | 5000 | 1800 | 20,100 |
| β2 | 103,333 | 128,000 | 163,300 |
| kNLSEF | 150 | 410 | 130 |
| δ | 0.5 | 0.4 | 0.4 |
| bc | 1 | 1 | 1 |
| η | 0.25 | 0.42 | 0.45 |
| η1 | 0.1 | 0.3 | 0.35 |
| η2 | 0.02 | 0.035 | 0.035 |
| η3 | 0.01 | 0.01 | 0.02 |
| η4 | 0.002 | 0.001 | 0.003 |
| α | 0.5 | 0.5 | 0.5 |
| Parameters | PID1 | PID2 | PID3 |
|---|---|---|---|
| kp | 2.5 | 12 | 6 |
| ki | 5 | 20 | 2.7 |
| kd | 0 | 2 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Liu, S.; Ding, H.; Ju, G.; Feng, L. An Improved ADRC Parameters Self-Tuning Controller for Multi-Color Register System in Unit-Type Flexographic Printing Machines. Electronics 2025, 14, 2162. https://doi.org/10.3390/electronics14112162
Zhao W, Liu S, Ding H, Ju G, Feng L. An Improved ADRC Parameters Self-Tuning Controller for Multi-Color Register System in Unit-Type Flexographic Printing Machines. Electronics. 2025; 14(11):2162. https://doi.org/10.3390/electronics14112162
Chicago/Turabian StyleZhao, Wenhui, Shanhui Liu, Haodi Ding, Guoli Ju, and Lei Feng. 2025. "An Improved ADRC Parameters Self-Tuning Controller for Multi-Color Register System in Unit-Type Flexographic Printing Machines" Electronics 14, no. 11: 2162. https://doi.org/10.3390/electronics14112162
APA StyleZhao, W., Liu, S., Ding, H., Ju, G., & Feng, L. (2025). An Improved ADRC Parameters Self-Tuning Controller for Multi-Color Register System in Unit-Type Flexographic Printing Machines. Electronics, 14(11), 2162. https://doi.org/10.3390/electronics14112162







