Gross Domestic Product Forecasting Using Deep Learning Models with a Phase-Adaptive Attention Mechanism
Abstract
1. Introduction
2. Related Work
3. Proposed Method
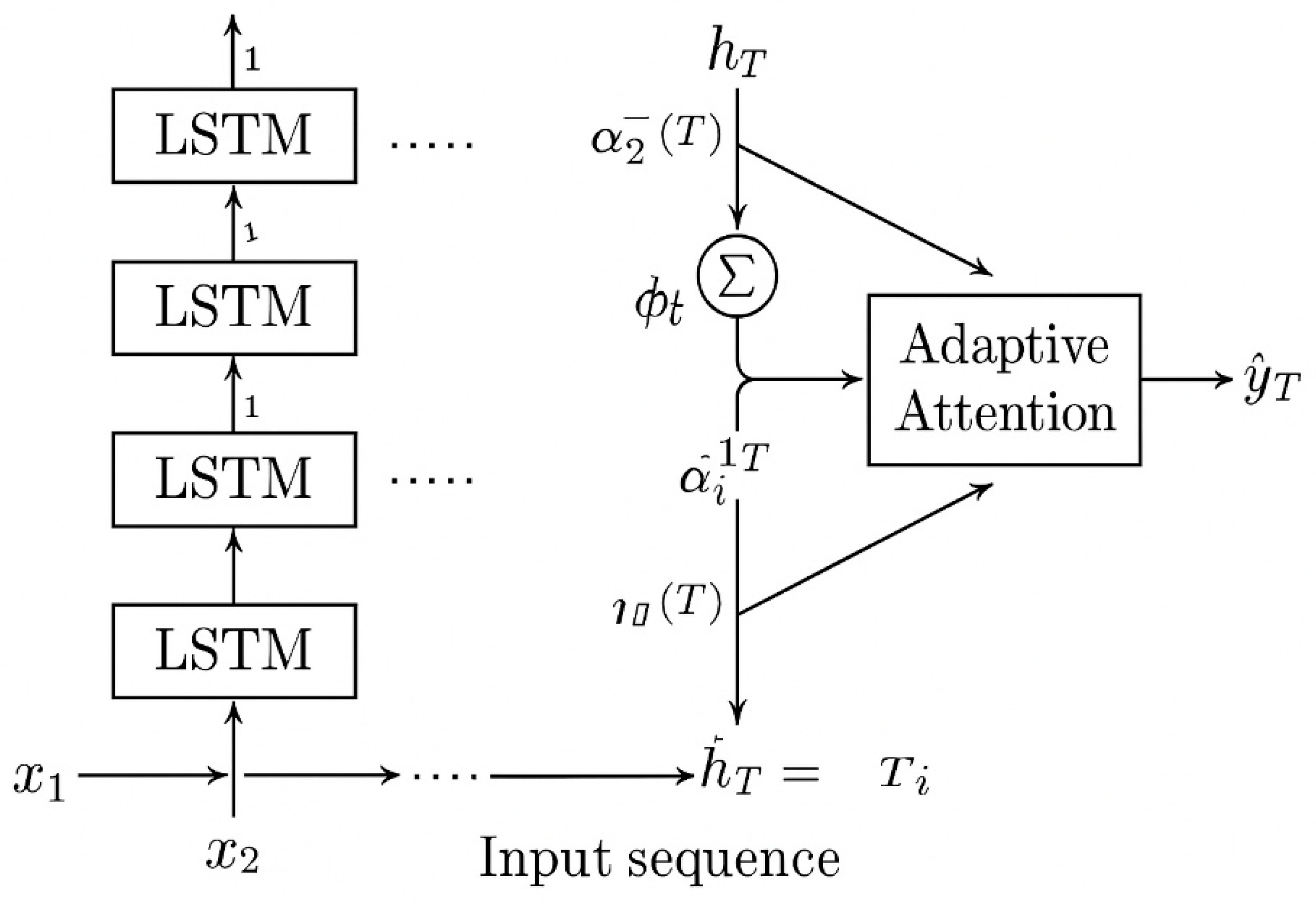
3.1. Model Architecture
- -
- Multi-layer LSTM: This component is responsible for extracting deep temporal features from the input time series, such as GDP growth, investment ratios, household consumption, and employment indicators. The use of multiple LSTM layers allows the model to learn abstract representations of macroeconomic dynamics;
- -
- Phase-Aware Adaptive Attention: Unlike standard attention mechanisms, this component is customized to adapt to each phase of the economic cycle (recession, recovery, expansion, and stagnation). Each phase is associated with a distinct set of attention parameters, enabling the model to prioritize critical time steps depending on the economic context;
- -
- Fully-connected output layer: This layer combines the contextual information from the LSTM and the attention mechanism to generate the final GDP growth forecast for the next time step.
3.2. Phase-Adaptive Attention Representation in Economic Cycles
- (1)
- Segmenting the economic cycle into phases;
- (2)
- Mapping phase-specific attention weights accordingly.
3.2.1. Economic Phase Segmentation
3.2.2. Phase-Specific Attention Design
- αₜᵖ: the attention weight at time t in phase p;
- wᵖ: the trainable attention weight vector for phase p;
- hₜ: the hidden output of the LSTM at time t.
| Algorithm 1 Pseudocode |
| Input: H = [h1, h2, …, hₜ] // Hidden states from LSTM P = [p1, p2, …, pₜ] // Phase labels for each time step Wᵖ, bᵖ for each phase p ∈ {Recession, Recovery, Expansion, Stagnation} Output: Context vector cₜ 1: Initialize attention weights α = [] 2: for t = 1 to T do 3: Identify phaseₜ ← P[t] 4: Retrieve parameters: W ← Wᵖ[phaseₜ], b ← bᵖ[phaseₜ] 5: Compute energy: eₜ ← tanh(W · hₜ + b) 6: Compute attention score: αₜ ← softmax(eₜ) 7: Append αₜ to α 8: end for 9: Compute context vector: cₜ = ∑ (αₜ · hₜ) 10: Return cₜ Illustrative Example Assume T = 3, and the LSTM outputs are scalar values, as follows: t = [1, 2, 3]; h = [0.5, 1.0, −0.2] Phase: Recession Let wrecession = 0.8, and brecession = 0.1 Energy calculation: e1 = tanh(0.8 × 0.5 + 0.1) = tanh(0.5) = 0.462 e2 = tanh(0.8 × 1.0 + 0.1) = tanh(0.9) = 0.716 e3 = tanh(0.8 × (−0.2) + 0.1) = tanh(−0.06) = −0.06 Softmax attention weights: α1 = ≈ 0.30 α2 = ≈ 0.47 α3 = ≈ 0.23 Context vector: Crecession ≈ 0.30 × 0.5 + 0.47 × 1.0 + 0.23 × (−0.2) ≈ 0.41 Phase: Expansion Let wexpansion = 0.2, and bexpansion = 0 Energy calculation: e1 = tanh(0.2 × 0.5) = tanh(0.1) = 0.1 e2 = tanh(0.2 × 1.0) = tanh(0.2) = 0.197 e3 = tanh(0.2 × (−0.2)) = tanh(−0.04) = −0.04 Softmax attention weights: α ≈ [0.31, 0.34, 0.35] Context vector: cexpansion ≈ 0.31 × 0.5 + 0.34 × 1.0 + 0.35 × (−0.2) ≈ 0.42 Interpretation |
3.3. Phase-Wise Training Strategy
- Phase-Based Data Segmentation
- Phase-Weighted Loss Function
- Phase-Specific Hyperparameter Optimization
- Phase-Wise Fine-Tuning
- Conditional Cross-Validation
3.4. Procedure
- Preprocess and normalize the entire dataset using z-score standardization;
- Segment the economic cycle into four phases: recession, recovery, expansion, and slowdown;
- Train the PAA-LSTM model using phase-wise fine-tuning strategies;
- Compare forecasting performance with baseline models: ARIMA, XGBoost, Transformer, LSTM, Bi-LSTM, and LSTM + Attention.
- Evaluate the models
4. Experiment and Discussion
4.1. Data and Scope
- Emerging economies: China, Russia;
- Developing economies: Vietnam, India;
- Developed economies: United States, Canada.
Data Preprocessing Steps
- Step 1: Remove missing, invalid, or inconsistent observations across data sources;
- Step 2: Construct additional economic interaction features, such as the product of human capital and employment rate (hc × emp), to enhance the model’s capacity to learn nonlinear patterns;
- Step 3: Structure the data as time series tables sorted by country and time, suitable for sequential deep learning training.
4.2. Experimental Results
- For countries with data from 1980 to 2019:
- ○
- Fold 1: Train = 1980–1999, Test = 2000–2004;
- ○
- Fold 2: Train = 1980–2004, Test = 2005–2009;
- ○
- Fold 3: Train = 1980–2009, Test = 2010–2014;
- ○
- Fold 4: Train = 1980–2014, Test = 2015–2019.
- For Russia (data from 1991 to 2019):
- ○
- Fold 1: Train = 1991–2010, Test = 2011–2014;
- ○
- Fold 2: Train = 1991–2014, Test = 2015–2019.
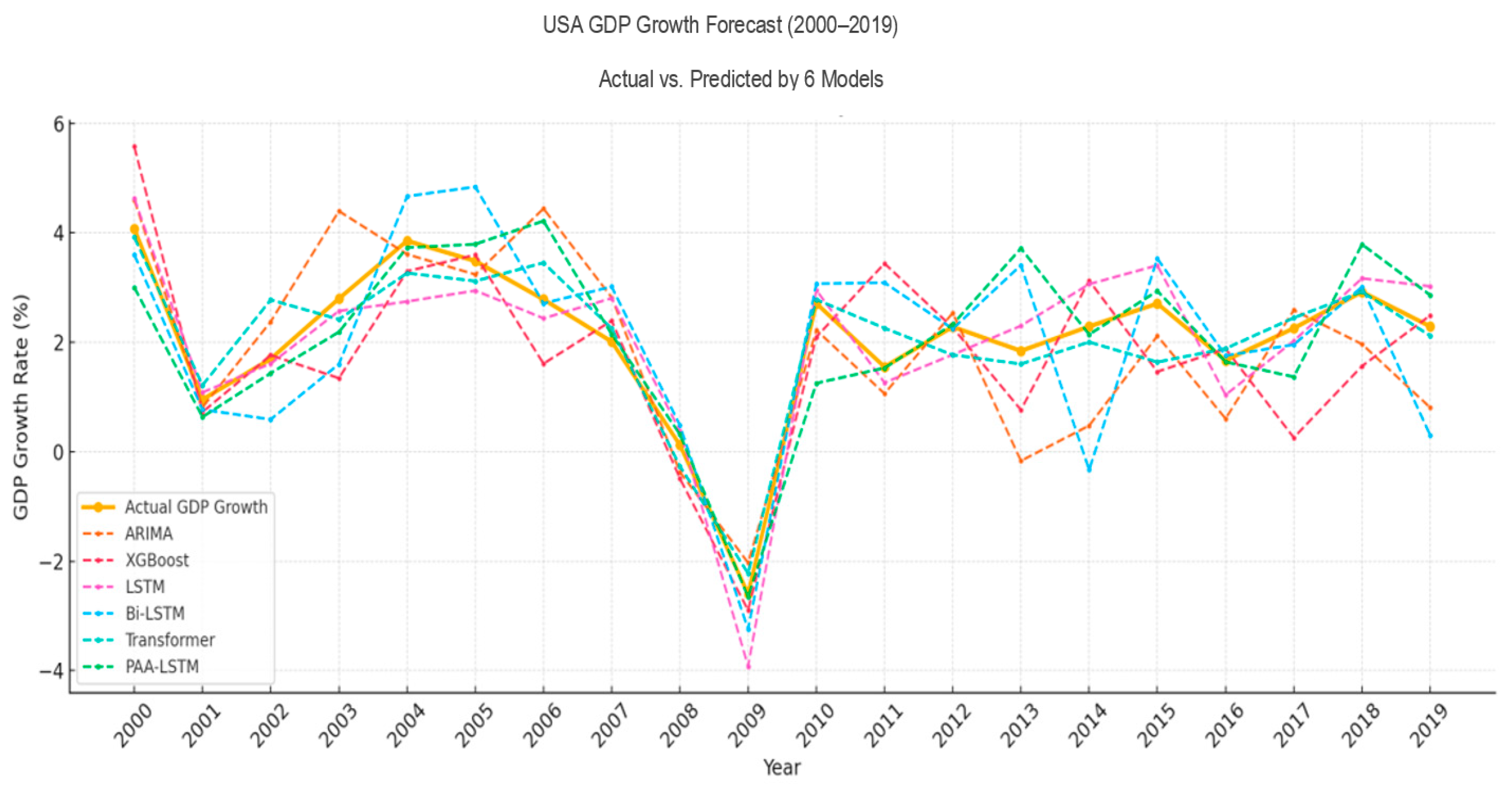
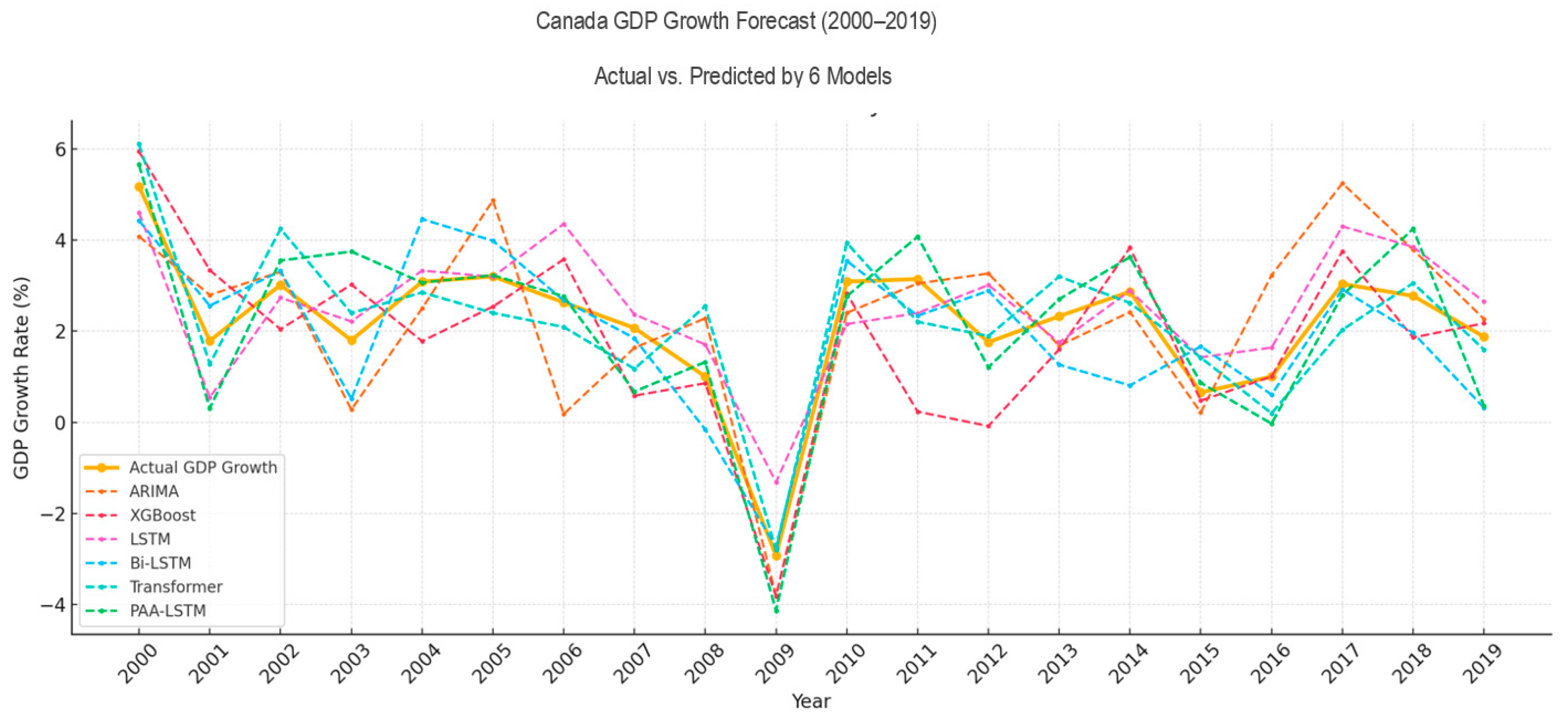
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- OECD. OECD Economic Outlook; OECD Publishing: Paris, France, 2023; Volume 2023, Issue 2; Available online: https://www.oecd.org/en/publications/oecd-economic-outlook/volume-2023/issue-2_7a5f73ce-en.html (accessed on 15 January 2025).
- IMF. World Economic Outlook, October 2023: Navigating Global Divergences; International Monetary Fund: Washington, DC, USA, 2023; Available online: https://www.imf.org/en/Publications/WEO/Issues/2023/10/10/world-economic-outlook-october-2023 (accessed on 15 January 2025).
- Păun, E.; Dima, M. The relevance of ARIMA models in financial forecasting under volatility and structural uncertainty. Theor. Appl. Econ. 2022, XXIX, 5–22. Available online: https://store.ectap.ro/articole/1222.pdf (accessed on 20 January 2024).
- MASEconomics. Structural Breaks in Time Series Analysis: Managing Sudden Changes. 2023. Available online: https://maseconomics.com/structural-breaks-in-time-series-analysis-managing-sudden-changes/ (accessed on 10 January 2025).
- Qin, Y.; Song, D.; Cheng, H.; Cheng, W.; Jiang, G.; Cottrell, G. A dual-stage attention-based recurrent neural network for time series prediction. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 2627–2633. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Burns, A.; Mitchell, W. Measuring Business Cycles; National Bureau of Economic Research: Cambridge, MA, USA, 1946. [Google Scholar]
- Hamilton, J.D. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Mourougane, A.; Roma, M. Can confidence indicators be useful to predict short-term real GDP growth? Appl. Econ. Lett. 2003, 10, 519–522. [Google Scholar] [CrossRef]
- Abeysinghe, T. Forecasting Singapore’s quarterly GDP with monthly external trade. Int. J. Forecast. 1998, 14, 505–513. [Google Scholar] [CrossRef]
- Meyler, A.; Kenny, G.; Quinn, T. Forecasting Irish Inflation Using ARIMA Models. Central Bank of Ireland, Technical Paper 3/RT/98. 1998. Available online: https://www.centralbank.ie/docs/default-source/publications/research-technical-papers/3rt98---forecasting-irish-inflation-using-arima-models-(kenny-meyler-and-quinn).pdf (accessed on 15 December 2024).
- Stock, J.H.; Watson, M.W. Core Inflation and Trend Inflation. Rev. Econ. Stat. 2016, 98, 770–784. [Google Scholar] [CrossRef]
- Abonazel, M.R.; Abd-Elftah, A.I. Forecasting egyptian gdp using arima models. Rep. Econ. Financ. 2019, 5, 35–47. Available online: https://www.m-hikari.com/ref/ref2019/ref1-2019/p/abonazelREF1-2019.pdf (accessed on 20 January 2024). [CrossRef]
- Voumik, L.C.; Smrity, D.Y. Forecasting GDP per capita in Bangladesh: Using ARIMA model. Eur. J. Bus. Manag. Res. 2020, 5, 1–5. [Google Scholar] [CrossRef]
- Ghazo, A. Applying the ARIMA Model to the Process of Forecasting GDP and CPI in the Jordanian Economy. Int. J. Financ. Res. 2021, 12, 70–85. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 2nd ed.; Monash University: Melbourne, Australia, 2018; Available online: https://otexts.com/fpp2/ (accessed on 20 January 2024).
- Sims, C.A. Macroeconomics and reality. Econom. J. Econom. Soc. 1980, 48, 1–48. [Google Scholar] [CrossRef]
- Robertson, J.C.; Tallman, E.W. Vector autoregressions: Forecasting and reality. Econ. Rev. Fed. Reserve Bank Atlanta 1999, 84, 4. [Google Scholar]
- Salisu, A.A.; Gupta, R.; Olaniran, A. The effect of oil uncertainty shock on real gdp of 33 countries: A global var approach. Appl. Econ. Lett. 2021, 30, 269–274. [Google Scholar] [CrossRef]
- Maccarrone, G.; Morelli, G.; Spadaccini, S. GDP Forecasting: Machine Learning, Linear or Autoregression? Front. Artif. Intell. 2021, 4, 757864. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Oancea, B. Advancing GDP Forecasting: The Potential of Machine Learning Techniques in Economic Predictions. arXiv 2025, arXiv:2502.19807. [Google Scholar] [CrossRef]
- Staffini, A. A CNN–BiLSTM Architecture for Macroeconomic Time Series Forecasting. Eng. Proc. 2023, 39, 33. [Google Scholar] [CrossRef]
- Fan, Y.; Tang, Q.; Guo, Y.; Wei, Y. BiLSTM-MLAM: A Multiscale Time Series Forecasting Model Based on BiLSTM and Local Attention Mechanism. Sensors 2024, 24, 3962. [Google Scholar] [CrossRef] [PubMed]
- Widiputra, H.; Mailangkay, A.; Gautama, E. Multivariate CNN-LSTM Model for Multiple Parallel Financial Time-Series Prediction. Complexity 2021, 2021, 9903518. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar] [CrossRef]
- Xu, C.; Li, J.; Feng, B.; Lu, B. A Financial Time-Series Prediction Model Based on Multiplex Attention and Linear Transformer Structure. Appl. Sci. 2023, 13, 5175. [Google Scholar] [CrossRef]
- Li, S.; Schulwolf, Z.B.; Miikkulainen, R. Transformer based time-series forecasting for stock. arXiv 2025, arXiv:2502.09625. [Google Scholar]
- Fischer, T.; Sterling, M.; Lessmann, S. Fx-spot predictions with state-of-the-art transformer and time embeddings. Expert Syst. Appl. 2024, 249, 123538. [Google Scholar] [CrossRef]
- Qiu, J.; Wang, B.; Zhou, C. Forecasting stock prices with long-short term memory neural network based on attention mechanism. PLoS ONE 2020, 15, e0227222. [Google Scholar] [CrossRef]
- Zhang, J.; Wen, J.; Yang, Z. China’s GDP forecasting using Long Short Term Memory Recurrent Neural Network and Hidden Markov Model. PLOS ONE 2022, 17, 1–17. [Google Scholar] [CrossRef]
- Zarnowitz, V. Business Cycles: Theory, History, Indicators, and Forecasting; University of Chicago Press: Chicago, IL, USA, 1992. [Google Scholar]
- Blanchard, O.; Johnson, D.R. Macroeconomics, 7th ed.; Pearson: Boston, MA, USA, 2017. [Google Scholar]
- Feenstra, R.; Inklaar, R.; Timmer, M. The next generation of the Penn World Table. Am. Econ. Rev. 2015, 105, 3150–3182. Available online: https://www.rug.nl/ggdc/productivity/pwt/ (accessed on 15 January 2024). [CrossRef]
- World Bank. World Development Indicators. Available online: https://data.worldbank.org (accessed on 15 January 2025).
- Hull, I. Machine Learning for Economics and Finance in TensorFlow 2: Deep Learning Models for Research and Industry; Apress: Berkeley, CA, USA, 2021. [Google Scholar]
- Chen, X.-S.; Kim, M.G.; Lin, C.; Na, H.J. Development of Per Capita GDP Forecasting Model Using Deep Learning: Incorporating CPI and Unemployment. Sustainability 2025, 17, 843. [Google Scholar] [CrossRef]
- Jallow, H.; Mwangi, R.W.; Gibba, A.; Imboga, H. Transfer Learning for Predicting GDP Growth Based on Remittance Inflows: A Case Study of The Gambia. Front. Artif. Intell. 2025, 8, 1510341. [Google Scholar] [CrossRef]
- Xie, H.; Xu, X.; Yan, F.; Qian, X.; Yang, Y. Deep Learning for Multi-Country GDP Prediction: A Study of Model Performance and Data Impact. arXiv 2024, arXiv:2409.02551. Available online: https://arxiv.org/abs/2409.02551 (accessed on 15 January 2025).
- Hamilton, J.D. A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica 1989, 57, 357–384. [Google Scholar] [CrossRef]
- Kant, D.; Pick, A.; de Winter, J. Nowcasting GDP using machine learning methods. AStA Adv. Stat. Anal. 2024, 109, 1–24. Available online: https://link.springer.com/article/10.1007/s10182-024-00515-0 (accessed on 16 January 2025).
- Vataja, J.; Kuosmanen, P. Forecasting GDP Growth in Small Open Economies: Foreign Economic Activity vs. Domestic Financial Predictors. SSRN Electron. J. 2023. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4415388 (accessed on 25 January 2024).
- Cui, Y.; Hong, Y.; Huang, N.; Wang, Y. Forecasting GDP Growth Rates: A Large Panel Micro Data Approach. SSRN Electron. J. Feb. 2025. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=5151633 (accessed on 5 May 2025).
- Choi, H.; Varian, H. Predicting the present with Google Trends. Econ. Rec. 2012, 88, 2–9. [Google Scholar] [CrossRef]
- Liu, D.; Chen, K.; Cai, Y.; Tang, Z. Interpretable EU ETS Phase 4 Prices Forecasting Based on Deep Generative Data Augmentation. Financ. Res. Lett. 2024, 61, 105038. [Google Scholar] [CrossRef]
- Gatti, R.; Lederman, D.; Islam, A.M.; Nguyen, H.; Lotfi, R.; Mousa, M.E. Data Transparency and GDP Growth Forecast Errors. J. Int. Money Financ. 2024, 140, 102991. Available online: https://openknowledge.worldbank.org/entities/publication/0fd1d195-9a75-430f-80ca-070332af36c6 (accessed on 15 January 2025). [CrossRef]
- Lesmy, D.; Muchnik, L.; Mugerman, Y. Lost in the fog: Growing complexity in financial reporting—A comparative study. Res. Sq. 2024; preprint. [Google Scholar] [CrossRef]
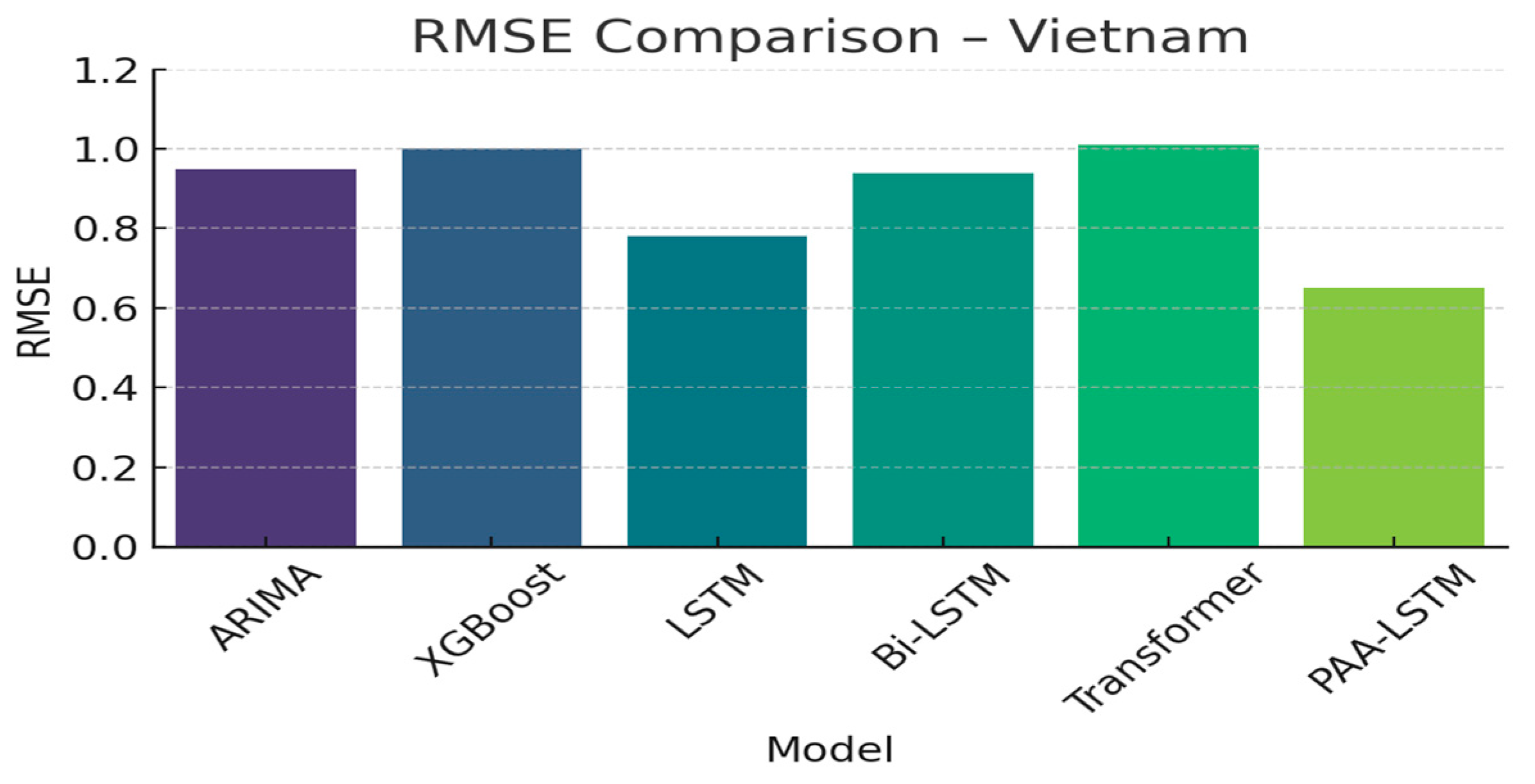
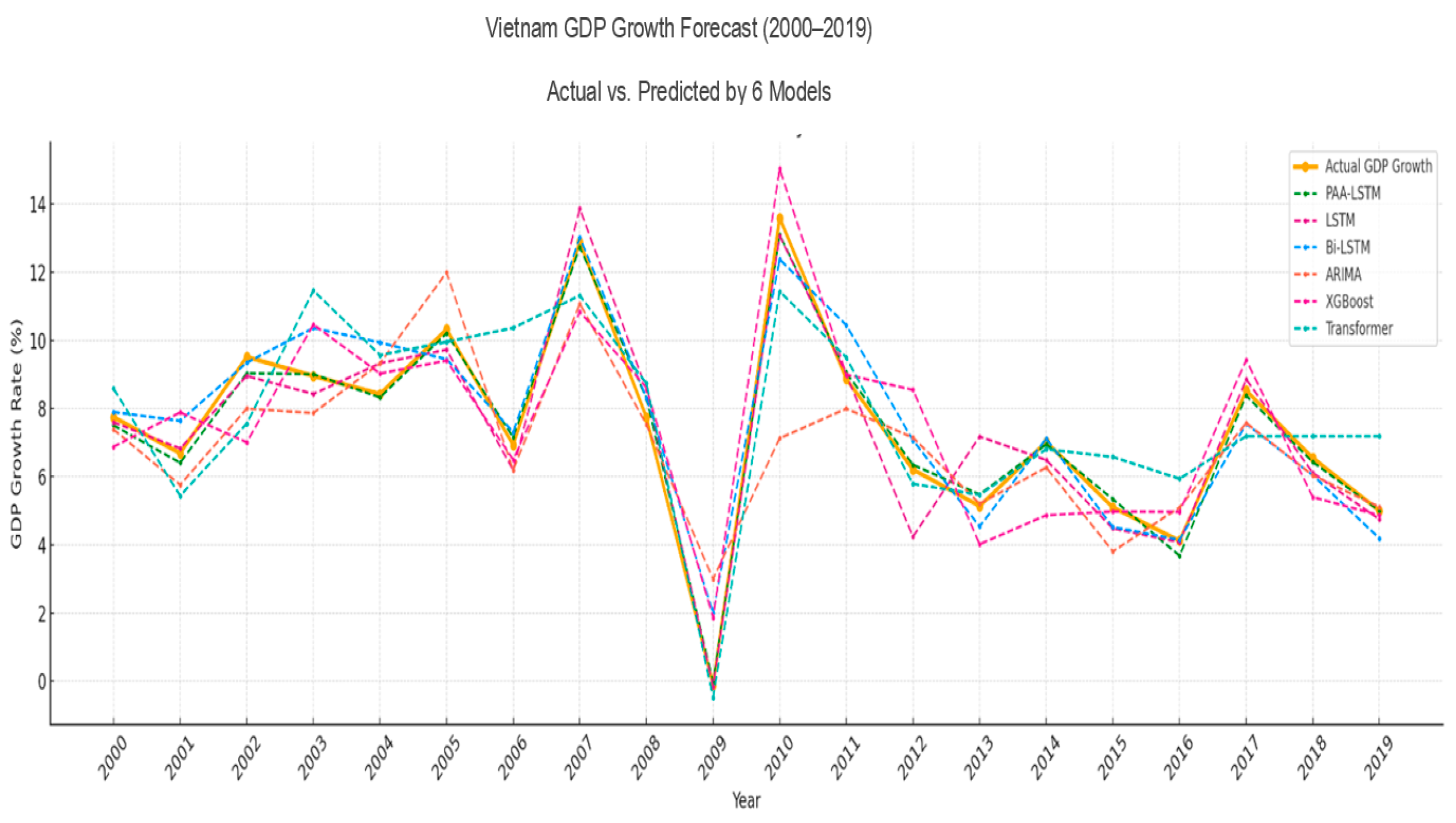
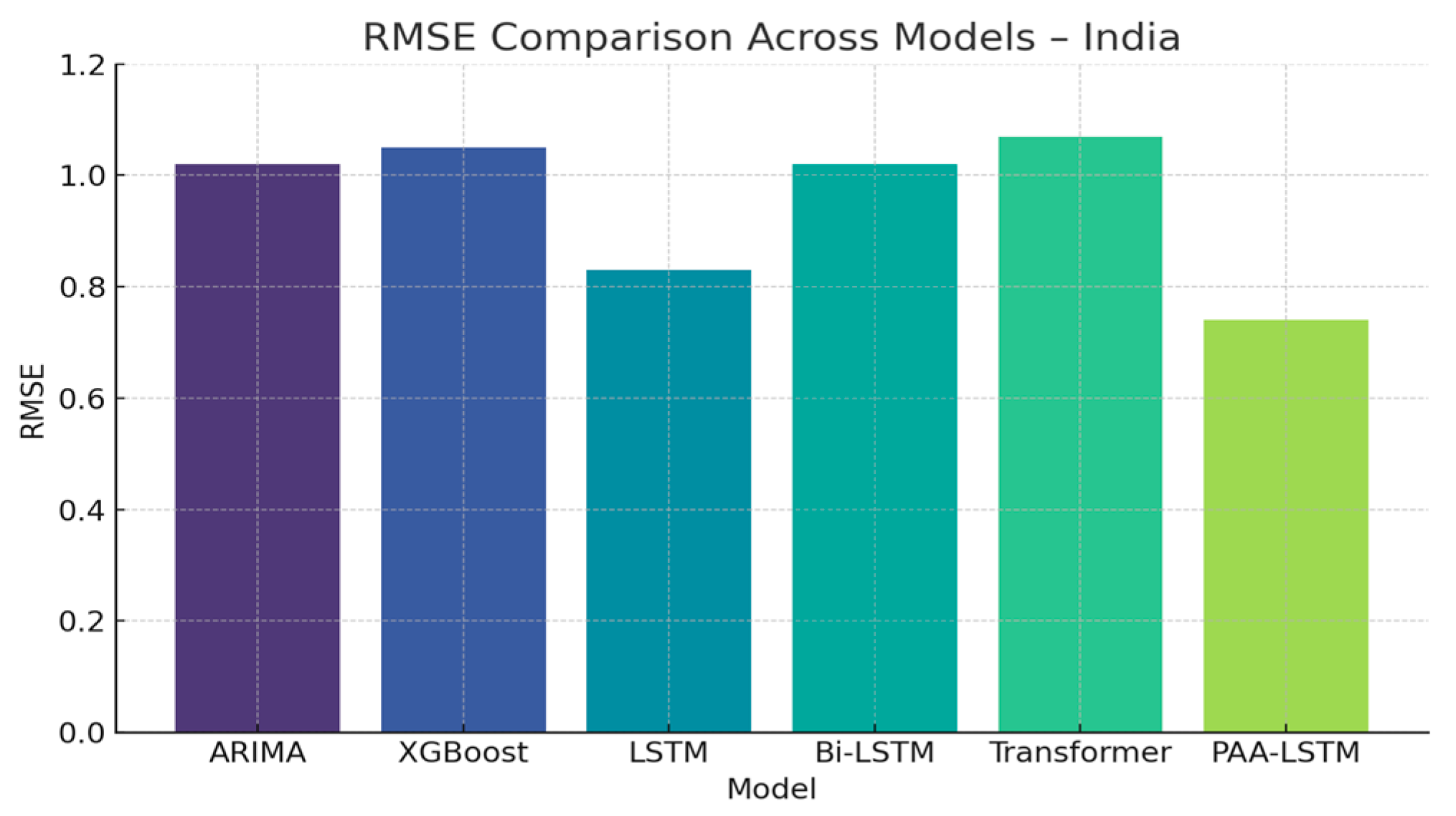
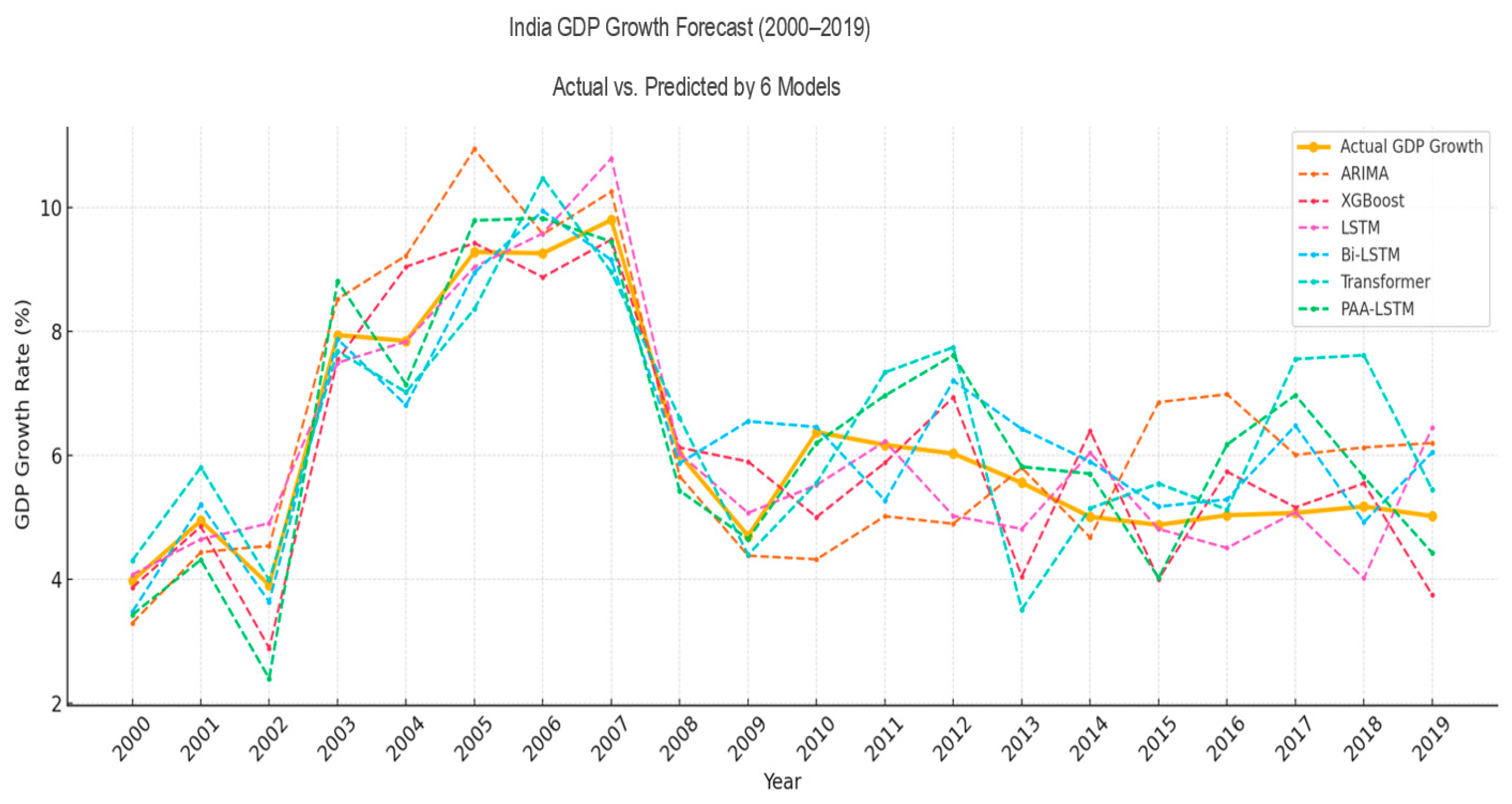
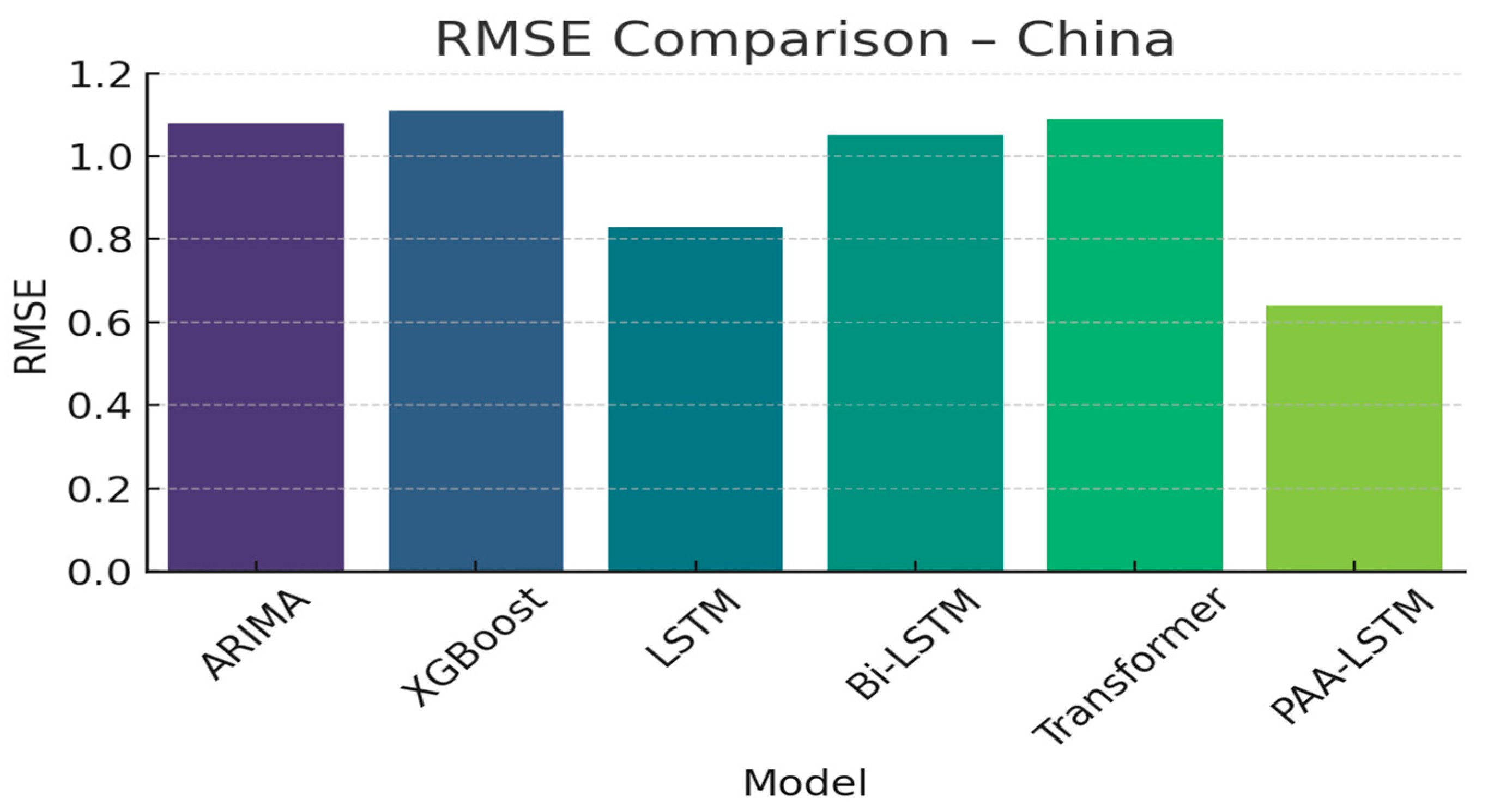
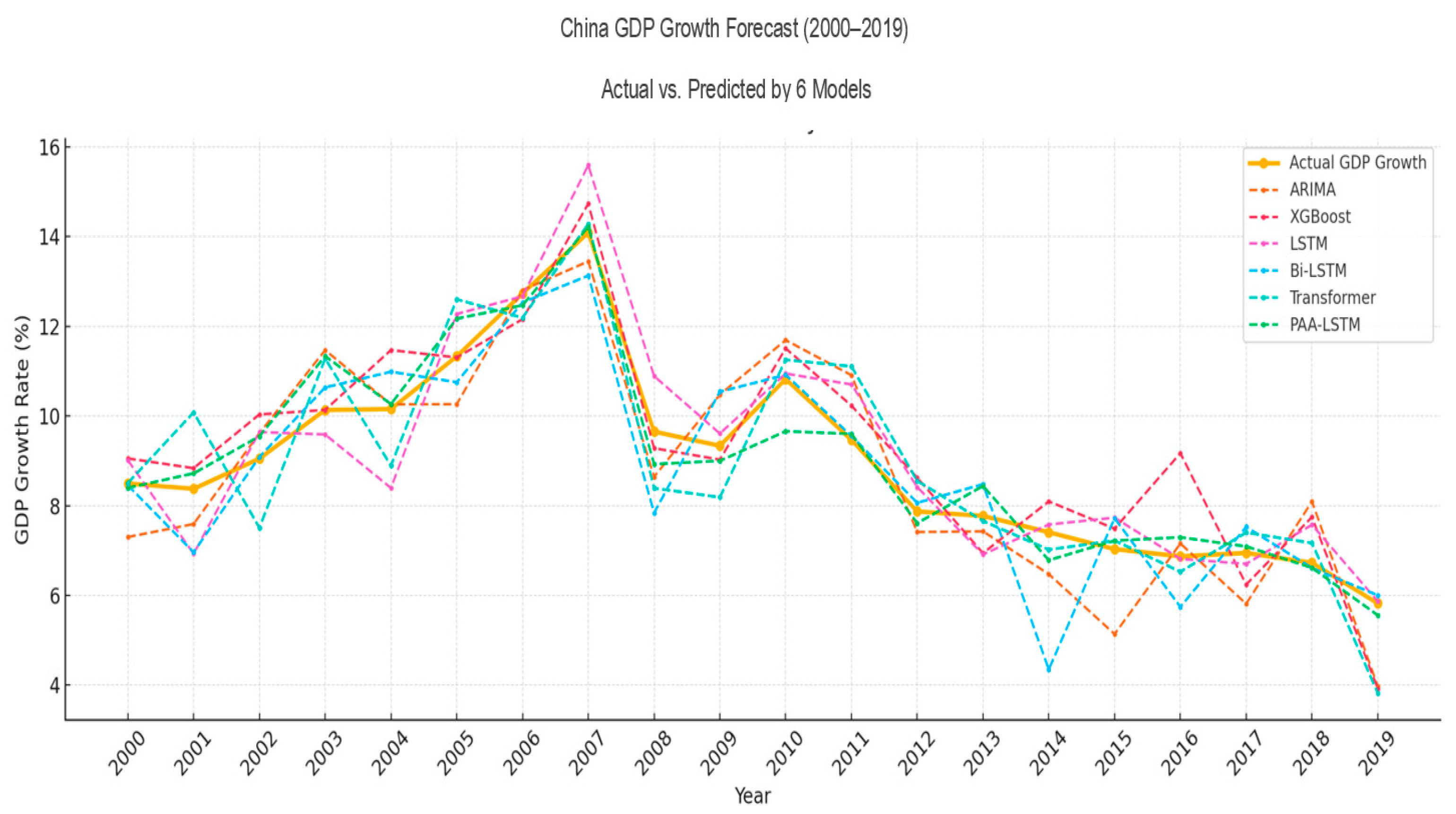

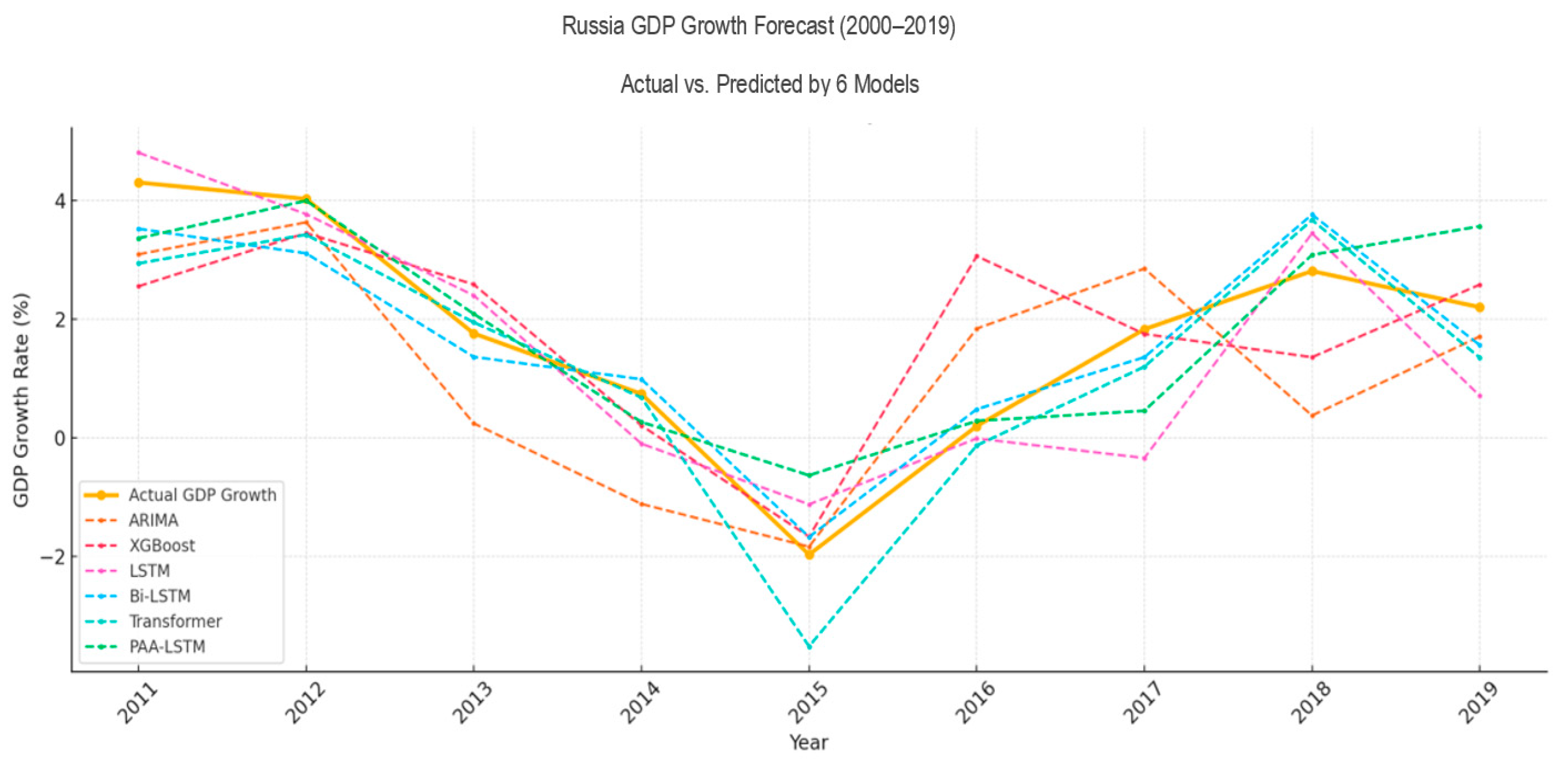
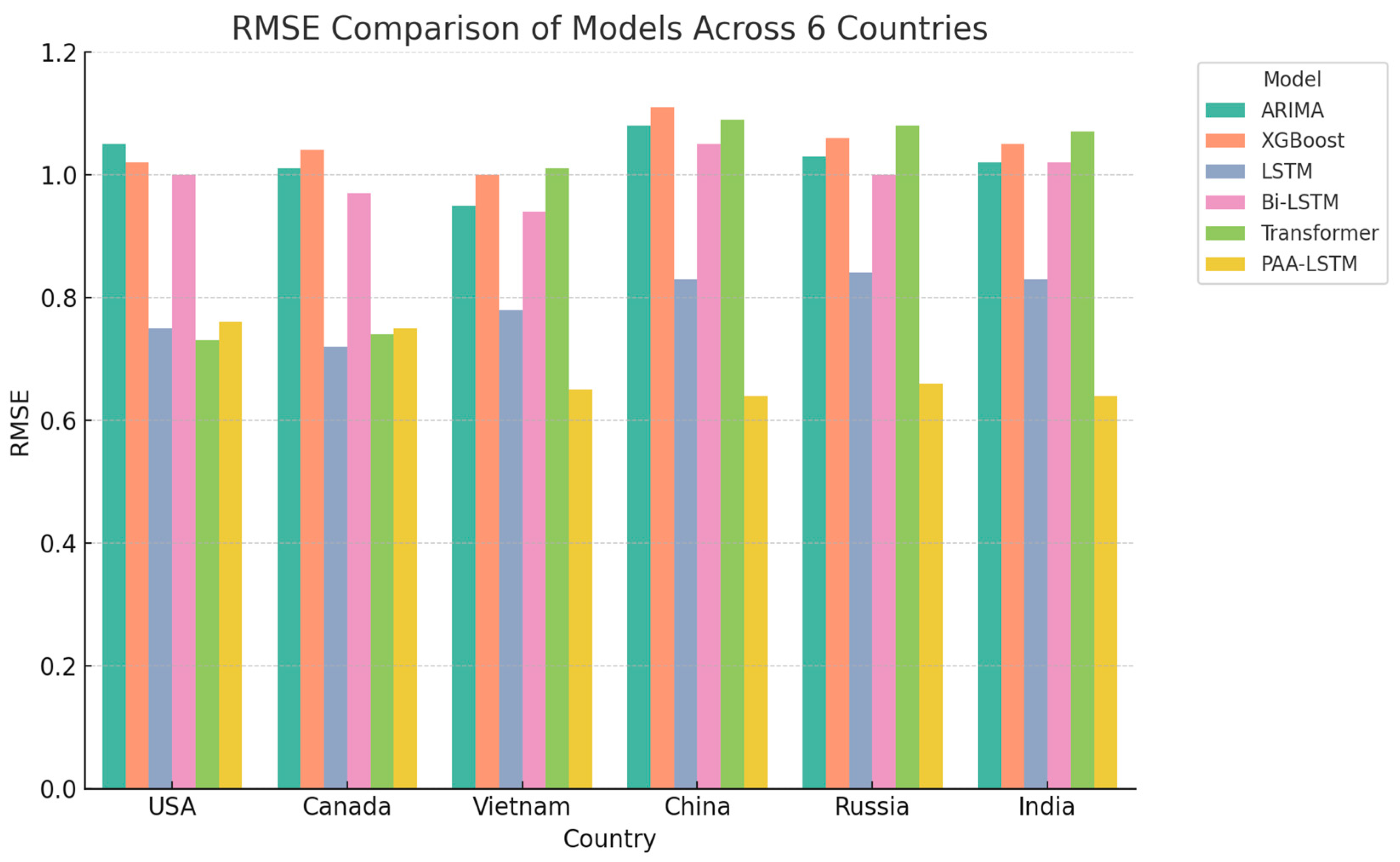
| Model | RMSE | MAE | R2 |
|---|---|---|---|
| ARIMA | 0.95 | 0.73 | 0.76 |
| XGBoost | 1.0 | 0.97 | 0.84 |
| LSTM | 0.78 | 0.61 | 0.75 |
| Bi-LSTM | 0.94 | 1 | 0.79 |
| Transformer | 1.01 | 0.83 | 0.82 |
| PAA-LSTM | 0.65 | 0.48 | 0.94 |
| Model | RMSE | MAE | R2 |
|---|---|---|---|
| ARIMA | 1.02 | 0.78 | 0.83 |
| XGBoost | 1.05 | 0.95 | 0.87 |
| LSTM | 0.83 | 0.66 | 0.77 |
| Bi-LSTM | 1.02 | 0.86 | 0.84 |
| Transformer | 1.07 | 0.91 | 0.84 |
| PAA-LSTM | 0.74 | 0.48 | 0.95 |
| Model | RMSE | MAE | R2 |
|---|---|---|---|
| ARIMA | 1.08 | 0.9 | 0.78 |
| XGBoost | 1.11 | 0.71 | 0.85 |
| LSTM | 0.83 | 0.55 | 0.85 |
| Bi-LSTM | 1.05 | 0.78 | 0.8 |
| Transformer | 1.09 | 0.86 | 0.82 |
| PAA-LSTM | 0.64 | 0.5 | 0.8 |
| Model | RMSE | MAE | R2 |
|---|---|---|---|
| ARIMA | 1.03 | 0.9 | 0.77 |
| XGBoost | 1.06 | 0.83 | 0.78 |
| LSTM | 0.84 | 0.61 | 0.78 |
| Bi-LSTM | 1.0 | 0.9 | 0.91 |
| Transformer | 1.08 | 0.96 | 0.83 |
| PAA-LSTM | 0.69 | 0.49 | 0.89 |
| Model | RMSE | MAE | R2 |
|---|---|---|---|
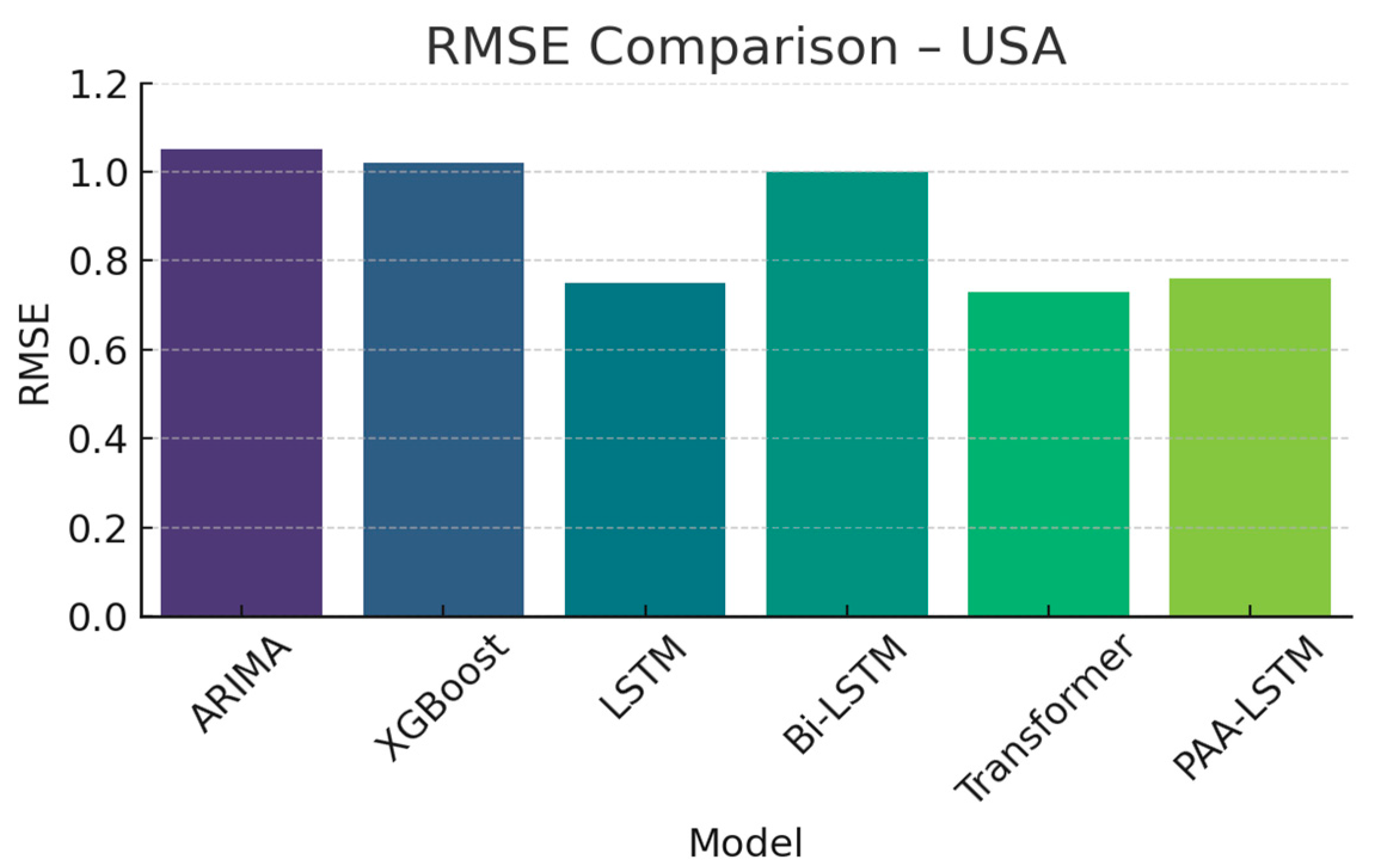
| ARIMA | 1.05 | 0.8 | 0.79 |
| XGBoost | 1.02 | 0.79 | 0.87 |
| LSTM | 0.75 | 0.57 | 0.81 |
| Bi-LSTM | 1 | 0.9 | 0.86 |
| Transformer | 0.73 | 0.98 | 0.76 |
| PAA-LSTM | 0.76 | 0.47 | 0.89 |
| Model | RMSE | MAE | R2 |
|---|---|---|---|
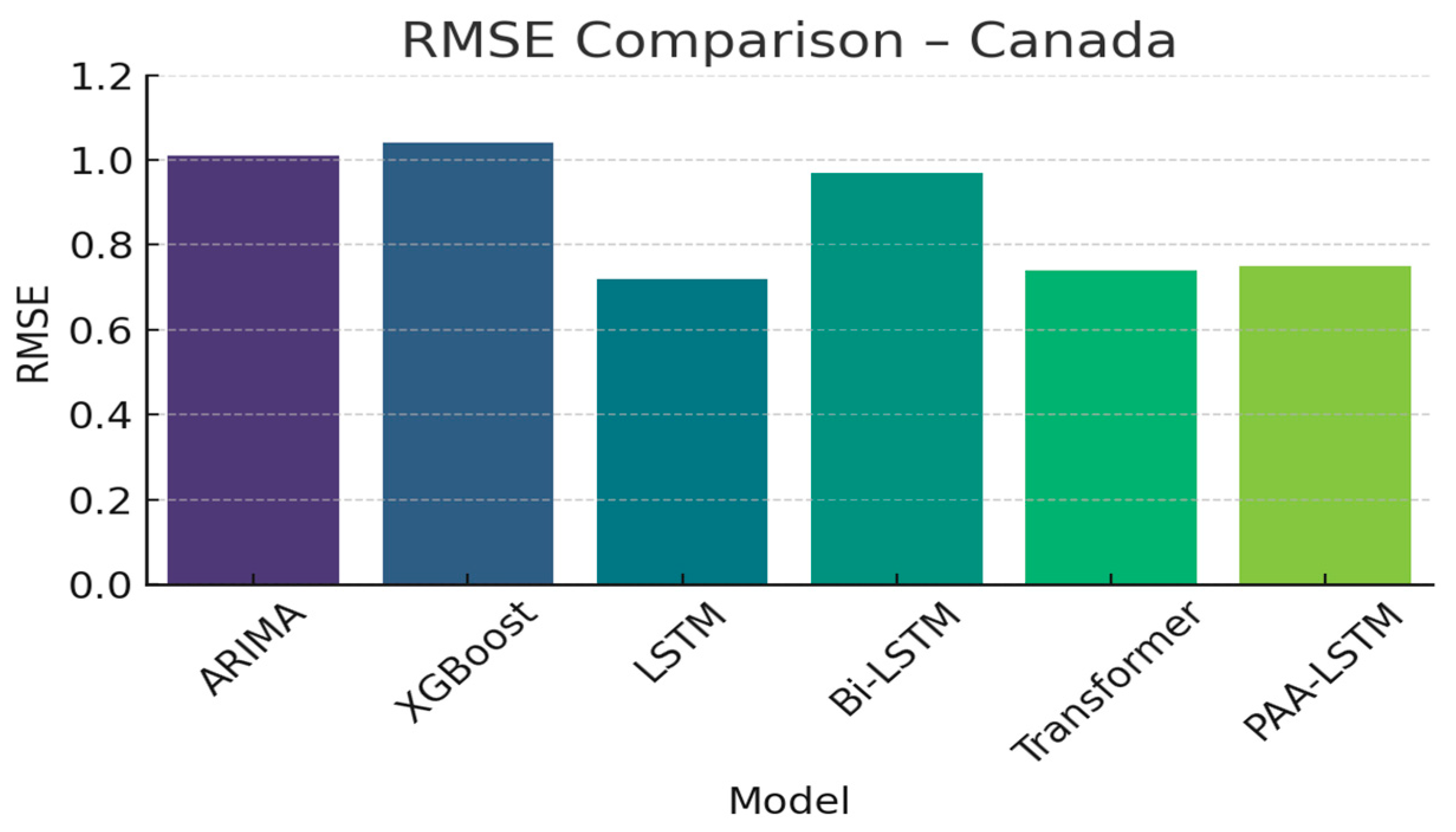
| ARIMA | 1.01 | 0.73 | 0.76 |
| XGBoost | 1.04 | 0.79 | 0.82 |
| LSTM | 0.72 | 0.59 | 0.82 |
| Bi-LSTM | 0.97 | 0.83 | 0.77 |
| Transformer | 0.74 | 0.98 | 0.82 |
| PAA-LSTM | 0.75 | 0.48 | 0.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong Thi Ngoc, L.; Hoan, N.D.; Nguyen, H.-N. Gross Domestic Product Forecasting Using Deep Learning Models with a Phase-Adaptive Attention Mechanism. Electronics 2025, 14, 2132. https://doi.org/10.3390/electronics14112132
Dong Thi Ngoc L, Hoan ND, Nguyen H-N. Gross Domestic Product Forecasting Using Deep Learning Models with a Phase-Adaptive Attention Mechanism. Electronics. 2025; 14(11):2132. https://doi.org/10.3390/electronics14112132
Chicago/Turabian StyleDong Thi Ngoc, Lan, Nguyen Dinh Hoan, and Ha-Nam Nguyen. 2025. "Gross Domestic Product Forecasting Using Deep Learning Models with a Phase-Adaptive Attention Mechanism" Electronics 14, no. 11: 2132. https://doi.org/10.3390/electronics14112132
APA StyleDong Thi Ngoc, L., Hoan, N. D., & Nguyen, H.-N. (2025). Gross Domestic Product Forecasting Using Deep Learning Models with a Phase-Adaptive Attention Mechanism. Electronics, 14(11), 2132. https://doi.org/10.3390/electronics14112132







