Classification of Whole-Slide Pathology Images Based on State Space Models and Graph Neural Networks
Abstract
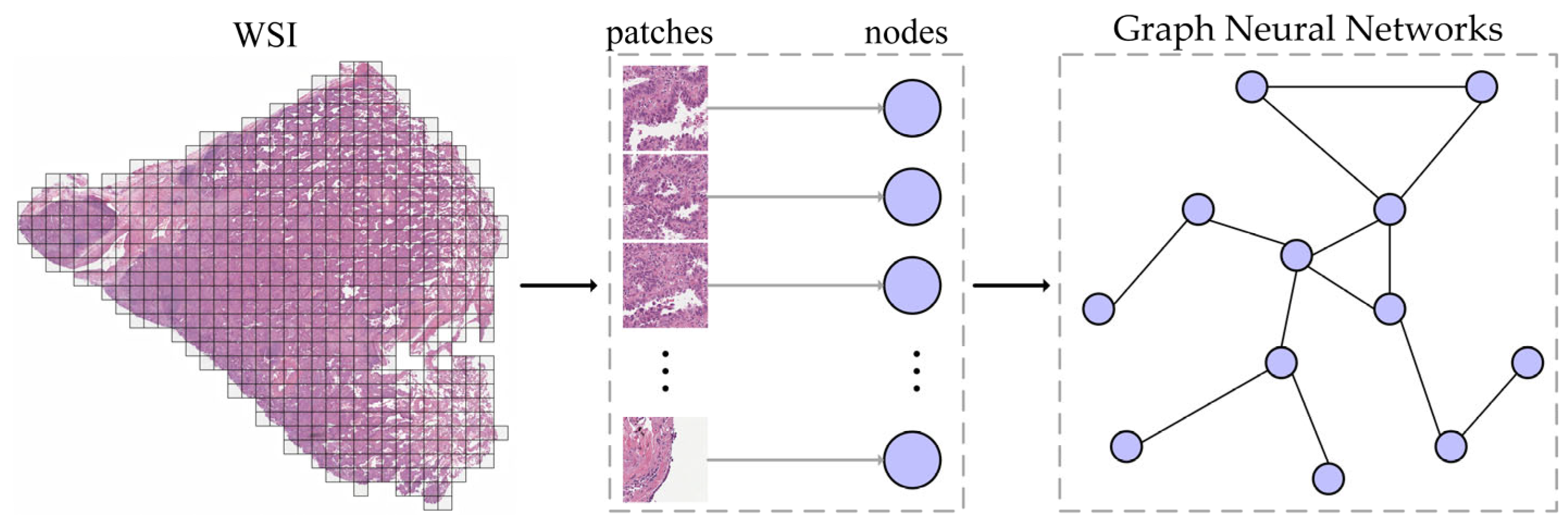
1. Introduction
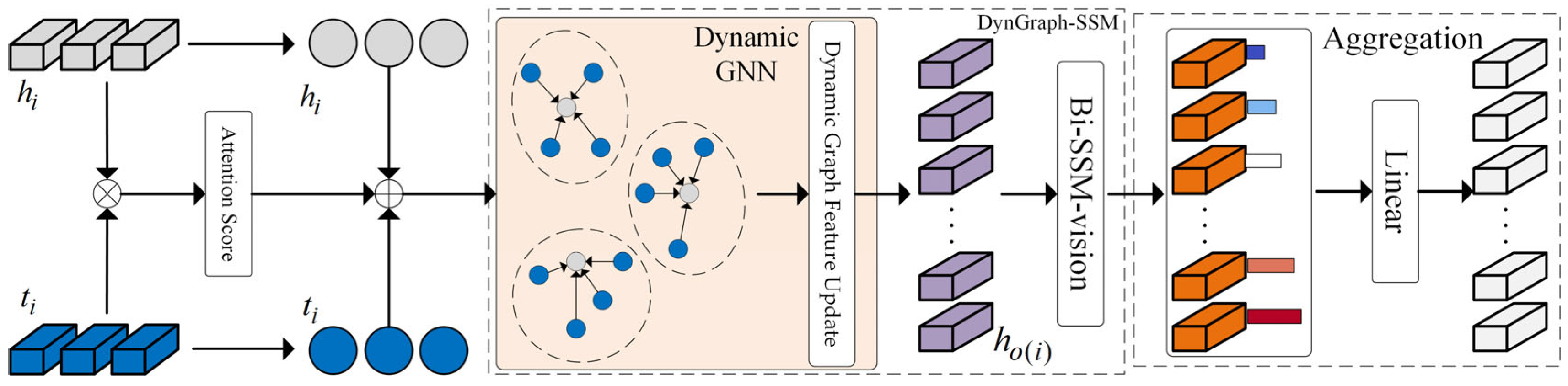
- We propose the DG-SSM-MIL framework, which consists of two parallel paths. The input feature vectors are separately fed into the DynGraph-SSM module as original features and GAT-processed features. This design enables more effective fusion of local and global information, allowing the model to better capture the spatial structure and interrelationships of image patches, thereby enhancing the multidimensional expressiveness of features and significantly improving their completeness and robustness.
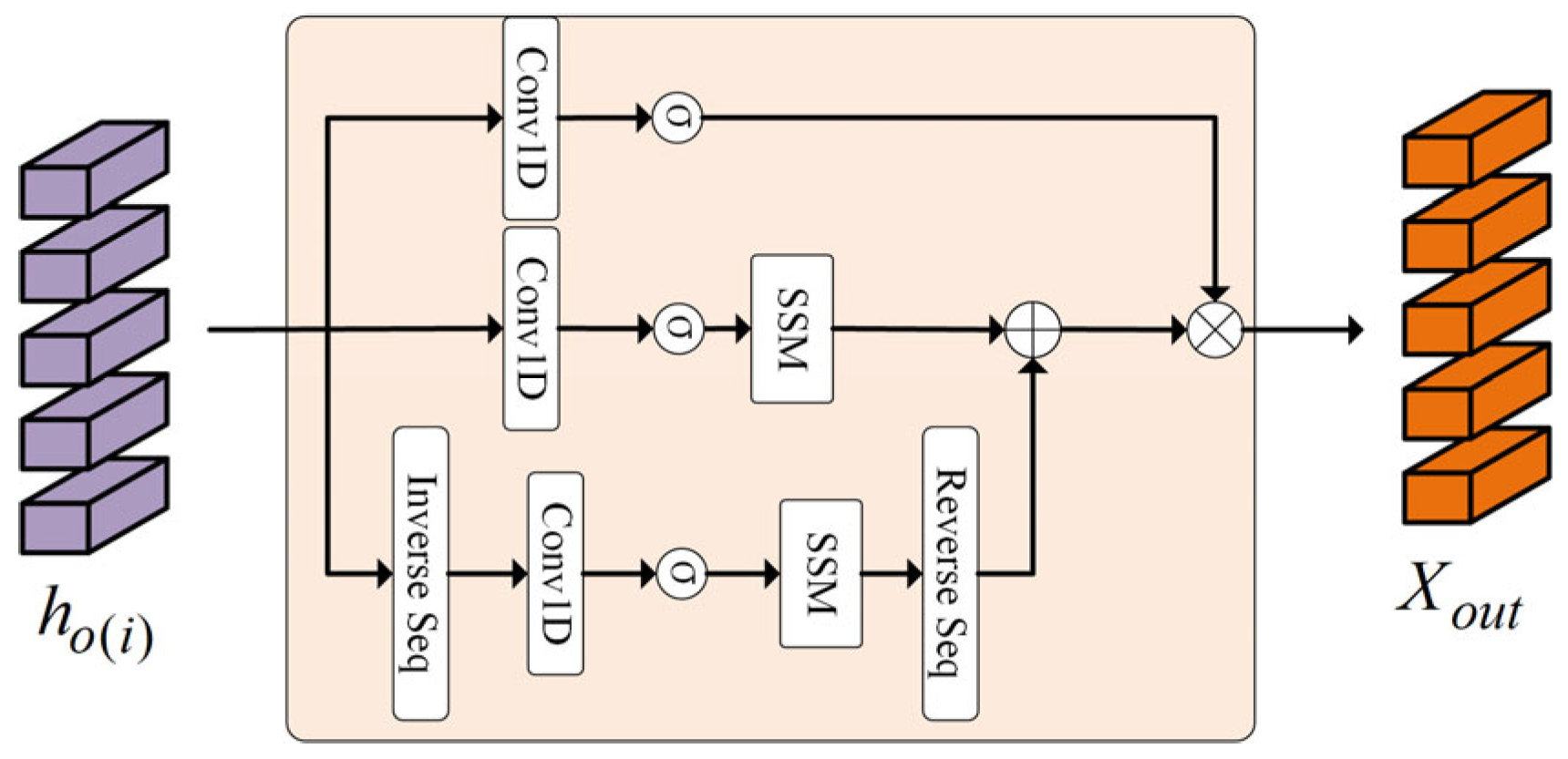
- We combine static and dynamic graph structures, enabling the model to more effectively capture correlations among positive regions and alleviate the limitation of Mamba’s unidirectional scanning, thereby improving classification performance. Meanwhile, we propose the Bi-SSM-vision module, an improved version of Bi-SSM tailored for image tasks. In this module, the original 1D causal convolutions are replaced with standard 1D convolutions to enhance compatibility with image processing. Additionally, we introduce an extra convolutional branch to extract local features from the dynamically updated representations, enabling joint modeling of local patterns and Mamba’s long-sequence modeling capabilities.
- We validate the model’s superior performance across multiple challenging tasks and datasets. Through extensive experiments on several public medical image datasets, including BRACS [21], NSCLC, RCC, and CAMELYON16 [22], our model demonstrates strong robustness and broad applicability. The results show that the improved model can leverage local and global information more effectively to enhance predictive performance.
2. Related Works
2.1. Graph Neural Networks
2.2. Application of Multiple Instance Learning in WSI Classification
2.3. Mamba: Evolution of State Space Models Based on Selective Mechanisms
3. Methods
3.1. Framework Overview
3.2. Graph Attention Network (GAT) Module
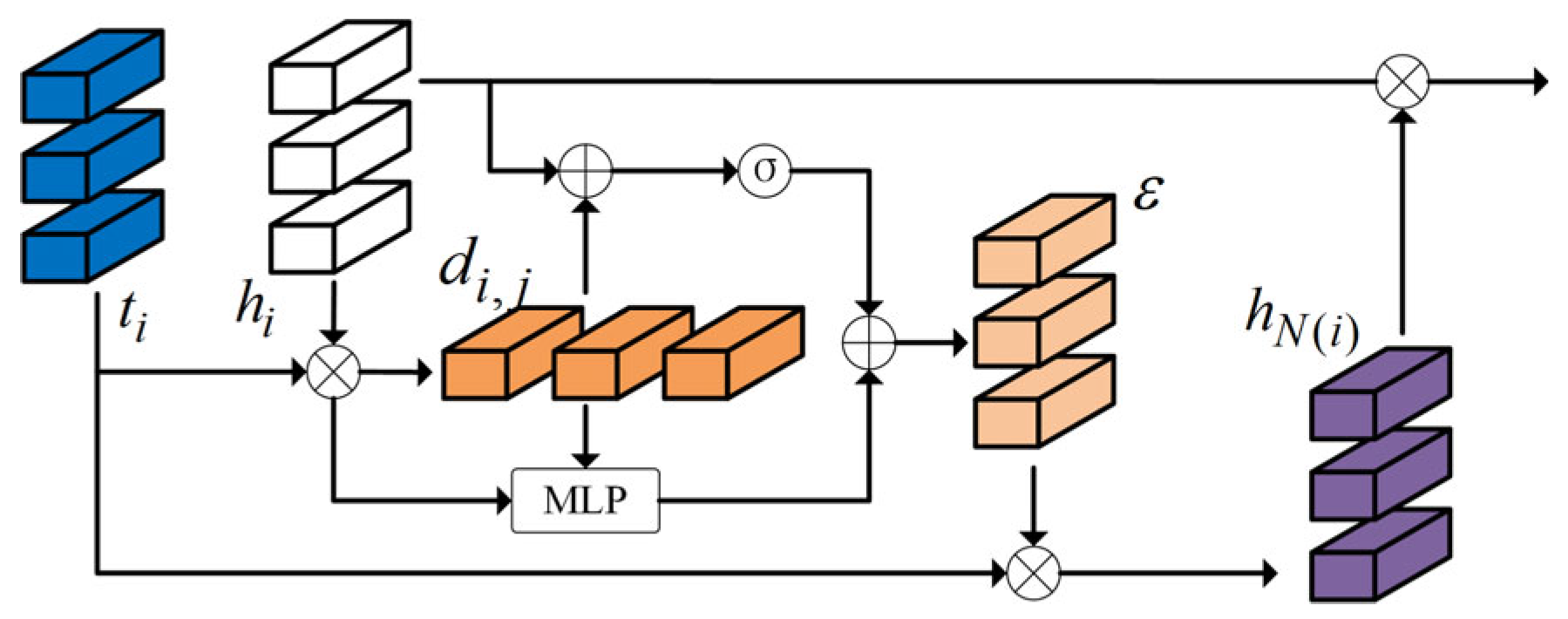
3.3. Dynamic Graph and State Space Model (DynGraph-SSM) Module
3.3.1. Dynamic Graph Structure
3.3.2. Bidirectional State Space Model for Vision (Bi-SSM-Vision) Module
| Algorithm 1 Bi-SSM-vision Module Process |
| Input: instance sequence :(B,S,D) Output: instance sequence :(B,S,D) # B: batch size, S:instance number, D: dimension ) #Forward Sequence: for #Backward Sequence: back # Convolutional Path: conv for o in {for,back} do )) )) ) , N , N ) end for ⊙⊙) )) ) return |
4. Experiments and Analysis
4.1. Experimental Setup
4.2. Datasets
4.3. Evaluation Metrics
4.4. Results Analysis
4.5. Sensitivity Analysis of the Hyperparameter
4.6. Ablation Study
4.7. Interpretability and Attention Visualization
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Cui, M.; Zhang, D.Y. Artificial intelligence and computational pathology. Lab. Investig. 2021, 101, 412–422. [Google Scholar] [CrossRef] [PubMed]
- Gurcan, M.N.; Boucheron, L.E.; Can, A.; Madabhushi, A.; Rajpoot, N.M.; Yener, B. Histopathological image analysis: A review. IEEE Rev. Biomed. Eng. 2009, 2, 147–171. [Google Scholar] [CrossRef]
- Bera, K.; Schalper, K.A.; Rimm, D.L.; Velcheti, V.; Madabhushi, A. Artificial intelligence in digital pathology—New tools for diagnosis and precision oncology. Nat. Rev. Clin. Oncol. 2019, 16, 703–715. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Li, C.; Rahaman, M.M.; Sun, H.; Li, X.; Wu, J.; Yao, Y.; Grzegorzek, M. A comprehensive review of computer-aided whole-slide image analysis: From datasets to feature extraction, segmentation, classification and detection approaches. Artif. Intell. Rev. 2022, 55, 4809–4878. [Google Scholar] [CrossRef]
- Afonso, M.; Bhawsar, P.M.; Saha, M.; Almeida, J.S.; Oliveira, A.L. Multiple Instance Learning for WSI: A comparative analysis of attention-based approaches. J. Pathol. Inform. 2024, 15, 100403. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Zhang, Y.; Wang, Z.; Zhang, J.; Ji, X.; Zhang, Y. Mammil: Multiple instance learning for whole slide images with state space models. In Proceedings of the 2024 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Lisboa, Portugal, 3–6 December 2024; pp. 3200–3205. [Google Scholar]
- Zhao, L.; Xu, X.; Hou, R.; Zhao, W.; Zhong, H.; Teng, H.; Han, Y.; Fu, X.; Sun, J.; Zhao, J. Lung cancer subtype classification using histopathological images based on weakly supervised multi-instance learning. Phys. Med. Biol. 2021, 66, 235013. [Google Scholar] [CrossRef]
- Zhao, W.; Guo, Z.; Fan, Y.; Jiang, Y.; Yeung, M.C.; Yu, L. Aligning knowledge concepts to whole slide images for precise histopathology image analysis. npj Digit. Med. 2024, 7, 383. [Google Scholar] [CrossRef]
- Ilse, M.; Tomczak, J.; Welling, M. Attention-based deep multiple instance learning. In Proceedings of the International conference on machine learning, Stockholm, Sweden, 10–15 July 2018; pp. 2127–2136. [Google Scholar]
- Lu, M.Y.; Williamson, D.F.; Chen, T.Y.; Chen, R.J.; Barbieri, M.; Mahmood, F. Data-efficient and weakly supervised computational pathology on whole-slide images. Nat. Biomed. Eng. 2021, 5, 555–570. [Google Scholar] [CrossRef]
- Zhang, H.; Meng, Y.; Zhao, Y.; Qiao, Y.; Yang, X.; Coupland, S.E.; Zheng, Y. Dtfd-mil: Double-tier feature distillation multiple instance learning for histopathology whole slide image classification. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 18802–18812. [Google Scholar]
- Li, B.; Li, Y.; Eliceiri, K.W. Dual-stream multiple instance learning network for whole slide image classification with self-supervised contrastive learning. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14318–14328. [Google Scholar]
- Shao, Z.; Bian, H.; Chen, Y.; Wang, Y.; Zhang, J.; Ji, X. Transmil: Transformer based correlated multiple instance learning for whole slide image classification. Adv. Neural Inf. Process. Syst. 2021, 34, 2136–2147. [Google Scholar]
- Chen, R.J.; Lu, M.Y.; Weng, W.-H.; Chen, T.Y.; Williamson, D.F.; Manz, T.; Shady, M.; Mahmood, F. Multimodal co-attention transformer for survival prediction in gigapixel whole slide images. In Proceedings of the IEEE/CVF international conference on computer vision, Montreal, BC, Canada, 11–17 October 2021; pp. 4015–4025. [Google Scholar]
- Li, H.; Yang, F.; Zhao, Y.; Xing, X.; Zhang, J.; Gao, M.; Huang, J.; Wang, L.; Yao, J. DT-MIL: Deformable transformer for multi-instance learning on histopathological image. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Proceedings, Part VIII 24. Strasbourg, France, 27 September–1 October 2021; pp. 206–216. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Gu, A.; Dao, T. Mamba: Linear-time sequence modeling with selective state spaces. arXiv 2023, arXiv:2312.00752. [Google Scholar]
- Hayat, M. Squeeze & Excitation joint with Combined Channel and Spatial Attention for Pathology Image Super-Resolution. Frankl. Open 2024, 8, 100170. [Google Scholar]
- Hayat, M.; Ahmad, N.; Nasir, A.; Tariq, Z.A. Hybrid Deep Learning EfficientNetV2 and Vision Transformer (EffNetV2-ViT) Model for Breast Cancer Histopathological Image Classification. IEEE Access 2024, 12, 184119–184131. [Google Scholar] [CrossRef]
- Zhu, L.; Liao, B.; Zhang, Q.; Wang, X.; Liu, W.; Wang, X. Vision Mamba: Efficient Visual Representation Learning with Bidirectional State Space Model. In Proceedings of the 41st International Conference on Machine Learning, Proceedings of Machine Learning Research, Vienna, Austria, 21–27 July 2024; pp. 62429–62442. [Google Scholar]
- Brancati, N.; Anniciello, A.M.; Pati, P.; Riccio, D.; Scognamiglio, G.; Jaume, G.; De Pietro, G.; Di Bonito, M.; Foncubierta, A.; Botti, G. Bracs: A dataset for breast carcinoma subtyping in h&e histology images. Database 2022, 2022, baac093. [Google Scholar]
- Ehteshami Bejnordi, B.; Veta, M.; Johannes van Diest, P.; van Ginneken, B.; Karssemeijer, N.; Litjens, G.; van der Laak, J.A.W.M.; the CAMELYON16 Consortium. Diagnostic Assessment of Deep Learning Algorithms for Detection of Lymph Node Metastases in Women With Breast Cancer. JAMA 2017, 318, 2199–2210. [Google Scholar] [CrossRef]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Khemani, B.; Patil, S.; Kotecha, K.; Tanwar, S. A review of graph neural networks: Concepts, architectures, techniques, challenges, datasets, applications, and future directions. J. Big Data 2024, 11, 18. [Google Scholar] [CrossRef]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. In Proceedings of the International conference on machine learning, Sydney, Australia, 6–11 August 2017; pp. 1263–1272. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Skarding, J.; Gabrys, B.; Musial, K. Foundations and modeling of dynamic networks using dynamic graph neural networks: A survey. IEEE Access 2021, 9, 79143–79168. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, J.; Kong, J.; Wang, F. Integrative Graph-Transformer Framework for Histopathology Whole Slide Image Representation and Classification. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Marrakesh, Morocco, 6–10 October 2024; pp. 341–350. [Google Scholar]
- Guan, Y.; Zhang, J.; Tian, K.; Yang, S.; Dong, P.; Xiang, J.; Yang, W.; Huang, J.; Zhang, Y.; Han, X. Node-aligned graph convolutional network for whole-slide image representation and classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 18813–18823. [Google Scholar]
- Adnan, M.; Kalra, S.; Tizhoosh, H.R. Representation learning of histopathology images using graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 13–19 June 2020; pp. 988–989. [Google Scholar]
- Behrouz, A.; Hashemi, F. Graph mamba: Towards learning on graphs with state space models. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Barcelona, Spain, 25–29 August 2024; pp. 119–130. [Google Scholar]
- Van der Laak, J.; Litjens, G.; Ciompi, F. Deep learning in histopathology: The path to the clinic. Nat. Med. 2021, 27, 775–784. [Google Scholar] [CrossRef] [PubMed]
- Deng, R.; Cui, C.; Remedios, L.W.; Bao, S.; Womick, R.M.; Chiron, S.; Li, J.; Roland, J.T.; Lau, K.S.; Liu, Q. Cross-scale multi-instance learning for pathological image diagnosis. Med. Image Anal. 2024, 94, 103124. [Google Scholar] [CrossRef] [PubMed]
- Chikontwe, P.; Kim, M.; Nam, S.J.; Go, H.; Park, S.H. Multiple instance learning with center embeddings for histopathology classification. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2020: 23rd International Conference, Lima, Peru, 4–8 October 2020; Proceedings, Part V 23, 2020. pp. 519–528. [Google Scholar]
- Song, A.H.; Chen, R.J.; Ding, T.; Williamson, D.F.; Jaume, G.; Mahmood, F. Morphological prototyping for unsupervised slide representation learning in computational pathology. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 11566–11578. [Google Scholar]
- Carbonneau, M.-A.; Cheplygina, V.; Granger, E.; Gagnon, G. Multiple instance learning: A survey of problem characteristics and applications. Pattern Recognit. 2018, 77, 329–353. [Google Scholar] [CrossRef]
- Gu, A.; Goel, K.; Ré, C. Efficiently modeling long sequences with structured state spaces. arXiv 2021, arXiv:2111.00396. [Google Scholar]
- Gu, A.; Johnson, I.; Timalsina, A.; Rudra, A.; Ré, C. How to train your hippo: State space models with generalized orthogonal basis projections. arXiv 2022, arXiv:2206.12037. [Google Scholar]
- Li, S.; Singh, H.; Grover, A. Mamba-nd: Selective state space modeling for multi-dimensional data. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; pp. 75–92. [Google Scholar]
- Xu, R.; Yang, S.; Wang, Y.; Du, B.; Chen, H. A survey on vision mamba: Models, applications and challenges. arXiv 2024, arXiv:2404.18861. [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. Automatica 1975, 11, 23–27. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Chen, R.J.; Ding, T.; Lu, M.Y.; Williamson, D.F.; Jaume, G.; Song, A.H.; Chen, B.; Zhang, A.; Shao, D.; Shaban, M. Towards a general-purpose foundation model for computational pathology. Nat. Med. 2024, 30, 850–862. [Google Scholar] [CrossRef]
- Ding, R.; Luong, K.-D.; Rodriguez, E.; da Silva, A.C.A.L.; Hsu, W. Combining graph neural network and mamba to capture local and global tissue spatial relationships in whole slide images. arXiv 2024, arXiv:2406.04377. [Google Scholar]
- Chen, R.J.; Lu, M.Y.; Shaban, M.; Chen, C.; Chen, T.Y.; Williamson, D.F.; Mahmood, F. Whole slide images are 2d point clouds: Context-aware survival prediction using patch-based graph convolutional networks. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Proceedings, Part VIII 24. Strasbourg, France, 27 September–1 October 2021; pp. 339–349. [Google Scholar]
- Li, J.; Chen, Y.; Chu, H.; Sun, Q.; Guan, T.; Han, A.; He, Y. Dynamic graph representation with knowledge-aware attention for histopathology whole slide image analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 11323–11332. [Google Scholar]
- Wang, X.; He, X.; Cao, Y.; Liu, M.; Chua, T.-S. Kgat: Knowledge graph attention network for recommendation. In Proceedings of the 25th ACM SIGKDD international conference on knowledge discovery & data mining, Anchorage, AK, USA, 4–8 August 2019; pp. 950–958. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE conference on computer vision and pattern recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Hoo, Z.H.; Candlish, J.; Teare, D. What is an ROC curve? Emerg. Med. J. 2017, 34, 357–359. [Google Scholar] [CrossRef] [PubMed]
- Cai, C.; Shi, Q.; Li, J.; Jiao, Y.; Xu, A.; Zhou, Y.; Wang, X.; Peng, C.; Zhang, X.; Cui, X. Pathologist-level diagnosis of ulcerative colitis inflammatory activity level using an automated histological grading method. Int. J. Med. Inform. 2024, 192, 105648. [Google Scholar] [CrossRef] [PubMed]

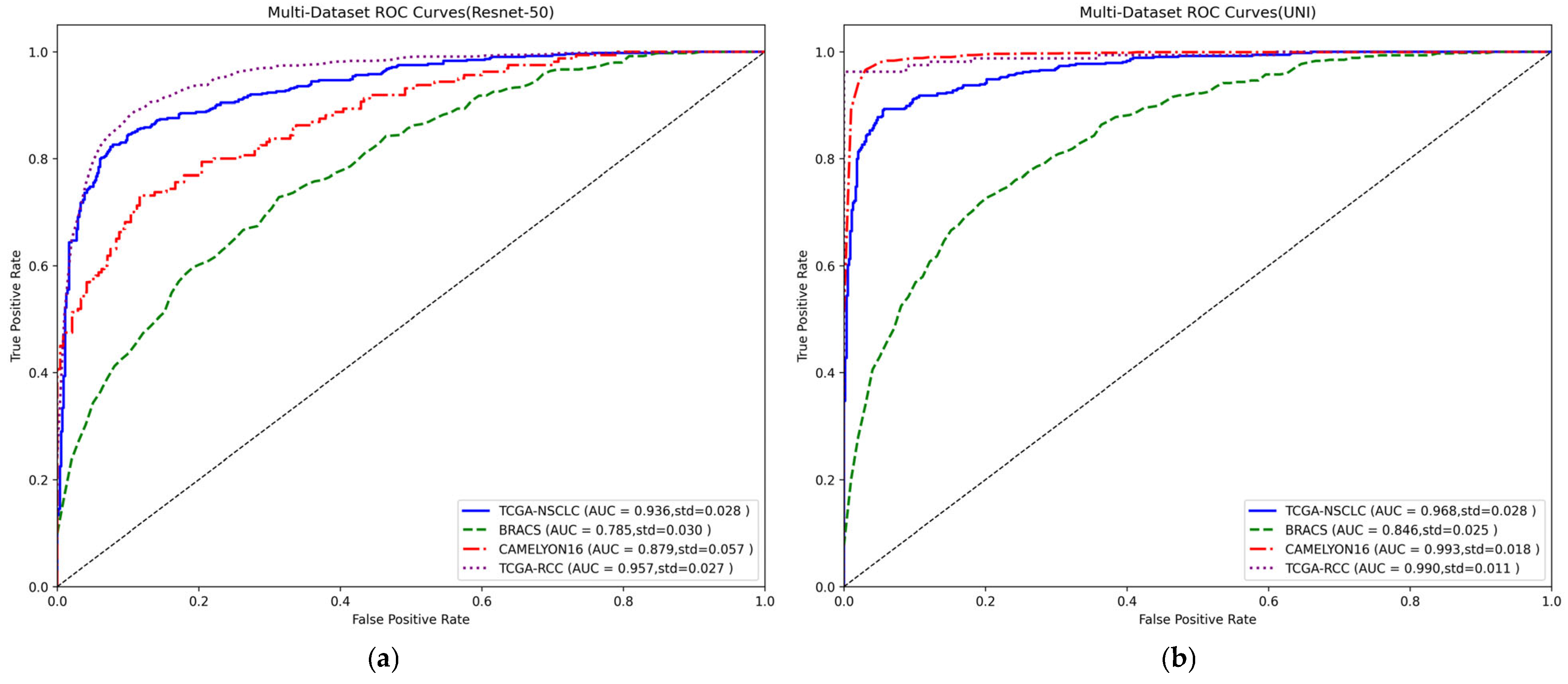
| Model | TCGA-NSCLC | BRACS | CAMELYON16 | TCGA-RCC | ||||
|---|---|---|---|---|---|---|---|---|
| AUC | ACC | AUC | ACC | AUC | ACC | AUC | ACC | |
| Max-Pooling | 0.928 ± 0.022 | 0.841 ± 0.029 | 0.723 ± 0.044 | 0.411 ± 0.043 | 0.846 ± 0.099 | 0.793 ± 0.081 | 0.947±0.026 | 0.913 ± 0.026 |
| Mean-Pooling | 0.907 ± 0.029 | 0.822 ± 0.031 | 0.727 ± 0.038 | 0.433 ± 0.059 | 0.795 ± 0.098 | 0.715 ± 0.077 | 0.940 ± 0.021 | 0.897 ± 0.039 |
| ABMIL | 0.918 ± 0.035 | 0.838 ± 0.045 | 0.759 ± 0.043 | 0.435 ± 0.057 | 0.856 ± 0.067 | 0.811 ± 0.054 | 0.941 ± 0.038 | 0.906 ± 0.028 |
| CLAM | 0.927 ± 0.033 | 0.849 ± 0.038 | 0.765 ± 0.045 | 0.466 ± 0.066 | 0.878 ± 0.050 | 0.802 ± 0.049 | 0.942 ± 0.022 | 0.915 ± 0.032 |
| TransMIL | 0.909 ± 0.041 | 0.833 ± 0.063 | 0.748 ± 0.032 | 0.423 ± 0.043 | 0.846 ± 0.075 | 0.783 ± 0.086 | 0.934 ± 0.036 | 0.886 ± 0.036 |
| S4MIL | 0.900 ± 0.028 | 0.812 ± 0.033 | 0.743 ± 0.041 | 0.429 ± 0.074 | 0.852 ± 0.098 | 0.765 ± 0.088 | 0.944 ± 0.027 | 0.914 ± 0.023 |
| MambaMIL | 0.907 ± 0.030 | 0.834 ± 0.034 | 0.778 ± 0.029 | 0.456 ± 0.073 | 0.846 ± 0.077 | 0.790 ± 0.060 | 0.946 ± 0.019 | 0.927 ± 0.024 |
| DG-SSM-MIL | 0.936 ± 0.028 | 0.857 ± 0.041 | 0.785 ± 0.030 | 0.480 ± 0.078 | 0.879 ± 0.057 | 0.831 ± 0.046 | 0.957 ± 0.027 | 0.936 ± 0.017 |
| Model | TCGA-NSCLC | BRACS | CAMELYON16 | TCGA-RCC | ||||
|---|---|---|---|---|---|---|---|---|
| AUC | ACC | AUC | ACC | AUC | ACC | AUC | ACC | |
| Max-Pooling | 0.954 ± 0.026 | 0.894 ± 0.042 | 0.812 ± 0.037 | 0.517 ± 0.071 | 0.988 ± 0.023 | 0.961 ± 0.019 | 0.980 ± 0.041 | 0.941 ± 0.013 |
| Mean-Pooling | 0.957 ± 0.024 | 0.885 ± 0.046 | 0.809 ± 0.031 | 0.509 ± 0.037 | 0.912 ± 0.066 | 0.845 ± 0.058 | 0.979 ± 0.023 | 0.935 ± 0.023 |
| ABMIL | 0.959 ± 0.028 | 0.899 ± 0.039 | 0.839 ± 0.028 | 0.544 ± 0.043 | 0.985 ± 0.022 | 0.970 ± 0.031 | 0.982 ± 0.018 | 0.931 ± 0.022 |
| CLAM | 0.965 ± 0.033 | 0.910 ± 0.040 | 0.847 ± 0.031 | 0.551 ± 0.057 | 0.980 ± 0.025 | 0.973 ± 0.032 | 0.983 ± 0.015 | 0.938 ± 0.018 |
| TransMIL | 0.956 ± 0.035 | 0.909 ± 0.039 | 0.821 ± 0.023 | 0.481 ± 0.049 | 0.991 ± 0.019 | 0.971 ± 0.028 | 0.970 ± 0.018 | 0.944 ± 0.026 |
| S4MIL | 0.964 ± 0.029 | 0.909 ± 0.031 | 0.835 ± 0.022 | 0.550 ± 0.068 | 0.990 ± 0.015 | 0.976 ± 0.021 | 0.982 ± 0.013 | 0.937 ± 0.014 |
| MambaMIL | 0.963 ± 0.024 | 0.901 ± 0.036 | 0.829 ± 0.033 | 0.537 ± 0.059 | 0.993 ± 0.014 | 0.975 ± 0.017 | 0.985 ± 0.021 | 0.942 ± 0.024 |
| DG-SSM-MIL | 0.968 ± 0.028 | 0.912 ± 0.034 | 0.846 ± 0.025 | 0.557 ± 0.066 | 0.993 ± 0.018 | 0.978 ± 0.014 | 0.990 ± 0.011 | 0.947 ± 0.021 |
| Pretrained Model | k = 4 | k = 8 | k = 12 | k = 16 | ||||
|---|---|---|---|---|---|---|---|---|
| AUC | ACC | AUC | ACC | AUC | ACC | AUC | ACC | |
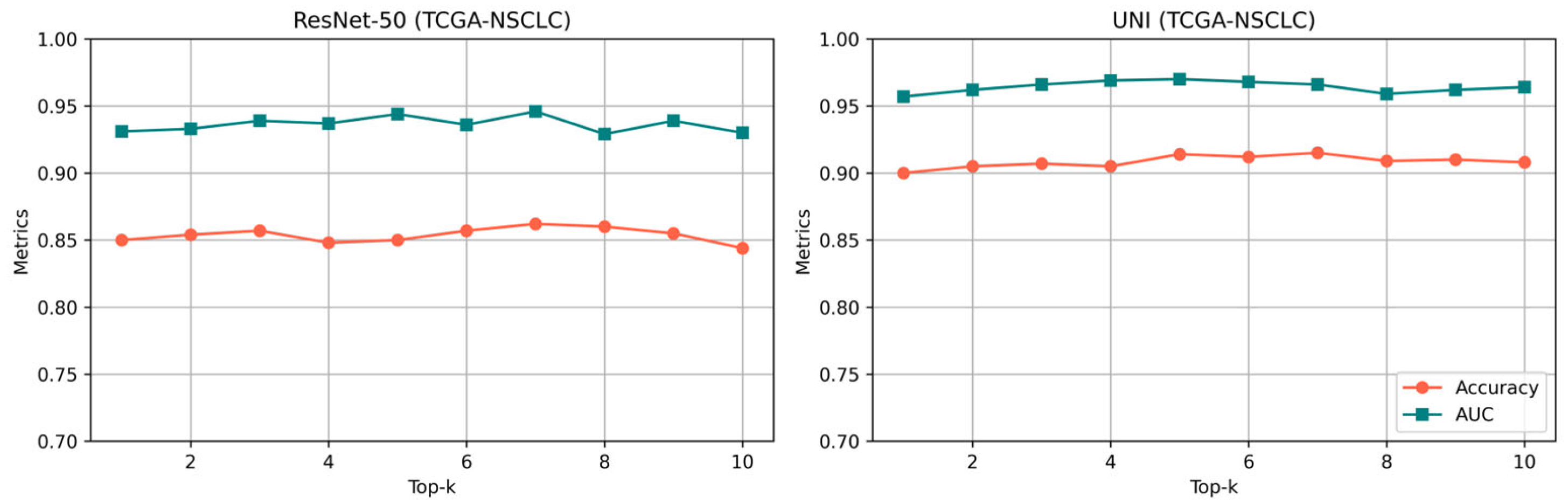
| ResNet-50 | 0.928 | 0.848 | 0.936 | 0.857 | 0.935 | 0.852 | 0.929 | 0.849 |
| UNI | 0.966 | 0.910 | 0.968 | 0.912 | 0.969 | 0.911 | 0.962 | 0.908 |
| Model | Designs in DG-SSM-MIL | Cancer Diagnosis | Cancer Subtyping | |||||
|---|---|---|---|---|---|---|---|---|
| DP | DG | BS | CR | ResNet-50 | UNI | ResNet-50 | UNI | |
| A | 0.856 | 0.985 | 0.905 | 0.959 | ||||
| B | √ | 0.864 | 0.988 | 0.921 | 0.963 | |||
| C | √ | √ | 0.872 | 0.988 | 0.929 | 0.966 | ||
| D | √ | √ | √ | 0.877 | 0.992 | 0.935 | 0.968 | |
| E | √ | √ | √ | √ | 0.879 | 0.993 | 0.936 | 0.968 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, F.; Cai, C.; Li, J.; Liu, M.; Jiao, Y.; Wu, Z.; Xu, J. Classification of Whole-Slide Pathology Images Based on State Space Models and Graph Neural Networks. Electronics 2025, 14, 2056. https://doi.org/10.3390/electronics14102056
Ding F, Cai C, Li J, Liu M, Jiao Y, Wu Z, Xu J. Classification of Whole-Slide Pathology Images Based on State Space Models and Graph Neural Networks. Electronics. 2025; 14(10):2056. https://doi.org/10.3390/electronics14102056
Chicago/Turabian StyleDing, Feng, Chengfei Cai, Jun Li, Mingxin Liu, Yiping Jiao, Zhengcan Wu, and Jun Xu. 2025. "Classification of Whole-Slide Pathology Images Based on State Space Models and Graph Neural Networks" Electronics 14, no. 10: 2056. https://doi.org/10.3390/electronics14102056
APA StyleDing, F., Cai, C., Li, J., Liu, M., Jiao, Y., Wu, Z., & Xu, J. (2025). Classification of Whole-Slide Pathology Images Based on State Space Models and Graph Neural Networks. Electronics, 14(10), 2056. https://doi.org/10.3390/electronics14102056







